摘要:镁颗粒因其能量密度高、点火特性和燃烧效率好的优势, 作为燃料或添加剂应用于爆震燃烧动力系统具有广阔的应用前景. 本文建立了镁颗粒-空气混合物的一维非稳态爆震波模型, 数值模拟爆震波传播过程及其内部流场分布. 研究结果表明, 爆震波传播过程中爆震波压力峰值和空间分布均存在小幅度波动. 考虑燃烧产物氧化镁在颗粒表面的沉积过程, 镁颗粒的反应速率和爆震波的稳定传播速度增大. 在考虑爆震管壁面损失的前提下, 随管径减小, 爆震波稳定速度和厚度均减小, 同时爆震波内未能反应的镁颗粒比例增大. 考虑壁面损失条件下, 爆震波稳定传播速度以及厚度均随颗粒初始粒径的增大而减小, 且镁颗粒初始为双粒径分布时对应的爆震波速度和厚度明显低于镁颗粒初始为统一单粒径的工况; 稳定传播速度随颗粒初始当量比的增大而先增后减, 厚度随初始当量比的增加单调递减. MgO熔化发生在CJ平面附近时, MgO熔化过程对爆震波传播稳定性无明显影响, 而爆震波厚度显著增大. 选取适当的点火区参数, 能够使爆震波达到稳定传播状态所经历的距离明显缩短.
关键词: 异相爆震/
镁颗粒燃料/
表面沉积/
壁面能量损失

English Abstract

全文HTML

--> --> -->

固体粉末燃料(镁、铝和硼等)因能量高、易存储、价格低廉, 不仅在常规的固体推进剂领域得到广泛应用, 还可应用于爆震推进系统, 如作为添加剂用于改善爆震波质量^[1], 提高脉冲爆震发动机性能^[2], 也作为连续旋转爆震燃烧室主要燃料^[3-7]等. 镁虽然能量密度低于铝和硼, 但镁金属较低的熔点和沸点使其点火特性和燃烧效率更优, 其燃烧过程以液态颗粒蒸发后的气相反应为主, 反应速度比铝和硼更快, 因此应用于爆震领域更有前景. 此外, 工业生产中, 镁因反应活性比铝和硼更高, 发生爆炸事故的潜在风险更高, 因此研究镁的爆震燃烧过程对工业生产安全也具有重要意义.
在此前的研究中^[8], 已针对镁颗粒-空气混合物爆震, 分析了来流速度、相变过程、颗粒初始浓度和颗粒初始粒径等因素对爆震波稳态传播特性的影响规律, 但研究仍存在如下不足.
1)文中采用的镁颗粒燃烧模型较为简单, 在镁颗粒达到沸点前反应速率采用经验公式^[9,10], 颗粒沸腾后汽化速率采用纯液滴蒸发公式^[10-12]. 而相关研究表明^[13,14], 镁颗粒实际燃烧过程与纯液滴燃烧存在不同, 其燃烧产物氧化镁中一部分会在颗粒表面凝结形成氧化帽. 氧化镁凝结时释放热量, 使颗粒反应速率增大, 同时生成的氧化帽则减小了颗粒表面的实际蒸发面积, 使颗粒反应速率减小, 因此有必要针对颗粒表面沉积对爆震波速度和结构的影响开展相关研究. 文献[8]中以镁颗粒的汽化速率代替镁颗粒汽化形成蒸气而后与氧气进行气相反应的总速率, 会导致贫氧工况下颗粒反应速率的计算值偏高. 此外, 文献[8]假设镁颗粒达到熔点后才开始反应, 而相关研究表明, 由于镁的氧化层为非致密结构^[15], 在镁颗粒达到熔点前, 氧气便可通过扩散穿过氧化层与镁发生表面反应, 只是熔化前镁的表面反应速率明显低于熔化后^[16-19].
2)文中未考虑爆震波在管道内传播时由壁面引起的损失. Zhang等^[10]认为管壁摩擦及换热损失会使前导激波后的气相工质更快加速至声速, 进而对爆震波结构产生影响. 洪滔等^[20]认为, 对于铝颗粒-空气混合物爆震, 在考虑管壁摩擦及换热损失的条件下, CJ面处有20%的铝颗粒尚未反应, 表明管壁造成的损失是影响爆震波传播过程的重要因素之一.
3)文中未能体现爆震波传播过程中的非稳态特性. 稳态模型^[8]的计算结果表明, 在一个镁颗粒初始浓度较低的小范围内(0.146—0.168 kg/m³), 受产物MgO的熔化过程的影响, 对应的爆震波无法以一个稳定的速度传播. 此不稳定传播过程的具体形式如何还需要通过非稳态模型开展进一步研究. 此外, 参照气相爆震过程^[21], 因点火能量不同导致的DDT过程不同和因反应速率量级不同导致传播过程中可能存在周期振荡等问题, 也需要开展相关研究.
鉴于现有研究存在的不足以及镁颗粒燃料应用于爆震燃烧的优势, 本文通过建立镁颗粒-空气一维非稳态两相爆震模型, 分析研究燃烧产物MgO在颗粒表面的凝结、爆震管壁面热损失、镁颗粒初始粒径、初始当量比等因素对爆震波传播速度和结构的影响, 以及初始点火能量、MgO熔化过程等因素对爆震波DDT过程、传播过程稳定性等非稳态特性的影响, 为镁粉燃料应用于爆震推进动力系统奠定理论基础.

为便于计算, 结合文献[10]中建立的气体颗粒两相爆震模型, 本文作出如下简化假设:
1)颗粒均匀弥撒分布, 作为连续介质处理, 颗粒内温度均匀分布, 且初始粒径相同. 关于非统一初始粒径的影响见本文3.4节;
2)在考虑表面沉积的条件下, 镁未完全蒸发前, 颗粒相温度不会超过镁的沸点;
3)忽略颗粒间相互作用, 忽略颗粒与壁面的作用, 颗粒相压强为0;
4)燃烧产物MgO算作气相组分, 氧化镁的离解温度当作沸点处理, 物质沸点由Clausius-Clapeyron方程确定^[22], 气相中仅气态工质(氧气、氮气、镁蒸气和气态氧化镁)对气相压强有贡献;
5)物质熔点为常数, 相变潜热包含在内能之中, 在氧化镁熔化、离解过程中, 气相温度分别维持在氧化镁熔点和离解温度;
6)当颗粒粒径减小至初始粒径的十分之一时, 颗粒质量仅为初始质量的千分之一, 此时不再计算两相间的相互作用^[20].
2

-->

2.1.流动控制方程组

流动控制方程组如下:

$\frac{{\partial {{U}}}}{{\partial t}} + \frac{{\partial {{F}}}}{{\partial x}} = {{J}},$

${{U}} = \left[\!\!{\begin{array}{*{20}{c}} {{\rho _{\rm{g}} }} \\ {{\rho _{\rm{g}} }{u_{\rm{g}} }} \\ {{\rho _{\rm{g}} }{E_{\rm{g}} }} \\ {{\rho _{{\rm{g}}, {{\rm{O}} _2}}}} \\ {{\rho _{{\rm{g}}, {\rm{MgO}} }}} \\ {{\rho _{{\rm{g}}, {\rm{Mg}} }}} \\ {{\rho _{\rm{p}} }} \\ {{\rho _{\rm{p}} }{u_{\rm{p}} }} \\ {{\rho _{\rm{p}} }{E_{\rm{p}} }} \\ {{n_{\rm{p}} }} \\ {{\rho _{{\rm{p}}, {\rm{MgO}} }}} \end{array}}\!\!\right]$, $~~{{F}} = \left[\!\!{\begin{array}{*{20}{c}} {{\rho _{\rm{g}} }{u_{\rm{g}} }} \\ {{\rho _{\rm{g}} }u_{\rm{g}} ^2 + p} \\ {{\rho _{\rm{g}} }{u_{\rm{g}} }{E_{\rm{g}} } + p{u_{\rm{g}} }} \\ {{\rho _{{\rm{g}}, {{\rm{O}} _2}}}{u_{\rm{g}} }} \\ {{\rho _{{\rm{g}}, {\rm{MgO}} }}{u_{\rm{g}} }} \\ {{\rho _{{\rm{g}}, {\rm{Mg}} }}{u_{\rm{g}} }} \\ {{\rho _{\rm{p}} }{u_{\rm{p}} }} \\ {{\rho _{\rm{p}} }u_{\rm{p}} ^2} \\ {{\rho _{\rm{p}} }{u_{\rm{p}} }{E_{\rm{p}} }} \\ {{n_{\rm{p}} }{u_{\rm{p}} }} \\ {{\rho _{{\rm{p}}, {\rm{MgO}} }}{u_{\rm{p}} }} \end{array}}\!\!\right]$, ${{J}} = \left[\!\!{\begin{array}{*{20}{c}} {{S_{\rm{d}} } - {S_{{\rm{d}}, {\rm{MgO}}, {\rm{cds}}}}} \\ {{S_{\rm{d}} }{u_{\rm{p}} } - {F_{\rm{d}} } - {{4{\tau _{\rm{w}} }} / {{d_{\rm{t}} }}}} \\ {{Q_{{\rm{c}}, {\rm{g}}}} - {Q_{\rm{d}} } - {F_{\rm{d}} }{u_{\rm{p}} } + {S_{\rm{d}} }{E_{\rm{p}} } - 4{{\left( {{q_{\rm{s}}} - \left| {{\tau _{\rm{w}} }{u_{\rm{g}} }} \right|} \right)} / {{d_{\rm{t}} }}}} \\ {{S_{{\rm{d}}, {{\rm{O}} _2}}}} \\ {{S_{{\rm{d}}, {\rm{MgO}} }}} \\ {{S_{{\rm{d}}, {\rm{Mg}} }}} \\ { - {S_{\rm{d}} } + {S_{{\rm{d}}, {\rm{MgO}}, {\rm{cds}}}}} \\ { - {S_{\rm{d}} }{u_{\rm{p}} } + {F_{\rm{d}} }} \\ {{Q_{{\rm{c}}, {\rm{p}}}} + {Q_{\rm{d}} } + {F_{\rm{d}} }{u_{\rm{p}} } - {S_{\rm{d}} }{E_{\rm{p}} }} \\ 0 \\ {{S_{{\rm{d}}, {\rm{MgO}}, {\rm{cds}}}}} \end{array}}\!\!\right],$
其中, ${E_{\rm{g}} } = {e_{\rm{g}} } + {{u_{\rm{g}} ^2} / 2}$, ${E_{\rm{p}} } = {e_{\rm{p}} } + {{u_{\rm{p}} ^2}/ 2}$, 下标g、p分别表示气相和颗粒相, 气相组分共有4种: 氧气、氧化镁、镁蒸气和氮气. 颗粒相组分包括镁和凝结在颗粒表面的氧化镁. ${n_{\rm{p}} }$表示单位体积内颗粒数. ${d_{\rm{t}} }$为爆震管内径. ${\tau _{\rm{w}} }$为气相与管壁间由黏性产生的摩擦力, ${q_{\rm{s}}}$表示气相与管壁间的对流换热损失. ${S_{\rm{d}} }$、${F_{\rm{d}} }$和${Q_{\rm{d}} }$分别表示单位体积内颗粒反应(蒸发)速率、颗粒相所受气相拖曳力以及两相间的对流换热量, ${S_{{\rm{d}}, i}}$表示第i种气相组分单位体积内的质量变化率, ${S_{{\rm{d}}, {\rm{MgO}}, {\rm{cds}}}}$表示单位体积内气相中氧化镁在颗粒相表面凝结的质量变化率, ${Q_{{\rm{c}}, {\rm{g}}}}$和${Q_{{\rm{c}}, {\rm{p}}}}$分别表示单位体积内气相吸收的反应放热速率和颗粒相吸收的反应放热速率.
2 -->

2.2.源项表达式

(1)质量源项
质量源项${S_{\rm{d}} }$分为异相反应${S_{{\rm{d}}, {\rm{het}} }}$和蒸发${S_{{\rm{d}}, {\rm{eva}} }}$两部分, 即${S_{\rm{d}} } = {S_{{\rm{d}}, {\rm{het}} }} + {S_{{\rm{d}}, {\rm{eva}} }}$. 根据文献[23]在颗粒完全熔化之前表面发生缓慢的异相反应:

$\begin{split}& \!S_{\rm d,het} = \\& \!\!\begin{cases}1.7 \!\times\! 10^9 \!\times\! 4\text{π} r^2 n_{\rm p}Y_{{\rm O} _2}\exp (-170000/RT_{\rm p})/\beta,\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad 873\;{{\rm K}} \!\leqslant\! T_{\rm p} \!\leqslant\! 923\;{\rm K}, \\ 0,\qquad\qquad\qquad\qquad\quad\quad\quad\quad{\rm else},\end{cases}\\[-20pt]\end{split}$

其中, R为通用气体常数, ${Y_{{{\rm{O}} _2}}}$为气相中氧气质量分数, $\beta $表示根据镁和氧气反应的化学计量比得到的氧气与镁的质量比, r表示颗粒半径. 为简化计算, 在缓慢氧化阶段(颗粒温度在873—923 K), 忽略颗粒表面生成的氧化镁对颗粒粒径的影响. 颗粒完全熔化后, 镁颗粒燃烧过程与液滴蒸发燃烧类似, 参照文献[23,24]中处理方法, 假设燃烧产物在颗粒表面沉积形成球冠状氧化帽, 此时颗粒表面蒸发速率为

$\begin{split}{S_{{\rm{d}},{\rm{eva}} }} =\;& {f_S}\left( {1 - \frac{{{h_{{\rm{cap}} }}}}{{2r}}} \right)\frac{{2{\text{π}}r{n_{\rm{p}} }{\mu _{\rm{g}} }Nu\ln \left( {1 + B} \right)}}{{Pr}},\\ &{T_{\rm{p}} } > 923\;{\rm{K}},\end{split}$

其中, $Pr$和$Nu$分别为Prandtl数和颗粒在强迫对流换热条件下的Nusselt数, ${\mu _{\rm{g}} }$为气相黏性系数, B为Spalding传递系数, 其表达式为

$B = \frac{{{Y_{{\rm{Mg}},{\rm{s}}}} + {{{Y_{{{\rm{O}} _2}}}} / \beta }}}{{{f_{\rm{S}} } - {Y_{{\rm{Mg}},{\rm{s}}}}}},$

${f_{\rm{S}} } = \frac{{{{\dot m}_{{\rm{Mg}} }}}}{{{{\dot m}_{{\rm{Mg}} }} - {{\dot m}_{{\rm{MgO}} }}}},$

其中, ${\dot m_{{\rm{Mg}} }}$和${\dot m_{{\rm{MgO}} }}$分别为无氧化帽覆盖情况下颗粒表面镁蒸气生成质量流率和氧化镁凝结质量流率. 不考虑颗粒表面凝结时, ${f_{\rm{S}} } = 1$; 当考虑凝结时, ${f_{\rm{S}} } > 1$. ${f_{\rm{S}} }$值越高表明颗粒表面沉积速率越大, 沉积在颗粒表面累积形成球冠状氧化帽, ${h_{\rm{cap}}}$为球冠状氧化帽的高. ${Y_{{\rm{Mg}}, {\rm{s}}}}$为镁颗粒表面镁蒸气质量分数, 根据Clausius-Clapeyron方程和道尔顿分压定律可得到:

${Y_{{\rm{Mg}},{\rm{s}}}} = \frac{{{M_{{\rm{Mg}} }}}}{{\bar M}}\frac{{{p_{{\rm{ref}} }}}}{p}\exp \left[ {\frac{{\Delta {h_{{\rm{Mg}},{\rm{b}}}}}}{{{R_{{\rm{Mg}} }}}}\left( {\frac{1}{{{T_{{\rm{ref}} }}}} - \frac{1}{{{T_{\rm{s}} }}}} \right)} \right]$

其中, ${T_{{\rm{ref}} }}$为镁颗粒在参考压力${p_{{\rm{ref}} }}$下的沸点, ${R_{{\rm{Mg}} }}$为镁蒸气的气体常数. ${M_{{\rm{Mg}} }}$和$\bar M$分别为镁蒸气的摩尔质量以及气相中气态物质的平均摩尔质量. 各组分反应源项表达式如下:

${Q_{{\rm{c}},{\rm{g}}}} = {S_{\hom }}{q_{{\rm{c}},{\rm{Mg}}}}$

${Q_{{\rm{c}},{\rm{p}}}} = {S_{{\rm{d}},{\rm{het}}}}{q_{{\rm{c}},{\rm{Mg}}}}$

${S_{\rm{d}},{{\rm{O}}_2}} = - \beta \left( {{S_{{\rm{d}},{\rm{het}}}} + {S_{\hom }}} \right)$

${S_{{\rm{d}},{\rm{MgO}}}} = \left( {1 + \beta } \right){S_{\hom }} - {S_{{\rm{d}},{\rm{MgO}},{\rm{cds}}}}$

${S_{\rm{d},\rm{Mg}}} = {S_{\rm{d},\rm{eva}}} - {S_{\hom }}$

其中, ${q_{{\rm{c}}, {\rm{Mg}}}}$表示镁的单位质量热值, ${S_{\hom }}$为单位体积内气相中镁蒸气的消耗速率, 根据文献[23,25]有

$ \begin{split}& {S_{{\rm{hom}}}} \!= \\& \left\{ {\begin{aligned}& 1.05 \!\times\! 10^8 \!\times \! \rho_{\rm g,Mg} \rho _{\rm g,O_2}\exp (\!-69010/R T_{\rm g})/M_{\rm O_2},\\ & \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad~~{{T_{\rm{g}}} < 2000\;{\rm{K}}},\\& 1.8 \!\times\! 10^6 \!\times\! \rho_{\rm g, Mg} \rho _{\rm g,O_2}/ M_{\rm O_2}, \;~~~ T_{\rm g} \geqslant 2000\;{\rm K},\end{aligned}} \right.\end{split}$

(2)两相间作用力源项
单位体积中气体对颗粒作用力${F_{\rm{d}} } = {n_{\rm{p}} }{f_{\rm{d}} }$, 有

${f_{\rm{d}} } = \frac{1}{2}{\text{π}}{r^2}{C_{\rm{D}} }{\rho _{\rm{g}} }\left| {{u_{\rm{g}} } - {u_{\rm{p}} }} \right|\left( {{u_{\rm{g}} } - {u_{\rm{p}} }} \right),$

由于镁颗粒燃烧过程类似液滴蒸发燃烧, 颗粒与气体之间存在质量交换, 阻力系数${C_{\rm{D}} }$表达式为

${C_{\rm{D}}} = \begin{cases}{27R{e^{ - 0.84}}},&{Re < 80},\\{0.27R{e^{0.217}}},&{80 \leqslant Re \leqslant {{10}^4}},\\2,&{Re > {{10}^4}},\end{cases} $

其中, $Re \!=\! 2\rho _{\rm g} r|u_{\rm g} \!-\! u_{\rm p}|/\mu_{\rm g}$为两相间的Renolds数.
(3)两相间换热源项
两相间对流热传导:

${Q_{\rm{d}}} = 4{\text{π}}{r^2}{n_{\rm{p}} }\frac{{{\lambda _{\rm{g}} }Nu\left( {{T_1} - {T_2}} \right)}}{{2r}}, $

其中, ${\lambda _{\rm{g}} }$为气相导热系数. 对于可压缩流动, 强迫对流换热条件下的Nusselt数, 根据文献[26]有:

$\begin{split}Nu =\; & \frac{{2\exp \left( { - Ma} \right)}}{{1 + {{17Ma}/ {Re}}}} + 0.459R{e^{0.55}}P{r^{0.33}} \\ & \times\frac{{1 + 0.5\exp \left( {{{ - 17Ma} / {Re}}} \right)}}{{1.5}},\end{split}$

其中, $Ma$为气固两相速度差与当地气相声速的比值.
(4)两相间换热源项
壁面产生的黏性摩擦力为

${\tau _{\rm{w}} } = 0.5{C_{\rm{f}} }{\rho _{\rm{g}} }u_{\rm{g}} ^2,$

其中, 摩擦系数${C_{\rm{f}} } = 0.074 Re_l^{ - 0.2}$, $R{e_l} = {{{\rho _{\rm{g}} }{u_{\rm{g}} }l}/ {{\mu _{\rm{g}} }}}$, l是网格点到前导激波阵面的距离. 黏性力做功为$\left| {{\tau _{\rm{w}} }{u_{\rm{g}}}} \right|$, 气相与管壁之间的对流换热损失为

${q_{\rm{s}}} = 0.5{C_{\rm{f}} }{\rho _{\rm{g}} }{u_{\rm{g}} }{c_{{\rm{p}},{\rm{g}}}}\left( {{T_{\rm{g}} } - {T_{\rm{w}} }} \right), $

其中, ${c_{{\rm{p}}, {\rm{g}}}}$为气相的定压比热容. 根据文献[8], 气相与颗粒相间的辐射换热量很小, 可以忽略不计, 且在爆震波内部有$\left( {T_{\rm{g}} ^4 - T_{\rm{p}} ^4} \right) \gg \left( {T_{\rm{p}} ^4 - T_{\rm{w}} ^4} \right)$, 因此颗粒与管壁间的辐射换热损失也可忽略不计.
2 -->

2.3.数值方法

本文数值计算方法采用CE/SE方法, 它是一种格式简单、精度高、捕获爆震波等强间断能力强的高精度计算格式, 文献[27,28]等将CE/SE方法应用于两相混合物爆震研究, 并验证了其可行性. 鉴于爆震问题中化学反应特征时间相对于对流特征时间要小得多, 在数值求解过程中每个时间步的求解思路为: 先不考虑方程组(1)中源项的影响, 用CE/SE方法求解纯流动方程组获得流场参数$\bar {{U}}$, 然后将$\bar {{U}}$作为初值, 用4阶Runge-Kutta法求解常微分方程组:

$\frac{{{\rm{d}}\bar {{U}}}}{{{\rm{d}}t}} = {{J}}, $

获得下一时间步的流场参数. 本文算例中Runge-Kutta法的时间步长为CE/SE法的1/10.
计算域左端为固体壁面, 右端为出口, 长度为40 m. 计算域初始条件为${\rho _{{\rm{g}}, 0}} = 1.29\;{\rm{kg}}/{{\rm{m}}^3}$、${\rho _{{\rm{p}}, 0}} = $ 0.445 kg/m³, ${u_{{\rm{g}}, 0}} = {u_{{\rm{p}}, 0}} = 0\;{\rm{m }}/ {\rm{s}}$, ${T_{{\rm{g}}, 0}} \!=\! {T_{{\rm{p}}, 0}} \!$ = 300 K, ${r_0} \!=\!$ 2.5 μm. 点火区位于固壁端, 其初始条件为${\rho _{{\rm{g}}, 0}} = 3\;{\rm{kg}}/{{\rm{m}}^3}$, ${u_{{\rm{g}}, 0}} = 2000\;{\rm{m / s}}$, ${T_{{\rm{g}}, 0}} = 3000\;{\rm{K}} $, 点火区长度${L_{{\rm{ign}} }} = 0.288\;{\rm{m}} $. 图1为t = 2.5 ms时刻, 网格大小分别为1 mm、0.5 mm、0.25 mm时所对应的流场中压力的分布. 算例中未考虑壁面摩擦、换热损失以及颗粒表面沉积. 由图可知, 1 mm网格计算结果与另外两组有明显差别, 0.5 mm和0.25 mm的压力分布几乎相同, 随着尺度减小, 激波间断面所在位置有向下游移动的趋势, 且压力峰值略有增加, 但总体差别不大. 为兼顾计算效率, 本文采用0.5 mm的网格尺度进行计算.
图 1 不同网格尺度对应的压力分布
Figure1. Spatial distribution of the gas-phase pressure with different grid sizes.

2

-->

3.1.不同颗粒燃烧模型对比

将计算域初始条件${\rho _{{\rm{g}}, 0}} = 1.29\;{\rm{kg}}/{{\rm{m}}^3}$, ${\rho _{{\rm{p}}, 0}} =$ 0.445 kg/m³, ${u_{{\rm{g}}, 0}} = {u_{{\rm{p}}, 0}} = $ 0 m/s, ${T_{{\rm{g}}, 0}} = {T_{{\rm{p}}, 0}} = $ 300 K, ${r_0} = 5$ μm定义为标准参考条件, 下文算例如无特别说明, 则计算域初始条件以上述条件处理.
图2为爆震波充分发展后趋于稳定传播的状态下, 不同时刻爆震波压力峰附近的压力分布情况, 时间间隔为0.05 ms. 由图可知, 在爆震波趋于稳定传播的状态下, 压力峰值和压力波形在传播过程中仍存在小幅振荡. 根据文献[21], 对于采用单步反应模型的一维气相爆震而言, 爆震波传播过程中出现周期性震荡主要与反应活化能和反应放热量有关. 活化能较大时对应的反应高温敏感性较高, 较小的温度扰动就会导致反应速率的大幅波动, 而对于较高的反应放热量, 扰动的物理效应也会增强. 对于镁颗粒-空气混合物爆震, 其反应活性低于常规气体燃料-空气混合物, 反应活化能较高, 且镁的理论当量空燃比较低, 在相同空气质量且当量比为1的条件下, 镁燃烧的反应放热量高于常规气体燃料. 以上原因导致在传播过程中燃烧区内镁颗粒反应速率存在波动, 因此镁颗粒-空气混合物一维非稳态爆震波传播过程中存在振荡现象. 上述状态下, 爆震波传播速度的振幅较小, 在±1 m/s范围内, 可将振荡平均值作为爆震波稳定传播速度. 后文如无特别说明, 爆震波稳定速度均为振荡平均值.
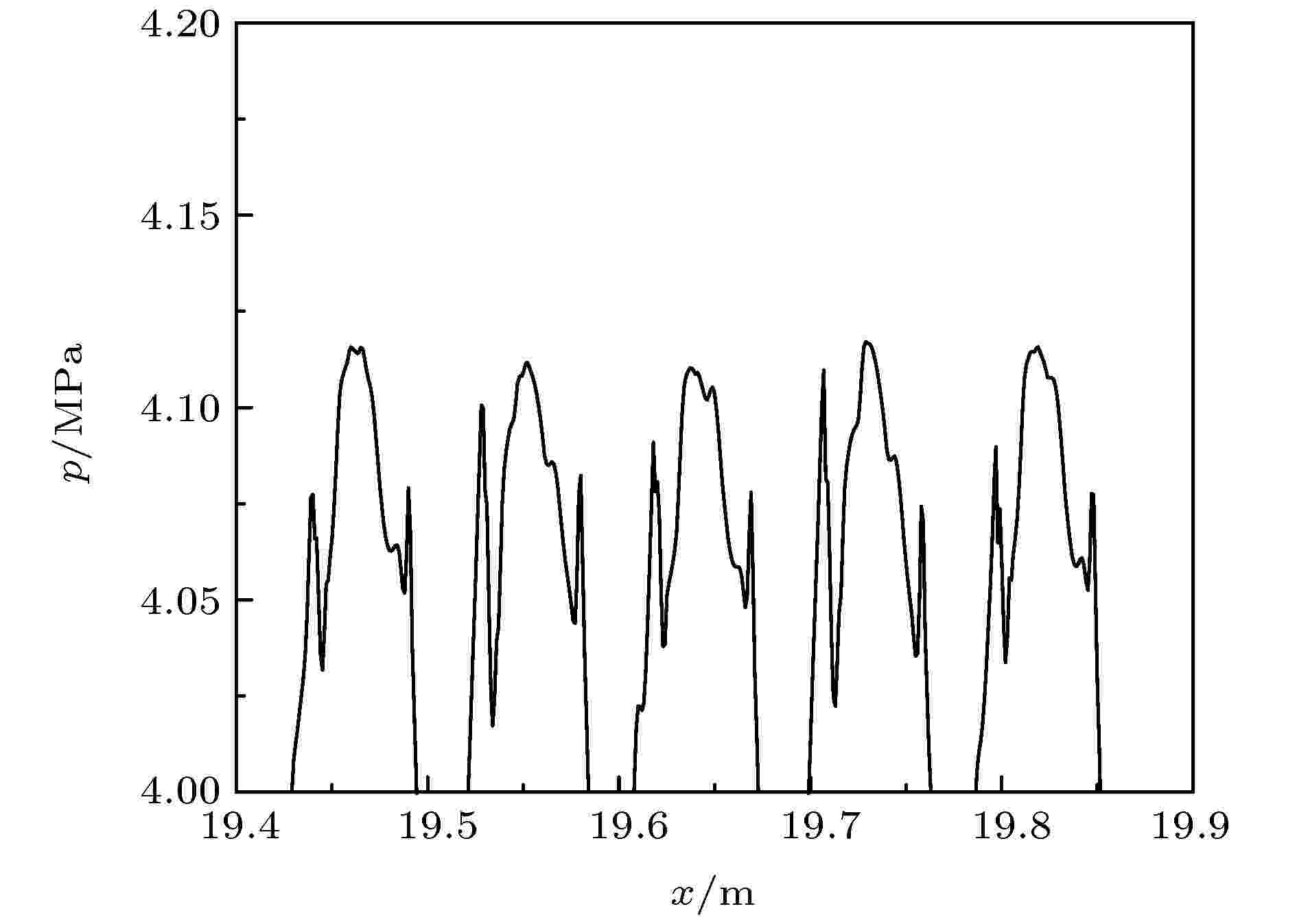图 2 不同时刻爆震波压力峰附近的压力分布
Figure2. Pressure distribution near peak at different time.

杨晋朝等^[29]提出了一种基于粉末冲压发动机燃烧室环境的镁颗粒点火燃烧模型, 能够较全面地反应镁粉尘云的燃烧过程, 在低速层流环境下计算结果与试验符合度较好. 在标准参考条件且不考虑侧壁面损失和颗粒表面凝结的前提下, 分别采用本文镁颗粒点火燃烧模型与文献[29]的镁颗粒点火燃烧模型, 获得爆震波内流场参数分布, 如图3所示. 由图可知, 两种模型计算得到的爆震波结构存在明显不同, 本文模型计算结果与Zhang等^[10]、Federov等^[30]描述的爆震波结构相符, 气相密度峰值、颗粒相密度峰值以及压力峰值均位于前导激波下游某处. 而采用文献[29]的镁颗粒点火燃烧模型得到的爆震波结构与气相燃料爆震类似, 前导激波处的压力和密度均为峰值. 这是由于文献[29]中的点火燃烧模型认为镁颗粒在完全熔化之后到沸腾之前这一阶段, 除了镁颗粒表面蒸发过程, 在颗粒表面还同时发生氧气与镁液滴的异相反应, 异相反应放热均被颗粒吸收, 模型中镁液滴与氧气异相反应的速率比熔化前固体镁与氧气的异相反应高出至少3个量级. 由图3(c)中模型的颗粒相温度曲线可知, 前导激波后颗粒温度迅速升高达到沸点, 几乎看不到颗粒熔化过程. 与之相比, 本文模型对应的颗粒温度曲线可以明显看出前导激波后镁颗粒历经的整个“升温-熔化-升温-沸腾”过程.
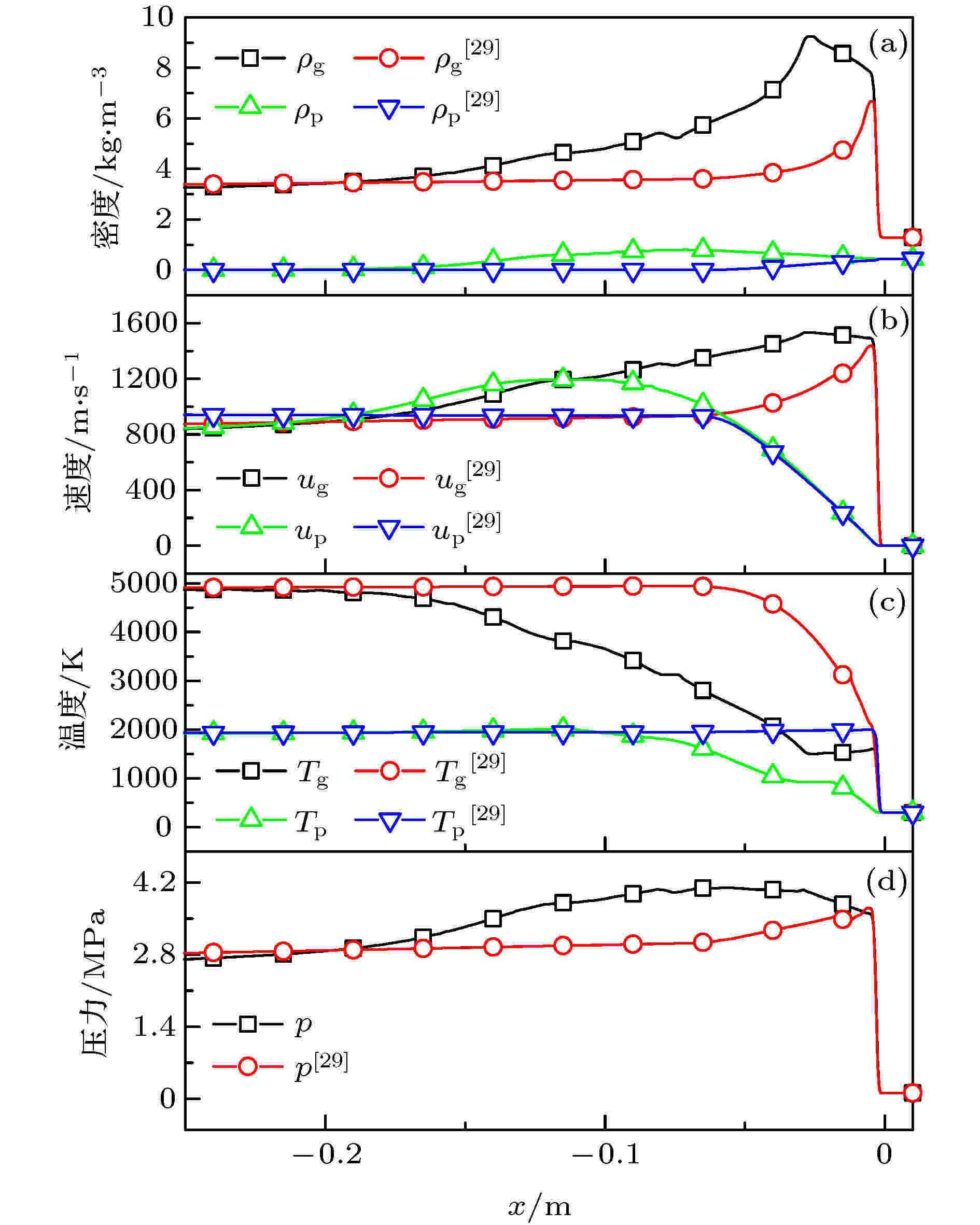图 3 不同燃烧模型对应的爆震波内流场参数分布　(a) 密度和浓度; (b) 速度; (c) 温度; (d) 压力
Figure3. Parameters distribution in detonation wave with different combustion models: (a) Density and concentration; (b) velocity; (c) temperature; (d) pressure.

采用本文点火燃烧模型模型、文献[29]中的点火燃烧模型以及文献[8]中的两相ZND模型分别计算得到的爆震波稳定传播速度和爆震波厚度结果如表1所示. 由表可知, 本文点火燃烧模型计算得到的爆震波速度和厚度与两相ZND模型基本一致, 采用文献[29]的镁颗粒点火燃烧模型计算得到的爆震波速度略高, 爆震波厚度明显缩短. 基于上述结果可知, 相比文献[29]中的模型, 本文模型更加适用于描述前导激波后高温高压强迫对流条件下的镁颗粒燃烧过程.

参数	本文模型	文献[29]模型	两相ZND模型
爆震波速度/(m·s–1)	1786	1789	1782.28
爆震波厚度/m	0.327	0.055	0.331

表1不同模型对应的爆震波稳定速度和厚度
Table1.Steady velocity and thickness of detonation wave with different models.

2 -->

3.2.颗粒表面沉积的影响

图4所示为${f_{\rm{S}} } = 1.1$时对应的稳定传播状态爆震波两相温度分布. 由图可知, 在CJ面上游, 由于颗粒相中的液态镁蒸发持续吸热, 颗粒相温度维持在镁的沸点. 经过CJ面, 下游颗粒相组分仅剩下沉积的氧化镁, 在相间传热作用下温度继续上升.
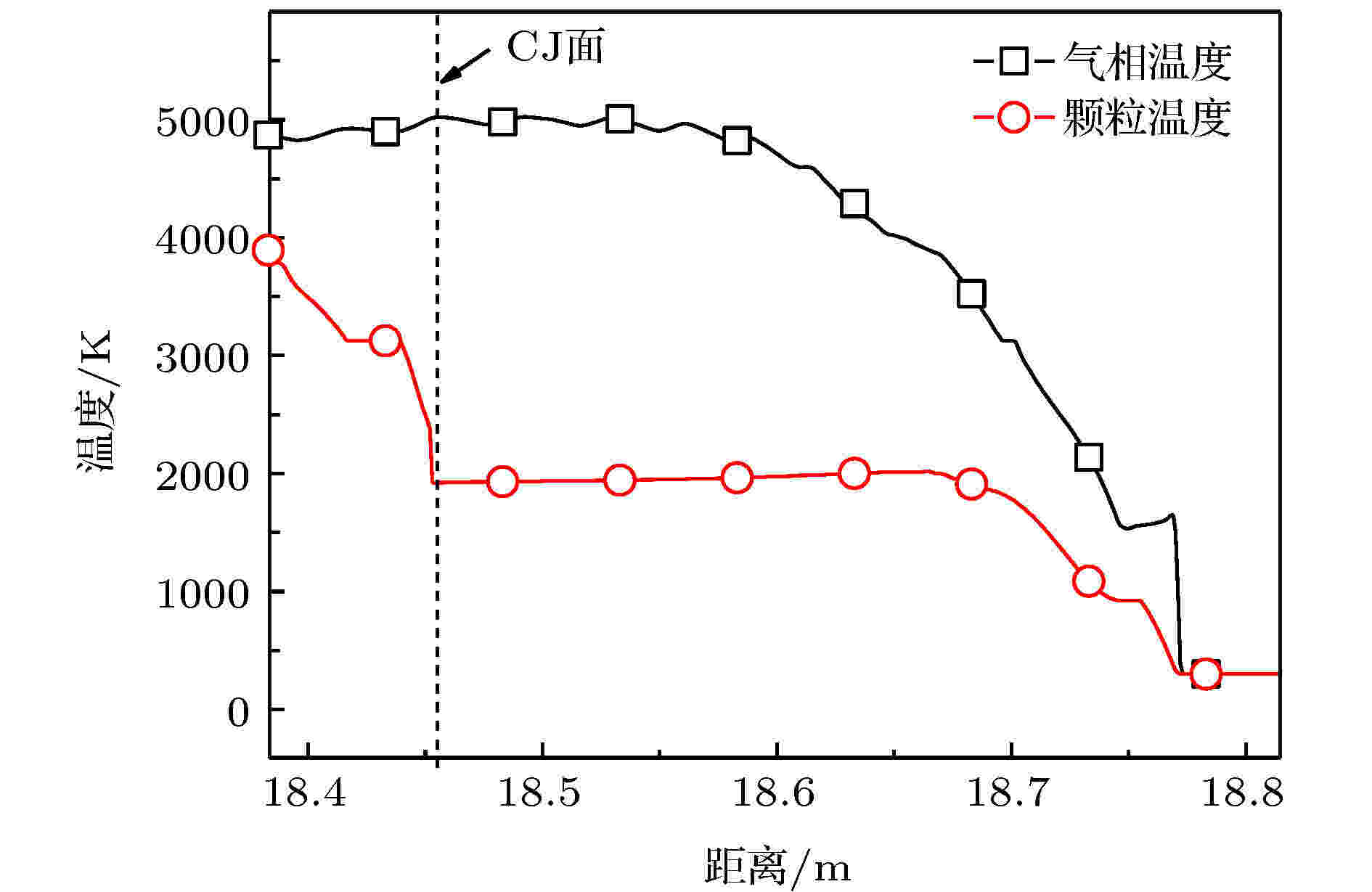图 4 在${f_{\rm{S}} } = 1.1$时对应的稳定传播状态爆震波两相温度分布
Figure4. Temperature distribution of gas and particle phases inside steady detonation wave with ${f_{\rm{S}} } = 1.1$.

图5所示为爆震波稳定后的爆震波厚度、CJ面两相温度、CJ面颗粒相浓度(镁和氧化镁沉积)和传播速度随${f_{\rm{S}} }$的变化规律. 由图5(a)可知, 爆震波厚度随${f_{\rm{S}} }$增加无明显变化. 由图5(b)和图5(c)可知, 随着${f_{\rm{S}} }$的增大, CJ面两相间温差和CJ面处沉积浓度均增大, 由于单位体积内产物沉积释放的热量与沉积浓度和两相间温差成正相关, 因此产物沉积释放的热量随${f_{\rm{S}} }$增大而增大. 氧化镁沉积在镁颗粒表面累积形成球冠状氧化帽, 此过程中释放的热量部分被气态工质吸收用于膨胀做功. 由于产物沉积释放的热量随${f_{\rm{S}} }$增大而增大, 因此气态工质膨胀做功随${f_{\rm{S}} }$增加而增加, 导致爆震波稳定传播速度随${f_{\rm{S}} }$增大而增大, 如图5(d)所示. 在爆震波厚度不变的情况下, 爆震波稳定传播速度升高, 镁颗粒在爆震波内的驻留时间变短. 图5(c)表明CJ面镁颗粒是完全反应的, 因此随着${f_{\rm{S}} }$增大, 镁颗粒反应速率整体增大. 氧化镁沉积对于镁颗粒反应速率的影响: 一方面形成的氧化帽减少镁颗粒表面有效蒸发面积, 导致镁颗粒反应速率降低; 另一方面氧化镁沉积放热提高了爆震波内的压力和温度, 促进镁颗粒蒸发, 使镁颗粒反应速率增大. 根据对计算结果的分析可知, 沉积放热对颗粒反应速率的影响占主导作用. 因此, 模型中考虑氧化镁的沉积过程, 会使镁颗粒的反应速率增大和爆震波的稳定传播速度增大.
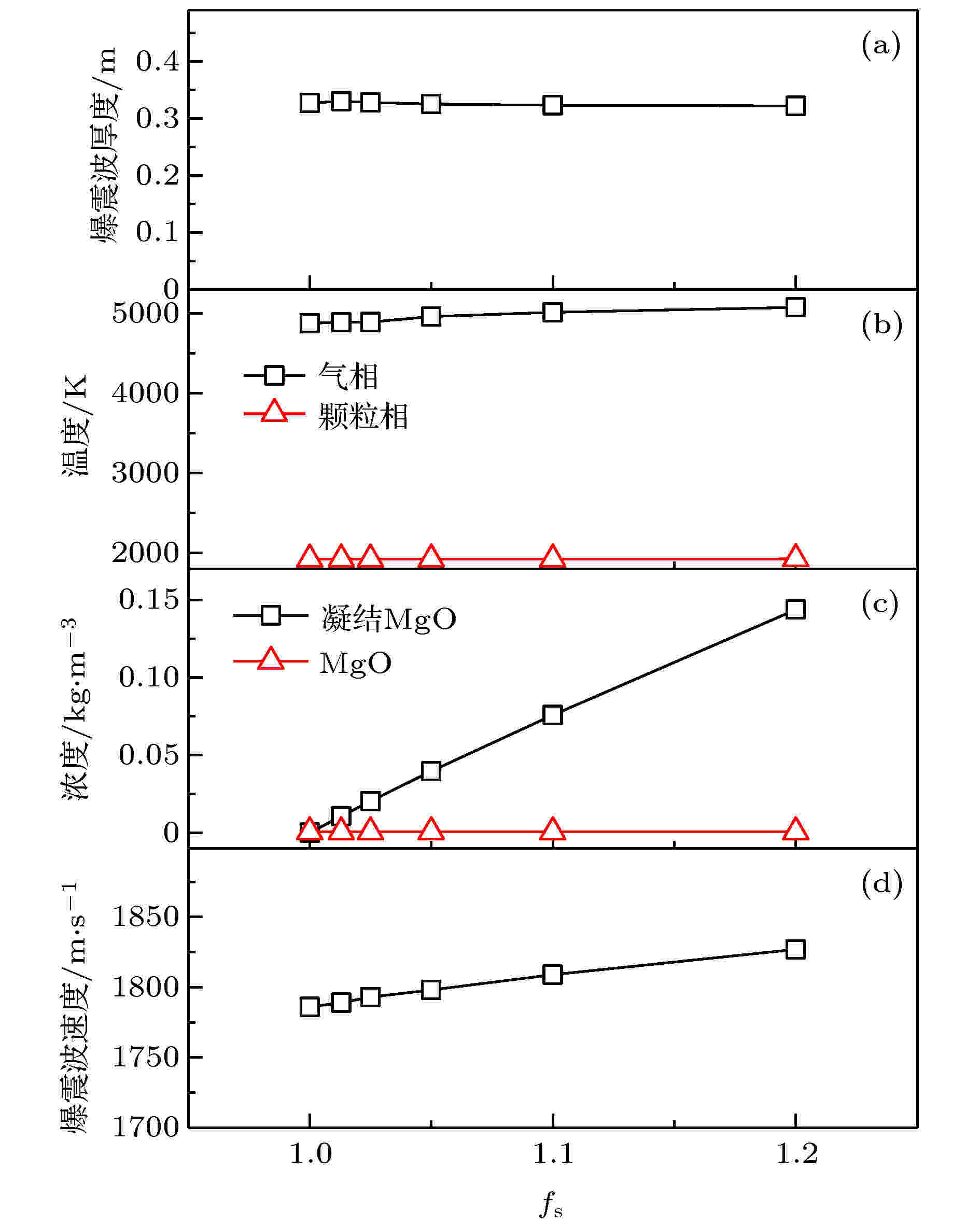图 5 爆震波参数随${f_{\rm{S}} }$的变化　(a) 爆震波厚度; (b) CJ面两相温度; (c) CJ面颗粒相浓度; (d) 爆震波速度
Figure5. Variation of detonation parameters with different value of ${f_{\rm{S}} }$: (a) Thickness; (b) temperature at CJ plane; (c) particle concentration at CJ plane; (d) velocity

2 -->

3.3.壁面能量损失的影响

根据文献[8]的研究结论可知, 在不考虑外界损失的理想条件下, 当且仅当来流速度条件为对应工况的特征值爆震速度时, 爆震波结构稳定且在CJ面处镁颗粒恰好完全反应. 当来流速度低于特征值爆震速度时, 在波后气相达到声速面处仍有颗粒燃料未反应, 导致出现奇点, 表明对应的爆震波无法稳定传播. 与理想条件相比, 引入侧壁面损失后, 反应释放的总能量有一部分通过侧壁面对流换热损失, 导致可转化气态工质膨胀功的能量比例减少, 不足以维持爆震波稳定传播, 爆震波传播速度必然降低. Zhang等^[10]在研究铝颗粒-空气混合物爆震的模型中考虑了爆震管侧壁面损失, 其处理方法是在气相动量方程和气相能量方程中引入了新的源项, 爆震波传播速度与波后膨胀功之间会达到一个新的平衡状态, 使爆震波能够以一个低于理想条件ZND特征值爆震速度的速度值稳定传播, 在这种情况下, 爆震波CJ面处颗粒燃料未完全反应, 这与理想情况下CJ面处颗粒燃料完全反应不同.
初始参数为标准参考条件, 点火区参数为${\rho _{{\rm{g}}, 0}}\! =\! 3\;{{{\rm{kg}}} / {{{\rm{m}}^3}}}$, ${u_{{\rm{g}}, 0}} \!=\! 2000\;{{\rm{m}} / {\rm{s}}}$, ${T_{{\rm{g}}, 0}} \!=\! 3000\;{\rm{K}} $, ${L_{{\rm{ign}} }} = 0.288\;{\rm{m}} $条件下, 不考虑颗粒表面凝结, 计算不同爆震管内径条件下对应的爆震波稳定传播速度、爆震波厚度(即前导激波至CJ面的距离)以及CJ面颗粒剩余量(r_CJ/r₀), 结果如表2所示.

管径	$\infty $	1 m	0.3 m	0.15 m	0.075 m
稳定速度/(m·s–1)	1786	1777.5	1758.5	1733	1691.5
爆震波厚度/m	0.327	0.297	0.254	0.234	0.2185
CJ面rCJ/r0	< 0.1	0.162	0.199	0.239	0.277
注: 管径$\infty $表示不考虑管壁损失的理想条件

表2不同爆震管内径条件下爆震波稳定传播速度、厚度和r_CJ/r₀
Table2.Steady velocity, thickness and r_CJ/r₀ at CJ plane of detonation wave with different tube inner-diameters.

由表2可知, 随着爆震管内径减小, 爆震波稳定传播速度减小, 爆震波厚度减小, CJ面处未反应颗粒所占比例增大. 稳定传播速度增大和CJ面处未反应颗粒比例增大是由于根据方程组(1)中气相动量方程和气相能量方程的源项部分, 侧壁面造成的损失大小与爆震管内径成反比所致. 当管径为1 m时, 管壁引起的损失相对较小, 而一些试验中常用的爆震管管径尺寸300 mm^[31,32]和150 mm^[33,34]左右等, 管壁造成的损失与理想条件相比已经非常明显. 下文涉及理想条件与考虑爆震管侧壁面损失的工况对比时, 无特别说明, 均以管径0.15 m为参考.
爆震波速度降低, 对应波后von Neumann状态的气相温度和压力降低. 图6(a)和6(b)为不同管径条件下爆震波内的压力和气相温度分布, 为方便对比, 将各算例结果对应的前导激波面置于同一坐标位置. 由图可知, 随着内径减小, 爆震波内的压力和气相温度整体降低, 但总的分布趋势不变. 随着压力和气相温度的降低, 对应的当地声速也随之减小. 在两相CJ模型中, 坐标系固定在前导激波上, CJ面对应的是波后气相达到当地声速的平面. 而在非稳态模型, 由于参考系的转换, CJ面对应的是波后气相与前导激波间的相对速度达到当地声速的平面. 由于侧壁面摩擦对波后气相有一个减速作用, 使得波后气相与前导激波之间的相对速度能够更快地达到当地声速, 因此随着爆震管内径减小, 爆震波厚度减小.
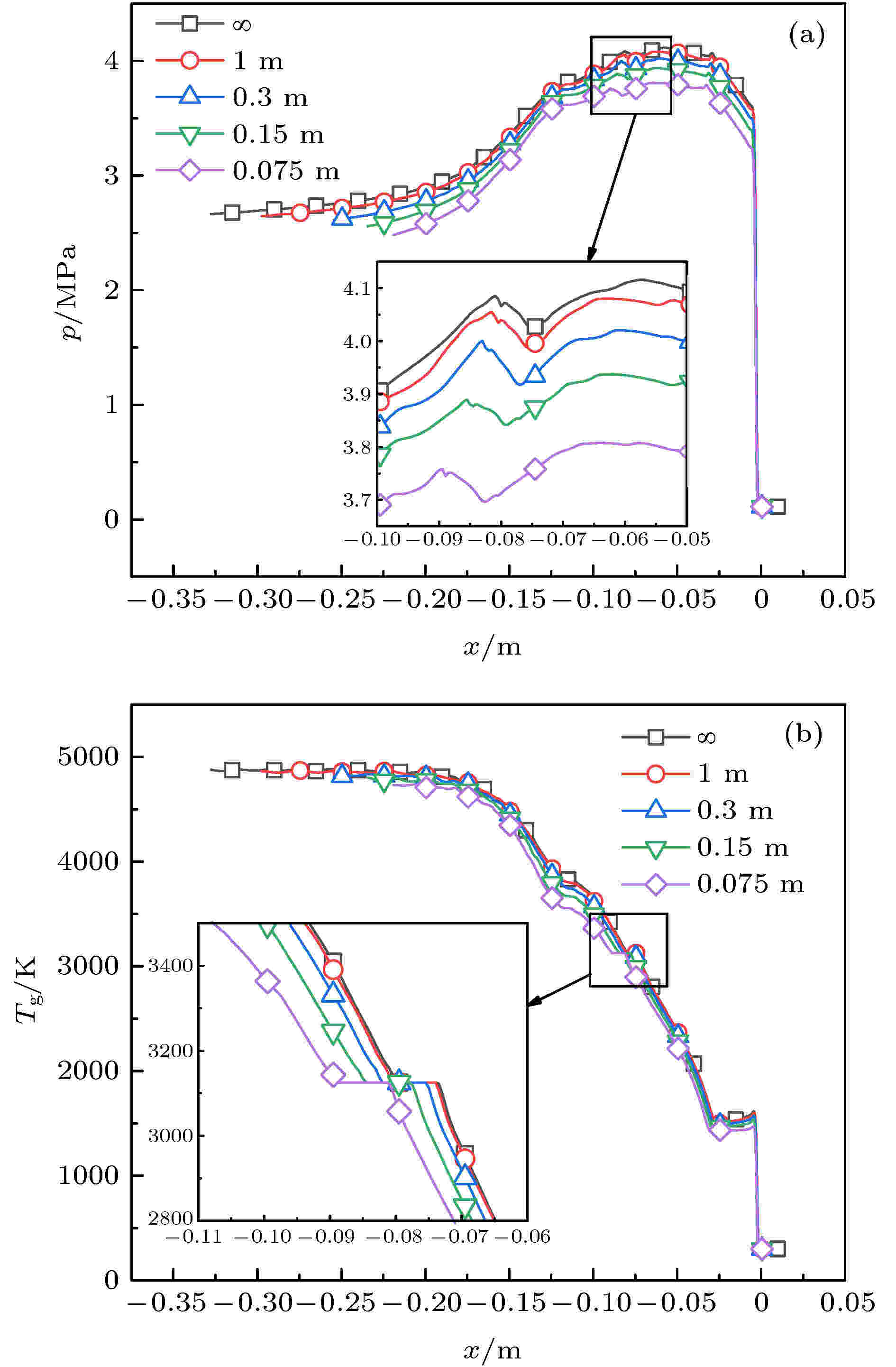图 6 不同管径条件下爆震波内的压力和气相温度分布　(a) 压力; (b) 气相温度
Figure6. Pressure and gas-phase temperature distribution inside detonation wave with different tube inner-diameters: (a) Pressure; (b) gas-phase temperature.

2 -->

3.4.颗粒初始粒径的影响

表3给出了在不同颗粒初始粒径条件下, 理想条件和管径为0.15 m时爆震波传播速度和厚度的计算结果. 根据表3可知, 在不考虑壁面损失的理想条件下, 爆震波稳定传播速度随粒径增大仍然保持不变, 爆震波厚度随粒径增大而增大, 这与文献[8]得到的结论一致. 这是由于理想条件下在CJ面处镁颗粒完全反应, 反应释放的总能量相同, 因此爆震波稳定速度保持不变, 而在镁颗粒初始质量相同的前提下, 初始粒径增加导致颗粒反应/蒸发表面积减大, 波后气相膨胀过程变缓, 最终导致爆震波厚度增加.

粒径		5 μm	10 μma	10 μmb	15 μm	20 μm
爆震波速度/(m·s–1)	无损失	1786	1786	1786	1786	1786
	有损失	1762	1733	1700	1702	1662
爆震波厚度/m	无损失	0.171	0.327	0.622	0.614	0.908
	有损失	0.099	0.234	0.446	0.425	0.666
注: a, 单一粒径; b, 5 μm和15 μm掺混后的平均粒径.

表3不同颗粒初始粒径对应的爆震波传播速度和厚度
Table3.Steady velocity and thickness of detonation wave with different initial particle diameter.

而在考虑壁面损失的条件下, 随着颗粒初始粒径的增大, 爆震波稳定速度与理想条件下的差值也随之增大, 这是由于侧壁面造成的换热损失与爆震波厚度呈正相关关系, 爆震波厚度越大, 对应的换热面积就越大, 爆震波内反应释放的总能量损失也越多, 爆震波稳定传播速度与理想条件下的差值也越大. 同时, 由表3可知, 与理想条件下相比, 爆震波厚度的减小量也随颗粒初始粒径的增大而增大. 这是由于爆震波所受壁面总黏性力的大小与爆震波厚度呈正相关关系, 爆震波厚度越大, 爆震波整体所受壁面总黏性力就越大, 根据3.3节的分析, 壁面黏性力能够使波后气相与前导激波之间的相对速度达到当地声速的过程加快, 因此爆震波厚度的减少量也会随壁面总黏性力的增大而增大. 综上所述, 在考虑爆震管侧壁面损失的情况下, 随着粒径增大, 爆震波稳定传播速度和爆震波厚度与理想条件下的差值也增大.
此外, 表3还给出了平均初始粒径为10 μm(5 μm和15 μm的镁颗粒按质量比1:10均匀混合)的计算结果, 可以看出, 与初始粒径统一为10 μm的工况相比, 双粒径分布对应的理想条件下爆震波稳定状态厚度明显增高, 甚至高于初始统一粒径为15 μm工况的厚度, 这是因为在双粒径分布的爆震波内, 小粒径镁颗粒很快被完全消耗, 剩余的大粒径15 μm颗粒, 颗粒数目较少, 反应表面积较少, 因而反应速率更低, 导致波后气相膨胀至与前导激波相对速度为当地声速需要的时间更长, 爆震波的厚度更大. 在考虑壁面损失的条件下, 双粒径分布对应的爆震波速度明显低于统一粒径的工况. 对于实际镁粉颗粒可以而言, 其粒径存在一个分布范围, 因此可以推测实际镁粉爆震试验得到的爆震波速度值可能低于按照平均粒径计算得到的爆震波速度值.
2 -->

3.5.初始当量比的影响

图7为理想条件和管径为0.15 m条件下, 稳定传播的爆震波速度和爆震波厚度随初始当量比的变化. 根据图7(a), 在理想条件下, 随着镁颗粒-空气当量比增大, 爆震波稳定传播速度先增大后减小, 速度最大值对应的当量比略小于1, 这与文献[8]中的结论一致. 根据图7(b), 在理想条件下, 爆震波厚度随当量比增加先减小后增大, 是因为在当量比小于1时, 随着当量比增大, 爆震波内颗粒反应面积增大, 反应速率增大, 放热率增大, 气相工质吸热膨胀速率增大, 波后气相与前导激波间的速度差达到当地声速所需时间更短, 因此爆震波厚度减小. 当量比大于1时, 在贫氧条件下, 未燃烧部分的镁颗粒吸热蒸发产生与镁沸点温度相同的蒸气, 使气相温度整体降低, 气相实际膨胀做功速率减小. 随着初始当量比增大, 镁颗粒蒸发面积随之增大, 蒸发速率随之增大, 实际气相膨胀做功速率随之减小, 波后气相与前导激波间的速度差达到当地声速所需时间更长, 因此爆震波厚度增大.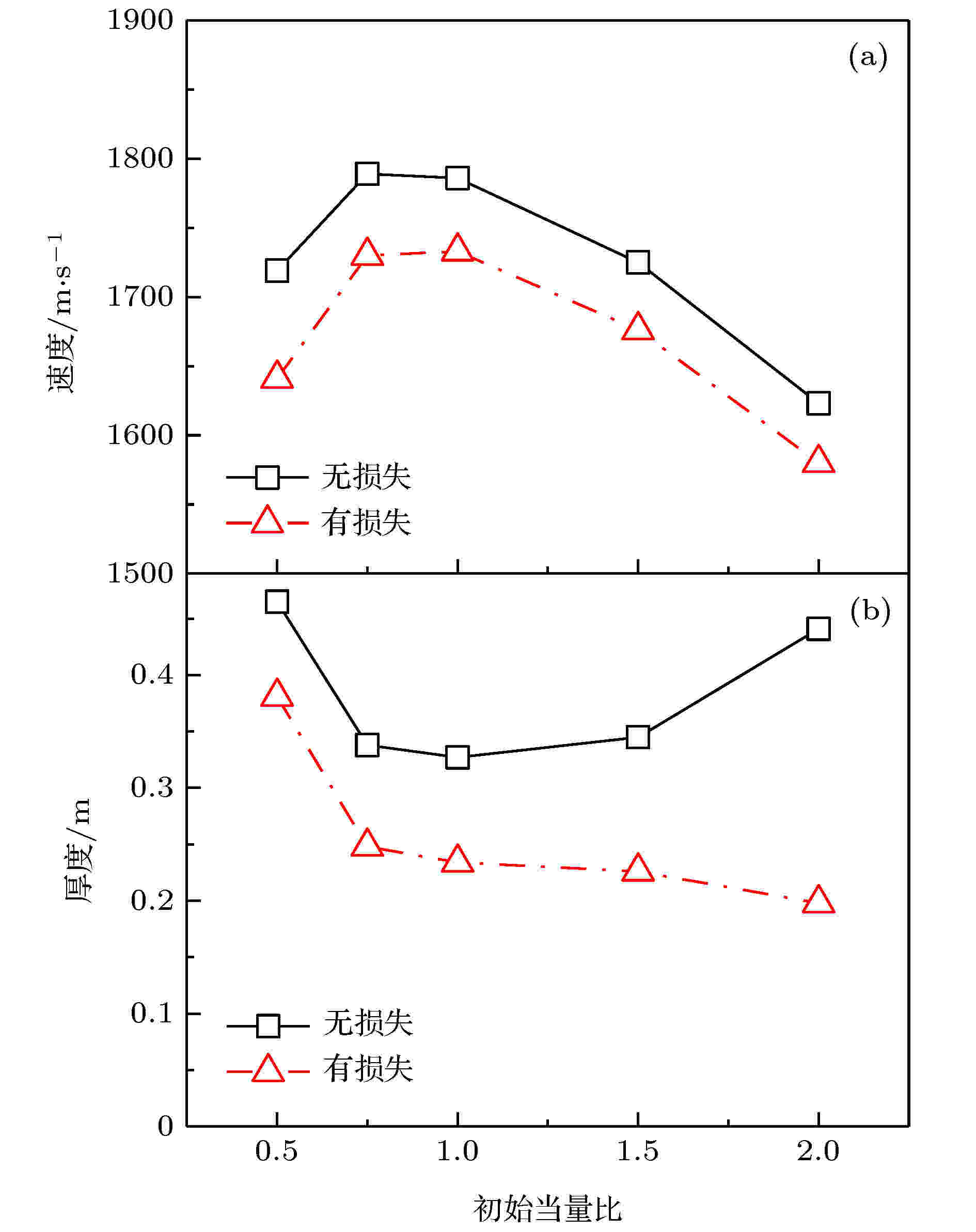
图 7 稳定传播的爆震波速度和爆震波厚度随初始当量比的变化　(a) 速度; (b) 厚度
Figure7. Variation of steady velocity and thickness of detonation wave with different initial equivalent ratio: (a) Velocity; (b) thickness.

在考虑管壁损失的条件下, 爆震波稳定速度随初始当量比的变化趋势与理想条件一致, 稳定传播速度与理想条件下的差值随当量比增大略有减小, 一方面是由于爆震波厚度随当量比增大而降低, 侧壁面换热面积随之减小, 另一方面是由于随着当量比增加, 贫氧工况下剩余的镁颗粒吸热增多, 气相与侧壁面间的温差减小, 上述两方面的原因共同导致侧壁面换热损失降低. 爆震波厚度随初始当量比的变化趋势与理想条件时不同, 初始当量比大于1的条件下, 爆震波厚度随初始当量比的增大仍然继续减小, 与理想条件爆震波厚度的差距进一步拉大. 如图8所示为初始当量比分别为1.0、1.5和2.0时, 在理想条件下和有壁面能量损失的条件下爆震波内气相密度分布. 由图可知, 气相密度整体随初始当量比增大而增大, 且在爆震波首段和末段差别明显. 这是由于在首段, 两相间速度差较大, 颗粒相对气相的压缩作用随初始当量比增大而增强; 在中段, 两相速度趋于一致, 压缩作用明显减弱; 在末段, 未反应镁蒸气的含量随着初始当量比的增加, 导致气相密度随初始当量比的增大而增大. 根据壁面黏性摩擦力公式(17), 壁面与气相间摩擦力大小与气相密度呈正比, 因此气相所受黏性力随当量比增大而增大, 导致爆震波厚度与理想条件爆震波厚度的差距随初始当量比的增大而增大.
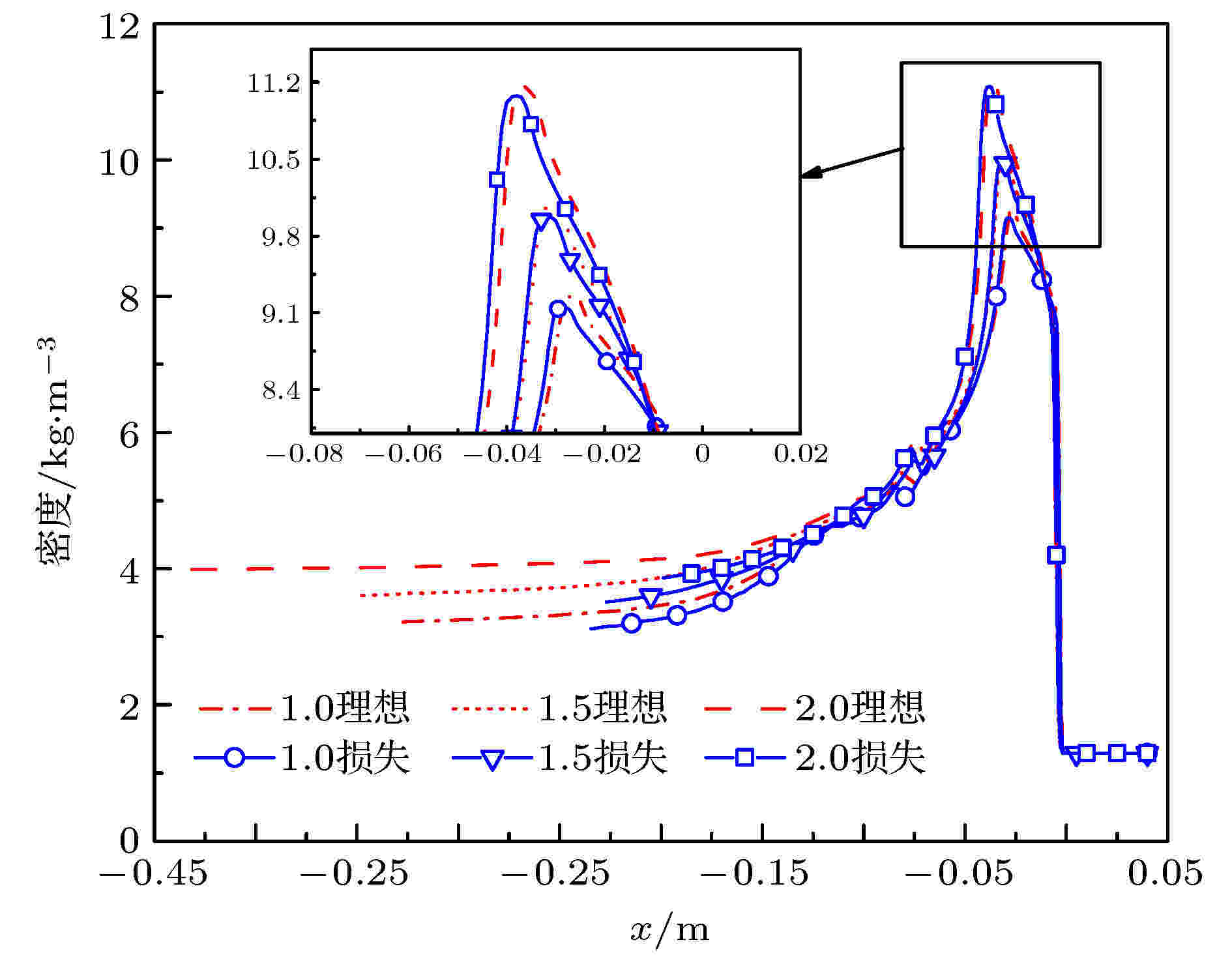图 8 不同当量比条件下爆震波内气相密度分布
Figure8. Gas-phase density distribution inside detonation wave with different initial equivalent ratio.

文献[8]中两相ZND模型的计算结果表明, 在一个镁颗粒初始浓度较低的小范围内(0.146—0.168 kg/m³), 由于产物MgO的熔化过程发生在气相相对前导激波的相对速度即将达到声速的阶段, 熔化吸热导致气相膨胀过程受到影响无法加速, 因而对应的爆震波无法以一个稳定的速度传播, 而可能是以某一速度为均值而进行振荡传播. 而本文的非稳态模型计算结果表明, 爆震波在传播过程中自身伴随着小幅振荡. 为进一步研究上述发生在临近爆震波末端的MgO熔化过程对爆震波传播稳定性和结构的影响, 以理想条件下初始当量比分别为0.315、0.337、0.382和0.5(对应镁颗粒初始浓度分别为0.14 kg/m³、0.15 kg/m³、0.17 kg/m³和0.222 5 kg/m³)的工况为例, 图9为不同初始当量比条件下充分发展后的爆震波内压力和气相温度分布. 由图9可知, 初始当量比为0.315对应的工况气相压力始终低于MgO熔点(3125 K), 表明此工况下爆震波内MgO未发生熔化; 初始当量比为0.5对应的工况在爆震波末端气相温度明显高于MgO熔点, 表明此工况下爆震波内MgO已完全熔化; 初始当量比为0.337对应的工况在爆震波内气相温度先升高达到MgO熔点后, 在爆震波末端气相温度又降至MgO熔点以下, 表明此工况下爆震波内MgO经历先部分熔化后又重新凝固的过程, 并且气相温度下降段对应的压力明显降低, 此过程中气相继续膨胀做功直至其与前导激波相对速度达到当地声速; 初始当量比为0.382对应的工况在爆震波内气相温度升高至MgO熔点后不再变化, 表明此工况下爆震波末端MgO始终处于熔化过程中, 根据压力分布可知, 在前导激波面下游约0.75 m处, 气态工质停止膨胀, 压力明显回升, 表明此工况下充分发展后的爆震波内的气态工质出现一个强度相对较低的二次压缩过程. 此外, 由图9还可以看出, 初始当量比为0.315和0.5时对应的爆震厚度大致相等, 而初始当量比为0.337和0.382时, 爆震波厚度显著增大, 表明发生在临近爆震波末端的MgO熔化过程使爆震波厚度显著增加. 图10为爆震波趋于稳定传播状态时在不同位置处的对应的爆震波压力峰值, 取样时间间隔为0.1 ms. 由图可知, 不同初始当量比条件下爆震波压力峰值均存在振荡, 且振幅大致相等, 约为0.05 MPa, 表明发生在临近爆震波末端的MgO熔化过程对爆震波传播稳定性的影响基本可以忽略不计.
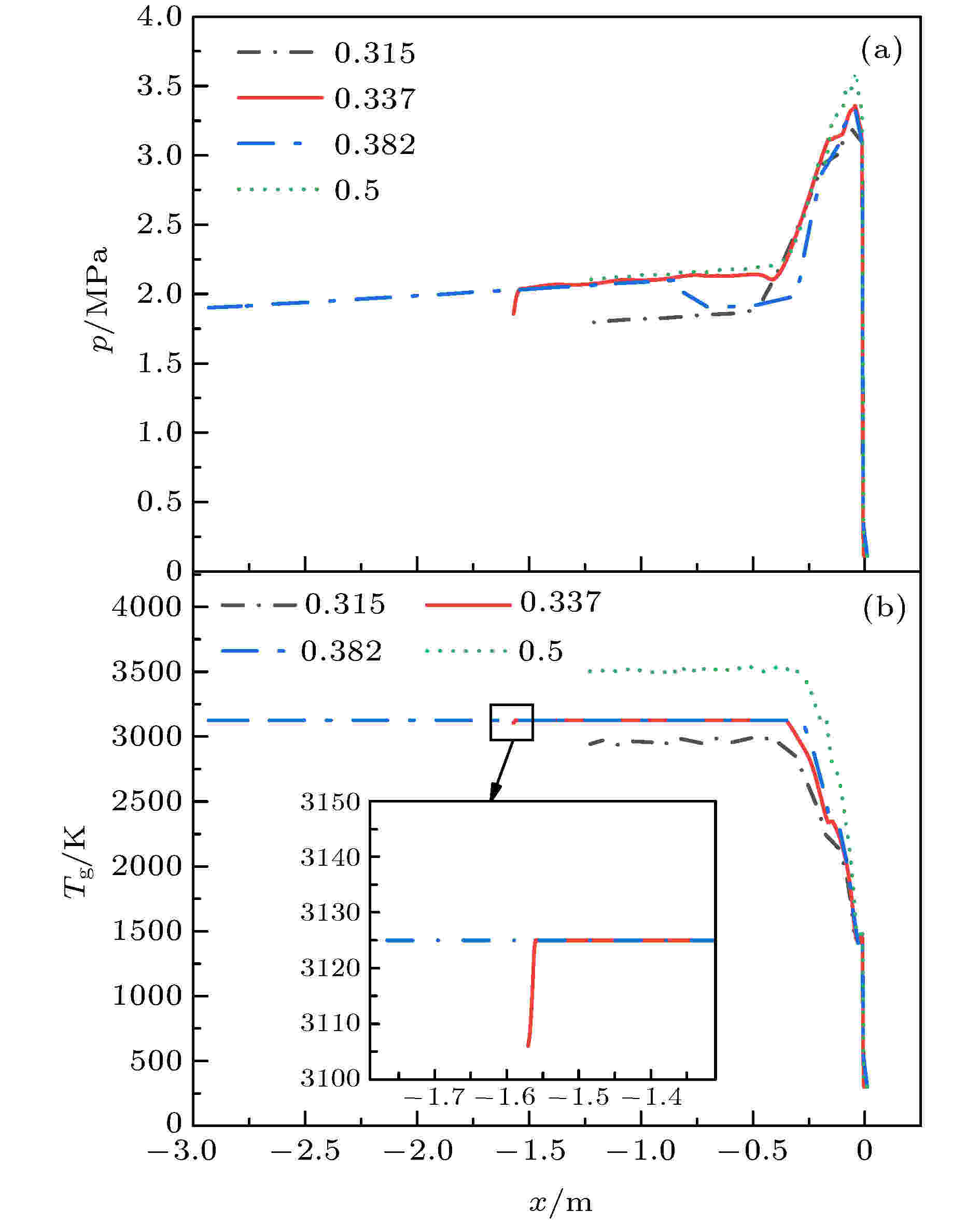图 9 不同初始当量比条件下爆震波内参数分布　(a)压力; (b)温度
Figure9. Parameters distribution inside detonation wave with different initial equivalent ratio: (a) Pressure; (b) temperature.

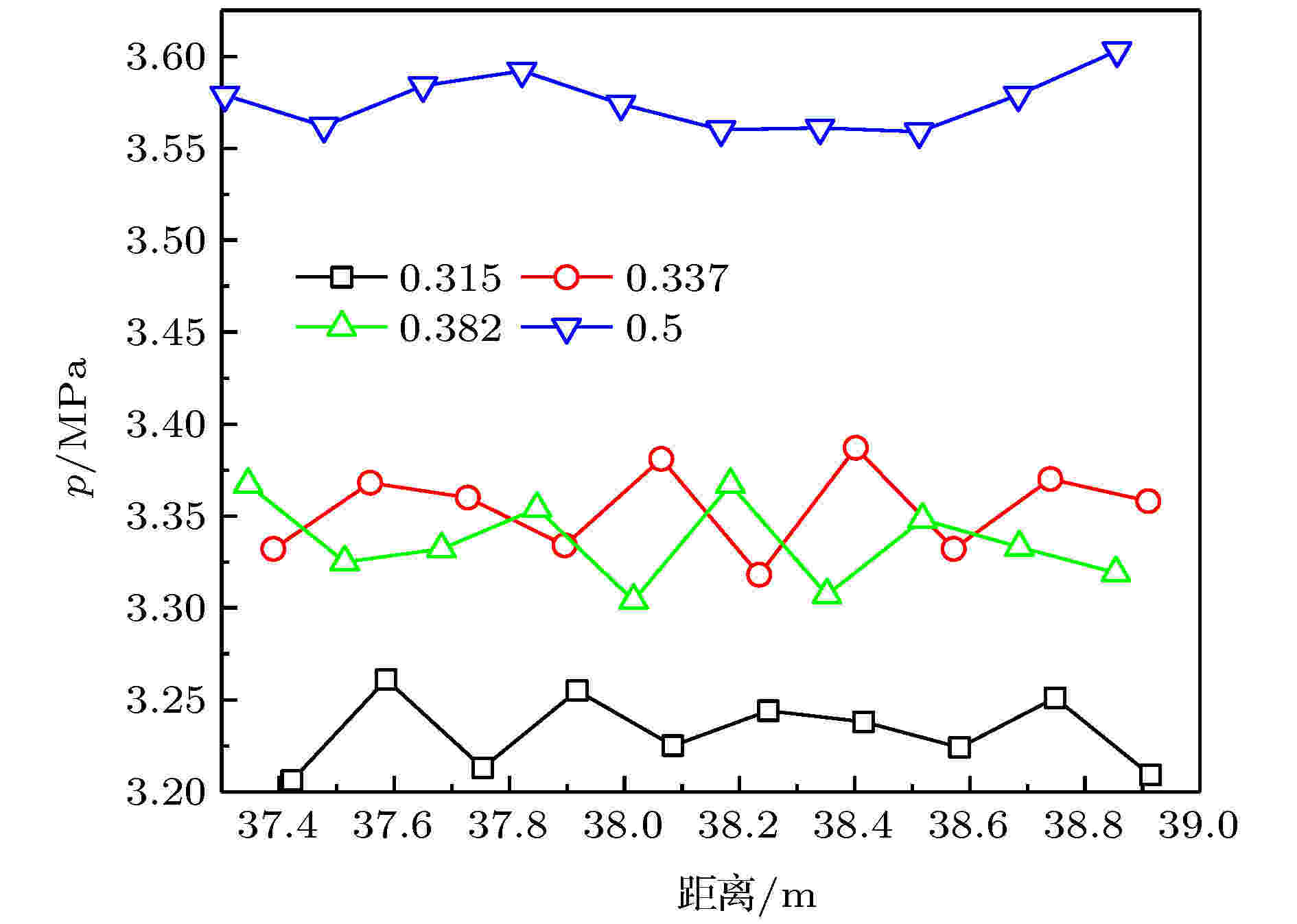图 10 不同初始当量比条件下不同位置处的爆震波压力峰值
Figure10. Pressure peak at different position with different initial equivalent ratio.

2 -->

3.6.初始点火条件的影响

根据标准参考工况条件下稳定传播的爆震波速度1786 m/s计算得到对应的正激波波后参数作为点火区的流场初值, 点火区大小分别取1倍、0.5倍、0.25倍和0.125倍稳定爆震波厚度, 得到冲击波诱导起爆条件下的前导激波面在发展成为稳定传播过程中的速度变化, 如图11所示. 点火区长度为0.125倍稳定爆震波厚度的情况, 爆震波起爆失败, 故其结果未在图中显示. 由图可知, 点火区长度为1倍和0.5倍爆震波厚度时, 前导激波在经过开始的一小段加速过程(分别对应2.319—2.83 m和2.017—2.315 m)后, 开始逐渐衰减直至达到稳定传播状态. 而当点火区长度为爆震波厚度的0.25倍时, 前导激波先是衰减, 速度降至稳定传播速度以下, 当速度降至1237 m/s时, 爆震波停止衰减, 并开始逐渐加速达到过驱爆震状态, 速度达到1953 m/s后, 前导激波开始逐渐衰减直至达到稳定传播状态. 开始的衰减是由于点火区较短, 初始膨胀波强度较大导致的. 当点火区厚度较大时, 初始膨胀波强度较弱, 对前导激波的削弱作用较小.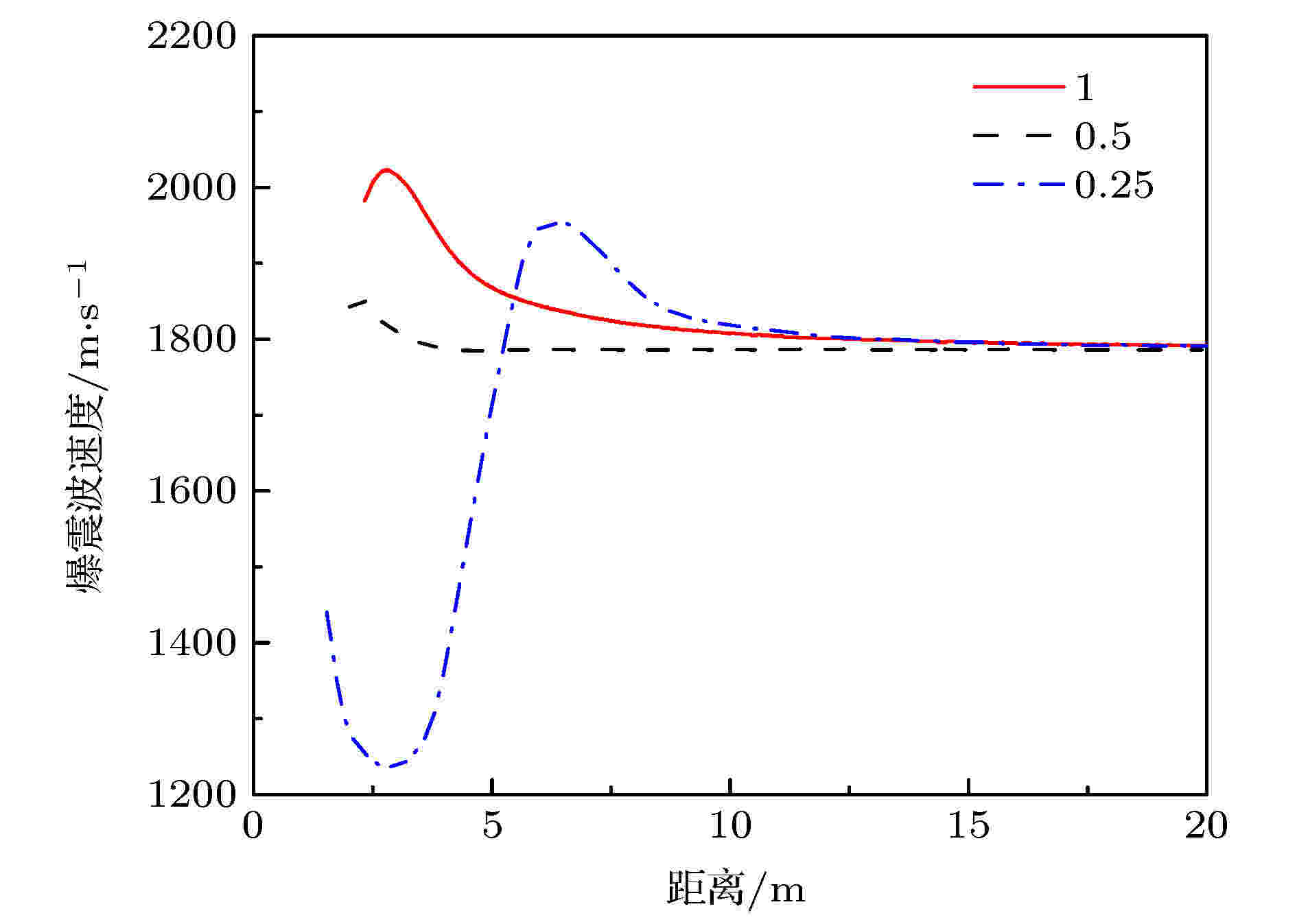
图 11 不同点火区长度对应的爆震波速度发展过程
Figure11. Development of detonation wave velocity with different length of ignition zone.

当点火区大小为1倍稳定厚度, 点火区流场参数初值分别为0.8倍、1.0倍和1.2倍爆震波稳定速度正激波后的von Neumann参数时, 计算得到前导激波面在发展成为稳定传播过程中的速度变化, 如图12所示. 1.2倍稳定速度的结果与1.0倍的趋势一致, 定量关系上其对应的前导激波速度更高. 0.8倍稳定速度的结果与另外两者明显不同, 是直接加速直至爆震波达到过驱状态, 再渐进衰减至稳定速度. 参考气相爆震冲击波起爆的研究结果^[21], 对于点火区的冲击波总能量, 存在起爆界限(下限)和过驱界限(上限). 对于镁颗粒-空气混合物而言, 当冲击波总能量高于上限时, 在爆震波发展至稳定传播过程中, 前导激波速度始终高于稳定速度(如图11中的曲线1.0和0.5以及图12中的曲线1.0和1.2). 当冲击波总能量低于下限时, 爆震波无法起爆. 在点火条件处于上限和下限之间, 则前导激波会经历速度衰减至稳定值以下, 而后爆震波加速至过驱状态(前导激波速度高于稳定速度), 再逐渐达到稳定速度的过程.
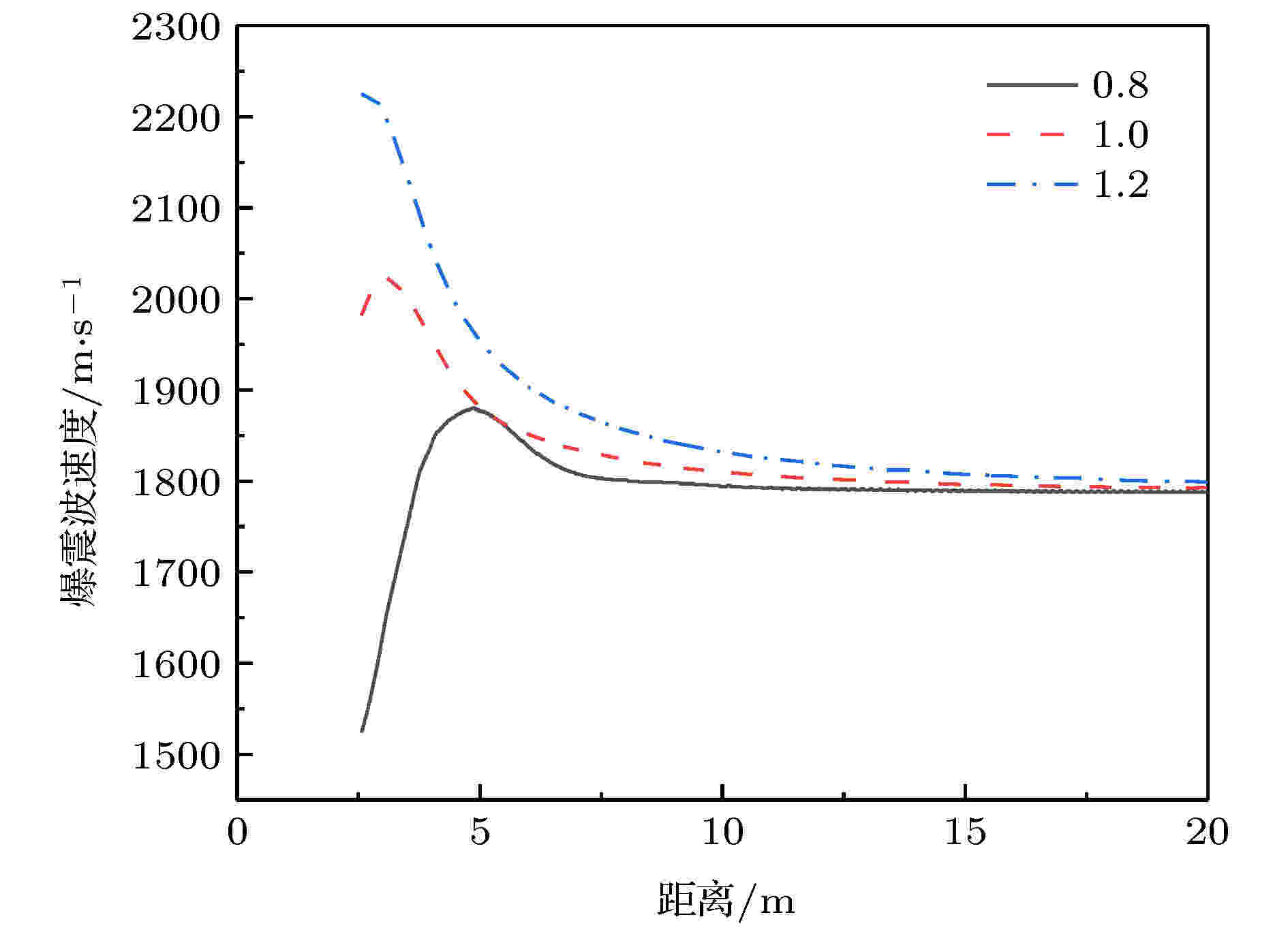图 12 不同点火区参数对应的爆震波速度发展过程
Figure12. Development of detonation wave velocity with different field parameters of ignition zone.

综合以上计算结果可以看出, 点火区参数对爆震波最终的稳定传播状态没有影响, 但会影响爆震波发展过程. 点火区参数和长度满足一定条件(如点火区长度为0.5倍稳定厚度, 流场参数为稳定波速对应的正激波后von Neumann参数), 能够使爆震波发展至稳定状态所传播的距离明显缩短. 这对于采用冲击波起爆方式的连续旋转爆震发动机尽快实现爆震波在燃烧室内的稳定传播具有重要指导意义.

本文针对镁颗粒-空气混合物爆震建立了一维非稳态模型, 通过数值模拟不同工况下的爆震波非稳态自维持传播过程, 获得了爆震波内流场参数的分布以及爆震管侧壁面损失、镁颗粒半径、镁颗粒初始当量比、颗粒表面沉积过程以及点火能量对爆震波结构和发展过程的影响规律. 研究表明, 充分发展后的镁颗粒-空气混合物一维非稳态爆震波在传播过程中存在振荡现象, 但振幅较小, 在 ± 1 m/s以内; 在考虑燃烧产物在颗粒表面沉积的情况下, 颗粒反应速率和爆震波稳定速度均随燃烧产物在颗粒表面的凝结速率的增大而增大, 对应的爆震波厚度基本保持不变.
在考虑爆震管侧壁面损失的条件下, 随着管径减小, 爆震波内的压力与温度均降低, 进而导致爆震波传播速度和爆震波厚度减小; 在不考虑管壁损失的理想条件下, 随着颗粒初始粒径增大, 爆震波稳定速度保持不变, 爆震波厚度单调递增. 考虑管壁损失时, 得到的爆震波稳定速度和厚度均低于同等初始条件下理想工况的结果, 且由于管壁造成的损失与爆震波厚度成正相关, 因此考虑损失和理想条件下爆震波速度和厚度的差值均随颗粒初始粒径的增大而增大; 初始粒径为双粒径分布的工况(5 μm和15 μm混合)与对应的初始单一粒径分布(10 μm)的工况相比, 小粒径镁颗粒很快被完全消耗, 剩余的大粒径颗粒数目较少, 反应表面积较少, 导致爆震波的厚度更大, 且在考虑壁面损失的条件下, 双粒径分布对应的爆震波速度明显低于统一粒径的工况. 对于试验用镁颗粒而言, 其粒径存在一个分布范围, 因此可以推测镁粉爆震试验得到的爆震波速度值可能低于按照平均粒径计算得到的爆震波速度值.
在颗粒初始当量比0.5—2范围内, 随初始当量比增大, 不考虑壁面损失的条件下爆震波稳定速度先增大后减小, 爆震波厚度先减小后增大. 在考虑壁面损失的条件下, 随着初始当量比增大, 稳定爆震波速度先降低后增大, 由于爆震波内气相密度随当量比增大而单调增大, 因此爆震波厚度随初始当量比增加而单调递减; 当初始颗粒初始当量比在一个较低范围内(0.337—0.382), 满足MgO熔化发生在CJ平面附近时, MgO熔化过程对爆震波传播稳定性无明显影响, 而对爆震波结构影响较大: 初始当量比偏低的情况下, 爆震波内MgO先部分熔化而后重新凝固, CJ面处的MgO为固态; 初始当量比偏高的情况下, CJ面处MgO仍处于熔化过程中, 且爆震波内存在一个强度较低的二次压缩过程.
点火区参数对爆震波最终的稳定传播状态没有影响, 但会影响爆震波发展过程: 当点火区能量高于上限时, 爆震波在发展至稳定传播过程中, 前导激波速度始终高于稳定速度; 当低于下限时, 爆震波无法起爆; 点火能量在上限和下限之间时, 前导激波会经历速度衰减至稳定值以下, 而后爆震波加速至过驱状态, 再逐渐达到稳定速度的过程. 合理设置点火条件, 可使得爆震波发展至稳定状态所传播的距离明显缩短. 这对于采用冲击波起爆方式的连续旋转爆震发动机尽快实现爆震波在燃烧室内的稳定传播具有重要指导意义.
本模型较全面地反映出管壁损失、颗粒初始粒径、颗粒初始当量比、颗粒表面沉积以及点火区参数对爆震波非稳态传播过程的影响, 对采用粉末燃料的爆震动力装置设计具有一定的指导意义. 基于本文的工作, 下一步可开展镁颗粒-空气混合物二维连续旋转爆震燃烧数值模拟的相关研究.