摘要: 众所周知, 量子态的演化可用与其相应的Wigner函数演化来代替. 因为量子态的Wigner函数和量子态的密度矩阵一样, 都包含了概率分布和相位等信息, 因此对量子态的Wigner函数进行研究, 可以更加快速有效地获取量子态在演化过程的重要信息. 本文从经典扩散方程出发, 利用密度算符的
P 表示, 导出了量子态密度算符的扩散方程. 进一步通过引入量子算符的Weyl编序记号, 给出了其对应的Weyl量子化方案. 另外, 借助于密度算符的另一相空间表示—Wigner函数, 建立了Wigner算符在扩散通道中演化方程, 并给出了其Wigner算符解的形式. 本文推导出了Wigner算符在量子扩散通道中的演化规律, 即演化过程中任意时刻Wigner算符的形式. 在此结论的基础上, 讨论了相干态经过量子扩散通道的演化情况.
关键词: Wigner函数 /
Weyl编序 /
量子扩散通道 /
演化规律 English Abstract Time evolution law of Wigner operator in diffusion channel Zhang Ke 1 ,Li Lan-Lan 1 ,Ren Gang 1 ,Du Jian-Ming 1 ,Fan Hong-Yi 2 1.School of Electronic Engineering, Huainan Normal University, Huainan 232038, China Fund Project: the National Natural Science Foundation of China (Grant No.11775208), the Natural Science Foundation of the Anhui Higher Education Institutions of China (Grant No. KJ2019A0688), and the Key Projects of Huainan Normal University, China(Grant No. 2019XJZD04)Received Date: 15 January 2020Accepted Date: 13 February 2020Published Online: 05 May 2020Abstract: As is well known, the evolution of quantum state can be replaced by its Wigner function’s time evolution. The Wigner function of a quantum state is the same as the density matrix of a quantum state, because they both contain many messages, such as the probability distribution and phases. Thus, the important information about the quantum state in the evolution process can be obtained more quickly and effectively by studying the Wigner function of a quantum state. In this paper, based on the classical diffusion equation, the diffusion equation of the quantum state density operator is derived by using the P representation of the density operator. Furthermore, by introducing the Weyl ordering symbol of the quantum operator, the corresponding Weyl quantization scheme is given. In addition, the evolution equation of Wigner operator in diffusion channel is established by using another phase space representation of density operator—Wigner function, and the solution form of Wigner operator is given. In this paper, we derive the evolution law of Wigner operator in quantum diffusion channel for the first time, that is, the form of Wigner operator at any time in the evolution process. Based on this conclusion, the evolution of coherent states through quantum diffusion channels is discussed.Keywords: Wigner function /Weyl ordering /quantum diffusion channel /evolution law 全文HTML --> --> --> 1.引 言 近来, 量子调控已经成为研究微观世界的一个重要手段, 而用单光子实现量子操控尤为可行, 例如向光腔中逐个注入光子制备非高斯态, 理论上这属于量子扩散机制[1 ,2 ] . 鉴于量子态的Wigner函数包含了量子态的概率分布和相位等信息, 量子态的演化可代之以研究相应的Wigner函数的演化[3 -5 ] . 本文旨在研究量子相空间的Wigner算符在量子扩散通道的时间演化规律, 它简洁而物理清晰, 展现了从点源函数$\dfrac{1}{2}\begin{array}{*{20}{c}} : \\ : \end{array}\delta \left( {{z^ * } - {a^\dagger }} \right)\delta \left( {z - a} \right)\begin{array}{*{20}{c}} : \\ : \end{array}$ 向$t$ 时刻高斯型函数$\dfrac{1}{{2 kt}}\begin{array}{*{20}{c}} : \\ : \end{array}\exp \left[ {\dfrac{{ - 1}}{{kt}}\left( {{a^\dagger } - {z^ * }} \right)\left( {a - z} \right)} \right]\begin{array}{*{20}{c}} : \\ : \end{array}$ 的演变, $k$ 是扩散系数, 这里$\begin{array}{*{20}{c}} : \\ : \end{array}\!\! \begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 代表Weyl编序; ${a^\dagger }, a$ 是玻色产生和湮灭算符. 用有序算符内的积分方法也可进一步将Wigner算符的Weyl编序式转化为其他排序形式, 如正规乘积序等, 为计算量子态的Wigner函数演化规律带来便利. 本文安排如下, 先从经典扩散方程推导出量子扩散方程, 并以相干光场为例, 讨论其量子扩散. 鉴于初始相干光场的反正规乘积形式是Delta函数, 其演化就体现在从$\delta \left( {z - a} \right)\delta \left( {{z^ * } - {a^\dagger }} \right)$ 演化为$ \vdots \begin{array}{*{20}{c}} {} \\ {} \end{array} \vdots $ 代表反正规排序[6 ,7 ] . 然后再讨论Wigner算符的量子扩散, 鉴于Wigner算符的Weyl排序形式是Delta函数,$\begin{array}{*{20}{c}} : \\ : \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 代表Weyl排序, 为范洪义首创, 所以可以立即从扩散方程导出Wigner算符在扩散通道中的演化规律.2.从经典扩散导出量子扩散方程 经典扩散方程是$k$ 是扩散率, $P\left( {z, t} \right)$ 是系统的某种密度分布函数. 下面推导相应的量子扩散方程. 我们将密度算符$\rho $ 用相干态表象中的$P $ -表示[8 ,9 ] :1 )式代入(4 )式即有$P\left( {z, t} \right)$ 消失, 则有$\dfrac{{{\partial ^2}}}{{\partial z\partial {z^ * }}}\left| {\left. z \right\rangle } \right.\left\langle {\left. z \right|} \right.$ , 注意到10 )式代入(6 )式得到3.相干光场的扩散 当初态是纯相干光场时,[10 ] 给出的把正规乘积排序变为反正规乘积排序的公式$P - $ 表示为$\dfrac{{\partial P\left( {z, t} \right)}}{{\partial t}} \!=\!$ $ - k\dfrac{{{\partial ^2}P\left( {z, t} \right)}}{{\partial z\partial {z^ * }}} $ 的解是$\delta \left( x \right) = \mathop {\lim }\limits_{t \to 0} \dfrac{1}{{\sqrt {\text{π}} t}}{{\rm{e}}^{ - {{{x^2}} / t}}}$ 的推广.${P_t}$ 是密度算符${\rho _t}$ 在相干态表象中的表示, 所以便可得到${\rho _t}$ 的反正规乘积形式为[11 ] 和有序算符内的积分技术[12 -14 ] 可以将它化为正规乘积,20 )式可发现它不再是纯态. 同时可验证${\rm{tr}}{\rho _t} = 1$ , 故而${\rho _t}$ 是一个新光场密度算符, 代表一个广义的混沌光场[15 ,16 ] . 计算$t$ 时刻的光子数:${\rm{tr}}\left( {{a^\dagger }a{\rho _0}} \right) = \left\langle {\left. z \right|{a^\dagger }a\left| {\left. z \right\rangle } \right.} \right.=$ ${\left| z \right|^2} $ , 可见光子数增加了$kt$ , 这是扩散的结果.4.Wigner算符的Weyl排序形式 现在讨论Wigner函数在扩散通道中的演化. 鉴于$t$ 时刻的密度算符$\rho \left( t \right)$ 的Wigner函数是[17 ,18 ] $\varDelta \left( {p, q} \right)$ 是Wigner算符, 所以也可转而讨论Wigner算符在扩散通道中的时间演化, 即从$\varDelta \left( {p, q, 0} \right)$ 演化为$\varDelta \left( {p, q, t} \right)$ . 历史上, Wigner算符最早是在坐标表象中定义的[19 ] ,$| {q \!+\! {v}/{2}}\rangle = {{\rm e}^{{{ - {\rm{i}}Pv} / 2}}} |q\rangle $ 和$\left| q \right\rangle \left\langle q \right| = \delta \left( {q - Q} \right)$ , $Q$ 是坐标算符, P 是动量算符, (23 )式可化为24 )式进行积分, 我们引入Weyl编序$\begin{array}{*{20}{c}} : \\ : \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 来标志已经Weyl排序好了的算符[20 -22 ] . 例如Weyl编序可以将经典量${q^m}{p^r}$ 通过积分变换(积分核就是Wigner算符$\varDelta \left( {q, p} \right)$ )量子化为$\begin{array}{*{20}{c}} : \\ : \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 标识,$\begin{array}{*{20}{c}} : \\ : \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 内部玻色算符是可交换的, 所以有$H\left( {P, Q} \right)$ 及其经典对应$h\left( {p, q} \right)$ 的Weyl对应式为[23 ] $H\left( {P, Q} \right)$ 的Weyl排序形式, 可以直接将$h\left( {p, q} \right)$ 中的$p \to P, q \to Q$ , 并放入$\begin{array}{*{20}{c}} : \\ : \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} : \\ : \end{array}$ 内得到. 例如, $\begin{array}{*{20}{c}} : \\ : \end{array}{{\rm{e}}^{{\rm{i}}Pv + {\rm{i}}Qu}}\begin{array}{*{20}{c}} : \\ : \end{array}$ 的经典对应是${{\rm{e}}^{{\rm{i}}pv + {\rm{i}}qu}}$ :5.扩散通道中Wigner算符的演化方程 由于Wigner算符满足:12 )式, 它所满足的扩散方程是37 )直接导出(具体详见附录A ).2 节内容可见此扩散方程的经典对应是$W$ 应该满足的扩散方程.6.Wigner算符的演化方程之解 初始的Wigner算符$\varDelta \left( {\alpha, {\alpha ^ * }, 0} \right)$ 在Weyl编序下是[24 -26 ] 2 节的结果可知:41 )式就是量子扩散通道中Wigner算符的演化律公式, 可以看出, 它简洁明了, 同时展现了从点源函数$\dfrac{1}{2}\begin{array}{*{20}{c}} : \\ : \end{array}\delta \left( {{z^ * } - {a^\dagger }} \right)\delta \left( {z - a} \right)\begin{array}{*{20}{c}} : \\ : \end{array}$ 向高斯型函数$\dfrac{1}{{2 kt}}\begin{array}{*{20}{c}} : \\ : \end{array}$ $\exp \left[ {\dfrac{{ - 1}}{{kt}}\left( {{a^\dagger } - {z^ * }} \right)\left( {a - z} \right)} \right]\begin{array}{*{20}{c}} : \\ : \end{array} $ 的演变, 所以此数学表达式的物理意义十分明晰.40 )式可知$\varDelta \left( {\alpha, {\alpha ^ * }, t} \right)$ 的经典对应是28 )式可知24 )式做积分可得:$\varDelta \left( {\alpha, {\alpha ^ * }, t} \right)$ 的正规乘积是40 )式的Weyl编序形式导出了其正规乘积形式. 另外, (45 )式还可进一步得到验证(具体详见附录B ), 即将正规乘积形式转化为Weyl编序形式. 举例, 当初态是纯相干态, 那么经过扩散通道后, 从(40 )式可知它的Wigner函数为图1 所示为Wigner算符的演化规律, 图1(a) 描绘了相干态初始的Wigner函数, 尖峰象征Delta函数; 图1(b) 描绘了$kt = 0.8$ 时高斯型Wigner函数. 对比两图中Wigner函数的峰值及形状, 可以看出相干态在耗散通道的演化情况.图 1 (a) $kt = 0$ , (b) $kt = 0.8$ 时, 相干态下Wigner算符的演化规律($\alpha = 1/2\left( {1 + i} \right)$ )Figure1. Evolution law of Wigner operator for the coherent state with $\alpha = 1/2\left( {1 + i} \right)$ for (a) $kt = 0$ ; (b) $kt = 0.8$ 7.结 论 本文引入算符的Weyl编序记号, 导出量子扩散通道中Wigner算符的演化律公式, 它简洁而物理清晰, 展现了从点源函数$k$ 是扩散系数. 由此也可转化为Wigner算符的其他排序形式, 如正规乘积序. 值得指出, 对于相干态的演化用了反正规乘积来讨论, 而对Wigner算符的演化用Weyl排序来讨论, 这两者的演化在数学形式上是一样的.附录A 相空间中Wigner算符所满足的扩散方程 本节验证Wigner算符所满足的扩散方程. 由${\rm{Wigner}}$ 算符的正规乘积表达式(44 )式可算出:36 )式.附录B 化算符为Weyl排序的公式 相干态$\left| z \right\rangle \left\langle z \right|$ 的经典对应是$\left| z \right\rangle \left\langle z \right|$ 的Weyl排序形式为2 )式得到$\left| \beta \right\rangle $ 为相干态, $\left| \beta \right\rangle = \exp \left[ {{{ - {{\left| \beta \right|}^2}} / 2} + \beta {a^\dagger }} \right]\left| 0 \right\rangle $ , 所以$\rho $ 为(45 )式时,B6 )式便可得到Weyl编序形式.40 )式. 


























































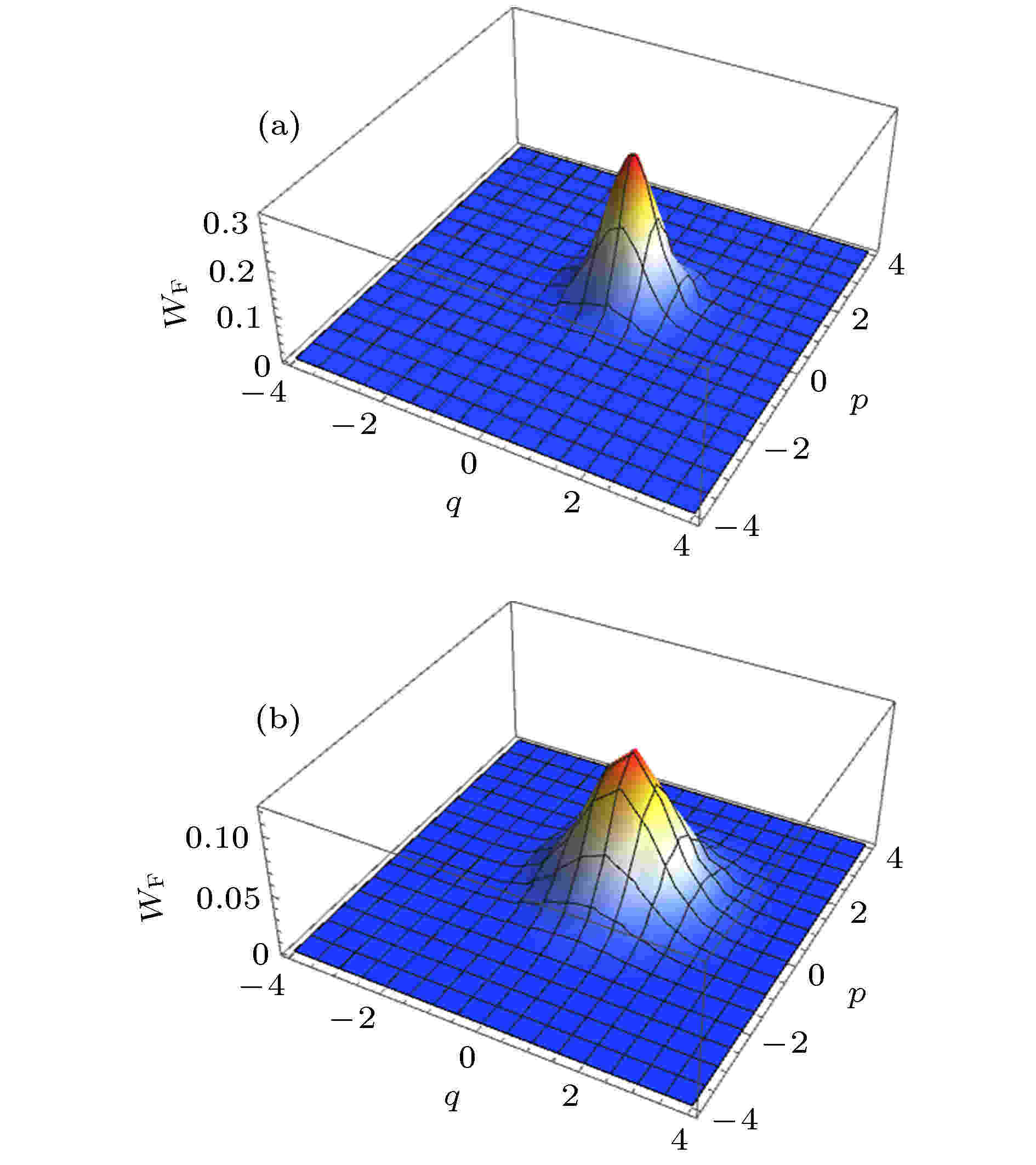 图 1 (a)
图 1 (a) 







































































 图 1 (a)
图 1 (a) 











