摘要:通过直接数值求解Navier-Stokes方程, 研究了入流激励下可压缩剪切层中Kelvin-Helmholtz (KH)涡结构的响应特性, 结果清晰地展示了KH涡的独特演化方式. 基于流动可视化数据, 采用两点相关性分析获得了流场拟序结构的空间尺寸和结构角分布. 通过分析不同激励频率下涡结构的动态特性, 揭示了入流激励下可压缩剪切层中KH涡结构的独特演化机理. 研究结果表明, 低频入流激励(f = 5 kHz)下KH涡尺寸在远场区域达到饱和后呈现锁频状态, KH涡量厚度稳定在12—14 mm之间; 与自由剪切层涡结构通过配对合并的方式实现生长的机理不同, 低频入流激励下剪切层的发展是通过中间涡核顺时针吞噬KH不稳定波诱导的一串外围小涡结构来实现生长. 此外, 针对高频激励 (f = 20 kHz)下的剪切层流动, 研究了涡结构特性和入流激励参数之间的定量关系, 发现均匀分布涡结构的尺寸近似等于对流速度与入流激励频率之比.
关键词: 可压缩剪切层/
入流激励/
Kelvin-Helmholtz涡/
生长特性

English Abstract

全文HTML

--> --> -->

近年来随着超燃冲压发动机技术以及高速导弹成像制导技术的发展, 可压缩剪切层流动得到了广泛的关注和持续不断的研究^[1,2]. 超燃冲压发动机有限的燃烧室尺寸内, 超声速空气与燃料剪切混合的时间尺度为毫秒量级, 如何在较短的时间内实现空气与燃料的充分混合成为其中最为核心的一项关键技术^[3,4]. 此外, 对于红外成像制导技术而言, 导弹以高马赫数飞行时, 其光学侧窗周围存在严重的气动光学效应, 使得目标图像出现偏移、抖动以及模糊. 这其中为消除气动热效应而采用的制冷剂喷流与外部来流形成的可压缩剪切层流场结构是产生气动光学效应的一个重要来源^[5]. 一系列工程应用上的需求使得可压缩剪切层流场结构的调控变得尤为迫切. 在科学价值方面, 剪切层流动存在速度拐点, 其诱导的Kelvin-Helmholtz (KH)不稳定波促成了流场中典型大尺度涡—KH涡的卷起, KH涡的发展和演化是剪切层实现增长的重要方式. 此外, 剪切层不受壁面干扰, 结构相对简单, 深入研究其流场中KH涡结构的相互作用及涡结构的生长特性具有重要的学术意义和理论价值.
Brown和Roshko^[6]于1974年首次在剪切层中发现KH不稳定波诱导的拟序结构, 且这些结构主导着剪切层的能量交换及动力学行为. 随后Ortwerth和Shine^[7]通过实验发现在可压缩状态下剪切层中同样存在着大尺度KH拟序涡结构, 但是可压缩效应的存在使得KH涡结构的增长受到显著抑制. 为了衡量压缩性对剪切层的影响, Papamoschou和Roshko^[8]基于大尺度KH涡结构首次提出了对流马赫数(convective Mach number, Mc)的概念, 这一无量纲量后来成为国内外****开展可压缩剪切层稳定性分析, 混合增强以及流动控制研究采用的重要参数.
针对剪切层主动流动控制的研究, 最早由Ho和Huang^[9]在低速剪切层中采用人工扰动的方式分析了流场中KH涡结构的演化及剪切层的增长情况, 其研究表明在流场中加入人工扰动可以实现对流场结构的控制. 随后McLaughlin等^[10]在可压缩剪切层中引入电火花激励, 通过电火花在流动入口处产生高频温度扰动, 激发出流场中的大尺度KH涡结构, 从而实现了可压缩条件下剪切层的流动控制, 但是受到实验条件的限制, 其研究结果并没有观察到人工激励下流场的精细结构以及KH涡结构的生长方式. Guo等^[11]基于气动光学研究背景, 采用大涡模拟方法研究了脉冲激励下可压缩剪切层的演化机理, 其研究基于涡核位置提取方法, 对流场中涡结构的空间尺寸和瞬时对流速度的动态特性进行了定量计算. Freeman和Catrakis^[12]采用等离子体激励的方式对剪切层涡结构演化特性进行了研究, 结果表明选择恰当的等离子体激励频率, 可以有效抑制涡结构的生长. 在周期性激励控制流动混合方面, Yu等^[13]的研究表明入口人工扰动下可压缩剪切层的增长率可以提高2—3倍; 然而Feng^[14]采用大涡模拟方法研究表明, 入口人工激励对剪切层演化的影响呈现出先促进增长, 后抑制增长的特性.
由此可见, 虽然国内外****对剪切层进行控制时采用的人工激励方式有差别, 但其本质上都是通过人工激励来调控流场中KH拟序涡结构的发展. 在周期性的人工激励下, 涡结构必然会呈现出某些特有的规律, 进而影响流场的发展和演化方式. 然而过去的研究更多的是对人工激励下可压缩剪切层中KH涡结构进行可视化分析^[12], 相关的定量分析如结构空间尺寸, 结构角分布等还缺乏深入的研究, 进而使得对人工激励下KH涡结构特有的响应特性和生长机理也缺乏足够的认识. 此外, 对比Yu等^[13]和Feng^[14]的研究可以发现, 在入口激励影响剪切层掺混方面, 前人的研究对于剪切层的增长特性也尚未达成共识.
基于此, 本文研究采用入流周期性激励的方式对可压缩剪切层添加人工扰动, 通过直接数值求解可压缩Navier-Stokes方程, 借助于KH涡量厚度分析, 空间相关性分析等研究手段对入流激励下剪切层的增长特性和KH拟序涡结构的空间尺寸, 结构角分布进行定量研究. 通过分析不同激励频率下流场中涡结构的动态演化过程, 获得了KH涡结构演化特性和入流激励参数之间的定量关系, 揭示了入流激励下可压缩剪切层KH涡结构的演化机理和独特生长特性.

2

-->

2.1.数值计算方法

通过直接数值求解可压缩Navier-Stokes方程获得流动的瞬时流场, 即各种尺度的随机运动, 从而获得流场的全部时空信息, 结合可视化和相关后处理方法揭示流场结构的发展演化特性. 计算采用的高精度数值计算方法由本课题组自行开发, 具有高精度, 高分辨率和强稳定性的特点, 已经在可压缩流动的研究中得到了一系列应用^[15,16]. 限于篇幅, 这里仅对格式的构造作简要介绍. 对于可压缩Navier-Stokes方程, 对流项采用具有5阶精度的WENO (weighted essentially non-oscillatory) 格式进行求解, WENO格式能够在克服ENO (essentially non-oscillatory) 格式带来的舍入误差大及经济性差的缺陷的同时保持较好的计算刚性和精度. 黏性项采用6阶精度中心差分格式离散, 时间推进上采用三阶精度具有TVD保持性质的Runge-Kutta方法, 库朗特数(CFL)选为0.1. 相关格式的具体构造方式可以参见^[17,18].
由于本研究并未关注KH涡转捩形成湍流的过程, 因此考虑到计算成本, 采用了二维模型进行计算, 如图1所示. 前人的研究亦表明, 如果仅仅关注剪切层中KH不稳定及KH涡的演化, 采用二维的计算模型是可行的^[19]. 计算中取混合区的流向长度为L = 600 mm, 横向长度2H = 200 mm, 流向长度和横向长度的比值为3. 在文献[19]中, 通过设置流向长度为横向长度的4倍来保证横向区域足够大, 从而有效减小上下边界对主流的影响. 本文取这一比值为3, 从而将影响进一步降低.
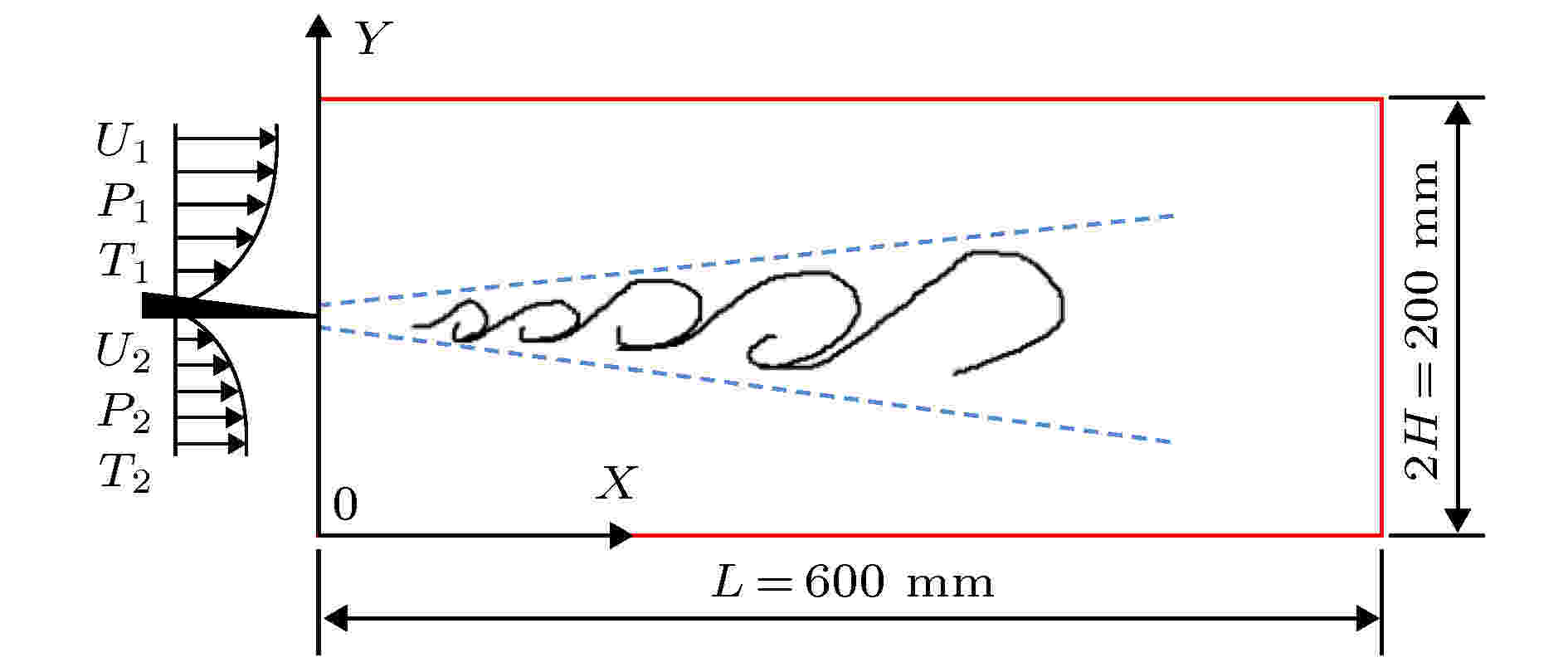图 1 计算模型示意图
Figure1. Schematic of computational model.

本次计算的来流参数如表1所列. 上下来流的速度分别为473 m/s和284 m/s, 当地声速可通过关系式获得

	速度 /m·s–1	马赫 数	密度 /kg·m–3	压力 /kPa	温度 /K	对流马 赫数Mc
上层 来流	473	2.15	0.983	34	120	0.4
下层 来流	284	1.12	0.737	34	160

表1数值计算来流参数
Table1.Inflow parameters of numerical simulation

$a = \sqrt {{\rm{\gamma R}}T} , $

其中γ为比热比, γ = 1.4. R为气体常数, 取R = 287 J·kg^–1K^–1. 由关系式Ma = U/a求得上下两层超声速来流的马赫数分别为2.15和1.12.
对于边界条件的处理, 由于上下两股来流均为超声速流动, 因此入口直接给定超声速入口边界条件, 即只提物理边界条件, 给定上下两层的来流参数. 出口只提数值边界条件. 上下边界均给无反射边界条件, 以保证边界的信息不会对剪切层主流产生影响. 对于5阶WENO格式, 3个子模板共涉及5个节点的信息. 对于边界部分的节点, 需要人为补充3个镜像点(ghost cells)来提供足够的网格点构造子模板.
2 -->

2.2.算例与网格无关性验证

采用Goebel-Dutton^[20]经典实验算例对本计算采用的数值格式进行验证. 为了将计算结果和Goebel-Dutton的实验结果相对比, 所有条件均与实验条件相对应, Goebel-Dutton实验来流条件如表2所列.

	速度 /m·s–1	马赫 数	密度 /kg·m–3	压力 /kPa	对流马 赫数Mc
上层 来流	519	2.04	1.00	46	0.2
下层 来流	409	1.40	0.76	46

表2Goebel-Dutton超声速混合层实验来流参数
Table2.Inflow parameters of supersonic mixing layer experiments conducted by Goebel and Dutton.

图2(a)对比了湍流发展到自相似区域时流场的时均速度剖面与Goebel-Dutton的实验结果, 其中ΔU = U₁ – U₂, U₁和U₂分别代表上下两层流体的速度. $ y^* $为纵向无量纲坐标,$ y^* = (y – y_0)/b $, y₀为流场y方向中心坐标, b为y方向对应速度值U = U₁ – 0.1ΔU和U = U₂ + 0.1ΔU之间的距离. 可以发现时均速度剖面与实验结果吻合的较好. 图2(b)对计算获得的流向脉动强度与实验结果进行了对比, 发现其结果同样具有较好的一致性. 通过对比流场的一阶量和二阶量验证了本次数值计算采用的DNS方法在模拟超声速混合层流场方面的有效性.
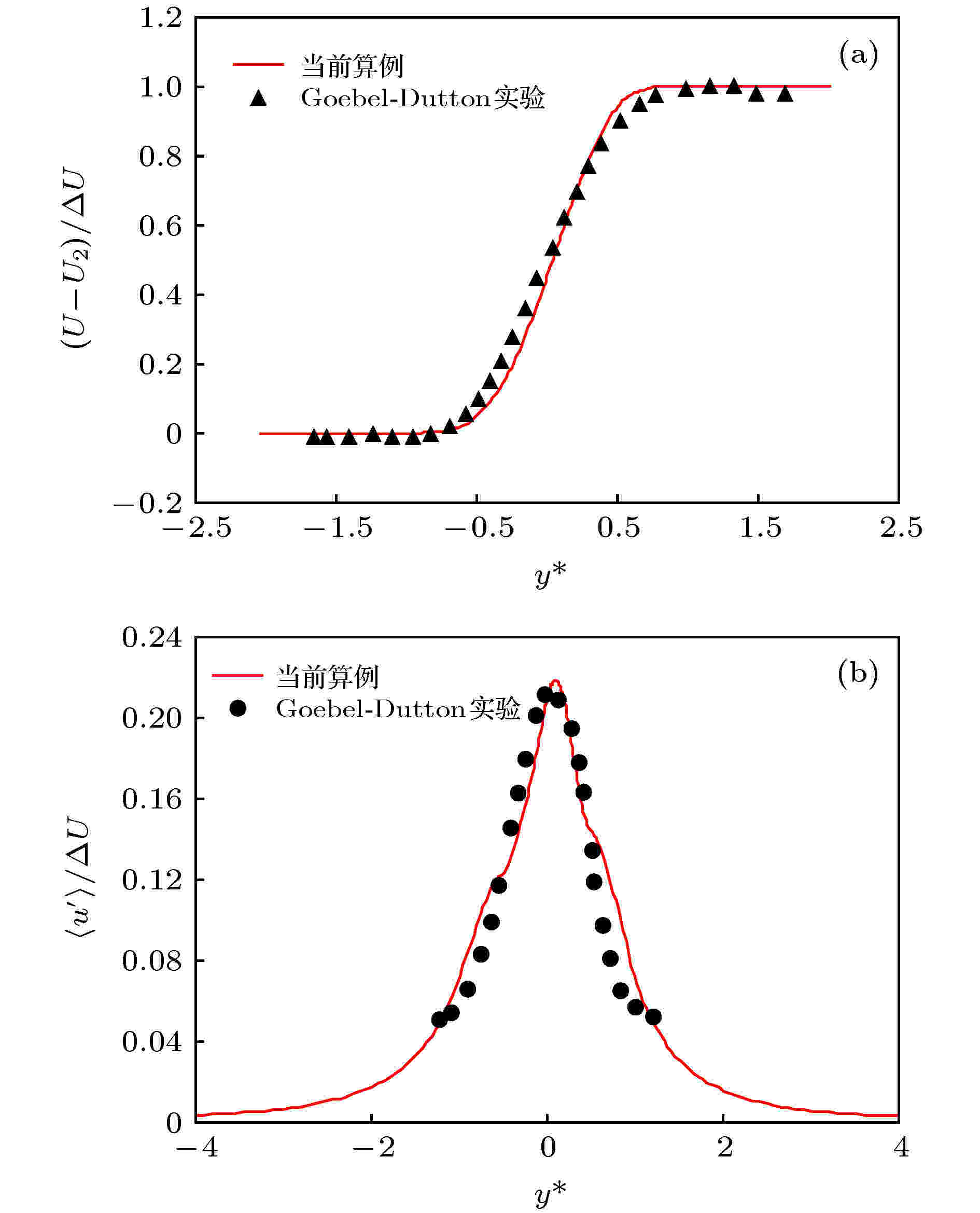图 2 数值与实验对比　(a) 时均速度; (b) 流向湍流强度
Figure2. Comparison between numerical and experimental results: (a) Mean velocity; (b) turbulent intensity.

此外为了进行网格无关性的验证, 本文采用了三套网格进行数值计算. 网格数量分别为960 × 240, 1440 × 240以及1920 × 240. 网格分布为流向均匀分布, 横向网格采用正切函数方式进行加密. 图3对比了不同网格条件下混合层的涡量厚度沿流向的变化情况. 涡量厚度${\delta _\omega }$定义为${\delta _\omega } = \Delta U/$${\left| {{\rm{d}}u/{\rm{d}}y} \right|_{\max }} $. 可以发现在1440 × 240以及1920 × 240 网格分布下, 混合层的涡量厚度沿流向的变化大体一致, 而在差网格条件下(960 × 240), 涡量厚度的变化与中等网格及精细网格条件下相差较大.
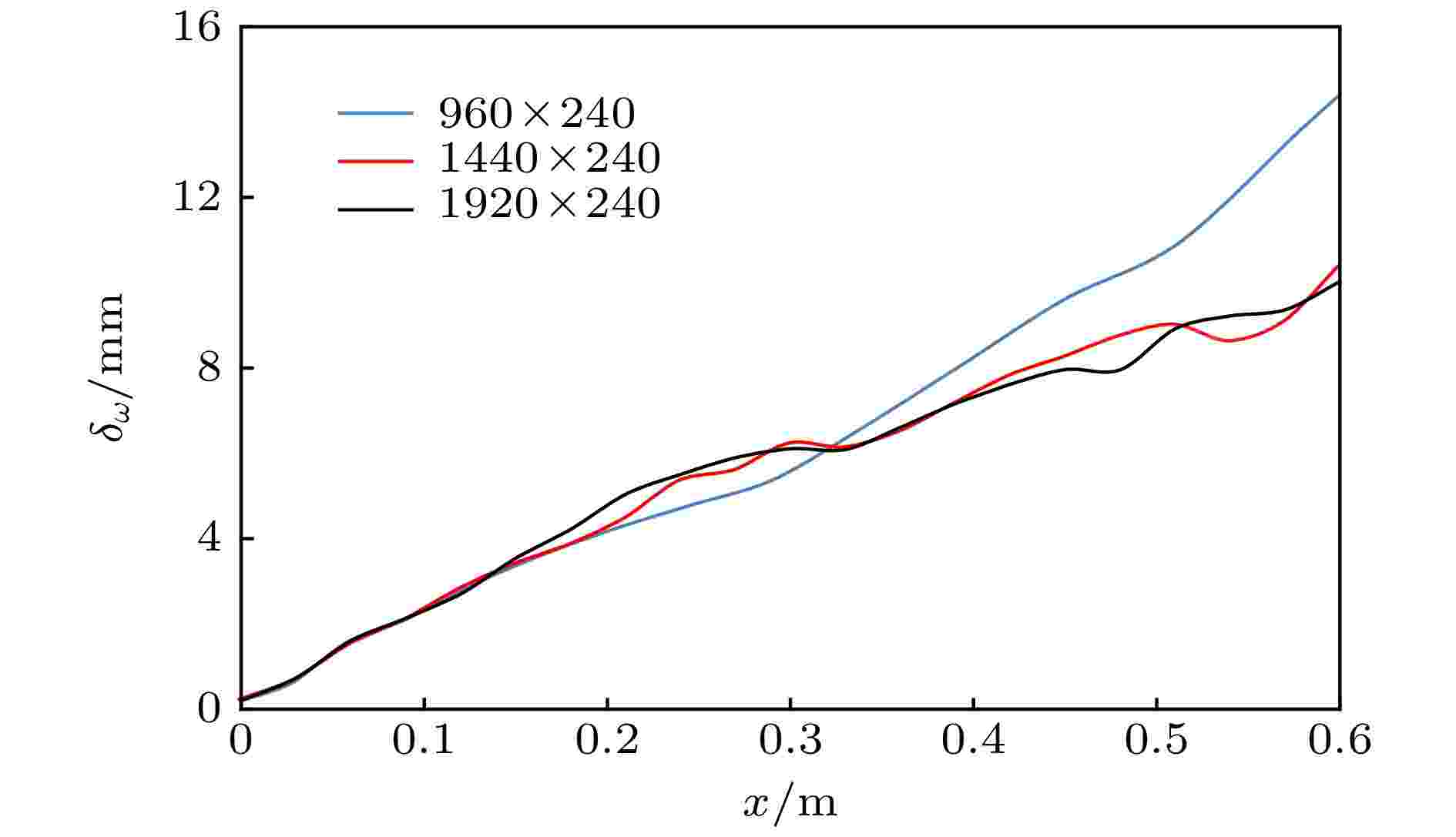图 3 不同网格条件下混合层的涡量厚度沿流向的变化
Figure3. Vorticity thickness variations versus stream wise direction for different mesh distributions.

此外, 对于一个可信的结果而言, 其最小网格尺度不能超过Kolmogorov尺度的几倍, 即最小网格尺度与Kolmogorov尺度至少在一个量级上^[19]. 可压缩剪切层剪切运动最剧烈的部分发生在剪切层的核心区域, 对于本文研究, 基于$\eta = {\left( {{\nu ^3}/\varepsilon } \right)^{1/4}}$获得的剪切层中心处的最小Kolmogorov尺度约为0.004 mm. 这里$\nu $和$\varepsilon $分别为动力黏性系数和湍动能耗散系数. 本文采用的网格在剪切层核心处的最小尺度为0.03 mm, 约为Kolmogorov尺度的7.5倍. 因此, 综合考虑计算精度和计算耗费资源, 本次计算采用1440 × 240的网格分布进行计算.
2 -->

2.3.激励方式

采用连续激励控制的方式来模拟对可压缩剪切层流场的周期性扰动. 采用的激励控制函数如下:

$f{'_{(y,t)}} = A \cdot C \cdot G(y)\sin (2{\text{π}}ft + \varphi ), $

式中, A为入口激励幅值, f为激励频率, $\varphi $为位于[–π, π]之间的随机相位. $G(y)$为y方向服从Y~N (0.1, 0.005²)的正态分布函数, 作用是来控制入流激励的影响区域, C为常数, 其取值依赖于G(y)的参数. 此处G(y)其表达式为

$G(y) = \frac{1}{{0.005 \times \sqrt {2{\text{π}}} }}{{\rm{e}}^{ - \frac{{{{(y - 0.1)}^2}}}{{2 \times {{0.005}^2}}}}}, $

则本文中C取值为$0.005 \times \sqrt {2{\text{π}}} $. 图4为连续控制信号的时序分布, 本次研究施加激励的周期T分别为50和200 μs, 分别对应于频率f为20和5 kHz. Grimshaw^[21]在其关于波涡作用理论的研究中指出, 相比于激励频率, 激励幅值的变化对剪切层流场结构演化的影响较小, 即频率的变化对流场结构的演化起主导所用. 因此本文并未针对振幅的变化进行研究.
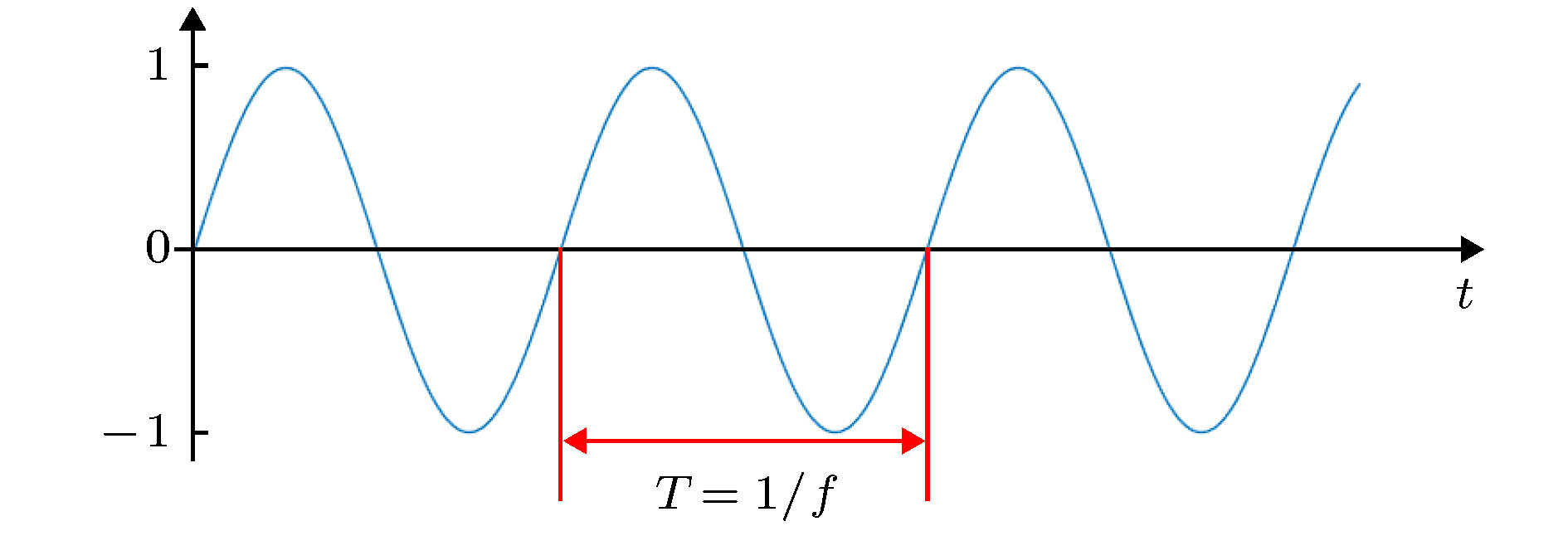图 4 连续控制信号分布
Figure4. Distribution of input continuous signal.

2

-->

3.1.流场可视化分析

为了和入流激励下剪切层的生长特性进行对比分析, 首先研究了可压缩自由剪切层流场结构的演化特性. 图5定性展示了自由剪切层中KH涡结构的演化过程. 流场区域采用横向半高H进行无量纲化, 涡量值采用来流对流速度U_c和入口动量厚度δ₍₀₎进行无量纲化. 由于剪切层涡量具有极大值, 速度分布具有拐点, 所以剪切层流动对于KH不稳定波的扰动是无黏不稳定的^[20]. 当流场中最不稳定模态幅值达到最大值时, 即在流场下游X/H = 0.3处, KH涡结构完成卷起. 同时, KH涡结构的生长是通过配对合并的方式来进行. 在时间间隔为200 μs内, 流场中的涡结构P和Q运动到P' 和Q' 的位置, 并且完成了配对与合并, 这种对并的方式是自由剪切层中KH涡结构的生长机理, 主导了剪切层的发展, ****Olsen和Dutton^[22]以及Zhang等^[23,24]也证实了这一生长机理的存在. 此外, 图5也定性地反映了自由剪切层是通过近似线性增长的方式来实现上下两层流体的掺混.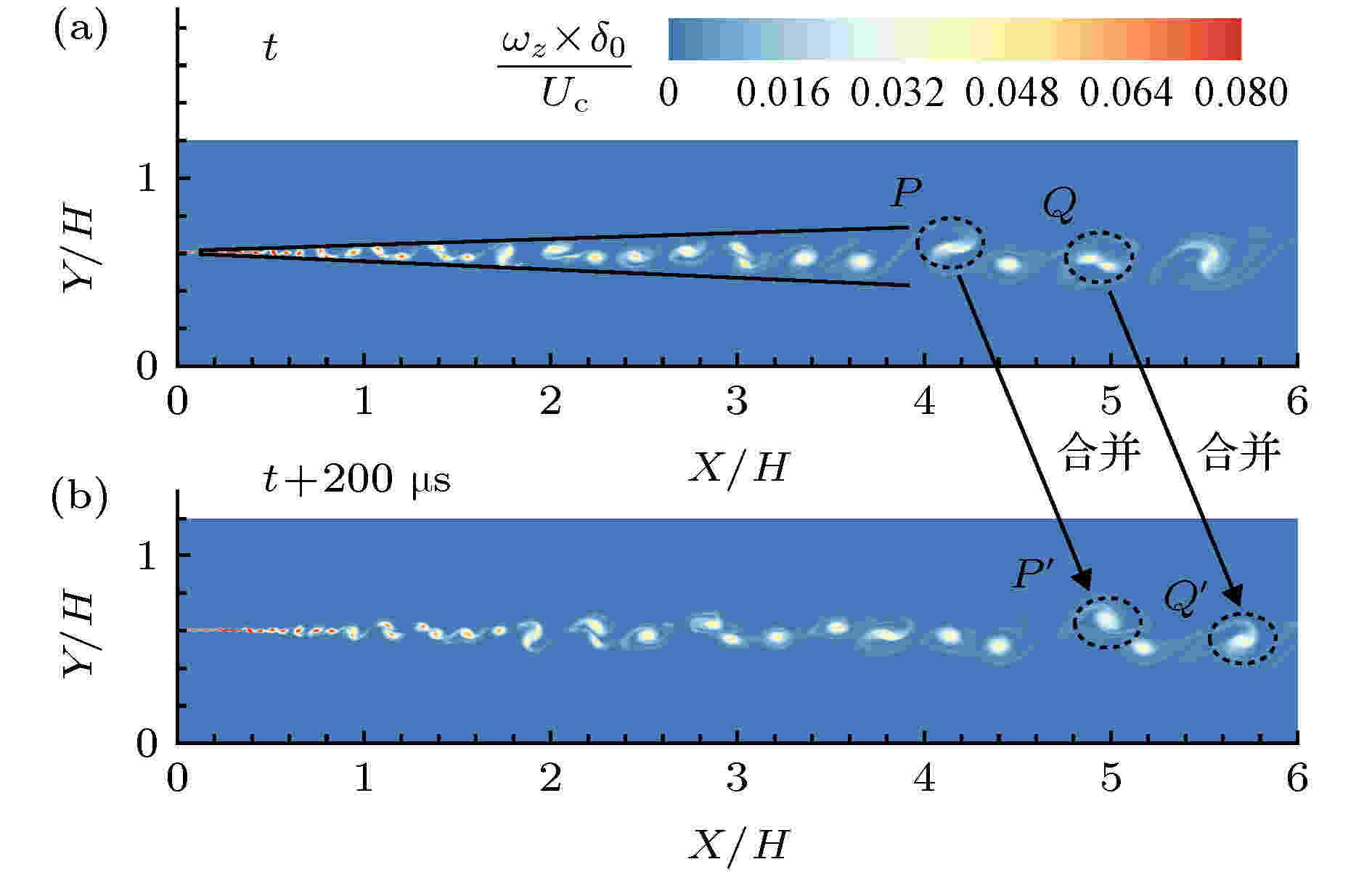
图 5 自由剪切层流场涡结构分布
Figure5. Distribution of vortex structures of free shear layers.

图6为高频入流激励(f = 20 kHz)条件下剪切层涡结构的分布, 上下两幅图的时间间隔为20 μs. 在高频激励下, 剪切层在下游X/H = 0.4处完成涡结构的卷起, 并且涡结构的尺寸很快达到饱和, 在流场向下游演化过程中, 涡结构始终保持饱和状态, 这种流动现象的出现说明流场中涡结构与入口扰动波发生了共振, 这一现象最早由Ho和Huang^[9]在不可压低速剪切层流动中发现, 此处在可压缩剪切层中也发生了这一共振效应. 此外, 在时间间隔为20 μs范围内, 涡结构并没有出现自由剪切层中通过“对并”来生长的现象, 而是自第一个涡结构卷起后, 即维持其饱和尺寸状态往下游发展.
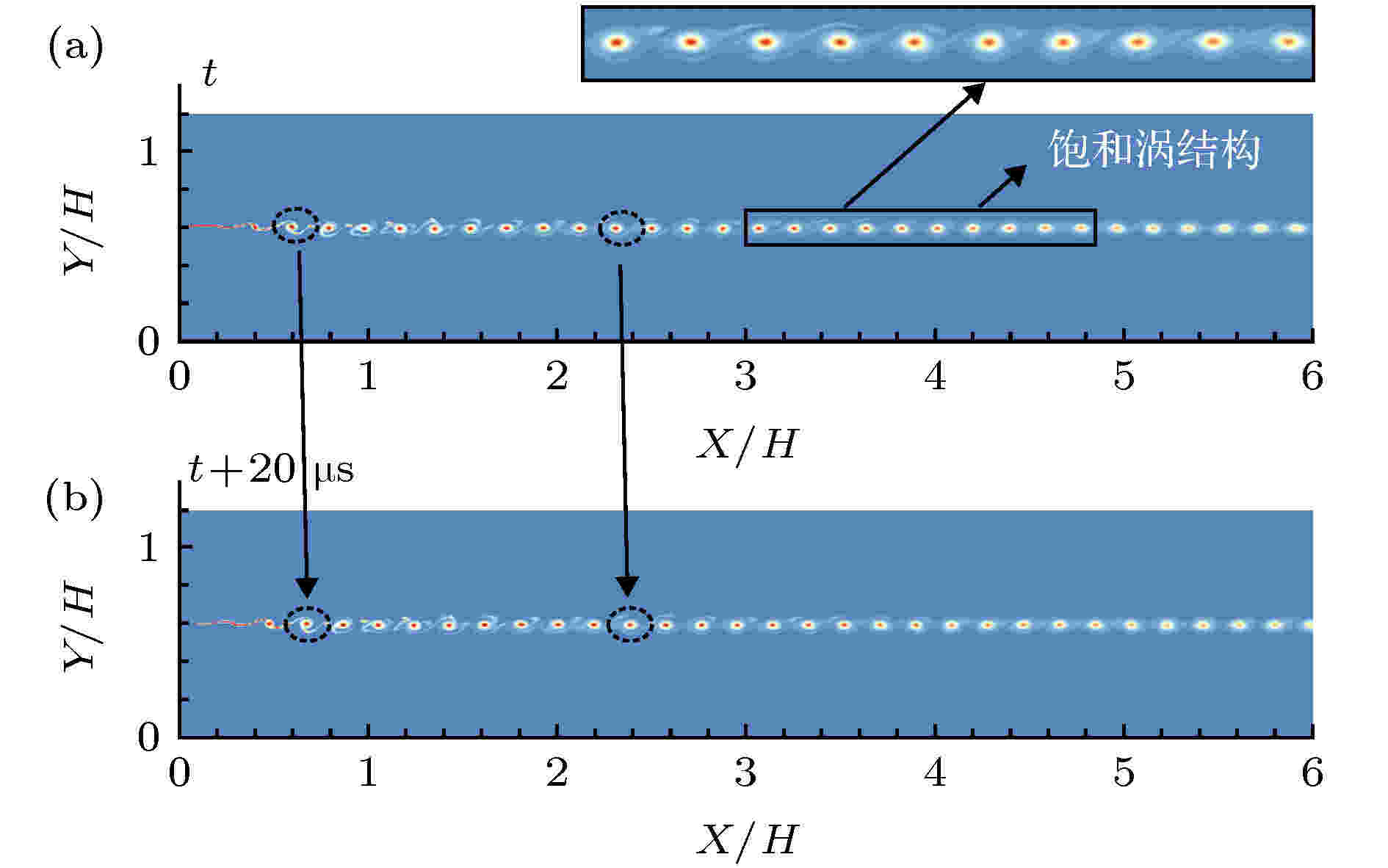图 6 高频入流激励下流场涡结构的分布 (f = 20 kHz)
Figure6. Vortex structures distribution under inlet forcing with high frequency (f = 20 kHz).

由于涡结构的尺寸在整个流场中保持一致, 因此有必要对其进行分析, 探究涡尺度与入流激励之间是否存在定量关系. 由于涡核处压力存在极小值^[14], 因此只要获得流场中的压力分布即可得到流场的涡结构尺寸. 这里定义涡尺寸为两个相邻涡核之间的距离λ. 图7为n = 10个涡核区域范围内的压力分布, 采样点的位置均位于横向Y/H = 0.6处. 涡尺寸可以用下式获得:
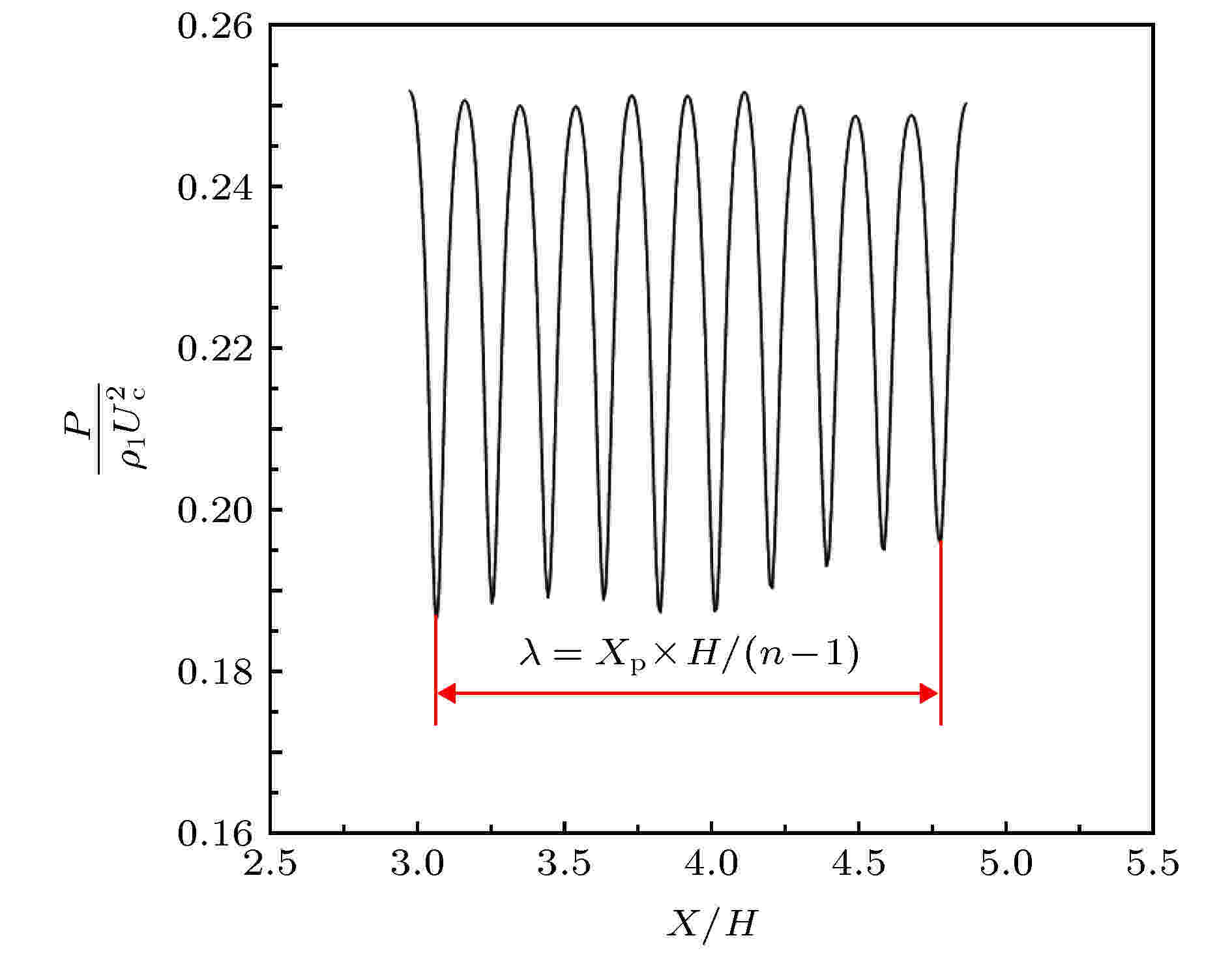图 7 流场涡核之间的压力分布
Figure7. Pressure distribution between the vortex core in the flow field.

$\lambda = {X_{\rm{p}}} \times H/(n - 1), $

其中X_p为10个涡核之间的无量纲距离, X_p = 1.706, 通过计算可得基于流场可视化得到的涡尺寸λ = 18.96 mm. 此外, Ghoniem和Ng^[25]研究表明, 剪切层流场内的特征涡尺度λ_v可以表达为

${\lambda _{\rm{v}}} = {{{U_{\rm c}}}/{{f_{\rm{v}}}}}, $

其中

${U_{\rm{c}}} = \frac{{{a_2}{U_1} + {a_1}{U_2}}}{{{a_1} + {a_2}}}, $

式中, U_c为剪切层的对流速度, a₁和a₂分别为上下两层的当地声速, 其值可通过 (1)式的声速关系式求得. f_v为流动的某种特征频率, 这里取f_v为入流激励频率, f_v = 20 kHz. 通过计算可得特征涡尺度λ_v为19.25 mm, 可以发现基于入流激励频率计算得到的涡尺度λ_v与λ相差在2%范围之内, 因此研究结果表明均匀分布的涡结构的尺寸近似等于对流速度与入流激励频率之比.
为了进一步验证此结论的正确性, 采用快速傅里叶变换(fast Fourier transform, FFT)提取了剪切层流场下游X/H = 1和4处的频谱分布, 采样点的位置均位于横向Y/H = 0.6处, 结果如图8所示. 与自由剪切层中存在各种谐波扰动不同, 高频激励下剪切层的流场特征频率锁定在20 kHz, 这正是入流激励施加的频率. 在X/H = 1处, 流场中仍然存在着少许呈规律分布的高频扰动波, 如图8(a)中黑色虚线框中所示. 随着流场向下游发展, 在X/H = 4处, 这种高频成分已经完全消失. 其原因在于, 入流高频激励在和剪切层固有的KH不稳定波相互作用过程中占据主导地位, 使得KH不稳定诱导的各种不稳定模态波在来流初始剪切处就开始被抑制. 随着流动的发展, 高频激励完全控制着涡结构的发展并实现了锁频的作用.
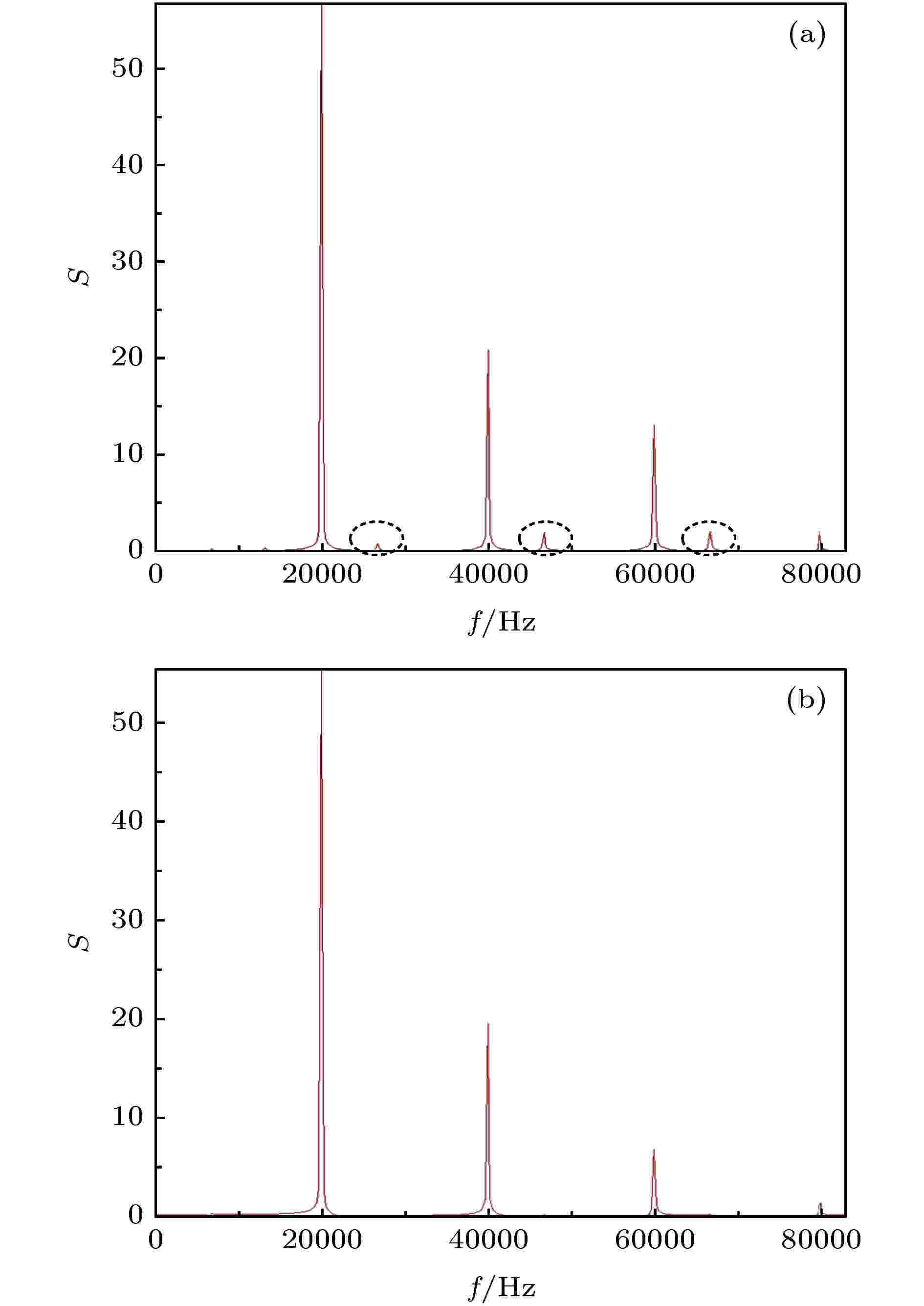图 8 高频入流激励下频谱分布 (f = 20 kHz)　(a) X/H = 1; (b) X/H = 4
Figure8. Frequency spectrum distribution under inlet forcing with high frequency (f = 20 kHz): (a) X/H = 1; (b) X/H = 4

为了进一步探究完善涡结构生长特性与不同入流激励条件之间的关系, 有必要分析低频激励下涡结构的运动特性. 图9展示了f = 5 kHz时剪切层流场的可视化结果, 图9(a)和图9(b)时间间隔为100 μs. 在100 μs的时间间隔内, 并没有出现自由剪切层中通过涡结构配对合并来实现剪切层增长的现象, 而是出现了一种新的涡结构生长方式: 在流场下游X/H < 2范围内, 出现了一串由KH不稳定波诱导的涡结构剪切带, 在X/H = 2处, 入流激励诱导的涡核开始出现, 外围剪切带围绕着涡核旋转并逐渐被涡核吞噬 (engulfment), 实现剪切层涡结构的生长. 这种吞噬的生长机制使得涡结构在剪切层近场处就能实现其尺寸的快速增长. 吞噬过程完成后, 涡结构达到饱和, 在向下游演化过程中其尺度不再变化, 剪切层的厚度近似呈现出先线性增长, 后保持不变的特性.
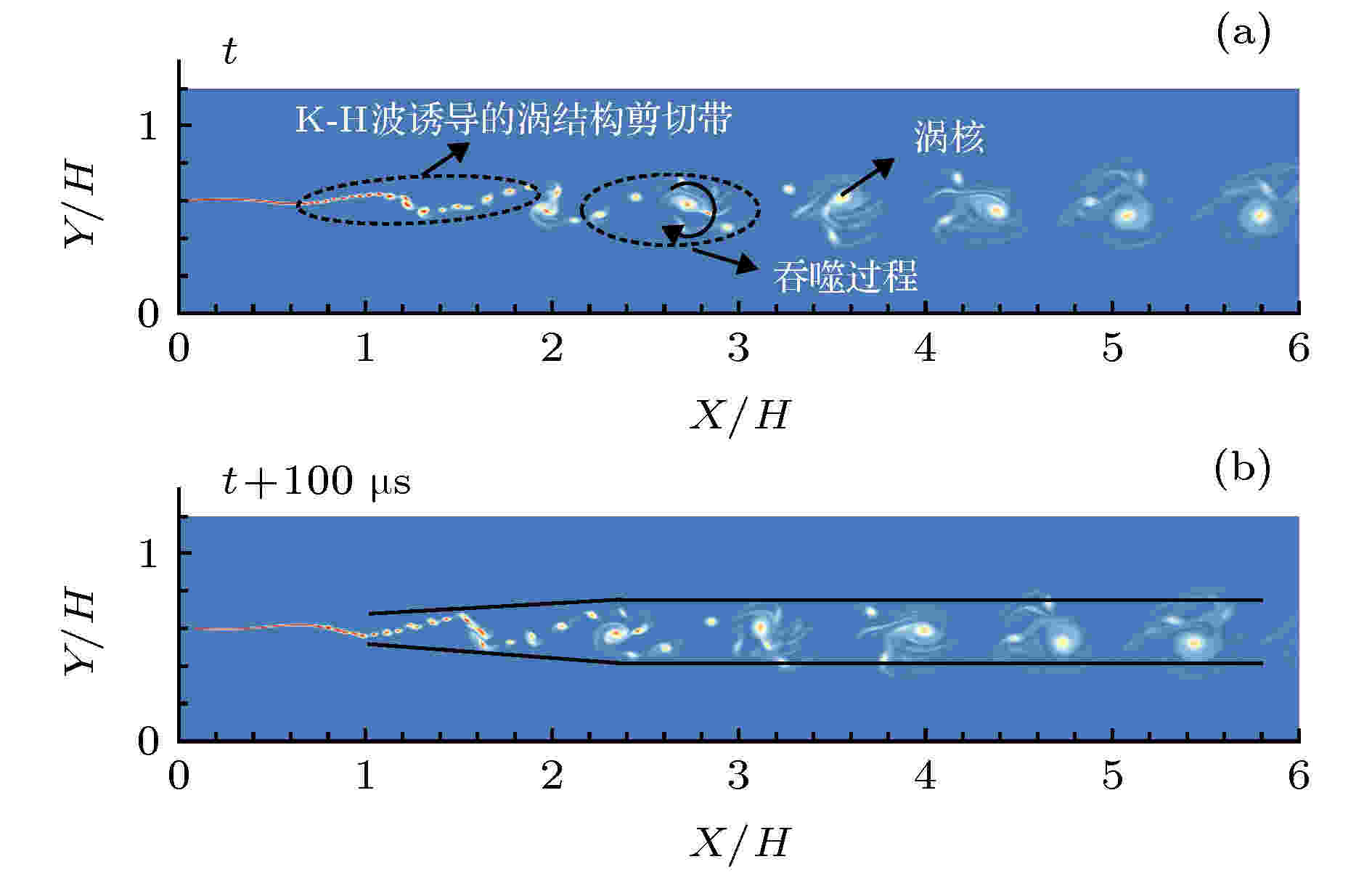图 9 低频入流扰动下剪切层流场涡结构分布 (f = 5 kHz)
Figure9. Vortex structures distribution under inlet forcing with low frequency (f = 5 kHz).

图10提取了低频激励下流向X/H = 1, 4, 横向均为Y/H = 0.6两处的流场速度振荡频谱分布. 在X/H = 1处, 入流激励频率及其倍频成分的幅值都很大, 基频5 kHz并没有完全突显出来, 在流场下游X/H = 4处, 入流激励实现了对流场涡结构的控制, 涡结构运动的频率锁定在5 kHz. 此外, f = 20 kHz的高频激励下流动近场处 (X/H = 1)的高频扰动波成分较少, 而f = 5 kHz时流动近场 (X/H = 1)处的高频扰动波成分显著增多, 表明相比于低频激励, 入流高频激励能够更快地实现对流场结构演化的主导和控制.
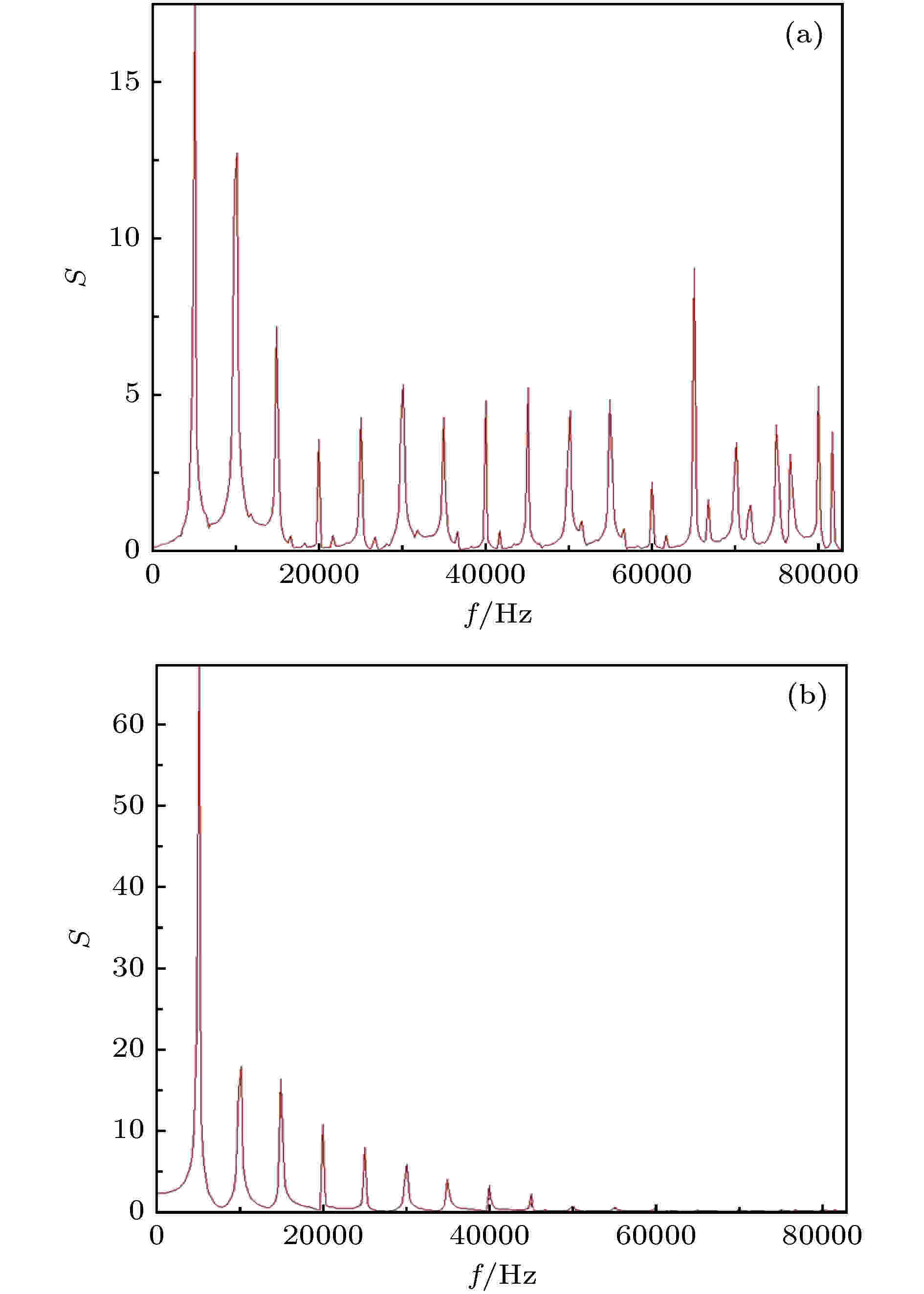图 10 低频入流激励下频谱分布 (f = 5 kHz)　(a) X/H = 1; (b) X/H = 4
Figure10. Frequency spectrum distribution under inlet forcing with low frequency (f = 5 kHz): (a) X/H = 1; (b) X/H = 4

为了更好地揭示低频激励下中间涡核对于外围剪切带的吞噬作用, 图11给出了流场中涡结构的动态演化过程. t = 0至t = T_ω对应于一个完整的吞噬过程. 在中间高速旋转的大涡M的作用下, t = 0时刻从剪切带脱落的KH涡N进入大涡M的作用区域, 直至t = T_ω被完全吞噬, 从而实现了涡结构尺寸的增长. 与自由剪切层中KH涡结构通过配对合并实现增长不同, 在整个吞噬过程中, 涡N的形状逐渐变得狭长, 而中间涡M的形状则保持的较好. 这表明中间大涡结构对于整个吞噬过程起主导作用. 此外, 另一个重要现象是中间大涡可以同时吞噬外围剪切带的多个小涡结构. 在t = 0.2T_ω时刻, 涡结构R进入了中间大涡的影响区域, 高速旋转的大涡结构使得涡结构N和R在这个周期内均完成了吞噬过程.
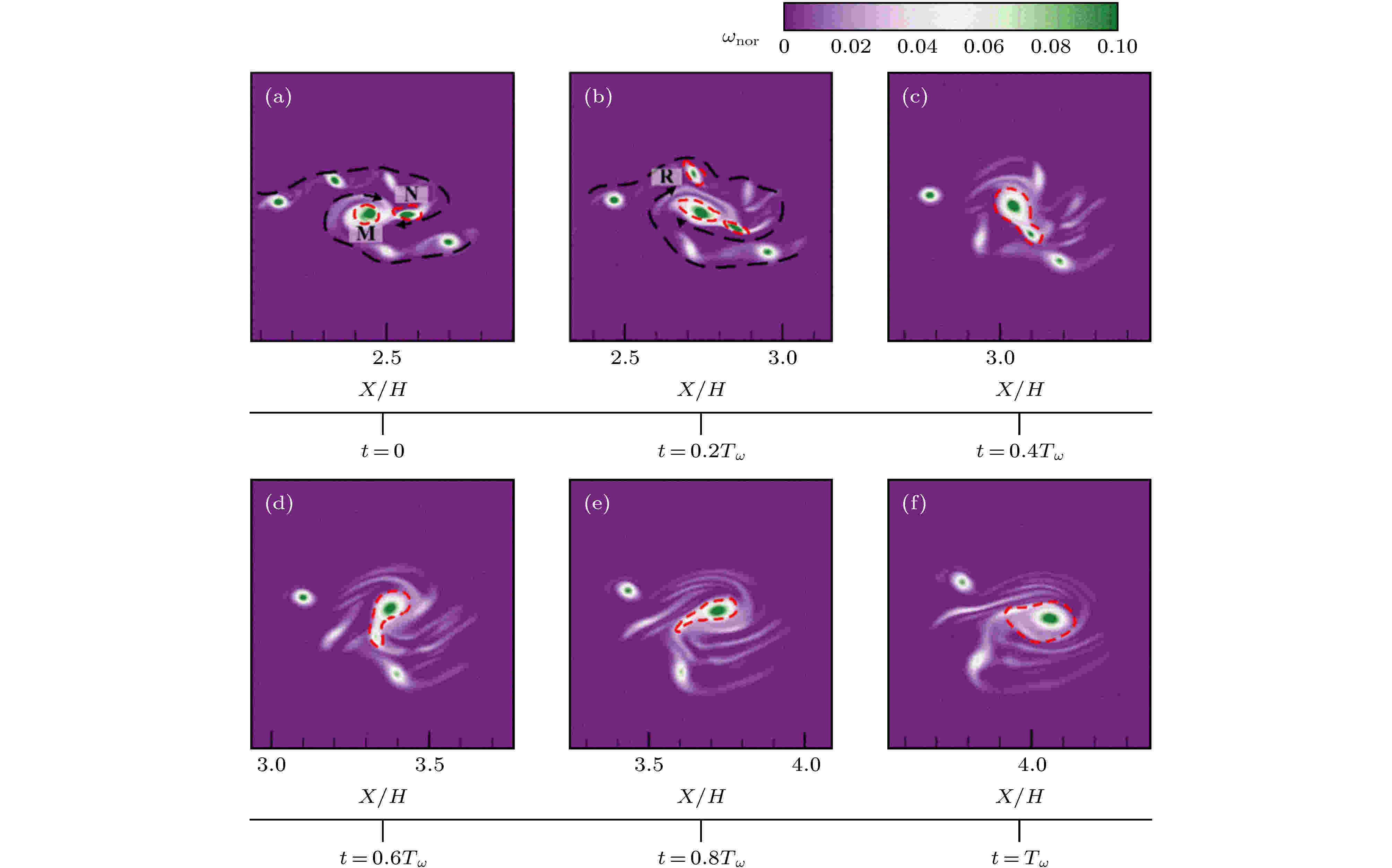图 11 涡结构的动态吞噬过程
Figure11. Dynamic engulfment process of vortex structures.

2 -->

3.2.KH涡增长特性

入流激励下KH涡结构展现出了独特的生长特性, 而与流场中拟序结构密切相关的剪切层必然也会呈现出不同的增长特性, 本文采用KH涡量厚度指标研究了涡结构生长对剪切层厚度的影响. 图12为自由剪切层和入流激励下剪切层涡量厚度随流向距离的分布. 在自由剪切层中, 涡量厚度呈现出近似线性增长的特点, 这与图5体现出的趋势相一致. 高频激励下(f = 20 kHz), 剪切层在经历入流的剪切过程后, 其涡量厚度值在涡结构达到饱和后, 稳定在3—4 mm之间, 表明高频扰动下, 无论是剪切层的近场区域还是远场区域, 其混合效果都没有得到改善. 低频激励下(f = 5 kHz), 在剪切层的近场区域, 剪切层的厚度快速增长, 涡核的吞噬作用明显促进了来流的混合. 在图12中蓝色虚线框中的分界处, 剪切层涡量厚度达到饱和. 在剪切层的远场处, 剪切层的涡量厚度稳定在12—14 mm之间, 入流周期性低频激励下(f = 5 kHz)剪切层的演化呈现出先加速增长, 后平稳过渡的特性.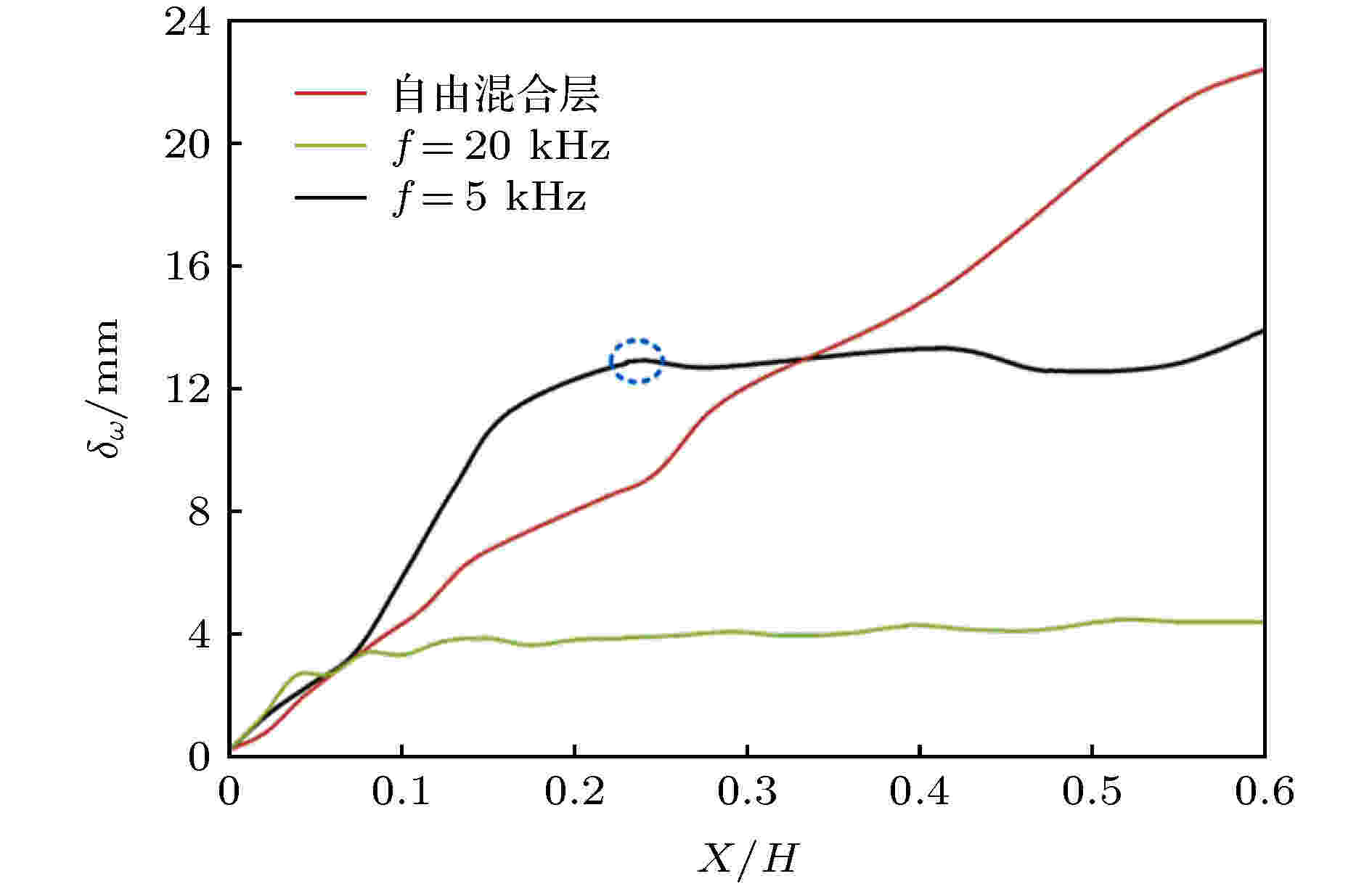
图 12 剪切层涡量厚度随流向距离的分布
Figure12. Vorticity thickness distribution versus streamwise direction.

2 -->

3.3.空间相关性分析

为了对可压缩剪切层的涡结构大小、形状以及结构角进行定量分析, 进一步明晰入流激励下涡结构的动力学特性, 本文基于计算结果, 采用空间两点相关性分析的方法, 研究了流向速度脉动在X-Y平面的空间相关系数分布, 采用的计算公式为

$\begin{split} & {C_{uu}}({x_0},\Delta x,{y_0},\Delta y) \\= \, & \frac{{u'({x_0},{y_0}) \cdot u'({x_0} + \Delta x,{y_0} + \Delta y)}}{{\sqrt {u'{{({x_0},{y_0})}^2}} \cdot \sqrt {u'{{({x_0} + \Delta x,{y_0} + \Delta y)}^2}} }}, \end{split}$

式中, (x₀, y₀)为相关性计算的参考点, u'代表流向速度的脉动均方根值. Bourdon和Dutton^[26]对两点相关性分析参数的研究表明, 当样本数为500左右时能够确保统计结果的稳定性.
图13为自由剪切层取不同流向和竖向参考点(X₀, Y₀)位置时的相关性分布, 图13(a)—(d)的参考点无量纲坐标分别为(1.5, 0.6), (2.4, 0.6), (3.5, 0.6), (5.1, 0.6). 定义中心点的值为1, 等值线从中心点向外围以0.05的间隔递减, 最外围等值线的数值为0.8.
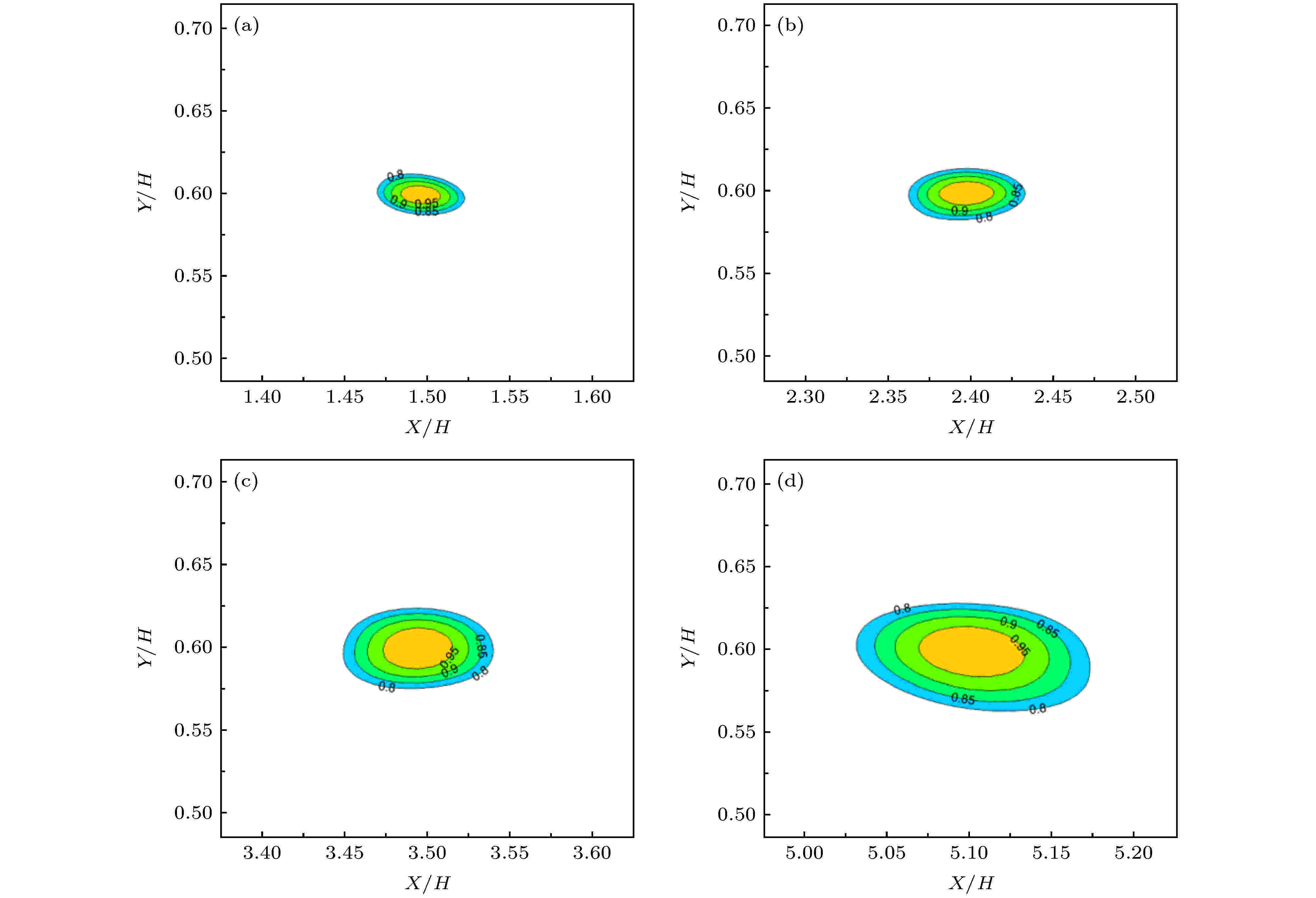图 13 自由剪切层中不同流向位置处空间相关性分布　(a) (1.5, 0.6); (b) (2.4, 0.6); (c) (3.5, 0.6); (d) (5.1, 0.6)
Figure13. Spatial correlation distributions of free shear layers in different streamwise positions: (a) (1.5, 0.6); (b) (2.4, 0.6); (c) (3.5, 0.6); (d) (5.1, 0.6).

在自由剪切层相关系数的等值线分布图中, 等值线的轮廓呈现出饱满的椭圆形. 同时随着流向距离的增加, 流场相关区域的面积增加. Bourdon和Dutton^[26]通过实验发现, 等值线代表拟序结构的平均结构, 因此随着流场往下游发展, 自由剪切层涡流场结构尺寸近似呈现出线性增长的趋势, 这与图12中自由剪切层的涡量厚度沿流向的分布相一致.
为了进行对比分析, 图14给出了入流低频激励下(f = 5 kHz)不同参考点处的空间相关系数分布, 图14(a)—(d)的参考点无量纲坐标分别为(2.0, 0.6), (2.7, 0.6), (3.5, 0.6), (5.1, 0.6). 与自由剪切层不同的是, 在(2.0, 0.6)和(5.1, 0.6)处, 流场结构呈现出饱满的椭圆形, 而在(2.7, 0.6)和(3.5, 0.6)处, 流场结构则趋于狭长的椭圆形. 对比图9可以发现, 在流向区域X/H = 2—4之间, 中间大涡结构通过吞噬一串外围剪切带来实现涡结构的生长. 与自由剪切层相比, 在这种新的涡结构生长机制下, 相关性系数分布的椭圆结构特性和结构角有着本质的变化. 对比图14(a)和图14(d), 发现经过中间大涡的吞噬作用后, 涡结构的尺寸实现了增长, 剪切层的厚度实现了增加.
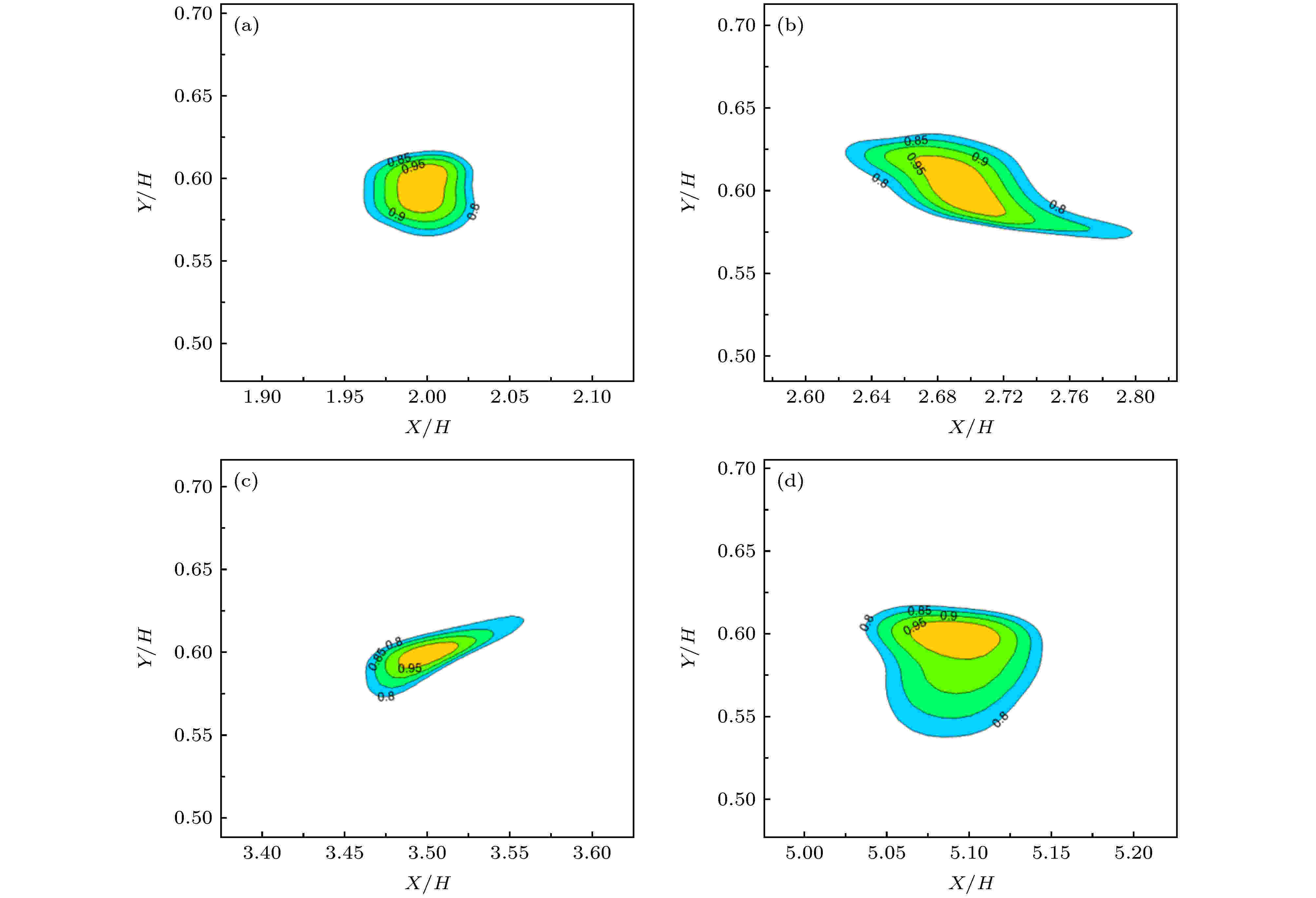图 14 低频激励下不同流向位置处空间相关性分布　(a) (2.0, 0.6); (b) (2.7, 0.6); (c) (3.5, 0.6); (d) (5.1, 0.6)
Figure14. Spatial correlation distributions with low frequency forcing in different streamwise positions: (a) (2.0, 0.6); (b) (2.7, 0.6); (c) (3.5, 0.6); (d) (5.1, 0.6).

Wu等^[27]的研究指出, 可以采用最小二乘拟合的方法对相关性分布的外围等值线进行椭圆拟合, 从而获得涡结构的大小和结构角分布. 本文对外围0.8等值线进行椭圆拟合, 如图15所示. 得到的椭圆长轴2d为相关性计算得到的拟序结构大小, α为结构角, α定义为拟合后椭圆长轴与流向的夹角.
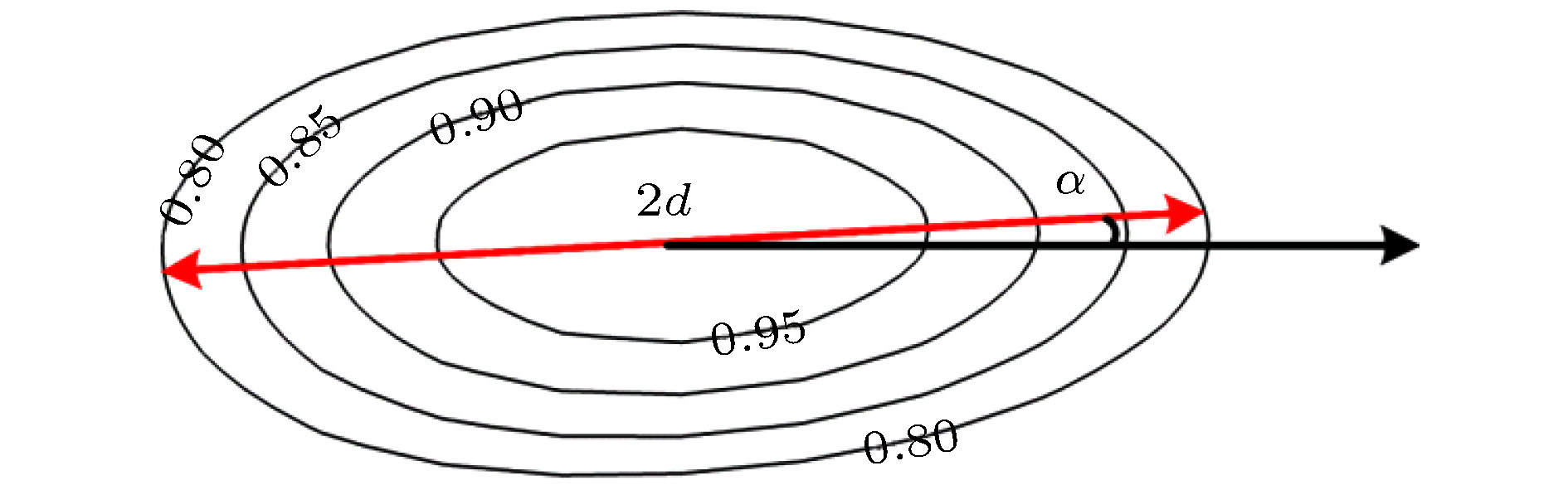图 15 拟序结构的大小和结构角示意图
Figure15. Schematic of vortex size and structure angle.

图16为通过椭圆拟合得到的自由剪切层和入流低频激励下 (f = 5 kHz)剪切层在不同参考点处无量纲结构大小δ_non的分布, 以自由剪切层在(1.5, 0.6)处的结构尺寸为1. 可以发现自由剪切层中, 由相关性分析得到的结构大小沿流向近似呈线性增长的趋势, 这与图12得到的自由剪切层涡量厚度的变化趋势相一致. 而低频激励下, 流向下游无量纲位置X/H = 2和2.7处结构尺寸的变化是先从1.31快速增长到3.17左右, 然后在X/H > 2.7时, 流场结构的大小逐步减小, 并在远场处维持在2.0左右. 结合上文分析的低频激励下涡结构的生长机理不难发现, X/H = 2.7位置附近正是中间大涡吞噬外围剪切带的区域, 吞噬作用是导致涡结构尺寸快速增长的重要原因.
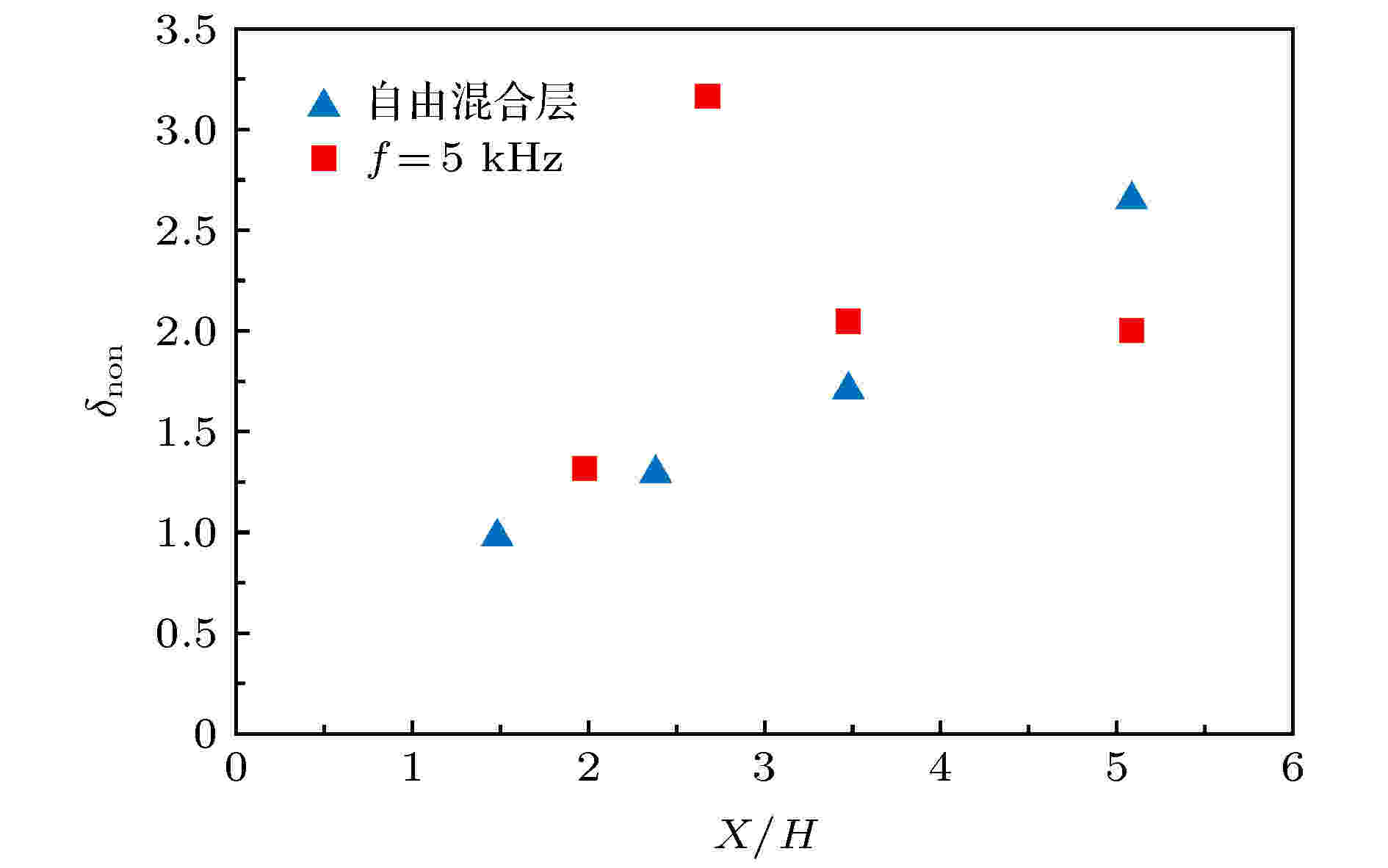图 16 无量纲结构大小沿流向的分布
Figure16. Non-dimensional structure size distribution versus streamwise direction.

图17给出了不同流向位置处自由剪切层和低频激励 (f = 5 kHz)剪切层的结构角分布. 自由剪切层中结构角沿流向的变化起伏较小, 这是由于无外加扰动的自由剪切层完全依靠涡结构的配对与合并来实现剪切层的增长, 这种近似线性的增长方式使得布置在剪切层核心发展区的参考点结构的旋转特性较为微弱. 而低频激励下结构角呈现出不同的变化趋势. 在近场X/H = 2处, 结构角较小; 在下游X/H = 2.7以及X/H = 3.5处, 流场结构表现出强烈的倾斜和旋转特性, 结构角分别达到157°和24°. 结合图14(b)和图14(c)中相关性系数在(2.7, 0.6)和(3.5, 0.6)处的分布可以发现, 在流场吞噬作用发生的区域, 外围剪切带被中间大涡吞噬使得流场结构的倾斜特征变得明显. 同时, 结构角的大小在X/H = 2.7, X/H = 3.5以及X/H = 5.1的变化趋势表明, 中间大涡对外围剪切带的顺时针吞噬作用是入流低频激励下剪切层实现增长的重要机理.
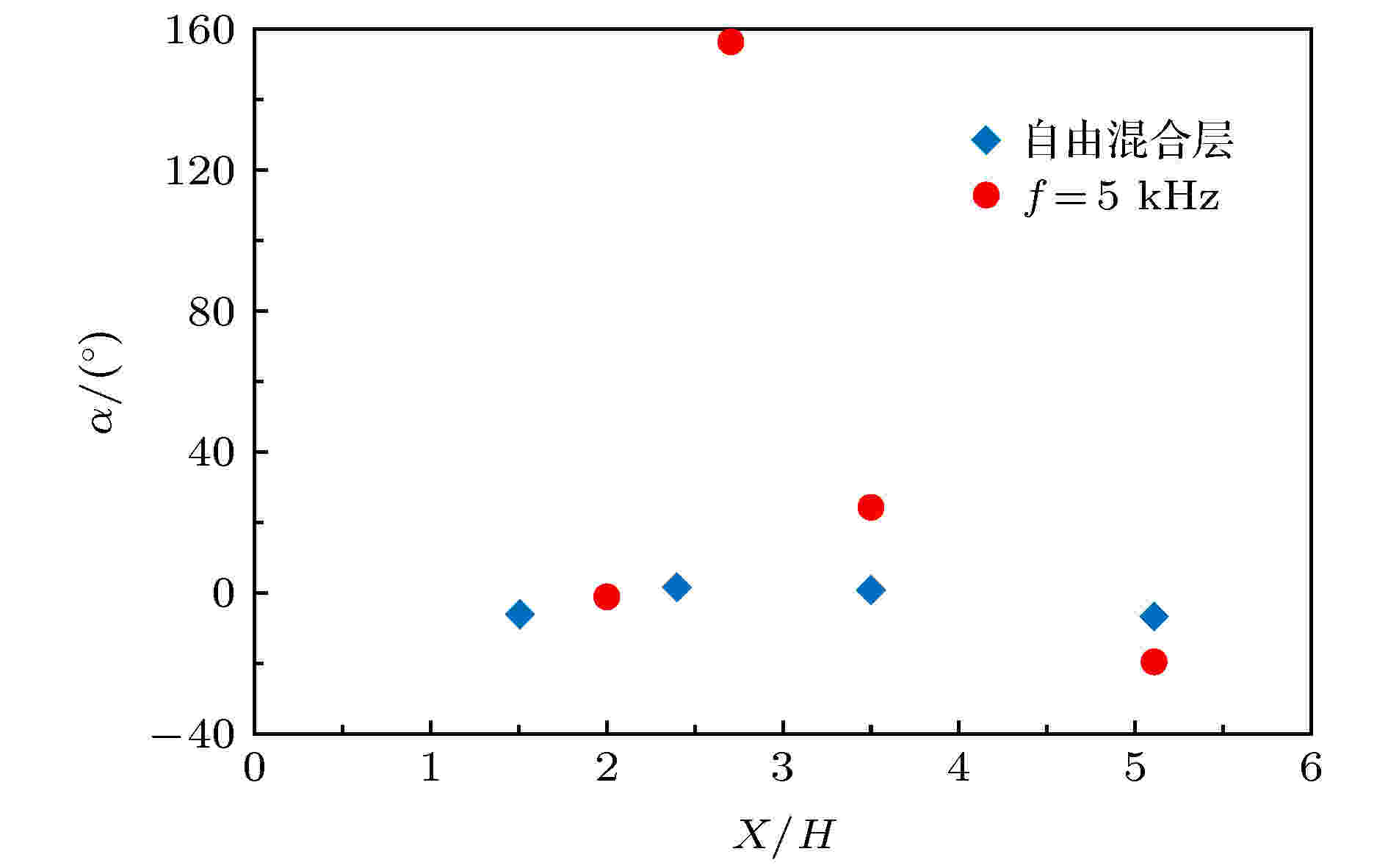图 17 结构角沿流向的分布
Figure17. Structure angle distribution versus streamwise direction.

通过直接数值求解Navier-Stokes方程, 研究了入流激励下可压缩剪切层中KH涡结构的响应特性. 计算结果清晰地展示了自由剪切层和入流激励下剪切层的流场拟序结构及其动态演化过程. 采用KH涡量厚度指标定量分析了剪切层的增长特性. 基于流动可视化结果, 结合空间相关性分析探究了流场结构尺寸和结构角分布, 揭示了入流激励下剪切层的混合特性及其涡结构的独特生长机理.
自由剪切层中, 流场KH涡结构通过配对与合并的方式实现涡结构的生长, 上下两层流体是通过近似线性增长的方式来实现掺混. 在入流高频激励下(f = 20 kHz), 涡结构在下游X/H = 0.3处卷起后很快达到饱和状态, 并且维持其饱和尺度往下游发展, 剪切层的厚度值稳定在3—4 mm之间, 这种由涡结构与入流扰动波发生共振效应导致的现象最早在Ho和Huang^[9]研究的不可压低速剪切层中发现. 此外高频激励下, 均匀分布饱和涡结构的尺寸近似等于对流速度与入流激励频率之比. 同时在流场下游, 入流高频扰动占据主导地位, 剪切层的流场特征频率锁定在20 kHz.
入流低频激励下(f = 5 kHz), 流场可视化结果表明拟序结构的生长是通过中间大涡的吞噬作用来实现, 这种吞噬的生长机制使得在剪切层近场处就能实现涡结构尺寸的快速增长. 空间相关性分析表明, 与自由剪切层中等值线轮廓呈现出饱满的椭圆形不同, 在吞噬作用发生的区域 (2.7, 0.6)和(3.5, 0.6), 等值线轮廓趋于狭长的椭圆形. 同时结构角分析表明, 在下游X/H = 2.7以及X/H = 3.5处, 低频激励下流场结构表现出强烈的倾斜和旋转特性, 结构角分别达到157°和24°. 结构角在流向的变化趋势表明, 中间大涡对于外围剪切带的顺时针吞噬作用是入流低频激励下剪切层实现增长的重要机理.