摘要:研究了行人在能见度受限情况下的疏散行为, 考虑行人对环境的熟悉程度, 将行人分为熟悉环境人群和不熟悉环境人群. 对于房间内熟悉环境的行人, 改进势函数元胞自动机模型来模拟其疏散行为. 对于不熟悉环境人群, 分析其在视野范围内的跟随行为, 并制定了不同跟随行为策略, 来研究其跟随行为特性. 仿真模拟了房间内熟悉环境人群的人数占比、房间内的视野半径大小以及行人密度等参数, 研究其对行人疏散的影响, 比较不熟悉环境人群采取的跟随策略的优劣. 发现疏散时间的大小与房间内视野半径的大小和房间内熟悉环境者密度的大小有关. 其次, 跟随策略的有效性与视野半径的大小和熟悉环境者密度有关. 而且在单一策略环境下, 有着同样的规律. 这些发现能对大型公共场所如超市、体育馆的应急疏散情况提供一些启示, 有助于在视野受限情况下制定一些有效的指导策略.
关键词: 元胞自动机/
视野范围/
环境熟悉度/
行人疏散

English Abstract

全文HTML

--> --> -->

随着社会经济的不断发展, 商场、剧院、体育馆、博物馆、车站、机场、综合交通枢纽等大型公众设施也在不断地发展和完善, 这极大地丰富和方便了居民生活, 行人的出行频率也大大提高. 但是行人在建筑物内易受突发事件(如拥挤、踩踏和火灾等情况)的影响, 引起重大的群体事故. 因此, 建筑物内的行人疏散一直是交通研究者研究的热点问题之一.
目前, 科学家们先后提出了一系列各具特色的计算机仿真模型来研究建筑物内的行人疏散行为, 越来越多的微观仿真模型被应用在建筑物疏散中. 其中, 最为广泛应用的微观模型包括: 社会力模型^[1-5]、格子气模型^[6-8]和元胞自动机模型^[9-17]. Helbing等^[1-4]提出的社会力模型是一个连续的仿真模型, 它研究了恐慌情形下行人的疏散行为, 发现了行人的自组织现象、出口处行人的聚集与成拱现象和快即是慢效应. Burstedde等^[12]提出的元胞自动机场域模型也能较好地模拟行人动态的聚集效应和自组织现象. 目前, 大多数模型都是在此基础上进行改进研究, 来模拟行人的疏散过程.
目前, 有部分研究者开始研究能见度受限情况下行人的疏散行为, 即考虑房间内部能见度的大小和行人对房间的熟悉程度. Hou等^[18]和Ma等^[19,20]建立社会力模型来研究有限能见度下行人的领导作用, 认为有效的领导力与视野半径范围的大小息息相关, 在有限能见度下行人的领导对疏散影响是双重的. Guo等^[21]通过真人疏散实验建立了零能见度下的元胞自动机模型, 仿真表明在零能见度条件下的行人速度约为正常能见度情况下行人速度的一半, 并且认为疏散演习有助于提高零能见度条件下行人疏散的效率. Frank和Dorso^[22]以及Wang和Cao^[23]都考虑了在视野受限的房间内, 行人疏散过程的不同行为(包括放牧、沿墙壁行走等). Li等^[24]建立了考虑视野受限的元胞自动机模型来分析视野半径对疏散行人的影响, 认为疏散时间依赖于房间内的初始密度和视野半径. Li和Han^[25]研究疏散房间内行人的环境熟悉程度和积极性行为来分析对疏散时间的影响, 认为疏散时间随着疏散人员对疏散路线熟悉程度的增加而呈指数下降.
而研究者们对疏散过程中行人的跟随行为研究较少, 大多数研究都是关于领导者和导游对行人的领导作用. 在社会力模型中, Hou等^[18]建立了具有领导效应的社会力模型来研究领导者对普通行人的领导作用, 研究了疏散领导者的数量和位置对能见度有限的疏散动力学的影响, 认为更多的领导者促使单出口房间的疏散更快, 但是一个或两个受过训练的领导者也足以加速动态疏散. Ma等^[19,20]改进社会力模型来研究人群疏散过程中的领导行为, 认为领导者和导游并不是越多越好, 一小部分领导者已经足以有效地引导整个人群. 而在元胞自动机模型中, 典型的楼层元胞自动机模型^[12]的主要思想是基于仿生学来捕捉行人的放牧行为, 以及在疏散过程中寻找最短路径的行为. 在双向行人流的研究过程中, Zhang^[26]改进势函数元胞自动机模型分析了双向行人流的跟随行为、推动行为和避让行为, 仿真结果显示改进模型更能表现行人合理性和多样性, 而且更能反映集体行为特征. Guo等^[27]建立了势函数模型来分析行人跟随行为和避碰行为的元胞自动机模型, 对双向行人流进行了仿真研究, 认为对于渠道的形成, 避碰行为更优于跟随行为. 在房间内行人疏散情况中, Yuan和Tan^[28]改进了元胞自动机模型, 模拟了行人“随流流动”的现象, 认为引导者的能见度和数量能显著影响疏散时间. 而Lu等^[29]改进场域模型来研究行人小团体的领导者-跟随者行为规则, 能够很好地捕获疏散过程中群体移动的特征, 并成功预测总疏散时间. Wang等^[30]建立了扩展的场域模型来研究疏散助手的位置和数量对行人疏散的影响, 建立了信息传递场表示对行人的领导作用, 认为在疏散出口的疏散助手更能有效地领导行人的疏散, 而过多的疏散助手并不能提高疏散效率. Fang等^[31]建立了基于代理的跟随者模型, 提出了一个领导者-跟随者模型来解释社会集体行为, 并且建模了逆流、排队行走和集体移动三种场景.
2012年, Zhang等^[16]建立了势函数场元胞自动机模型, 该模型考虑了行人的行走时间和周围行人引起的不适成本, 以便行人移动到空的相邻元胞. 移动产生的费用将简单地测量当前元胞和目的地之间的距离, 类似于场域模型中的静态场^[12]. 同时又考虑行人的行程中的负舒适度(周围密度的增函数), 而负舒适度的作用类似于场域模型中的动态场^[12]. 2014年, Jian等^[17]提出了一种感知的势函数元胞自动机模型, 该模型考虑聚集力场和可视度的影响, 得到考虑聚集力场的预测费用势函数场模型, 并合理再现了有瓶颈或转角区域内的行人流现象. 本文考虑行人对环境的熟悉程度, 将行人分为熟悉环境人群和不熟悉环境人群, 由于势函数元胞自动机模型^[16]能模拟行人沿着疏散时间最短线路进行疏散, 能更切合实际地模拟熟悉环境人群的疏散行为, 因此本文采用改进势函数元胞自动机模型来模拟熟悉环境人群的疏散行为. 而对于不熟悉环境人群来说, 考虑其在视野半径内的跟随策略, 元胞自动机能较好地制定不熟悉环境者的跟随规则, 这些在周金旺等^[13]、永贵等^[14]、岳昊等^[15]的研究中也有所体现. 而且, 本文对行人高密度下的疏散进行了仿真, 元胞自动机模型能再现各类复杂的疏散现象的特点. 综合考虑, 本文采取元胞自动机模型进行建模, 来模拟行人跟随疏散行为.
在大多数与上述研究相关的行人疏散模拟中, 研究者们研究了房间内能见度受限或视野较差的情况, 但忽视了行人对环境的熟悉程度这一重要的因素. 因此本文考虑在房间内能见度受限情况下, 将行人分为熟悉环境人群和不熟悉环境人群综合考虑其疏散行为, 这比以往的研究更贴近实际情况. 而且, 上述文献对疏散过程中行人的跟随行为考虑较少, 大多数研究都是研究从众行为、领导者和导游对行人的领导作用, 而本文考虑了在能见度受限情况下, 不熟悉环境人群的跟随行为, 不熟悉环境人群采取不同跟随策略, 依赖视野范围内的其他行人进行移动, 从而达到安全疏散的目的. 因此, 本文相比其他文献, 分析了不熟悉环境人群的跟随策略, 并充分考虑了其疏散过程中的跟随行为, 更符合实际疏散情况.
因此, 与以往的研究相比, 本文研究的行人疏散行为同时考虑了能见度受限和行人对环境熟悉度的不同情况. 改进费用势场元胞自动机模型来模拟熟悉环境者人群的疏散, 同时考虑不熟悉环境者的跟随行为, 制定其跟随策略和规则, 对其跟随行为进行仿真研究, 并分析熟悉环境人群的比例数量、房间内行人密度和房间内不熟悉环境人群的可视半径等参数对行人疏散时间以及行人疏散演化过程的影响.

疏散模型建立在房间内部为(L + 2) × (L + 2)的二维离散元胞网格系统内. 黑色边框表示障碍物墙壁, 把行人疏散空间的移动区域分割为L × L个大小相等的离散元胞空格. 每个元胞网格可以是空的或被行人占用, 并且其大小可被近似视为0.4 m × 0.4 m^[12], 而W表示房间出口宽度. 每个行人也只能占据一个元胞空格, 行人的仿真过程也被离散化为相等的时间步长, 在每个离散的时间步长内, 行人仅仅能移动一个元胞的位置. 每个时间步长为0.3 s, 行人移动速度为1时间步一个元胞, 则行人移动速度为1.33 m/s. 在每个时间步长内, 行人或停止等待, 或以最大的速度移动, 且行人不能穿越和跨越围墙. 如图1所示, 整个系统分为两个区域: 一个表示可见出口区域A、一个表示不可见出口区域B. 白色区域为行人的走行区域, 并且假设每个行人的视野半径相等, 为R, 如图1所示, 红色实心圆表示位于视野半径为R中心的行人.
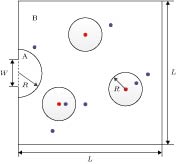图 1 行人视野图
Figure1. Visibility of pedestrian.

本文考虑行人对房间的熟悉程度, 将行人分为熟悉环境人群和不熟悉环境人群, 假定熟悉环境者能清楚地知道安全出口的位置, 即使是在视野较差的情况下, 也能知道最短路线和时间最短路线. 因此本文采用势函数元胞自动机模型来进行建模, 而不是考虑距离最短的场域模型进行建模.
2

-->

2.1.改进的势函数场

势函数场元胞自动机模型由Zhang等^[16]定义, 表示为当前小区移动到目的地的最低成本. 对于势函数场元胞自动机模型来说, 起关键性作用的因素是局部费用分布函数. 引入局部费用分布函数, 使得势函数场成为静态场和动态场的结合体, 模型可以被应用于模拟正常情况下行人运动达到系统费用最优时的运动状态.
费用分布函数表示: 一个是由行人的步行速度和从当前位置到目标位置的距离确定的行进时间的成本; 另一个是取决于周围密度的不舒服的成本. 对于费用函数来说, 在固定时刻t, 在元胞相应的位置(x, y)处的费用分布函数为^[16]

$\tau \left( {x,y,t} \right) = \frac{1}{{{v_{\max }}}} + g\left( {\rho \left( {x,y,t} \right)} \right),$

其中等式右边第一部分${1}/{v_{\max }}$代表行人的步行速度和从当前位置到目标出口的距离确定的移动时间的成本, 等式右边第二部分$g\left( {\rho \left( {x, y, t} \right)} \right)$代表与密度有关的行人的不适成本. 而假设^[16]

$\tau \left( {x,y,t} \right) = \frac{1}{{{v_{\max }}}} + {g_0}{\rho ^r}.$

从当前位置$\left( {x, y} \right)$走向安全出口位置$({x_0}, {y_0})$的总费用为^[16]

$\begin{split} & \varphi \left( {x,y,t} \right) \\ =\, & \int_{\left( {x,y} \right)}^{({x_0},{y_0})} {\tau \left( {x,y,t} \right)} {x{'}}(s){\rm{d}}x + \tau \left( {x,y,t} \right){y{'}}(s){\rm{d}}y.\end{split}$

假设积分与路径无关, 即^[16]:

${\varphi _x}\left( {x,y,t} \right) = - \tau \left( {x,y,t} \right){x{'}}(s),$

${\varphi _y}\left( {x,y,t} \right) = - \tau \left( {x,y,t} \right){y{'}}(s).$

上述的模型为Zhang等^[16]建立的势函数场域模型, 而本文认为熟悉环境者在其视野范围内, 在其移动方向上存在和不熟悉环境者移动方向的冲突, 因此考虑引入视野范围内不熟悉环境者的干扰函数, 来进一步表示影响熟悉环境者的不舒适度, 而视野范围为当前行人行驶方向的半圆区域, 如图2所示, 而干扰函数定义如下.
图 2 其他行人对熟悉环境者行人影响图
Figure2. Influence of the moving direction for surrounding pedestrian on the desired moving direction for the center pedestrian.

考虑当前行人行驶方向的左右90°扇形区间, 在此视野范围内, 影响该行人运动的干扰计算如下.
对于左侧90°区域, 计算此区域其他行人与当前运动行人的冲突, θ为其他行人移动方向和当前行人移动方向的逆时针夹角,

$\theta = \arccos \left\langle {{e_{({x_0},{y_0})}},{e_{(x,y)}}} \right\rangle ,$

如果θ为[180°, 360°), 则$N{l_i} = 0$, 如果θ为(0, 180°), 则$N{l_i} = 1$.

$Nl = \sum\limits_{i = 1}^n {N{l_i}} .$

对于右侧90°区域, 计算此区域其他行人与当前运动行人的冲突, θ为其他行人移动方向和当前行人移动方向的逆时针夹角,

$\theta = \arccos \left\langle {{e_{({x_0},{y_0})}},{e_{(x,y)}}} \right\rangle ,$

如果θ为(0, 180°)则$N{r_i} = 0$, 如果θ为[180°, 360°), 则$N{r_i} = 1$.

$Nr = \sum\limits_{i = 1}^n {N{r_i}} .$

因此, 其干扰函数为

$\eta = \frac{{Nl + Nr}}{N}.$

同时, 考虑原势函数模型的不舒适成本, 也就是视野范围内行人密度引起的不舒适成本, 视野范围内行人密度p为视野范围内总人数Na与视野面积之比r²,

$p = \frac{{Na}}{{{r^2}}}.$

参考文献[16], 视野半径为1 m时, r = 3, 半径大于等于2 m时, 认为r = 5.
因此本文将不适的原始成本分为两部分: 一部分与视野范围内行人密度有关, 另一个是由视野范围内其他行人运动变化引起的. 因此, 将成本函数重新定义为

$\tau \left( {x,y,t} \right) = \frac{1}{{{v_{\max }}}} + a{p^\alpha } + b{\eta ^\beta }.$

参考文献[16], 这里选择相应的系数为a = 0.075, b = 0.025, $\alpha = \beta = 2$.
2 -->

2.2.不熟悉环境者走行策略及规则

在房间内能见度受限时, 不熟悉环境者的行人有多种疏散策略, 本文考虑以下五种跟随策略作为不熟悉环境者的移动策略, 不熟悉环境人群策略如图3所示.
图 3 不熟悉环境人群策略图
Figure3. Diagram of uninformed pedestrian strategies.

策略S0　如果不熟悉环境者处在可见安全出口区域, 意味着此类行人能够清晰地知道出口位置, 此区域内的行人遵守静态场域模型^[12]的行走规则. 房间内区域分布如图4所示.
图 4 房间内区域分布图
Figure4. Illustration of different areas.

在可见安全出口区域内构建静态场模型, 模型采用元胞位置距安全出口的最短距离表示房间内不同位置对行人的吸引程度. 距安全出口内最近元胞的距离值作为元胞位置距安全出口的最短距离. 元胞位置距安全出口的最短距离由下式计算^[12]:

${S_{ij}} \!=\! {\rm min}\left({{\rm min}_n}\left(\sqrt {{{({x_i} \!-\! {x_n})}^2} \!+\! {{({y_j} \!-\! {y_n})}^2}} \right)\right),$

${S_{xy}} \!=\! {\rm min}\left({{\rm min}_n}\left(\sqrt{ (x- {x_n})^2 + {(y - {y_n})^2}}\right)\right),$

式中${S_{ij}}$为元胞$\left( {x, y} \right)$周边邻域距安全出口的最短距离, ${S_{xy}}$为元胞$\left( {x, y} \right)$距离安全出口的最短距离; $({x_i}, {y_j})$为元胞$\left( {x, y} \right)$在疏散系统中邻域的坐标; $({x_n}, {y_n})$为出口内第n个元胞在疏散系统中的坐标.
如果不熟悉环境者处在不可见安全出口区域, 采取四种跟随策略进行移动.
策略S1　视野范围内存在其他行人, 会等概率地选择视野范围内一个行人进行跟随, 跟随其方向进行移动. 在跟随过程中, 若被跟随者消失在自己视野范围内, 则会重新选择周边行人继续跟随. 如图5所示, 红圈代表跟随的行人. 其跟随规则为
图 5 策略S1跟随示意图
Figure5. Following strategy S1.

${S_m} = {\rm{min}}\left(\sqrt {{{({x_i} - {x_1})}^2} + {{({y_j} - {y_1})}^2}}\right),$

其中$\left( {x, y} \right)$表示当前元胞坐标, $({x_1}, {y_1})$表示被跟随元胞坐标, $({x_i}, {y_j})$表示跟随者周边邻域的八个位置的坐标, ${S_m}$表示邻居元胞距被跟随者的最短距离.
策略S2　行人考虑视野范围内的8个区域, 向视野范围内行人最多的区域进行移动, 表示从众跟随行为, 而跟随方向为Moore^[12]邻域的八个方向之一, 如图6所示, 行人对八个方向区域的人数进行判断, 每两块扇形区域代表一个方向. 其跟随规则如下:
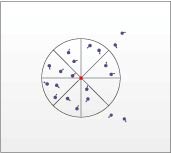图 6 策略S2, S3跟随示意图
Figure6. Following strategy S2 and S3.

$h = \max \{ {N_q}\} ,$

其中h表示下一步的方向, ${N_q}$表示视野范围内区域的人数.
策略S3　行人根据视野范围内大多数行人的移动方向来确定自己的移动方向, 行人跟随多数人的移动方向进行移动. 一个时间步计算一次, 即跟随上一时间步视野范围内行人最多进行移动的方向, 采用Moore^[12]邻域, 走行方向如图6所示, 表示跟随众多行人移动方向行走. 走行规则如下:

$h = \max \{ {N_{ e}}\} ,$

其中h表示下一步的方向, ${N_{ e}}$表示视野范围内八个移动方向的人数.
策略S4　行人坚定自己的方向, 选择不跟随他人, 按照最初设定的方向一直移动, 到达可见墙壁区域后, 往墙壁方向移动, 随机选择顺时针或逆时针方向, 跟随墙壁行走, 直到找到出口.
对于选择S1, S2和S3策略的行人, 若开始疏散时其视野范围内没有其他行人, 则按照S4策略进行移动, 直到视野范围内存在其他行人, 后采取跟随策略. 假定一旦选择跟随策略就不能改变, 一直以此策略运动下去, 直到走到出口或者停留在某个区域, 对于停留在某个区域的行人来说, 在停留t步之后, 按照S4策略所定规则进行移动.
2 -->

2.3.移动概率

本文采用Moore^[12]邻域, 被占用的小区有8个相邻小区, 各个小区的移动概率${P_{i, j}}$计算过程如下, 行人邻域及其移动概率示意图如图7所示.
图 7 行人邻域及概率示意图　(a)当前元胞及8个邻居元胞图; (b)当前元胞移动概率图
Figure7. Neighboring cell and moving probabilities of pedestrian: (a) An occupied cell and its eight neighboring cells; (b) the corresponding probabilities for occupation in the next update step.

对于熟悉环境人群来说, 其移动概率如下.
对于元胞$(i, j) \!\!\in\! {S_0} \!=\!\! \left\{\!{(i, j)|(i, j)\!\! \in \!{S_{0, 0}}{\text{为空元胞}}}\!\right\}$, 计算差商$\delta {\phi _{i, j}}(0) \equiv (\phi _{i, j}^n - \phi _{0, 0}^n)/{d_{i, j}}$, 其中, ${d_{i, j}}$为元胞$(i, j)$和$(0, 0)$之间的距离; 构造集合S_m = $ \{ (i, j)|\delta {\phi _{i, j}}(0) = \delta {\phi _{\min }}(0)\} \subseteq {S_0}$, 其中, $\delta {\phi _{\min }}(0) = $$ {\min _{(i, j) \subseteq {S_0}}}\delta {\phi _{i, j}}(0)$; 因此, 定义可移动概率为:

$\begin{aligned} & \qquad\ {\text{当}}{S_m} \ne \varnothing,\;\;{\text{且}}\delta {\phi _{\min }}(0) < 0\;{\text{时}},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\& \qquad\qquad{P_{i,j}} = \left\{\begin{aligned}& 1/|{S_m}|,\quad {(i,j) \in {S_m},}\\& 0,\quad\quad\quad\; {(i,j) \notin {S_m},}\end{aligned}\right.\\ & {\text{否则}}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\& \qquad\qquad{P_{i,j}} = \left\{\begin{aligned}& 1,\quad {(i,j) \in {S_m},}\\& 0,\quad {(i,j) \notin {S_m},}\end{aligned}\right. \end{aligned}$

其中$|{S_m}|$代表集合${S_m}$的元素个数.
对于不熟悉环境人群来说, 位于可见出口区域, 采取S0策略静态场域进行移动, 而对于静态场移动概率如下.
对于静态场移动概率来说, 对于元胞$ (i, j) \in $${S_0} = \left\{ {(i, j)|(i, j) \in {S_{0, 0}}{\text{为空元胞}}} \right\}$, 计算差商$ \Delta S = $${S_{xy}} - {S_{ij}}$, 构造集合${S_n} = \{ (i, j)|\max \Delta S\}$$ \subseteq {S_0} $; 因此, 定义可移动概率为:

$\begin{split} &\qquad {\text{当}}{S_n} \ne \varnothing,\;\;\;{\text{且}}\max \Delta S > 0{\text{时}},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\& \qquad\qquad {P_{i,j}} = \left\{ \begin{aligned}& 1/|{S_n}|, \;\;\;\;\; (i,j) \in {S_n},\\& 0, \;\;\;\;\;\;\;\;\;\;\;\; (i,j) \notin {S_n},\end{aligned} \right.\\ & {\text{否则}}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\& \qquad\qquad {P_{i,j}} = \left\{ \begin{aligned} & 1, \;\;\;\;\;\;\;\;\;\; (i,j) \in {S_n},\\& 0, \;\;\;\;\;\;\;\;\;\; (i,j) \notin {S_n},\end{aligned} \right. \end{split}$

其中$|{S_n}|$代表集合${S_n}$的元素个数.
而对于不熟悉环境人群采取其他四种跟随策略的行人, 按照上节所述的规则进行行走, 所以此处不再定义其移动概率.
2 -->

2.4.模型仿真步骤

仿真采用并行更新的规则来更新行人位置, 模型步骤描述如下(图8所示).
图 8 仿真步骤
Figure8. Simulation step diagram.

步骤1　在房间内随意分配密度为ρ的行人, 其中密度ρ为总人数N除以内部房间格子数$L \times L$.
步骤2　设置熟悉环境者比例Ks, 即熟悉环境行人为$N \times Ks$若干, $N - N \times Ks$为不熟悉环境行人, 不熟悉环境行人采取四种跟随策略进行移动, 四种跟随行人的数量为$(N - N \times Ks)/4$. 熟悉环境者计算势函数场进行移动, 其他行人按照疏散策略进行移动.
步骤3　如果存在多个行人竞争一个空元胞时, 随机选择一个行人进入该元胞, 其他行人退回自己原位置.
步骤4　当疏散行人移动到安全出口内时, 在下一时间步, 行人将移出系统. 当所有疏散行人都移出系统后, 仿真过程结束.
在并行更新机理的演化规则中, 模型在每个时间步长内需要并行地把行人的移动规则应用到每一个人, 并做相应的数据统计工作.

在仿真研究中, 疏散行人流的密度ρ定义为系统内的行人数量N与元胞个数$L \times L\;\;$之比, $L = 25$个元胞. 熟悉环境者密度定义为熟悉环境者的数量与初始时刻房间行人数量之比, 行人的疏散时间T定义为系统内所有行人离开房间所需要的时间步数, 为减少仿真初始状态对各项统计指标的影响, 每项统计指标分别取20次运行指标的平均值. 在仿真的初始时刻, 所有疏散行人随机地分布在房间内, 安全出口内没有设置行人. 待行人全部离开房间后, 仿真过程终止. 对于停留在某个区域的不熟悉环境者, 认为其停留t步之后, 按照策略S4进行移动. 由于停留步数t不能小于出口处正常排队时行人停留的最大步数, 通过仿真不同密度下疏散情况, 在密度0.1时, t = 30, 密度0.2时, t = 50, 密度为0.3时, t = 80, 密度为0.4时, t = 100. 仿真相关参数说明如表1所列.

变量	名称		名称	物理意义		名称	物理意义
L	房间长度		ρ	行人密度		${\rm{S1}}, {\rm{S2}}, {\rm{S3}}, {\rm{S4}}$	行人移动策略
W	出口宽度		Ks	熟悉环境者密度		TS1, TS2, TS3, TS4	策略疏散时间
N	行人总人数		R	行人视野半径		T	行人疏散总时间

表1参数说明
Table1.Parameters description.

2

-->

3.1.视野半径和熟悉环境者密度对疏散时间的影响

疏散房间定义为10 m × 10 m, 即为25 × 25个元胞, 在本节仿真中, 考虑视野半径R以及熟悉环境者密度Ks对疏散时间的影响. 由于房间为10 m × 10 m, 考虑视野半径为1—5 m, 熟悉环境者密度Ks为0—0.9. 如果超过400个时间步, 房间内行人还未能全部疏散, 则认为最大疏散时间为400步. 仿真结果如图9所示.
图 9 环境熟悉度与疏散时间的关系图　(a) R = 1 m; (b) R = 2 m; (c) R = 3 m; (d) R = 4 m; (e) R = 5 m
Figure9. Relationship between environmental familiarity and evacuation time: (a) R = 1 m; (b) R = 2 m; (c) R = 3 m; (d) R = 4 m; (e) R = 5 m.

图9(a)显示了视野半径为1 m时, 在不同密度下, 疏散时间随熟悉环境者密度的增加而减少. 在人流密度较大时, 疏散时间曲线先缓慢地下降, 然后迅速地下降. 而在人流密度为0.1时, 疏散时间曲线一直平缓地下降. 图9(b)的变化趋势和图9(a)类似, 不同的是在熟悉环境者密度达到0.6时, 疏散时间开始保持缓慢地减少.
图9(c)—(e)三幅图的疏散时间变化趋势相似, 随着熟悉环境者密度的增加先缓慢地减少, 然后迅速地减少, 最后保持平缓. 不同的是, 图9(c)和图9(d)中, 熟悉环境者密度达到0.4时, 曲线保持平缓. 而在图9(e)中, 熟悉环境者密度达到0.2时, 曲线开始保持平缓.
因此, 视野半径一定时, 疏散时间随着熟悉环境者密度的增加而持续减少. 意味着房间内熟悉环境者人数的增多, 更多的人准确知道出口位置, 从而引导不熟悉环境者向出口方向移动, 这在不同视野半径下有着相同的规律. 而对于视野半径R ≥ 2 m时, 疏散时间在熟悉环境者密度为0.4之后保持稳定. 因此, 考虑熟悉环境密度为0—0.5时, 分析视野半径对疏散时间的影响.
从图10(a)—(d)四幅图可以看出, 相同人流密度下疏散时间随视野半径的变化保持相同的趋势, 随着视野半径的增加, 疏散时间保持缓慢的下降. 而图10(e), 在熟悉环境者密度为0.4时, 当视野半径为1—3 m时, 疏散时间下降的速率较大, 视野半径为4—5 m时, 疏散时间基本保持不变. 图10(f)和图10(e)的变化趋势一致, 不同的是, 疏散时间曲线在视野半径2 m处保持平缓.
图 10 视野半径与疏散时间的关系图　(a) Ks = 0; (b) Ks = 0.1; (c) Ks = 0.2; (d) Ks = 0.3; (e) Ks = 0.4; (f) Ks = 0.5
Figure10. Relationship between different visibilities and evacuation time: (a) Ks = 0; (b) Ks = 0.1; (c) Ks = 0.2; (d) Ks = 0.3; (e) Ks = 0.4; (f) Ks = 0.5.

因此, 熟悉环境者密度一定时, 疏散时间随着行人视野半径的增加而持续减少. 意味着房间内能见度越好, 更多的行人能准确知道出口位置, 向出口方向移动, 不熟悉环境者的跟随策略也越有效, 从而导致疏散时间减少.
行人密度为0.3, 熟悉环境者密度为0.4, 视野半径为3 m时, 行人疏散流演化过程如图11所示.
图 11 行人疏散流演化过程($\rho = 0.3, Ks = 0.4, R = 3$)　(a) T = 0; (b) T = 20; (c) T = 40; (d) T = 60; (e) T = 90; (f) T = 110
Figure11. Evacuation evolution ($\rho = 0.3, Ks = 0.4, R = 3$): (a) T = 0; (b) T = 20; (c) T = 40; (d) T = 60; (e) T = 90; (f) T = 110

2 -->

3.2.视野半径对四类跟随策略疏散时间的影响

由3.1节可知, 疏散时间在熟悉环境者密度$Ks = 0.4$后开始趋于平缓, 因此本节考虑在熟悉环境者密度为0.4, 房间内行人密度为0.1—0.4, 各疏散策略的疏散时间随着视野半径的变化情况. 同时, 将策略S1, S2, S3和S4的疏散时间分别用T_S1, T_S2, T_S3和T_S4表示.
从图12(a)可以看出, 房间内行人密度为0.1, 四种跟随策略疏散的时间随着视野半径的增大而减少. 在房间内视野半径小于7 m时, 四种疏散时间大小关系为T_S2 > T_S1 > T_S4 > T_S3. 表明策略S2 (从众跟随)的疏散时间最大, 而策略S1 (跟随周围行人)跟随时间较大, 策略S4 (跟随墙壁移动)疏散时间与策略S3 (跟随较多行人方向)的时间较小, 这是因为采取S4策略靠墙行走的行人在墙壁、拐角和出口处的行人存在冲突. 而在视野半径大于7 m时, 四种策略的疏散时间相差不大, 这是由于此时行人都具有清晰的视野, 不论采取何种跟随策略的行人都明确地知道疏散出口的位置, 从而采取相同的移动规则直接向出口方向移动.
图 12 不同密度下各策略视野半径与疏散时间的关系　(a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$
Figure12. Relationship between different visibilities and evacuation time under different density: (a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$.

图12(b)显示到, 房间内行人密度为0.2, 四种跟随策略的疏散时间随着视野半径的增大先迅速减少再缓慢地减少. 在视野半径小于7 m时, 四种疏散时间大小关系为 T_S2 > T_S1 > T_S3 ≥ T_S4. 而图12(c)和图12(d)变化趋势和图12(b)相似, 不同的是, 在视野半径小于4 m时, 四种疏散时间大小关系为T_S2 > T_S1 > T_S3 ≥ T_S4, 在4—7 m时, S1, S3和S4策略疏散时间基本一致. 而且三幅图相同的是, 在视野半径大于7 m后, 四种策略疏散时间相差不大.
因此, 对于跟随策略S1和S2来说, 视野半径越大则其疏散时间越小, 而且在R = 2, 3, 4 m处疏散时间有显著变化, 而在视野半径大于5 m后, 疏散时间缓慢减少而后趋于稳定. 对于跟随策略S3来说, 视野半径对其疏散时间影响较大, 密度大于0.1, 在视野半径为1和2 m时, 受视野的影响, 疏散时间T_S3较大. 对于策略S4来说, 由于采取靠墙行走策略, 即使在视野较差时, 也能找到出口. 总体来说, 在密度为0.2—0.4时, 各策略基本保持相同的变化趋势, 而S1, S2和S3受视野半径影响较大, 在视野半径小于7 m时, T_S2 > T_S1 > T_S3 ≥ T_S4, 而视野半径大于7 m后, T_S2 = T_S1 = T_S4 = T_S3, 各策略疏散时间无明显差异.
2 -->

3.3.熟悉环境者密度对四类跟随策略疏散时间的影响

由3.1节可知, 疏散时间在视野半径R = 3 m后保持缓慢地减少, 因此本节研究在房间内行人密度为0.1—0.4, 视野半径为3 m时, 四类疏散策略下的疏散时间T_S1, T_S2, T_S3和T_S4随着熟悉环境者密度的变化情况, 来比较熟悉环境者密度对四种跟随策略的影响. 当熟悉环境者密度较大时, 不熟悉环境者密度较小, 导致选择跟随策略人数较少, 为比较不熟悉环境者的四类跟随策略的优劣, 本文考虑熟悉环境者比例为0—0.6.
从图13(a)可以看到, 在密度为0.1, 视野半径为3 m, 熟悉环境者密度小于0.2时, 四类跟随疏散时间大小为T_S2 > T_S1 > T_S3 > T_S4. 而在熟悉环境者密度大于0.2时, T_S2 > T_S1 > T_S4 > T_S3. 这是由于选择策略S4的行人靠墙进行运动, 不受熟悉环境者密度大小的影响, 因此疏散时间保持平缓地减少. 而对于选择策略S3的行人来说, 熟悉环境者密度越大, 房间内知道出口方向的行人越多, 因此策略S3就越有效. 同样, 图13(b)和图13(a)的变化趋势一致.
图 13 不同密度下各策略环境熟悉度与疏散时间的关系　(a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$
Figure13. Relationship between environmental familiarity and evacuation time under different density: (a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$.

从图13(c)和图13(d)可以看出, 疏散时间随熟悉环境者密度的变化曲线相似, 在熟悉环境者密度小于0.5时, T_S2 > T_S1 > T_S3 > T_S4. 而在熟悉环境者密度大于0.5时, 四种策略疏散时间相差不大, 这是因为房间内熟悉环境者占了大多数, 大多数人能准确地知道出口方向, 对于S1, S2, S3这三种策略, 不论行人采取何种跟随策略都能准确地进行跟随, 从而找到正确的疏散出口, 因此这三种跟随策略疏散时间相差不大.
因此, 熟悉环境者密度的大小影响着S1, S2, S3这三种跟随策略的疏散, 在熟悉环境者密度小于0.5时, T_S2 > T_S1 > T_S3, 这是由于熟悉环境者密度较小时, 房间内知道出口的行人较少, 而采取跟随策略S1和S2的行人都无法进行正确的跟随, 但随着熟悉环境者密度的增加, 房间内知道准确出口的行人变多, 策略S1和S2也能准确地进行跟随. 而在熟悉环境者密度大于0.5时, 三种策略都能取得较好的效果, 疏散时间相差不大, 因为采取三种跟随策略都能找到准确的出口. 对于疏散策略S4来说, 采取靠墙行走的方式, 几乎不受熟悉环境者密度的影响.
2 -->

3.4.单一策略条件下视野半径对疏散时间的影响

以上部分讨论了在同一房间, 采取多种疏散策略的疏散情况. 为了进一步比较四类跟随策略的优劣, 本节考虑房间内采取单一跟随策略的疏散情况, 研究视野半径的变化对各类跟随策略疏散时间的影响, 从而进一步比较四类跟随策略的优劣.
从图14(a)和图14(b)可以看到, 策略S1和S2随着视野半径的增加, 疏散时间缓慢地减少, 直到视野半径为8 m时, 疏散时间基本保持不变. 可以理解的是, 对于策略S1和S2, 当视野半径较小时, 采取策略S1和S2的行人没有具体的跟随方向, 而随着视野半径的增加, 在出口附近的行人能看到疏散出口位置, 从而直接移动到出口.
图 14 单一策略下不同密度的视野半径与疏散时间的关系　(a)策略S1; (b)策略S2; (c)策略S3; (d)策略S4
Figure14. Relationship between different visibilities and evacuation time at different densities under a single strategy: (a) Strategy S1; (b) strategy S2; (c) strategy S3; (d) strategy S4.

从图14(c)可以看到, 对于策略S3, 随着视野半径的增加, 疏散时间首先迅速减少, 然后缓慢减少, 最后疏散时间保持不变. 而在视野半径小于3 m时, 疏散时间较大, 随着视野半径的增大疏散时间迅速减少, 这是由于策略S3对视野半径比较敏感, 在可见出口区域有行人往出口移动, 会引导其他行人往出口方向移动, 从而疏散时间迅速减少. 而在视野半径$R \geqslant 3$ m后, 疏散时间曲线保持缓慢减少.
图14(d)和图14(c)的疏散时间变化趋势类似, 不同的是选择策略S4的行人在视野半径较小时, 也能沿着墙壁行走且顺利找到出口, 所以疏散时间较S3来说较小. 同样, 随着房间内视野条件变好, 可视出口的范围越大, 在可视出口区域的行人可以直接向出口进行移动, 从而导致疏散时间较少.
图15显示了在视野半径下四种疏散策略疏散时间的变化. 可以发现, 在不同密度下, 各策略疏散时间变化趋势一致, 而且各策略的疏散时间关系与视野半径的大小密切相关, 如下所示:
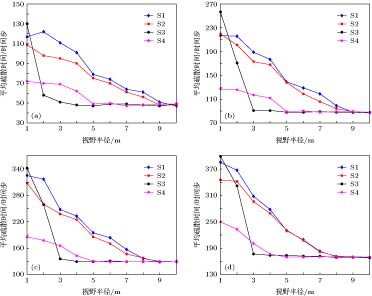图 15 不同密度下各策略的视野半径与疏散时间的关系　(a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$
Figure15. Relationship of different strategy between different visibilities and evacuation time at different densities: (a) $\rho = 0.1$; (b) $\rho = 0.2$; (c) $\rho = 0.3$; (d) $\rho = 0.4$.

$\begin{split}& R = 1\;{\rm{m}}{\text{时}},\;{T_{{\rm{S3}}}}>{T_{{\rm{S1}}}}>{T_{{\rm{S2}}}}>{T_{{\rm{S4}}}};\\& 1\;{\rm{m}} < R < 9\;{\rm{m}}{\text{时}},\;{T_{{\rm{S1}}}}>{T_{{\rm{S2}}}}>{T_{{\rm{S4}}}} \geqslant {T_{{\rm{S3}}}};\\& R = 9,10\;{\rm{m}}{\text{时}},\;{T_{{\rm{S1}}}}={T_{{\rm{S2}}}}={T_{{\rm{S4}}}}={T_{{\rm{S3}}}}.\end{split}$

结果表明, 各类跟随策略的疏散时间与视野半径的大小有关. 在视野半径较小时, 如R = 1 m, 跟随策略S4效果最优; 而视野半径较大时, 视野半径大于2 m小于5 m时, 跟随策略S3才是更好的疏散策略; 视野半径更大时, 如视野半径大于5 m小于8 m时, 跟随策略S3和S4的疏散时间相差不大, 效果都较好; 而视野半径大于8 m时, 四种跟随疏散策略没有优劣, 疏散时间基本一致.

本文研究了疏散行人的跟随行为特性, 建立了元胞自动机模型来仿真能见度受限和熟悉环境者人数变化下的行人跟随行为表现, 改进势函数元胞自动机模型来模拟熟悉环境人群的疏散行为, 对不熟悉环境人群制定跟随策略来模拟其跟随行为, 观察模拟仿真情况后, 得出以下结论.
1)房间内视野条件越好或熟悉环境人群数量越多, 则行人疏散时间越少. 而且当熟悉环境者密度Ks = 0.4或视野半径R = 3 m时, 疏散时间开始变得较小, 意味着行人能开始得到快速的疏散.
2)跟随策略的有效性和视野半径的大小有关, 在熟悉环境者密度一定, 视野半径很小时, 跟随策略S4效果最好; 视野半径较小时, 跟随策略S4和S3效果较好, 跟随策略S1和S2效果较差, 此时疏散时间大小关系为T_S2 > T_S1 > T_S3 ≥ T_S4. 而在视野半径继续增大时, 四种疏散策略时间没有较大差异.
3)当视野半径一定且熟悉环境者密度小于0.5时, 跟随策略S3效果最好, 而跟随策略S1, S2, S4效果较差, 此时疏散时间大小关系为T_S2 > T_S1> T_S4 > T_S3. 在熟悉环境者密度大于0.5时, 三种策略都能取得较好的效果, 疏散时间相差不大. 而且策略S4受熟悉环境者密度影响不大.
4)在单一策略下, 视野半径对跟随策略影响很大. 在视野半径较小时, 疏散策略S4效果最优, 此时跟随墙壁行走为更好的策略; 在视野半径较大时, 跟随策略S3效果最好, 这和Wang和Cao^[23]的研究表现一致, 由于策略S4的行人在墙壁、拐角和出口处存在较多冲突, 而策略S3对视野半径比较敏感, 在可见出口区域有行人往出口移动, 会引导S3策略行人往出口方向移动, 从而疏散时间较策略S4更小; 而当房间内视野半径更好时, 四种策略疏散时间没有较大差异.
本文的研究结果和其他研究者的结果有一定的区别和相似之处. Hou等^[18]、Ma等^[19,20]建立社会力模型来研究有限能见度下行人的领导作用, 结果表明有限能见度下领导作用对疏散影响是双重的. Ma等^[20]认为在视野半径较大时, 未看到出口的行人都会向领导者靠拢, 而不同领导者所处房间位置不同, 而增加了疏散时间. 而本文的研究结果为, 视野条件越好行人疏散时间越少, 因为视野条件越好, 知道出口的行人越多, 则跟随效果越好, 这与本文所考虑的跟随行为有关. Frank和Dorso^[22]以及Wang和Cao^[23]考虑了在视野受限的房间内, 行人疏散过程的放牧、沿墙壁行走等行为, 他们的实验表明疏散时间随着视野半径的增大而变小, 这和本文有着相同的结论. Wang和Cao^[23]也在考虑行人视野受限时, 建立了社会力模型研究行人的疏散策略包括跟随平均位置、平均移动方向和沿墙行走等行为, 他们认为单一策略下沿墙行走和跟随平均移动方向等策略更有效. 这和本文研究结果在单一策略环境下有相似之处, 而与多种策略并存情况下有些区别, 由于Wang和Cao^[23]只考虑了单一策略下疏散行为, 而本文考虑了熟悉环境人群疏散和多种跟随策略下行人的疏散, 更综合地分析了行人的疏散行为, 认为在多种跟随策略下, 能见度较差时, 跟随策略S4 (沿墙行走)更有效, 而能见度较好时, 跟随策略S3 (跟随最多移动方向)更有效.
本文研究的内容更切合实际地分析了房间内的疏散行为, 研究了不熟悉环境人群在能见度受限下采取不同跟随策略的表现, 此项工作能对大型公共场所如超市、体育馆的应急疏散情况和视野条件较差时提供一些启示, 有助于制定一些有效的指导策略. 但是本文研究的模拟环境较为基础, 在未来的研究过程中需要研究出口宽度、多出口条件下以及障碍物情况下的疏散情况, 以研究这些跟随策略在未来的适用性. 而且, 目前本文的研究仅处于理论层面, 暂未进行真人实验来标定和验证, 在未来的研究中, 可结合实际条件对现实场景进行真人实验以进一步研究跟随策略的有效性和适用性.