删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

二维相敏检波器及其在调幅图像解调中应用

本站小编 Free考研考试/2021-12-29
摘要:采用二维空间调制解调技术可以提高低照度及高噪声环境条件下光电探测目标对象的能力, 本文提出了对二维空间调幅信号进行高精度检波的二维相敏检波器(two-dimensional phase-sensitive detector, 2D PSD)方法. 介绍了二维相敏检波器提取二维调幅图像中调制信号的工作原理, 并对二维相敏检波器抑制噪声、从噪声淹没的调幅图像中提取信号的能力进行了模拟仿真; 为消除屏蔽玻璃中金属丝网产生的网格调幅图像对屏蔽玻璃缺陷检测的影响, 对比分析了频域直接滤波方法、整流加滤波方法和二维相敏检波器等方法对调幅图像进行检波、提取缺陷和抑制噪声的效果. 介绍了通过外加载波和二维相敏检波方法检测普通玻璃缺陷的原理和实验结果. 模拟仿真及实际检测结果表明二维相敏检波方法可用于空间二维调幅图像解调, 大大提高输出图像的信噪比, 具有提取淹没在噪声中的调幅图像中调制信号的能力, 提高检测精度.
关键词: 二维相敏检波器/
二维调幅图像/
信噪比/
玻璃缺陷检测

English Abstract


全文HTML

--> --> -->
1.引　言
光电探测技术是根据被探测对象辐射、反射、散射的光波的特征来探测和识别对象的一种技术, 在水下目标探测[1,2]、舰用光电探测[3]、空间目标[4,5]、物质特性检测[6]等领域应用广泛. 在信噪比较低的环境条件下, 普通成像方法成像质量差甚至无法分辨出图像中的目标物体, 对光波参量[7] (幅度、频率、相位、偏振等)进行调制和解调是提高信噪比的有效方法. 目前, 光强时域调制方法是应用最广泛的方法, 杨鲁新等[8]利用脉冲光源驱动发光二极管(LED), 消除背景光对位置敏感探测器(PSD)的影响, 提高了精密位移测量系统的测量精度. 郝勤正等[9]在双光路能见度仪中采用正弦波光源调制方法去除了背景光噪声, 提高了能见度仪的测量精度. 除此之外, 这种时域强度调制技术还用在泵浦探测技术[10]、微分表面等离子体共振成像(DSPR)[11]和伪外差干涉法[12]等领域.
二维相机在这些应用中受到限制, 因为它们能够解调的信号的最高频率远小于帧速率, 而且传统的测量调制光信号的实验设备是光电二极管和锁相放大器, 对所有像素都进行光电检测和锁相放大显然不切实际. 基于此原因, 常用单点扫描系统实现二维检测, 如刘灏等[13]在水下成像系统中利用激光光源强度调制技术抑制水下目标成像过程中前向和后向散射光的影响, 并顺序扫描目标上每个点, 得到了高质量目标图像. 然而, 单点扫描方式速度慢、价格昂贵、更加复杂, 且在扫描帧上受到运动伪影的影响. Johnston等[14]设计的256 × 256相机的每一个像素包含一个光电二极管及其复位开关和四个相互独立的控制开关, 通过快速获取时域调制周期内相位相差90°的四幅图像, 通过简单的后处理就可以提取出调制幅度、相位以及光信号的直流量, 取代了探测器、锁相放大器和机械扫描台等硬件, 不仅在成本和实验时间上有很大的优势, 而且可以提供无运动伪影的图像. Hornbeck[15]发明的数字微反射镜器件(digital micro-mirror device, DMD)是一种基于MEMS和CMOS大规模集成电路技术制成的电寻址空间光调制器, 已应用于散射介质聚光[16]、自适应高动态范围成像[17]、数字光刻[18]、近红外光谱仪[19]、物体三维测量[20]和超高清激光电视系统[21]等领域. 其中吴传奇[22]利用DMD进行光信号的编码调制, 基于互补S矩阵编码、全哈达玛矩阵编码以及最大光通量矩阵编码等空间编码和解码多通道测量方法重建出实际场景图像, 提高了信噪比, 改善了成像质量. 吉莉[23]分析了哈达玛编码探测重建信号时噪声信号独立性和相邻信号噪声相关性, 提出一种基于邻域平均的哈达玛重建图像降噪方法.
光波强度时域调制方法可以抑制噪声的影响, 但需要多次对信号或图像进行采集, 检测耗时; 基于空间调制的编码多通道探测技术, 具有高信噪比、高光通量和高分辨率的特点, 在弱光信号探测中具有一定优势, 但重建目标图像中依然残留明显噪声, 而且信号探测和重建过程繁琐. 如果在探测过程中采用非编码空间二维调制和解调方法可以大大简化信号探测和重建过程, 但目前还没有能够从淹没的噪声中提取出有用信号的有效的解调方法. 因此, 提出了用于二维空间调幅图像解调的二维相敏检波方法, 抑制二维图像中的噪声, 大大提高了输出图像的信噪比. 文中介绍了二维相敏检波器提取二维正弦调幅图像中调制信号的工作原理, 对二维相敏检波器抑制噪声、提取微弱图像信号的能力进行仿真, 将二维相敏检波器用于屏蔽玻璃缺陷和普通玻璃缺陷的检测, 验证其抗干扰和抑制噪声特性.
2.二维相敏检波器原理及噪声抑制特性
2
2.1.二维相敏检波器组成及工作原理
-->

2.1.二维相敏检波器组成及工作原理

调制和解调是信号检测中常用的有效抑制噪声和干扰的方法, 其中基于相敏检波原理的锁相放大器已经成为微弱信号检测领域的必备仪器. 针对二维空间检测领域抑制干扰和噪声的实际需求提出了二维相敏检波的概念. 二维空间调制采用的载波信号为频率较高的二维空间信号, 对二维载波信号的调制过程是将二维低频测量信号的频谱搬迁到高频载波频率附近的非线性过程. 二维相敏检波的基本思想来自于相干检测理论, 也就是引入一个和二维载波信号频率一样的二维参考信号, 通过乘法器、开关器等非线性运算将载波信号频率附近的低频测量信号频率成分重新搬回到低频位置, 并且利用二维低通滤波器滤除载波频率及其他高频成分, 提取出二维低频测量信号. 利用二维相敏检波器非常好的选频特性, 实现二维调幅信号的精密检波, 抑制噪声和干扰.
如图1所示, 二维相敏检波器由乘法器和低通滤波器两部分组成, 乘法器的输入信号${u_i}(m, n)$为如(1)式所示的二维幅度调制信号, ${u_{{\rm{sinal}}}}(m, n)$为二维变量, ${u_{{\rm{sinal}}}}(m, n)$为二维低频测量信号, $\cos(\alpha m)\cos(\beta n)$为二维载波信号, $\alpha $和$\beta $分别为m和n两个方向的高频载波频率. 乘法器的另一路输入信号${u_r}(m, n)$((2)式所示)为与高频载波信号频率一样的参考信号. 乘法器的输出信号${u_{o1}}(m, n)$中包含五个乘积项((3)式所示), 由于${{\cos}}(2\alpha m + 2\beta n)$, $\cos (2\alpha m - 2\beta n)$, $\cos(2\alpha m)$和$\cos (2\beta n)$为高频分量, 根据积化和差公式, ${u_{{\rm{sinal}}}}(m, n)$和这四项高频分量相乘, 从频域来看相当于将${u_{{\rm{sinal}}}}(m, n)$信号频谱搬迁到这些高频分量附近, 这四个乘积项通过低频滤波器后将被滤除, 当选择低通滤波器的截止频率大于${u_{{\rm{sinal}}}}(m, n)$信号频率时, $({1}/{4}){u_{{\rm{sinal}}}}(m, n)$项信号可以通过低通滤波器输出((4)式所示). 因此, 二维相敏检波器可以从二维调幅信号中解调出二维低频测量信号.
图 1 二维相敏检波器组成
Figure1. Block diagram of 2D PSD.

${u_i}(m,n) = {u_{{\rm{sinal}}}}(m,n)\cos(\alpha m)\cos(\beta n), $
${u_r}(m,n) = \cos(\alpha m)\cos(\beta n), $
$\begin{split}& {u_{o1}}(m,n) = {u_i}(m,n) \times {u_r}(m,n)\\ =\, & \cos(\alpha m)\cos(\beta n) \times {u_{{\rm{sinal}}}}(m,n)\cos(\alpha m)\cos(\beta n)\\ =\, & \frac{1}{4}{u_{{\rm{sinal}}}}(m,n{{)[\cos}}(2\alpha m) + 1{{][\cos}}(2\beta n) + 1]\\ =\, & \frac{1}{4}{u_{{\rm{sinal}}}}(m,n)[\cos(2\alpha m)\cos(2\beta n) \\ & + \cos(2\beta n) + \cos(2\alpha m) + 1]\\ =\, & \frac{1}{4}{u_{{\rm{sinal}}}}(m,n)\Big[\frac{1}{2}\cos(2\alpha m + 2\beta n) + \frac{1}{2}\cos(2\alpha m \\ & - 2\beta n) + \cos(2\beta n) + \cos(2\alpha m) + 1\Big], \\[-16pt]\end{split}$
${u_o}(t) = \frac{1}{4}{u_{{\rm{sinal}}}}(m,n).$

2
2.2.调幅图像二维相敏检波仿真
-->

2.2.调幅图像二维相敏检波仿真

在光学检测中经常需要对二维空间调制图像进行解调, 提取二维低频图像信号, 下面对二维图像调制和采用二维相敏检波器解调原理进行仿真. 图2(a)、图2(b)和图2(c)所示分别为二维调制信号的空间域$(m, n)$2D显示、频域$(u, v)$2D显示和频域$(u, v)$3D网格显示, 二维调制信号的像素尺寸为$(2000, 2000)$, 有用信号为一个直径大小为500像素的圆, 二维调制信号的主要频率成分为以$(1001, 1001)$为中心的低频分量; 图2(d)、图2(e)和图2(f)所示分别为二维载波信号的空间域2D显示、频域2D显示和频域3D网格显示, 二维载波信号的像素尺寸为$(2000, 2000)$, $(m, n)$方向的角频率都为$2{\text{π}}\times 0.01$弧度/像素, 周期为100个像素, 二维载波信号包含(981, 981)、(1021, 981)、(981, 1021)、(1021, 1021)四个频率分量; 图2(g)、图2(h)和图2(i)所示分别为二维调幅信号的空间域2D显示、频域2D显示和频域3D网格显示, 二维调幅信号的像素尺寸为$(2000, 2000)$, 在空间域相当于调制信号和载波信号相乘, 在频域相当于低频调制信号的频谱(图2(c))搬迁到载波信号各个频率分量(图2(f))(981, 981), (1021, 981), (981, 1021), (1021, 1021)的位置; 图2(j)、图2(k)和图2(l)为二维相敏检波器中乘法器的输出结果, 分别为空间域2D显示、频域2D显示和频域3D网格显示, 图2(g)和图2(j)对比可知, 在空间域乘法器输出信号频率提高, 图2(h)和图2(k)对比可知, 乘法器的作用相当于将低频调制信号的频谱从载波信号各个频率分量(981, 981), (1021, 981), (981, 1021), (1021, 1021)的位置搬迁到(961, 961), (1001, 961), (1041, 961), (961, 1001), (1001, 1001), (1041, 1001), (961, 1041), (1001, 1041), (1041, 1041)各个频率位置; 图2(m)、图2(n)和图2(o)为二维相敏检波器中低通滤波器的输出结果, 分别为空间域2D显示、频域2D显示和频域3D网格显示, 低通滤波器的作用相当于将(961, 961), (1001, 961), (1041, 961), (961, 1001), (1041, 1001), (961, 1041), (1001, 1041), (1041, 1041)各个频率位置的高频分量滤除, 只剩下(1001, 1001)位置的低频分量, 实现了二维调幅信号的解调.
图 2 二维空间调制及二维相敏检波过程　(a) 二维调制信号空域图像; (b) 二维调制信号频域2D图像; (c) 二维调制信号频域3D网格图像; (d) 二维载波信号空域图像; (e) 二维载波信号频域2D图像; (f) 二维载波信号频域3D网格显示; (g) 二维调幅信号空域图像; (h) 二维调幅信号频域2D图像; (i) 二维调幅信号频域3D网格图像; (j) 乘法器输出信号空域图像; (k) 乘法器输出信号频域2D图像; (l) 乘法器输出信号频域3D网格图像; (m) 相敏检波器输出信号空域图像; (n) 相敏检波器输出信号频域2D图像; (o) 相敏检波器输出信号频域3D网格图像
Figure2. Simulation of 2D spatial modulation and 2D PSD: (a) Spatial image of 2-D modulating signal; (b) frequency domain image of 2D modulating signal; (c) frequency domain 3D mesh image of 2D modulating signal; (d) spatial image of 2D carrier signal; (e) frequency domain image of 2D carrier signal; (f) frequency domain 3D mesh image of 2D carrier signal; (g) spatial image of 2D modulated signal; (h) frequency domain image of 2D modulated signal; (i) frequency domain 3D mesh image of 2D modulated signal; (j) output spatial image of multiplier; (k) output frequency domain image of multiplier; (l) output frequency domain 3D mesh image of multiplier; (m) output spatial image of 2D PSD; (n) output frequency domain image of 2D PSD; (o) output frequency domain 3D mesh image of 2D PSD.

由(1)—(4)式以及图2(a)—(o)可见, 通过二维低频测量信号和二维高频载波信号相乘实现二维调制的主要目的是将低频信号频谱(图2(b))搬迁到了二维载波频率(图2(e))的附近(图2(h)), 以便区分其他干扰和噪声. 二维调幅信号解调的目的是提取二维调幅信号中的二维低频测量信号. 二维相敏检波器解调算法包括乘法器和低通滤波器两个部分(图1), 首先通过乘法器的非线性作用、利用积化和差公式((3)式)将低频测量信号的频谱成分从载波信号附近(图2(h))搬迁到直流频率附近以及更高的频率附近(图2(k)), 然后利用低通滤波器的低通特性获取直流附近的低频测量信号, 滤除载波以及更高频率信号. 设计的低通滤波器的截止频率要大于信号频率, 远小于载波的频率.
3.二维相敏检波器噪声抑制特性
本节将通过与整流 + 滤波检波方法对比分析二维相敏检波方法噪声抑制特性. 图3(a) 所示为整流 + 滤波检波方法仿真流程, 低频调制信号${I_i}(m, n)$和载波信号${I_c}(m, n)$相乘形成调幅信号$I(m, n)$, 利用加噪函数对调幅信号$I(m, n)$模拟加入不同程度的高斯白噪声, 形成混有噪声的二维调幅信号${I_{1 a}}(m, n)$. 整流 + 滤波检波方法的第一步是整流, 整流通过减去平均值再取绝对值来实现, 整流后的信号${I_{1 b}}(m, n)$通过FFT变换成频域信号${F_{1 a}}(u, v)$, 再通过低通滤波器滤除高频分量得到频域信号${F_{1 b}}(u, v)$, 再通过IFFT得到低频信号${I_{1 o}}(m, n)$. 图3(b) 所示为二维相敏检波方法仿真流程, 低频调制信号${I_i}(m, n)$和载波信号${I_c}(m, n)$相乘形成调幅信号$I(m, n)$, 利用加噪函数对调幅信号$I(m, n)$模拟加入不同程度的高斯白噪声, 形成混有噪声的二维调幅信号${I_{2 a}}(m, n)$. 二维相敏检波方法的第一步是乘法器, 调幅信号${I_{2 a}}(m, n)$和载波信号${I_c}(m, n)$相乘产生信号${I_{2 b}}(m, n)$, ${I_{2 b}}(m, n)$信号中包含高频成分和低频信号, ${I_{2 b}}(m, n)$通过FFT变换成频域信号${F_{2 a}}(u, v)$, 并利用低通滤波器滤除其高频成分、提取低频分量${F_{2{\rm{b}}}}(u, v)$, 最后通过IFFT得到低频信号${I_{2 o}}(m, n)$.
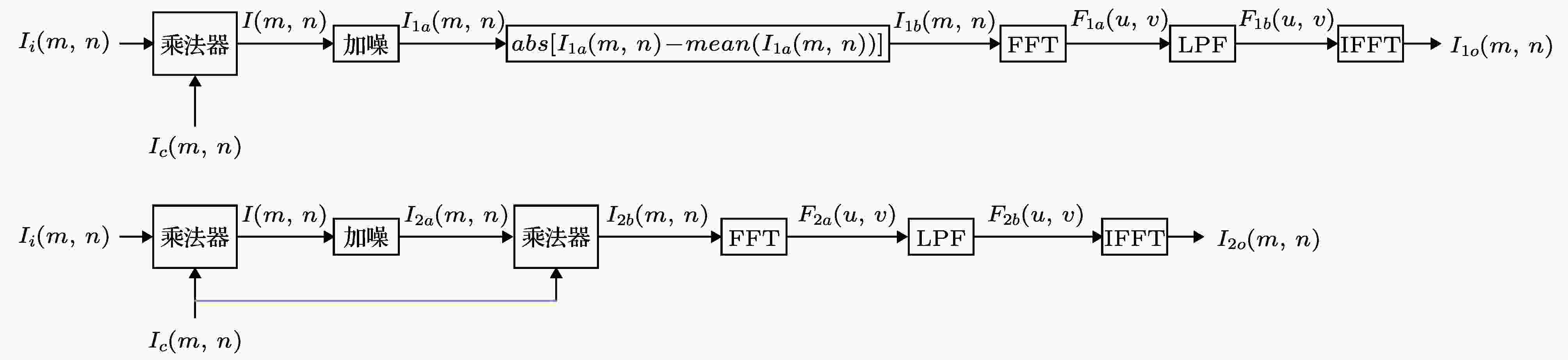图 3 两种不同检波器检波方法及噪声抑制特性仿真流程　(a) 整流滤波方法; (b) 二维相敏检波方法
Figure3. Simulation flow of demodulation and noise suppression of two different demodulation methods: (a) Rectifier + filtering method; (b) 2D PSD.

图4所示为二维调幅信号在加入不同噪声情况下整流 + 滤波检波方法和二维相敏检波方法检波输出的噪声抑制特性比较. 图4(a) 所示为加入了噪声、信噪比为60 dB的二维调幅信号, 图4(b) 和图4(c) 所示为二维相敏检波输出图像的空间域2D显示和3D网格显示, 图4(d) 和图4(e) 所示为整流 + 滤波检波方法输出图像的空间域2D显示和3D网格显示, 通过图4(b)、图4(c)和图4(d)、图4(e)比较可知, 在噪声较小的情况下两种检波方法都可以比较精确地提取出低频的圆形调制信号, 输出图像信号的信噪比都为4.0. 此处信噪比的定义如(5)式所示: 图像的标准差和平均值之比. 图4(f) 所示为加入了噪声、信噪比为0 dB的二维调幅信号, 图4(g) 和图4(h) 所示为二维相敏检波输出图像的空间域2D显示和3D网格显示, 图4(i) 和图4(j) 所示为整流 + 滤波检波方法输出图像的空间域2D显示和3D网格显示, 通过图4(g)、图4(h)和图4(i)、图4(j)比较可知, 在噪声增加的情况下两种检波方法都可以提取出低频的圆形调制信号, 但二维相敏检波方法输出信号的信噪比为3.9, 而整流 + 滤波检波方法输出图像信号的信噪比降为0.63. 图4(k) 所示为加入的噪声已经淹没了信号、信噪比为–30 dB的二维调幅信号, 图4(l) 和图4(m) 所示为二维相敏检波输出图像的空间域2D显示和3D网格显示, 图4(n) 和图4(o) 所示为整流 + 滤波检波方法输出图像的空间域2D显示和3D网格显示, 通过图4(l)、图4(m)和图4(n)、图4(o)比较可知, 在图像信号被噪声淹没的情况下整流 + 滤波检波方法已经无法提取出低频的圆形调制信号, 而二维相敏检波方法仍然可以提取出低频的圆形调制信号, 输出信号的信噪比达到2.0.
图 4 二维调幅信号在加入不同噪声情况下两种检波方法噪声抑制特性　(a) 信噪比60 dB调幅信号; (b) 输入60 dB, 二维相敏检波输出空域2D图像; (c) 输入60 dB, 二维相敏检波输出空域3D网格图像; (d) 输入60 dB, 整流 + 滤波方法输出空域2D图像; (e) 输入60 dB, 整流 + 滤波方法输出空域3D网格图像; (f) 信噪比0 dB调幅信号; (g) 输入0 dB, 二维相敏检波输出空域2D图像; (h) 输入0 dB, 二维相敏检波输出空域3D网格图像; (i) 输入0 dB, 整流 + 滤波方法输出空域2D图像; (j) 输入0 dB, 整流 + 滤波方法输出空域3D网格图像; (k) 信噪比–30 dB调幅信号; (l) 输入–30 dB, 二维相敏检波输出空域2D图像; (m) 输入–30 dB, 二维相敏检波输出空域3D网格图像; (n) 输入–30 dB, 整流 + 滤波方法输出空域2D图像; (o) 输入–30 dB, 整流 + 滤波方法输出空域3D网格图像
Figure4. Noise suppression characteristics of two demodulation methods in different noise background: (a) Amplitude-modulated signal of 60 dB; (b) output spatial image of 2D PSD in case of 60 dB; (c) output spatial domain 3D mesh image of 2D PSD in case of 60 dB; (d) output spatial image of rectifier + filtering method in case of 60 dB; (e) output spatial domain 3D mesh image of rectifier + filtering method in case of 60 dB; (f) amplitude-modulated signal of 0 dB; (g) output spatial image of 2D PSD in case of 0 dB; (h) output spatial domain 3D mesh image of 2D PSD in case of 0 dB; (i) output spatial image of rectifier + filtering method in case of 0 dB; (j) output spatial domain 3D mesh image of rectifier + filtering method in case of 0 dB; (k) amplitude-modulated signal of –30 dB; (l) output spatial image of 2D PSD in case of –30 dB; (m) output spatial domain 3D mesh image of 2D PSD in case of –30 dB; (n) output spatial image of rectifier + filtering method in case of –30 dB; (o) output spatial domain 3D mesh image of rectifier + filtering method in case of –30 dB.

$S/N = \frac{{{\rm std}(I(m,n))}}{{{\rm mean} (I(m,n))}}.$
图5所示为二维调幅信号在加入不同噪声情况下整流 + 滤波检波方法和二维相敏检波方法输出图像信噪比随输入图像信噪比变化曲线. 从图5仿真结果可见, 在输入不同信噪比的调幅信号情况下, 二维相敏检波方法输出信号的信噪比远大于整流 + 低通滤波方法输出信号的信噪比. 从图4典型仿真输出的三维网格显示图像和信噪比数值对比(图4(c)和图4(e)、图4(h)和图4(j)、图4(m)和图4(o))可以明显看到: 输入相同信噪比的调幅图像, 二维相敏检波方法与整流 + 低通滤波方法相比较抑制噪声的能力强, 输出信号的信噪比高, 即使信号图像被噪声淹没, 也可以检测出被测图像, 具有提取淹没在噪声中的信号的能力. 二维相敏检波方法之所以有此特性, 主要在于二维相敏检波方法引入了一路和载波信号频率一样的参考信号, 具有好的频率选择性, 即只有载波附近的低频测量信号才能通过乘法器频率搬迁、低通滤波后输出, 而其他频率的信号无法输出. 整流 + 低通滤波方法不具有频率选择特性, 抑制噪声能力弱.
图 5 两种不同检波方法输出信噪比随输入信噪比的变化
Figure5. Variation curve of output signal-to-noise ratio with input signal-to-noise ratio for two demodulation methods.

4.二维相敏检波方法应用
2
4.1.二维相敏检波方法在屏蔽玻璃缺陷检测中应用
-->

4.1.二维相敏检波方法在屏蔽玻璃缺陷检测中应用

3
4.1.1.屏蔽玻璃及其缺陷检测方法
-->
4.1.1.屏蔽玻璃及其缺陷检测方法
电磁波辐射不仅影响电子设备的工作, 还对人体有极大的危害, 在军事领域的电磁辐射有可能导致国家机密信息的泄露. 为了消除电磁辐射带来的危害, 电磁屏蔽技术显得十分重要. 电磁屏蔽玻璃是经过特殊工艺处理, 在玻璃表面覆盖导电涂层或在玻璃中夹入金属丝网, 实现对电磁波的阻挡和衰减. 屏蔽玻璃除了具有透光性和可视性之外, 必须要有良好的屏蔽性能, 而屏蔽玻璃的缺陷会直接影响其作用的发挥, 因此, 对屏蔽玻璃进行缺陷检测是十分重要的一个环节, 可以避免瑕疵产品进入民用和军事应用领域.
屏蔽玻璃缺陷检测一般采用机器视觉方法, 选择合适波长的光源照明被检测对象, 通过高分辨率相机采集屏蔽玻璃二维图像, 利用图像处理算法判别屏蔽玻璃有无缺陷. 图6所示为屏蔽玻璃典型缺陷二维图像, 由于屏蔽玻璃缺陷的高精度检测要求(小于10 μm), 图像中可以看到金属丝网背景图像, 影响到缺陷的可靠识别. 由于金属丝网图像具有周期性, 可以把屏蔽玻璃二维图像看作以金属丝网周期性图像为载波, 缺陷为调制信号的二维调幅信号, 因此, 可以利用二维相敏检波器抑制噪声能力强的特点对二维调幅信号进行检波, 提取缺陷图像.
图 6 屏蔽玻璃典型缺陷图像　(a) 黑点; (b) 划痕; (c) 白线
Figure6. Typical defect images of shielding glass: (a) Black spot; (b) scratch; (c) white line.

3
4.1.2.屏蔽玻璃缺陷检测方法对比
-->
4.1.2.屏蔽玻璃缺陷检测方法对比
图7所示为四种屏蔽玻璃缺陷检测算法图像处理流程. 图7(a) 所示为直接滤波方法, 屏蔽玻璃二维图像$I(m, n)$通过FFT变换成频域信号${F_{1 a}}(u, v)$, 通过低通滤波器滤除高频分量得到频域信号${F_{1 b}}(u, v)$, 再通过IFFT得到低频的缺陷信号${I_{1 o}}(m, n)$. 图7(b) 所示为整流 + 滤波方法, 屏蔽玻璃二维图像$I(m, n)$减去平均值再取绝对值实现$I(m, n)$的整流, 整流后的图像${I_{2{\rm{a}}}}(m, n)$通过FFT、低通滤波和IFFT等过程得到低频的缺陷信号${I_{2 o}}(m, n)$. 图7(c) 所示为二维相敏检波方法之一(近似提取载波), 由于屏蔽玻璃二维图像$I(m, n)$中主要成分是载波信号, 因此利用$I(m, n)$减去其平均值的方法近似提取载波信号${I_{3 a}}(m, n)$, 通过二维相敏检波方法的相乘和低通滤波两个过程提取低频的缺陷信号${I_{3 o}}(m, n)$. 图7(d) 所示为二维相敏检波方法之二(精确提取载波)图像处理流程, 缺陷识别过程中信号如图8所示. 屏蔽玻璃原始二维图像$I(m, n)$如图8(a)所示, 为精确提取载波信号, 将$I(m, n)$通过FFT变换为频域信号${F_{4 a}}(u, v)$, ${F_{4 a}}(u, v)$的幅值的2D显示和3D网格显示如图8(b)和图8(c); 通过设定阈值, 将${F_{4 a}}(u, v)$中幅值大于阈值的部分${F_{4 b}}(u, v)$认为是载波信号的频谱, ${F_{4 b}}(u, v)$的幅值的2D显示和3D网格显示如图8(d)和图8(e)所示, 再经过IFFT提取出载波信号${I_{4 a}}(m, n)$(图8(f)); 载波信号${I_{4 a}}(m, n)$和输入原始图像$I(m, n)$相乘后, 得到空域信号${I_{4 b}}(m, n)$(图8(g)), 再经过FFT得到其频谱${F_{4 c}}(u, v)$, 从${F_{4 c}}(u, v)$的幅值的2D显示(图8(h))和3D网格显示(图8(i))可见, 相乘后信号的频谱成分向高频方向迁移, 有利于提高低通滤波效果; 低通滤波器的频域特性如图8(j)所示, ${F_{4 c}}(u, v)$经过此滤波器滤波后形成低频缺陷图像对应的频谱${F_{4 d}}(u, v)$, ${F_{4 d}}(u, v)$的幅值的2D显示和3D网格显示分别如图8(k)和图8(l); 通过IFFT得到低频的缺陷图像${I_{4 o}}(m, n)$, 其2D显示和3D网格显示分别如图8(m)和图8(n); 二值化图像${I_{4 o}}(m, n)$(图8(o))可以指出缺陷所在位置.
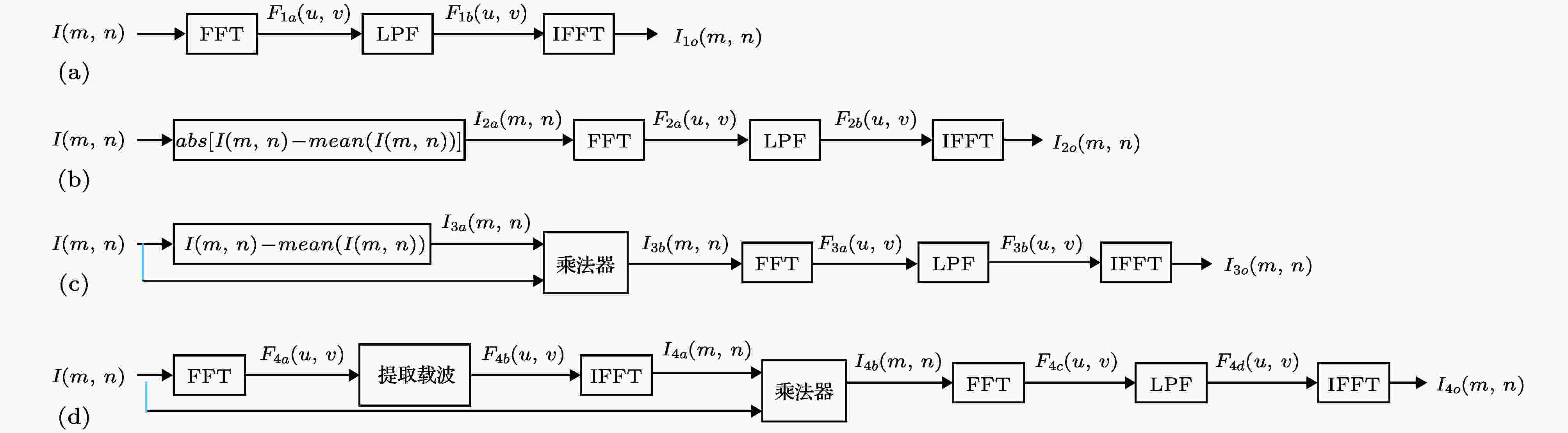图 7 屏蔽玻璃缺陷检测算法流程　(a) 直接滤波方法; (b) 整流 + 滤波方法; (b) 二维相敏检波方法之一(近似提取载波); (d) 二维相敏检波方法之二(精确提取载波)
Figure7. Flow chart of defect detection algorithm for shielding glass: (a) Direct filtering method; (b) rectifier + filtering method; (c) 2D PSD(extracting carrier approximately); (d) 2D PSD(extracting carrier accurately).

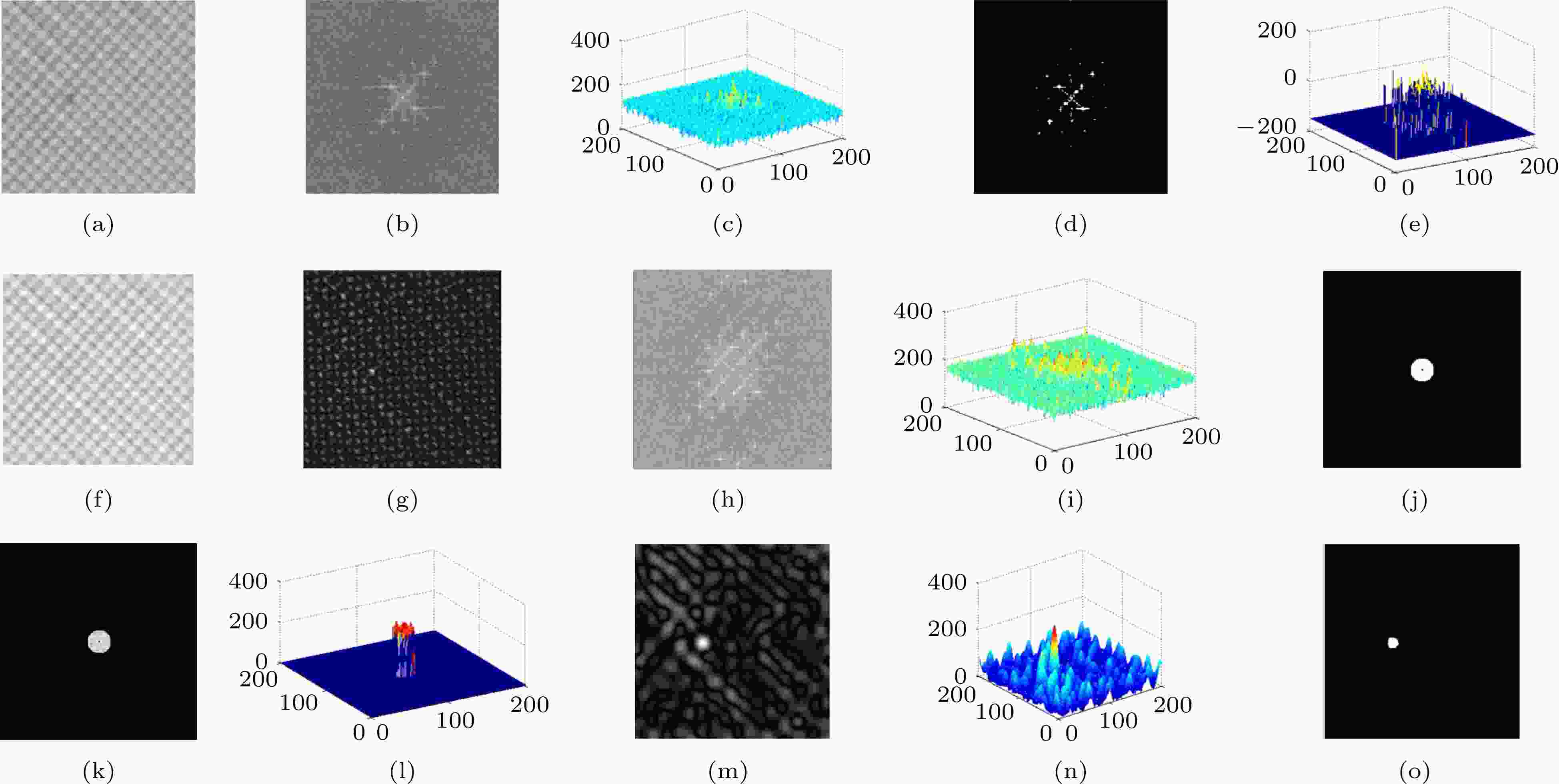图 8 二维相敏检波方法屏蔽玻璃缺陷识别过程　(a) 屏蔽玻璃原始二维图像; (b) 原始二维图像幅度谱2D显示; (c) 原始二维图像幅度谱3D网格显示; (d) 载波幅度谱2D显示; (e) 载波幅度谱3D网格显示; (f) 提取的载波图像; (g) 乘法器输出图像; (h) 乘法器输出图像幅度谱2D显示; (i) 乘法器输出图像幅度谱3D网格显示; (j) 滤波器幅度谱; (k) 滤波器输出图像幅度谱2D显示; (l) 滤波器输出图像幅度谱3D网格显示; (m) 滤波器输出图像2D显示; (n) 滤波器输出图像3D网格显示; (o) 缺陷二值化图像
Figure8. Detection process of defects in shielding glass for 2D PSD: (a) Original 2D image of shielding glass; (b) amplitude spectrum 2D display of original image; (c) amplitude spectrum 3D mesh display of original image; (d) amplitude spectrum 2D display of carrier; (e) amplitude spectrum 3D mesh display of carrier; (f) extracted carrier image; (g) output image of multiplier; (h) amplitude spectrum 2D display of output image of multiplier; (i) amplitude spectrum 3D mesh display of output image of multiplier; (j) amplitude spectrum 2D display of filter; (k) amplitude spectrum 2D display of output image of filter; (l) amplitude spectrum 3D mesh display of output image of filter; (m) 2D display of output image of filter; (n) 3D mesh display of output image of filter; (o) binary image of defect.

利用图7所示四种屏蔽玻璃缺陷检测算法对图6所示三种屏蔽玻璃典型缺陷图像进行缺陷识别, 识别结果如图9所示, 在此采用(5)式所示的信噪比的定义评价输出图像的质量. 直接滤波方法输出噪声较多, 信噪比最低; 整流 + 滤波方法信噪比有所提高; 两种不同载波提取方法实现的二维相敏检波都可以得到信噪比高的缺陷图像.
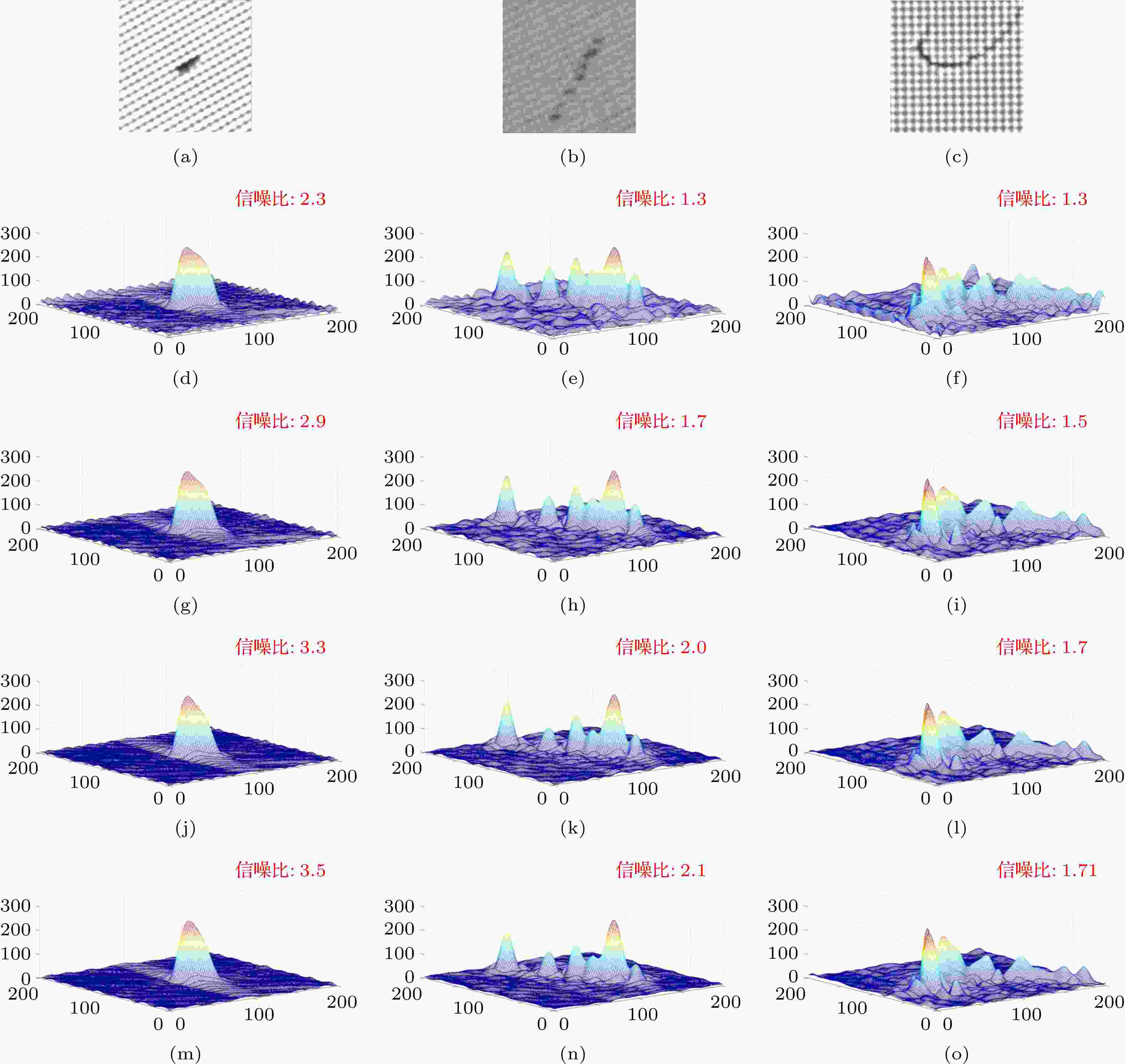图 9 四种屏蔽玻璃缺陷检测算法输出图像信噪比对比　(a) 黑点缺陷原始图像; (b) 划痕缺陷原始图像; (c) 白线缺陷原始图像; (d) 黑点缺陷直接滤波方法输出图像; (e) 划痕缺陷直接滤波方法输出图像; (f) 白线缺陷直接滤波方法输出图像; (g) 黑点缺陷整流滤波方法输出图像; (h) 划痕缺陷整流滤波方法输出图像; (i) 白线缺陷整流滤波方法输出图像; (j) 黑点缺陷二维相敏检波方法(近似提取载波)输出图像; (k) 划痕缺陷二维相敏检波方法(近似提取载波)输出图像; (l) 白线缺陷二维相敏检波方法(近似提取载波)输出图像; (m) 黑点缺陷二维相敏检波方法(精确提取载波)输出图像; (n) 划痕缺陷二维相敏检波方法(精确提取载波)输出图像; (o) 白线缺陷二维相敏检波方法(精确提取载波)输出图像
Figure9. Signal-to-noise ratio of defect output images for different detection methods: (a) Original 2D image of black spot defect; (b) original 2D image of scratch defect; (c) original 2D image of white line defect; (d) image of black spot defect achieved by filtering method; (e) image of scratch defect achieved by filtering method; (f) image of white line defect achieved by filtering method; (g) image of black spot defect achieved by rectifier + filtering method; (h) image of scratch defect achieved by rectifier + filtering method; (i) image of white line defect achieved by rectifier + filtering method; (j) image of black spot defect achieved by 2D PSD (extracting carrier approximately) method; (k) image of scratch defect achieved by 2D PSD (extracting carrier approximately) method; (l) image of white line defect achieved by 2D PSD (extracting carrier approximately) method; (m) image of black spot defect achieved by 2D PSD (extracting carrier accurately) method; (n) image of scratch defect achieved by 2D PSD (extracting carrier accurately) method; (o) image of white line defect achieved by 2D PSD (extracting carrier accurately) method.

2
4.2.二维相敏检波方法在普通玻璃缺陷检测中的应用
-->

4.2.二维相敏检波方法在普通玻璃缺陷检测中的应用

由于屏蔽玻璃中的金属丝网起到载波调制的作用, 因此在屏蔽玻璃缺陷检测中不需要外加载波信号, 而普通玻璃缺陷检测中为了消除各种环境光的影响, 可以采用对外加载波进行调制和解调的方法. 图10(a)所示为通过计算机软件生成的二维载波图像; 图10(b)为相机采集到的通过投影仪投射的未被调制的载波图像; 图10(c)为相机获取的、已被玻璃调制的图像; 图10(d)为强环境光下的已调制图像; 图10(e)为叠加了噪声的已调制图像; 图10(f)为(c)图所示已调制图像和(d)图强环境光下已调制图像解调后的图像; 图10(g)为(c)图所示已调制图像和(d)图强环境光下已调制图像解调后图像的3D网格显示; 图10(h)为(e)图所示叠加了噪声的已调制图像解调后图像的3D网格显示. 图10(f)和10(g)结果显示, 只要相机没有出现饱和的情况下, 环境光对玻璃缺陷的检测毫无影响, 图10(h)结果显示, 二维相敏检波方法可以有效抑制噪声对玻璃缺陷检测的影响.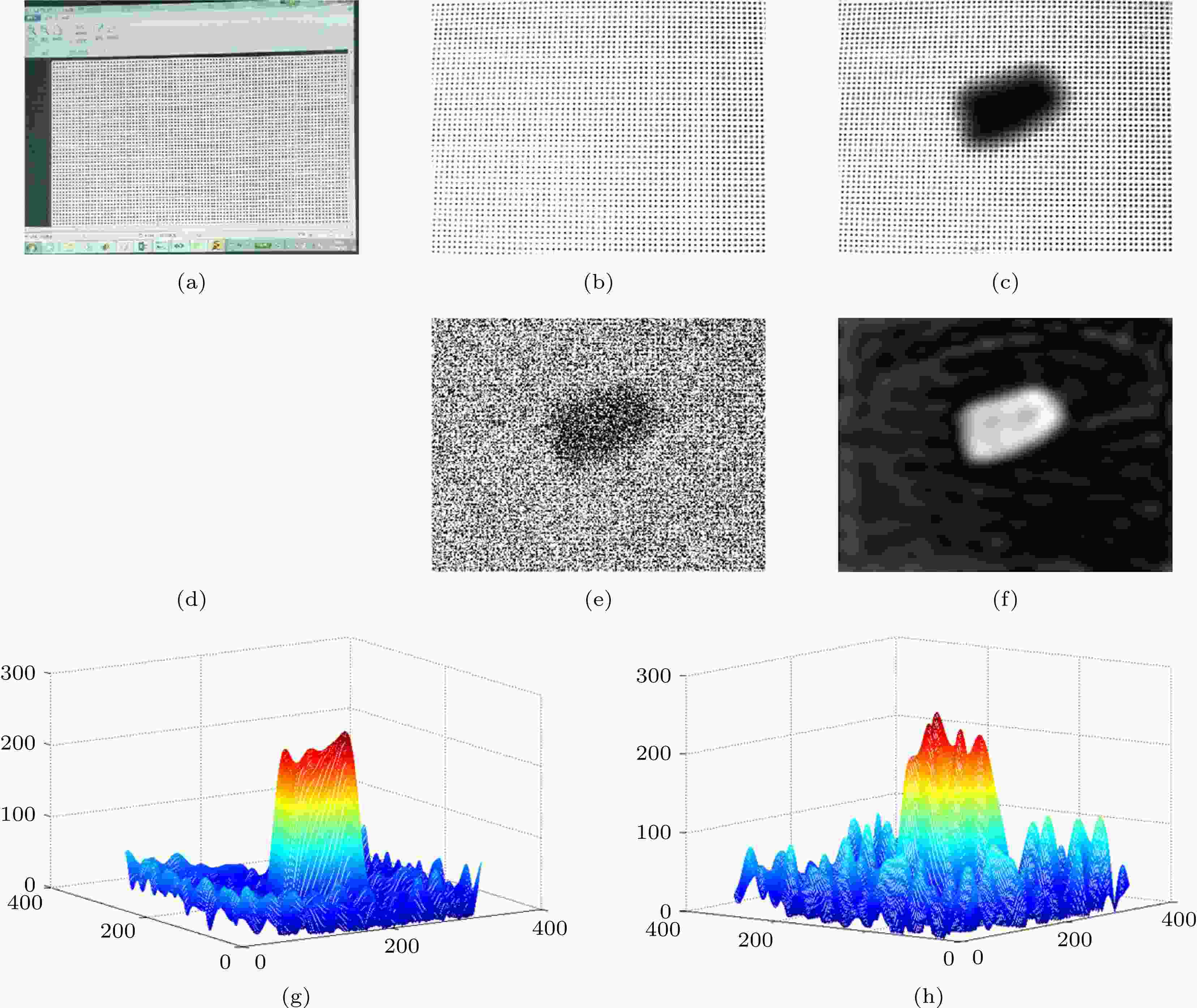
图 10 外加载波方法普通玻璃缺陷检测结果　(a) 软件生成的二维载波图像; (b) 投影仪投射的未加调制的载波图像; (c) 相机获取的已调制图像; (d) 强环境光下的已调制图像; (e) 叠加了噪声的已调制图像; (f)图(c)和(d)解调后的2D图像; (g)图(c)和(d)解调后的3D网格显示图像; (h) 图(e)解调后的3D网格显示图像
Figure10. Detection results of glass defects by using external carrier method: (a) 2D carrier image generated by software; (b) unmodulated carrier image projected by projector; (c) 2D modulated image acquired by camera; (d) modulated image in strong ambient light: (e) modulated image superimposed with noise; (f) demodulated 2D image of (c) and (d); (g) demodulated 3D mesh image of (c) and (d); (h) demodulated 3D mesh image of (e).

5.讨　论
在二维图像检测过程中容易受到各种干扰和噪声的影响, 降低检测的精度和目标识别的可靠性. 通过调制以后可以降低低频背景噪声的影响, 此外通过二维相敏检波方法可以大大抑制噪声, 提高输出信噪比. 二维相敏检波的本质是利用参考信号和被检波的调幅信号中的载波的相关性, 通过相乘的非线性作用将低频调制信号的频谱从高频载波的位置搬迁到更高频的位置以及低频位置, 再利用低通滤波器的选频特性提取低频调制信号; 二维相敏检波输出的频率范围是以载波频率为中心, 低通滤波器截止频率为半径的区域, 输出噪声的频谱也在此范围内, 因此, 当低频信号的频率非常低时, 可以设置非常低的低通滤波器截止频率, 输出噪声减少, 可以从噪声淹没的调幅信号中提取出低频信号; 在文中给出了正弦信号为载波的二维信号调制和解调过程, 在实际应用中以方波信号为载波的调制和解调过程具有方便、简单的特点, 同样可以提高抗干扰能力, 但输出噪声比正弦调制高; 二维相敏检波的对象是调幅信号, 调幅信号的形成可以采用照明光源载波驱动方式、机械调制方式等主动调制, 也可以采用像屏蔽玻璃这种检测对象自带载波形式.
6.结　论
文章提出了一种提高二维信号或二维图像输出信噪比的二维相敏检波器方法, 介绍了二维相敏检波器组成以及利用乘法器的非线性特性和低通滤波器选频特性抑制噪声原理; 利用二维相敏检波方法和整流 + 低通滤波方法实现了对二维调幅信号的解调, 并且验证了二维相敏检波方法与整流 + 低通滤波方法相比较抗干扰能力强, 具有提取淹没在噪声中的信号的能力; 把二维相敏检波方法用于实际的屏蔽玻璃缺陷和普通玻璃缺陷二维图像的处理, 与其它几种图像处理方法进行了对比, 结果表明二维相敏检波方法可以明显提高输出缺陷图像的信噪比, 有利于可靠、精确地识别缺陷的位置和大小. 在光学测量中如果采用主动调制方法, 二维相敏检波器可以利用已知的载波信号和被检的调幅波信号相乘; 如果载波信号未知, 则可以利用调幅信号的频域特征提取载波信号后再与被检的调幅信号相乘, 将二维相敏检波方法应用于光学检测等领域将极大提高检测微弱二维信号的能力. 虽然一维相敏检波器在锁相放大器领域得到广泛应用, 在一维的微弱信号检测中发挥了至关重要的作用, 在光学检测领域目前应用较多的是利用一维信号的时域调制减小背景光对测量的影响, 空域二维调制的应用还比较少. 本文提出的二维相敏检波方法将在空间调幅信号解调方面发挥其噪声抑制能力强的优势; 如果空间调制方式与时间调制方式相结合, 将在光学相干层析成像(OCT)等三维检测领域发挥其作用; 此外, 在光学成像过程中不仅混有噪声, 而且还会受到光学系统点扩张函数的影响, 因此, 将来结合点扩张函数影响的研究将有助于更好地发挥二维相敏检波器的作用.
相关话题/信号 图像 空间 测量 过程
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 人工磁导体对无线能量传输空间场的调控
    摘要:为了提高无线能量传输系统的传输效率,将正六边形人工磁导体结构引入非共振双线圈无线能量传输系统中,展开对空间场调控的研究.研究结果发现,在人工磁导体介入非共振双线圈无线能量传输系统后,在发射线圈和接收线圈之间的电磁场发生了变化,这是由于近磁场激发了人工磁导体的多个谐振模式,同时人工磁导体屏蔽了磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用海洋环境噪声空间特性估计浅海海底分层结构及地声参数
    摘要:海洋环境噪声场中包含了海洋中的诸多信息,海底地声参数是影响海洋环境噪声场空间分布的主要因素之一.对于不同的海底分层结构,海底反射损失会根据沉积层厚度和各层声速呈现出不同的临界角和干涉条纹结构.本文利用Harrison能流理论,从理想反射系数出发,分别考虑了声速、密度、衰减系数、沉积层厚度等几种 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种随机共振增强正弦信号的二次多项式接收方法
    摘要:针对雷达、通信系统的正弦中频信号在低信噪比中难以接收的问题,提出一种经随机共振增强正弦信号的接收方法.通过分析正弦信号的随机共振机理,引入判决时刻,将非自治的福克-普朗克方程(Fokker-PlanckEquation,FPE)转化为自治方程求解,得到FPE的含时间参量的周期定态解;在得到随机 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 氩气空心阴极放电复杂动力学过程的模拟研究
    摘要:利用流体模型模拟研究了氩气空心阴极放电的动力学过程.数值模型考虑了直接基态电离、基态激发、分步电离、潘宁电离、解激发、两体碰撞、三体碰撞、辐射跃迁、弹性碰撞和复合反应等31个反应过程.计算得到了电子密度,Ar+密度,激发态氩原子Ar4s、Ar4p、Ar3d能级的密度,电势和电场强度等的分布特性 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种基于压缩感知和多维混沌系统的多过程图像加密方案
    摘要:随着计算机科学的快速发展,信息的存储和传播常常在各类计算机硬件以及多种网络之间进行,传统的信息加密方案已逐渐不再适用.因此,基于计算机的信息加密算法近年来逐步成为研究热点.通过结合小波包变换、压缩感知、混沌系统等理论,一种基于压缩感知和多维混沌系统的多过程图像加密方案被提出.该加密方案实现了针 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用Kapitza-Dirac脉冲操控简谐势阱中冷原子测量重力加速度
    摘要:利用Feynman路径积分研究了简谐势阱中冷原子受到两次Kapitza-Dirac脉冲的干涉机制.理论研究表明:当初始态为简谐势阱的基态时,外场使不同模式的演化路径相对于没有外场情况下的路径发生偏离;同时外场强度和测量时刻相邻模式的相位差成线性关系;当外场为重力场时,测量重力加速度的精度可达1 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 扫频光学相干层析角膜图像轮廓自动提取算法
    摘要:在扫频光学相干层析系统中,远心扫描模式造成角膜图像中存在伪影、部分结构缺失及低信噪比区域,影响了角膜轮廓提取的精度.针对该问题,本文提出了一种针对低质量角膜图像的轮廓自动提取算法.该算法首先依据图像标准差分布将图像划分为高、低信噪比区域;针对高信噪比区域,通过峰值点定位法获取角膜轮廓;针对低信 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种精确测量原子喷泉冷原子团温度的方法
    摘要:冷原子团的高斯半径和温度是用来描述冷原子团,反映冷原子特性的主要参数.本文提出了一种新型的测量冷原子团高斯半径和温度的方法,采用过饱和近共振激光束照射冷原子团,原子由于吸收了光子动量偏离原来的运动轨道,而不能被探测系统所探测.根据冷原子团的原子分布规律,理论上构建了物理模型,通过改变作用于冷原 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于心脏电影磁共振图像的一种新的右心室多图谱分割方法
    摘要:基于心脏电影磁共振图像的右心室(RV)分割,对心脏疾病的诊疗及预后有着十分重要的意义.右心室结构复杂,传统图像分割方法始终未能达到较高的精度.多图谱方法通过配准和融合来实现RV分割,是近几年RV分割中的主要方法之一.本文提出一种新的右心室多图谱分割方法,能够实现RV的全自动准分割.本文首先采用 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 拉曼激光边带效应对冷原子重力仪测量精度的影响
    摘要:电光调制技术是产生拉曼光的几种方法之一,其优点是系统简单、易搭建且环境适应性强.然而,这种调制技术会产生额外的边带光,并影响冷原子干涉绝对重力仪的测量精度.本文利用自行研制的可移动冷原子重力仪,研究了边带效应对冷原子重力仪测量精度的影响.详细分析了拉曼反射镜的位置、拉曼脉冲的作用时刻及其间隔、 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.