摘要:针对表面声波作用下含不溶性活性剂的部分润湿薄液膜的铺展过程, 推导出了液膜厚度和表面活性剂浓度的无量纲演化方程组, 通过数值计算研究了声波引起的漂移流主导的液膜铺展过程及漂移流与毛细力共同控制的铺展过程. 结果表明表面声波驱使液膜铺展及移动, 而活性剂进一步促进了液膜的铺展过程, 且当活性剂存在时受漂移流与毛细力共同控制的铺展过程中出现了铺展半径收缩的现象, 使得液膜达到平衡状态所需的时间更长. 另外, 液膜最大厚度和铺展半径的变化速度随着分离压与活性剂浓度的相关系数α值、Marangoni数M值的增大而加快.
关键词: 表面声波/
活性剂/
铺展/
部分润湿薄液膜

English Abstract

全文HTML

--> --> -->

液滴或液膜的铺展过程在电子系统冷却^[1]、镀膜、喷墨印刷等领域具有广泛的应用^[2,3]. 常用的促进液滴铺展的手段有施加电场^[4] (电润湿)或磁场^[5], 添加表面活性剂或对液膜加热以引起Marangoni效应^[3]. 近年来, ****们发现以表面声波(surface acoustic wave, SAW)形式传播的MHz级高频振动可驱使位于固体基底上的完全润湿液膜铺展甚至移动^[6,7], 而部分润湿液膜只有在添加活性剂使其表面张力减小后才可在SAW作用下铺展^[8,9]. 深入研究活性剂对SAW作用下部分润湿液膜铺展的影响有助于精准控制液膜运动, 进而改进工艺和提高产品质量.
由Friend和Yeo领导的研究组在2011—2015年间对SAW作用下的液滴或液膜铺展现象进行了一系列研究^[6,7,10,11]. 2011年, 他们通过实验观察到在声波引起的MHz级振动作用下的液滴平衡状态取决于它所在基底的润湿性, 进一步分析发现声辐射压使液滴在垂直方向上变形, 而边界层流驱使接触线移动及液滴铺展^[10]. 2012年, Rezk等^[7]发现固着油滴在SAW作用下产生了所谓的“声润湿”现象、指进不稳定现象和类孤子波. Rezk等^[6]通过另一个实验发现受SAW作用的硅油液膜的稳定状态与液膜厚度有关, 且在薄膜的铺展过程中出现了两次流动方向的转变. 2015年, Manor等^[11]推导出了液膜在SAW作用下铺展的具有普适性的控制方程, 并根据该控制方程分析了液膜的铺展动力.
上述研究对象均是完全润湿液膜, 而之前的研究表明部分润湿液膜无法在高频振动作用下铺展, 若振动强度进一步提升则会发生雾化^[12,13]. 但Altshuler和Manor^[8,9]发现往水膜添加表面活性剂使其表面张力减小后, 水膜可以在SAW作用下进行铺展. 他们的实验结果表明振动强度一定时, 液膜前缘的移动速度和活性剂浓度正相关; 提高振动强度可以加快液膜前缘的移动速度, 且移动速度随θ³/We的减小而增大, 其中θ表示三相接触角, We为Weber数. 在理论研究方面, Altshuler和Manor^[8]考虑毛细力、声辐射压、分离压作用, 分别建立了不含活性剂的薄液膜厚度方程和不含活性剂的厚液膜厚度方程, 提出用无量纲数θ³/We来阐述控制部分润湿水膜铺展的动力学机理. 2016年, Altshuler和Manor^[9]又通过数值计算求解不含活性剂的薄液膜厚度演化方程, 分别探究了部分润湿薄液膜铺展过程受声波引起的漂移流主导和受毛细力、漂移流共同控制及受毛细力主导时的动力学特征.
研究表明, 活性剂的存在可以通过两种途径影响液膜的流动: 首先, 活性剂会降低液体的表面张力, 因而活性剂浓度分布不均将导致液体由高浓度区(低表面张力)流向低浓度区(高表面张力), 即引发Marangoni效应, 促使浓度分布趋于均匀, 加速液膜变薄^[14]; 其次, 活性剂的特性和浓度将影响分离压^[15]. 一般认为, 纯水中由于水偶极子的吸附作用而使界面带负电荷^[16], 当纯水中加入表面活性剂时, 活性剂的类型和浓度均会对静电作用力产生影响^[17], 进而影响分离压. 而分离压是影响超薄液膜去润湿稳定性的主要因素^[11].
综上所述, SAW作用下的液膜铺展实验已开始涉及表面活性剂的影响, 但该领域已有的理论模型尚未将这一影响加以考虑. 因此, 本文在已有的SAW驱动液膜流动的模型中引入活性剂浓度对分离压和表面张力的影响, 利用数值模拟研究部分润湿薄液膜在声波与毛细力不同相对贡献度下的铺展过程, 并讨论了分离压和Marangoni效应对铺展过程的影响.

如图1(a)所示, 有一厚度为h ^*(x ^*, t ^*)的含活性剂水膜放置在SAW器件的压电铌酸锂(lithium niobate, LN)基底上(上角标*表示有量纲量, 下同). SAW器件上的叉指换能器(interdigital transducer, IDT)通过逆压电效应将输入的高频电信号转换成高频声信号, 此声信号沿LN基底表面传播. 水膜的有量纲静态三相接触角为θ ^*, 初始时固体表面和液膜均处于平衡状态, 液膜在频率为f ^* = 20 MHz的瑞利SAW的激励下沿声波传播方向铺展. 声波在水中传播的声速v _l ^*约为1500 m/s^[11], 则渗透进液膜的声波波长λ_l ^* = v _l ^*/f ^* ≈ 75 μm.
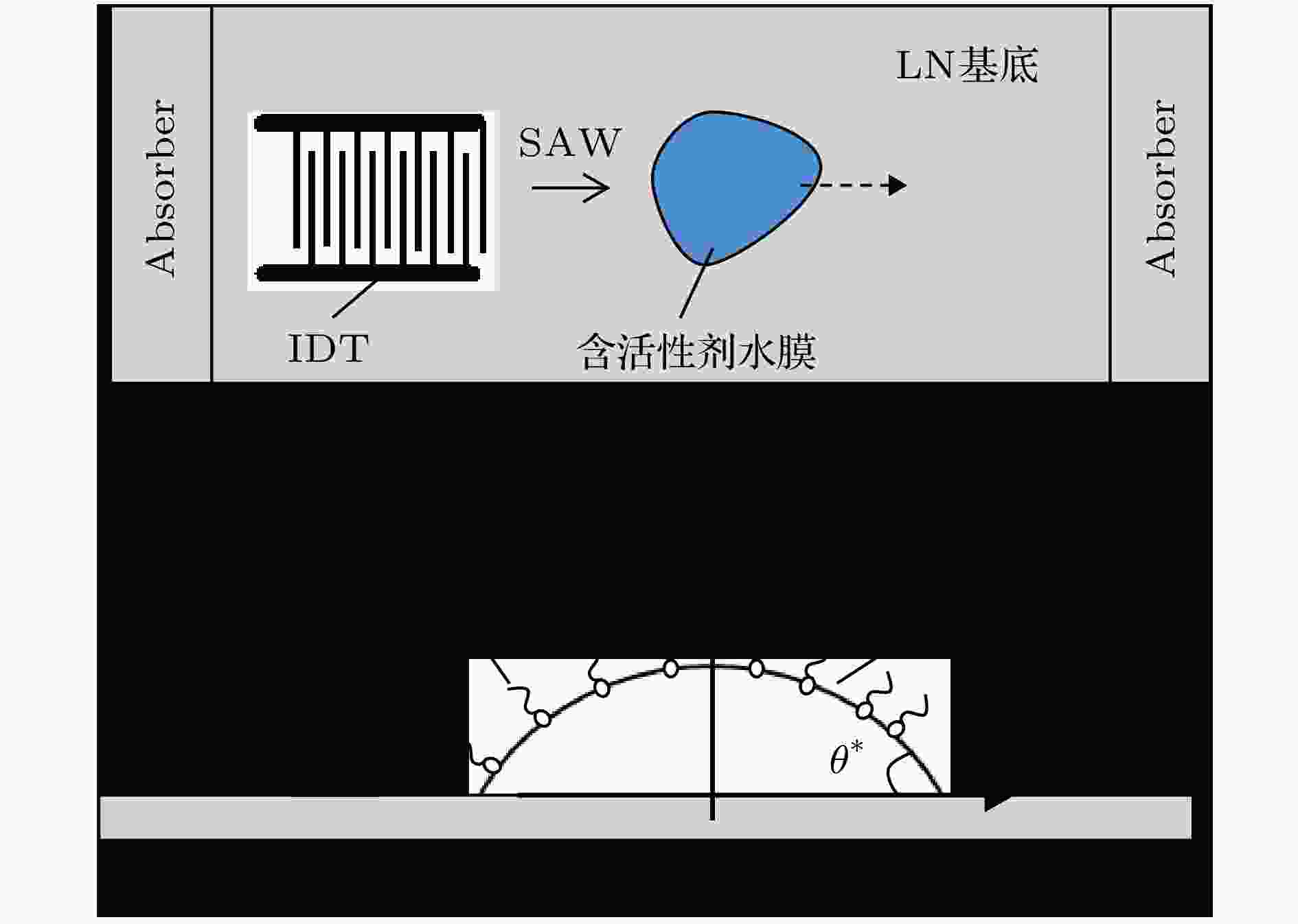图 1 放置在SAW器件上的含活性剂薄水膜示意图　(a)俯视图; (b)正视图
Figure1. Schematic diagram of thin water film with surfactant on a SAW device: (a) Top view; (b) front view.

本文研究的薄液膜厚度h^* $\ll $ λ_l^*, 此时声波渗透并在液膜内积累的能量较少, 声波在液体里面的衰减程度也很小, 故声辐射压和Eckart流的影响可以忽略不计^[6,11].
液膜运动过程的控制方程包括连续性方程和动量方程:

${\nabla ^ * } \cdot {{ u}^ * } = 0,$

$ {\rho ^ * }\left( {{\partial _{{t^ * }}}{{{u}}^ * } + {{{u}}^ * } \cdot {\nabla ^ * }{{{u}}^ * }} \right) + {\nabla ^ * }{p^ * } - {\mu ^ * }{\nabla ^ {*2} }{{{u}}^ * } = 0, $

其中${{{u}}^{*}} = \left( {u_{{x^ * }}^ *,u_{{y^ * }}^ * } \right)$, $u_x^ * $, $u_y^ * $为液膜的水平速度分量和纵向速度分量; ${\partial _{\left[ \cdot \right]}}$表示对参数[·]求导, ${\nabla ^ * }$为梯度算子; t^*表示时间; ρ^*, μ^*, p^*分别为液体的密度、动力黏度和压强.
本文研究中活性剂为不溶性, 即活性剂仅存在于液膜表面, 不存在y方向上的扩散. 表面活性剂浓度的对流扩散方程为^[15,18]

${\partial _{{t^ * }}}{G^ * } = - {\partial _{{x^ * }}}\left( {u_x^{{\rm s} * }{G^ * }} \right) + D_{\rm{s}}^ * {\partial _{{x^ * }{x^ * }}}{G^ * },$

式中D_s^*为扩散系数, $u_x^{{\rm s} * }$为水平表面速度, G^*表示活性剂浓度.
固体表面的速度边界条件为

${\left( \begin{aligned}u_x^ * \\u_y^ * \end{aligned} \right)_{{y^ * } = 0}} = \left( \begin{aligned}& {U^ * }\cos \left( {{\omega ^ * }{t^ * } - {k^ * }{x^ * }} \right)\\& \chi {U^ * }\cos \left( {{\omega ^ * }{t^ * } - {k^ * }{x^ * } - {\varphi ^ * }} \right)\end{aligned} \right),$

式中, U^*, ω^*, φ^*, k^*分别为声波的振动速度幅值、角频率、横向分量和纵向分量的相位差、声波波数. χ为液膜的纵向速度幅值和横向速度幅值的比值, 本文取χ = 1.
运动学边界条件为

${\partial _{{t^ * }}}{h^ * } + {u_{{x^ * }}}{\partial _{{x^ * }}}{h^ * } = u_{{y^ * }}^ *, y=h^*.$

表面张力与活性剂浓度间的关系为

${\gamma ^ * }\left( {{G^ * }} \right)=\gamma _0^ * - {\varSigma ^ * }{G^ * },$

其中${\gamma ^ * }\left( {{G^ * }} \right)$为表面张力, $\gamma _0^ * $为液膜不含活性剂时的表面张力; Σ ^*为由浓度引起的表面张力梯度, Σ^* = dγ ^*/dG ^*.
考虑活性剂浓度对表面张力的影响, 在液膜表面切应力${\tau ^ * }$与表面张力梯度${\partial _{{x^ * }}}{\gamma ^ * }$近似平衡, 因此结合(6)式可得

${\tau ^ * } \approx {\partial _{{x^ * }}}{\gamma ^ * } = - {\varSigma ^ * }{\partial _{{x^ * }}}{G^ * }.$

气液界面上的切应力和法向应力满足

${\left( \begin{aligned} {\partial _{{y^ * }}}u_{{x^ * }}^ * \\ {\partial _{{y^ * }}}u_{{y^ * }}^ *\end{aligned} \right)_{{y^ * } = {h^ * }}} \!=\!\left( \begin{aligned}& - {\mu ^{ * - 1}}{\varSigma ^ * }{\partial _{{x^ * }}}{G^ * } \\& {\left( {2{\mu ^ * }} \right)^{ - 1}}\left[ {2(\gamma _0^ * \!-\! {\varSigma ^ * }{G^ * }){\kappa ^ * } \!-\! {\varPi ^ * }} \right]\end{aligned} \right),$

式中, ${\kappa ^ * }$为液膜曲率, 近似等于${\partial _{{x^ * }{x^ * }}}{h^ * }$; ${\varPi ^ * }$表示分离压.
考虑活性剂浓度对分离压的影响, 采用如下模型^[19]:

${\varPi ^ * } = - \left[ {A{A^ * }{\left( {\frac{{h_{\rm{f}}^ * }}{{{h^ * }}}} \right)^3} - B{B^ * }{\left( {\frac{{h_{\rm{f}}^ * }}{{{h^ * }}}} \right)^2}} \right]\left( {\frac{{h_{\rm{f}}^ * }}{{{h^ * }}} - C} \right),$

式中$h_{\rm{f}}^ * $为预置液膜厚度, C为分离压稳定常数. 为考虑活性剂浓度对分离压的影响, 以文献[17]的实验结果为基础, 令系数BB与活性剂浓度相关, 而AA为常数, 即$A{A^ * } \!=\! 3h_{\rm{f}}^{ * 3}\gamma _0^ * \varepsilon {\theta ^2}/h_{\rm{f}}^{ * 4}$, $B{B^ * }\! =\! 3h_{\rm{f}}^{ * 3}\gamma _0^ * \varepsilon {\theta ^2}/ $ $h_{\rm{f}}^{ * 4} + {\alpha ^ * }{G^ * }$. 其中$\varepsilon ={\left( {{\delta ^ * }/{H^ * }} \right)^{\frac{1}{3}}}$, δ ^*, H ^*分别表示SAW的黏性渗透长度和初始时刻液膜厚度的最大值; θ为无量纲接触角, 为了能更好地与Altshuler和Manor^[8]的实验进行对比, 结合实验数据及本文数值计算取值推算出接触角无量纲化时的相对角度为120°, 即$\theta = {\theta ^ * }/{120^ {\circ} }$; ${\alpha ^ * }$为分离压与活性剂浓度的线性相关系数.
借鉴Altshuler等^[8]和Morozov等^[20]建立理论模型的方法, 采用如下转换式对上述方程进行无量纲化:

$\begin{split}\left( {{h^ * },h_{\rm{f}}^ * } \right) \, & = {H^ * }\left( {h,{h_{\rm{f}}}} \right), \\\left( {{p^ * },{\varPi ^ * }} \right)& = \left( {\gamma _0^ * {\theta ^2}{\varepsilon ^2}/{H^ * }} \right)\left( {p,\varPi } \right),\; {G^ * } = G_m^ * G,\\{x^ * } \, & = \left( {{H^ * }/\theta \varepsilon } \right)x,\;{t^ * } = \left( {{H^ * }/Re{U^ * }\theta \varepsilon } \right)t,\end{split}$

其中$ Re = {\rho ^ * }{U^ * }{\delta ^ * }/{\mu ^ * }$.
由于SAW在液膜中会引起对流漂移流^[21], 液膜在漂移流驱动下铺展及移动^[8,9], 因此液膜运动过程中的惯性效应不能忽略. 本文考虑的是不可压缩流的二维流动, 故在建模过程中引入流函数$\psi $来代替$\left( {{u_x},{u_y}} \right)$以减少未知数个数, 速度分量与流函数关系为$\left( {{u_x},{u_y}} \right) = \left( {{\partial _y}\psi, - {\partial _x}\psi } \right)$. 将流函数渐近展开, 通过时均计算忽略周期分量的影响并提取出稳定分量, 即将惯性项的作用简化为对流项. 最终得到液膜厚度h和表面活性剂浓度G的无量纲演化方程组:

$\begin{split} {\partial _t}h =\; & - \frac{{{\theta ^3}}}{{3We}}{\partial _x}\left[ {{h^3}\phi {\partial _{xxx}}h} \right] \\ & + \frac{{{\theta ^3}}}{{3We}}{\partial _x}\left( {{h^3}{\partial _x}\varPi } \right) - {\partial _x}\left[ {hf(\xi)} \right] \\ & + \frac{M}{2}{\partial _x}\left( {{h^2}{\partial _x}G} \right), \end{split}$

${\partial _t}G = - {\partial _x}(u_x^{\rm{s}}G) + \frac{{\theta \varepsilon }}{{Re}}\frac{1}{{Pe}}{\partial _{xx}}G, \qquad$

$u_x^{\rm{s}} = R\left( \xi \right) + \frac{1}{2}\frac{{{\theta ^3}}}{{We}}{h^2}\left[ {\phi {\partial _{xxx}}h - {\partial _x}\varPi } \right] - Mh{\partial _x}G,$

其中$\xi = {H^ * }h/{\delta ^ * }$, $ \phi =1 - {{\varSigma ^ * }G_m^ *}G / {{\gamma _0^ * }}$; Weber数$We = \rho^ * {U^{ * 2}}{H^ * }/ {\gamma _0^ * }$, Peclet数$Pe ={{{U^ * }{L^ * }}}/{{D_s^ * }}$, Marangoni数$M ={\theta \varepsilon {\varSigma ^ * }G_m^ *}/ \rho^ * {\delta ^ * }{U^{ * 2}}$; ${L^ * }$为特征长度, H ^*/L ^* = 0.01. θ³/We表征毛细力作用和SAW作用的相对大小, 当θ³/We < 1, 毛细力较小, 薄液膜铺展过程主要受SAW引起的漂移流控制; 当θ³/We = 1, 毛细力影响增大, 漂移流和毛细力共同主导铺展过程; 当θ³/We > 1, 毛细力控制铺展过程^[8]. (11)式中, f(ξ)为SAW引起的无量纲拖拽速度(dragging velocity),

$ \begin{split} & f\left( \xi \right) \\ = \, & \frac{1}{{4\xi }}\left(\!{\frac{{\xi \sinh \left( {2\xi } \right) - \xi \sin \left( {2\xi } \right) + 2\cos \left( \xi \right)\cosh \left( \xi \right)}}{{\cos \left( {2\xi } \right) + \cosh \left( {2\xi } \right)}} - 1}\!\right).\end{split}$

(13)式中, R(ξ)为

$R\left( \xi \right) = \frac{{\sinh (2\xi) - \sin (2\xi)}}{{4\left[ {\cos \left( {2\xi } \right) + \cosh \left( {2\xi } \right)} \right]}}.$

方程(11)右侧第一项表征毛细力作用; 第二项为分离压作用; 第三项是SAW引起的质量漂移流带来的影响, 即对流作用项; 最后一项则是表面活性剂对流扩散形成浓度梯度的影响. 这四个作用项决定了液膜流量. 当G为0时, (11)式与Altshuler和Manor^[9]推导出的不含活性剂的薄液膜厚度方程完全相同.
水膜添加表面活性剂后表面张力和接触角减小, 液膜性质接近于完全润湿液膜, 因此在本文中采用预置液膜以解决三相接触线处的应力集中问题^[2]. 设置初始时刻的液膜形状为抛物形, 活性剂浓度在液膜表面均匀分布, 在预置液膜区域为0:

$\begin{split} h\left( {x,0} \right) =\, & \left( {1 + b - {x^2}} \right)\left[ {F\left( {1 - x} \right) - F\left( { - 1 - x} \right)} \right] \\ & + b\left[ {F\left( {x - 1} \right) + F\left( { - 1 - x} \right)} \right], \\[-15pt]\end{split}$

$G\left( {x,0} \right) = {G_0}\left[ {F\left( {1 - x} \right) - F\left( { - 1 - x} \right)} \right],$

(17)式中G₀表示初始状态下最大的无量纲活性剂浓度; $F\left( x \right) = 0.5\left[ {1 + \tanh (100x)} \right]$为海氏阶跃函数; 无量纲预置液膜厚度$b = h_{\rm{f}}^ */{H^ * }$. 预置液膜的实际厚度约为1—10 nm^[22,23], 但在数值模拟中当h_f^*取值较小时计算过程无法顺利进行. 因此借鉴Altshuler和Manor^[8,9]的经验, 我们适当放大预置液膜厚度的取值, 令b = 0.1.
计算中边界条件为

${\partial _x}h\left( {{x_{ - \infty }},t} \right) = {\partial _{xxx}}h\left( {{x_{ - \infty }},t} \right)=0,$

${\partial _x}h\left( {{x_{ + \infty }},t} \right) = {\partial _{xxx}}h\left( {{x_{ + \infty }},t} \right)=0,$

${\partial _x}G\left( {{x_{ - \infty }},t} \right) = {\partial _x}G\left( {{x_{ + \infty }},t} \right) = 0.$

本文采用PDECOL程序求解上述演化方程, 如无特殊说明, 计算区域取[–150, 150]. 初步计算时, 尝试时间步长分别取10^–14, 10^–15和10^–16, x方向的网格数分别取2000, 3000和4000, 将时间步长和网格数两两组合进行计算, 发现当网格数为3000, 时间步长为10^–15时可同时满足精确性与高效性的要求. 参照文献[8, 9, 19, 24, 25], 可得液膜有量纲基本参数的取值范围(表1)和无量纲参数的取值范围(表2), 下文数值计算中相关参数的取值即以此为基础. 其中, 表面活性剂相关参数取值参照Altshuler和Manor^[8,9]在实验中所采用的表面活性剂SDS(十二烷基硫酸钠)取值.

有量纲参数	符号	单位	取值范围
表面张力系数	${\varSigma ^ * }$	N·m2/mol	5 × 10–3
液膜无活性剂时表面张力	γ0*	N/m	0.072
液体黏度	μ*	Pa·s	0.001
液体密度	ρ*	kg/m3	1000
SAW速度振幅	U *	m/s	0.1—0.26
液膜最大厚度	H *	m	10–7—9 × 10–6
液膜特征长度	L*	m	10–5—9 × 10–4
临界胶束浓度	Gm*	mol/L	0.0086
初始时刻最大活性剂浓度	G0*	mol/L	0.002—0.0086
有量纲三相接触角	θ*	(o)	3—28
表面扩散系数	Ds*	m2/s	10–8—10–6
黏性渗透长度	${\delta ^ * }$	m	10–7

表1有量纲参数取值范围
Table1.Order of magnitude estimates for dimensional parameters.

无量纲参数	定义	取值范围
无量纲预置液膜厚度	hf	0.1
分离压稳定常数	C	0.5
初始活性剂浓度的 最大值	G0	0.2—1
厚度小量	ε = (δ */H *)1/3	0.22—1
分离压与活性剂 浓度的相关系数	α	–100—100
无量纲三相接触角	θ = θ */120°	0.025—0.233
Marangoni数	$ M = \theta \varepsilon \varSigma ^ * G_m^ */{\rho ^ * }{\delta ^ * }{U^{ * 2} }$	0.1—100
Weber数	We = ρ*U*2H*/γ0*	10–5—5 × 10-3
Reynolds数	Re = ρ*U*δ*/μ*	0.01—0.03
Peclet数	Pe = U*L*/Ds*	1—1000

表2无量纲参数取值范围
Table2.Order of magnitude estimates for nondimensional parameters.

2

-->

3.1.漂移流起主导作用时液膜的铺展过程

对于声波引起的漂移流起主导作用时的液膜铺展过程, 为突出声波作用并验证完全润湿液膜铺展过程, 取θ^* = 3°, θ³/We = 0.01, 计算区域为[–2, 18]. 计算中其他参数的取值为H ^*/δ ^* = 4, U ^* = 0.25 m/s, G₀ = 0.93, Pe = 200, α = 40, M = 8, 此时部分润湿液膜和完全润湿液膜的铺展过程相近. 如图2所示, 液膜的铺展过程分为两个阶段. 在第一阶段(t = 0—74)中, 液膜后缘流体在漂移流作用下不断向前缘输运, 流体在前缘的积累使得液膜曲率增大, 从而表面张力和液膜厚度增加, 接触角也随之变大, 因此液膜前缘x _f在漂移流的作用下迅速向声波传播方向移动; 反之, 后缘液膜厚度不断降低, 固体基底与液膜的接触角减小, 后缘x _r移动极其缓慢; 液膜铺展半径、最大厚度分别随时间快速增大和减小, 表面活性剂在对流作用下迅速向两端扩散. 到了第二阶段(t = 74—200), 液膜铺展速度减小, 液膜最大厚度缓慢降低, 铺展半径增大速度相比第一阶段明显减慢, 活性剂浓度分布接近均匀.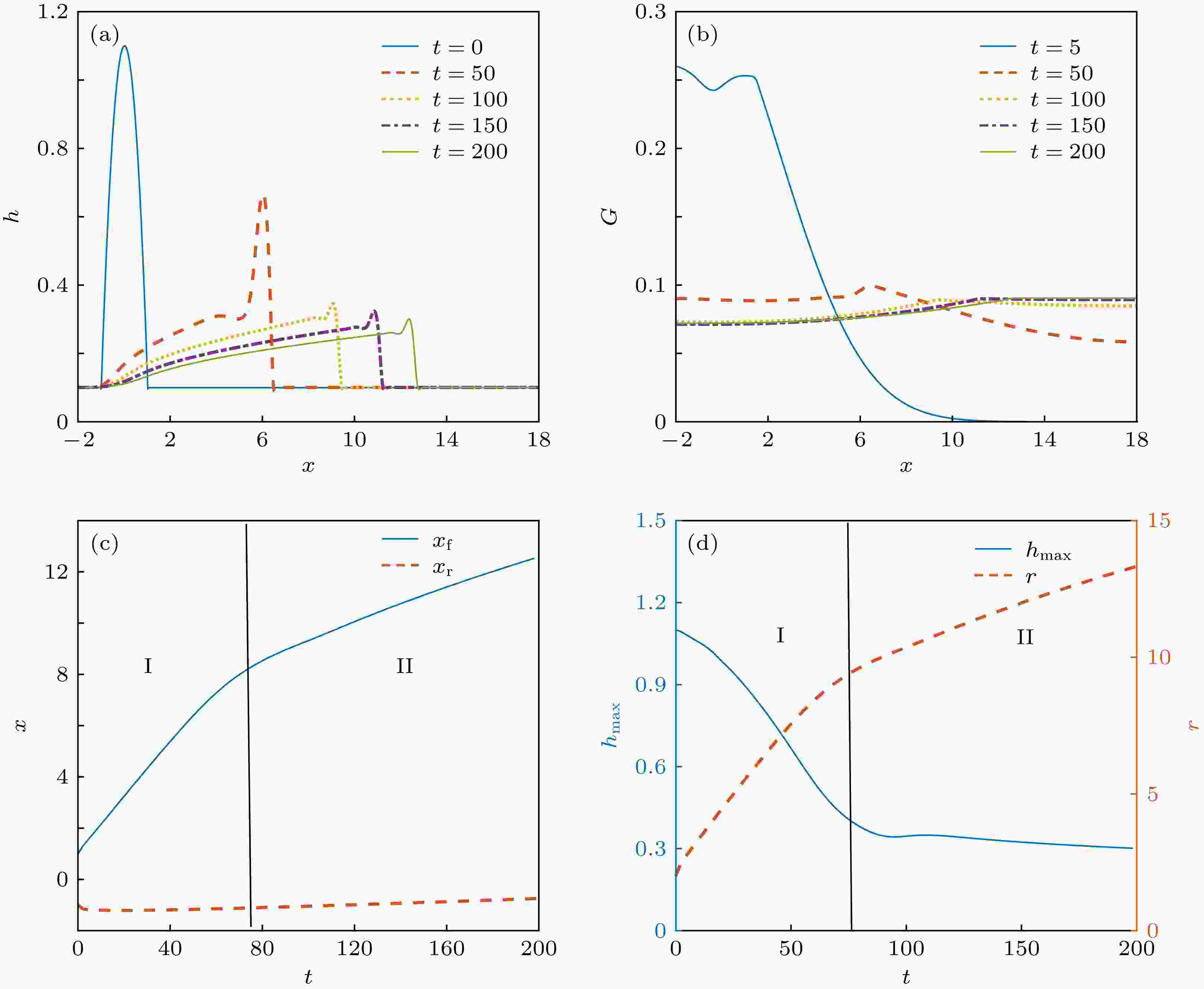
图 2 漂移流起主导作用, 考虑活性剂影响时水膜的铺展过程　(a)液膜厚度; (b)活性剂浓度; (c)液膜前缘x_f与后缘x_r; (d)最大厚度与铺展半径
Figure2. Spreading process when the drift of mass governs the film dynamics: (a) Film thickness; (b) surfactant concentration; (c) the position of the front x_f and the rear x_r of the liquid film; (d) maximal thickness and spreading radius of the liquid film.

为进一步讨论液膜内部液体的流动情况, 绘制了t = 10 (第一阶段)和t = 100 (第二阶段)时的流线图和水平速度等值图, 如图3所示. 在图3(a)中, 液膜内部的液体水平速度均大于0, 说明液体在漂移流带动下总是沿声波传播方向流动; 在垂直方向上, 液膜上部的流线呈开口向下的抛物线形状, 说明液体运动轨迹为从液膜后缘往顶部移动再回流到前缘, 这正是液膜顶部形成小锥形的原因. 比较图3(a)和图3(b)可知, 两者的流动趋势大体一致, 但前者的水平速度是后者的水平速度的好几倍, 这解释了第二阶段液膜铺展速度比第一阶段慢得多的原因.
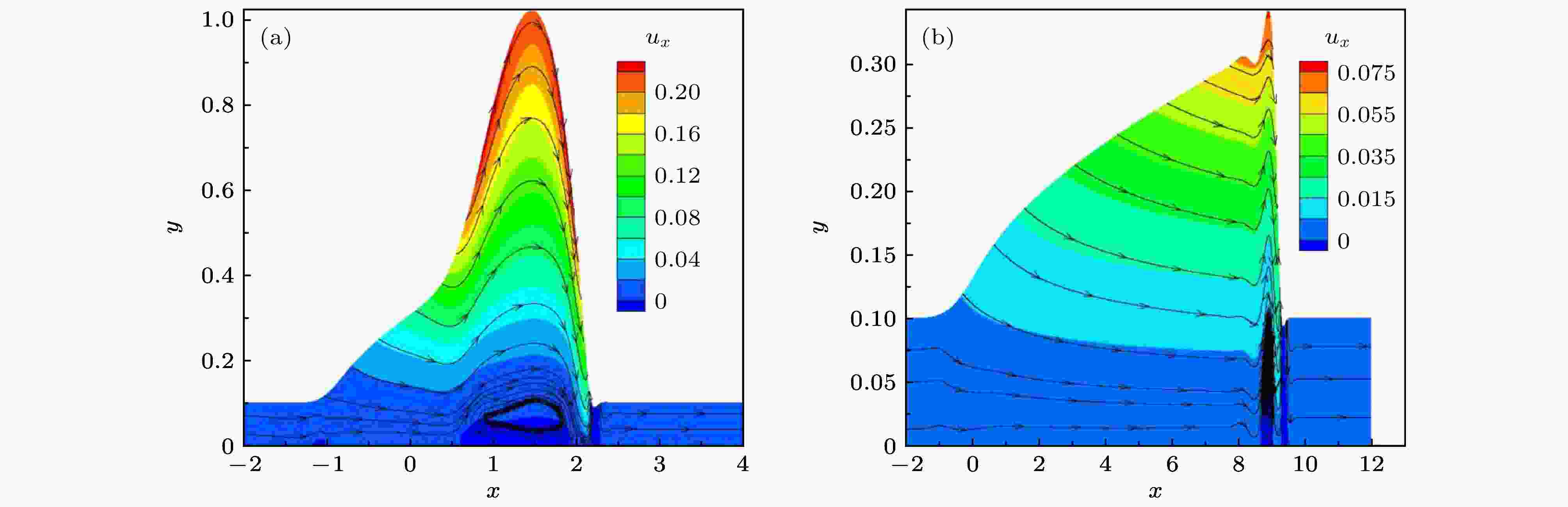图 3 不同时刻下液膜内部的流线与水平方向分速度　(a) t = 10; (b) t = 100
Figure3. Horizontal velocity contour within the film along with streamlines at different time: (a) t = 10; (b) t = 100.

图4比较了其他参数取值相同, 考虑活性剂影响和不考虑活性剂影响两种情况下液膜的铺展过程. 可以发现考虑活性剂影响时, 液膜的铺展速度在第一阶段更快, 但到了第二阶段后则不再有“优势”. 这是因为初始时刻时, 含活性剂液膜中部的活性剂浓度高, 表面张力较小, 两端活性剂浓度低, 表面张力较大, 液体在Marangoni效应的推动下向外流动. 当铺展过程进行到第二阶段后, 活性剂浓度分布趋于均匀, Marangoni效应较弱, 而SAW引起的漂移流拖拽速度随着液膜厚度降低而减小^[20], 因此含活性剂液膜沿声波传播方向铺展的速度逐渐减慢. 当含活性剂液膜的厚度与不含活性剂液膜趋于一致时, 两者铺展速度相近, 前缘间的距离几乎不变.
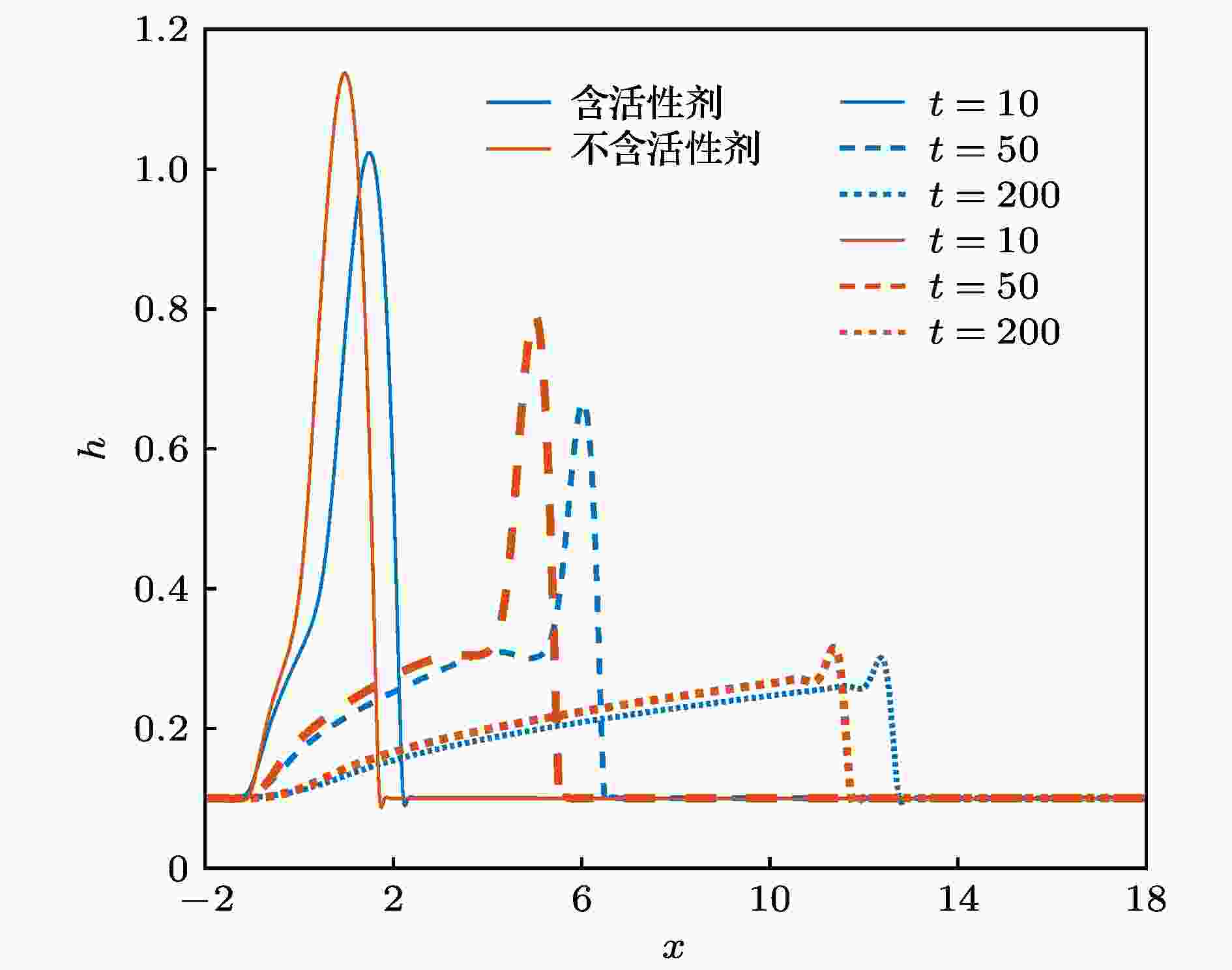图 4 漂移流主导时, 考虑活性剂影响和不考虑活性剂影响的液膜演化过程对比
Figure4. Film profiles at different times during the drift governed spreading process with (blue line) and without (orange line) considering the effect of surfactant.

Rezk等^[6]将μ^* = 50 mPa﹒s的硅油液膜放置在LN基底上, 液膜在f ^* = 19.5 MHz, U ^* = 0.1 m/s的SAW作用下沿声波传播方向铺展, 其前缘位置与时间满足x_f^*～t^*n的规律, 指数n从最初的1.55逐渐减小, 当时间t^*超过110 s后, 该指数趋近于0.25, 如图5所示. 另外, Rezk等^[7]又通过实验发现黏度为100 mPa﹒s的硅油液膜在频率为19.5 MHz的SAW作用下铺展时, 在对数坐标下, 液膜前缘的移动速度dx_f ^*/dt^*随着振动速度幅值U ^*的平方的增大呈线性增加, 如图6所示. 当θ³/We = 0.01时, 本文中水膜的铺展过程与完全润湿硅油膜类似. 将有量纲化后的模拟结果与Rezk等在文献[6]中的实验结果比较, 总体趋势符合良好, 但幂指数n的值有微小差异(图5). 对比有量纲化后的数值计算结果与Rezk等在文献[7]中的实验结果, 发现模拟结果和实验结果的规律相同, 但硅油膜前缘移动速度大于水膜前缘的移动速度, 如图6所示. 造成速度不同的原因可能是虽然硅油膜的黏度大于水膜, 但硅油液膜的表面张力比水膜小, 而液膜的铺展速度随着表面张力的减小而加快^[8].
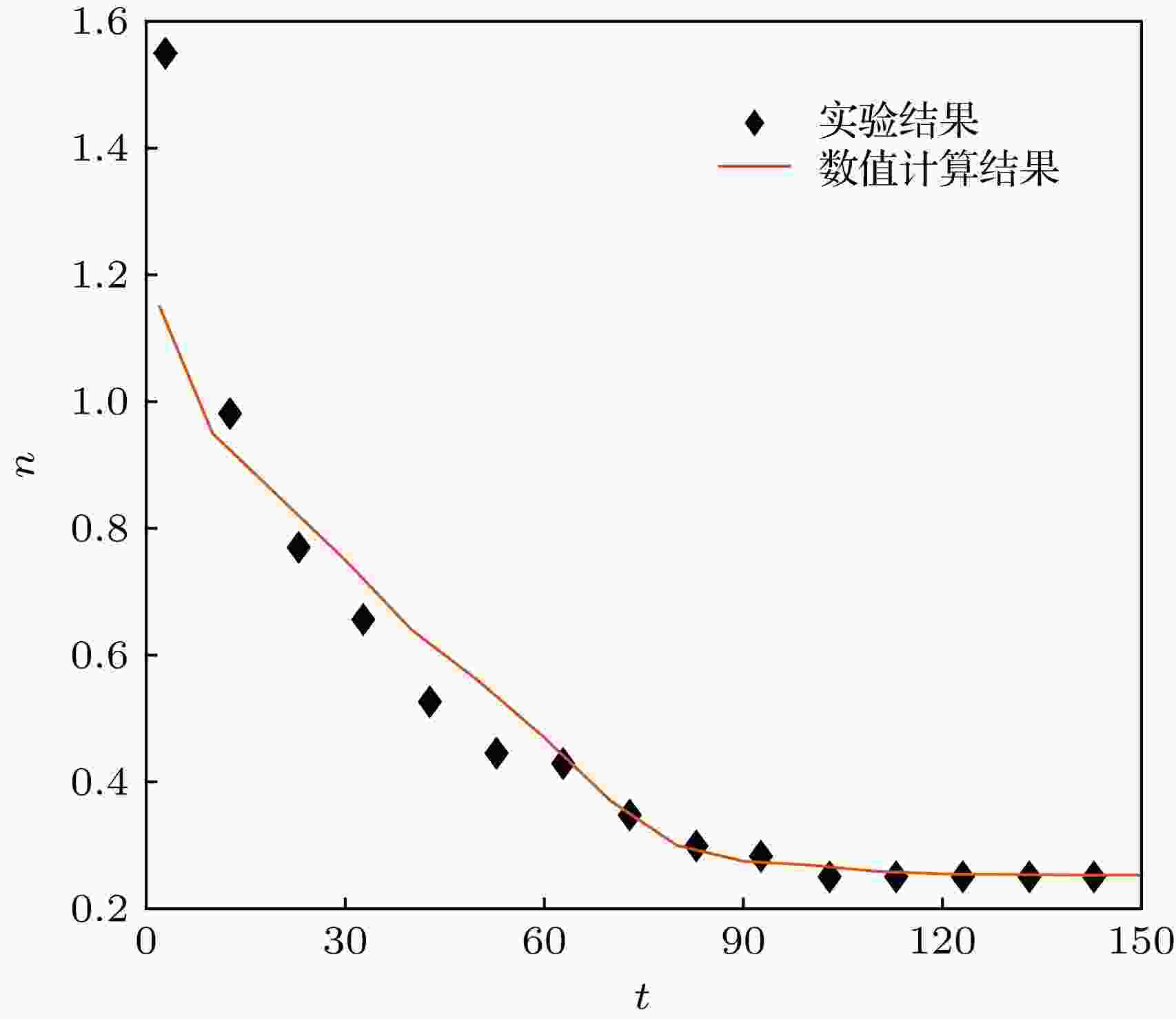图 5 漂移流主导时, 幂指数n随时间t^*的变化与Rezk等^[6]的实验结果的对比(液膜前缘位置与时间满足规律x_f^*～t^*n)
Figure5. Comparison between simulated and experimental^[6] results for the variation of exponent n with dimensional time during the drift governed spreading process (the variation of the position of the front of the film with time accords to the power laws x_f^*～t^*n).

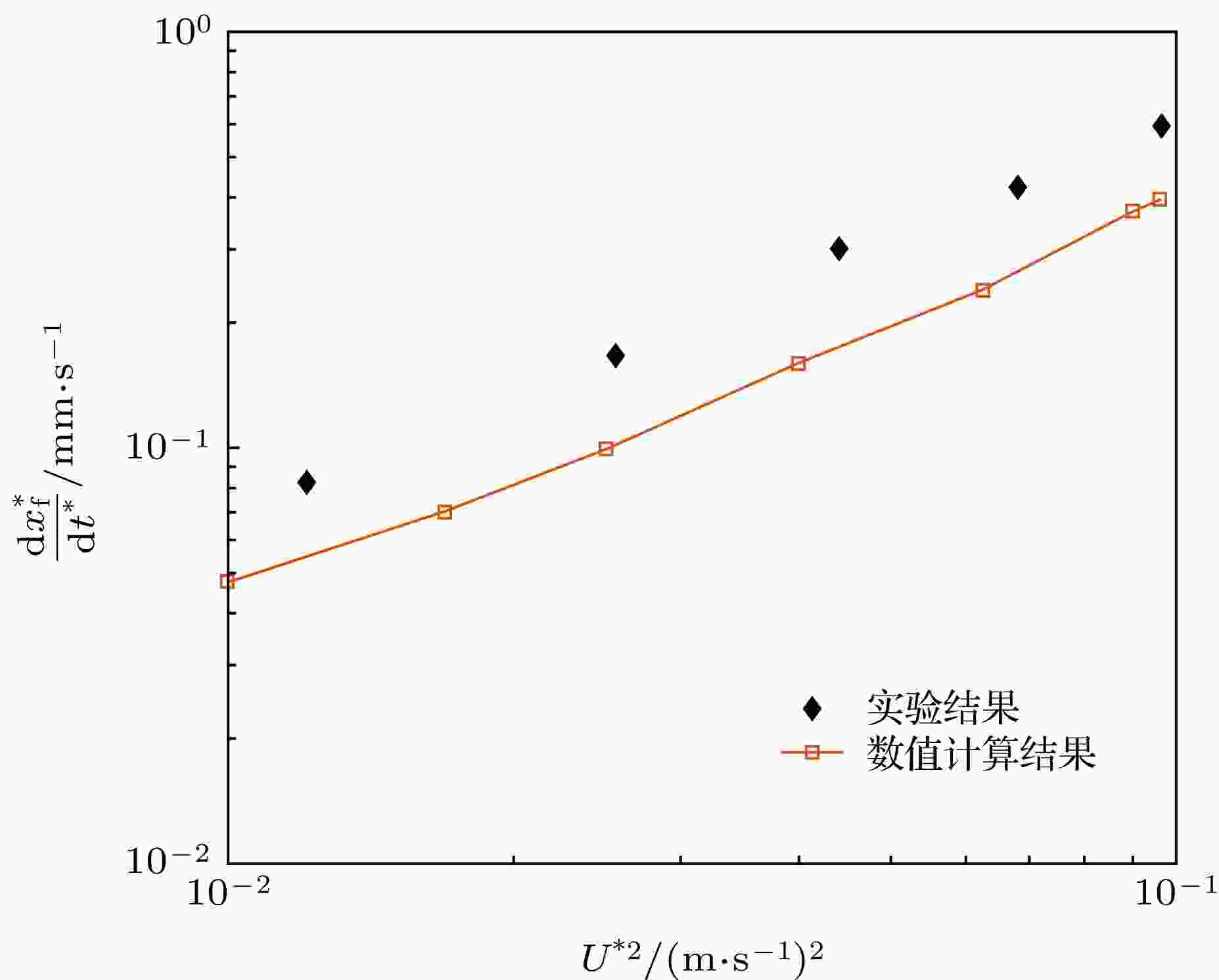图 6 漂移流主导时, 液膜前缘移动速度dx_f^*/dt^*随U ^*2的变化与Rezk等^[7]实验结果的对比
Figure6. Comparison between simulated and experimental^[7] results for the variation of dimensional velocity dx_f^*/dt^* with U ^*2 during the drift governed spreading process

2 -->

3.2.毛细力与漂移流影响相当时液膜的铺展过程

为讨论毛细力与漂移流影响相当时含活性部分润湿液膜的铺展过程, 取$\theta=13^\circ$, H ^*/δ ^* = 40, U ^* = 0.10 m/s, G₀ = 0.70, Pe = 200, α = 40, M = 8, 则θ³/We = 1. 从图7(a)—(d)可看出, 液膜铺展过程大致分为三个阶段. 在第一阶段(t = 0—45), 初始时刻表面活性剂浓度梯度的存在引起Marangoni效应, 与漂移流、分离压共同作用推动液膜迅速向两边铺展, 使得液膜半径和厚度分别急剧增大和降低; 在第二阶段(t = 45—243), 分离压和漂移流逐渐稳定, 毛细力影响缓慢增大, 驱使液膜表面积缩小, 液膜后缘移动速度稍大于前缘, 铺展半径呈现收缩的趋势, 最大液膜厚度缓慢增大; 到了第三阶段(t = 243—400), 液膜在毛细力的作用下保持最小表面积, 液膜铺展半径和最大厚度保持稳定, 铺展过程进入平衡状态. 在图2(d)和图7(d)中, 液膜铺展半径随时间出现振荡变化. 文献[26, 27]中的润湿过程也伴随着类似的振荡现象, 这可能是接触线附近分子间作用力的吸引力和排斥力相互作用引起的, 其间蕴含着复杂的分子动力学机理, 有待****的进一步研究.
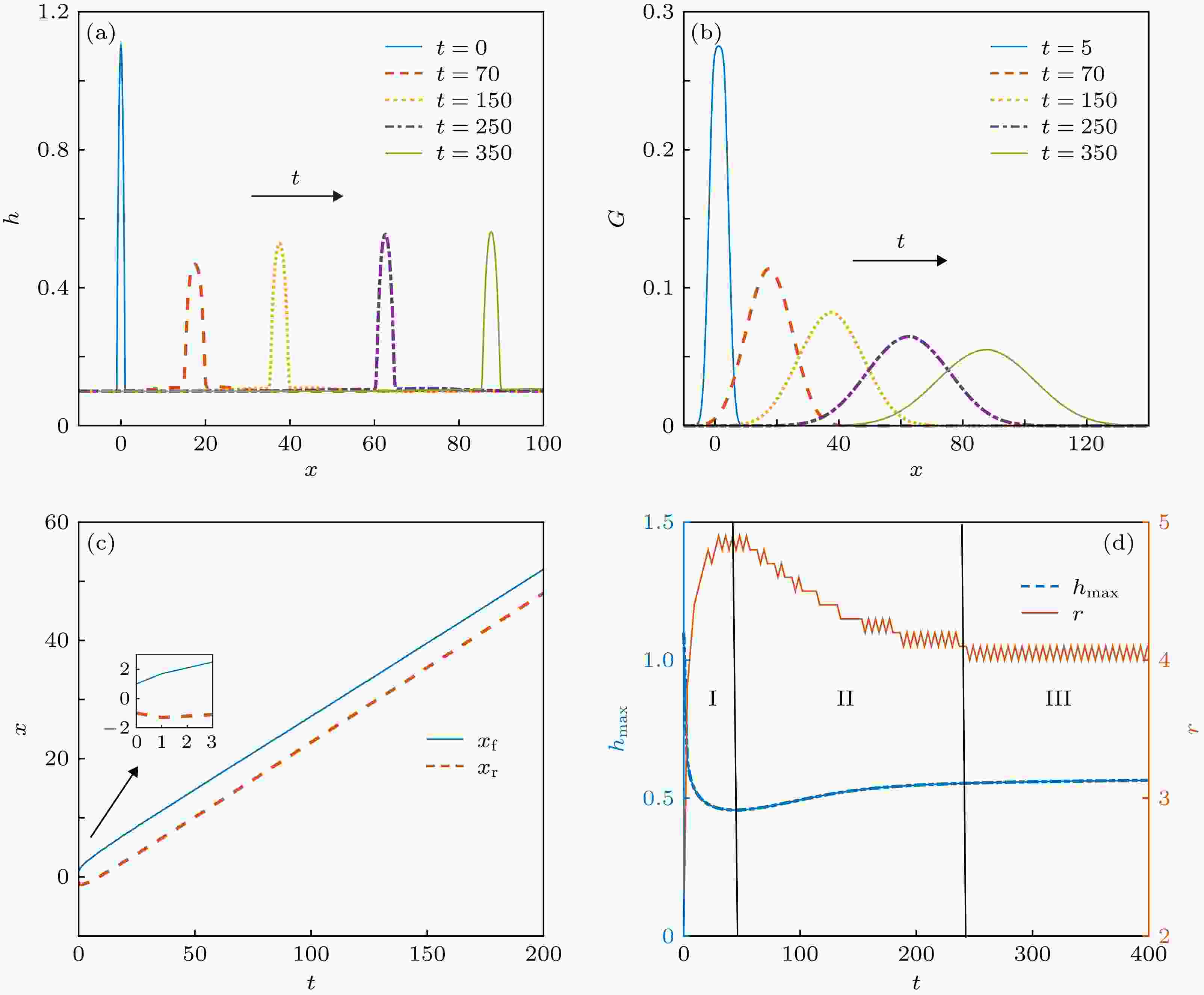图 7 毛细力和漂移流作用相当, 考虑活性剂影响时水膜的铺展过程　(a)液膜厚度; (b)活性剂浓度; (c)液膜前缘x_f与后缘x_r; (d)液膜最大厚度h_max与铺展半径r
Figure7. Spreading process when the equal effect of drift and the capillary stress is considered: (a) Film thickness; (b) surfactant concentration; (c) the position of the front x_f and the rear x_r of the liquid film; (d) maximal thickness and spreading radius of the liquid film.

图8比较了其他参数取值相同, 考虑活性剂影响和不考虑活性剂影响两种情况下的液膜演化过程. 可以发现, 含活性剂液膜在第一阶段的铺展速度更快; 含活性剂液膜的最大厚度经历了先减小再增大最后达到平衡的3个阶段, 铺展半径则经历了先增大再减小最后平衡的三个阶段. 而不含活性剂液膜的最大厚度和铺展半径在整个演化过程分别呈单调减小和单调增大; 在同一时刻, 不含活性剂液膜的最大厚度的数值更大, 铺展半径更小, 且最大厚度达到最小值和铺展半径达到最大值的时刻更早.
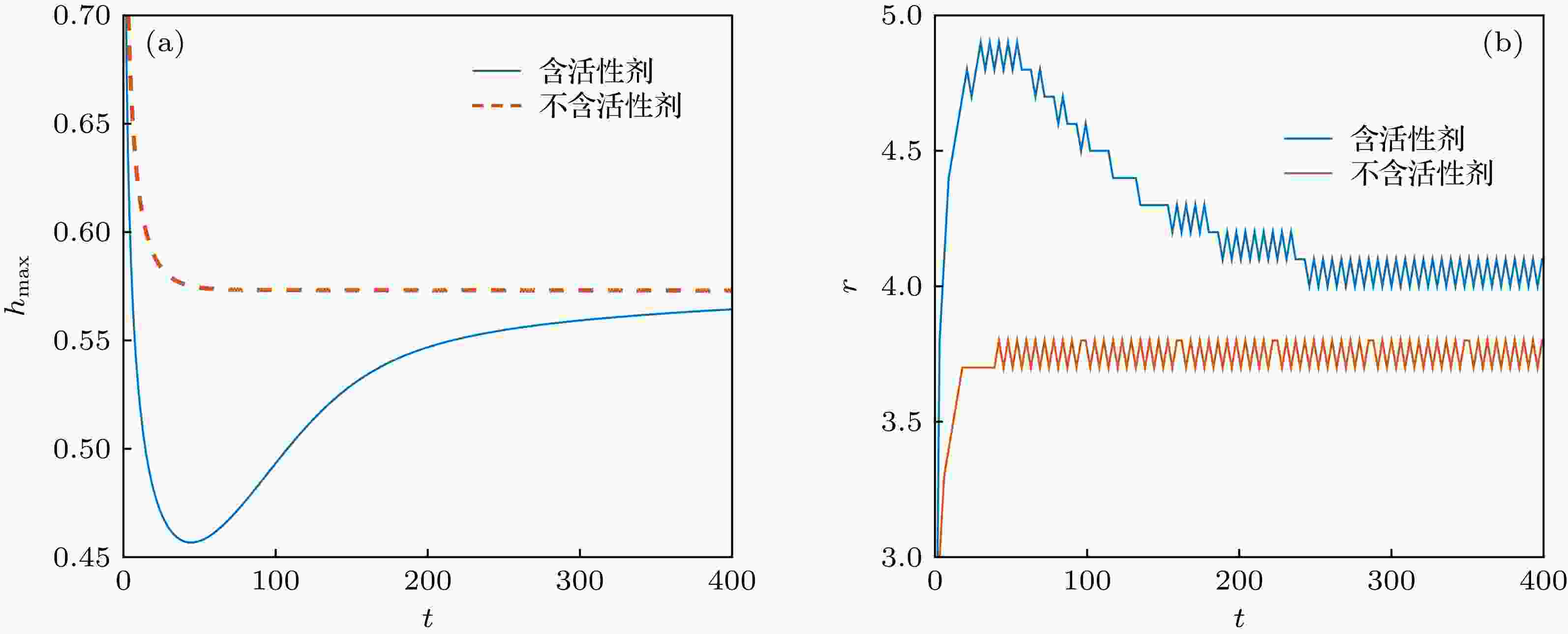图 8 考虑活性剂影响和不考虑活性剂影响的液膜演化过程对比　(a)液膜最大厚度; (b)液膜铺展半径
Figure8. Film spreading when both the capillary stress and the drift govern the dynamics of the film with (blue line) and without (orange line) considering the effect of surfactant: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.

Altshuler和Manor^[8]使用信号发生器和放大器向IDT施加正弦电压以产生频率为30 MHz的瑞利SAW, 观察含活性剂去离子水膜在SAW器件LN基底上的动力学特性, 发现水膜前缘的无量纲移动速度随着无量纲数θ³/We的增大呈线性减小. 对比本文模拟结果与Altshuler和Manor在文献[8]的实验结果, 发现两者趋势一致, 但模拟结果稍大于实验结果, 如图9所示. 这可能是如下原因所致: 第一, 计算中所用的声波振动强度、液膜高度等参数和实验无法一一对应; 第二, 实验中声波作用除了漂移流外还有声辐射压及Eckart流, 后两者是引起液膜逆流的主要因素^[21], 虽然当液膜厚度较薄时声辐射压和Eckart流作用不显著, 但影响仍然存在; 第三, 本文建立的是二维模型, 和实际的三维物体存在一定偏差.
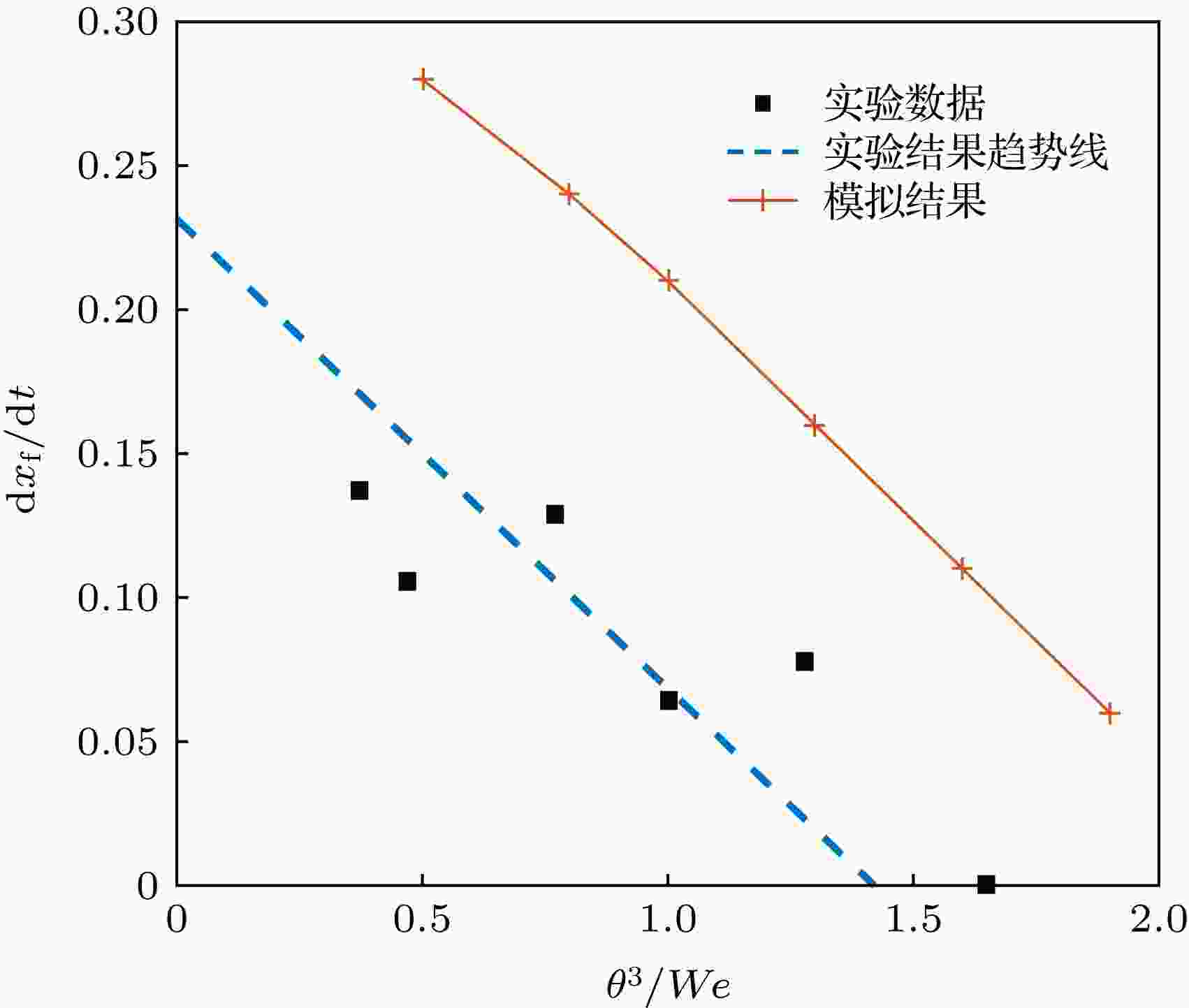图 9 漂移流和毛细力作用相当时, 液膜前缘移动速度的模拟结果和文献[8]的实验结果对比
Figure9. Comparison between simulated and experimental^[8] results for the variation of velocity dx_f/dt with θ³/We when both the capillary stress and the drift govern the dynamics of the film.

图10对比了Marangoni数M = 10, 分离压与活性剂浓度的相关系数α取不同值时的液膜铺展过程. α值越大, 活性剂对分离压的影响越强. 结果表明, 在同一时刻液膜的铺展程度与α值呈正相关关系; 在铺展过程的第一阶段和第二阶段, 最大厚度和铺展半径的变化速度随着α值的增大而加快. 这是因为由(9)式给出的分离压形式可知, 当h > h_f /C = 0.2, 分离压Π < 0, 此时分离压对液膜总压力起正贡献作用, 促进液膜铺展. 而α值越大, Π绝对值越大, 分离压呈现的吸引效应也越强, 使得液膜的失稳性随着α值的增大而变强.
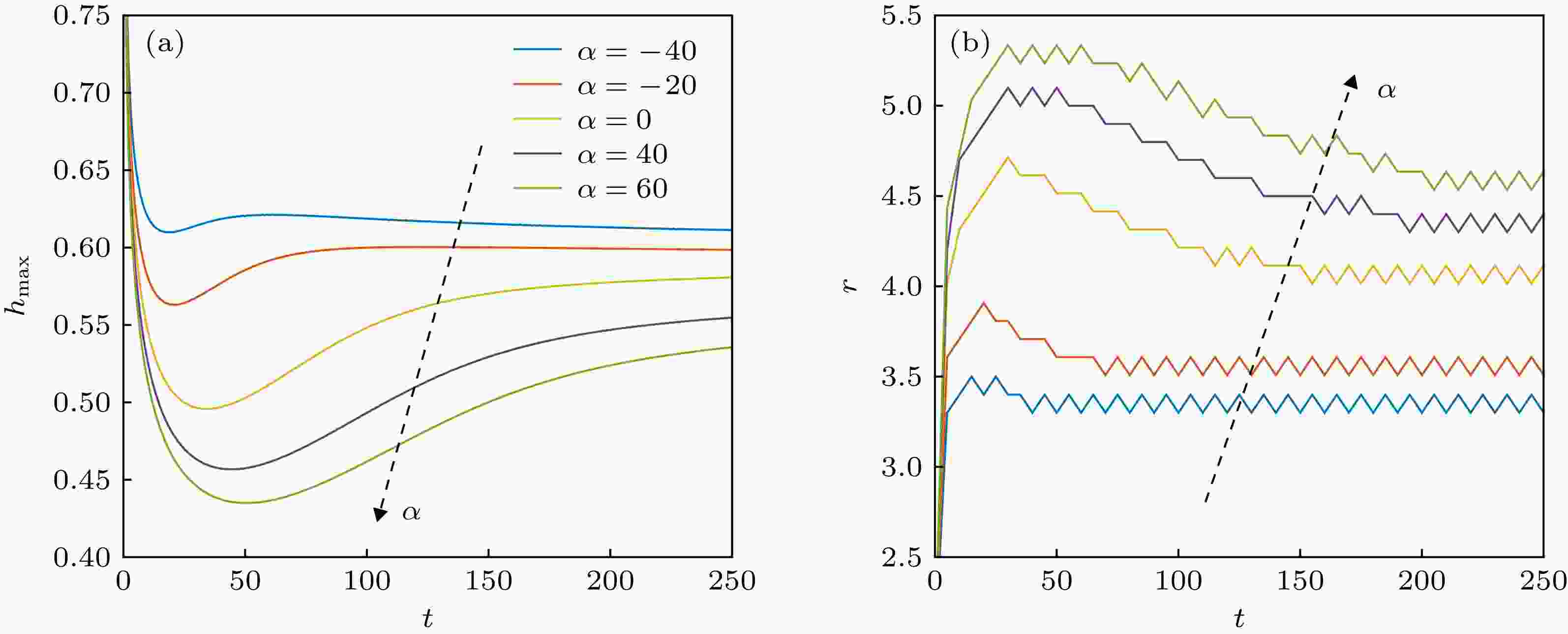图 10 不同α下部分润湿薄液膜的铺展过程对比　(a)最大厚度; (b)铺展半径
Figure10. Evolution of partially wetting film with different values of α: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.

为进一步研究Marangoni效应的影响, 其他参数保持不变, 令α = 20, 改变M值, 液膜铺展过程如图11所示. 可以看出, M越大, Marangoni效应影响越大, 初始时刻液膜在Marangoni效应推动下铺展得越快, 最大厚度降低的程度和铺展半径扩张的程度越大. 到了第二阶段, 活性剂浓度分布趋于均匀, Marangoni效应减弱, 在毛细力约束下液膜最大厚度升高和铺展半径收缩的速度随着M值的增大而加快. 在平衡阶段, M值越大, 液膜形状与初始形状相差越大. 由此可见, 部分润湿液膜的稳定性随着M值的增大而减弱.
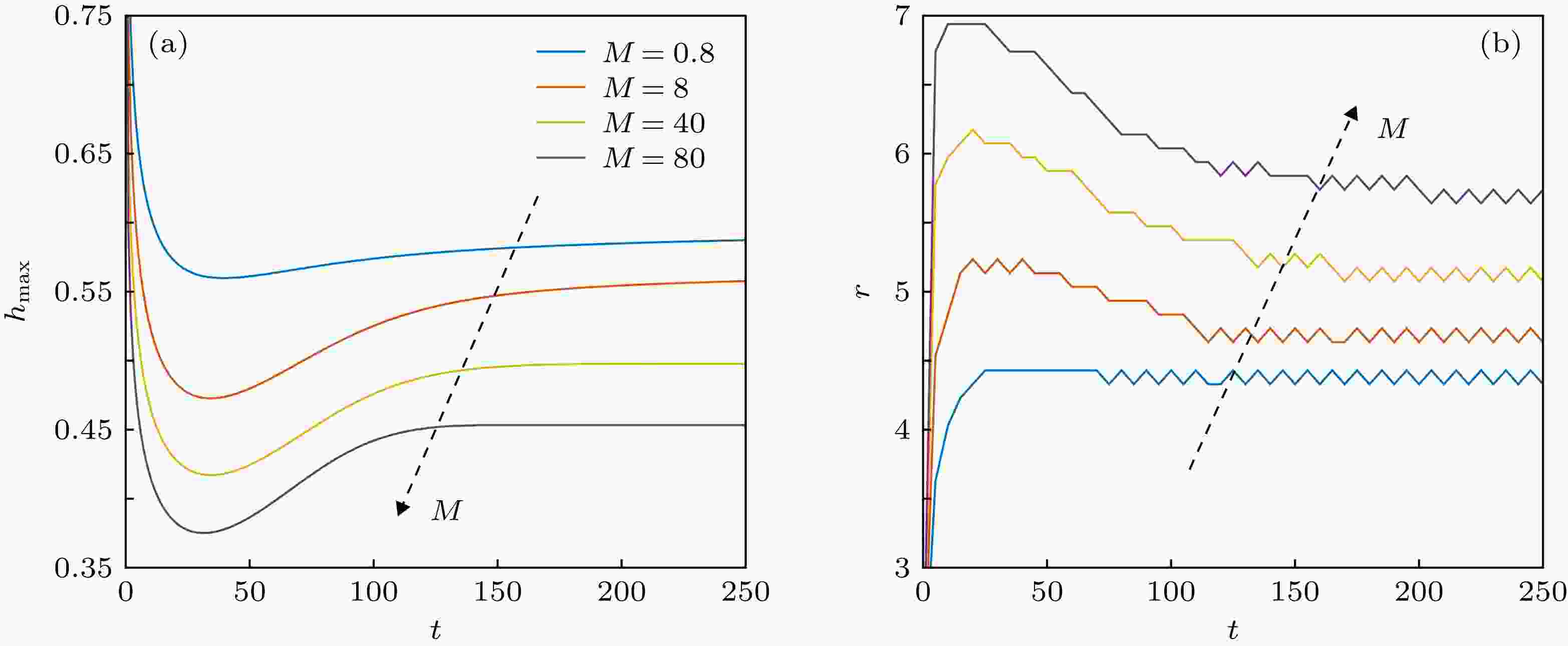图 11 不同M下部分润湿薄液膜的铺展过程对比　(a)最大厚度; (b)铺展半径
Figure11. Evolution of partially wetting film with different values of M: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.

本文以无量纲参数θ³/We来表示毛细力和漂移流的相对作用大小, 在理论建模过程中引入与表面活性剂浓度有关的分离压和表面张力表达式, 通过数值计算的方式分析了不溶性活性剂对SAW作用下部分润湿薄液膜铺展的影响.
当θ³/We $\ll 1 $, 含活性剂液膜铺展过程主要受漂移流控制, 此时部分润湿液膜的铺展过程趋近于完全润湿液膜, 分为快速铺展和平衡两个阶段. 对比考虑活性剂浓度分布影响与不考虑活性剂影响的液膜铺展过程, 可以发现活性剂浓度分布不均引起的Marangoni效应使得液膜在第一阶段铺展得更快, 但到了第二阶段Marangoni效应减弱后, 厚度更低的含活性剂液膜的铺展速度逐渐减慢, 当含活性剂液膜的厚度与不含活性剂液膜相近时, 两者铺展速度趋于一致.
当θ³/We = 1, 毛细力和漂移流共同主导铺展过程, 液膜铺展过程分为铺展、收缩和平衡三个阶段. 对比考虑活性剂浓度分布影响与不考虑活性剂影响的液膜铺展过程可知, 活性剂的存在加快了液膜的铺展速度, 但当Marangoni效应减弱, 毛细力作用逐渐显现, 含活性剂液膜经历了第二阶段的收缩过程, 因此需要更长的时间才能达到平衡状态.
在本文中, 分离压和Marangoni效应均促进液膜铺展. 当毛细力与漂移流共同主导铺展过程时, 在铺展过程的第一阶段和第二阶段, 液膜的铺展程度和α值、M值呈正相关关系, 最大厚度和铺展半径的变化速度随着α值、M值的增大而加快.
对于θ³/We $\gg 1 $, 毛细力主导液膜铺展动力学过程的情形, 因为数值计算的困难, 在本文暂不做研究. 另外, 建立三维模型、研究铺展过程中振荡的机理也留待将来研究.