删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

深海大接收深度海底混响研究

本站小编 Free考研考试/2021-12-29
摘要:海洋混响对主动声纳工作性能的影响不可忽略, 一直是水声学研究中的一个重要课题. 在南海实验中获取了深海混响实验数据, 包含近海底大接收深度的混响信号, 其强度随时间变化存在锯齿形结构. 为对混响数据进行深入分析, 基于射线理论提出了一种深海海底混响模型,能够计算本地混响和异地混响强度, 并可解释深海混响信号的产生过程. 该模型首先对海底散射体进行网格式划分, 然后根据每个网格内散射体产生混响信号的准确时间进行混响计算, 对于传播路径丰富的深海环境比传统按圆环或椭圆环处理散射体的方式更加精确. 在多种收发距离和接收深度条件下, 将数值模拟结果与实验数据进行比较. 结果表明: 对于大接收深度, 混响整体吻合较好; 而靠近海面处的混响, 二者的一致性下降. 分析结果表明, 使用的海底散射系数参数适用于该实验海区, 同时验证了该散射系数模型对于小掠射角海底散射更加准确, 对应深海大接收深度混响.
关键词: 海底混响/
深海/
大接收深度/
射线理论

English Abstract


全文HTML

--> --> -->
1.引　言
混响是海洋声学领域的一个重要课题. 海洋混响通常是主动声纳的主要背景干扰, 同时也因携带丰富的海洋信息可用于环境参数反演而受到广泛关注.
国内外对于浅海混响的研究相对较多, 建立了简正波混响理论[1-3]、射线混响理论[4-7]和抛物方程混响理论[8,9]等. 简正波混响理论最早由Bucker和Morris[1]提出, Zhang和Jin[2]对其进一步发展, 推导出了浅海远程混响强度的一般表达式, 并分析了负跃层浅海中平均混响强度的衰减规律. 射线方法是对波动理论的近似, 具有物理意义直观、运算简单等特点, 应用射线理论研究海底混响已经取得了丰富的成果. 射线理论一般更多地被应用于近程混响计算, 在一定海底散射模型假设前提下, 可以很好地解释实验结果, 同时射线方法也是研究深海混响的首选. 抛物方程混响理论适用于水平变化的复杂海洋环境, 但随着频率的增加计算量会迅速增加. 射线方法是波动理论的近似, 具有物理意义直观、运算简单等特点, 应用射线理论研究海底混响已经取得了丰富的成果. 射线理论一般更多地应用于近程混响计算, 同时也是研究深海混响的首选. 此外, 李风华等[10]提出了射线-简正波相干混响理论, 并解释了浅海混响强度的振荡现象. 刘建军等[11,12]根据射线-简正波混响理论和三维海底散射模型, 给出了浅海异地混响衰减和混响垂直相关的一般表达式, 并由此有效地反演了海底反射损失与海底散射系数. 吴金荣等[13]研究了倾斜海底环境下近程混响强度的衰减特性, 并讨论了海水及海底多种因素对混响衰减特性的影响.
深海混响与浅海混响的特性有明显区别, 对其分析手段和数值建模方法都有所不同. Mackenzie[14]计算了特定频率下近海底声源和接收器的深海海底混响, 并说明了散射公式的适用角度范围. Urick和Saling[15]计算了爆炸声源激发的海底背向散射, 并得出了散射强度随角度的变化曲线. Ellis等[16,17]将Lambert散射模型和基于Kirchhoff近似的表面散射函数相结合, 提出了包含背向散射和侧向散射的三维海底散射函数, 将其用于深海异地混响的数值仿真, 并与实验测量结果进行了对比分析. Williams和Jackson[18]利用Kirchhoff近似和微扰理论描述海底背向散射, 同时讨论了海底沉积层和基底对散射的影响. 翁晋宝等[19]通过射线方法对本地深海海底混响进行了数值仿真, 并对实验数据进行了初步解释和分析. 郭熙业等[20]基于射线理论提出了收发合置的非相干海底混响信号模型, 简化了混响信号预报的计算过程. Xu等[21]计算了声波经第一次海底反射产生的深海混响, 得到了与实验数据一致的数值结果. Yang等[22]在Jackson射线混响模型的基础上[23], 结合有限元法提出了深海异地海底混响模型, 并用其有效反演了海底声学参数. 海洋混响主要是由于海底、海面和海洋介质的不均匀性对声波的散射引起的, 从实验观测来看, 对深海混响而言, 海底散射是主要的贡献.
本文基于射线理论, 使用包含背向散射和侧向散射的三维海底散射系数, 提出了一种深海海底混响模型, 可对本地和异地混响进行计算. 该模型首先对海底散射体进行网格式划分, 可以更加准确地获取不同路径声线的传播时间, 从而精确、快速计算得到混响强度. 在海上实验中获取了大接收深度的深海混响信号, 对其特性进行了分析, 并将实验数据与数值模拟结果进行对比, 获得实验海区的海底散射系数.
2.深海混响实验及数据分析
2
2.1.实验简介
-->

2.1.实验简介

2018年4月, 中国科学院声学研究所声场声信息国家重点实验室在南海进行了一次综合性海上声学实验, 深海混响是其主要内容之一. 实验采用单船结合深海声学接收潜标的作业方式进行, 如图1所示. 接收潜标系统由20个自容式水听器(USR)组成, USR以非等间距方式布放在85—3400 m深度范围内, 接收灵敏度为–170 dB, 信号采样率为16 kHz. 围绕接收潜标, “实验1号”船在声传播测线上间隔约6 min投掷一枚标定深度为200 m的1 kg TNT当量宽带爆炸声源.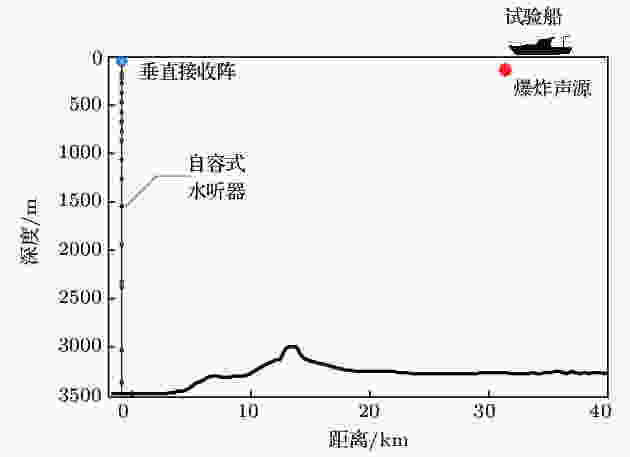
图 1 实验设备布放位置及作业方式示意图
Figure1. Configuration of the deep-water reverberation experiment.

图1给出了传播测线上的海深变化, 垂直阵处海深约为3472 m, 0—8 km距离范围内海底地形相对平坦, 更远处海深发生明显变化. 本文对混响的分析假设海底是水平不变的, 所以只选取0—8 km距离范围内爆炸声源产生的混响信号. 图2给出了实验海域及实验过程的俯视示意图, 除图1给出的实验条件外, 还存在一个小海底山距垂直阵约14 km, 会对接收的混响信号产生一定影响, 在后面将对此进行分析. 实验期间测量的该海区海水声速剖面如图3所示, 其中0—1700 m深度范围内的声速为实测数据, 由于声道轴以下的声速结构具有稳定性, 1700 m以深的声速数据由水文数据库获得, 将其与实测深度的声速通过插值连接得到整个水体的声速剖面.
图 2 实验海域及实验过程俯视图
Figure2. Vertical view of experimental area and process.

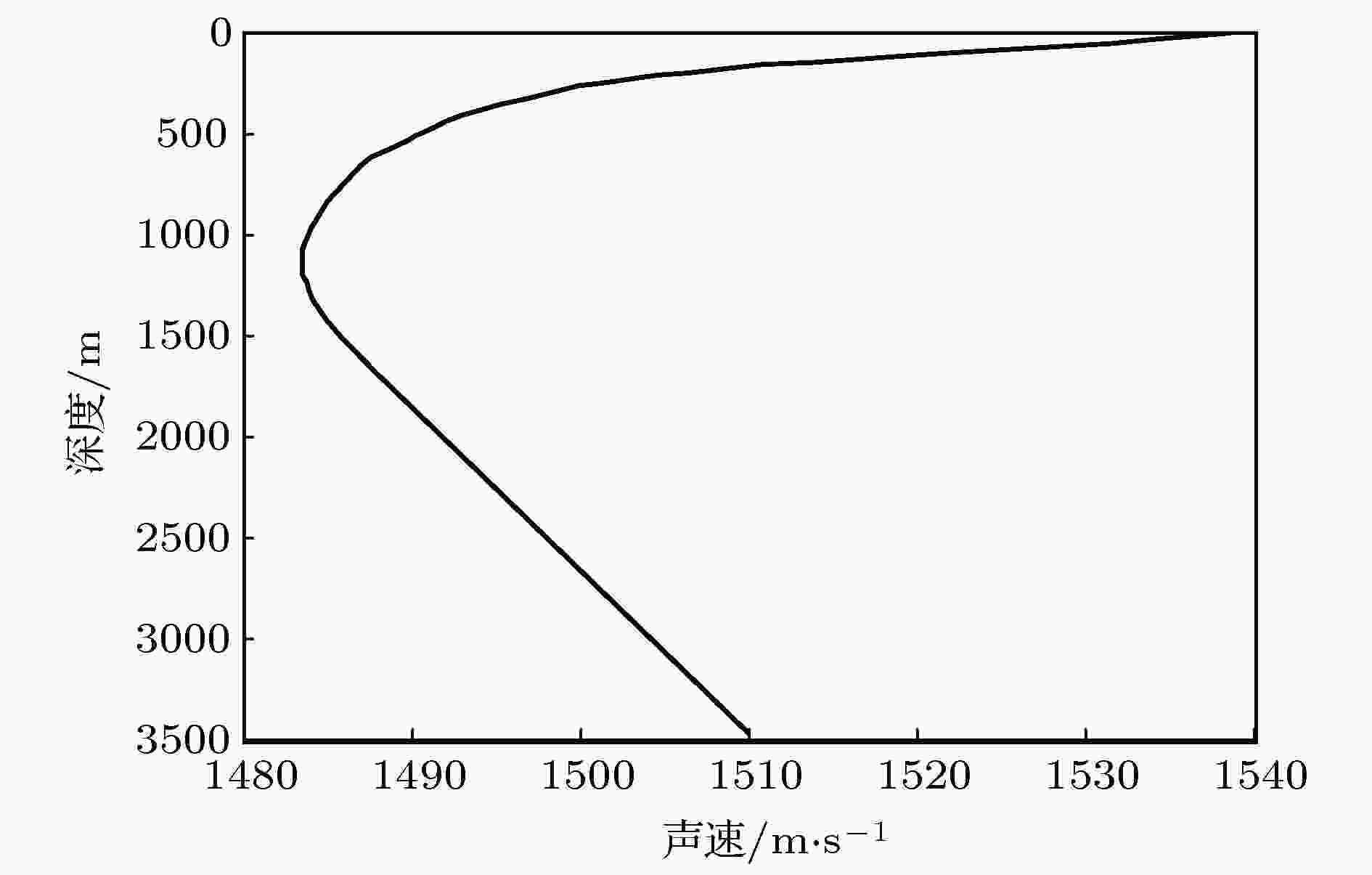图 3 实验海域海水声速剖面
Figure3. Sound speed profile of seawater in experimental area.

2
2.2.实验数据处理
-->

2.2.实验数据处理

图4给出了实验中不同深度水听器记录爆炸声源激发的声信号, 声源与接收阵的水平距离为0.76 km. 将接收到的时域信号记为$x\left( t \right)$, 认为${t_i}$时刻附近短时间内的信号是平稳的, 记为$x\left( {{t_i}} \right)$. 对其进行离散傅里叶变换得到信号的频谱Xi, 并在中心频率的1/3倍频程带宽内取平均, 可以得到窄带信号的平均功率:
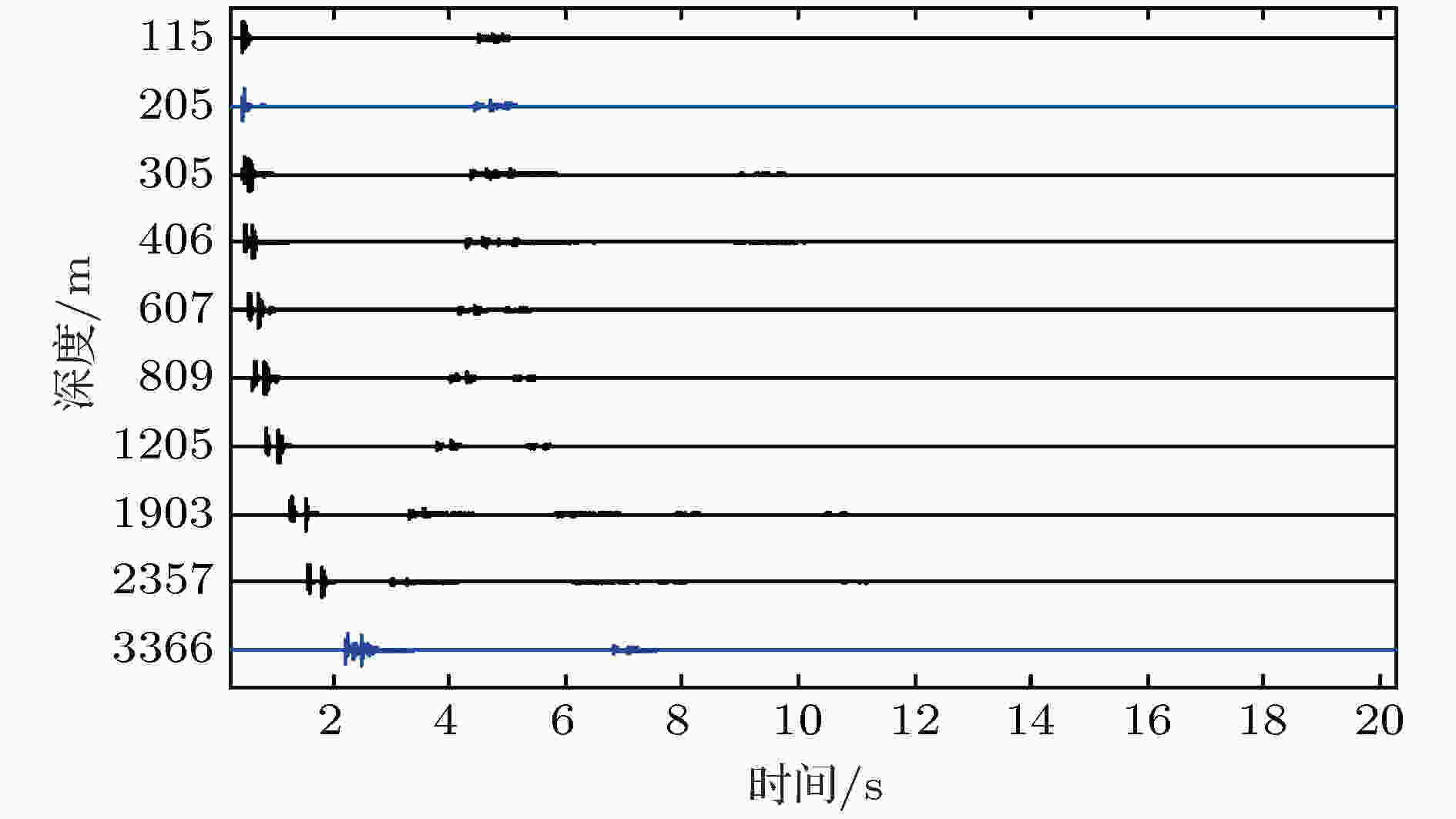图 4 不同深度水听器接收到的声信号, 声源与接收阵的水平距离为0.76 km
Figure4. Sound signals received by hydrophones at different depth. The horizontal distance between the source and the receiving array is 0.76 km.

${P_i}\left( {{f_0}} \right) = \frac{2}{{N{f_{\rm{s}}}{\rm{(}}n{f_2} - n{f_1} + 1{\rm{)}}}}\sum\limits_{k = n{f_1}}^{n{f_2}} {{{\left| {{X_i}{\rm{(}}k{\rm{)}}} \right|}^2}},$
其中, ${f_0}$为中心频率,${f_{\rm{s}}}$为采样率,N为数据的点数,$n{f_1}$和$n{f_2}$分别为频率的下限和上限对应的频点数. 实验的混响强度可以用对数的形式表示为:
$RL = 10\lg \left[ {{P_i}\left( {{f_0}} \right)} \right] - b - SL\left( {{f_0}} \right),$
其中$SL$和b分别表示声源的谱级和水听器的灵敏度, 单位均为dB.
通过上述方法对图4中接收深度为205和3366 m的声信号(蓝色曲线)进行处理, 图5给出了混响强度随时间变化的曲线, 可见多个明显的峰值. 图5(a)为205 m接收深度的结果, 其中第一个峰值对应的是声源到接收器的直达波及经海面反射的声波, 之后强度迅速减小, 对应的是海面混响与体积混响信号, 不包含海底散射信号; 第二个峰值为一次海底反射波, 此后强度逐渐下降, 此时声信号主要由声波经海底散射后传播回接收器的信号组成. 之后随着时间的增加, 出现的峰值分别对应不同次数的海底反射声波, 每个峰值后声强逐渐下降, 对应的是经海底反射后的混响信号. 从图中可以看出, 经海底反射之后到达水听器的声信号明显高于直达声之后的海面混响和体积混响信号, 因此可知, 水听器接收到的混响信号主要贡献来自海底散射, 在经由海底散射之后的混响信号中, 海面混响和体积混响可以忽略. 图5(b)为大接收深度数据的处理结果(3366 m), 其各个峰值的位置与图5(a)明显不同. 由于接收器距离海底较近, 直达声波和一次海底反射波到达接收器的时间十分接近, 因此二者在时间上重合形成了第一个峰值. 后面的多个峰值对应不同次数的海底反射波, 每个峰值后逐渐下降的部分为海底混响信号. 值得注意的是, 第一个峰值之后海底混响强度明显小于其他时间, 这与所对应的海底散射掠射角较小有关.
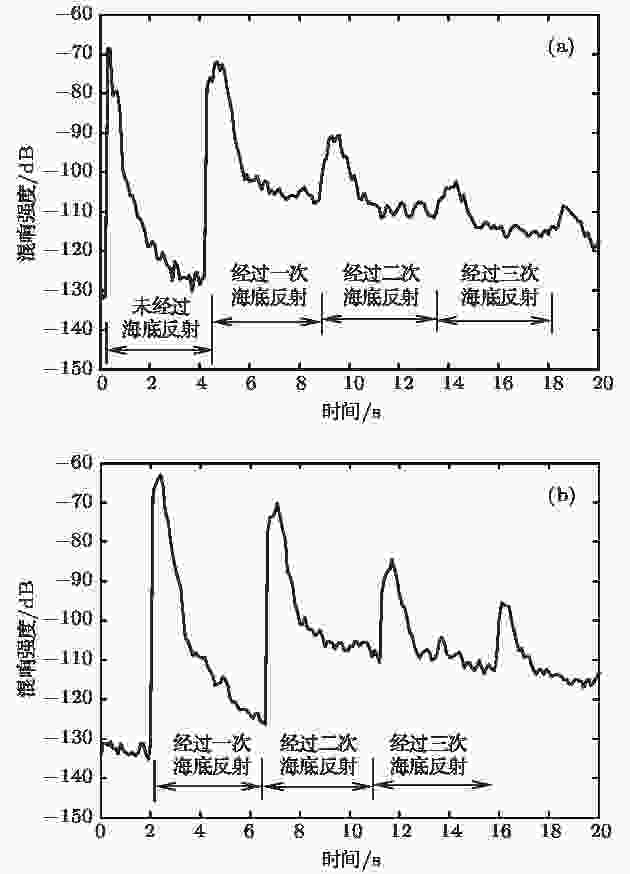图 5 混响强度实验数据处理结果　(a)接收器深度205 m; (b)接收器深度3366 m
Figure5. Reverberation from experimentdata: (a) Receiver depth is 205 m; (b) receiver depth is 3366 m

3.混响模型
为深入分析实验测量的混响信号, 本节通过射线理论建立深海海底混响模型. 对于混响信号, 可以表述为从声源激发的声信号传播到达海底散射体后经过散射后传播回接收器的过程. 根据射线理论, 声源位于$\left( {{\rm{0}},{z_0}} \right)$, 其激发的声波在散射体$\left( {{{r}},{z_{\rm{b}}}} \right)$处的声压可以表示为
$\begin{split}p\left( {{{r}},{z_{\rm{b}}}} \right) =\;&\sum\nolimits_{n = 1}^N {{p_n}} =\\ \sum\nolimits_{n = 1}^N &{{A_n}\left( s \right){\phi _n}\left( s \right){{\rm{e}}^{{\rm{i}}\omega {\tau _n}\left( s \right)}}}, \end{split}$
其中r为散射体的水平位置, zb为海深, N为声线总数, An(s)为第n条声线的幅度, ?n(s)为声线束幅度的函数, ω为声源角频率, ${\tau _n}\left( s \right) = \int_0^s {\displaystyle\frac{1}{{c\left( {s'} \right)}}{\rm{d}}s'} $为声线从声源到散射点的延迟时间, s代表射线束的路程, $c\left( {s'} \right)$为声线上的海水声速. 当声源至散射体距离足够远时, 声波在波导中的传播可以近似为平面波, 因此点声源在散射体处激发的入射声场可以近似表示为N个平面波的叠加.
根据互易原理, 距声源水平距离为r的水听器接收到单位面积上散射体对应的散射声压可以表示为(省略了海深${z_{\rm{b}}}$)
$\begin{split} p\left( r \right) =\; &\sum\limits_{i = 1}^N \sum\limits_{j = 1}^M {p_{{\rm{inc}},i}}({r_i})\\&\times {p_{{\rm{scatt}},j}}({r_j}) \times g({\theta _{{\rm{inc,}}i},{\theta _{{\rm{scatt}},j}},\varphi )},\end{split}$
其中, ${p_{{\rm{inc,}}i}}$表示入射声波传递函数, ${p_{{\rm{scatt}},j}}$表示散射声波传递函数, ${r_i}$表示第i条入射声线从声源到散射体的水平距离, ${r_j}$表示第j条散射声线从散射体到接收器的水平距离, N和M分别表示入射声线和散射声线总条数;$g{\rm{(}}{\theta _{{\rm{inc}},i}},{\theta _{{\rm{scatt}},j}},\varphi{\rm{)}}$为三维散射函数, 指在入射平面波作用下单位面积海底散射的平面波幅值. 在本地混响计算中, 入射和散射声线始终在一个竖直平面内, 所以散射函数只与入射掠射角${\theta _{{\rm{inc,}}i}}$和散射掠射角${\theta _{{\rm{scatt}},j}}$两个变量有关. 而对于异地混响, 通常存在入射声线和散射声线不在同一个竖直平面内的情况, 所以除入射掠射角和散射掠射角外, 还需要引入散射方位角$\varphi$来描述散射函数, 如图6所示.
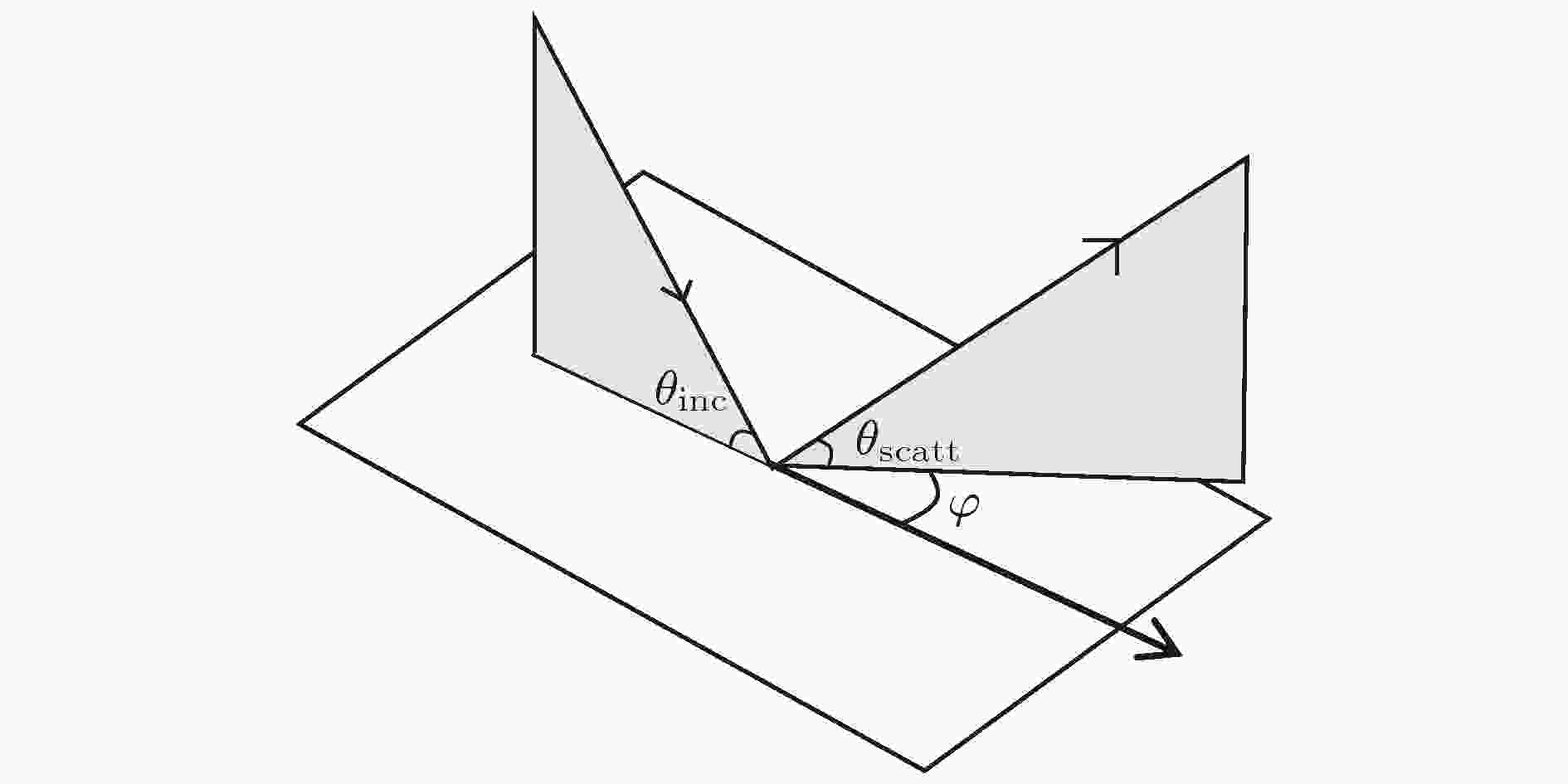图 6 海底散射示意图
Figure6. Bottom scatteringgeometry.

Ellis和Haller[16]在Lambert背向散射模型的基础上建立了适用于异地混响的三维散射模型, 其散射系数表示为
$\begin{split} S\left( {{\theta _{{\rm{inc}},i}},{\theta _{{\rm{scatt}},j}},\varphi } \right) &= {\left| {g\left( {{\theta _{{\rm{inc}},i}},{\theta _{{\rm{scatt}},j}},\varphi } \right)} \right|^2}\\&= \mu {\rm{sin}}{\theta _{{\rm{inc}},i}}{\rm{sin}}{\theta _{{\rm{scatt}},j}} \\&\quad + \upsilon {{\rm{(}}1 + \Delta \varOmega {\rm{)}}^2}{{\rm{e}}^{\frac{{ - \Delta \varOmega }}{{2{\sigma ^2}}}}},\end{split}$
式中第二个等号后第一项为Lambert散射系数, 由背向散射引起; 第二项为侧向散射引起的, 是在Kirchhoff近似及Helmholtz方程的基础上, 假设海底各向同性且界面粗糙程度是符合高斯分布条件下提出的; μ为背向散射强度, υ为侧向散射强度, σ为侧向散射偏差. $\Delta \varOmega $表示散射声线对镜反射方向的偏离, 由下式确定:
$\begin{split}&\quad \Delta \varOmega \\&= \frac{{{\rm{co}}{{\rm{s}}^2}{\theta _{{\rm{inc}},i}} + {\rm{co}}{{\rm{s}}^2}{\theta _{{\rm{scatt}},j}} - 2{\rm{cos}}{\theta _{{\rm{inc}}.i}}{\rm{cos}}{\theta _{{\rm{scatt}},j}}{\rm{cos}}\varphi }}{{{{{\rm{(sin}}{\theta _{{\rm{inc}},i}} + {\rm{sin}}{\theta _{{\rm{scatt}},j}}{\rm{)}}}^2}}}.\end{split}$
根据 (4) 式, 水听器接收到单位面积上散射体对应的海底混响强度可以表示为
$\begin{split}{I_{{\rm{scatt}}}} =\;& \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{{\left| {{p_{{\rm{inc}},i}}{\rm{(}}{r_i}{\rm{)}}} \right|}^2}{{\left| {{p_{{\rm{scatt}},j}}{\rm{(}}{r_j}{\rm{)}}} \right|}^2}} }\\& \times S{\rm{(}}{\theta _{{\rm{inc}},i}},{\theta _{{\rm{scatt}},j}},\varphi {\rm{)}}.\end{split}$
假设声源发出信号脉冲强度为${I_0}\left( \tau \right)$, 脉冲长度为${\tau _0}$, 则t时刻的混响强度可以表示为该时刻接收到的散射信号的叠加,
$R(t) = \int_0^{{\tau _0}} {{I_0}\left( \tau \right)} {I_{{\rm{scatt}}}}{\rm{d}}A\left( {t,\tau } \right),$
其中到达时间$t = {\tau _{{\rm{inc}},i}} + {\tau _{{\rm{scatt}},j}}$, ${\tau _{{\rm{inc}},i}}$和${\tau _{{\rm{scatt}},j}}$分别为声线从声源到达散射体和散射体到达接收器的时间; ${\rm{d}}A\left( {t,\tau } \right)$表示散射面积. 将散射面积共分为K个散射面元, 用$\Delta {s_k}$表示第k个散射面元的面积, 则水听器接收到的混响强度可用离散的形式表示为
$R\left( t \right) = {I_0}\sum\limits_{k = 1}^K {{I_{{\rm{scatt}}}}} \Delta {s_k}.$
在以往文献中, 本地海底混响计算时声源和接收器在同一水平位置, 通常将对某一时刻混响有贡献的散射区域视作一个圆环. 同理, 对于异地海底混响的计算, 认为同一时刻在接收器接收到的散射声波来自于一个椭圆环状的散射区域, 发射换能器与接收水听器分别位于椭圆环的两个焦点. 需要说明的是, 如文献[3]所述, 上述处理方法是假定在计算混响时不同传播路径的声线到达同一个散射体的时间相同. 但是在深海环境下, 声线从声源到达同一散射体进而到达接收器的传播路径多样, 且传播时间存在明显差别, 因此对某时刻混响有贡献的区域并不是一个圆环或椭圆环. 为了得到精确的计算结果, 本文不使用圆环或椭圆环的散射体划分方式, 而是通过网格的方式对海底进行划分, 把海底划分成大量相接的矩形散射体, 如图7所示.
图 7 网格法散射体划分示意图
Figure7. Sketch of grid method for dividing scatterers.

在图7中, 当划分的网格足够小时, 可以认为每条声线到达同一个散射体不同区域的传播方式和能量都是相同的, 就可以使用散射体上一个点的传播情况代替整个散射面元的计算, 通过每个散射元上的计算结果乘以散射面积进而求和得到接收点的混响信号. 对海底散射体划分的网格越密集, 得到的计算结果就越精确, 但同时也会增加计算时间. 为了在保证计算精度的同时提高计算效率, 在划分网格时对散射体大小进行区分, 对距声源和接收器较近的散射体进行密集划分, 对距声源和接收器较远的散射体的划分相对稀疏, 然后对不同的散射面积分别进行计算.
海底散射体、声源和接收器所处的坐标系中(见图7), 四个象限的散射体几何位置是对称的, 但是声源与接收器的所处的深度通常不同, 即y坐标轴的左右散射体对混响的影响并非完全对称, 但关于x坐标轴是对称的. 所以, 混响计算时只考虑第一、二象限的散射体, 然后对计算结果做双倍处理得到最终的混响强度.
针对实验海区的环境, 图8(a)给出了一个混响强度的计算结果, 使用的具体参数为: 声源频率为500 Hz, 声源深度为200 m, 接收深度为3021 m, 声源与接收器的距离为5 km, 海底声学参数及散射系数的选取与下一节相同, 不影响这里的问题分析, 暂不做说明. 对于9 s时刻(见图8(a), 时间处于第二次和第三次海底反射之间)的混响强度, 首先确定所有经声源-散射体-接收器传播/散射历经9 s的声线, 然后计算每条声线所对应散射体对该时刻混响强度的贡献值, 即产生混响信号的强度, 将其标注在散射体各自所处的网格上, 得到图8(b)中海底不同位置散射体对其贡献的大小. 可见, 在该计算条件下(声源和接收器的水平位置和深度均不同), 对该时刻混响结果有影响的散射体不在同一个椭圆环上, 而是分布于若干圆环, 对应不同的传播方式. 随着混响时间的增加, 对应的椭圆环会不断扩大, 直至下一个混响峰值出现, 即出现了新的海底反射, 然后不同的传播路径将有新的椭圆环与之相对应.
图9给出了图8(b)中不同散射体圆环所分别对应的声波传播方式. 可以看出, 靠近声源有4个椭圆环, 分别对应4种传播方式的声线: 海底-海面-海底反射、海底-海面反射、海面-海底-海面-海底反射、海面-海底-海面反射; 靠近接收器有2个椭圆环, 分别对应两种传播方式的声线: 海底-海面-海底反射、海面-海底-海面-海底反射. 对混响信号产生贡献的海底散射体圆环的大小和位置与声源和接收器的相对位置有关, 椭圆环的个数和海底反射次数正相关. 由上面分析可知, 对于深海环境, 声源到达接收器的传播路径较多, 通常将海底散射体按照圆环或椭圆环进行划分的传统方式不能准确得到混响结果. 本文预先将海底散射体进行网格式划分, 然后根据实际的传播路径及对应的传播时间选择相应的散射元, 可提高混响的计算精度.
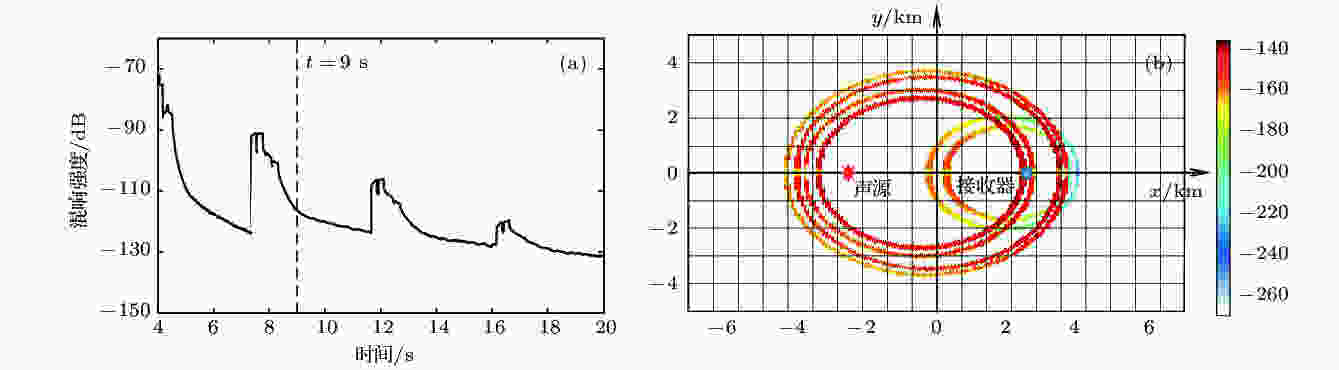图 8 海底不同位置散射体对同一时刻混响强度的贡献　(a)数值计算的混响强度; (b) 海底散射体对(a)中9 s时刻混响强度的贡献
Figure8. Contribution of scatterers at different locations to reverberation at fixed time: (a) Numerically calculated reverberation; (b) contribution of bottom scatterers to reverberation at 9-s moment in (a).

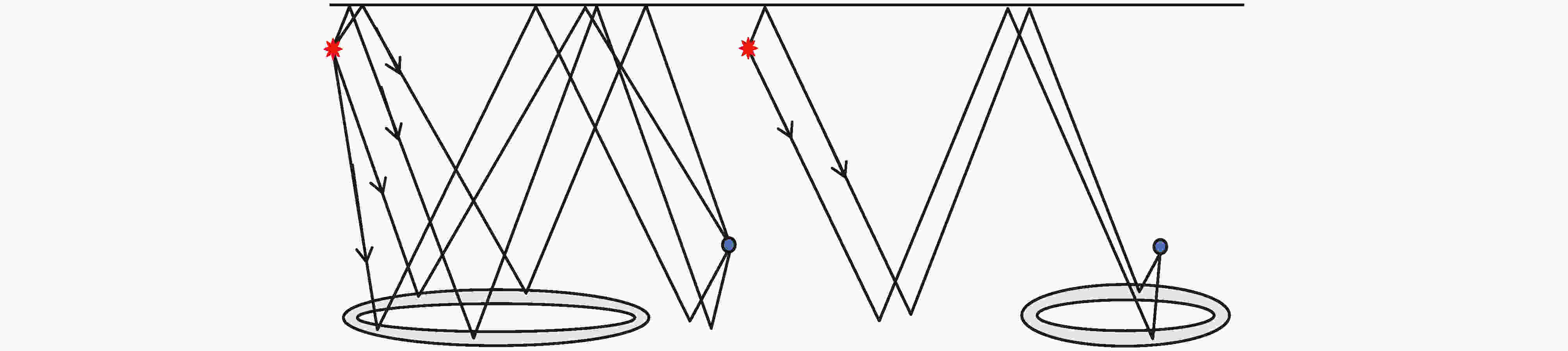图 9 不同散射体椭圆环对应的声线传播方式示意图
Figure9. Schematic diagram of sound propagation corresponding to different elliptical rings of bottom scatterers.

4.深海海底混响数值模拟及与实验结果对比分析
使用第3节提出的深海海底混响模型, 计算不同条件下的混响强度. 在数值模拟中, 假设海深不随距离变化, 取图1中接收潜标处的深度, 为3472 m, 使用图3所示的海水声速剖面. 海底使用液态半无限空间单层模型, 声学参数为: 声速1580 m/s, 密度1.6 g/cm3, 吸收系数0.3 ${\rm{dB/\lambda }}$, 该参数代表的海底底质特性与实验过程中海底采样获取的样品测量参数基本一致. 使用 (5) 式给出的散射系数, 其中的具体参数与文献[17]基本相同, 分别为: $10\lg \nu = - 10$, $10\lg \mu = - 32$, $\left( {{{180}^ \circ }/{\text{π}}} \right)\sigma = {10^ \circ }$.
图10给出了声源频率500 Hz时不同接收距离和大接收深度下的数值模拟结果, 并将其与实验获取的混响结果进行对比. 从图中可以看出, 数值计算得到的混响强度结果与实验数据整体吻合较好, 说明选取的海底散射系数适用于该实验海区. 从对比的细节看, 可以发现模拟结果与实验数据在三个部分相差较大, 以图10(a)为例, 分别出现在1—3.5 s, 28—34 s, 以及每一个峰值处, 图10中的其他子图均与之类似, 具体时间有所不同. 每一个峰值处的计算结果比实验混响强度偏小, 是由于实验结果峰值处的能量主要由海底、海面反射信号组成, 但数值计算时没有专门考虑这部分反射信号, 而是通过 (5) 式中散射系数第二项镜反射方向的散射信号来体现, 存在一定程度的能量缺失. 在1—3.5 s范围内, 实验结果在第一个峰(直达声)之后迅速下降, 由于这部分是声波在海底反射之前产生的, 因此主要是体积混响和海面混响. 混响模型只考虑了海底混响, 所以不能给出这部分结果. 另外, 在28—34 s附近, 实验的混响信号出现明显增强. 从图2可知, 在距离接收阵约14 km处有一个海底山, 该时间段内的峰值是声信号传播到海底山然后经反射再传播到接收阵产生的.
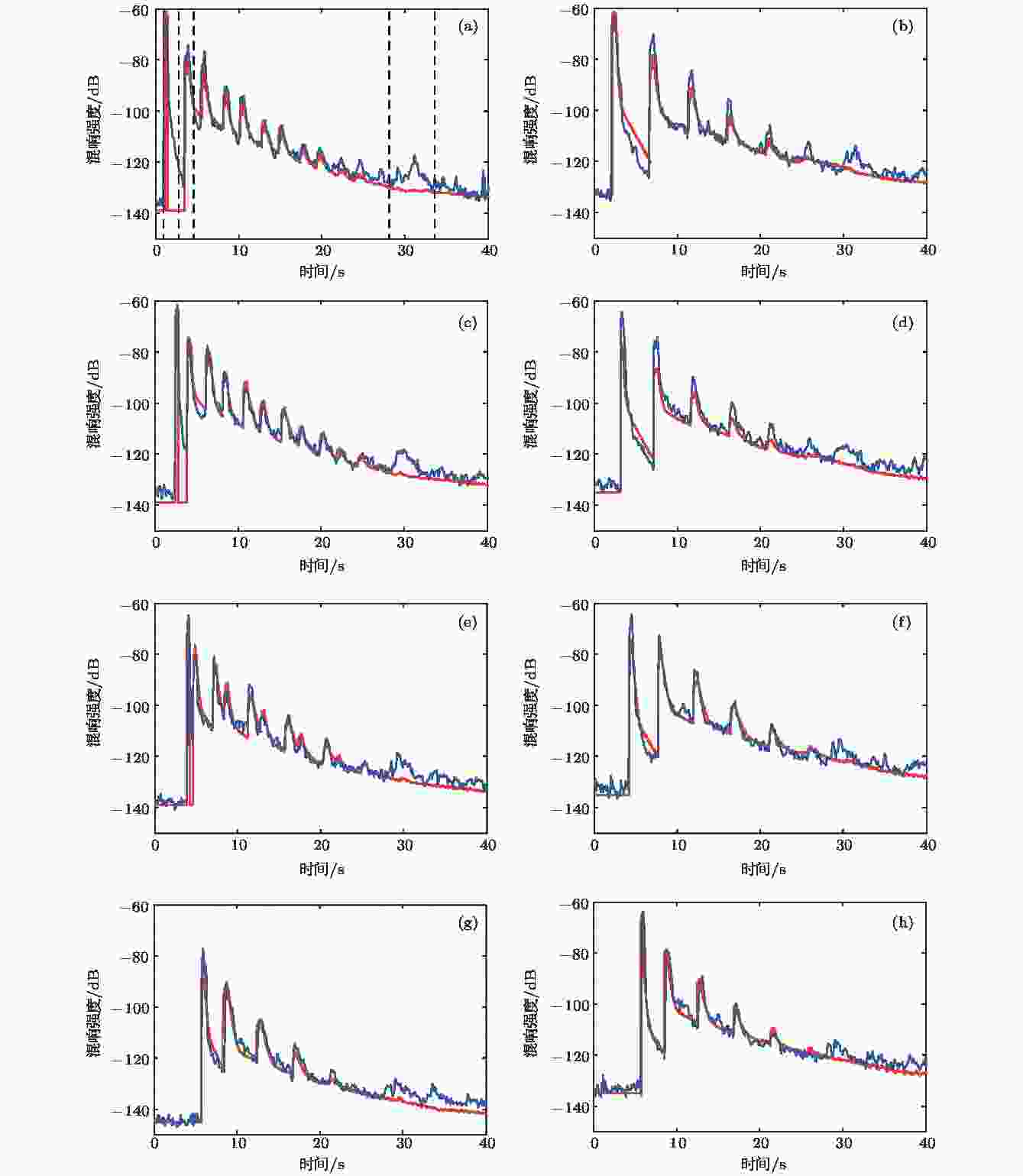图 10 数值模拟的大接收深度混响强度与实验结果对比. 声源频率500 Hz, 图中蓝色曲线为实验结果, 红色曲线为数值模拟结果.　(a) 收发相距0.76 km, 接收深度1903 m; (b) 收发相距0.76 km, 接收深度3366 m; (c) 收发相距3.19 km, 接收深度2306 m; (d) 收发相距3.19 km, 接收深度3366 m; (e) 收发相距5.45 km, 接收深度2357 m; (f) 收发相距5.45 km, 接收深度3366 m; (g) 收发相距7.75 km, 接收深度3021 m; (h) 收发相距7.75 km, 接收深度3366 m
Figure10. Comparison of reverberation at large receiving depths between numerical simulations and experimental results. The source frequency is 500 Hz. In each subgraph, the blue curve denotes the experimental result, and the red curve indicates the numerical simulation result. The distance from source to receiver and the receiving depth is (a) 0.76 km and 1903 m, (b) 0.76 km and 3366 m, (c) 3.19 km and 2306 m, (d) 3.19 km and 3366 m, (e) 5.45 km and 2357 m, (f) 5.45 km and 3366 m, (g) 7.75 km and 3021 m, (h) 7.75 km and 3366 m.

图10中均为大接收深度的混响结果, 深度范围在1903—3366 m, 在这种情况下, 海底散射掠射角${\theta _{{\rm{scatt}}}}$较小. 文献[17]指出, Lambert散射系数((5) 式第一项)在散射掠射角较小时更有效, 所以用其数值计算得到的混响强度与实验结果吻合较好. 图11给出了接收器靠近海面的混响强度结果. 图11(a)对应的收发距离很近, 可以看到第二到第四个峰值之间的数值和实验结果吻合较差, 这是由于该时间范围内对应的声波散射掠射角较大造成的. 但经过多次海底反射, 从远处散射体散射回的声波角度会变得相对较小, 所以之后的结果吻合较好. 图11(b)对应的收发距离较大, 一方面散射角度始终较小, 另一方面背向散射对混响的贡献也较小, 侧向散射的贡献较大, 所以整体吻合较好.
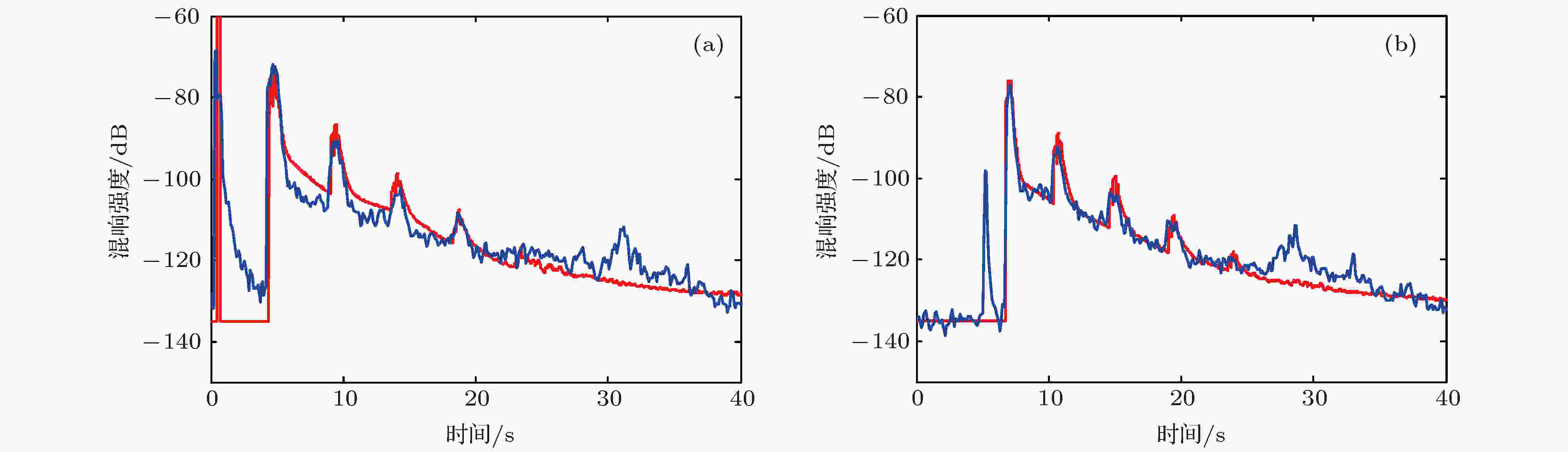图 11 接收器靠近海面时的混响强度. 声源频率500 Hz, 图中蓝色曲线为实验结果, 红色曲线为数值模拟结果;　(a)收发相距0.76 km, 接收深度205 m; (b)收发相距7.75 km, 接收深度205 m
Figure11. Reverberation for receiving depth near the sea surface. The source frequency is 500 Hz. In each subgraph, the blue curve denotes the experimental result, and the red curve indicates the numerical simulation result. The distance from source to receiver and the receiving depth is (a) 0.76 km and 205 m, (b) 7.75 km and 205 m.

5.总　结
基于射线理论建立了一种深海海底混响模型, 该模型与传统方法不同, 不是将对某一时刻混响有贡献的散射区域按圆环或椭圆环处理, 而是首先对海底散射区域进行网格式划分, 然后根据每个网格内散射体产生混响信号的准确时间进行混响计算, 该模型能够更加准确地计算深海本地混响和异地混响. 分析了爆炸声源激发的深海混响实验数据, 给出不同接收距离和深度条件下的结果, 并将其与数值模拟结果进行对比, 较好地解释了实验现象, 并由此确定了实验海区的散射系数. 实验与数值结果对比分析表明, 经典海底散射系数模型对于小掠射角海底散射更加准确, 对应于本文深海大接收深度混响.
感谢参加2018年春季南海海上声学综合实验的全体工作人员, 他们的辛勤劳动为本文提供了宝贵的实验数据.
相关话题/实验 信号 计算 传播 数据
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 三价镨离子掺杂对铽镓石榴石晶体磁光性能影响的量子计算
    摘要:在铽镓石榴石(TGG)晶体中掺杂Pr3+离子能够有效提升材料的磁光性能,但目前缺乏系统的理论计算阐明此问题.本文根据量子理论,分析了掺杂Pr3+离子的影响机理并进行了定量计算.根据微扰理论解算久期方程,得到自旋-轨道耦合、晶场、有效场及离子之间的超交换作用下,Tb3+,Pr3+离子的能级位移及 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 蒙特卡罗临界计算全局计数问题新策略研究
    摘要:基于一个裂变源分布对应香农熵序列的在线收敛性诊断方法,为提高全局计数整体效率的均匀裂变点算法将在首次激活迭代步和首次判断收敛迭代步的最大值之后启动.之后,整体精度指标将每隔固定迭代步数计算一次,一旦达到事先设定的精度标准,整个临界迭代计算将提前终止.这一判断过程将一直持续到事先设定的最大迭代步 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 1064 nm固体激光器和光纤激光器在制备压缩真空态光场实验中的对比研究
    摘要:实验和理论研究了单频固体激光器和单频光纤激光器的相对强度噪声对压缩真空态光场测量精度的影响.在实验中分别采用单频固体激光器和单频光纤激光器作为实验系统的光源,直接探测到的压缩真空态光场的压缩度分别为(13.2±0.2)dB和(10±0.2)dB.通过理论计算得知本实验中影响可测压缩度的主要因素 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于反转路径差信号的兰姆波成像方法
    摘要:针对传统基线相减成像方法受环境温度影响的问题,考虑到反转路径下超声波在缺陷处散射场的差异性,提出了一种基于反转路径差信号的兰姆波稀疏阵列成像方法.通过数值仿真,对反转路径差信号的来源进行了分析,并研究了缺陷与两个传感器的夹角及路径差对反转路径差信号幅值的影响规律.在此基础上,通过数值仿真及检测 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高效率三倍频产生355 nm皮秒激光的实验研究
    摘要:具有高重复频率、高平均功率的皮秒放大激光在科学研究和工业生产中有着重要的应用,尤其是在脆性材料的加工领域,绿光或紫外皮秒激光具有独特的优势.基于我们研制的平均功率23.2W、重复频率500kHz、脉冲宽度13.4ps的Nd:YVO4激光器,开展了LBO晶体高效率二倍频与三倍频的研究.通过优化相 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维含多孔介质周期复合结构声传播分析
    摘要:为取得理想的隔声性能,本文结合多孔介质和周期结构两类声振调控方案,讨论了一种新型含多孔介质周期复合结构;采用等效模型描述振子系统,利用薄板理论和Biot理论建立了相应的声振耦合理论模型.利用此模型计算得出的结果与文献中数据吻合良好.研究结果表明,采用简单振子系统或组合振子系统都可以在其特征频率 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于加权<i>K</i>-阶传播数的节点重要性
    摘要:节点重要性对于分析网络结构具有重要意义.为了充分刻画网络全局和局部特性,本研究基于网络拓扑结构对疾病传播过程进行了抽象,分别设置各个节点为传染源,在经历传播时长K后,将网络中已感染节点的数量定义为K-阶传播数,最终基于不同K值下的K-阶传播数得到节点重要性结果.对Watts-Strogatz小 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 2 μm波段再入射离轴积分腔输出光谱设计与实验
    摘要:离轴积分腔输出光谱技术(off-axisintegratedcavityoutputspectroscopy,OA-ICOS)是一种高灵敏度的激光光谱测量技术.但由于使用密集的高阶模进行光谱探测,OA-ICOS输出信号强度较低,使得探测灵敏度高度依赖于光源功率.针对该问题,本文引入光学再入射的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于冗余图态的多人协作量子计算
    摘要:量子计算是一种基于量子力学基本原理设计的新型计算模型,在某些特定问题上表现出了远超经典计算机的处理能力.随着量子计算任务复杂度的提高,如何分配量子计算资源,实现多方协作的量子计算,将成为量子计算领域待解决的一个重要问题.本文在一次性量子计算的基础上,提出了基于冗余图态的多人协作量子计算方案.不 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于计算全息和<i>θ</i>调制的彩色图像加密方法
    摘要:提出了一种基于计算全息和θ调制的彩色图像光学加密新方法.该方法利用彩色三基色原理和计算全息编码技术,首先将彩色图像的红、绿、蓝三基色分量进行随机相位调制和菲涅耳衍射变换,然后经过θ调制后进行图像叠加并编码为计算全息图,即加密过程是将一幅彩色图像加密为一幅实值的二元计算全息图,得到单幅密文.解密 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.