摘要:深海声场垂直相关特性对提高垂直阵阵列增益和水下目标探测性能具有重要意义. 基于2014年南中国海实验大跨度垂直阵接收的声信号, 分析了深海直达区、影区和会聚区等不同距离下的大深度声场垂直相关特性, 并使用射线理论解释了深海垂直相关随空间变化机理. 在直达声区内, 声场垂直相关半径几乎可以覆盖整个水深, 且随着深度增加, 直达声和海面反射声到达时间差增加, 相关略有下降. 在声影区内, 声场能量主要来源为经一次海底反射和一到两次海面反射的声线, 垂直相关整体偏低. 第一会聚区内垂直相关系数随着接收深度的增加而周期性振荡, 并且与声能量在深度上的分布具有相似结构, 这是高声强区域两组反转声线在垂直方向上周期性干涉的结果.
关键词: 垂直相关/
深海声场/
振荡结构

English Abstract

全文HTML

--> --> -->

声场垂直相关性表征了垂直空间上两个接收点声场的相似程度, 既是利用垂直阵进行匹配场定位的物理基础, 也是基于垂直阵声呐设计及获取空间增益的重要参数^[1], 在实际海洋环境中, 多途干涉效应会使得声场的垂直相关性降低, 进而影响垂直阵列波束形成和水下目标探测性能, 因此声场垂直相关性研究一直是海洋声学的重要课题之一.
国内外对声场垂直相关性展开了大量研究^[1-14]. 我国对声场垂直相关性的研究多集中在浅海. 2001年, Guo等^[2]对浅海远距离声场的垂直相关性进行了研究, 发现垂直相关系数随着距离的增加呈现出先减小后增大的趋势. 2004年, Li等^[3]利用垂直相关特性随距离的变化反演海底吸收系数. 2009年, Wan等^[4]通过两个L型接收阵同步研究了浅海声场的垂直相关性和水平相关性. 在浅海不平海底条件下声场空间相关研究方面, 赵梅和胡长青^[5]发现在浅海倾斜海底条件下, 空间相关性随着倾斜角度和阵元间距的增加而减小, 并且与收发深度有关; 2011年, 王鲁军等^[6]发现与水平海底相比, 下坡海底会增加声场的空间相关性, 上坡海底会减小声场的空间相关性.
在深海声场空间相关方面, Urick等^[10,11]提出, 会聚区声场的空间相关性明显高于影区, 而且随着阵元间距的增加衰减更慢. 1998年, 周士弘等^[1]发现, 多途干涉越复杂, 垂直相关系数变化越复杂, 而且垂直相关性与声源深度、频率以及声源与接收器的距离等有关. 2013年, Colosi等^[12]分别利用耦合模式传输理论和绝热模式近似理论分析了深海环境下的垂直相关, 并研究了深海垂直相关半径随着频率和距离的变化规律. Li等^[13]和李鋆^[14]对深海声场空间相关特性进行了研究, 发现声场的空间相关系数的空间分布结构与传播损失的空间分布结构基本一致, 高声强区内的声场主要是由一组相位相近的简正波或在水体中折射的射线组成, 其声场具有相似性. 胡治国等^[15-17]分析了在存在海底斜坡和海底小山丘的海底地形条件下, 声传播规律和声场的水平纵向相关性. 但是, 国内对深海大深度声场垂直相关性的研究还鲜有报道.
本文利用2014年南中国海的一次深海实验数据, 分区域探究了深海中直达声区、声影区和会聚区等不同距离位置的大深度声场垂直相关性, 并给出了相应的物理解释, 对提高深海环境下垂直阵列的阵增益和水下目标的探测性能等具有重要意义.

2014年6月, 声场声信息国家重点实验室在南中国海进行了一次深海声传播实验. 海上实验设备布放示意图如图1所示, 27个自容式水听器(USR)组成的潜标垂直阵被锚定在O2位置, 水听器呈不等间隔布放在102—1866 m深度范围内. 水听器的灵敏度为–170 dB, 通道的采样率为16 kHz. 实验船以4节航速拖曳发射换能器声源从O2接收阵位置向O1点行驶. O2到O1方向上声传播距离的总长度约172 km, 覆盖了3个会聚区.
图 1 海上实验设备布放示意图
Figure1. The configuration of the experiment.

拖曳发射换能器的深度约为126 m. 发射声信号是中心频率为310 Hz、带宽为100 Hz的双曲调频信号(HFM). 发射信号形式如图2所示, 先发射20 s, 停10 s, 重复四次, 再停40 s, 然后依次重复发射. 拖曳声源的声源级标定为181 dB. 图3是实验1号科考船上的万米测深仪测量的海深随距离的变化, 可见O2到O1 传播路径上海底整体比较平坦, 平均深度约为4300 m. 图4为实验期间的全海深声速剖面, 其中声道轴深度约为1150 m, 最小声速为1484 m/s, 海底附近海水声速(1533 m/s)小于海面处海水声速(1541 m/s), 为典型的不完全深海声道. 在这种海洋环境下, 海底反射作用对在声影区内的声场影响较大. 实验期间也进行了海底底质柱状采样测量, 经对3 m长的柱状沉积物样品分析表明: 实验海区的底质类型以粘土质粉砂为主, 具体分段测量的沉积物类型、密度、声速和中值粒径等参数如表1所示, 为海底声学参数的选取提供参考依据.
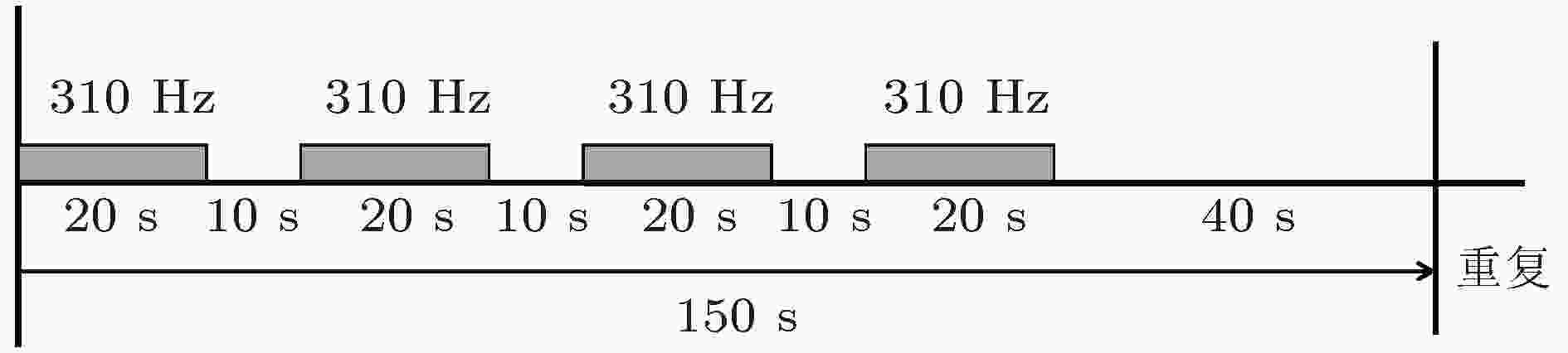图 2 拖曳换能器发射声信号的周期
Figure2. The cycle of the source signals from a towed transducer.

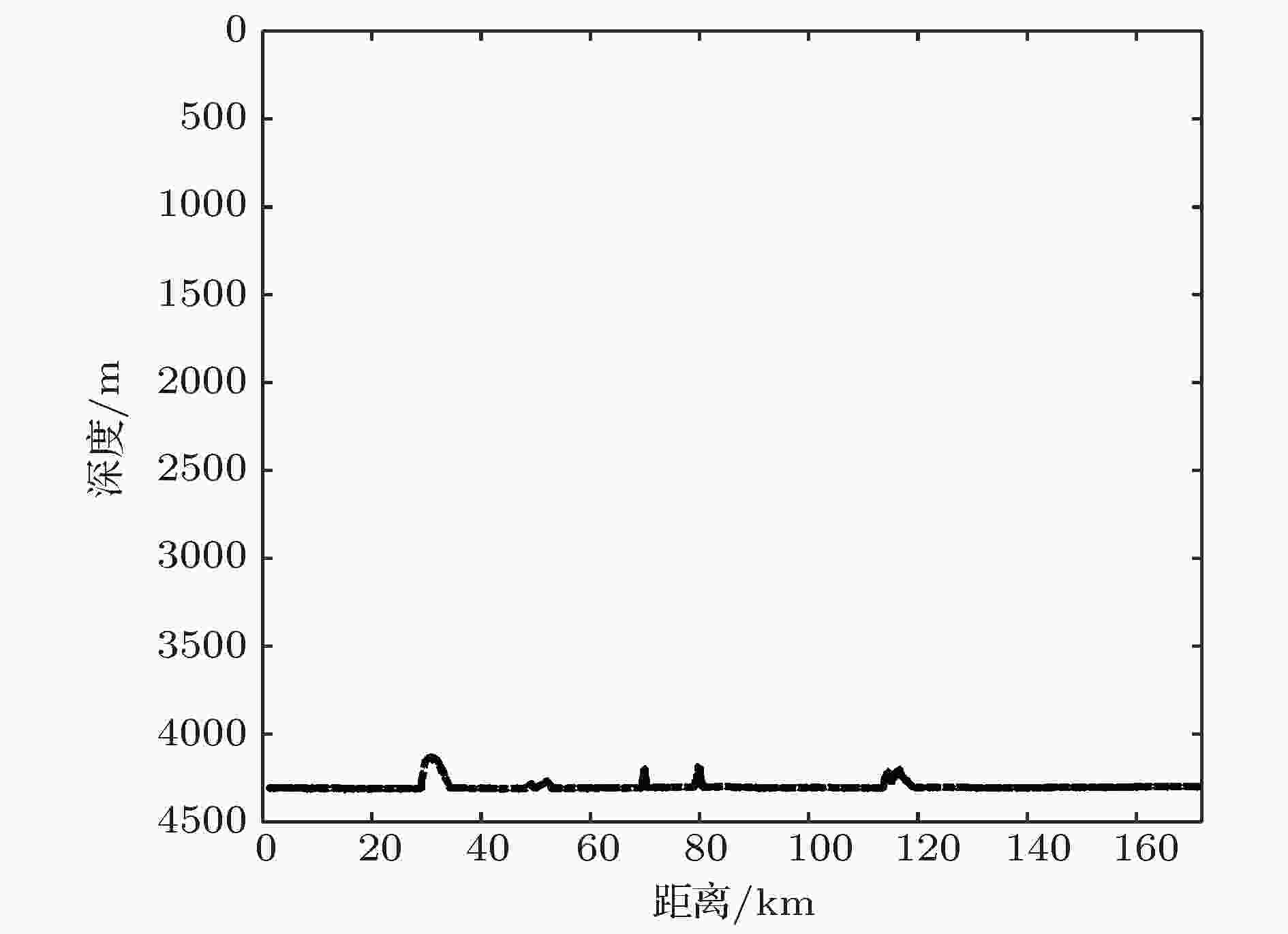图 3 O2到O1传播路径上海深随距离的变化
Figure3. The bathymetry along the propagation track from O2 to O1.

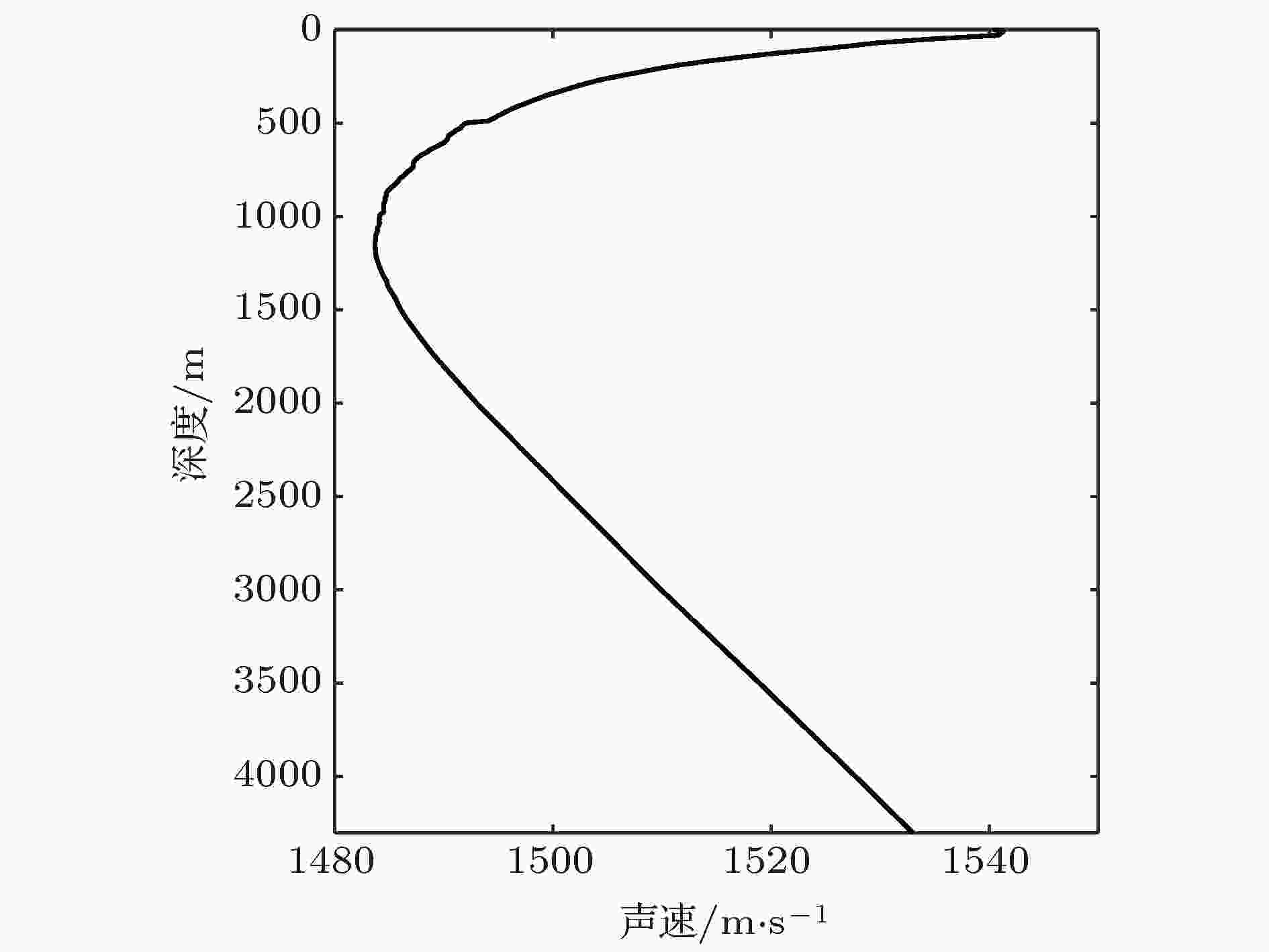图 4 实验期间的海水声速剖面
Figure4. Sound speed profile during the experiment.

深度范围/cm	实测声速/m·s–1	湿密度/g·cm–3	声衰减系数/dB·m–1	孔隙度/%	中值粒径/mm	沉积物类型
0–28	1583	1.65	137.06	62.60	0.0053	粘土质粉砂
28–55	1597	1.56	74.02	65.08	0.0274	粉砂
55–80	1663	1.57	118.80	67.59	0.0287	粉砂
80–105	1695	1.45	127.50	74.93	0.0127	粘土质粉砂
105–130	1631	1.55	108.91	68.22	0.0157	粉砂
130–155	1516	1.44	104.86	75.38	0.0062	粘土质粉砂
155–180	129	1.37	66.73	77.98	0.0059	粘土质粉砂
180–205	1508	1.33	127.47	80.77	0.0052	粘土质粉砂
205–230	1540	1.30	111.89	84.07	0.0046	粘土质粉砂
230–250	1533	1.26	121.37	85.00	0.0050	粘土质粉砂
250–280	1547	1.26	159.41	85.55	0.0057	粘土质粉砂
280–305	1565	1.21	255.70	83.24	0.0045	粘土质粉砂
平均值	1584	1.41	126.14	75.87	0.0106	–-

表1海底底质采样测量样品分析参数表
Table1.Sediment parameters analyzed from core sampling.

将声源发射的双曲调频信号设为是s(t), 则接收阵接收的声压信号p_R(r,z,t)可表示为

${p_{\rm{R}}}\left( {r,z,t} \right) =\displaystyle\int S\left( \omega \right)H\left( {r,z;\omega } \right)\exp \left( { - {\rm{i}}\omega t} \right){\rm{d}}\omega,$

其中S(ω)为s(t)对应的频谱, H(r,z;ω)为声源至接收器之间海洋声信道的传输函数, ω为角频率. 实验时可以通过脉冲压缩来提高信噪比. 脉冲压缩是将声源发射的信号s(t)与接收阵接收的信号p_R(r,z,t)做相关, 即:

$ {p_{\rm{c}}}\left( {r,z,t} \right) =\displaystyle \int { \left|{S\left( \omega \right)} \right|^2}H\left( {r,z;\omega } \right)\exp \left( { - {\rm{i}}\omega t} \right){\rm{d}}\omega, $

对应的频谱X_i可以由p_c(r,z,t)经过Fourier变换得到. 将X_i在实验发射信号的带宽内取平均, 得到信号的平均声能量:

$E\left( {{f_0}} \right) = \frac{2}{{F_{\rm{s}}^2}}{\rm{mean}} ({{{\left| {{X_i}} \right|}^2}} ),\left( {i = n{f_1}:n{f_2}} \right),$

其中f₀为信号的中心频率, F_s为信号的采样率, nf₂和nf₁分别为频率上、下限对应的频点数. 声传播损失(TL)的实验结果由下式计算:

${\rm{TL}}({f_0}|\left( {r,z} \right)) = {\rm{SL}}\left( {{f_0}} \right) - \left( {10\lg \left[ {E\left( {{f_0}} \right)} \right] - {M_v} - {E_{\rm{C}}}} \right),$

式中SL(f₀)代表发射换能器声源级, 本实验中为181 dB; M_v代表接收水听器灵敏度, 大小为–170 dB; E_C代表脉冲压缩获取的时频增益, 根据发射声源信号时间带宽计算得约为66.6 dB.
声场垂直相关指的是与声源水平距离相同, 深度不同的两个接收点接收到的声信号之间的互相关. 假设两个接收点位置分别为(r,z)和(r,z+${\Delta z}$), 其中r为与声源的水平距离, z为水听器深度. 垂直相关系数定义为两个接收水听器同时接收到声信号之间的互相关程度:

$\begin{split} &\rho \left( {\Delta z} \right) \\= &\mathop {\max }\nolimits_\tau \frac{{\displaystyle\int_{ - \infty }^\infty {p_z}\left( t \right){p_{z + \Delta z}}\left( {t + \tau } \right){\rm{d}}t}}{{\sqrt {\displaystyle\int_{ - \infty }^\infty {{\left| {{p_z}\left( t \right)} \right|}^2}{\rm{d}}t} \sqrt {\displaystyle\int_{ - \infty }^\infty {{\left| {{p_{z + \Delta z}}\left( t \right)} \right|}^2}{\rm{d}}t} }},\end{split}$

其中p_z(t)和$p_{z+{\Delta z}}(t)$分别代表两个水听器接收到的声压时域信号, ${\Delta z}$是水听器在垂直方向的间隔. 一般浅海远场垂直阵接收信号的波阵面可以近似为同时到达, 只需要做零时延相关. 与浅海中不同, 在深海中不同深度上波阵面到达时间差别较大, 所以垂直相关处理中 $p_{z+{\Delta z}}(t)$(t+τ)表示将其中一个信号做时延τ之后再做互相关. 频域内的垂直相关系数可以通过Fourier变换得到:

$\rho \left( {\Delta z} \right) = \mathop {\max }\nolimits_\tau \dfrac{{{\rm{Re}}\left[\displaystyle\int_{{\omega _0} - \tfrac{{\Delta \omega }}{2}}^{{\omega _0} + \tfrac{{\Delta \omega }}{2}} {P_z}\left( \omega \right)P_{z + \Delta z}^*\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega \tau }}{\rm{d}}\omega\right]}}{{\sqrt {\displaystyle\int_{{\omega _0} - \tfrac{{\Delta \omega }}{2}}^{{\omega _0} + \tfrac{{\Delta \omega }}{2}} {{\left| {{P_z}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } \sqrt {\displaystyle\int_{{\omega _0} - \tfrac{{\Delta \omega }}{2}}^{{\omega _0} + \tfrac{{\Delta \omega }}{2}} {{\left| {{P_{z + \Delta z}}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }},$

其中P_z(ω)和$P_{z+{\Delta z}}(\omega)$分别表示两个接收点位置的声场, *表示复数共轭. ω₀和$\Delta \omega$分别表示中心频率和带宽.
在下面的垂直相关性分析中, 采用(5)式对接收水听器接收的时域声压信号进行处理得到实验垂直相关系数, 用声传播模型计算频域声场经(6)式相关处理得到垂直相关理论结果.
为了比较垂直相关性的大小, 引入参考相关系数. 一般认为, 归一化相关系数大于参考相关系数0.707的两点间声场相关性较好.

2

-->

4.1.声传播损失

利用(2)式对垂直阵列接收的信号进行匹配滤波处理可得脉冲传播信号, 然后由(4)式计算得到O2到O1 传播路径上二维声传播损失（TL）, 结果如图5(a)所示. 作为比较, 图5(b)给出用抛物方程近似声场模型RAM-PE^[18,19]计算的不同距离和深度上的TL^[15,16]. 计算中, 采用声学互易原理^[20], 将声源设定在0 km, 不同的水听器所在深度, 在原拖曳声源深度的不同距离处接收信号. 仿真时频率范围与实验一致, 为260―360 Hz, 频点间隔为10 Hz. 根据表1的海底采样测量结果及声影区传播损失反演可获得的等效海底参数^[21], 海底模型设置为两层液态海底^[15], 沉积层声速1555 m/s, 密度1.6 g/cm³, 海底衰减系数 0.35 dB/λ, 厚度为20 m; 无限大基底声速为1650 m/s, 密度为1.8 g/cm³, 海底衰减系数$0.517 \!\times\! f^{1.07}~\text{dB}/\lambda$^[21,22], 其中频率 f的单位为kHz. 该海底模型及参数可较好地用于南海深海声传播损失计算^[15]. 海水吸收系数α(单位dB/km)则用以下公式计算^[20]:

$\alpha \cong 3.3 \times {10^{ - 3}} + \frac{{0.11{f^2}}}{{1 + {f^2}}} + \frac{{44{f^2}}}{{4100 + {f^2}}} + 3.0 \times {10^{ - 4}}{f^2},$

对比图5(a)和图5(b)可见, 在最大传播距离172 km以内, 基本上覆盖了3个会聚区, 实验结果空间分布与模型计算的影区及会聚区的相对强度一致, 表明不同距离上信号都具有较强的信噪比, 且第一会聚区以内声场信噪比更高. 过去受到实验条件限制, 我国对深海大深度声场垂直相关性的研究起步比较晚. 所以, 本节将选用O2到O1 传播路径上的实验数据, 分为直达声区、声影区和会聚区三个部分, 探究平坦海底环境下大深度声场的垂直相关特性. 实验选用O2潜标接收阵上所有27个水听器接收的数据, 并与RAM-PE模型计算结果进行对比. RAM-PE模型计算时选择与实验信号一致的频率范围, 即260—360 Hz, 选取101个频点, 频点间隔为1 Hz, 其他环境参数与计算图5(b)声传播损失时相同.
图 5 O2到O1 传播路径上二维声传播损失对比　(a)实验结果; (b) RAM模型计算结果
Figure5. TL along the propagation track from O2 to O1: (a) Experimental result; (b) numerical result.

2 -->

4.2.直达区声场垂直相关

实验中O2垂直阵的最大接收深度为1866 m, 在此深度下直达区宽度大约为10 km. 首先, 选取收发距离为2.0和4.2 km两个直达区内的典型收发距离进行垂直相关特性分析.
3 -->

4.2.1.距离2.0 km处声场垂直相关

先对收发距离2.0 km处的声场垂直相关特性进行研究. 图6 给出的是潜标垂直接收阵上不同水听器之间的声场自相关与互相关系数, (a)是实验结果, (b)是模型计算结果, 模型结果与实验结果符合较好. 互相关图以对角线为中心上下对称, 中间的斜对角线是各阵元的自相关结果, 归一化相关系数为1. 从图中可以看出, 2.0 km处接收阵的垂直相关性总体比较高. 图7是以第1阵元(平均深度102 m)为参考阵元, 与各个通道接收的信号做相关得出的垂直相关系数随着垂直间隔变化的实验结果和模型计算结果(即图6中第一行结果), 两者符合较好. 可见, 在距离2.0 km处, 垂直相关系数较高, 随着垂直间隔的增加, 垂直相关系数缓慢下降, 但基本保持在参考相关系数0.707(图中蓝色虚线, 下同)以上.
图 6 距离2.0 km处垂直阵声场垂直互相关　(a) 实验结果; (b) 模型结果
Figure6. The vertical cross-correlation of sound fields in the whole array at the range of 2.0 km: (a) Experimental results; (b) numerical results.

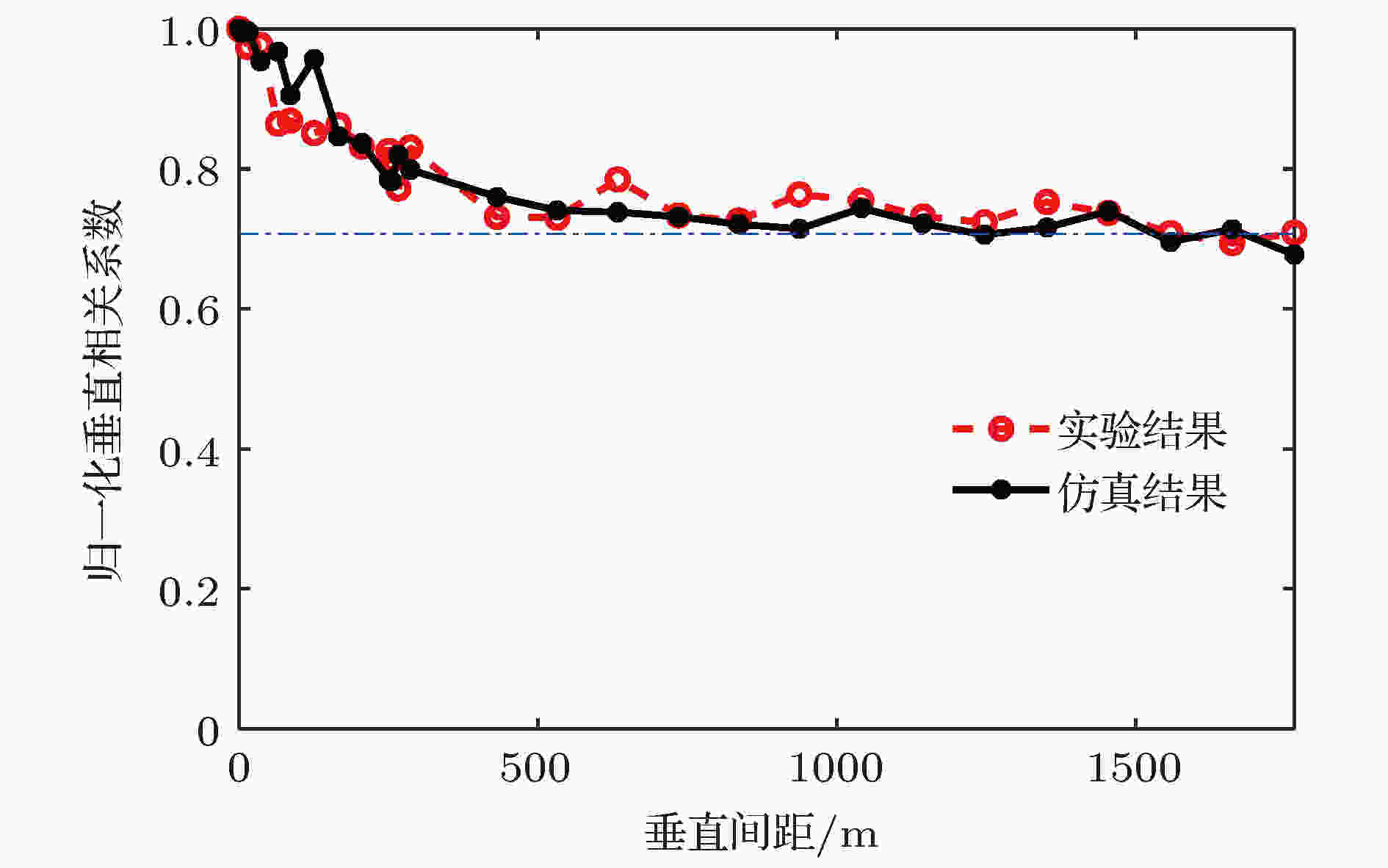图 7 距离2.0 km处声场垂直相关随间距的变化, 其中参考阵元深度102 m, 虚线为参考值0.707
Figure7. The vertical correlation coefficients at the range of 2.0 km for the reference depth at 102 m, where the dashed line representing the reference value 0.707.

深海声场中有效简正波号数比较多, 而射线声学物理图像清晰, 在深海环境中能较好地反映声波在海水中的传播特性. 以高斯波束追踪法^[23]为基础的BELLHOP射线模型可以计算水平变化环境中声线轨迹、时间到达结构和声强. 这里用BELLHOP模型对2.0 km处垂直相关系数的变化结果进行定性分析和机理解释.
图8给出距离2.0 km, 声源深度126 m, 接收深度分别为167 m, 357 m 和1453 m时的本征声线及时间到达结构. 为了使结果更加直观, 对不同大小掠射角的本征声线用不同颜色进行区分, 小于10°为青色, 10°—20°为红色, 20°—40°为深蓝色, 40°—65°为绿色, 后文均采用相同的颜色标注. 从图8可以看出, 到达垂直阵的声线多为直达声线(DR)和一次海面反射声线(SR), 且随着接收深度增加, 两条声线之间到达时间差逐渐增大. 图9给出整个垂直阵深度上的时间到达结构实验结果与BELLHOP计算结果的对比. 从图中可以看出, 两者比较符合, 直达区2.0 km处接收声信号主脉冲结构简单, 垂直相关性整体较高. 随着接收深度增加, 两条声线到达时间差逐渐增大, 信号多途畸变更明显, 从而导致图7中垂直相关系数随着垂直间隔增加而下降.
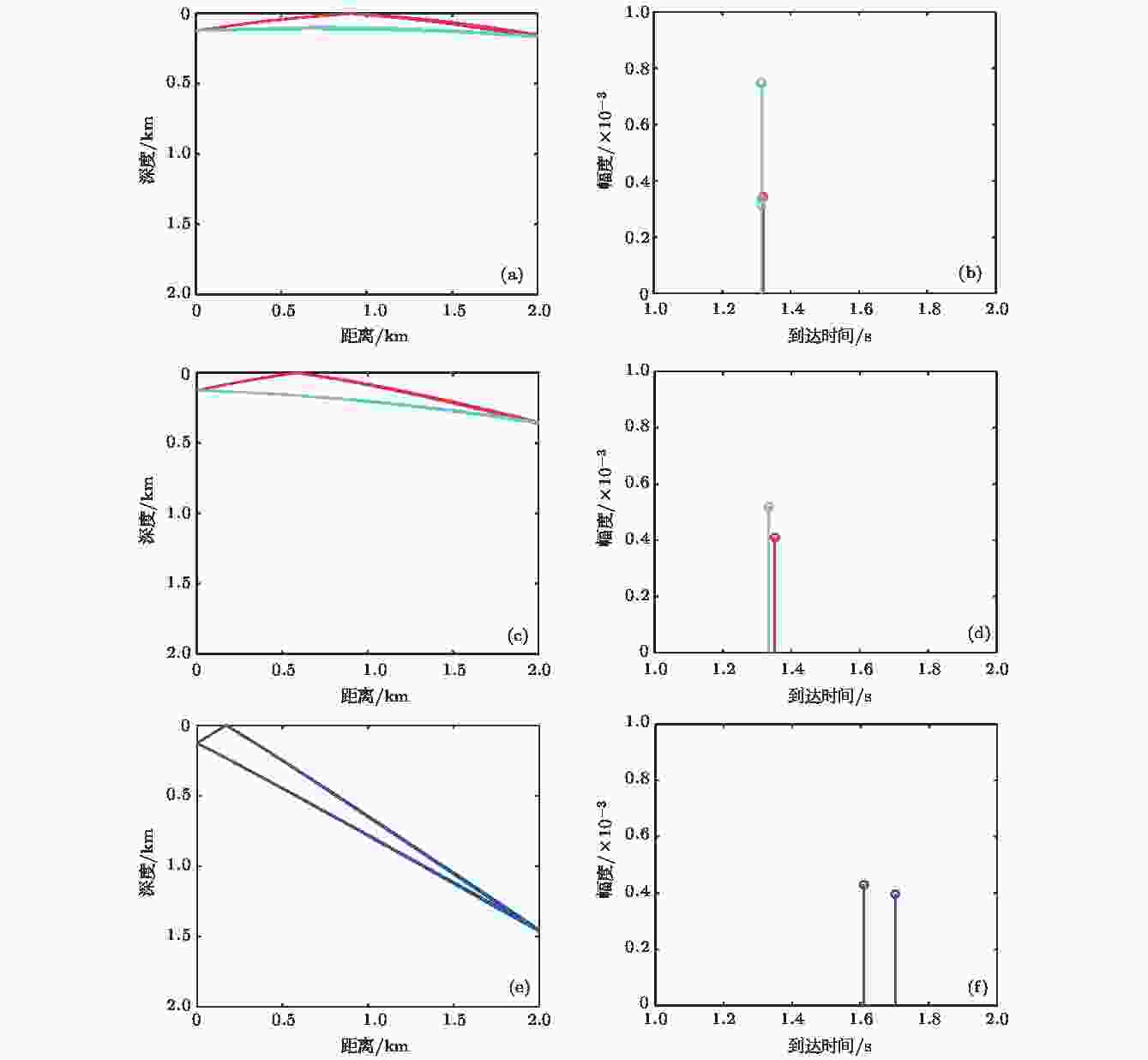图 8 直达区内2.0 km距离处不同接收深度本征声线和时间到达结构 (a), (b) 167 m; (c), (d) 357 m; (e), (f) 1453 m
Figure8. Eigenrays and arrivals received at three different depths at the range of 2.0 km in the direct zone: (a), (b) 167 m; (c), (d) 357 m; (e), (f) 1453 m.

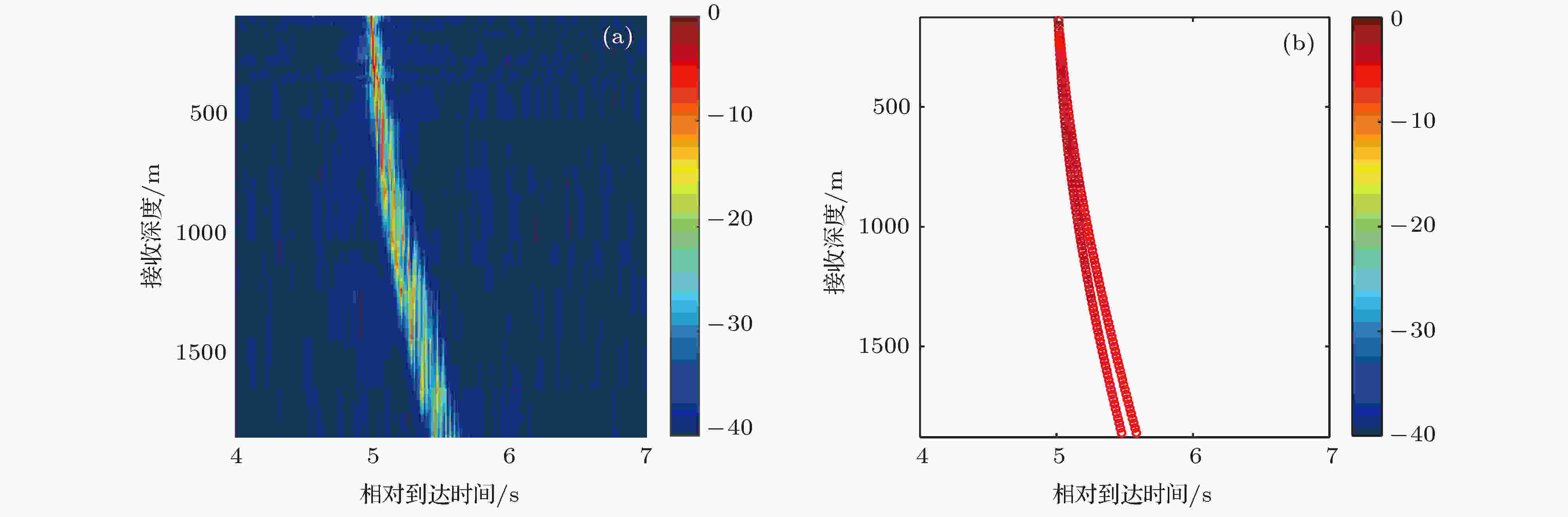图 9 直达区内2.0 km距离处不同接收深度多途到达结构比较　(a) 实验结果; (b) 模型结果
Figure9. Comparison of the experimental multipath structures on the vertical line array at the range of 2.0 km in the direct zone with numerical ones: (a) Experimental result; (b) numerical result.

下面将使用射线声学理论对直达区声场的垂直相关性进行定量分析和近似推导. 由于近场声波经海底大角度反射后的声能量衰减较大, 故只考虑对直达区声场起主要贡献的DR和SR, 即图10所示的两条声线. 图11给出了这两条声线的声源掠射角和时间到达结构, 直达区接收点接收到的声压可以近似表示为^[24]
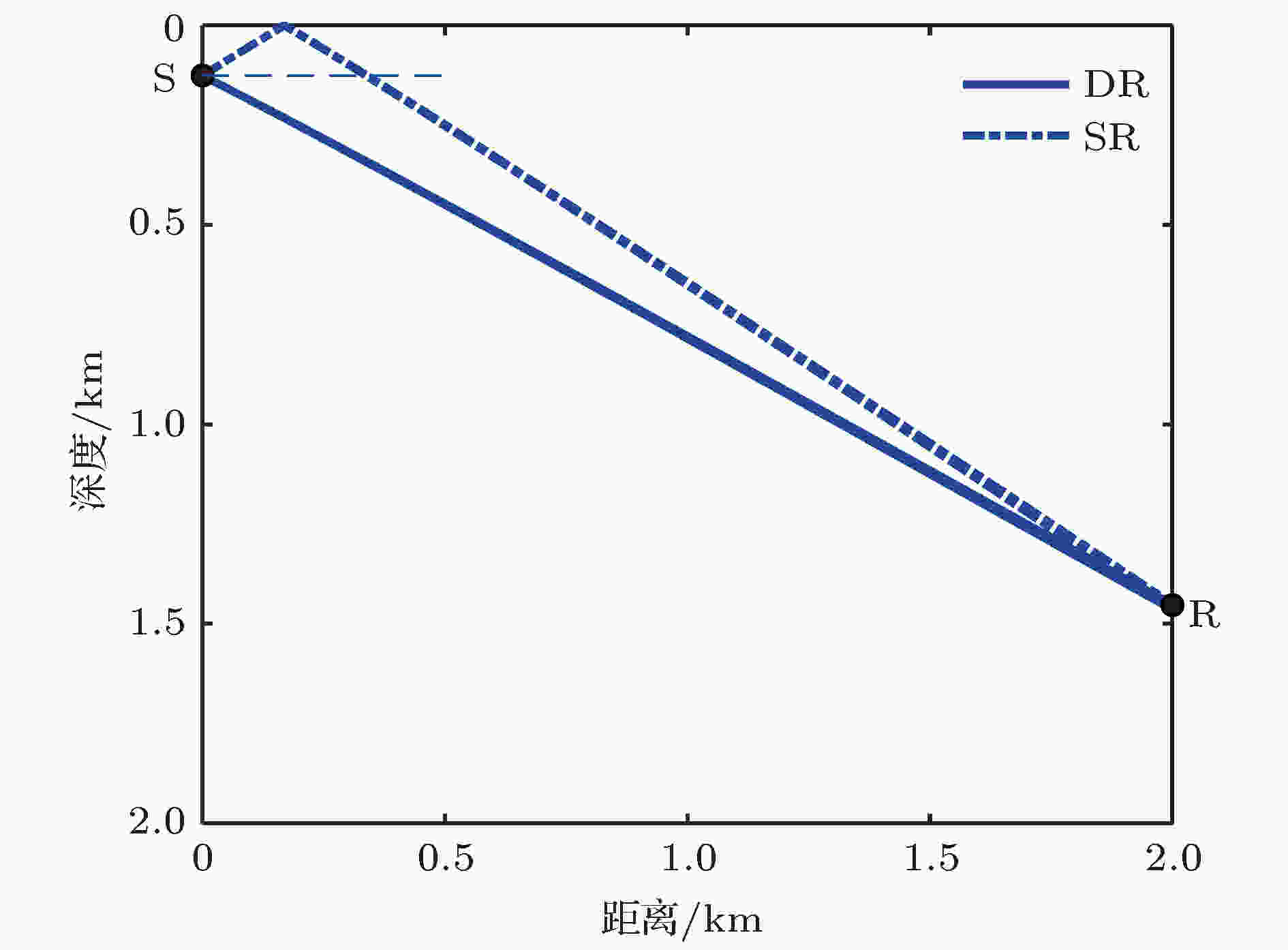图 10 直达区内对声场起主要贡献的两条声线, 其中声源深度126 m, 接收深度1453 m
Figure10. The two main rays contributing to the sound field in the direct zone, where the source and receiver are at the depth of 126 and 1453 m, respectively.

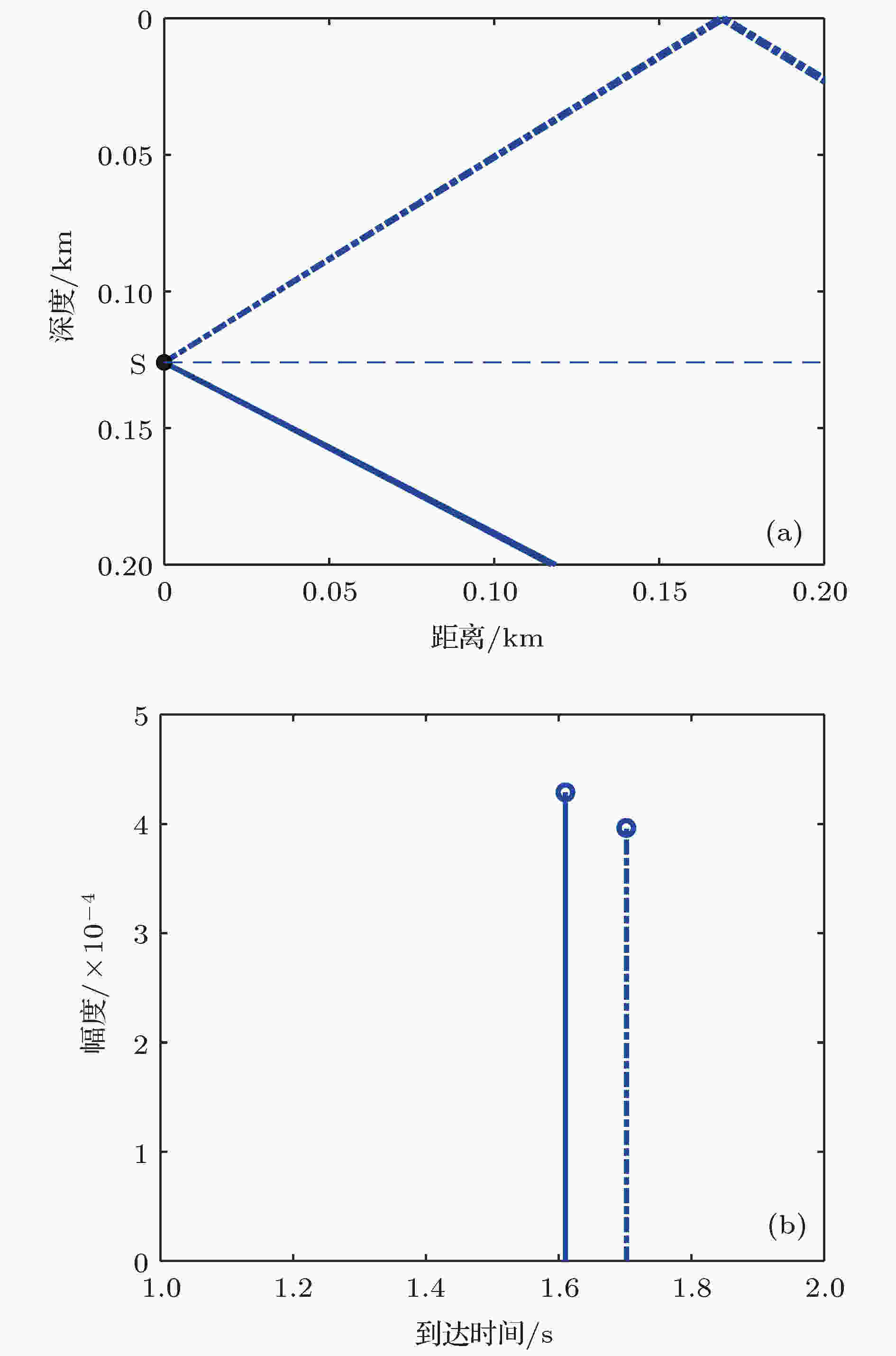图 11 直达区内对声场起主要贡献的两条声线的初始掠射角及时间到达结构　(a) 声源处的掠射角; (b) 时间到达结构(声源深度126 m, 接收深度1453 m)
Figure11. The two main rays contributing to the sound field in the direct zone: (a) The grazing angles at source location; (b) the arrivals of the two rays (The source and receiver are at the depth of 126 and 1453 m, respectively).

$P(r,z;\omega) \!\cong\! \frac{{S(\omega)\!\sqrt W }}{{4{\text{π}}}}\left( {\frac{{\sqrt {{F_1}} }}{{{R_1}}}{{\rm{e}}^{{\rm{i}}\omega {t_1}}} \!-\! \frac{{\sqrt {{F_2}} }}{{{R_2}}}{{\rm{e}}^{{\rm{i}}\omega {t_2}}}} \right),$

其中S(ω)表示声源的频谱, W为单位立体角内的辐射声功率, F_i表示第i条声线的聚焦因子, R_i表示第i条声线的斜距, t_i(i = 1,2)表示第i条声线的传播时间.
因为声源深度较浅, 两条声线的轨迹基本一致, 声源掠射角的绝对值近似相等, 即|α₁|≈|α₂|, 同时可以认为聚焦因子F和斜距R基本一致. 令Δt = t₂–t₁, 则(8)式中两条声线的相干叠加部分可以近似表示为

$P\left( {r,z;\omega } \right) \cong {A_z}\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega {t_1}}}\left( {1 - {{\rm{e}}^{{\rm{i}}\omega \Delta t}}} \right),$

其中${A_z}\left( \omega \right) = \dfrac{{S\left( \omega \right)\sqrt W }}{{4{\text{π}}}}\dfrac{{\sqrt {{F_1}} }}{{{R_1}}}$为幅度值.
因为两条声线满足|α₁|≈|α₂|, Δt可以近似表示为^[24]

$\Delta t \approx \frac{{2\displaystyle\int_0^{{z_s}} \sqrt {{n^2}\left( z \right) - {\rm{co}}{{\rm{s}}^2}{\alpha _2}} {\rm{d}}z}}{{{c_0}}},$

由(10)式可知, Δt随着声源深度z_s的增加而增大. 在典型深海条件下, 当收发距离不变时, |α₂|的值随着深度的增加而增大, 因此两条声线的到达时间差Δt随着接收深度的增加而增大.
同理, 接收点(r,z+Δz)处的声压可以表示为

$P\left( {r,z \!+\! \Delta z;\omega } \right) \cong {A_{z + \Delta z}}\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega t_1'}}\left(\! {1 - {{\rm{e}}^{{\rm{i}}\omega \Delta t'}}}\!\right) ,$

其中${A_{z + \Delta z}}\left( \omega \right) = \dfrac{{S\left( \omega \right)\sqrt W }}{{4{\text{π}}}}\dfrac{{\sqrt {F_1'} }}{{R_1'}}$为幅度值.
在窄带带宽Δω内, 有${A_z}\left( \omega \right) \approx {A_z}\left( {{\omega _0}} \right)$, ${A_{z + \Delta z}}\left( \omega \right) \approx {A_{z + \Delta z}}\left( {{\omega _0}} \right)$. 将(9)式和(11)式代入(6)式, 分子分母同时约去幅度项, 可得:

$\rho \left( {\Delta z} \right) \approx \mathop {\max }\limits_\tau \frac{{{\rm{Re}}\left[\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\rm{e}}^{{\rm{i}}\omega \left( {{t_1} - t_1' + \tau } \right)}}\left( {1 - {{\rm{e}}^{{\rm{i}}\omega \Delta t}}} \right)\left( {1 - {{\rm{e}}^{ - {\rm{i}}\omega \Delta t'}}} \right){\rm{d}}\omega\right]}}{{\sqrt {\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\left| {1 - {{\rm{e}}^{{\rm{i}}\omega \Delta t}}} \right|}^2}{\rm{d}}\omega } \sqrt {\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\left| {1 - {{\rm{e}}^{{\rm{i}}\omega \Delta t'}}} \right|}^2}{\rm{d}}\omega } }}.$

由于参考点(r,z)选定后, t₁和Δt为定值, 时延τ可以使${{\rm{e}}^{{\rm{i}}\omega \left( {{t_1} - t_1' + \tau } \right)}}$项实部近似等于最大值1, 故(12)式中的相位变化主要取决于ωΔt^'.
根据上述理论分析, 收发距离2.0 km处, 以第一阵元(平均深度102 m)为参考阵元, 用BELLHOP模型计算得到的DR和SR的到达时间差和相位差随深度的变化如图12所示. 从图中可以看出, 随着接收深度的增加, 两条声线的到达时间差逐渐增大, 而相位差在$\left[ {0,2} {\text{π}}\right]$内无规则振荡变化. 最后, 用近似公式(12)式计算得到参考深度为102 m时垂直相关系数随垂直间隔的变化, 如图13中青色曲线所示. 从图13结合图9可以看出, 近似公式只考虑两条声线, 而实际接收的信号及宽角RAM-PE计算的信号里包括一定角度范围内的声能量, 所以(12)式计算得到的相关系数在500 m以浅与实验结果及RAM-PE模型^[18]计算结果有0.15左右的偏差, 但是基本能够反映直达区声场的高垂直相关性.
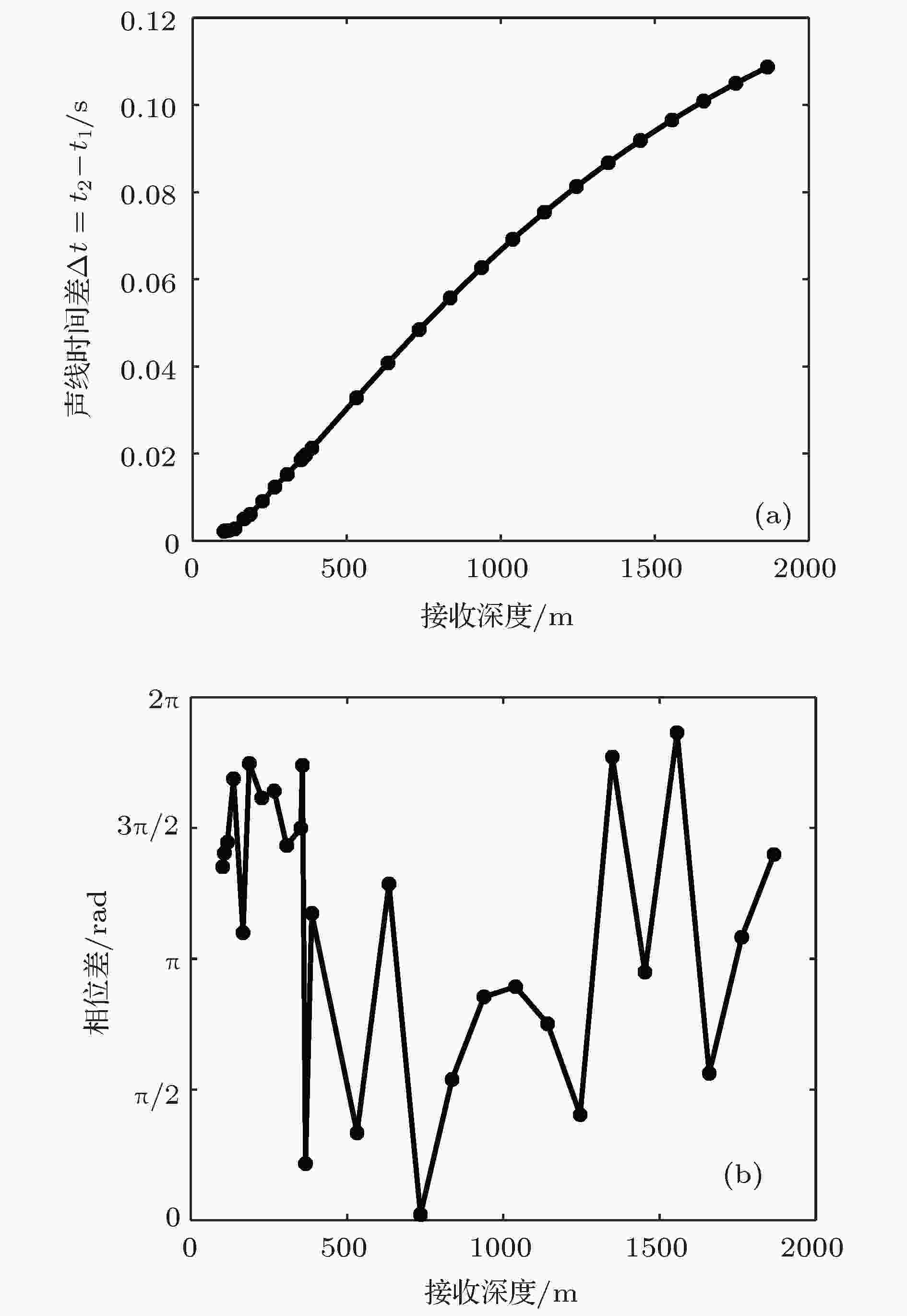图 12 由射线模型计算的距离2.0 km处对声场起主要贡献的两条本征声线DR和SR的(a) 到达时间差和(b) 相位差随接收深度的变化
Figure12. Numerical travel time differences (a) and phase differences (b) of the two eigenrays (DR and SR) with the increase of the receiving depth at the range of 2.0 km from Bellhop model.

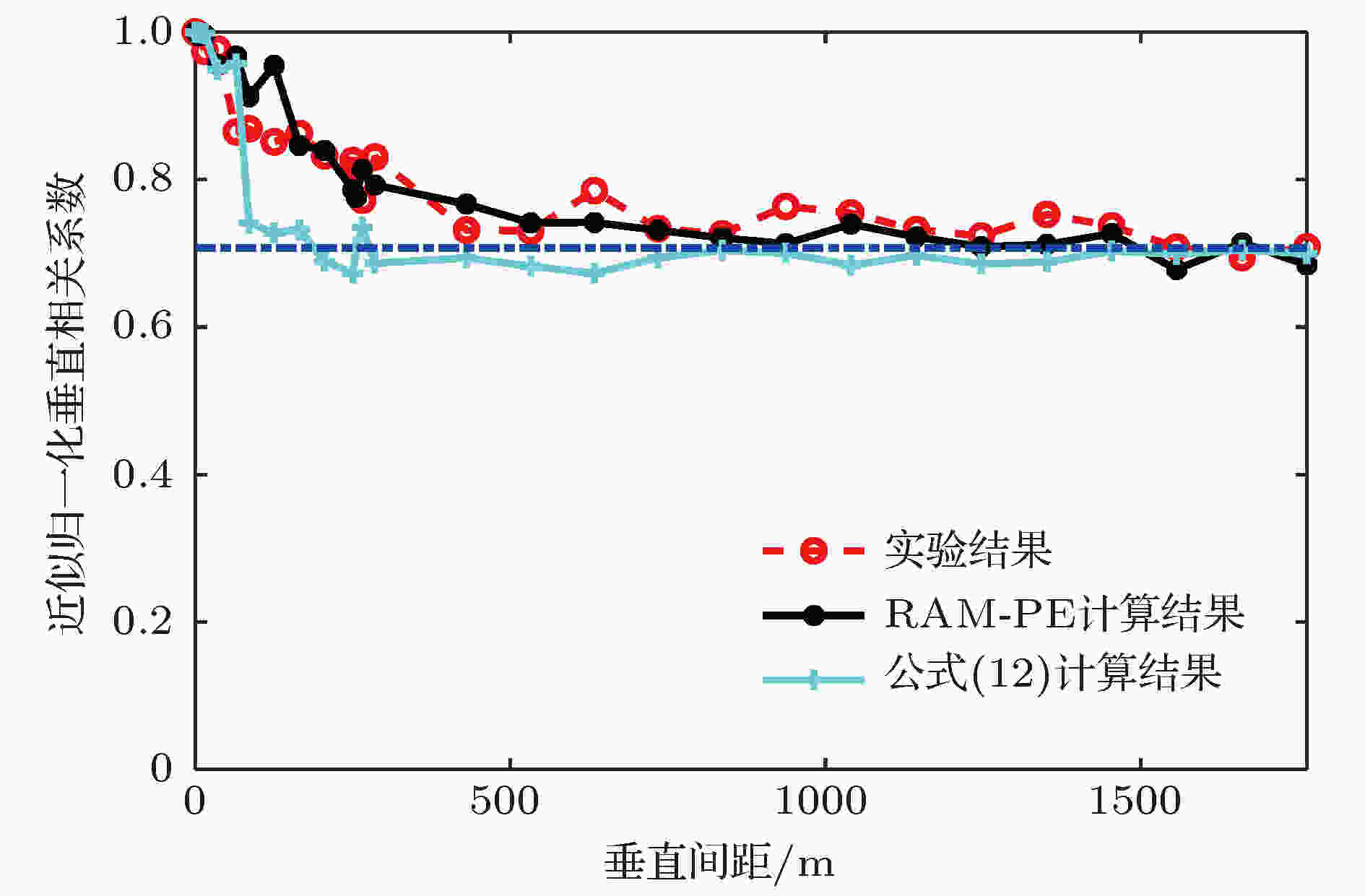图 13 由近似公式(12)式计算的垂直相关系数随着垂直间距变化与实验结果及RAM-PE模型结果的对比
Figure13. Comparison of the numerical vertical correlations computed by Eq. (12), with the experimental data and RAM-PE model results at the range of 2.0 km.

3 -->

4.2.2.距离4.2 km处声场垂直相关

当收发距离增加到4.2 km时, 潜标垂直接收阵较浅深度的水听器处在声影区内, 而部分较深的水听器处在直达声区内. 图14给出了各水听器接收声信号的互相关实验结果和模型计算结果, 可以看出, 与收发距离2.0 km处的结果相比, 编号较小的阵元所在的浅层深度声场垂直相关性显著偏低, 而在11阵元(平均深度357 m)以下, 阵元间的垂直互相关性较高. 为了分析垂直相关性随深度的变化情况, 图15给出了参考深度分别为102 m和357 m时的垂直相关系数随着垂直间隔变化的曲线, 可以看出, 参考深度为102 m时垂直相关系数随着垂直间距下降迅速, 并很快维持在0.3左右, 而以第11阵元为参考阵元的垂直相关系数随着深度增加下降缓慢, 与收发距离2.0 km处的情况比较类似, 相关系数基本维持在0.707上下.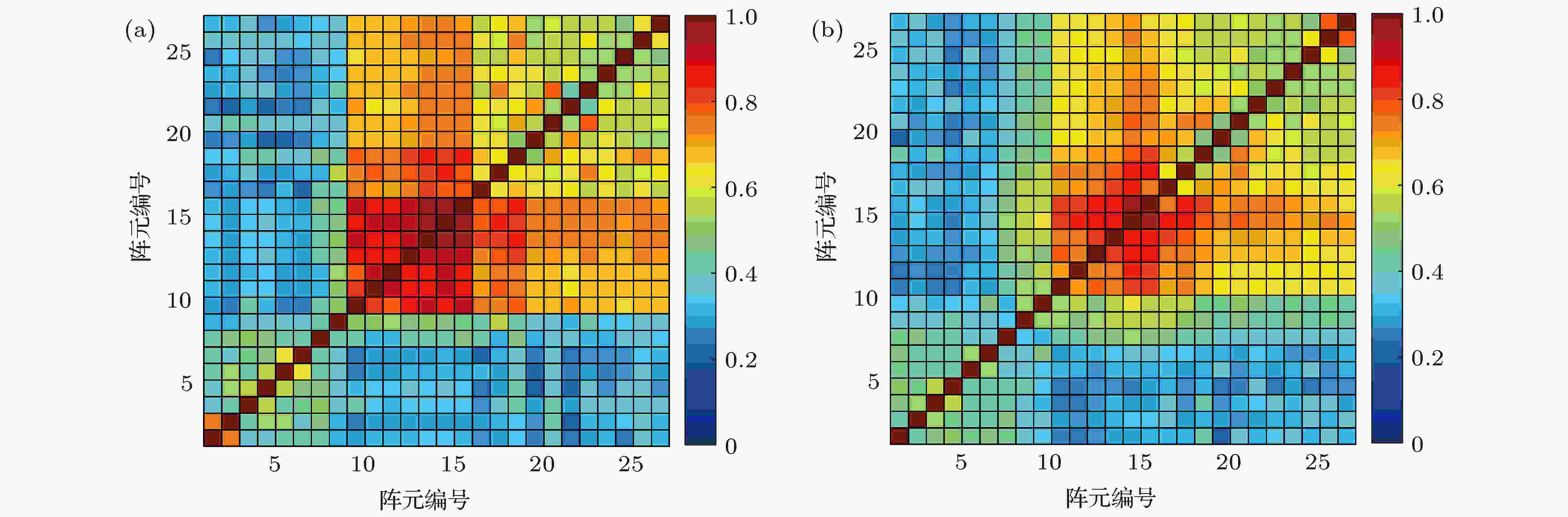
图 14 距离4.2 km处垂直阵声场垂直互相关　(a) 实验结果; (b) 模型结果
Figure14. The vertical cross-correlation of sound fields in the whole array at the range of 4.2 km: (a) Experimental results; (b) numerical results.

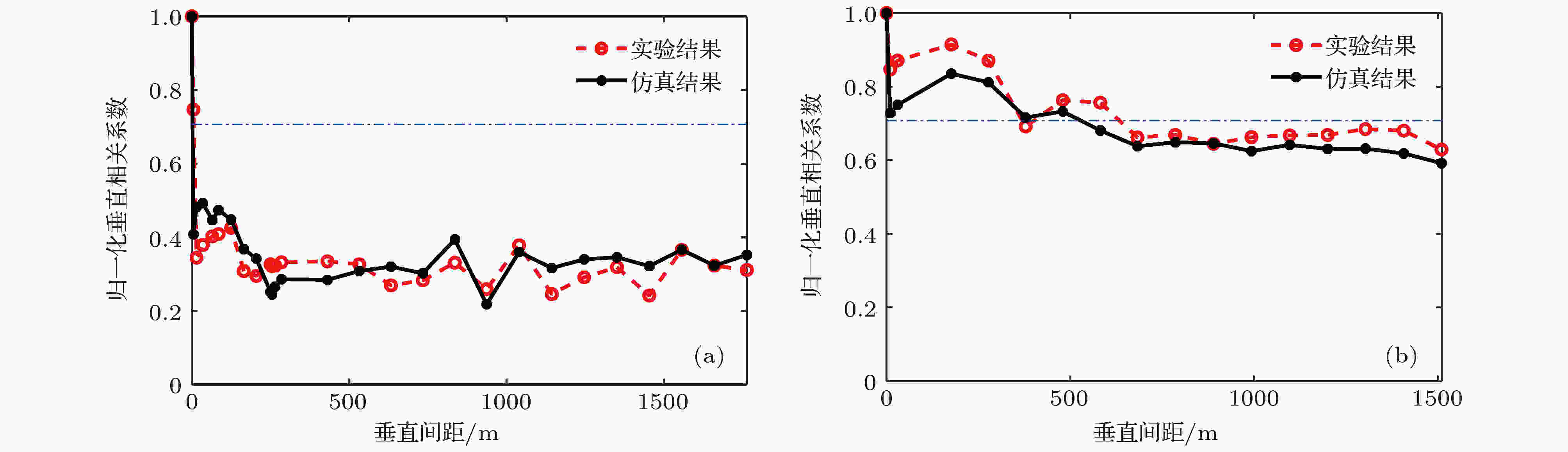图 15 距离4.2 km处两个不同参考深度上声场垂直相关随间距的变化　(a) 参考深度102 m; (b) 参考深度357 m
Figure15. The vertical correlation coefficients at two different reference depths at the range of 4.2 km: (a) For reference depth 102 m; (b) for reference depth 357 m.

图16是用BELLHOP模型计算得到的距离4.2 km处声源深度126 m, 接收深度分别为167 m, 357 m和1453 m的本征声线和时间到达结构. 图17是时间到达深度结构的实验结果与BELLHOP计算结果比较. 对比图16和图17可以看出, 4.2 km处深度较大的地方仍然处于直达区, 对声场起主要贡献的是两条声线DR和SR, 声信号主脉冲结构简单, 相关性较高, 垂直相关系数随着垂直间隔的增加下降缓慢. 而357 m以浅的接收深度处于影区, 经历一次海底反射的声线对声场的贡献占主, 声信号主脉冲多途到达结构复杂, 使得这部分阵元接收到的信号与其他深度阵元接收到的信号之间相关性较差, 垂直相关系数降低, 且随着深度增加下降较快.
图 16 直达区内4.2 km距离处不同接收深度的本征声线和时间到达结构　(a), (b) 167 m; (c), (d) 357 m; (e), (f) 1453 m
Figure16. Eigenrays and arrivals received at three different depths at the range of 4.2 km in the direct zone: (a), (b) 167 m; (c), (d) 357 m; (e), (f) 1453 m.

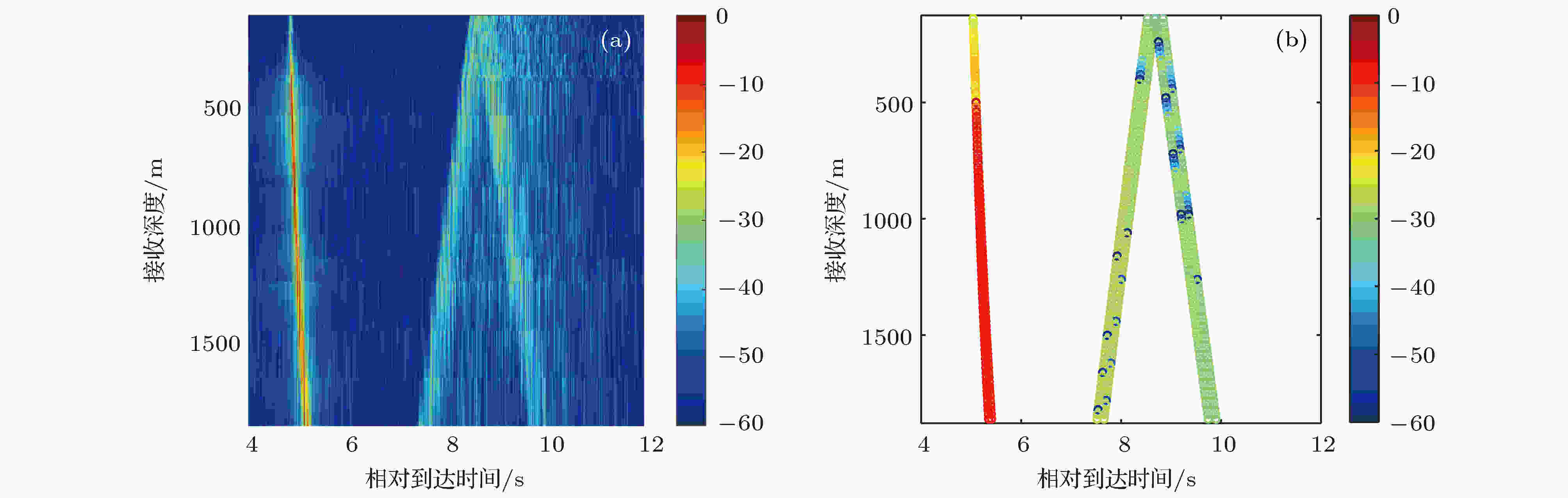图 17 直达区内4.2 km距离处垂直阵深度覆盖范围内的多途到达结构比较　(a) 实验结果; (b) 模型结果
Figure17. Comparison of the experimental multipath structures from the receivers on the vertical line array at the range of 4.2 km in the direct zone with numerical ones: (a) Experimental result; (b) Numerical result.

2 -->

4.3.声影区声场垂直相关

图18和图19分别给出第一影区内13.6 km和33.2 km两个不同距离处的接收阵各水听器接收声场的垂直互相关实验结果和模型计算结果的比较. 从图18和图19可以看出, 与图6和图7的直达区结果相比, 声影区内声场垂直相关系数整体偏小, 而距离33.2 km处的垂直相关比13.6 km处的稍高, 并且从实验结果和模型计算结果中都可以看到随着间隔增大声场垂直相关系数有较小幅度起伏. 为了进一步说明第一影区声场垂直相关特性的变化, 图20给出了参考深度为102 m时两个收发距离的垂直相关系数随垂直间隔的变化曲线. 从图中可以看出, 同一收发距离下, 垂直相关系数随垂直间距下降明显, 垂直相关性整体较低. 距离33.2 km处的垂直相关系数比13.6 km处平均高0.2左右, 而且垂直相关系数随间隔的周期性变化更加明显.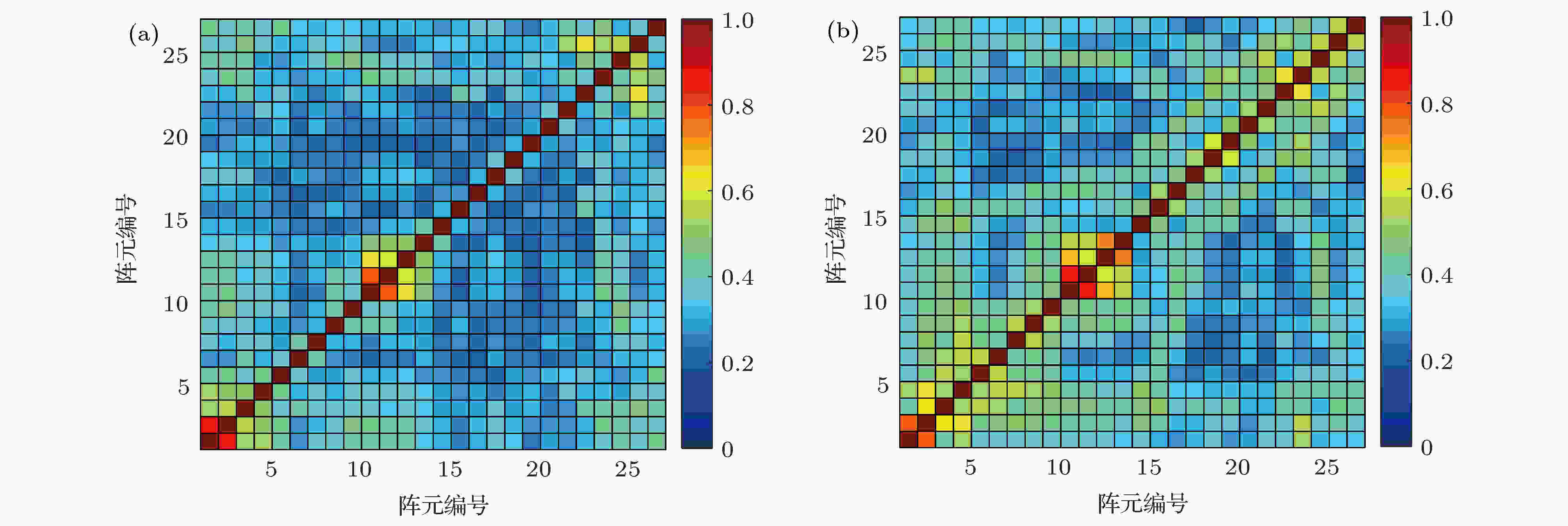
图 18 距离13.6 km处垂直阵声场垂直互相关　(a) 实验结果; (b) 模型结果
Figure18. The vertical cross-correlation of sound fields in the whole array at the range of 13.6 km: (a) Experimental results; (b) numerical results.

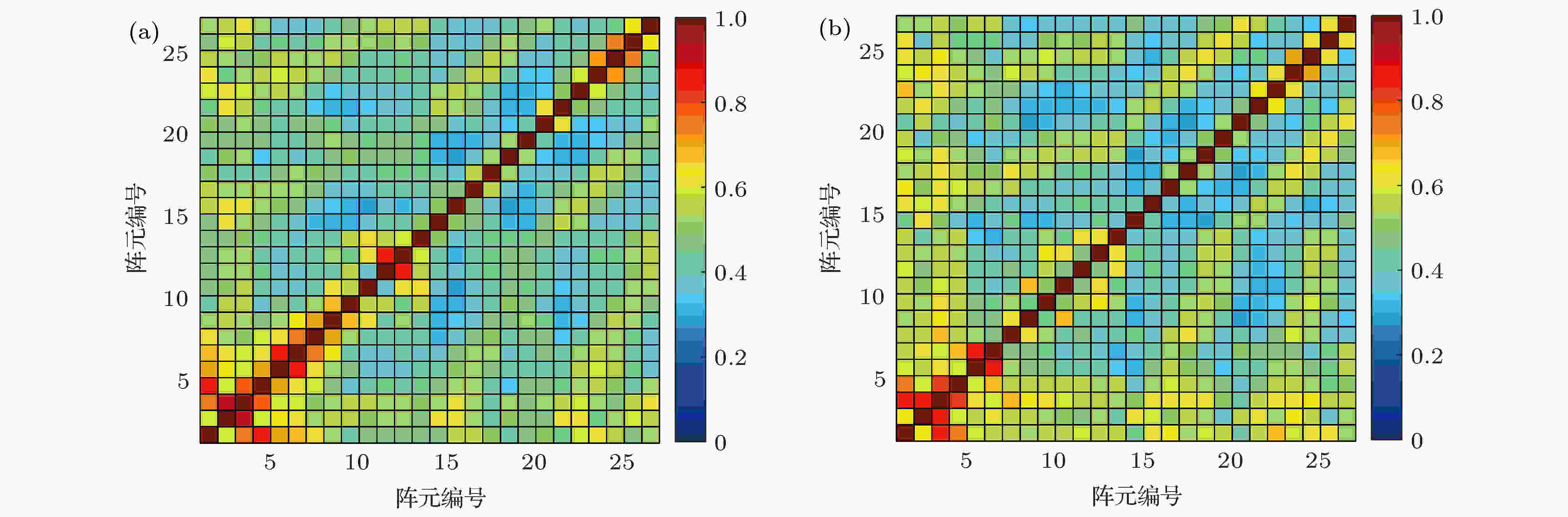图 19 距离33.2 km处垂直阵声场垂直互相关　(a) 实验结果; (b) 模型结果
Figure19. The vertical cross-correlation of sound fields in the whole array at the range of 33.2 km: (a) Experimental results; (b) numerical results.

图 20 第一影区内两个不同距离处声场垂直相关随间距的变化, 其中参考深度102 m, 接收距离分别为13.6 km 和33.2 km
Figure20. Comparison of the vertical correlation coefficients at two different ranges of 13.6 km and 33.2 km in the first shadow zone for the reference depth at 102 m.

图21给出了用BELLHOP模型计算得到的两个收发距离处的本征声线和时间到达结构, 声源深度126 m, 接收深度865 m. 图22和图23分别是距离13.6 km和33.2 km处的时间到达深度结构的实验结果和BELLHOP模型计算结果, 可以观测到经过一次和两次海底反射的声能量到达. 对比图21—图23可以看出, 进入影区之后, 对声场起主要贡献的从直达声线变成了海底反射声线, 它们构成的声信号主脉冲随着深度的增加逐渐分裂为声源(-海面)-海底-接收和声源(-海面)-海底-海面-接收的两部分能量相近的脉冲. 它们对声场垂直相关性的影响主要体现在以下两个方面: 1)随着深度的增加两部分声线到达时间差增大, 多途干涉更加复杂, 进而导致声场垂直相关性降低; 2)随着距离的增加, 到达接收阵的海底反射声线掠射角减小, 两部分声线路程差相对减小, 到达时间差减小; 对比两个不同距离处的时间到达深度结构可以看出, 随着距离增大, 多途展宽变窄, 到达结构反而变得更加简单, 从而提高了垂直相关性.
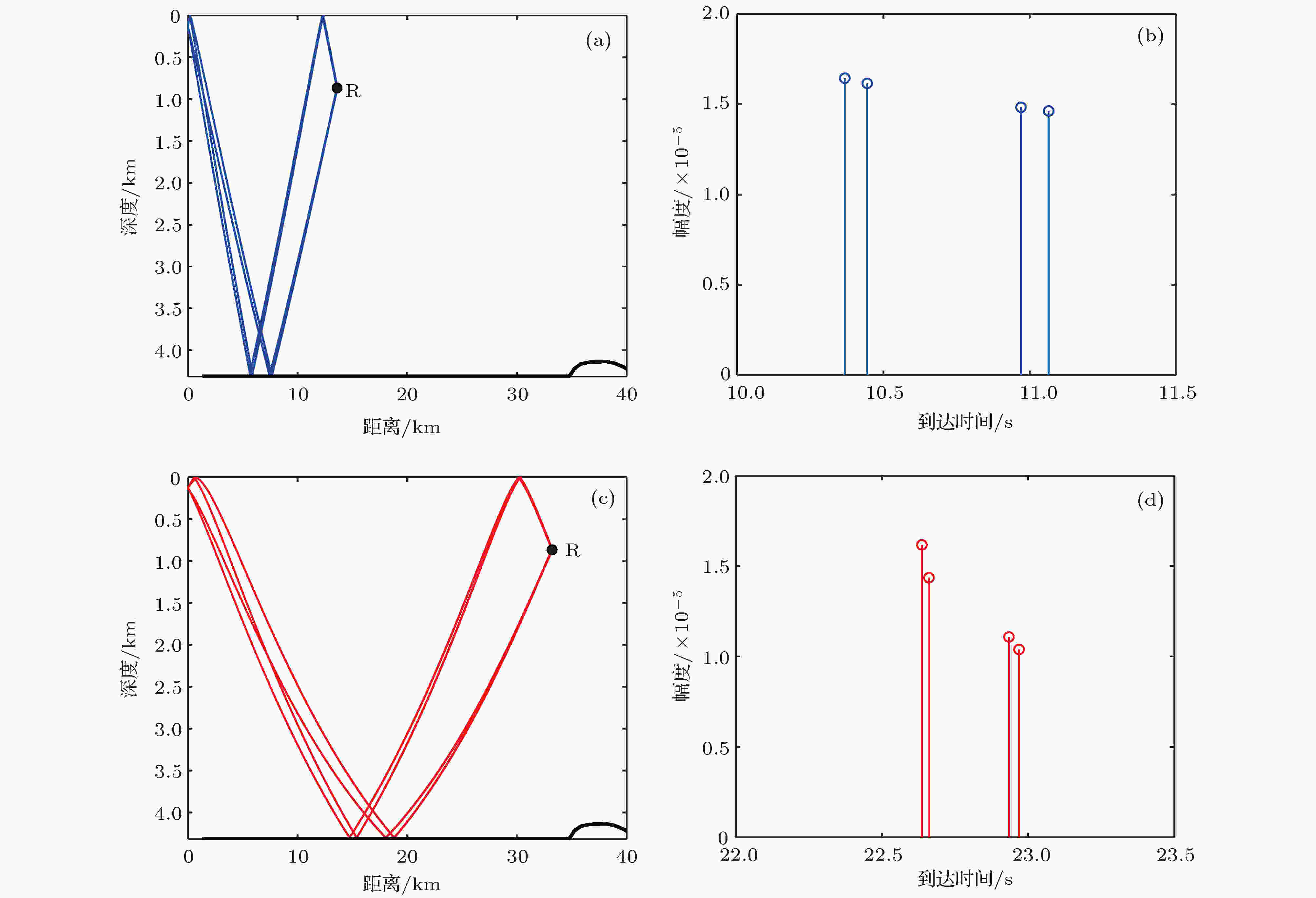图 21 第一影区内接收深度865 m处不同收发距离的本征声线和时间到达结构　(a), (b) 13.6 km; (c), (d) 33.2 km
Figure21. Eigenrays and arrivals received at the depth of 865 m for two different ranges in the first shadow zone: (a), (b) 13.6 km; (c), (d) 33.2 km.

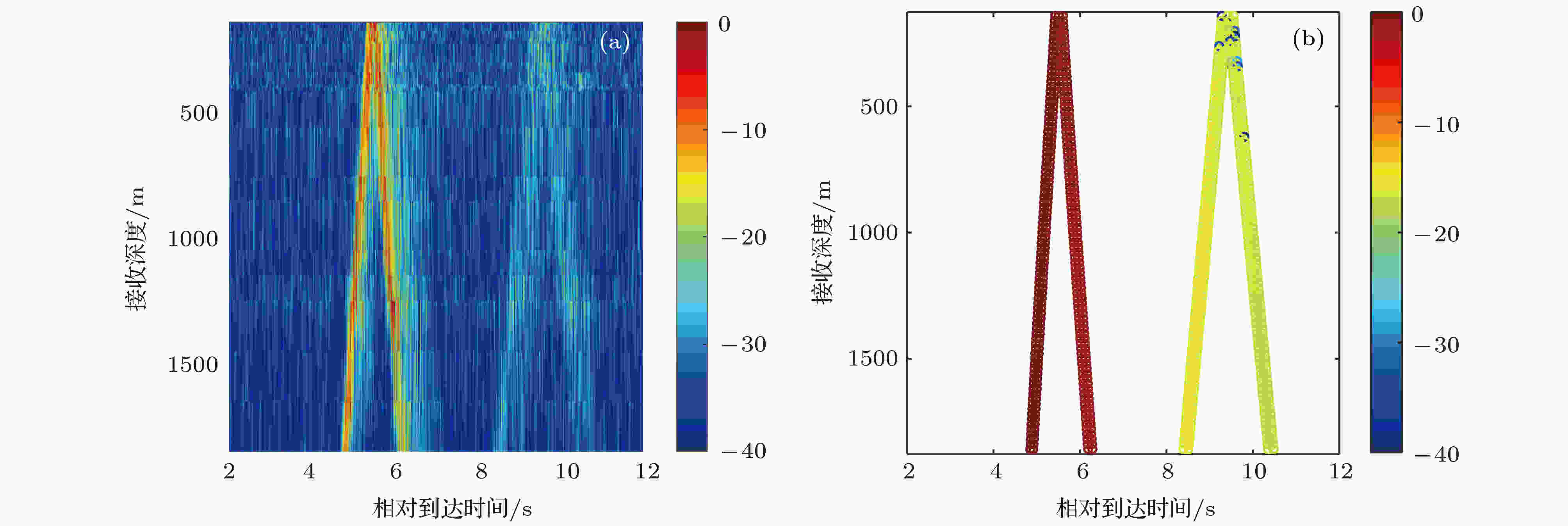图 22 第一影区内距离13.6 km处垂直阵深度覆盖范围内的多途到达结构比较　(a) 实验结果; (b) 模型结果
Figure22. Comparison of the experimental multipath structures from the receivers on the vertical line array at the range of 13.6 km in the first shadow zone with numerical ones: (a) Experimental result; (b) numerical result.

图 23 第一影区内距离33.2 km处垂直阵深度覆盖范围内的多途到达结构比较　(a) 实验结果; (b) 模型结果
Figure23. Comparison of the experimental multipath structures from the receivers on the vertical line array at the range of 33.2 km in the first shadow zone with numerical ones: (a) Experimental result; (b) numerical result.

2 -->

4.4.第一会聚区声场垂直相关

从图5的传播损失结果可见, 不同深度处的第一会聚区大约位于50 — 60 km附近. 为了探究第一会聚区附近垂直相关性的变化规律, 不失一般性, 选取50 km位置进行第一会聚区声场垂直相关性研究. 第二、第三会聚区具有和第一会聚区相似的规律, 这里不再展开讨论.
图24给出距离50 km处接收阵各通道声场垂直相关的实验结果和模型计算结果的比较. 图25给出参考深度分别为102 m (第1阵元)和634 m (第15阵元)时垂直相关系数随着接收深度的变化曲线. 从图24和图25可见, 50 km处垂直相关性整体比较高, 并且随着接收深度的增加呈现出周期性振荡趋势.
图 24 距离50 km处垂直阵声场垂直互相关　(a) 实验结果; (b) 模型结果
Figure24. The vertical cross-correlation of sound fields in the whole array at the range of 50 km: (a) Experimental results; (b) numerical results.

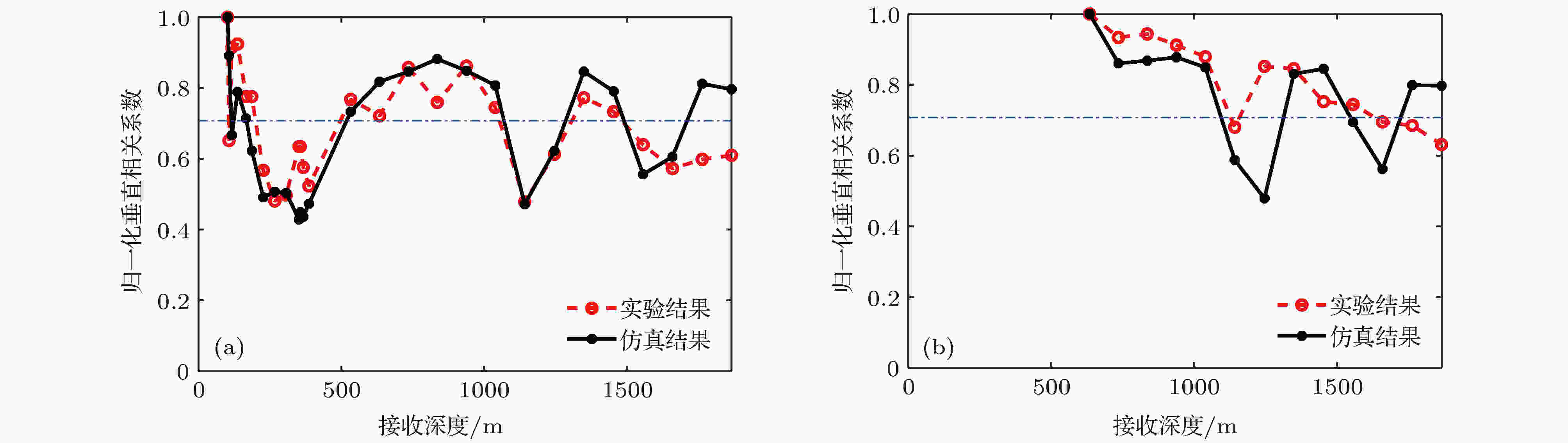图 25 距离50 km处两个不同参考深度上声场垂直相关随间距的变化　(a) 参考深度102 m; (b) 参考深度634 m
Figure25. The vertical correlation coefficients at two different reference depths at the range of 50 km: (a) For reference depth 102 m; (b) for reference depth 634 m.

图26给出了第一会聚区附近(50—60 km)接收深度范围内传播损失的实验结果和RAM-PE模型计算结果的比较. 从图中可以看出, 在会聚区附近的高声强区域, 声能量分布在空间垂直方向上呈现出清晰的明暗相间条纹. 仔细观察可见, 图26中50 km处的声能量在垂直方向上的振荡与图25中垂直相关系数的振荡现象具有较强的相似性. 为了进一步探究声能量的振荡规律与垂直相关性之间的关联性, 给出50 km处归一化声能量在垂直深度上的分布, 如图27所示. 对比图25和图27可以看出, 声能量随着接收深度的增加呈现出振荡趋势, 并且振荡规律与垂直相关系数随接收深度变化的振荡规律基本一致, 二者具有较强的关联性.
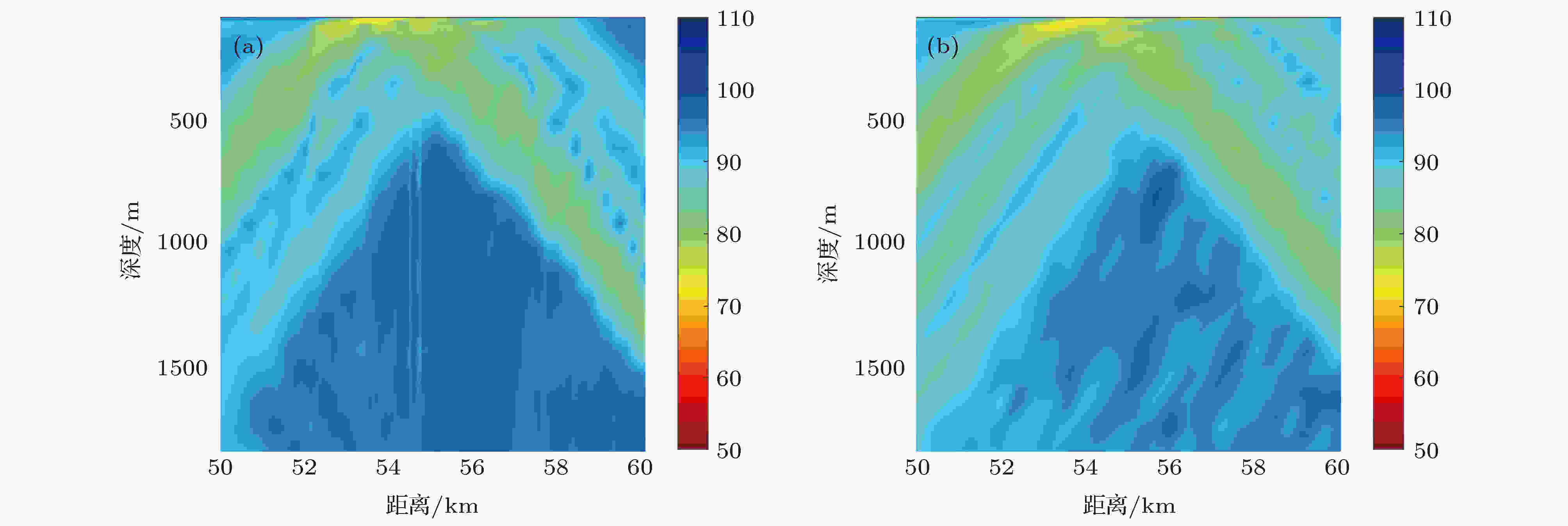图 26 第一会聚区附近(50?60 km)声传播损失比较　(a) 实验结果; (b) 模型结果
Figure26. TL results near the first convergence zone (50?60 km): (a) For experimental result; (b) for numerical result.

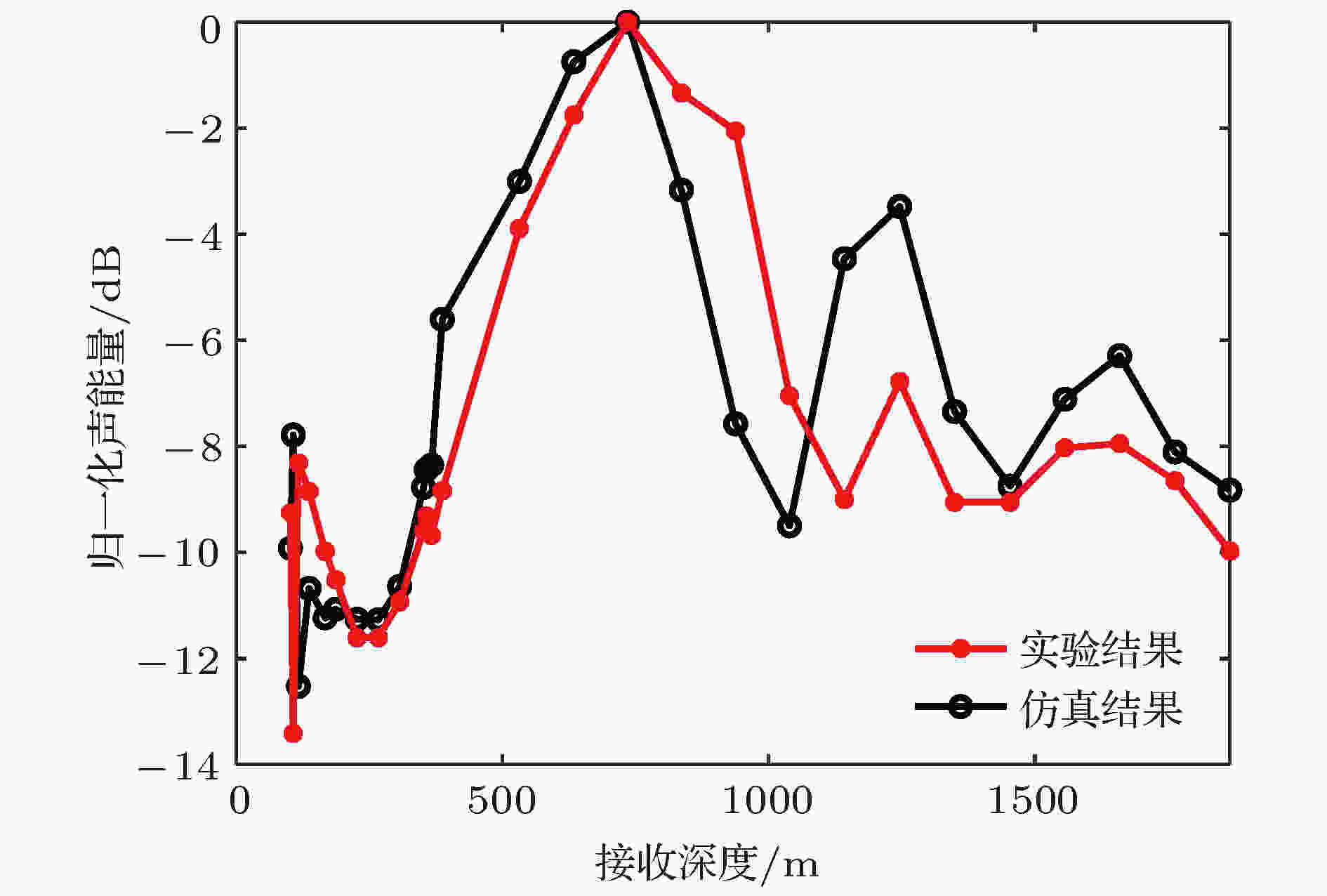图 27 距离50 km处归一化声强随接收深度变化的实验结果与仿真结果对比
Figure27. Comparison of the normalized experimental sound energy with numerical results at the range of 50 km.

下面使用射线理论, 分析50 km处声能量及垂直相关系数随接收深度增加而振荡的原因以及两者之间的关联.
针对收发距离50 km处3个典型接收深度(167 m, 836 m和1453 m)进行分析, 分别代表经海底小角度反射后的声场能量为主、及水体中折射加上海面反射时延不同导致干涉现象的差异, 图28给出了BELLHOP射线模型计算的主要本征声线和时间到达结构. 图29为50 km距离处的时间到达深度结构的实验结果和模型计算结果比较. 结合图27不同接收深度的相对强度可以看出, 对600 m以浅的声场起主要贡献的是四条一次海底反射声线, 声线与海底作用能量损失较大且接收声信号主脉冲多途干涉复杂, 声场的垂直相关性相对较低. 而对600—1550 m深度范围内的声场起主要贡献的是来自水体中的两条反转声线(声源-接收点和声源-海面-接收点), 它们没有与海底发生作用, 主脉冲到达结构简单, 对应的声传播损失小, 声场的垂直相关性较高, 而在垂直方向上两条反转声线之间的周期性干涉导致垂直相关系数随着深度增加出现周期振荡现象. 随着深度增加, 对1550—1866 m(最大接收深度1866 m, 第27阵元)深度范围内声场起主要贡献的是一条经声源-海面-接收的反转声线, 周期性振荡不如浅深度处剧烈, 此时声传播损失增大, 声场的垂直相关性有所下降. 从图3的海深中可以看出距离O2接收阵35—40 km附近存在一个海底小山丘会改变50 km处的二次海底反射到达声线的路径, 但对声信号的主脉冲结构没有影响, 其作用可以忽略不计.
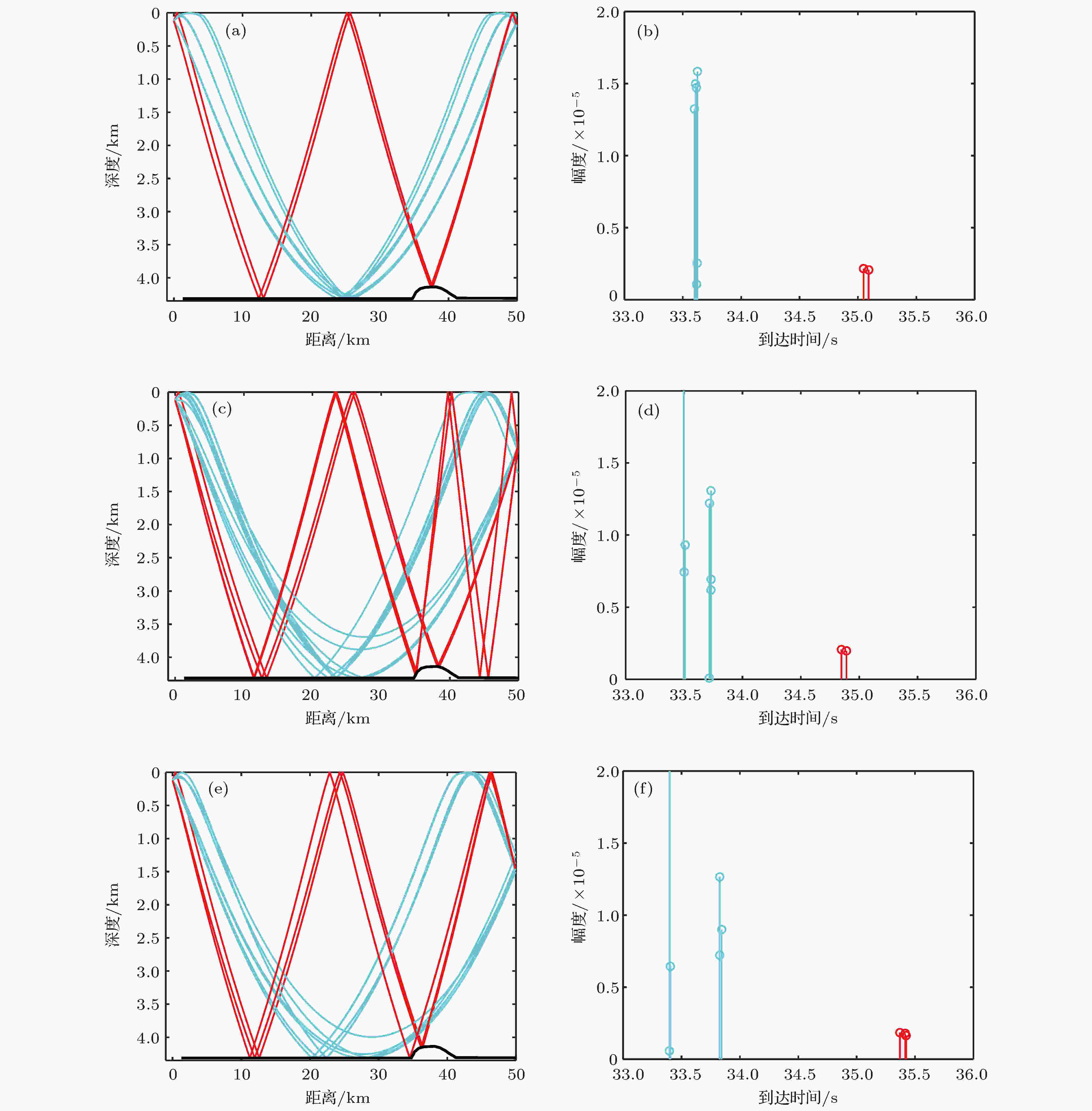图 28 第一会聚区附近50 km距离处不同接收深度的本征声线和时间到达结构　(a), (b) 167 m; (c), (d) 836 m; (e), (f) 1453 m
Figure28. Eigenrays and arrivals at three different depths at the range of 50 km near the first convergence zone: (a), (b) 167 m; (c), (d) 836 m; (e), (f) 1453 m.

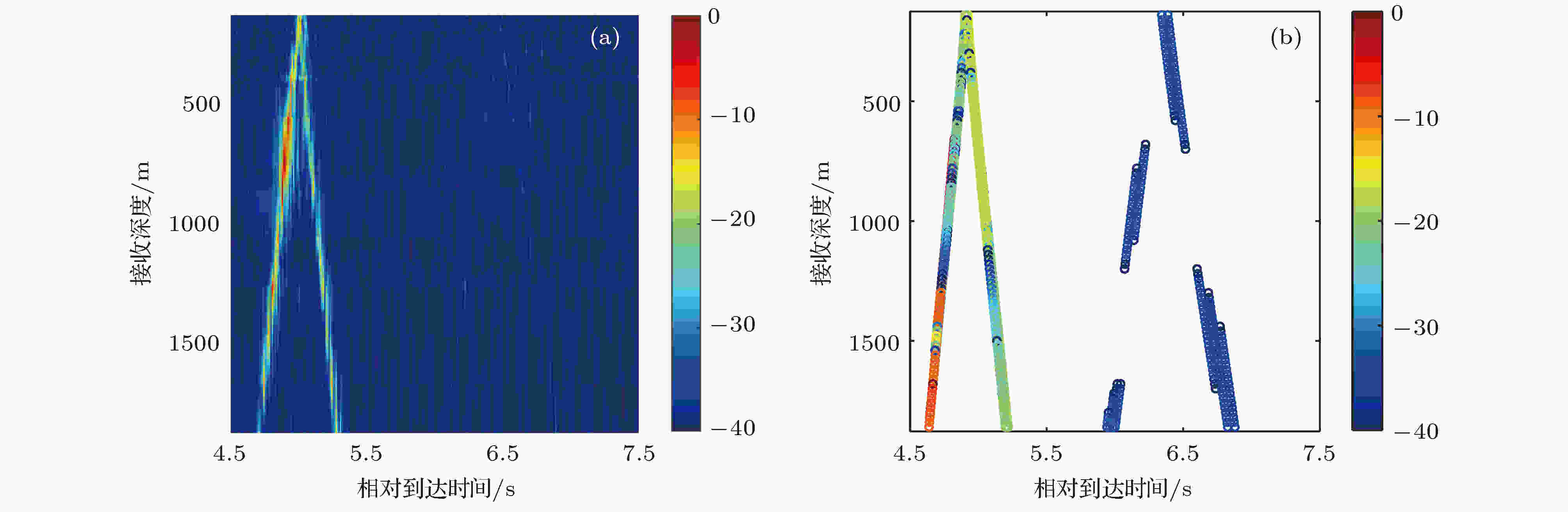图 29 第一会聚区附近距离50 km处垂直阵深度覆盖范围内的多途到达结构比较　(a) 实验结果; (b) 模型结果
Figure29. Comparison of the experimental multipath structures from the receivers on the vertical line array at the range of 50 km near the first convergence zone with numerical ones: (a) Experimental result; (b) numerical result.

下面进一步定量分析和解释第一会聚区附近声能量和垂直相关系数随着深度增加出现振荡现象的机理.
先考虑接收阵元位于600—1550 m深度范围内的情况. 由于一次海底反射声线与海底作用之后损失较大, 只考虑两组水体中反转声线的贡献, 则接收到的声压可以表示为^[23]

$\begin{split}& P\left( {r,z;\omega } \right) \cong \frac{{S\left( \omega \right)\sqrt W }}{{4{\text{π}}}}\\ &\times\left( {\frac{{\sqrt {{F_1}} }}{{{R_1}}}{{\rm{e}}^{ - {\rm{i{\text{π}} }}/2}}{{\rm{e}}^{{\rm{i}}\omega {t_1}}} + \frac{{\sqrt {{F_2}} }}{{{R_2}}}{{\rm{e}}^{ - {\rm{i{\text{π}} }}}}{{\rm{e}}^{{\rm{i}}\omega {t_2}}}} \right),\end{split}$

其中S(ω)表示声源的频谱, W为单位立体角内的辐射功率, F_i表示第i组声线的聚焦因子, R_i表示第i组声线的斜距, t_i(i = 1, 2)表示第i组声线的传播时间.
当声源位于海水表层时, 两组声线的传播轨迹基本一致, 可以认为声源掠射角的绝对值基本相等, 即|α₁|≈|α₂|, 同时可以认为聚焦因子F和斜距R基本一致. 令Δt = t₂–t₁, 则(13)式中两组声线相干叠加后的声压可以近似表示为

$P\left( {r,z;\omega } \right) \cong {A_Z}{e^{{\rm{i}}\omega {t_1}}}\left( { - {\rm{i}} - {e^{{\rm{i}}\omega \Delta t}}} \right),$

其中${A_Z} = \dfrac{{S\left( \omega \right)\sqrt W }}{{4{\text{π}}}}\dfrac{{\sqrt {{F_1}} }}{{{R_1}}}$, 为声压幅度. 同理可得, 接收点(r,z+Δz)处的声压可以表示为

$P\left( {r,z + \Delta z;\omega } \right) \cong {A_{z + \Delta z}}{e^{{\rm{i}}\omega t_1'}}\left( { - {\rm{i}} - {e^{{\rm{i}}\omega \Delta t'}}} \right).$

由(14)式, 经过推导可以得到声强的近似表示为

${\left| {P\left( {r,z;\omega } \right)} \right|^2} \cong 2A_Z^2\left[ {1 + \sin \left( {\omega \Delta t} \right)} \right],$

当掠射角满足|α₁|≈|α₂|时, Δt可以近似表示为^[24,25]

$\Delta t \approx \frac{{2\displaystyle\int_0^{{z_{\rm{s}}}} \sqrt {{n^2}\left( z \right) - {\rm{co}}{{\rm{s}}^2}{\alpha _2}} {\rm{d}}z}}{{{c_0}}},$

从(17)式可以看出, 两组声线的时间间隔Δt随着深度z_s的增加而增大. 在典型的深海条件下, 收发距离保持不变时, 声线2掠射角的绝对值|α₂|随着深度的增加而增大, 因此声线1, 2的到达时间差Δt随着深度的增加而增大, 这与图29中时间到达深度结构的结果一致, 从而导致声场相位随深度发生周期性变化.
根据上述推导结果, 可以采用下面的公式计算带宽内的平均声强:

$\overline {{{\left| {P\left( {r,z;\omega } \right)} \right|}^2}} = \frac{1}{N}\mathop \sum \nolimits_{i = 1}^N {\left| {P\left( {r,z;{\omega _i}} \right)} \right|^2},$

实验时中心频率为310 Hz, 带宽为100 Hz, 频带间隔为1 Hz, 则频点数N等于101.
图30给出了距离50 km处, 以第15阵元(深度634 m)为参考阵元, 由BELLHOP射线模型计算得到的两组声线到达时间差和相位差随着接收深度的变化. 可见, 随着接收深度增加, 对第一会聚区声场起主要贡献的两组反转声线到达时间差逐渐增大, 相位差在$\left[ {0,2} {\text{π}}\right]$内发生周期性变化, 这是导致多途声线叠加干涉时相位出现周期性起伏的原因^[26,27]. 图31给出由近似公式(18)式计算得到的带宽内平均声强随着接收深度的变化, 同时给出了归一化声能量的实验结果和模型计算结果, 三者符合程度较好, 都随着接收深度的增加呈现周期性振荡.
图 30 由射线模型计算的距离50 km处对声场起主要贡献的两组水体反转声线的到达时间差(a)和相位差随接收深度(b)的变化
Figure30. Numerical travel time differences (a) and phase differences (b) of the two groups of refraction eigenrays from water volume with the increase of the receiving depth at the range of 50 km from Bellhop model.

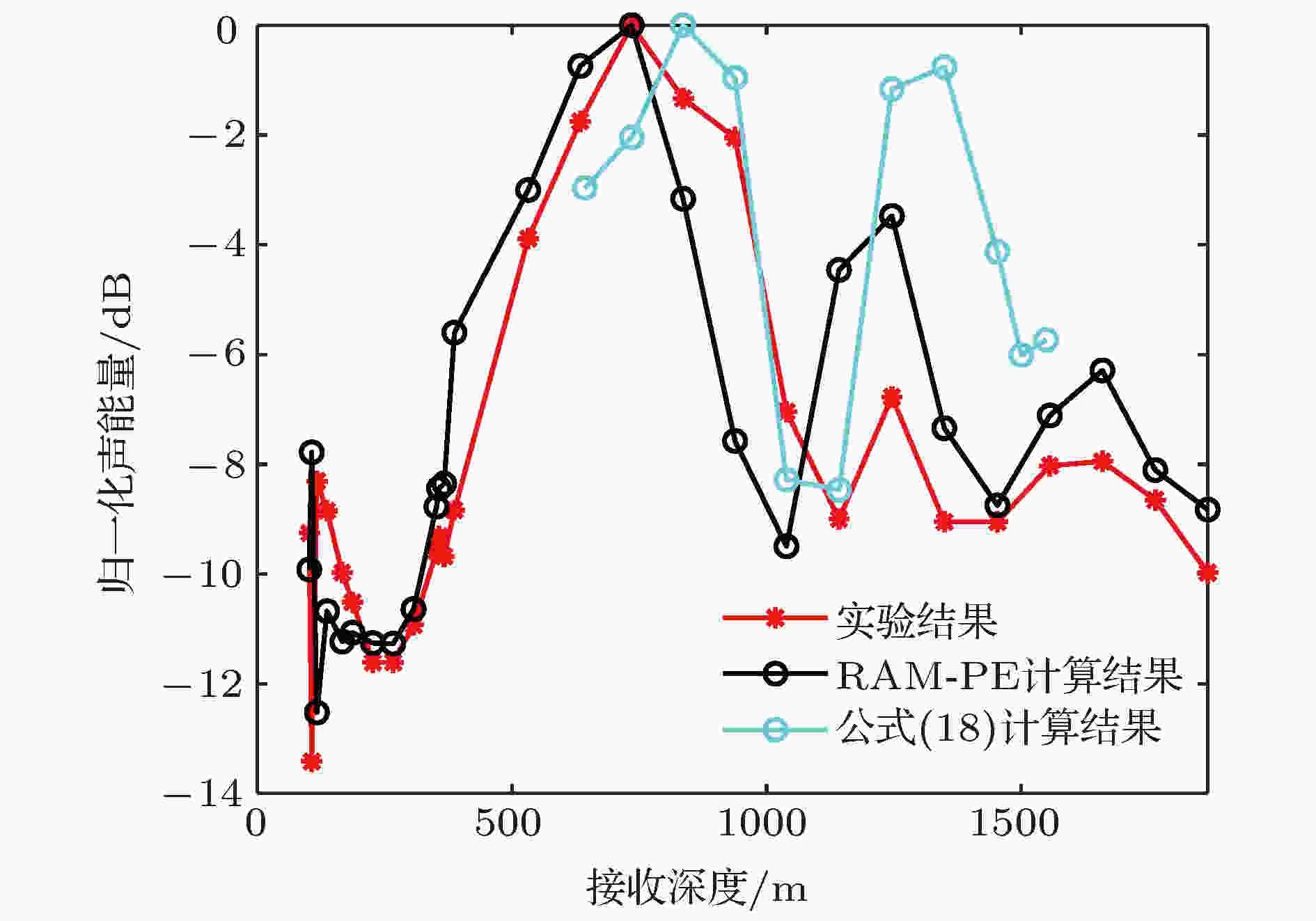图 31 由近似公式(18)式计算50 km处归一化声强随着接收深度变化与实验结果及RAM-PE模型结果的对比
Figure31. Comparison of the numerical sound intensities computed by Eq. (18) with the experimental data and RAM-PE model results at the range of 50 km.

在窄带带宽Δω内, 可以近似认为幅度$ {A_z}\left( \omega \right) \approx$ $ {A_z}\left( {{\omega _0}} \right)$, ${A_{z + \Delta z}}\left( \omega \right) \approx {A_{z + \Delta z}}\left( {{\omega _0}} \right)$. 将(14)式和(15)式代入(6)式, 分子分母同时约去幅度项, 可得:

$\rho \left( {\Delta z} \right) \approx \mathop {\max }\limits_\tau \frac{{{\rm{Re}}\left[\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\rm{e}}^{{\rm{i}}\omega \left( {{t_1} - t_1' + \tau } \right)}}\left( { - {\rm{i}} - {{\rm{e}}^{{\rm{i}}\omega \Delta t}}} \right)\left( {{\rm{i}} - {{\rm{e}}^{ - {\rm{i}}\omega \Delta t'}}} \right){\rm{d}}\omega\right]}}{{\sqrt {\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\left| {\left( { - {\rm{i}} - {{\rm{e}}^{{\rm{i}}\omega \Delta t}}} \right)} \right|}^2}{\rm{d}}\omega } \sqrt {\displaystyle\int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {{\left| { - {\rm{i}} - {{\rm{e}}^{{\rm{i}}\omega \Delta t'}}} \right|}^2}{\rm{d}}\omega } }},$

图32是用近似公式(19)式计算得到的以第15阵元为参考阵元的垂直相关系数随着接收深度变化的结果. 可见, 由近似公式计算得到的结果与实验结果及模型计算结果较为一致, 都呈现出明显的周期性振荡的趋势. 将图31与图32进行对比可以发现, 在会聚区附近50 km处的高声强区域内, 由两组水体反转声线干涉叠加推导得到的近似公式计算的声强和垂直相关系数在垂直方向上的分布非常相似. 实验海洋环境和RAM-PE模型计算中, 实际上是由两组相近的声线族干涉而成, 所以细节上会有一定的差别.
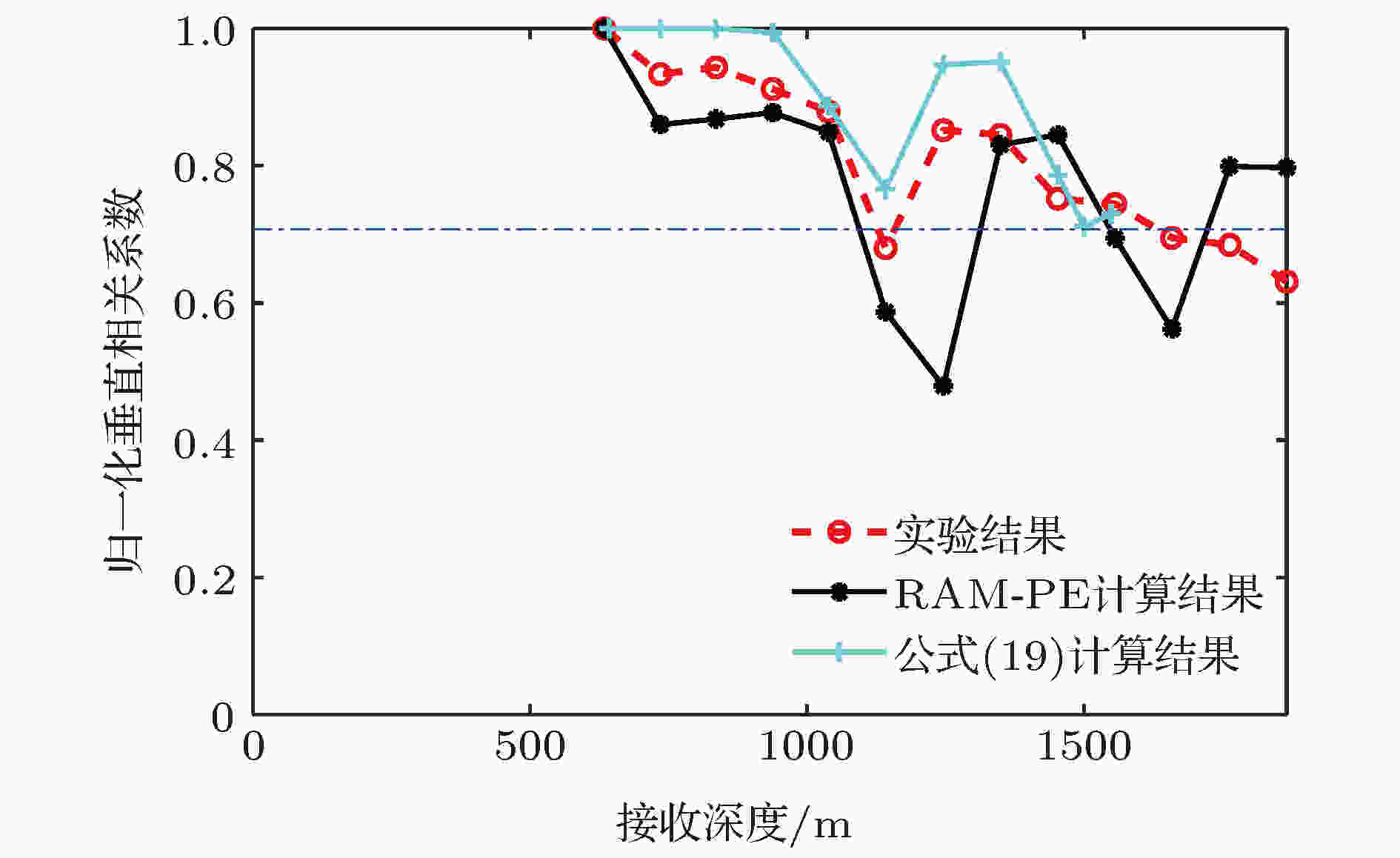图 32 由近似公式(19)式计算得到的参考深度634 m时垂直相关系数随着接收深度的变化与实验结果及RAM-PE模型结果的对比
Figure32. Comparison of the numerical vertical correlations for the reference depth 634 m computed by Eq. (19) with the experimental data and RAM-PE model results at the range of 50 km.

在会聚区附近的高声强区域(深度范围600—1550 m), 对声场起主要贡献的是两组水体内反转的声线, 其幅度相当, 随着深度的增加, 到达时间差增大, 使得相位差在$\left[ {0,2} {\text{π}}\right]$内周期性变化. 两组声线之间的互相干涉导致声能量和垂直相关系数随着接收深度振荡变化. 在同相相干的深度范围内, 声信号主要由两组水体反转声线构成, 它们的多途到达结构简单, 所以在该深度范围内声场的垂直相关性比较高; 而在反相相干的深度范围内, 两组反转声线(部分)干涉相消, 海底反射声线对声场的作用不能忽略, 此时多途干涉变得复杂, 导致垂直相关性在该深度范围内有所下降. 所以, 在会聚区附近的高声强区域内, 是两组水体反转声线的周期性干涉导致了垂直相关曲线和归一化声能量在垂直方向上相似的振荡结构.
对于约1550—1866 m深度范围内的声场来说, 由于只有一组水体反转声线能量占主, 无法形成两组反转声线之间的周期性干涉现象, 垂直相关系数和声能量随接收深度振荡的幅度显著降低, 振荡现象不再明显.

利用2014年南中国海一次深海声传播实验数据, 分区域对不同距离位置处的大深度声场垂直相关特性进行了系统分析, 并利用射线理论从物理机理方面对深海垂直相关特性随距离和深度的变化进行了解释, 主要结论如下:
1)在直达声区内, 对声场起主要贡献的是直达声线和一次海面反射声线, 声信号主脉冲到达结构简单, 垂直相关性较好, 随深度增加下降缓慢, 垂直相关系数基本维持在0.707左右;
2)在声影区内, 对声场起主要贡献的是海底反射声线, 随着接收深度增加, 声线的到达时间差逐渐增大, 声信号主脉冲多途到达结构复杂, 垂直相关系数随着深度增加下降明显. 随着接收距离的增加, 同一接收深度接收的声线到达时间差逐渐减小, 声信号主脉冲多途到达结构变得简单, 使得影区内的垂直相关随着接收距离增加略微增大;
3)在第一会聚区附近, 对高声强区内的声场起主要贡献的是水体内反转的两组声线, 它们幅度相当, 到达时间差随着接收深度的增加而增大, 相位差在$\left[ {0,2} {\text{π}}\right]$内周期性起伏, 这种深度上周期性干涉导致声能量和垂直相关系数在垂直方向上的周期性振荡. 在同相干涉的深度上, 对声场起主要贡献的是两组反转声线, 主脉冲到达结构简单, 该深度与同一距离其他深度接收的声信号之间相关性较高. 在反相干涉深度, 海底反射声线对声场的贡献相对增大, 它们的到达结构复杂, 导致垂直相关性下降. 因此, 在第一会聚区附近, 垂直相关性随着接收深度的增加出现周期性干涉现象, 并且垂直相关性和声能量在深度上具有相似的振荡结构.
作者对参加2014年南中国海海上实验的全体工作人员表达由衷的谢意, 是他们的辛勤工作为本文提供了宝贵的实验数据.