摘要: 最近Vafa等人提出了两个弦沼泽地的判据, 并且在研究宇宙学中两个弦沼泽地判据所施加的约束条件时, 发现暴胀模型通常与这两个判据很难相容. 将这两个判据应用于当前时期宇宙的加速膨胀时, 发现特定的quintessence模型可以满足这些限制, 同时满足根据当前观测所施加的约束. 基于大尺度洛伦兹破缺的宇宙学模型, 我们得到了修正的Friedmann方程, 在计算的过程中给出了三种可行的近似, 并定义了一个有效的真空能量密度
$ {\varLambda _{{\rm{eff}}}}$ , 其行为对于弦景观表现为单调下降的类quintessence势能, 对于大部分具有裸的正真空能量密度的沼泽地, 有效宇宙学常数随时间的演化会出现局域极小. 将光度距离的计算结果与天文观测值做对比, 我们得到负宇宙学常数也可以使宇宙产生加速膨胀, 因而用亚稳的de Sitter真空来解释宇宙后期的加速膨胀是不必要的, 沼泽地猜想所导致的沼泽地模型与后期宇宙加速膨胀不相容性的困难也就不存在了.
关键词: 弦沼泽地 /
洛伦兹破缺 /
暗能量 /
宇宙加速膨胀 English Abstract Effective quintessence from string landscape Zhai Han-Yu 1 ,Shen Jia-Yin 1 ,Xue Xun 1,2 1.Department of Physics, East China Normal University, Shanghai 200241, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11435005, 11775080, 11865016).Received Date: 01 March 2019Accepted Date: 25 April 2019Available Online: 01 July 2019Published Online: 05 July 2019Abstract: Recently, Vafa et al. proposed two string swampland criteria, and studying the constraints imposed by the two string swampland criteria on cosmology, they found that the inflationary models are generally difficult to be compatible with these two criteria. Applying these two criteria to the accelerated expansion of the universe during the current period, it was found that the specific quintessence model can satisfy these constraints while satisfying the constraints imposed by the current observations. Applying the gravitational theory of large scale Lorentz violation to cosmology, the vacuum energy density is not the only cause of the accelerated expansion of the universe. The large scale Lorentz violation combined with the cosmological constant term results in the observed accelerated expansion of the late universe. The vacuum energy density is a bit like a naked cosmological constant. The equivalent energy density considering the large scale Lorentz violation effect is the effective cosmological constant that determines the evolution of the universe. In this way, we find that the negative cosmological constant in the string landscape can also accelerate the expansion of the universe, and compared with the $ {\varLambda _{{\rm{CDM}}}}$ model, it leads to a cosmological constant as an effective vacuum energy density. Effective vacuum energy density behaves as a monotonically decreasing quintessence potential energy for the string landscape, for most of the naked positive vacuum energy densities in the swampland, the evolution of effective cosmological constant with time will show a local minimum. Comparing the calculated results of the distance modulus withthe astronomical observations, we can obtain that a negative cosmological constant also accelerates the expansion of the universe. Thus, the vacuum energy density derived from the string landscape will give quintessence potential that satisfies the swampland criterion, while the evolution of vacuum energy density given by the swampland model of the metastable dS vacuum is not quintessence potential, so it cannot satisfy the second de Sitter criterion. Therefore, the effective potential leading to the accelerated expansion of the late universe can only come from the string landscape, which is naturally UV completion. Therefore, it gives that the accelerated expansion of the late universe is the feature of early quantum gravity. It is not necessary to use the metastable de Sitter vacuum to explain the accelerated expansion of the late universe. The difficulty of incompatibility between the swampland model and the accelerated expansion of the late universe caused by the swampland conjecture will be eliminated.Keywords: string swampland /Lorenz violation /dark energy /accelerated expansion of the universe 全文HTML --> --> --> 1.引 言 从弦理论约化到描述低能物理的有效场论时, 需要将多出来的六个空间维度紧致化到非常小的微观尺度, 这一处理方法被称之为弦理论的紧致化. 在紧致化后, 便可以用一个低能有效理论来描述熟悉的四维世界[1 ,2 ] . 弦论有10500 种之多的紧致化方案, 其中所有不等价的低能有效理论, 其真空能的取值形成了一个复杂的“山脉地形图”, 构成了所谓的弦景观[3 ] .[4 ,5 ] 在2005年提出了沼泽地的概念, 即弦景观被一个更广阔的沼泽地所包围, 并非所有的自洽有效场理论都可以从弦理论中导出, 有许多看似自洽的有效场理论实际上和量子引力理论并不兼容, 不具有紫外完备性, 不属于弦景观, 只能被排除到所谓的“沼泽地”当中. Vafa等提出了两个拟议的沼泽地判据并研究了其宇宙学含义, 指出对于宇宙的后期加速膨胀来说, 第二个沼泽地判据 (对于任何自洽的量子引力理论的标量势V , 当$V > 0$ 时, 存在下限$\left| {{\nabla _\phi }} \right.\left. V \right|/V > c \sim {\rm O}\left( 1 \right)$ , c 是正的常数, 单位为约化的普朗克单位)与亚稳 dS势能不相容, 但是quintessence类型的势能以及弦景观的反德西特(anti-de Sitter, AdS)真空势能可以与这两个判据相容[6 ,7 ] .V [8 ,9 ] ,图1 所示.图 1 亚稳态dS的标量势V Figure1. The scalar potential V for a metastable dS.图2 所示.图 2 不稳定dS的标量势V Figure2. The scalar potential V for an unstable dS.[10 ,11 ] . 按照现在宇宙学的标准模型, 业界相信宇宙首先经历了量子引力主导的时期, 随后经历暴胀, 暴胀结束后才开始正常膨胀, 然后在近期又开始了加速膨胀, 现在的可观测宇宙是由量子引力主导时期的一个非常小的时空区域经历暴胀所得到的. 量子引力的一个普遍的特征是洛伦兹破缺和非局域性, 暴胀前洛伦兹破缺的时空区域尺度会随着早期宇宙暴胀超出视界, 在暴胀结束后的某个时间有可能又重新进入视界或者尚未进入视界, 洛伦兹破缺时空区域的各个部分因为暴胀被急速拉开远离, 因而失去相互作用, 使得洛伦兹破缺被冻结在大尺度上[12 ] . 因此, 当我们在研究宇宙学问题时需要将大尺度上的洛伦兹破缺效应考虑在内[12 —17 ] .[18 —20 ] , 但是涉及大尺度的天文观测现象也有许多与单纯广义相对论预言不符合的现象. 最困扰物理学界的就是为解释宇宙加速膨胀而引进的宇宙学尺度上斥力存在的暗能量假说, 暗能量最简单的唯象模型是用宇宙学常数来描述暗能量, 也就是所谓的${\varLambda _{{\rm{CDM}}}}$ 模型. ${\varLambda _{{\rm{CDM}}}}$ 模型的问题在于当我们将宇宙学常数看成真空能量密度时, 天文观测与理论预言之间存在很大差距, 理论预言比天文观测大了54到112个数量级, 这就必须使用精细调节机制, 理论的置信度就被极大地降低. 所以, 导致宇宙后期加速膨胀的暗能量机制依然是一个亟待解决的问题.[21 —31 ] , 我们从冻结在大尺度上的洛伦兹破缺导致物质的暗伴的角度来思考这一机制是一个全新的视角. 这样我们发现弦景观中裸宇宙学常数为负时也可以使宇宙产生加速膨胀, 并在与${\varLambda _{{\rm{CDM}}}}$ 模型做对比时, 导致一个作为有效真空能量密度的宇宙学常数, 其行为对于弦景观表现为单调下降的类quintessence势. 对于大部分具有裸的正真空能量密度的沼泽地, 有效宇宙学常数随时间的演化会出现局域极小, 与单调下降的quintessence势所导致的演化不符. 从而源自弦景观的真空能量密度会给出满足沼泽地判据的quintessence势, 而亚稳的dS真空正宇宙学常数的沼泽地模型给出的真空能量密度演化不是quintessence势, 也就不能满足第二个dS判据. 因此导致后期宇宙加速膨胀的有效势只能来自弦景观, 其自然具有紫外完备性, 所以给出了后期宇宙加速膨胀是早期量子引力的特征, 从而避免了Vafa等文章中指出的弦沼泽地与后期加速膨胀难以相容的问题. 另外基于弦理论, 其真空为AdS类型, 在用${\varLambda _{{\rm{CDM}}}}$ 模型解释宇宙后期加速膨胀时就需要正的宇宙学常数, 于是弦理论学家不得不构造一些不自然的模型, 将稳定的AdS真空能量密度提升至正值, 变成亚稳的dS真空. 我们通过考虑大尺度洛伦兹破缺效应, 自然地实现了从裸的负真空能量密度提升至正的有效真空能量密度, 避免了很多不自然的技术, 也避开了沼泽地猜想的第二判据.2.大尺度洛伦兹破缺下的引力理论 要构造包含大尺度洛伦兹破缺下的引力理论, 可以借助规范原理, 将局域对称性加以约束进行破缺[12 ] . 为引入局域$SO\left( 3 \right)$ 不变洛伦兹boost破缺的约束条件, 我们先考察洛伦兹规范势在局域$SO\left( 3 \right)$ 下的变换性质. 规范势$A_{b\mu }^a$ 在局域洛伦兹变换$x \mapsto \varLambda \left( x \right)x$ 下满足$\varLambda \in SO\left( 3 \right)$ , 可以证明${A_u}$ 所满足的约束条件为${f_\mu }\left( x \right)$ 可以认为是洛伦兹破缺的量度, 并且是参考系依赖的.${\lambda ^u}$ ${\varLambda _0}$ 是真空能量密度给出的裸宇宙学常数, R 为曲率标量. 需要注意的是, 由于拉格朗日乘子项的存在, 其对联络的运动方程的贡献相当于一个有效的角动量张量, 所以即使引力场的物质源是无旋的, 联络的运动方程也会偏离广义相对论中的形式, 一般的联络是有挠的, 而非广义相对论中的Levi-Civita联络.$\dfrac{{\delta S}}{{\delta {h^a}_u}}$ , 可以得到标架运动方程${\left( {{{ T}_M}} \right)^a}_b$ 是能动张量, ${{ G}^a}_b$ 为爱因斯坦张量. 需要注意的是这里的联络不再是Levi-Civita联络, 由于联络是有挠的, 可以一般的将联络写为Levi-Civita项和contortion的分解[15 ] ${\varGamma ^a}_{bu}$ 是Levi-Civita项, ${K^a}_{bu}$ 是contortion项.ρ 和压强p 来描述, 即${\left( {{{ T}_M}} \right)^a}_{\rm{b}} = {\rm{diag}}\left( {\rho, - p, - p, - p} \right)$ . 由方程(7 )得到${{ G}^a}_b$ 必须是对角矩阵, 由此可以解出${K^0}_{11}$ , ${K^0}_{22}$ , ${K^0}_{33}$ 可以非0, 其他的contortion分量皆为0. 又由于宇宙学原理要求${{ G}^a}_b$ 只能是宇宙时t 的函数, 所以${f_\mu }$ 与${\cal{K}}\left( t \right)$ 的关系${f_\mu }$ 中的三个自由度是由标架的选取而被确定, 剩余的一个自由度以${\cal{K}}\left( t \right)$ 表达. 注意到(7 )式中的爱因斯坦张量${{ G}^a}_b$ 其联络${A^a}_{bu}$ 是有挠的, 记${A^a}_{bu}$ 的无挠部分Levi-Civita联络${\varGamma ^a}_{bu}$ 所产生的相应几何量为${{\tilde G}^a}_b$ , ${{\tilde R}^a}_b$ 和${\tilde R}$ , 且7 )式的标架场方程改写为${T_\varLambda }{^a_b} = \dfrac{{{c^4}}}{{8{\text{π}}G}}\left( {{{{\tilde G}}^a}_b - {{ G}^a}_b} \right)$ , 可以看作物质分布的暗伴, 其效应导致了宇宙的加速膨胀.7 )式, (11 )式和(14 )式可以得到, 对于理想流体${\left( {{{ T}_M}} \right)^a}_{\rm{b}} = {\rm{diag}}\left( {\rho, - p, - p, - p} \right)$ , 暗伴的有效能量动量张量为${\rho _{_\varLambda }} = - \dfrac{{{c^4}}}{{8\operatorname{p} G}}\left( {3{{\cal{K}}^2} + 6{\cal{K}}\dfrac{{\dot a}}{a} - {\varLambda _0}} \right)$ ,${p_{\varLambda} } = \dfrac{{{c^4}}}{{8{\text{π}}G}}\left( {{{\cal{K}}^2} + 4{\cal{K}}\dfrac{{\dot a}}{a} + 2{\dot {\cal{K}}} - {\varLambda _0}} \right)$ , $a\left( t \right)$ 为宇宙尺度因子. 由于观测表明宇宙是空间平直的, 所以我们只考虑$k = 0$ 的情况. 并采用几何单位制$\dfrac{{8{\text{π}}G}}{{{c^4}}} = 1$ , 可得大尺度洛伦兹破缺下修正的Friedmann方程11 )可知宇宙的加速膨胀解应该满足11 )式中的${\cal{K}}$ 不能由(11 )式确定, 即便是给出了宇宙介质的状态方程. 由(12 )式可知, ${\cal{K}}$ 可以用${f_\mu }$ 来表示. ${f_\mu }$ 是我们之前唯象引入的, 其演化应该由量子引力和暴胀模型给出, 目前的模型不能给出${f_\mu }$ 或${\cal{K}}$ 的演化, 为了确定${\cal{K}}$ 的演化规律, 我们不得不做一些近似. 因为${\varLambda _{{\rm{CDM}}}}$ 模型是一个非常好的宇宙学唯象模型, 可以借助其给出${\cal{K}}$ 的演化近似, 基于${\varLambda _{{\rm{CDM}}}}$ 模型的Friedmann方程${\rho _{\varLambda 1}} = \varLambda $ , ${p_{\varLambda 1}} = - \varLambda $ .16a )和(18a )式我们可以得到${\cal{K}}\left( t \right)$ 的初始条件${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( { \pm \sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , 且${\varLambda _0} \geqslant - \dfrac{2}{5}\varLambda $ .3.三种近似下的模型 第一种近似CaseA:16 )式和(18 )式, 我们可以将${\cal{K}}\left( t \right)$ 与${\varLambda _{{\rm{CDM}}}}$ 模型中的宇宙学常数Λ 建立联系$p\left( t \right) = w\left( t \right)\rho \left( t \right)$ , 代入到(16 )和(18 )式整理可得$ {\varLambda _{{\rm{CDM}}}}$ 模型21 )式和(22 )式可以得到${p_{\varLambda} } = {w_0}{\rho _\varLambda }$ , 由${{ T}_{\varLambda} }{^a_c} = {\rm{diag}}\left( {{\rho _{\varLambda} }, - {p_{\varLambda} }, - {p_{\varLambda} }, - {p_{\varLambda} }} \right)$ 整理可得20 ), (23 ), (24 )式分别与(16 )式结合并有初始条件${H_0} = H\left( {{t_0}} \right)$ , ${t_0} \simeq {H_0}^{ - 1}$ 是宇宙的当今时刻, 可以确定${\cal{K}}\left( t \right)$ 和哈勃参数$H\left( t \right)$ 的演化. 修正的Friedman方程(16 )式有两个不同的解$H = \sqrt {\dfrac{{\rho + {\varLambda _0}}}{3}} - {\cal{K}}$ 和$H = - \sqrt {\dfrac{{\rho + {\varLambda _0}}}{3}} - {\cal{K}}$ , 从${\varLambda _{{\rm{CDM}}}}$ 模型的解$H = \sqrt {\dfrac{{\rho + \varLambda }}{3}} $ 来看, 第一个解更合理. 我们只考虑物质为主的时期即$w\left( t \right) \approx 0$ , 表1 对上述情况进行了汇总. ${\cal{K}}\left( {{t_0}} \right)$的值 ${\cal{K}}\left( t \right)$的方程 CaseA1 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $H\left( t \right){\cal{K}}\left( t \right) + {\dot {\cal{K}}}\left( t \right) = \dfrac{1}{3}\left( {{\varLambda _0} - \varLambda } \right);$ CaseA2 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $H\left( t \right){\cal{K}}\left( t \right) + \dot {\cal{K}}\left( t \right) = \dfrac{1}{3}\left( {{\varLambda _0} - \varLambda } \right);$ CaseB1 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $\dot {\cal{K}} + 2H{\cal{K}} + \dfrac{1}{2}{{\cal{K}}^2} = \dfrac{1}{2}\left( {{\varLambda _0} - \varLambda } \right);$ CaseB2 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $\dot {\cal{K}} + 2H{\cal{K}} + \dfrac{1}{2}{{\cal{K}}^2} = \dfrac{1}{2}\left( {{\varLambda _0} - \varLambda } \right);$ CaseC1 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $\begin{array}{l} \left( {3{w_0} + 1} \right){{\cal{K}}^2} + \left( {6{w_0} + 4} \right)H{\cal{K}} + 2\dot {\cal{K}} = \left( {{w_0} + 1} \right){\varLambda _0}; \\ \end{array} $ CaseC2 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $\begin{array}{l} \left( {3{w_0} + 1} \right){{\cal{K}}^2} + \left( {6{w_0} + 4} \right)H{\cal{K}} + 2\dot {\cal{K}} = \left( {{w_0} + 1} \right){\varLambda _0}. \\ \end{array} $
表1 Lorentz破缺宇宙学的几种模型Table1. Proposed models of Lorentz violation cosmology.图3 和图4 给出了不同初值下哈勃参数随着时间的演化曲线. 可以看出在哈勃时间附近的范围内, 这几种模型的宇宙演化非常近似. 在长期的演化中, CaseB1与${\varLambda _{{\rm{CDM}}}}$ 模型的演化结果趋近于完全相同, CaseA1和${\varLambda _{{\rm{CDM}}}}$ 模型的结果相比要比CaseB1的差别大一些, CaseC1和${\varLambda _{{\rm{CDM}}}}$ 模型的演化结果相比差别很大, 并且随着${\varLambda _0}$ 的增大, CaseA1, CaseC1与${\varLambda _{{\rm{CDM}}}}$ 模型的差别也在逐渐缩小. CaseB2与${\varLambda _{{\rm{CDM}}}}$ 模型的结果也趋近于完全相同, 相比于CaseA1和CaseC1, CaseA2与CaseC2要比${\varLambda _{{\rm{CDM}}}}$ 模型的演化结果偏差更大. 图5 和图6 给出了不同初值下${\cal{K}}$ 随宇宙时的演化曲线, 可以看出, CaseA1和CaseB1在哈勃时间附近的范围内趋近于完全一致, 并且在长期的演化过程中也非常相近, CaseC1和CaseA1, CaseB1的演化结果偏离的较大. CaseA2, CaseB2和CaseC2在哈勃时间附近的范围内也趋近于完全一致, 并且在长期的演化过程中CaseC2与CaseA2, CaseB2的偏差比CaseC1与CaseA1, CaseB1的偏差要小.图 3 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , ${w_0} = - 0.88$ 时哈勃常数随时间的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure3. The Hubble constant evolves with the time when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) $ {\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .图 4 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ , ${w_0} = - 0.88$ 时哈勃常数随时间的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure4. The Hubble constant evolves with the time when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) $ {\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .图 5 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , ${w_0} = - 0.88$ 时${\cal{K}}$ 随时间的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure5. ${\cal{K}}$ evolves with the time when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .图 6 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ , ${w_0} = - 0.88$ 时${\cal{K}}$ 随时间的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure6. ${\cal{K}}$ evolves with the time when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .$ {a_0} = a\left( {{t_0}} \right).$ k = 0, 由光度距离${d_{\rm{L}}}\left( z \right)$ 的定义[32 ] 可得[32 ] 25 ), (26 )式可以将(16 )和(20 ), (23 ), (24 )式转化为以红移z 为变量的${\cal{K}}\left( z \right)$ 和${d_{\rm{L}}}\left( z \right)$ 的方程组:图7 和图8 给出了不同初值下光度距离随红移的演化结果. 在长期的演化中, CaseB1和${\varLambda _{{\rm{CDM}}}}$ 模型的结果趋近于完全相同, 相较于CaseB1的演化结果, CaseA1和CaseC1与${\varLambda _{{\rm{CDM}}}}$ 模型的演化结果对比差别要大些. 并且CaseB2在长期的演化中也和${\varLambda _{{\rm{CDM}}}}$ 模型的结果趋近于完全相同, 但CaseA2, CaseC2的演化结果与${\varLambda _{{\rm{CDM}}}}$ 模型相比要比差别要比CaseA1和CaseC1大.图 7 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , ${w_0} = - 0.88$ 时光度距离随红移的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure7. The luminosity distance evolves with the redshift when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .图 8 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ , ${w_0} = - 0.88$ 时光度距离随红移的演化 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure8. the luminosity distance evolves with the redshift when ${w_0} = - 0.88$ , ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ .4.计算结果与数据分析 图9 和图10 给出了距离模数的测量值与理论期望值的对比. 比较(16a )和(18a )式发现${\rho _\varLambda }$ 扮演了有效宇宙学常数的角色. 由此我们可以定义${\varLambda _{{\rm{eff}}}}\left( t \right) = {\varLambda _0} - 3\left( {{\cal{K}}{{\left( t \right)}^2} + 2{\cal{K}}\left( t \right)\dfrac{{\dot a\left( t \right)}}{{a\left( t \right)}}} \right)$ , 表现为类标量场的有效势能. 对于所有的近似情况, 可以求解${\varLambda _0}$ 临界值的情况, 它表示${\varLambda _{{\rm{eff}}}}$ 从单调下降的quintessence类型到有效宇宙学常数随时间的演化出现局域极小类型转变的临界值.图 9 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , ${w_0} = - 0.88$ 时距离模数测量值与理论期望值的对比 (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure9. Comparison of the measured distance moduluswith its expected value when ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ , ${w_0} = - 0.88$ : (a) ${\varLambda _0} = - {\rm{0}}.{\rm{2}}\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) $ {\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda$ 图 10 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ , ${w_0} = - \dfrac{8}{9}$ 时距离模数实验测量值与理论期望值的对比 (a) ${\varLambda _0} = - 0.2\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) ${\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda $ Figure10. Comparison of the measured distance moduluswith its expected value when ${\cal{K}}\left( {{t_0}} \right)\!=\!- {H_0}\left(\!{\sqrt {1\!-\!\dfrac{{\varLambda\!-\!{\varLambda _0}}}{{3{H_0}^2}}}\!+\!1}\!\right)$ , ${w_0} = - \dfrac{8}{9}$ : (a) ${\varLambda _0} = - 0.2\varLambda $ ; (b) ${\varLambda _0} = 0$ ; (c) $ {\varLambda _0} = {\rm{0}}.{\rm{2}}\varLambda$ .表2 给出了不同模型下${\varLambda _0}$ 的临界值情况, 图11 和图12 将${\varLambda _{{\rm{eff}}}}$ 在临界值附近随时间的演化曲线清楚地表示了出来. 对于CaseC, 当${w_0} > $ $ - \dfrac{8}{9}\left(\!{ - \dfrac{8}{9} \approx - 0.889}\!\right)$ , ${\cal{K}}\left(\!{{t_0}} \right) \!=\!{H_0}\left(\!\!{\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1}\!\right)$ 时, 对于所有${\varLambda _0}$ , ${\varLambda _{{\rm{eff}}}}$ 表现为单调下降的类quintessence势, 并且由图9 可知, 通过天文观测可以将${w_0} > - \dfrac{8}{9}$ 时, ${\varLambda _0}$ 大于0的情况排除. 对于所有有临界值的情况, ${\varLambda _{0 - {\rm{crit}}}}$ 近似为0, 我们可以推测${\varLambda _{0 - {\rm{crit}}}}$ 与0的偏差可能是由近似所引起的, 在一个更详细精准的模型中, 它可能会有${\varLambda _{0 - {\rm{crit}}}} = 0$ . ${\cal{K}}\left( {{t_0}} \right)$的值 ${\varLambda _0}$的临界值 CaseA ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $ - 0.05\varLambda $ ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $ - 0.187\varLambda $ CaseB ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $ - 0.066\varLambda $ ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $ - 0.2144\varLambda $ CaseC (${w_0} = - 1$) ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $0.00001\varLambda $ ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $0.00001\varLambda $ CaseC(${w_0} = - {8}/{9}$) ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ $0.119\varLambda $ ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $0.075\varLambda $ CaseC(${w_0} = - {7}/{9}$) ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ 无 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $0.152\varLambda $ CaseC(${w_0} = - {2}/{3}$) ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ 无 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $0.225\varLambda $ CaseC(${w_0} = - {1}/{3}$) ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ 无 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ $0.397\varLambda $
表2 在不同模型下有无${\varLambda _0}$ 的临界值Table2. Whether there are critical values of ${\varLambda _0}$ under different models图 11 ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ 时${\varLambda _{{\rm{eff}}}}$ 从单调的quintessence类型到随时间的演化出现局域极小类型的转变 (a) CaseA1; (b) CaseB1; (c) CaseC1, ${w_0} = - 1$ ; (d) CaseC1, ${w_0} = - \dfrac{8}{9}$ Figure11. ${\varLambda _{{\rm{eff}}}}$ shifts from a monotonically decreasing quintessence type to a local minimal type transition with time evolution when ${\cal{K}}\left( {{t_0}} \right) = {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} - 1} \right)$ (a) CaseA1; (b) CaseB1; (c) CaseC1, ${w_0} = - 1$ ; (d) CaseC1, ${w_0} = - \dfrac{8}{9}$ .图 12 ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ 时${\varLambda _{{\rm{eff}}}}$ 从单调的quintessence类型到随时间的演化出现局域极小类型的转变 (a) CaseA2; (b) CaseB2; (c) CaseC2, ${w_0} = - 1$ ; (d) CaseC2, ${w_0} = - \dfrac{8}{9}$ Figure12. ${\varLambda _{{\rm{eff}}}}$ shifts from a monotonically decreasing quintessence type to a local minimal type transition with time evolution when ${\cal{K}}\left( {{t_0}} \right) = - {H_0}\left( {\sqrt {1 - \dfrac{{\varLambda - {\varLambda _0}}}{{3{H_0}^2}}} + 1} \right)$ (a) CaseA2; (b) CaseB2; (c) CaseC2, ${w_0} = - 1$ ; (d) CaseC2, ${w_0} = - \dfrac{8}{9}$ .${\varLambda _{{\rm{eff}}}}$ 表现为类quintessence类型的标量势所驱动的演化, 它满足这两个弦沼泽地判据. 也就是说dS真空并不是宇宙加速膨胀所必需的, 宇宙加速膨胀与量子引力是相容的. 对于具有裸的正宇宙学常数的弦沼泽地, 在最合理的近似下, 有效宇宙学常数${\varLambda _{{\rm{eff}}}}$ 随着时间的演化会出现局域极小, 如果有标量场的势能驱动其演化的话, 必然不是quintessence类型.5.总结与展望 实际上, 从上文的分析可以看出, CaseC并不是一个很好的近似, 原因可能是在暗能量部分的状态方程中使用固定的${w_0}$ . 根据光度距离观测值与理论期望值的比较, 以及对${\varLambda _0}$ 临界值在不同模型下的分析, 可以得出结论: 从弦景观中能够产生有效的类quintessence势, 我们推测从单调下降的quintessence势能类型到有效宇宙学常数 (或者说类标量场的有效势能) 随时间的演化出现局域极小类型转变的临界值${\varLambda _0}$ 为零. 在我们的讨论中事实上没有涉及标量场, 也没有涉及标量场的势能, 我们给出的是有效宇宙学常数随时间的演化. 如果将这个有效宇宙学常数用一个标量场的真空势能来等效地实现, 这个标量场应该具有quintessence的行为, 后续的研究将给出一个由quintessence势能驱动的加速膨胀宇宙, 其标量势随时间的演化与我们在这里的有效宇宙学常数预言之间的比较.${\cal{K}}\left( t \right)$ 的演化规律, 这样就可以用观测去检验大尺度洛伦兹破缺模型的正确性. 另外洛伦兹破缺区域进入视界也是具有不确定性的, 目前我们并没有足够的信息来确定其何时进入视界, 进入视界时间的不同会导致洛伦兹破缺区域尺度大小的不同, 也会对于理论的预言造成差别, 但是这些差别都可以通过观测进行鉴别. 我们目前的洛伦兹破缺引力模型是基于规范原理对广义相对论的修正, 实现洛伦兹破缺不见得一定要通过规范原理. 尤其是有研究指出考虑量子引力修正之后, 时空的对称性一般不是李代数, 而是更一般的Hopf代数[33 ] , 规范原理应用于Hopf代数没有现成的理论可以借鉴, 需要寻求实现洛伦兹破缺的其他途径. 广义相对论的黎曼几何框架是表述引力的一种最常用的框架, 研究证明绝对平行引力的框架完全等价于广义相对论非黎曼几何表述的一种, 另外基于非不可度量性的几何的表述也是等价于广义相对论的. 对于后两种的大尺度洛伦兹破缺的修正与我们的模型是否一致也是值得研究的, 我们的结论是否是模型不依赖的还需要检验. 

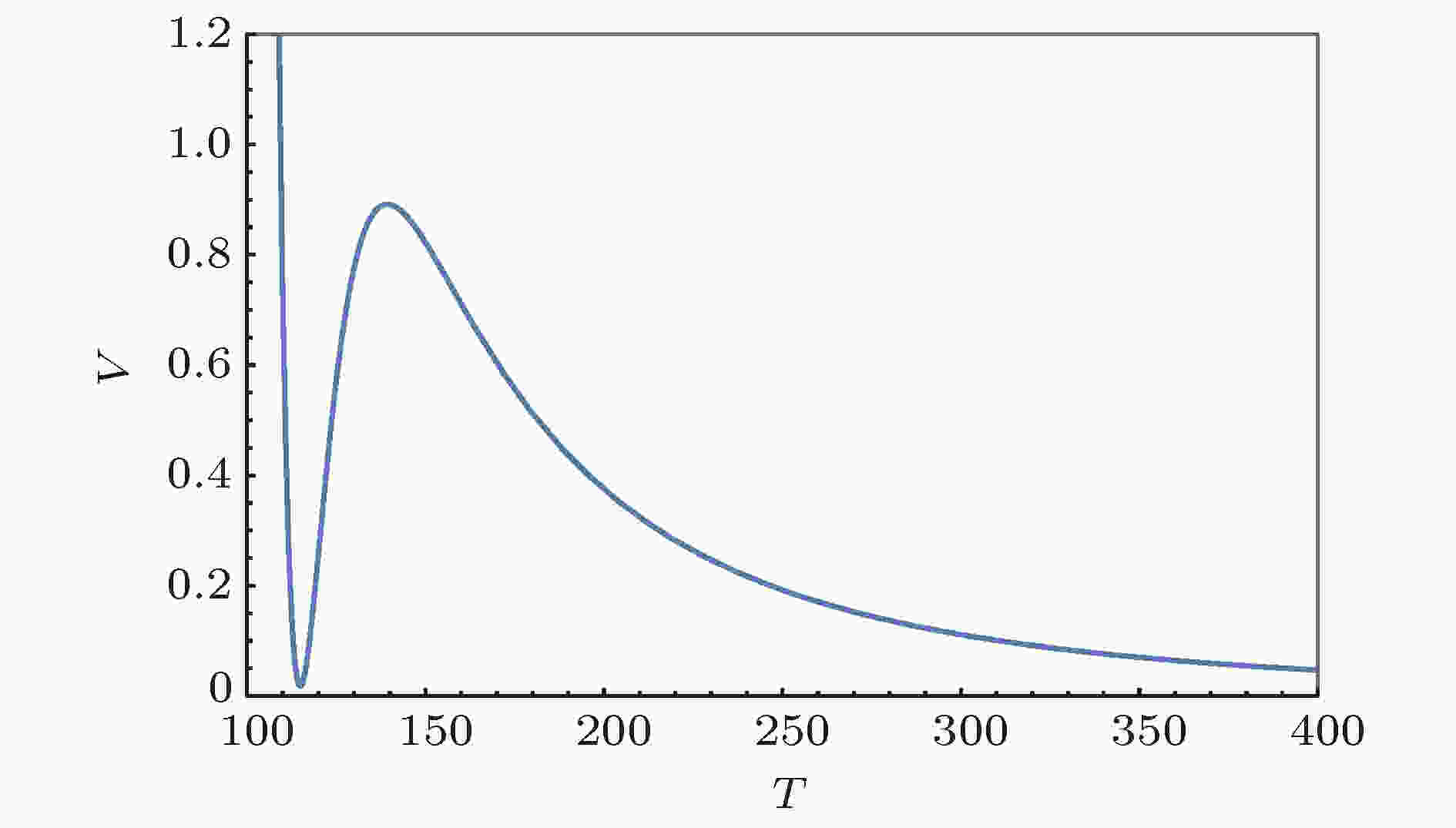 图 1 亚稳态dS的标量势V
图 1 亚稳态dS的标量势V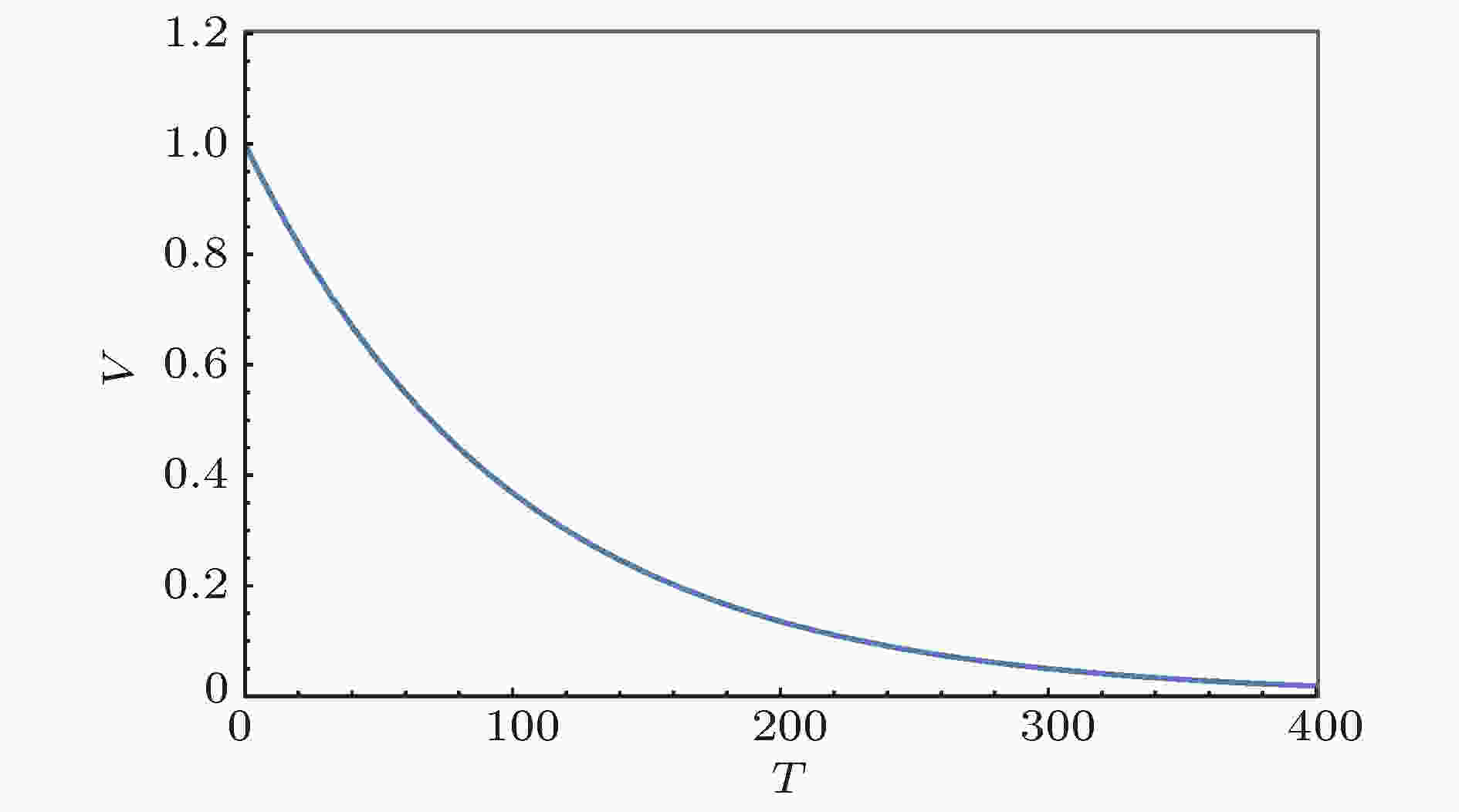 图 2 不稳定dS的标量势V
图 2 不稳定dS的标量势V



















































































































































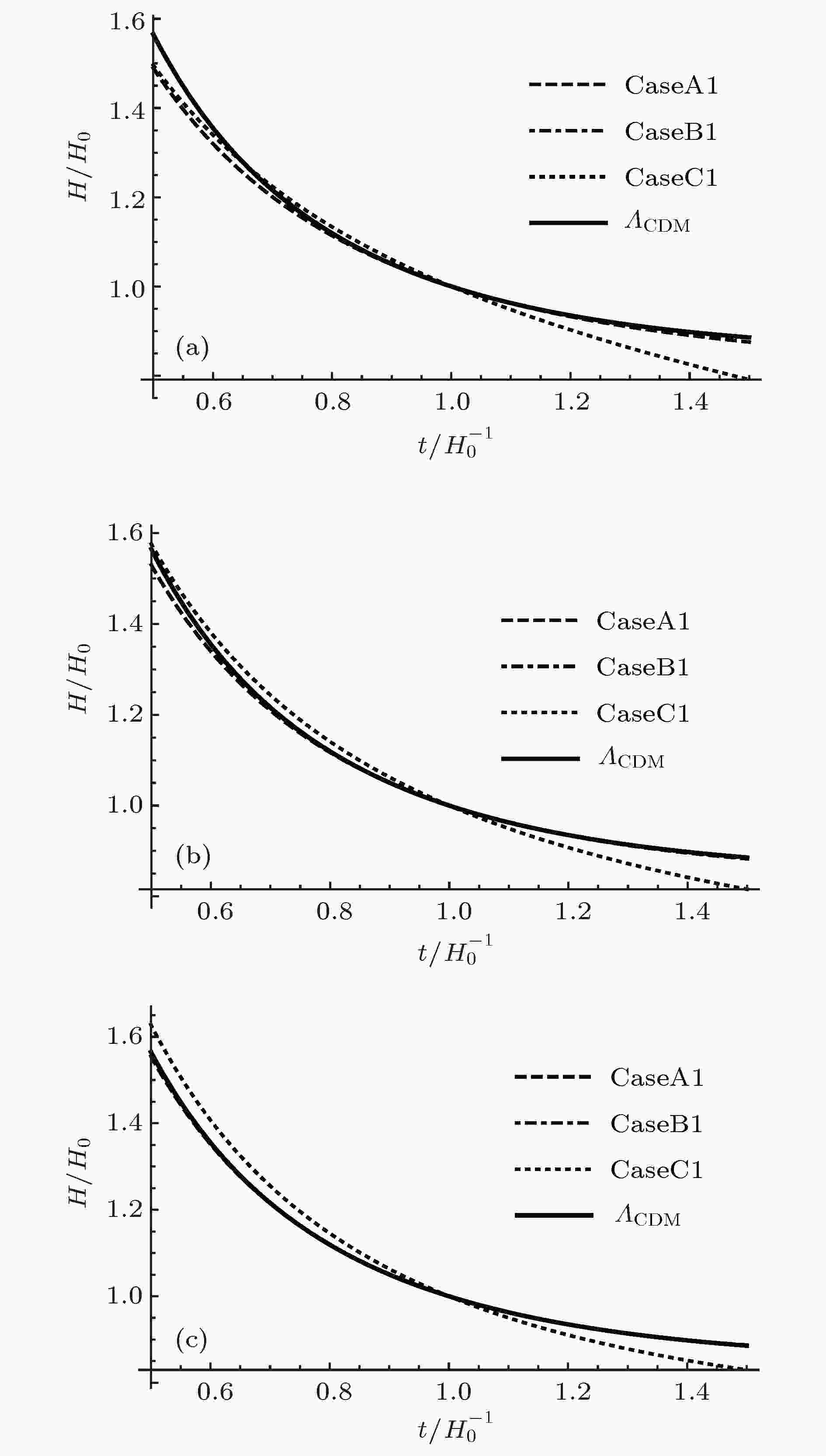 图 3
图 3 









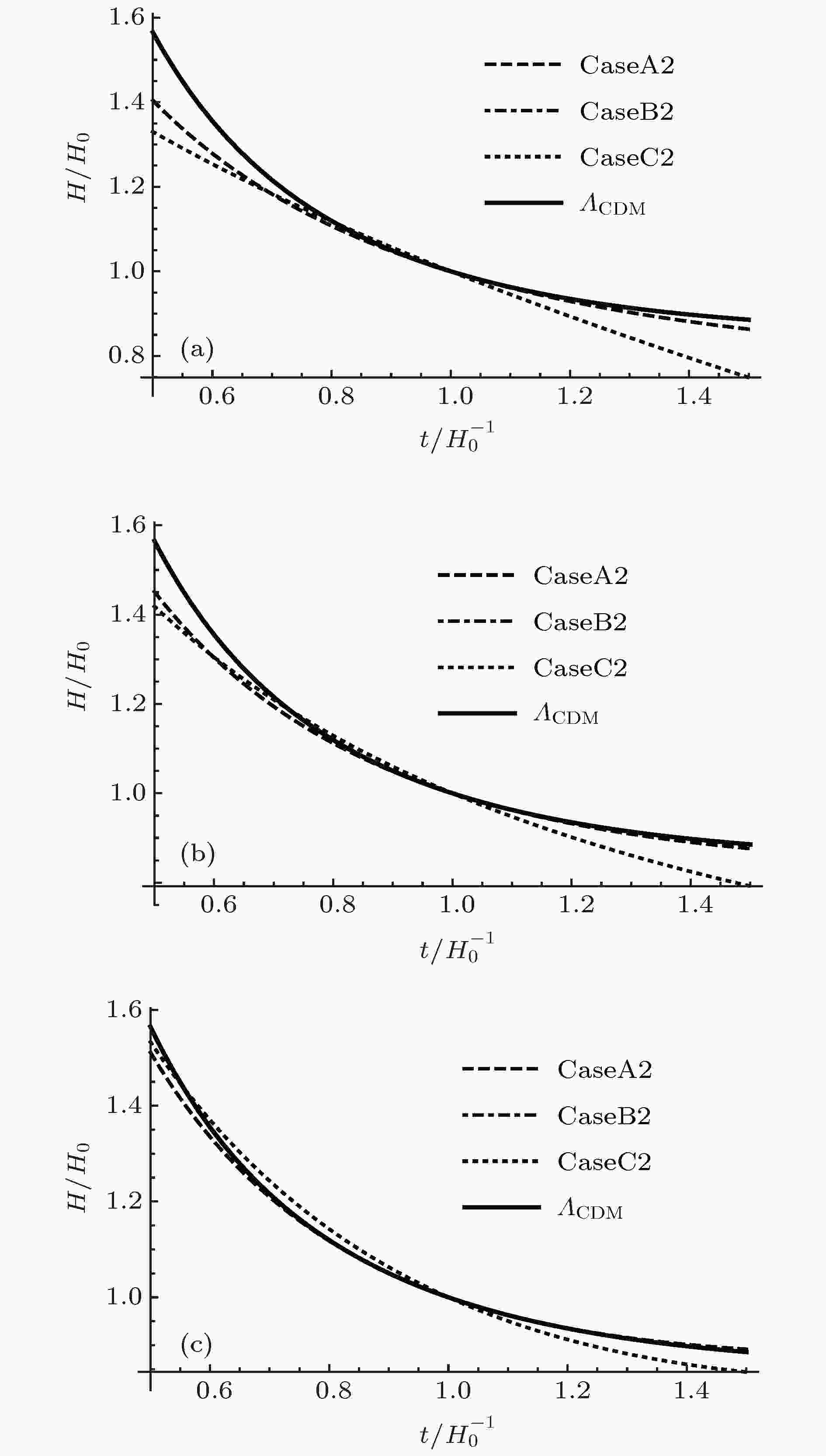 图 4
图 4 









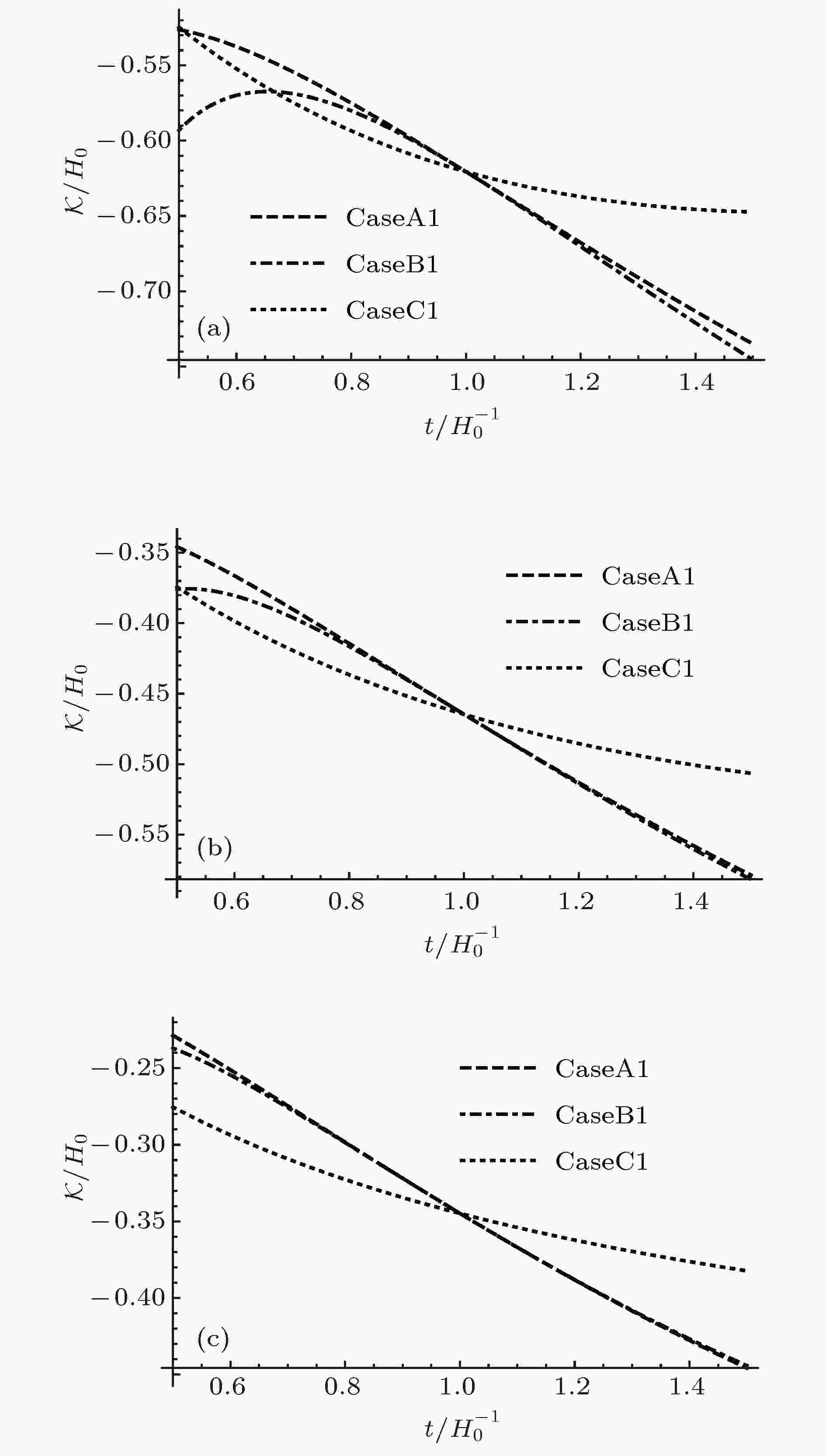 图 5
图 5 











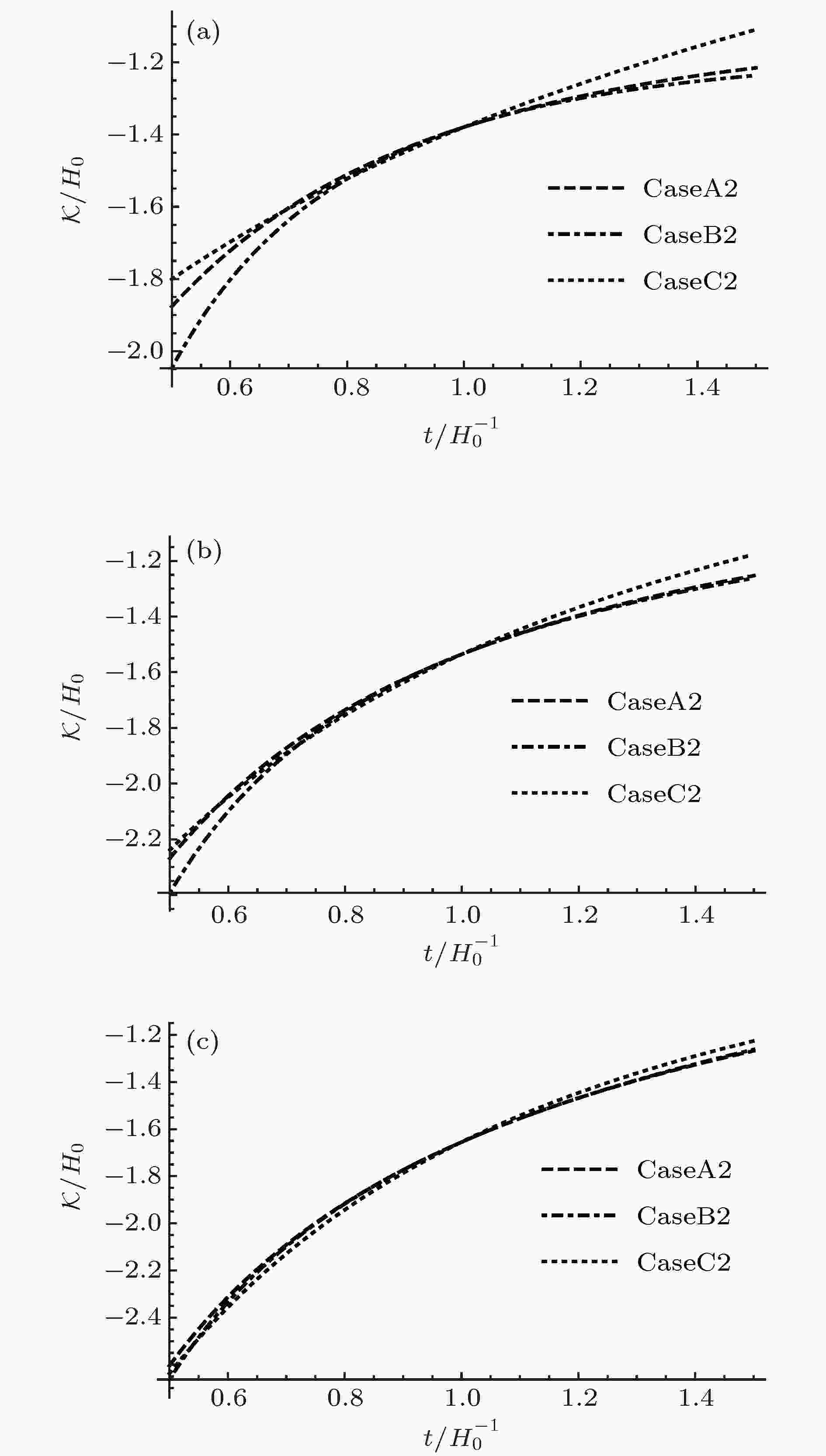 图 6
图 6 































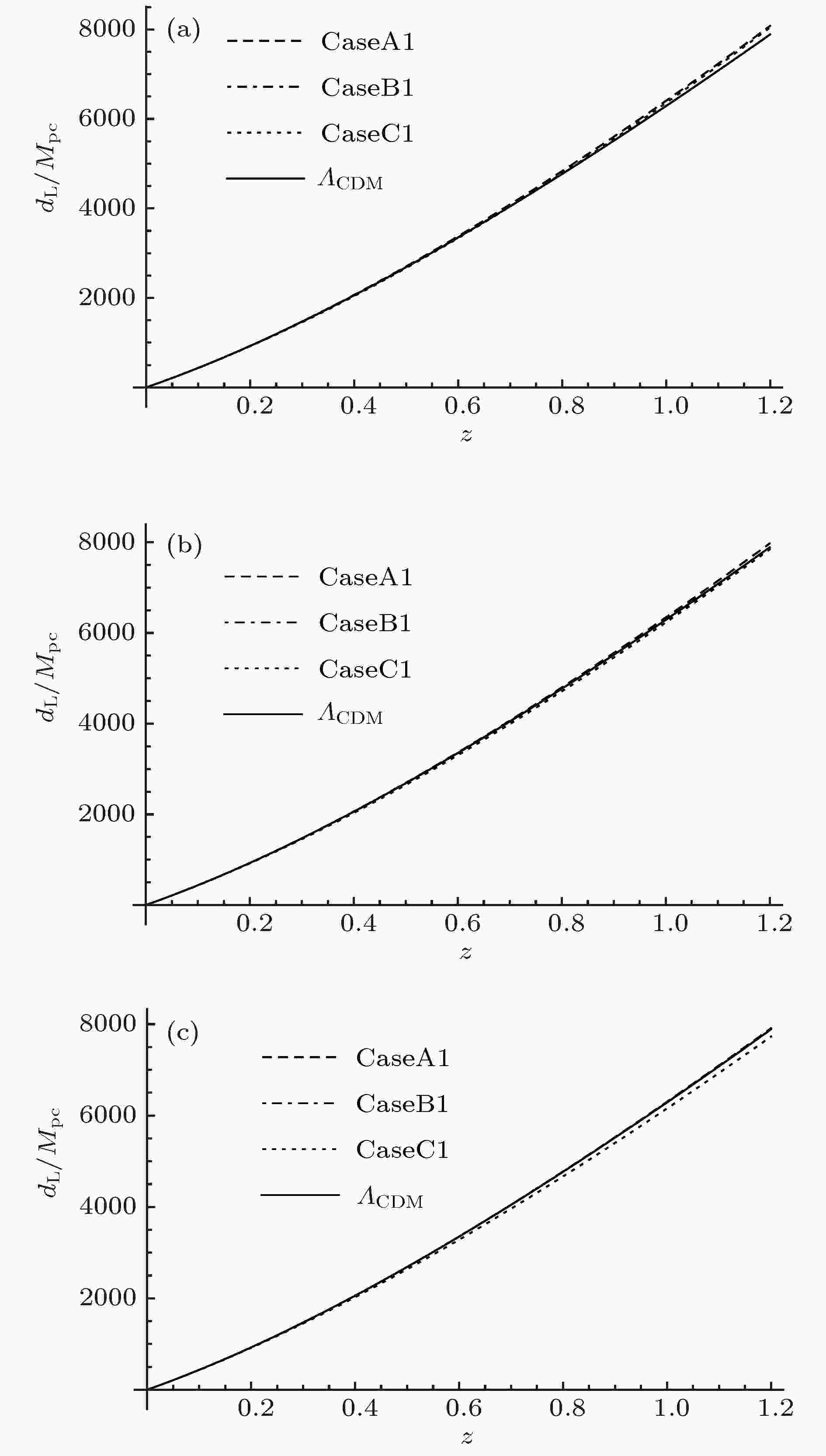 图 7
图 7 









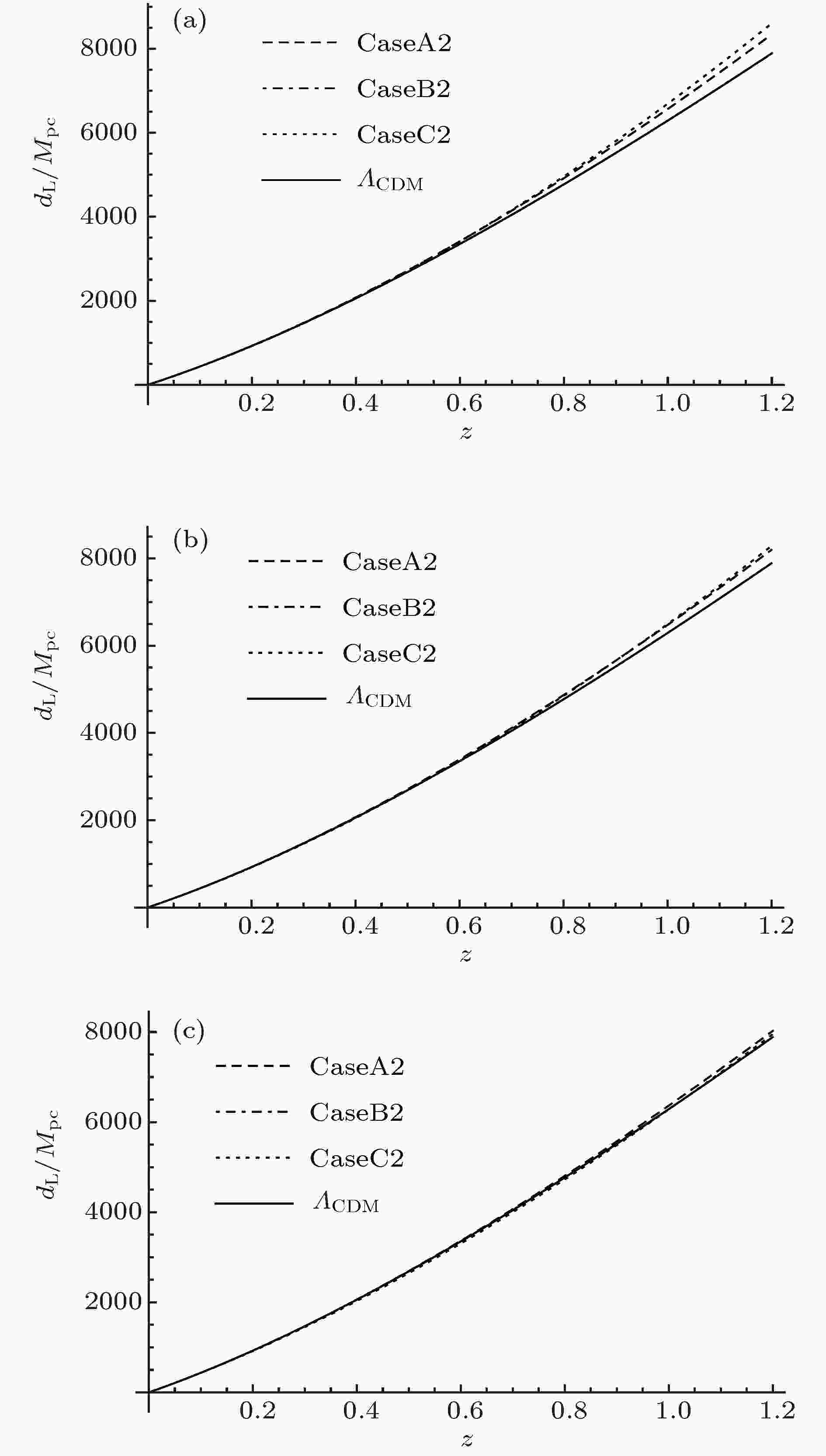 图 8
图 8 













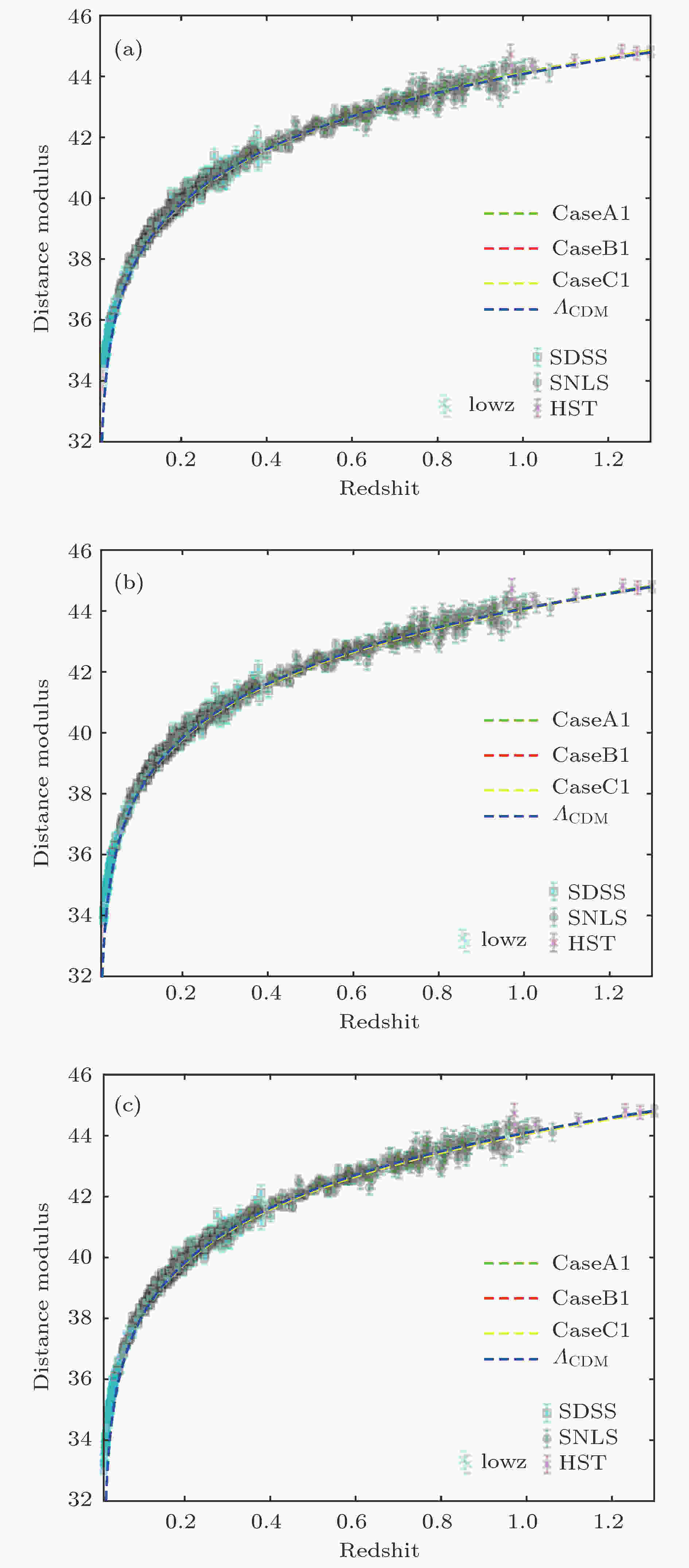 图 9
图 9 









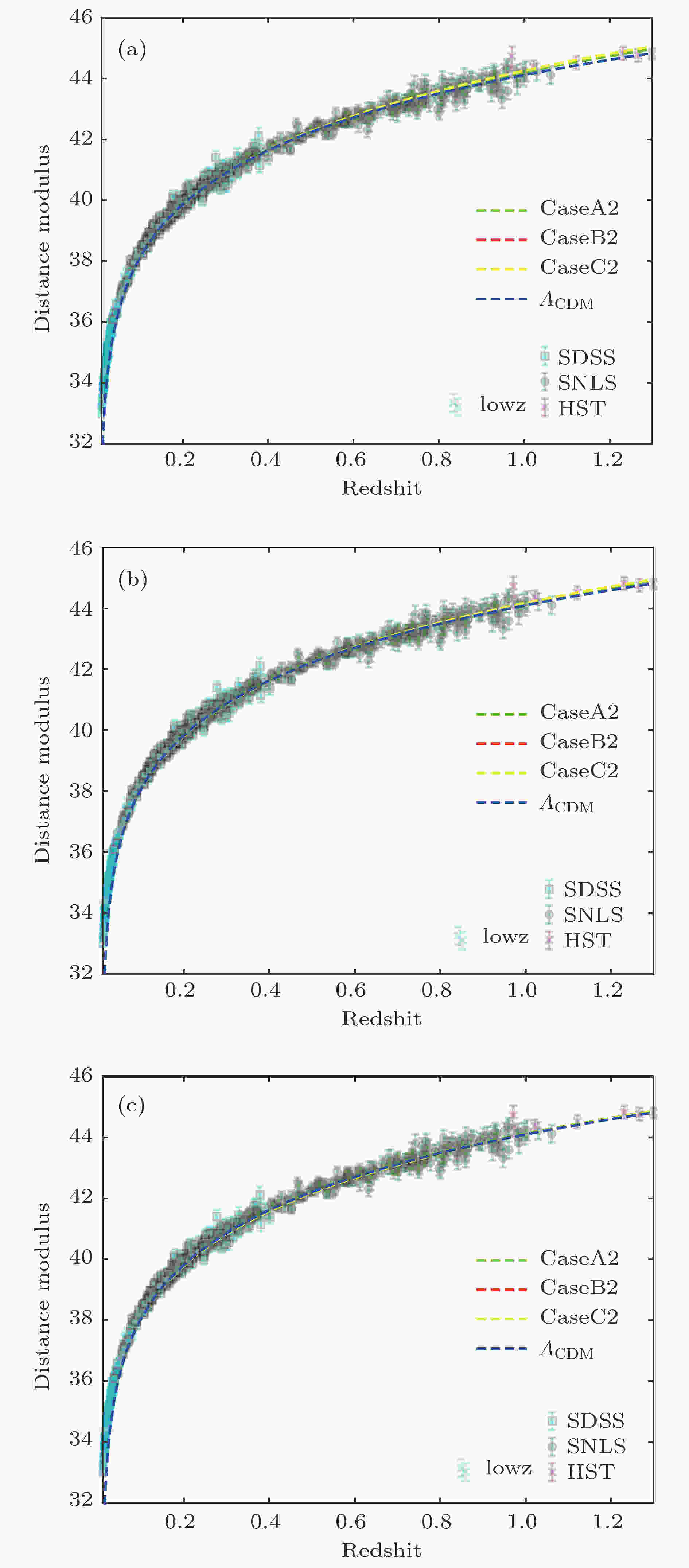 图 10
图 10 

































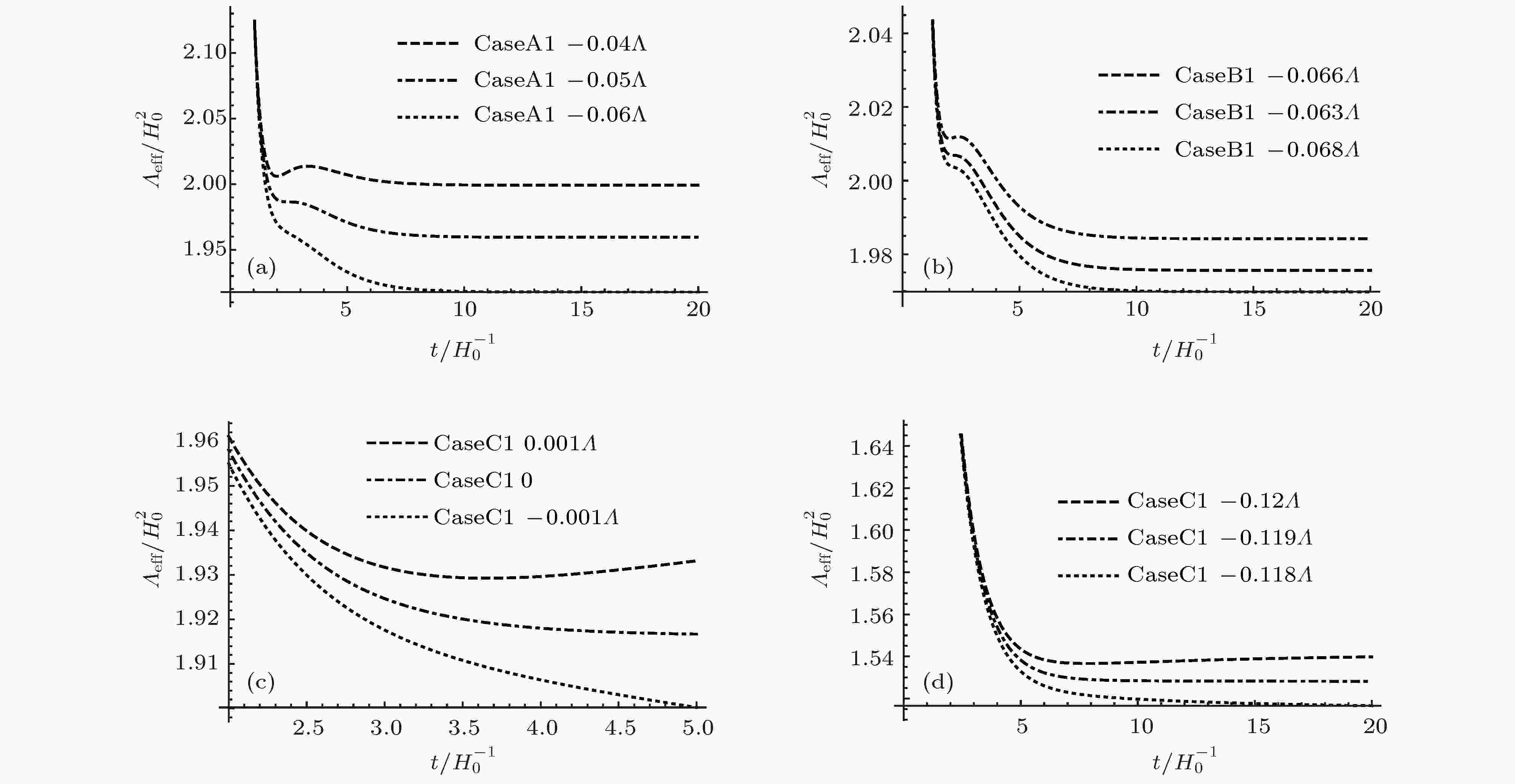 图 11
图 11 







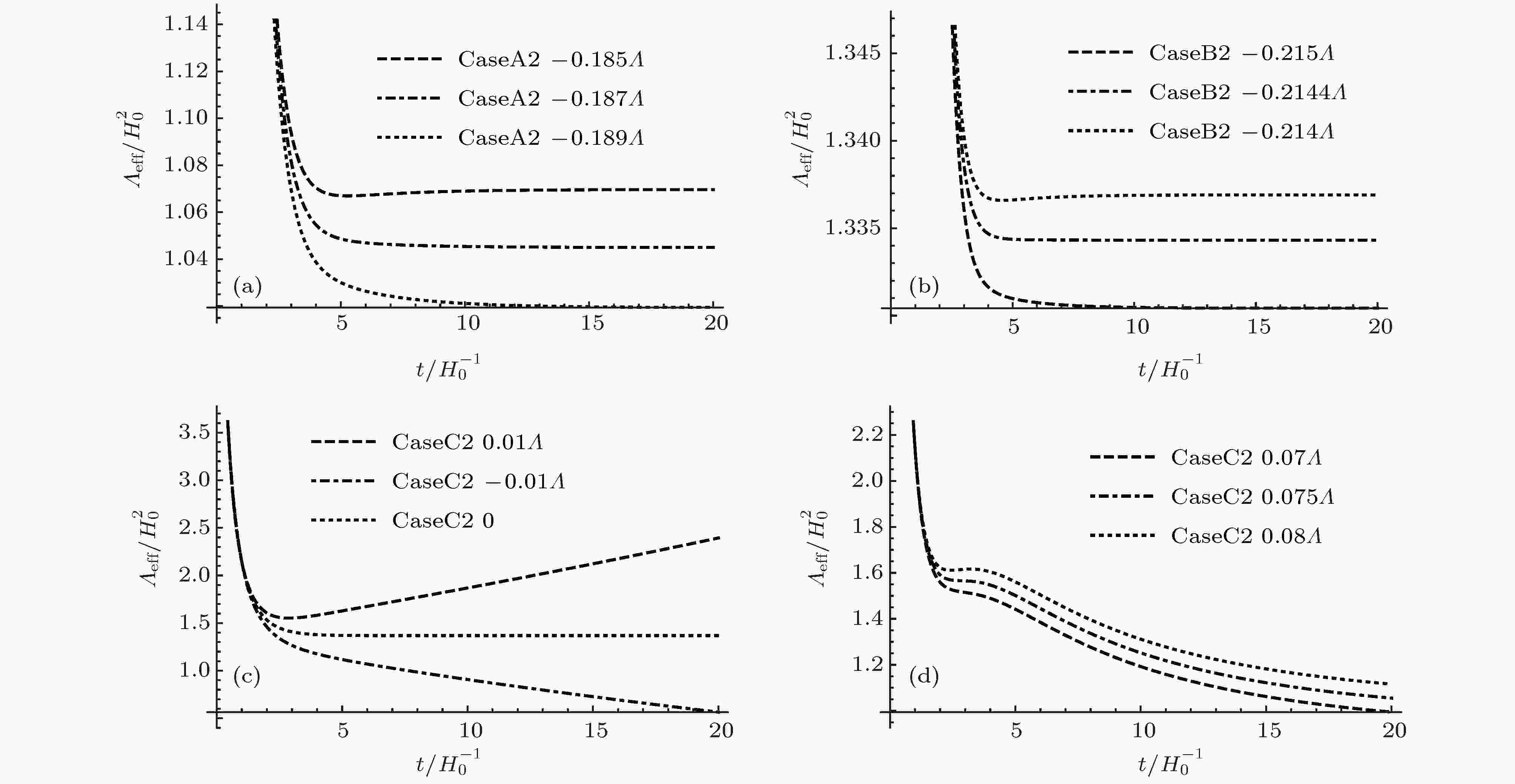 图 12
图 12 



















