摘要: 在浅海, 尤其是负梯度声速剖面和海面较为平静的浅海波导, 海底界面反向散射是浅海混响的主要来源. 经验散射模型只适用于分析浅海混响平均强度衰减特性, 而基于物理机理建立的反向散射模型克服了这一缺陷, 但同时也引入了其受地声模型约束的问题. 本文结合了海底反射系数的三参数模型, 对浅海远场海底反向散射模型进行了简化, 以减少地声模型的输入参数. 理论分析了海底反射系数的相移参数可以描述海底对声场的散射作用, 无需任何海底地声参数的先验知识. 通过对海底反向散射模型近似简化, 结果表明在临界角附近和甚小掠射角范围内的海底粗糙界面反向散射模型的角度特性和强度特性受海底沉积层的影响不同: 在临界角附近, 海底反向散射的角度特性受海底反射系数的相移参数加权,而其散射系数则近似与相移参数无关; 对于甚小掠射角, 海底反向散射的角度特性近似与海底反射系数的相移参数无关, 其散射系数则近似与相移参数的4次方成正比.
关键词: 海底反向散射模型 /
强度特性 /
角度特性 /
小掠射角近似 English Abstract Simplification of roughness bottom backscattering model at small grazing angle in shallow-water Hou Qian-Nan Wu Jin-Rong Key Laboratory of Underwater Acoustic Environment, IACAS, Beijing 100190, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11374323, 11774375).Received Date: 02 August 2018Accepted Date: 25 December 2018Available Online: 01 February 2019Published Online: 20 February 2019Abstract: Bottom backscattering due to roughness seafloor is the main source of shallow water reverberation, especially in the waveguide with downward reflection profile or a calm sea-surface. Empirical backscattering models with a simple form has an important limitation to analyzing other characteristics of reverberation except for the intensity characteristics, which originates from optics and describes the relationship between the bottom backscattering strength and scattering grazing angle of plane-wave in half-infinite space. In the shallow water, such a plane-wave backscattering model cannot be used due to frequency dispersion. The model of bottom backscattering based on physical scattering principle is made to relieve such a limitation, but thereby bringing about another restraint by a geoacoustics model. The bottom backscattering model, which is formulated during modeling the full-wave reverberation theory at small grazing angle in range-independent shallow water waveguide, is simplified by combining with bottom reflection coefficient model which is independent of the geoacoustics model. The bottom reflection coefficient model as referred to the proposed phase parameter P in this paper is equivalent to velocity and density of sediment to describe sound field interacted with sea-bottom. Therefore simplification of bottom backscattering model can be handled by the phase parameter without any knowledge of bottom geoacoustic parameters. The angular dependency and intensity dependency of bottom backscattering due to roughness seafloor at small grazing angle are studied more in depth through such a simplified model. Marking 2/P as the cut-off point, the grazing angle is divided into two stages. Near the critical angle, as grazing angle is greater than 2/P and less than critical grazing angle, the angular dependency of bottom backscattering due to roughness seafloor is weighted by phase parameter of bottom reflection coefficient, while the intensity dependency is independent of phase parameter. At each small grazing angle, as grazing angle is less than 2/P , the angular dependency of bottom backscattering due to roughness seafloor is proportional to incident and scattering grazing angle squared and irrespective of phase parameter of bottom reflection coefficient which is like the empirical bottom backscattering model, while the intensity dependency is proportional to the fourth power of phase parameter. So the bottom has different influences on the angular dependency and intensity dependency of bottom backscattering in different stages of grazing angle.Keywords: bottom sackscattering model /intensity dependency /angular dependency /small grazing angle approximation 全文HTML --> --> --> 1.引 言 海底作为浅海混响的主要散射源, 浅海海底界面混响是很多****探究的课题. 浅海混响根据其形成过程可以分为传播和散射两个过程. 入射声传播和散射声传播过程同属信道声传播问题, 研究较为完善. 而散射过程则比较复杂, 散射强度的测量也较难实现, 尤其是小掠射角的反向散射的测量, 所以针对散射的研究相对比较受限. 在混响研究伊始, 各国****均采用经验的散射模型描述海底对声场的散射作用. 由于其形式较为简单, 运算速度较快, 在主动声纳预报系统中有很大的优势[1 -4 ] , 至今仍被延续使用. 但是该类型的散射模型也存在着很大的局限性, 很难分析海底散射机理. 最初的经验散射模型是借鉴光学理论中提出的半无限自由空间中的Lambert散射定律给出的海底散射模型, 是海底散射强度与平面波掠射角之间的关系. 而在波导环境中, 由于频散效应的存在, 平面波散射理论不再适用于声场处理, 遂采用简正波理论, 避免了频散产生的多途现象. 然而简正模态的掠射角不同于平面波的掠射角, 因此对波导环境中的声散射问题不能够直接采用经验的Lambert散射模型. 近年来, 越来越多的****开始从海底散射的物理机理着手建立散射模型. 国际上关于物理散射模型的建模方法包括有限元方法[5 ] 、Kirchhoff近似方法[6 ] 、微扰近似方法[7 -10 ] . 国内关于物理散射模型的研究最具代表性的是中国科学院声学研究所的高天赋和尚尔昌. Shang等[11 ] 在Gao[12 ] 和Tang[13 ] 的研究基础上提出了全波动混响理论, 并对该模型进行了一系列的发展. 2001年, Gao等[14 ] 提出了依据混响数据反演海底反向散射矩阵的方法. Wu等[15 ,16 ] 将海底反射模型引入到浅海混响模型中简化了混响衰减特性与海底沉积层参数之间的关系, 为海底地声参数的反演提供了一种新方法.2.浅海全波动混响理论 在浅海波导环境中, 海底粗糙界面是海底混响的主要散射源. 在图1 所示的浅海波导环境中, 平坦海底的平均海深为${H_0}$ , 任意水平位置$r$ 的海底粗糙界面相对于平均海深的起伏高度为$\eta (r)$ , 其量值远小于${H_0}$ , 均值为0, 方差为$\sigma _\eta ^{\rm{2}}$ . 海底粗糙界面对声场的散射强度远小于入射声场的强度, 即满足弱散射的条件. 海底为半无限均匀介质, 其声速、密度和声吸收系数分别为$ {c_b},{\rho _b}\,{\text{和}}\,\alpha _b^{(w)} $ (声吸收系数的单位是${{{\rm{dB}}}/{\rm{\lambda }}}$ ). 海面为平坦的自由边界, 不考虑其对声场的散射作用.图 1 浅海波导环境Figure1. Shallow water waveguide environment.2.1.浅海海底粗糙界面散射 2.1.浅海海底粗糙界面散射 全波动混响理论的基础思想是将海底粗糙界面对声场的散射作用看作是“二次声源”向外辐射声能量, 从而将海底粗糙界面的散射作为“声源”向波导环境中辐射声能量[11 ] . 该“声源”的声源强度与入射声强度成正比关系. 在水平均匀的波导环境中, 单位简谐点源入射声场满足波动方程为${{{R}}_0} = {\rm{(}}{r_{\rm{s}}},{z_0}{\rm{)}}$ , ${{{R}}_1} = ({r_1},{H_0})$ 分别是声源和散射点的空间位置, 两者之间的水平距离差为$r = |{r_{\rm{s}}} - {r_1}|$ ; $ u_{\rm{w}}, u_{\rm{b}}$ 分别是水介质和沉积层介质中“二次源”的辐射声场(下脚标w和b分别代表水介质和沉积层介质); ${k_{{\rm{w,b}}}}$ 是水介质和沉积层介质中的波数, 与声源频率$f$ 和介质声速有关; ${c_{\rm{H}}} = $ $ {c_{\rm{w}}}{\rm{(}}{H_0}{\rm{)}}$ 是海深处的声速, 沉积层介质和水介质的密度比用$\kappa $ 表示; ${G^{\rm{i}}}{\rm{(}}{{{R}}_1},{{{R}}_0}{\rm{)}}$ 是波导环境中初级声场的格林函数. 根据简正波理论的思想, 在浅海波导环境中, ${G^{\rm{i}}}{\rm{(}}{{{R}}_1},{{{R}}_0}{\rm{)}}$ 可以表示为简正模态${\phi _m}({H_0})$ (实际上是${\phi _m}(z)$ , $z$ 是接收深度, 在这里的接收深度为海深${H_0}$ )叠加的形式, 如(4 )式所示, km 和${\beta _m}$ 分别是简正模态本征值的实部和虚部. $V({{{R}}_1})$ 和$p({{{R}}_1})$ 则分别是质点振速算子和压力算子, 作用到初级声场的格林函数${G^{\rm{i}}}{\rm{(}}{{{R}}_1},{{{R}}_0}{\rm{)}}$ , 得到海底粗糙界面的“二次速度源”的声源强度$V{\rm{(}}{{{R}}_1}{\rm{)}}{G^{\rm{i}}}{\rm{(}}{{{R}}_1},{{{R}}_0}{\rm{)}}$ 和“二次压力源”的声源强度$p{\rm{(}}{{{R}}_1}{\rm{)}}{G^{\rm{i}}}{\rm{(}}{{{R}}_1},{{{R}}_0}{\rm{)}}$ . 在瑞利参数较小的情况下, Bass给出了(5 )式和(6 )式的近似表达式. ${\nabla _ \bot }$ 为水平梯度算子,${{R}} = {\rm{(}}{r_{\rm{r}}},z{\rm{)}}$ 处的辐射声场可以通过格林函数$G_{{\rm{w,b}}}^{\rm{V}}{\rm{(}}{{R}},{{{R}}_1}{\rm{)}}$ 给出形式解. 辐射声场的格林函数满足11 )式的形式解,$G_{\rm{w}}^{\rm{p}}{\rm{(}}{{R}},{{{R}}_1}{\rm{)}}$ 是“二次压力源”的辐射声场的格林函数. 根据边界处法向振速与压力之间的关系, 不难得到$G_{\rm{w}}^{\rm{p}}{\rm{(}}{{R}},{{{R}}_1}{\rm{)}}$ 与$G_{\rm{w}}^{\rm{V}}{\rm{(}}{{R}},{{{R}}_1}{\rm{)}}$ 满足11 )—(13 )式代入(14 )式, 得到海底粗糙界面散射声场的一般形式解15 )式进行简化得到${r_{\rm{s}}} = {r_{\rm{r}}} = 0$ . 将(4 )—(6 )式代入(17 )式, 并通过分部积分法得到简谐点源的海底粗糙界面的反向散射声场, 将其描述为简正模态的叠加形式[11 ] ,2.2.浅海海底粗糙界面混响 -->2.2.浅海海底粗糙界面混响 实际上(18 )式是平坦波导环境中海底粗糙界面散射场的稳定解形式. 对于声源脉冲信号s (t ), 其功率谱$F\left( \omega \right)$ 满足Fourie变换s (t )的海底散射声场为$F\left( \omega \right)$ 和(18 )式代入(22 )式, 同时取水平波束在中心频率处的两阶泰勒级数展开, 进而得到脉宽为$\tau $ 声源信号s (t )的反向散射声场,t 0 是信号的传播时间, 与散射环的水平距离满足${t_0} \approx {{2r}/{{c_{\rm{H}}}}}$ .$\Delta r = {{{c_{\rm{H}}}\tau }/2}$ 的散射圆环, 其内径为${r_{{\rm{in}}}} = r - \displaystyle\frac{{{c_{\rm{H}}}\tau }}{4}$ , 外径为${r_{{\rm{ex}}}} = r + $ $ \displaystyle\frac{{{c_{\rm{H}}}\tau }}{4}$ . 对(23 )式计算强度, 并在散射环面积上进行积分得到海底粗糙界面混响平均强度$ {\rm{[}}u_{\rm{w}}^{s{\rm{(}}t{\rm{)}}}{\rm{]}}^* $ 是$u_{\rm{w}}^{s{\rm{(}}t{\rm{)}}}$ 的复共轭.24 )式进一步简化为23 )式代入(25 )式, 并假设脉宽远小于混响时间t , 将声源强度近似为${S^\eta }(2{k_0})$ 是海底界面的粗糙度谱, 与海底沉积层的地声参数无关, 只是声源频率的函数; $S_{mn}^\eta $ 是海底粗糙界面引起的入射模态和散射模态之间的耦合系数, 反映海底粗糙界面的反向散射能力, 由海底界面粗糙度谱和地声参数决定. 定义3.海底反射系数的三参数模型 尚尔昌在1979年提出了海底反射系数的三参数模型[17 ] , 随后给出了海底小掠射角的反射系数幅值和相移与掠射角之间的量化关系, 该参数与地声模型无关. 海底反射系数的幅值用Q 参数表示P 参数表示$\theta $ 是海底界面处入射声波的掠射角; Q 参数反映海底声吸收效果, 体现声能量的衰减; P 参数则描述各阶简正模态在海深处的能量, 即控制各阶简正模态的水平波数. 海底反射系数的相移参数P 与地声参数之间的转换关系满足[18 ,19 ] $\upsilon = {{{c_{\rm{b}}}}/{{c_{\rm{H}}}}}$ 表示沉积层介质和水介质的声速比; $\kappa $ 是密度比, 如(7 )式所示; $ \theta ^{*}$ 是临界掠射角.33 )式和(34 )式分别给出了不同海底掠射角时海底反射系数的相移参数的不同形式. ${P^{{\rm{Low}}}}$ 是甚小掠射角处的海底反射系数相移参数, 是海底沉积层和水介质的声速比和密度比的函数; ${P^{Crit}}$ 是临界角附近海底反射系数的相移参数, 是临界角的函数.Q 与地声参数之间的转换关系满足[18 ,19 ] $\alpha _b^{\left( w \right)}$ 是海底沉积层的声吸收系数, 单位是$dB/\lambda $ .$\upsilon $ 与临界掠射角之间满足36 )式代入(34 )式, 临界角附近的海底反射系数的相移参数${P^{Crit}}$ 与声速之间满足37 )式和(33 )式得到甚小掠射角的海底反射系数的相移参数${P^{Low}}$ 与密度之间满足关系式37 )式和(38 )式分别是海底反射系数的参数与等效的均匀半无限海底介质的地声参数之间的转换关系.4.海底粗糙界面反向散射模型 常用的经验散射模型如(39 )式所示:${\mu _{\rm{E}}}$ 是经验散射系数, 反映反向散射强度; $\theta $ 是入射掠射角; $\varphi $ 是散射掠射角. 当$l = k = 1$ , 是经验的Lambert散射模型. 该类型的散射模型是可分离的经验海底反向散射模型, 不可分离的经验散射模型(参见附录)也被用来描述海底反向散射.30 )式的海底反向散射模型是根据波导环境建立的散射模型, 明确了入射简正模态、散射简正模态以及海底地声参数对反向散射的强度特性和角度特性的影响. 浅海波导环境中简正模态是受格林函数严格约束的稳定解, 与海底沉积层的介质参数和水文环境有关. 在掠射角小于临界角的条件下, 忽略各阶简正模态的水平波数(掠射角)之间的差异, 即${k_m} \approx {k_n} \approx {k_{\rm{w}}}$ , 则(19 )式可以近似描述为与模态无关的量.37 )式和(38 )式代入(40 )式, 用海底反射系数的相移参数代替地声参数, 得到${P^{Low}}$ 和${P^{Crit}}$ 之间的差异, 文献[18 ]中也说明了这种近似的合理性.$P$ 决定了各阶简正模态在海底粗糙界面平均深度处的能量, 即41 )式和(43 )式代入(30 )式得到远距离(小掠射角)条件下的海底反向散射核函数,$\theta = {\theta _m}$ 为入射掠射角, $\varphi = {\theta _n}$ 为散射掠射角.$P$ 描述海底反射系数, 明确了海底对声散射的物理机理, 不同于经验反向散射模型.4.1.角度特性 4.1.角度特性 在远距离条件下, (44 )式表明, 海底反向散射的角度特性受海底反射系数的相移参数$P$ 的影响, 不同于经验散射模型. 在临界角附近,$\displaystyle\frac{{P\theta }}{2}$ 为宗量, 不能对$\sin \left(\displaystyle\frac{{P\theta }}{2}\right)$ 进行小角度近似, 所以在临界角附近, (44 )式所描述的反向散射模型随掠射角并不满足线性变化的关系.${{P\theta }/2} = 1$ 为分界点, 当${{P\theta }/2} < 1$ 时, 为甚小掠射角范围, 小角度近似引起的海底反向散射强度小于3 dB, 在实际应用中可忽略不计; 当${{P\theta }/2} > 1$ 时, 为临界角附近, 小角度近似使海底反向散射强度出现大于3 dB的误差, 实际应用中不可忽略. 所以, 在随后的分析中, 对反向散射模型的强度特性和角度特性进行分段处理.${{P\theta }/2} > 1$ , 即${2/P} < \theta < \theta *$ 时, (44 )式不能进行小角度近似, 其随角度的变化关系受P 参数加权.${{P\theta }/2} < 1$ , 即$\theta < {2/P}$ 时, 对(44 )式的角度项进行小角度近似,48 )式代入(44 )式得到39 )式的经验散射模型进行小角度近似得到$l = k = 2$ 时, 比较(51 )式和(49 )式具有相同的角度关系. 所以当掠射角$\theta < {2/P}$ 时, 基于物理散射机理的反向散射模型与$l = k = 2$ 的可分离经验散射模型具有一致的角度特性.4.2.强度特性 -->4.2.强度特性 通过4.1节的分析, 掠射角不同时, 海底反向散射的角度特性不同, 同时也反映了海底反向散射系数的差异.47 )式指出, 在临界角附近, 海底反向散射系数由海底反射系数的相移参数P 、海底界面粗糙度谱, 海深以及声源信号的频率决定. 忽略临界角附近以及甚小掠射角的P 参数之间的差异[18 ] , 则(42 )式中等式右边第三项相比前两项为小量, 可以忽略不计. 第二项中采用小角度近似,42 )式中的第二项近似与P 参数无关, 所以$ \varsigma (P) \approx 0.73 $ . 图2 也表明了$\varsigma (P)$ 随P 参数的变化不是很明显. 所以, 在临界角附近的海底反向散射系数近似与海底沉积层介质无关, 只是海底界面粗糙度谱、海深以及声源频率的函数.图 2 $\zeta $ 随P 参数的变化Figure2. $\zeta $ varied with P parameters near critical angle.50 )式. 结合$\varsigma (P)$ 近似为常数的结果, (50 )式可以近似为与${P^4}$ 成正比, 即图3 以第一类海底为例说明了这种近似结果的合理性. 图中给出了甚小掠射角的海底反向散射系数随$P$ 参数的变化曲线(仿真参数: 海深为50 m, 声源频率为600 Hz, 海底粗糙界面的标准差为$0.1\;{\rm{m}}$ , 相关尺度为${\rm{10}}\;{\rm{m}}$ , 计算得到Goff-Jordan谱[20 ] 为-32.8 dB)以及对其进行$P$ 参数的四次方拟合结果, 两者的变化趋势基本一致. 所以, 在甚小掠射角的条件下, 海底反向散射系数与海底反射系数的相移参数$P$ 密切相关, 即与海底沉积层的声速比和密度比有关, 与声吸收系数无关.图 3 海底甚小掠射角反向散射系数对P 参数的依赖Figure3. Relationship between P and bottom backscattering coefficient at very low grazing angle.图3 的仿真参数, 海底是第一类均匀半无限介质, 声速为$18{\rm{36}}\;{\rm{m/s}}$ , 密度为${\rm{2}}{\rm{.03}}\;{\rm{g/c}}{{\rm{m}}^{\rm{3}}}$ , 声吸收系数为$0.88\;{\rm{dB/}}\lambda $ , 海深为50 m, 水介质为1500 m/s的等声速剖面的均匀水体. 声源频率为600 Hz, 发射深度为10 m, 接收深度为30 m. 计算水平散射距离从5 km到50 km的混响平均强度衰减曲线. 图4中实线是根据(30 )式仿真的非近似混响平均强度衰减曲线; “○ ”是根据(46 )式和(53 )式仿真的临界角的近似结果, 与非近似的混响平均强度衰减曲线在13 km以前完全重合; 随着水平距离的增加, 两者相差逐渐增大; “$ \bullet $ ”是根据(49 )式和(54 )式仿真的甚小掠射角的近似结果, 在20 km以前, 与非近似结果之间的差异随水平距离的增大而减小, 在20 km以后两者基本吻合. 在散射距离较近时, 掠射角相对较大, 临界角附近近似的海底反向散射模型与真实结果更接近; 在散射距离较远时, 掠射角相对较小, 甚小掠射角的近似结果与真实结果更接近.图 4 海底反向散射模型的比较Figure4. Compare with bottom backscattering model with different approximate.5.结 论 在浅海混响平均强度模型中, 经验散射模型在混响特性分析中存在明显的局限性, 而现有的物理散射模型受地声模型的影响较大. 本文以全波动混响理论的物理散射模型为基础, 结合海底反射系数的三参数模型, 将海底反射系数的相移参数等效代替地声参数, 描述海底对声场的散射作用, 简化了海底反向散射模型. 通过理论分析, 明确了海底掠射角以${2/P}$ 为分界点, 海底反向散射的角度特性和强度特性对海底反射系数的相移参数存在不同的依赖关系. 在掠射角满足$\theta < {2/P}$ 时, 海底反向散射的角度特性近似描述为与可分离经验散射模型的角度特性一致, 与$P$ 参数无关; 而其散射系数则近似描述为与P 4 线性增强. 当海底掠射角满足${2/P} < \theta < \theta ^{*}$ 时, 海底反向散射的角度特性是受$P$ 参数加权的, 即受海底地声参数的影响; 而其散射系数则近似为与$P$ 参数无关. 所以不同掠射角范围, 海底对反向散射声场的强度特性和角度特性的贡献不同. 掠射角较大时海底对反向散射声场的影响主要体现在其角度特性; 掠射角非常小时, 海底的影响主要体现在其强度特性.${\mu _{\rm{E}}}$ 是海底反向散射系数; $l,k$ 取不同的值对应不同的散射模型. 常见的Lambert散射模型则是(A1 )式中$l = k = 1$ 时的散射模型. 该模型最初是Mackenzie[1 ] 在处理深海海底混响模型时由光学的散射原理引入, 给出经验的海底反向散射模型, 随后根据实验数据与理论结果对比得到${\mu _{\rm{E}}}$ 的分贝值大约在-27 dB左右, 也就是说${\mu _{\rm{E}}} \approx {10^{ - 2.7}}$ . 当$l = 1,k = 0$ 表示散射源强正比于$\mu {\rm{sin}}\theta $ 的均匀散射; 当$l = 0,k = 0$ 表示与角度无关的均匀散射; 同时也存在$l = k = 2$ 的反向散射模型. 








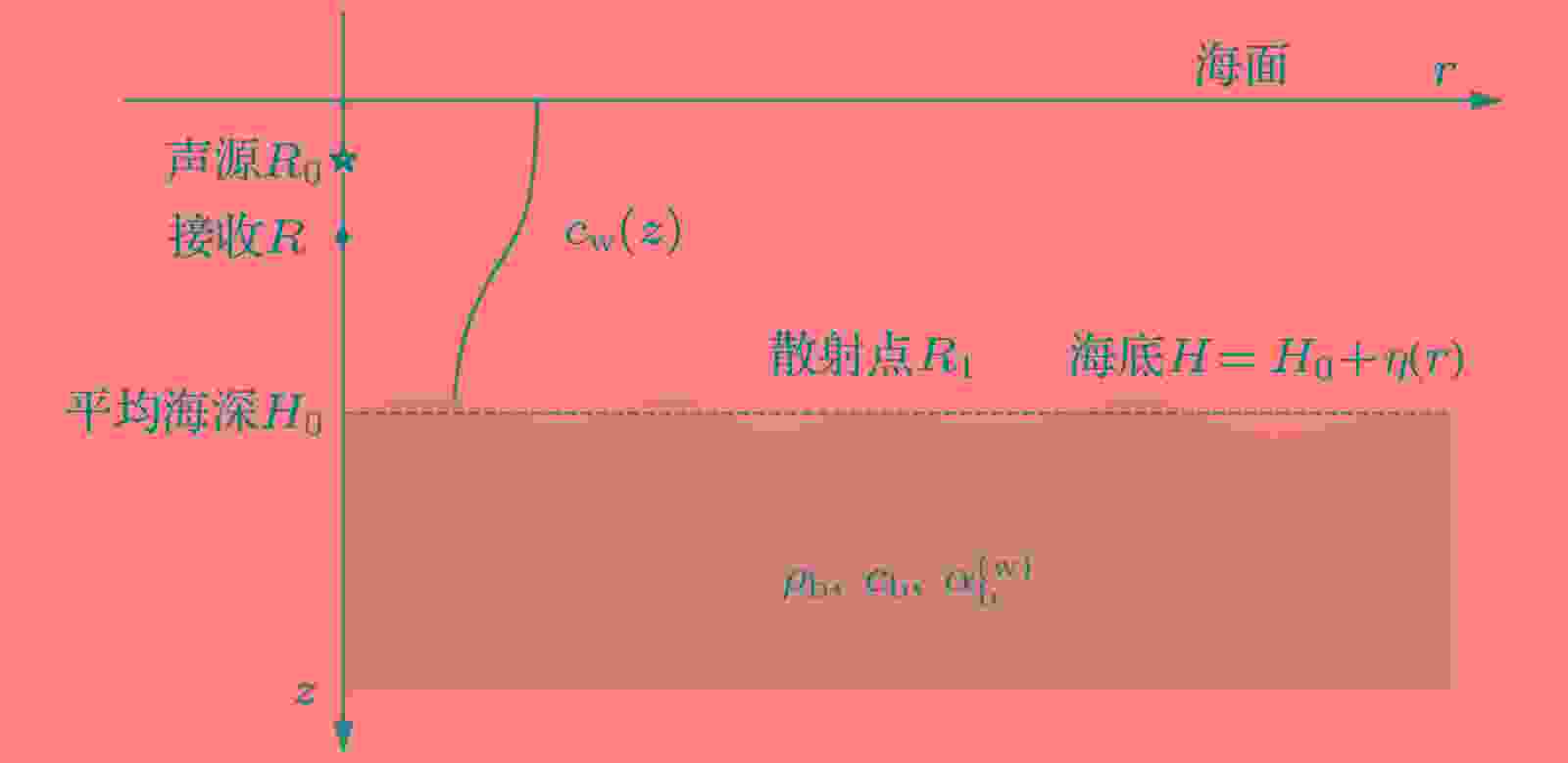 图 1 浅海波导环境
图 1 浅海波导环境






















































































 图 2
图 2 














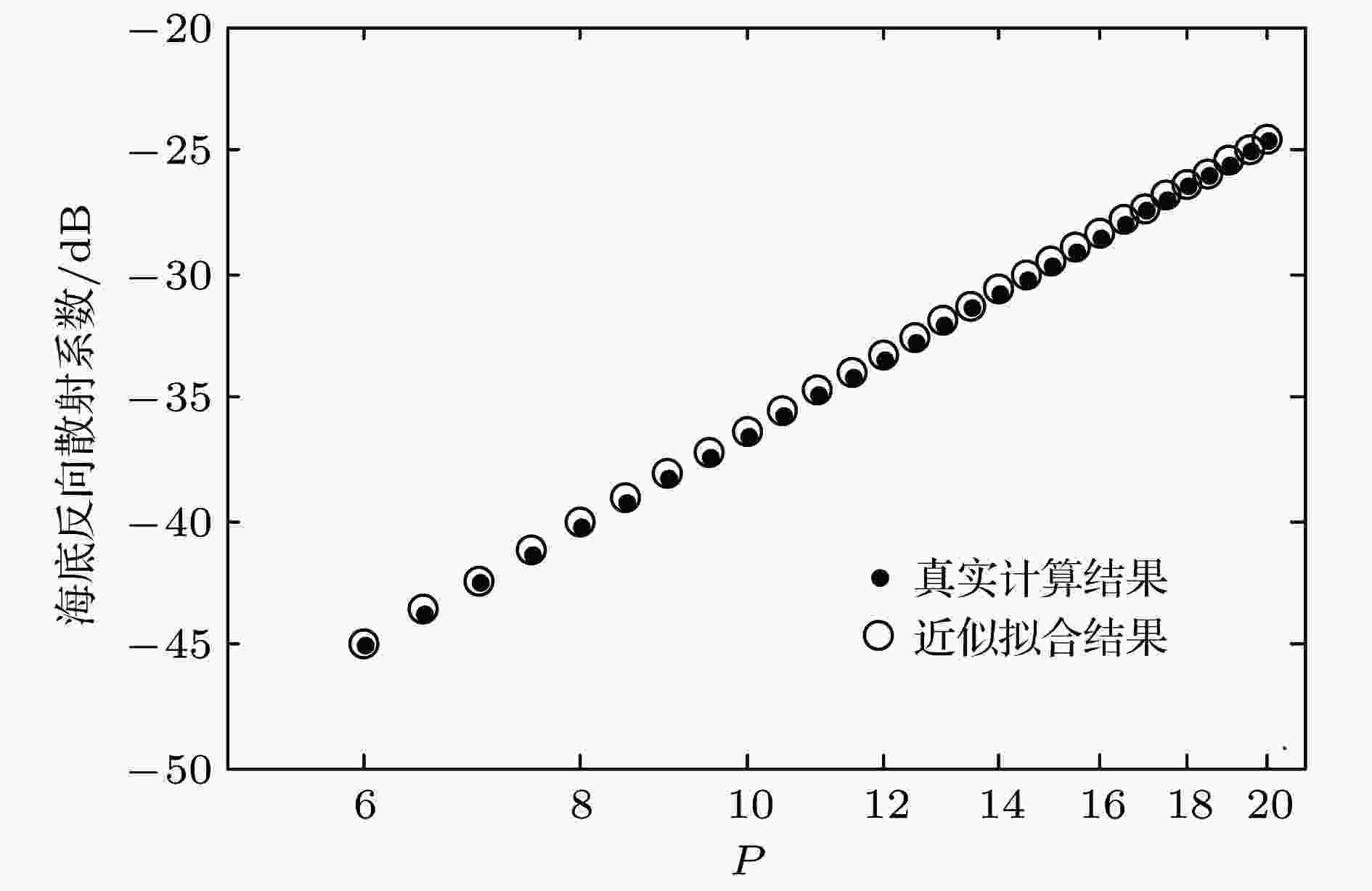 图 3 海底甚小掠射角反向散射系数对P参数的依赖
图 3 海底甚小掠射角反向散射系数对P参数的依赖



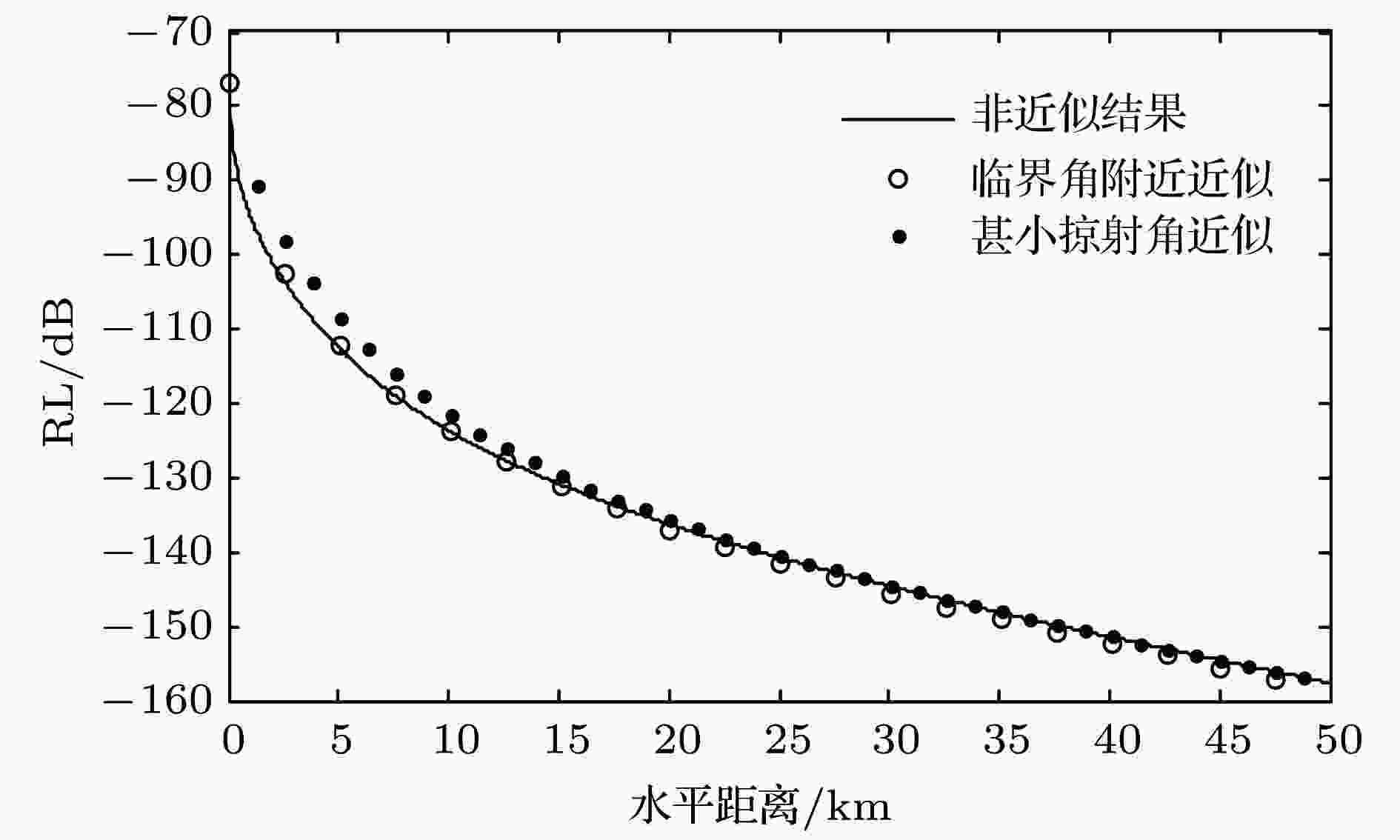 图 4 海底反向散射模型的比较
图 4 海底反向散射模型的比较






















