 , 白先勇1,2,3, 冯志伟1,2,4, 王东光1,2,3, 邓元勇1,2,3
, 白先勇1,2,3, 冯志伟1,2,4, 王东光1,2,3, 邓元勇1,2,3 1. 中国科学院 国家天文台, 北京 100101;
2. 中国科学院大学, 北京 100049;
3. 中国科学院 太阳活动重点实验室, 北京 100101;
4. 中国科学院 天文光学重点实验室, 北京 100101
2019-10-22 收稿, 2019-11-20 录用
基金项目: 国家自然科学基金(11973061,11873062,11673038)和国家重大科研仪器研制项目〈部门推荐〉(11427901)资助
*通讯作者: 张志勇
摘要: 为应对大口径天文望远镜因结构弯沉和形变导致的次镜姿态失调、系统像质退化等问题,本文提出了采用小口径平行光源构造人工星点,配合夏克哈特曼波前传感器,利用局部口径波前探测获得局部波像差信息以计算次镜失调量,并结合精密六足位移平台实现次镜姿态实时校正的方法。本文基于目前正在研制中的1 m口径离轴格里高利太阳望远镜实际参数,采用光学软件模拟和数学仿真方法,分析了局部口径的波前探测可行性。仿真结果表明,当选取局部口径直径为200 mm、波前传感器像点质心偏移探测精度达到0.01 μm时,即可有效提取波像差信息,以此计算次镜姿态并加以校正,可满足望远镜光学系统像差要求。
关键词: 大口径太阳望远镜次镜失调波前畸变夏克哈特曼波前传感器仿真分析
An Alignment Strategy for Secondary Mirror of Large Aperture Solar Telescope Based on Wavefront Detection of Sub-aperture
XUN Hui1,2,3, ZHANG Zhiyong1,2,3
 , BAI Xianyong1,2,3, FENG Zhiwei1,2,4, WANG Dongguang1,2,3, DENG Yuanyong1,2,3
, BAI Xianyong1,2,3, FENG Zhiwei1,2,4, WANG Dongguang1,2,3, DENG Yuanyong1,2,3 1. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, P. R. China;
2. University of Chinese Academy of Sciences, Beijing 100049, P. R. China;
3. Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, P. R. China;
4. Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, P. R. China
Abstract: In order to cope with the problem of secondary mirror misalignment due to structural deflection and deformation of the large aperture telescope and the degradation of the image quality, we came up with a strategy that collimated light is proposed to construct artificial star points, and the Shark Hartman wavefront sensor is used to detect wavefront of sub-aperture. We use local distorted wavefront to calculate the secondary mirror misalignment and combine the precise hexapods to realize the real-time correction. Based on the actual parameters of the 1 m aperture off-axis Gregory solar telescope under development, the optical software simulation and mathematical simulation methods are used to analyze the feasibility of wavefront detection of sub-aperture. The simulation results show that when the local aperture of 200 mm is selected and the detection accuracy of the centroid offset reaches 0.01 μm, the wave aberration information can be extracted effectively, so that the telescope meets optical quality after the real-time correction.
Key words: large solar telescopesecondary lens misalignmentdistorted wavefrontShark-Hartman wavefront sensorsimulation analysis
追求更高分辨率是建造大口径天文望远镜的主要目标之一,然而随着口径增大,望远镜的桁架结构也越来越庞大。在望远镜不同指向过程中,由桁架弯沉和形变所产生的次镜相对于主镜的姿态变化,将导致像质退化,从而无法达到设计的分辨率。以目前正在研制中的“用于太阳磁场精确测量的中红外观测系统”(An infrared system for the accurate measurement of solar magnetic field, AIMS)望远镜为例,该望远镜为通光口径1 m的离轴格里高利系统,因采用了离轴光学系统,其桁架结构设计重量达到约6.8 t。根据AIMS望远镜设计公差要求,次镜相对于主镜平移量小于2.5 μm,倾斜量小于2″。然而在力热耦合有限元分析中发现,望远镜在对太阳进行跟踪观测的过程中,桁架因重力和温度等因素,次镜相对于主镜所产生的平移量达到数十微米,倾斜量达到3″,远超出望远镜公差范围,将严重影响光学系统的成像质量。
这种因结构形变所致的像质退化几乎是地基大型望远镜不可避免的共性问题。目前应对这种结构形变,通常的解决方法是采用夏克哈特曼波前传感器[1](Shack-Hartman wavefront sensor, S-H WFS)探测系统的波前像差,计算次镜相对于主镜姿态的失调量,然后采用精密多维位移台作用于次镜予以补偿。目前美国大熊湖1.6 m GST望远镜[2]、德国1.5 m GREGOR望远镜[3],以及正在建设中的4 m DKIST望远镜[4]均采用类似方案。然而对于太阳观测而言,波前探测技术面临两个方面的困难:首先是受限于白天较差的大气视宁度条件,大气扰动将导致图像的高频随机抖动,会降低提取次镜姿态变化信息的灵敏度和可靠性。其次,太阳是面源,在进行波前探测时,需要以一定视场内的日面特征作为信标进行相关计算。但当太阳表面没有黑子、暗条、谱斑等较高对比度的活动区时,基于相关算法的扩展目标波前探测会有较大的困难[5, 6]。在太阳活动极小年阶段,日面没有明显活动区的情况通常会持续数月之久,这对太阳宁静区的观测研究极为不利。因此目前的方法还存在一定的局限性,应用效果并不令人满意。
针对上述的困难,我们创新性提出利用小口径平行光源构造人工星点,基于局部口径波前探测,实时校正望远镜次镜姿态的方法。因为望远镜主次镜面型由其机械结构和主动光学设计来保证,所以由面型变化导致的波前畸变通常忽略不计。而光学系统局部口径波前是全口径波前的子集,所以由次镜姿态失调导致的波前畸变信息亦包含在局部口径波前中。这种方法优势在于:其一,平行光源靠近望远镜入瞳入射,空气链路短,大气扰动对波前探测影响相对较小;其二,利用人工星点进行波前探测,可以不依赖低对比度面源的互相关计算,计算速度更快,准确性更高。
本文基于正在研制中的AIMS望远镜的实际参数,采用光学设计软件模拟和数学仿真协同分析的方法,建立了基于局部口径波前探测计算的次镜姿态校正量计算模型,验证了计算模型的正确性和该方法的可行性。本文研究可以为AIMS望远镜及未来大口径望远镜次镜姿态校正提供有效的数据支持。
1 局部口径次镜姿态校正方法及原理1.1 次镜姿态校正方法局部口径波前探测方法如图 1所示,采用小口径平行光源构造人工星点,使其入射方向平行于望远镜主光线方向,且其出瞳靠近望远镜入瞳,入射望远镜的局部区域。在望远镜的焦面后设计准直光路,与波前传感器的参数相匹配,并在光路中放置对应波段的窄带滤光片。平行光源安装于精密平移装置上,可在进行校正时切入光路,校正结束后移出光路。次镜安装于精密六足位移平台上,实现姿态精密补偿。在进行校正时,移入折轴反射镜M3,将光路切换至检测光路。由主控计算机对获得的波前数据进行计算,并驱动精密六足位移平台进行补偿,以达到像质要求。
图 1
 | 图 1 基于局部口径波前探测次镜姿态校正方法示意图 1.主镜;2.次镜;3.望远镜入瞳位置;4.六轴位移台;5.平行光源;6.太阳入射光线;7.检测光线;8.折轴反射镜;9.视场光阑;10.准直镜组;11.窄带滤光片;12.波前传感器;13.主控计算机 |
1.2 原理1.2.1 波前探测在实际天文望远镜光学系统中,通常使用波前传感器探测波前信息,波前函数W通常表示为Zernike多项式[7]之和:
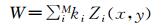 | (1) |
波前探测原理是:当标准平面波前入射微透镜阵列后,会形成一组分布规则的标准点阵,而当入射波前发生畸变时所成点阵会相对于标准点阵产生偏移,该偏移量对应各子单元波前的斜率。经过质心算法获得每个子单元像点偏移量,依据归一化算法将各个参数统一到待测系统坐标系,进一步可计算出光瞳面波前各个子单元对应的波前斜率[8]:
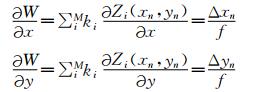 | (2) |
根据每个子单元的斜率(2)式建立超定方程组(3)式,再通过相应的算法[9]求解最小二乘解,即可得Zernike系数ki,最终得到重构的波前函数。
 | (3) |
1.2.2 基于灵敏度矩阵法的失调量计算光学系统中光学元件的位置参数偏离设计理想值将会引入波像差,因而这种波像差可以表示为元件位置参数的函数。由于失调量主要导致初级像差,而高级像差的变化相对于初级像差较小,因此光学失调量校正时基于初级像差信息,主要控制初级球差、彗差和像散。Zernike系数可以与常用的Seidel像差系数建立联系,系数k2~k9代表初级像差,其中k4代表离焦,k5代表 0°或90°方向的像散,k6代表 45°方向的像散,k7代表X方向的彗差,k8代表Y方向的彗差,k9代表球差,所以用于计算校正量的Zernike系数选取k2~k9。
基于灵敏度矩阵法[10, 11],在失调量很小的情况下,光学系统的像差和失调量近似为线性关系。建立光学系统失调量与系统像差系数(Zernike系数)的关系,可获得灵敏度矩阵A。将光学元件沿x、y、z轴平移记为X、Y、Z,绕x、y轴旋转记为U、V。将望远镜初始设计状态记为理想波前,其Zernike系数设为Kinitial。当望远镜次镜姿态失调后,畸变波前Zernike系数为K,Zernike系数变化量为:
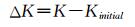 | (4) |
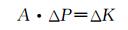 | (5) |
求解方程组(5)可得失调量ΔP,再输入精密六足位移平台以补偿望远镜光学系统次镜姿态失调。因此校正望远镜次镜姿态失调的步骤如下:
1) 由波前传感器探测获得点偏移量信息;
2) 经波前重构获得代表波像差的Zernike系数;
3) 采用灵敏度矩阵计算出导致像差的次镜姿态失调量;
4) 将数据输入精密六足位移平台,校正望远镜次镜姿态。
2 基于AIMS望远镜实际参数的仿真分析2.1 局部口径选取我们以正在研制中的1 m口径的AIMS望远镜主次镜光学系统为对象进行仿真分析,计算波前探测的灵敏度和精度需求,以验证基于局部口径波前探测校正次镜姿态的方法和应用于大口径太阳望远镜的可行性。AIMS望远镜为离轴格里高利系统,光路如图 2所示,主镜为离轴抛物镜,次镜为离轴椭球镜,系统等效焦距为10 m。
图 2
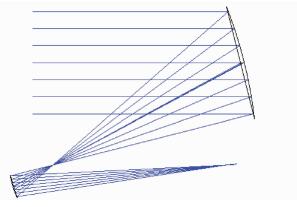 | 图 2 AIMS望远镜光学系统 |
在ZEMAX软件中,分别选取直径为150、200和250 mm的局部口径区域进行光学追迹,如图 3所示。根据次镜位置公差表(见表 1),模拟次镜单个姿态公差失调量,波前畸变如表 2所示,其中λ=633 nm。由数据可见,在相同的望远镜次镜姿态失调量下,局部口径的波前畸变程度明显低于全口径,其数值近似于两者口径之比,即表明利用局部波前探测需要更高的探测精度和灵敏度。当次镜沿Z轴方向位移1.5 μm时,产生最小的波前畸变,200 mm局部口径的波前PV为0.071λ,约为λ/14。从数值上看,该畸变量仍在现有波前传感器的精度范围之内(通常能达到PV为λ/20)。因此结合性能参数和重量体积等实际因素综合考虑,我们选择200 mm局部口径区域进行波前探测。
图 3
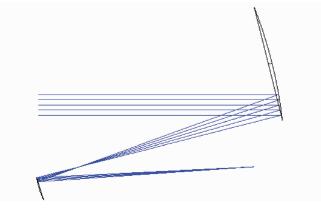 | 图 3 局部口径波前探测光路 |
表1
| 表 1 AIMS次镜M2位置公差表 |
表2
| 表 2 入射畸变波前PV模拟结果 |
2.2 计算模型及结果采用光学设计软件模拟和数学仿真协同分析的方法建立计算模型,流程如图 4所示。
图 4
 | 图 4 计算仿真流程 |
第一步,利用ZEMAX软件模拟局部口径的波前畸变。不失一般性,我们随机产生一组失调量(表 3),针对AIMS望远镜200 mm局部口径进行波前探测模拟,可得理论畸变波前Wd的PV=0.1845λ,RMS=0.0436λ,Zernike系数如表 4所示。
表3
| 表 3 次镜随机施加失调量 |
表4
| 表 4 理论入射畸变波前Zernike系数 |
第二步,利用MATLAB仿真模拟波前传感器点阵坐标。我们选择口径为5 mm的波前传感器,微透镜阵列为10×10排布,每个子单元口径为0.5 mm,焦距为15 mm,其中有效子单元数76个。根据(2)式对理论入射畸变波前函数Wd求偏导数,可以模拟畸变波前在波前传感器每个子单元像点的理论偏移量;而后,利用理论点阵偏移量数据,分别模拟0.1、0.01和0.001 μm的点阵质心计算精度模型,以模拟获得不同测量误差条件下的点偏移量;最后由上述误差条件下的点偏移量,利用波前重构算法计算畸变波前Zernike系数。
第三步,基于失调灵敏度矩阵模型,根据上述波前重构的畸变波前Zernike系数,计算望远镜次镜姿态失调量,即为校正量。以此补偿已知施加的失调量得到校正后的望远镜次镜位置,以及校正后整个望远镜系统的波像差,如表 5所示。分析校正后的望远镜次镜位置和主次镜光学系统波像差是否满足要求,并分析像点偏移测量精度与校正量计算误差间的作用规律。
表5
| 表 5 模拟计算校正结果 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
根据模拟不同的精度模型可知,模拟测量点阵偏移量精度越高,次镜姿态失调量的计算越准确,残差越小。当点阵质心计算精度优于0.01 μm时,失调次镜经过校正后的次镜位置满足公差要求,表明当波前探测精度较高时,局部波前探测可以有效提取望远镜光学系统的像差信息,并且可以准确地计算出导致波前畸变的次镜姿态失调量。因为根据目前波前传感器产品水平和现有质心算法精度,点偏移量测量精度通常能达到上述精度要求,所以基于局部波前探测实时校正次镜的方法可行。
3 结论本文基于望远镜局部口径波前探测方法计算次镜姿态失调量,采用光学设计软件模拟和数学仿真协同分析的方法研究了局部口径波前探测的灵敏度和可行性。根据AIMS望远镜实际参数的仿真结果表明,当选取直径为200 mm局部口径、波前传感器像点质心偏移探测精度达到0.01 μm时,即几百分之一像素,即可有效提取波像差信息,以此计算次镜姿态失调量并加以校正,可满足望远镜光学系统像差要求。本文研究成果为下一步实验研究提供数据保障,也将为AIMS望远镜以及未来大口径太阳望远镜研制提供技术参考。
参考文献
| [1] | Platt B C, Shack R V. History and principles of Shack-Hartmann wavefront sensing[J]. Journal of Refractive Surgery, 2001, 17(5): 573-577. DOI:10.3928/1081-597X-20010901-13 |
| [2] | Cao W, Gorceix N, Coulter R, et al. Scientific instrumentation for the 1.6 m new solar telescope in Big Bear[J]. Astronomische Nachrichten, 2010, 331(6): 636-639. DOI:10.1002/asna.201011390 |
| [3] | Berkefeld T, Schmidt D, Soltau D, et al. The GREGOR adaptive optics system[J]. Astronomische Nachrichten, 2012, 333(9): 863-871. DOI:10.1002/asna.201211739 |
| [4] | Upton R. Optical control of the advanced technology solar telescope[J]. Applied Optics, 2006, 45(23): 5881-96. DOI:10.1364/AO.45.005881 |
| [5] | 饶长辉, 张学军, 姜文汉. 太阳米粒结构相关哈特曼-夏克波前传感模拟研究[J]. 光学学报, 2002, 22(3): 285-289. Rao C H, Zhang X J, Jiang W H. Simulation study on correlating Hartmann-Shack Wavefront sensor for solar granulation[J]. Acta Optica Sinica, 2002, 22(3): 285-289. DOI:10.3321/j.issn:0253-2239.2002.03.007 |
| [6] | 饶长辉, 姜文汉, 凌宁, 等. 太阳表面米粒结构观测对比度分析[J]. 天文学报, 2001, 42(2): 134-139. Rao C H, Jiang W H, Ling N, et al. Analysis of the observed R.M.S. contrast in solar granulation[J]. Acta Astronomica Sinica, 2001, 42(2): 134-139. DOI:10.3321/j.issn:0001-5245.2001.02.004 |
| [7] | Noll R J. Zernike polynomials and atmospheric turbulence[J]. Journal of the Optical Society of America, 1976, 66(3): 207-211. DOI:10.1364/JOSA.66.000207 |
| [8] | Lane R G, Tallon M. Wave-front reconstruction using a Shack-Hartmann sensor[J]. Applied Optics, 1992, 31(32): 6902-6908. DOI:10.1364/AO.31.006902 |
| [9] | Qi B, Chen H, Dong N. Wavefront fitting of interferogram with Zernike polynomials[J]. Optical Engineering, 2002, 41(7): 1565-1569. DOI:10.1117/1.1481726 |
| [10] | 杨晓飞, 张晓辉, 韩昌元. Zemax软件在离轴三反射镜系统计算机辅助装调中的应用[J]. 光学精密工程, 2004, 12(3): 270-274. Yang X F, Zhang X H, Han C Y. Application of Zemax software in alignment of three-mirror off-axis aspherical optical system[J]. Optics and Precision Engineering, 2004, 12(3): 270-274. DOI:10.3321/j.issn:1004-924X.2004.03.005 |
| [11] | 巩盾, 田铁印, 王红. 利用Zernike系数对离轴三反射系统进行计算机辅助装调[J]. 光学精密工程, 2010, 18(8): 1754-1759. Gong D, Tian T Y, Wang H. Computer-aided alignment of off-axis three-mirror system by using Zernike coefficients[J]. Optics and Precision Engineering, 2010, 18(8): 1754-1759. |
