
 , 张丰收
, 张丰收 河南科技大学 医学技术与工程学院, 河南 洛阳 471000
2019-05-16 收稿, 2019-06-05 录用
基金项目: 国家科技部专项(2017YFB0306401)资助
*通讯作者: 宋卫东, E-mail: 496979605@qq.com
摘要: 锥束CT具有成像质量高、低辐射、操作简单等优点,近几年得到迅速发展。锥束CT几何参数的精确获取是得到高质量图像的关键因素。针对FDK算法要求的条件以及现有的几何参数获取方法,本文提出了一种基于四椭圆快速获取全参数的方法。首先介绍了锥束CT中的关键参数,然后提出了四椭圆全参数获取原理并设计出通用标定模体。本标定模体可用于任何锥角不同的锥束CT系统。通过标定模体在空间的几何关系获取系统中所有几何参数。最后针对该方法进行了实验论证,结果表明,本方法获取的几何参数精度高。综上所述,可证实该算法具有一定的工程实用价值。
关键词: 锥束CT数学模型几何参数标定模体
Study on Four-elliptic Method of Cone Beam X-CT System to Obtain Full Geometric Parameters
ZHANG Zhen, SONG Weidong

 , ZHANG Fengshou
, ZHANG Fengshou School of Medical Technology and Engineering, Henan University of Science and Technology, Luoyang 471000, Henan, P. R. China
*Corresponding author: SONG Weidong, E-mail: 496979605@qq.com
Abstract: Cone beam CT has the advantages of high image quality, low radiation, and simple operation. It has developed rapidly in recent years. Accurate acquisition of geometric parameters of cone beam CT is a key factor in obtaining high quality images. Aiming at the conditions required by the FDK algorithm and the methods of acquiring geometric parameters, this paper proposes a method for quickly obtaining full parameters based on four ellipse. Firstly, the key parameters of cone beam CT are introduced. Then the principle of four ellipse full parameter acquisition is proposed and the universal calibration mode is designed. The calibration phantom can be used in any cone beam CT system with different cone angles. Accurately acquire all geometric parameters in the system by calibrating the geometric relationship of the phantom in space. Finally, the experimental demonstration is carried out for the method. The experimental results show that the geometric parameters obtained by this method have high precision, and the algorithm has certain engineering practical value.
Key words: cone beam CTmathematical modelgeometric parameterscalibration phantom
锥束X-CT系统相比传统CT系统有许多优点,随其不断发展,在医学成像和工业无损检测中占据着重要地位。其成像质量受制于安装误差,安装误差如果不加以校正,会引起重建图像出现环形伪影[1],所以对锥束X-CT系统进行几何参数标定是很有必要的。近年来各种标定方法层出不穷,其中Sun和侯颖等[2, 3]设计了一个钻有4个小孔的金属板作为校准模板, 并通过在一个投影角度下得到投影数据,利用解析法得出相关参数。此方法前提是需要将模板摆放到旋转台的中心位置,有一定的精度要求。刘晓鹏等[4]提出了利用细琴弦和带豁口的钢尺得到几何参数。Meng[5]和Yang等[6]提出了无模体标定的方法,陈炼等[7]提出了利用一个简单的校正模型得到少量的投影,计算出几何参数的方法,此方法在计算之前运用了一定的假设。李晓晴等[8]提出了平行双丝法来获取几何参数,此方法虽然模体制造简单、计算速度较快,但是此模体求得的参数不全,而且在计算参数时默认探测器无倾斜角和扭转角,实际安装中难以实现。王珏等[9]在点模型求解方法上进行了改进,有效降低了在求解几何参数时对标定模体安装精度的要求。黄秋红等[10]研究了在不考虑成像系统畸变的情况下,静态系统射线源阵列的几何参数标定方法。杨帅和周凌宏等[11, 12]分别从图像质量以及成像系统方面研究几何参数标定方法,杨帅等人提出的方法比较耗时,周凌宏等人提出的方法对标定环境因素要求较高。
1 锥束CT系统扫描结构及其关键几何参数定义锥束CT系统的扫描结构如图 1所示,左侧O-XYZ坐标系为平板探测器,中间A-MNL坐标系为待检测物体,右侧S为射线源。将探测器中间行和中间列相交的焦点定义为中心,用右手法则建立O-XYZ坐标系,以转轴为L轴建立A-MNL坐标系,L轴为旋转中心轴。S(sx, sy, sz)定义为射线源焦点的坐标,并定义S在探测器上的投影坐标为P(px, O, pz)。DAO为探测器到旋转中心的距离,DSA为旋转中心到射线源的距离,DSO为射线源到探测器的距离。并且存在射线源主射线SO与旋转轴垂直。理想状态下,投影坐标P(px, O, pz)在O-XYZ坐标系的原点上。主射线SO是L轴和Z轴的公垂线,探测器不存在任何的绕X轴倾斜、绕Z轴扭转以及在XOY平面上的旋转。但是由于安装误差不可避免,制造误差也会导致出现探测器倾斜、扭转以及射线源焦点投影不在探测器中心等情况,这样会造成重建结果出现伪影,直接影响重建结果的精确度。如图 2所示,定义α角为探测器绕Z轴旋转的角度,β角为绕X轴旋转的角度,γ角为探测器在XOZ面旋转的角度,ΔX为探测器在X轴方向的误差,ΔZ为探测器在Z轴上的误差,需要求得的参数为DSA、DSO、DAO、α、β、γ、ΔX、ΔZ。
图 1
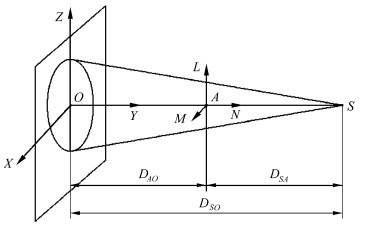 | 图 1 锥束CT系统结构图及其相关几何参数 Cone beam CT system structure diagram and the related geometric parameters |
图 2
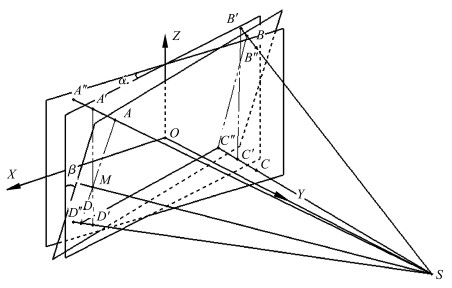 | 图 2 探测器安装误差示意图 Detector installation error |
2 四椭圆法基本原理本文中提出的方法是基于圆轨道扫描为假设前提,其使用的标定模体如图 3所示,需要两个有机玻璃管(2),每个有机玻璃管内包含两个直径为2 mm的小钢珠(1)。由于2个有机玻璃管内各有两个小钢珠,钢珠的运动轨迹为4个椭圆,故称为四椭圆法。在设计时,标定模体的2个有机玻璃管应尽量保证与旋转平台垂直,因为其垂直度会影响成像的质量,如果误差较大,会导致计算所得参数误差增大。为保证垂直度要求,文中标定模体设有2个有机玻璃管的固定底座,底座上有2个和有机玻璃管外直径相等的装配孔,装配孔采用基轴制加工,以保证玻璃管与固定底座的垂直度。其次应保证固定底座的平面度,平面度可以用机加工设备来保证。其中一个有机玻璃球管远离旋转中心,另外一个有机玻璃球管离旋转中心距离较近,旋转中心与两有机玻璃球管三者构成不等边三角形,且4个小钢珠中有2个为固定,另外2个为可调节钢珠,适用于任意锥束角不同的锥束CT系统的参数标定。四椭圆法获取全参数的基本思想为:将制成的标定模体放在待测物体转台上,首先把标定模体上2个有机玻璃管旋转到主射线的任意一侧,固定钢珠一端靠近射线源,调节可调节钢珠位置,使4个钢珠在探测器上的投影为2个点,并保证2个有机玻璃管与转台平面垂直,转台旋转一周,获取标定模体360°投影图像,然后对投影图像进行数据处理,计算出需要得到的各个标定参数。
图 3
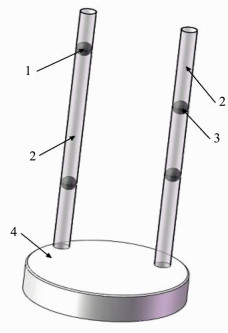 | 图 3 锥束CT系统标定体模三维模型 1.可调节小钢珠,2.有机玻璃管,3.固定钢珠,4.固定底座 Cone beam CT system calibration phantom three-dimensional model 1. Adjustable small steel ball, 2. plexiglass tube, 3. fixed steel ball, 4. fixed base |
2.1 探测器投影视图参数预处理根据锥束CT系统中各参数敏感度,本文方法先计算ΔX、DSO,以减少成像误差。在操作过程中,将调整好的标定模体放在转台平面上,并让有机玻璃与旋转轴平行。旋转一周,可得到4个小钢珠的运动轨迹。在理想状态下,探测器成像轨迹为4个规则的椭圆,但是由于安装误差,会出现轨迹倾斜的情况。如图 4所示,在理想探测器的条件下ABCD四点组成的四边形应该为矩形,而在实际过程中,ABCD四点组成的为不规则四边形。根据小球的投影轨迹可以拟合出4个椭圆参数,在投影过程中,间隔180°的两质点坐标确定一条直线,所有的直线必相交于一点,这样就可以建立一个方程组,用最小二乘法求出方程组的解,即椭圆的中心记为(u, v)。然后拟合椭圆,并用来计算椭圆参数。假设一组椭圆质心坐标记为(ui, vj),那么由这组投影点即可得到一个椭圆方程:
 | (1) |
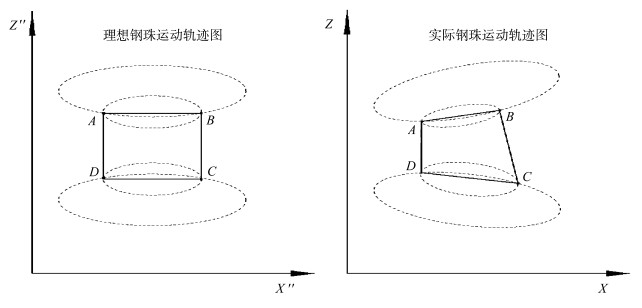 | 图 4 理想探测器与实际探测器投影轨迹示意图 Schematic diagram of the projected path of the ideal detector and the actual detector |
其中,椭圆参数a、b、c、u、v均可通过(ui, vj)拟合出来。一共4组数据,可以得到4个不同的轨迹方程,2个轨迹方程联立可解出A(xa, za)、B(xb, zb)、C(xc, zc)、D(xd, zd)四点的坐标。可以得到:
直线AB的长度lAB:
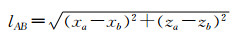 | (2) |
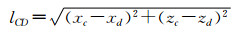 | (3) |
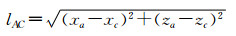 | (4) |
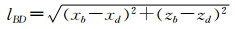 | (5) |
图 5
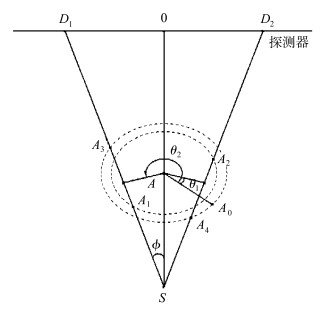 | 图 5 px和Dso的计算模型示意图 Schematic diagram of the calculation model of px and Dso |
过旋转中心A分别做SD1和SD2的垂线,则几何关系可得:
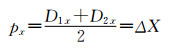 | (6) |
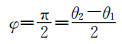 | (7) |
则射线源到平板探测器的距离:
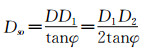 | (8) |
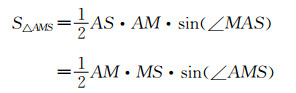 | (9) |
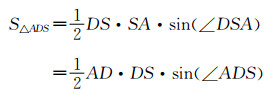 | (10) |
 | 图 6 ADS面视图 View(seen from ADS) |
由式(9)和式(10)相除可得到:
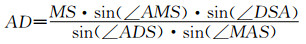 | (11) |
其中,∠S可由标定模体中4个小钢珠位置相对关系求出,AD为已知。
图 7为俯视图,过M点做ME垂直于SO并交SO于E。在图 7中可得如下几何关系:
 | (12) |
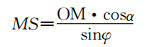 | (13) |
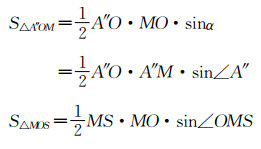 | (14) |
 | (15) |
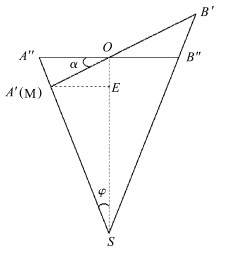 | 图 7 α角计算示意图 Schematic diagram of α angle solution |
由式(14)和式(15)相除可得到:
 | (16) |
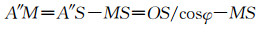 | (17) |
2.4 探测器在ZOX平面内旋转γ角的计算方法γ角为探测器在ZOY平面内的旋转角,在本方法所用的模体中,模体旋转一周,得到运动模体运动轨迹参数。在探测器绕p点旋转γ角度时,投影图像如图 8所示。实线表示实际投影图形,虚线表示理想投影图形。J、K点分别为上下椭圆的中心为已知,则可由J、K点坐标求得γ角。
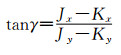 | (18) |
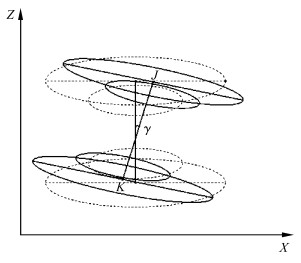 | 图 8 γ角计算示意图 Schematic diagram of γ angle solution |
2.5 射线源到旋转中心的距离DSA及旋转中心到探测器的距离DAO计算方法在旋转过程中,标定体模4个小球所确定的平面存在总是两次与锥束主射线垂直,小球在探测器上的投影总存在以下几何关系,如图 9所示。
图 9
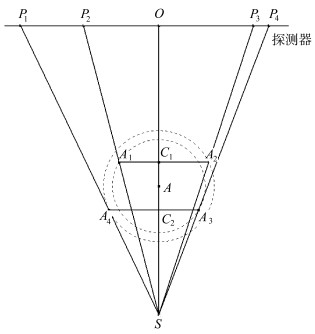 | 图 9 DSA计算模型示意图 Schematic diagram of the calculation model of DSA |
直线A1A2表示在第一次4个小球确定的平面与折射线垂直时的情况,直线A4A3表示第二次4个小球确定的平面与折射线垂直时的情况。两个小球之间的法向距离为d,其测量实现方法为已知钢珠球的直径为a mm,有机玻璃管壁厚b mm。采用数码游标卡尺多次测量2个玻璃管外壁之间的距离,记录测量次数和每次测量值,最后求取平均值x,则d=x-a-2b。OA2=R,OA2=r,则由相似三角形定理可得:
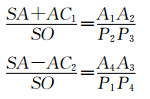 | (19) |
 | (20) |
图 10
 | 图 10 ΔZ计算模型示意图 Schematic diagram of the calculation model of ΔZ |
Z为旋转中心A在探测器的投影点,C点为过A点到直线SD1的垂足点,根据上图几何关系可知:△SAC≈△SD1Z。
 | (21) |
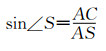 | (22) |
 | (23) |
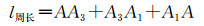 | (24) |
 | (25) |
 | (26) |
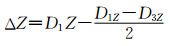 | (27) |
3.1 具体实验操作方案1) 把标定模体垂直放置在旋转台上,旋转一定角度,使两个有机玻璃管位于主射线的同一侧,固定位置钢珠所在的有机玻璃管靠近X射线源一侧,然后调整标定模体,使两个不同有机玻璃管内的小钢珠投影重合。标定体模调整结束,开始标定。
2) 使旋转台顺时针和逆时针旋转一周,得到4个小球的运动轨迹。根据文中提到的计算方法拟合椭圆参数方程,并计算出4个相应的交点坐标。
3) 记录旋转台旋转到两次投影重合时的角度,计算相应的ΔX和射线源到探测器之间的距离DSO。
4) 根据文中计算α、β、γ的方法,计算出结果,并校准α、β、γ的角度。
5) 记录4个小钢珠所在的平面与探测器平行时,标定体模上4个小钢珠的投影横坐标,并计算射线源到旋转中心的距离DSA以及旋转中心到探测器的距离DAO。
6) 在小钢珠投影重合时根据几何关系,计算出最后一个几何参数ΔZ。
图 11为搭建的实验平台。
图 11
 | 图 11 实验平台实物图 Experimental platform |
3.2 实验结果从表 1中可知,由本文中提到的基于四椭圆锥束CT系统几何参数的算法得出来的计算值与设计时的真实值相比较,求得的全参数误差相对很小,满足实际的应用需求。
表1
| 表 1 实际几何参数与计算几何参数比较 Comparison of actual geometric parameters and calculated geometric parameters |
为了验证本方法的实际效果,利用河南科技大第一附属医院实际人体口腔数据进行重建,其重建算法为圆轨迹滤波反投影FDK重建算法,重建过程为:1)对得到的投影数据进行加权预处理,即对得到投影数据与滤波函数进行卷积操作;2)把预处理过的数据进行一维的斜坡滤波;3)对滤波后的数据做锥形束的加权反投影。图 12和图 13为校正前和校正后重建的图像,从图中可以看出校正前图像环影较重,而且细节处模糊不清,轮廓处有伪影。校正后伪影基本消除,清晰度较高。为了更直观地分析结果,计算出了两个图像的峰值信噪比。其计算流程为:1)把两个重建的图像分别导入MATLAB中,并添加相同的椒盐噪声;2)生成系统预定义的3×3滤波器对两张添加噪声的图像进行均值滤波;3)求得两张图像的均值误差MSE;4)求得两张图像的峰值信噪比PSNR。最后求得参数未校正图像的峰值信噪比为11.0487,参数校正后图像的峰值信噪比为14.0413。显然参数校正后得到的图像比未校正得到的图像质量更好,可满足正常医用的要求。
图 12
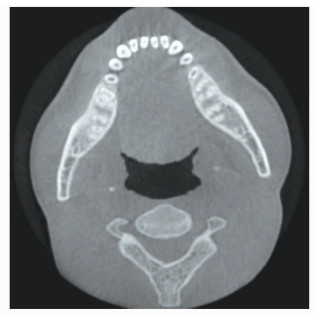 | 图 12 参数未校正重建的图像 Image reconstructed with uncorrected parameter |
图 13
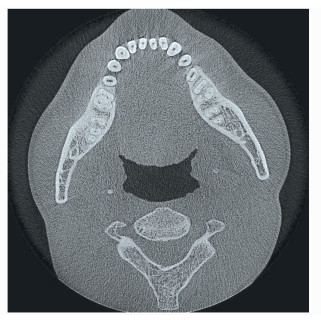 | 图 13 本文方法参数校正之后重建的图像 Image reconstructed after parameter correctionin this paper |
4 结论基于小球的椭圆轨迹法以及平行双丝法,本文设计了一种通用标定模体并提出基于本标定模体的几何全参数解析算法,从成像敏感参数出发环环相扣,得到的几何参数比较精确。改善了目前标定方法在解析计算标定过程中标定模体的单一性、标定参数不全、参数获取过程中计算较为复杂等缺点。本文设计的这种可调节的通用标定模体,可以适用于任意不同锥角的几何参数标定。在标定前只需要相应调整标定模体,标定过程中,通过简单的几何数学模型,即可获取锥束X-CT系统中的几何参数。实验结果表明,该方法对标定锥束CT系统几何参数是有效的,使用的标定模体通用性强、结构简单,适用于各种CT参数标定。但是目前使用该方法存在一个前提:标定前需要调整模体,使两个小钢珠投影相重合,这一条件是非常难以精确满足的。因此今后我们将进一步研究如何得到一种与标定体模初始状态无关的几何参数标定方法。
参考文献
| [1] | 张定华, 黄魁东, 程云勇. 锥束CT技术及其应用[M]. 西安: 西北工业大学出版社, 2010: 26-27. Zhang D H, Huang K D, Cheng Y Y. Cone Beam CT Technology and Its Application[M]. Xi'an: Northwestern Polytechnical University Press, 2010: 26-27. |
| [2] | Sun Y, Hou Y, Zhao F Y, Hu J S. A calibration method for misaligned sacanner geometry in cone-beam computed tomography[J]. NDT and E International, 2006, 39(6): 499-513. DOI:10.1016/j.ndteint.2006.03.002 |
| [3] | 侯颖, 孙怡. 锥束X-CT系统校准方法的实际应用分析[J]. CT理论与应用研究, 2011, 20(2): 211-220. Hou Y, Sun Y. A practical application analysis of cone beam X-CT system calibration method[J]. CT Theory and Applied Research, 2011, 20(2): 211-220. |
| [4] | 刘晓鹏, 张定华. 锥束CT系统安装参数确定技术研究[J]. 计算机工程与应用, 2006, 42(20): 170-173. Liu X P, Zhang D H. Study on the determination technology of installation parameters of cone beam CT system[J]. Computer Engineering and Applications, 2006, 42(20): 170-173. DOI:10.3321/j.issn:1002-8331.2006.20.052 |
| [5] | Meng Y Z, Hui G, Yang X Q. Online geometric calibration of cone-beam computed tomography for arbitrary imaging objects[J]. IEEE Transactions on Medical Imaging, 2013, 32(2): 278-288. DOI:10.1109/TMI.2012.2224360 |
| [6] | Yang M, Wang X L, Liu Y P. Automatic calibration method of voxel size forcone-beam 3D-CT scanning system[J]. Chinese Physics C, 2014, 38(4): 75-80. |
| [7] | 陈炼, 吴志芳, 刘锡明, 姚明. 锥束CT系统几何参数校正的解析计算[J]. 清华大学学报(自然科学版), 2010, 50(3): 418-421. Chen L, Wu Z F, Liu X M, Yao M. Analytical calculation of geometric parameter correction for cone beam CT system[J]. Journal of Tsinghua University(Science and Technology), 2010, 50(3): 418-421. |
| [8] | 李晓晴, 刘锡明, 苗击臣, 吴志芳. 锥束CT平行双丝法获取几何参数研究[J]. 原子能科学技术, 2018, 2(26): 1-7. Li X Q, Liu X M, Miao J C, Wu Z F. Study on geometric parameters of cone beam CT parallel double wire method[J]. Atomic Energy Science and Technology, 2018, 2(26): 1-7. |
| [9] | 王珏, 葛敏雪, 蔡玉芳, 向前. 基于线框模型的锥束CT几何参数校正方法[J]. 仪器仪表学报, 2018, 26(19): 177-184. Wang J, Ge M X, Cai Y F, Xiang Q. A method for correcting geometric parameters of cone beam CT based on wireframe model[J]. Journal of Instrumentation, 2018, 26(19): 177-184. |
| [10] | 黄秋红, Cao G H, 赵敏, 邱宗明, 朱凌建. 静态锥束CT成像系统的几何标定方法研究[J]. 仪器仪表学报, 2015, 36(10): 2339-2346. Huang Q H, Cao G H, Zhao M, Qiu Z M, Zhu L J. Study on geometric calibration method of static cone beam CT imaging system[J]. Chinese Journal of Scientific Instrument, 2015, 36(10): 2339-2346. DOI:10.3969/j.issn.0254-3087.2015.10.023 |
| [11] | 杨帅, 齐宏亮, 吴书裕, 徐圆, 周凌宏. 基于图像质量优化的锥束CT几何校正法[J]. 核电子学与探测技术, 2015, 36(7): 697-701. Yang S, Qi H L, Wu S Y, Xu Y, Zhou L H. A cone beam CT geometric correction method based on image quality optimization[J]. Nuclear Electronics & Detection Technology, 2015, 36(7): 697-701. |
| [12] | 周凌宏, 李翰威, 徐圆, 骆毅斌, 齐宏亮. 锥束CT圆轨道扫描的几何校正[J]. 光学精密工程, 2014, 22(10): 2847-2854. Zhou L H, Li H W, Xu Y, Luo Y B, Qi H L. Geometric correction of cone beam CT circular orbital scan[J]. Optical Precision, 2014, 22(10): 2847-2854. |
