
1. 北京理工大学 深圳研究院, 广东 深圳 518057;
2. 北京理工大学 光电学院, 北京 100081;
3. 河北工程大学 数理科学与工程学院, 河北 邯郸 056038
2019-10-14 收稿, 2019-11-11 录用
基金项目: 深圳市科技创新项目(JCYJ20170817114558026,JCYJ20170817115139963)资助
*通讯作者: 程灏波
摘要: 针对基于激光照明的离轴全息显微成像系统存在散斑和寄生条纹噪声,以及基于部分相干光照明的离轴数字全息显微技术存在相干条纹对比度差的问题,本文提出了一种基于单色LED照明的衍射相位显微成像系统。该系统利用大数值孔径物镜及光栅对物光进行多级衍射,并采用4f系统和空间滤波器分离出0级和+1级信息,分别作为参考光和物光,最终两束光在CCD阵面上干涉产生离轴全息图,从而形成共光路全息成像结构。通过理论分析和计算,对实验用到的光学元器件进行选型,确保衍射光频谱信息能够分开且满足抽样条件。最后与传统激光离轴数字全息显微成像检测结果进行对比,实验结果表明,本文提出的系统能够获得较高的成像准确度和信噪比。
关键词: 数字全息定量成像衍射光栅数值孔径共路离轴
Research on Multi-diffraction Phase Imaging Restricted by Large Numerical Aperture Optical Lens
WANG Qian1,2, CHEN Xin1,2, WEN Yongfu1,2, YANG Hao1, WANG Huaying3, CHENG Haobo1,2

1. Shenzhen Research Institute, Beijing Institute of Technology, Shenzhen 518057, Guangdong, P. R. China;
2. School of Optics and Photonics, Beijing Institute of Technology, Beijing 100081, P. R. China;
3. School of Mathematics and Physics, Hebei University of Engineering, Handan 056038, Hebei, P. R. China
*Corresponding author: CHENG Haobo
Abstract: Digital holographic microscopy imaging technology is a quantitative phase imaging technology combined with digital holography technology and traditional optical microscopy imaging technology. Owing to there are speckles and parasitic stripe noise in traditional laser off-axis holographic microscopy imaging system and the traditional off-axis digital holographic microscopy of partial coherent light illumination has the problem of poor contrast of coherent fringes, the diffraction phase microscopy imaging system with monochromatic LED illumination is putted forward in this paper. Grating is used to obtain multi-level diffraction of object light. And 0th and +1st order light are separated by 4f system and spatial filter, which are used as reference light and signal light, respectively. Two beams interfere with each other on the CCD and generate off-axis hologram. Thereby a common-path and off-axis holographic imaging structure is formed. Through theoretical analysis and calculation, the optical components used in the experiment are picked to guarantee that the diffracted light spectrum information can be separated and accord with the sampling conditions. In conclusion, the experimental results demonstrate that the proposed system can derive higher imaging accuracy and signal-to-noise ratio than the traditional laser off-axis digital holographic microscopy imaging results.
Key words: digital holographyquantitative imagingdiffraction gratingNAcommon-path and off-axis
基于激光照明的离轴数字全息系统[1, 2],采用高相干光(激光)作为照明光源,会产生无法消除的激光散斑和相干寄生条纹噪声,影响测量的精度。采用低相干光源[3](白光、LED等)能够很好地抑制这些噪声[4-8],但是由于低相干光相干长度短,采用传统基于部分相干光照明的离轴数字全息显微干涉结构,存在相干条纹对比度差及不能实现全视场清晰成像等问题。Popescu等先后提出了衍射相位显微系统(diffraction phase microscopy, DPM)[9, 10]和白光衍射相位显微系统(white diffraction phase microscopy, wDPM)[11]两种装置,消除了激光照明光源产生的激光散斑和相干寄生条纹噪声对系统测量精度的影响,同时其共路离轴的光路结构使得参物光路光程相等,保证了低相干光干涉条纹的对比度。wDPM采用卤素灯光源照射透明相位式物体,利用光栅对物光进行多级衍射,并采用4f系统和空间滤波器筛选出0级和+1级,分别作为物光场和参考光场,最终在CCD上获取到全息干涉图。但由于白光是复合光,单色性较差,极易产生光晕现象,造成相位测量不准确,因此需要在聚光镜中加入合适的小孔,提高光源空间相干性[12]。本文提出了一种单色LED照明的衍射相位显微系统(monochromatic LED diffraction phase microscopy, MLED-DPM),该系统具有较高的时间相位灵敏度[9, 13](即帧到帧的最小相移)和空间相位灵敏度[14-17](即同一帧内点到点的最小相位变化),可对相位型物体的形态特征进行成像,而不需要外加造影剂。首先,本文介绍了数字全息技术的记录原理及本文中用于恢复相位信息的角谱算法和最小二乘解包裹算法;其次,详细介绍了单色LED照明的衍射相位显微系统,通过理论分析和计算,对实验用到的光学元器件进行选型,确保衍射光频谱信息能够分开且满足CCD采样条件;最后,将由该系统测量得到的实验结果与传统激光离轴数字全息显微成像检测结果进行了对比,结果表明本文提出的光路系统能够获得较高的成像准确度和时空信噪比。
1 基本原理1.1 衍射相位显微成像原理在全息记录过程中,将被测物体的衍射光波和参考光波分别表示为:
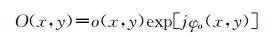 | (1) |
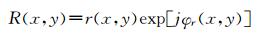 | (2) |
 | (3) |
在全息再现过程中,可通过算法将被测样品的全部信息恢复出来[18]。全息再现算法有菲涅耳积分变换法、卷积法、角谱法等,本文采用角谱法进行数值重建,得到的被测样品的物光波复振幅分布u(x, y)公式如下:
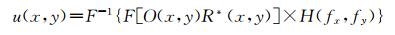 | (4) |
 | (5) |
由式(4)可得被测物体的光强和相位分布为:
 | (6) |
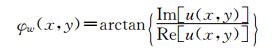 | (7) |
由于在提取相位信息时引入了反正切函数,故使得到的相位值分布在[-π, π]区间,是四象限包裹相位值,需采用解包裹算法对相位进行展开,以得到被测物体真实的相位分布。本文采用离散余弦变换(discrete cosin transform, DCT)最小二乘算法对相位进行解包裹[19, 20]。该算法解包裹速度较快、抗噪能力较高且算法易于实现。
本文提出的单色LED衍射相位显微成像系统如图 1所示,该系统主要分为两部分,照明系统和衍射相位成像系统。光路系统中采用了单色LED作为照明光源,并采用了科勒照明(K?hler illumination)的照明方式,既消除了LED发光灯芯的成像,又使得系统可以通过调节孔径光阑的大小来增强光束的空间相干性[21]。LED光源经科勒照明结构产生一束质量均匀的平行光,用于照明被测物体。物光束经镜筒透镜准直为平行光,照射在光栅上。在光栅衍射相位成像系统中,光栅放置在由透镜L1和L2组成的4f系统前焦面,CCD放置在4f系统的后焦面。利用光栅的分束功能,平行物光被分成多个携带物体全部空间信息的衍射光束。在4f系统的频谱面放置含一大一小两个孔的滤波器,只允许0级光的直流部分和+1级光束完整通过。其中0级光经针孔低通滤波后,不含物体信息,作为参考光;+1级光包含物体的全部信息,作为物光,两束光在CCD上进行干涉。
图 1
 | 图 1 单色LED衍射相位显微系统原理图 |
在该系统中,CCD记录面和光栅平面共轭,由费马定理可知,共轭面上的点通过系统成像时经过的光程相等,故光程差为0,确保了低相干光源干涉条纹的对比度。干涉条纹的周期由0级光和+1级光等相面的夹角决定[22]。光栅衍射成像原理图如图 2所示。
图 2
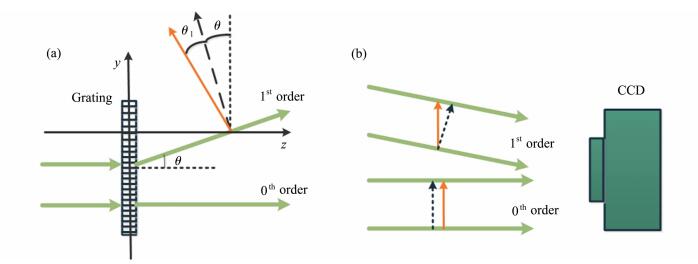 | 图 2 光栅衍射成像原理示意图(a)光栅衍射示意图,黑色虚线是+1级光的等相面(垂直于+1级光传播方向),橙色实线是+1级光的相干平面;等相面和相干平面有一夹角θ1; (b)最终干涉时,0级和+1级光束的等相面和相干平面分布 |
在单色LED光栅衍射相位显微成像系统中,用到的关键元器件理论分析与计算如下:根据离轴全息图的三项分离条件,在非相干光系统中,光栅平面调制得到的参考光载频至少为样品在该平面最高频率的4倍,可得光栅常数必须满足[6, 23]:
 | (8) |
考虑CCD相机能够对全息图进行正确采样,采样频率需满足奈奎斯特采样定理,可推出4f系统的横向放大倍率M4f需满足:
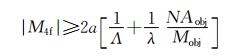 | (9) |
在透镜L1和L2的参数选择上,除了要满足4f系统的横向放大倍率,还需满足0级和+1级光波场能够完整地通过4f系统。透镜L1和L2的数值孔径NA1和NA2的计算公式为:
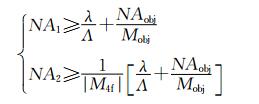 | (10) |
系统中采用的照明光源为绿色LED光源,光源中心波长为λmean=536 nm,用光谱仪HR4000测量得到的光谱分布曲线如图 3所示。该曲线可以近似为高斯分布,等效功率谱带宽(power-equivalent bandwidth, PEB)为35 nm。将上述参数代入公式lc=(2ln2/π)(λ2/Δλ)中,可计算得到该光源的相干长度lc=3.622 μm。
图 3
 | 图 3 单色LED光源光谱分布曲线 |
搭建的实验光路系统见图 4照片。为减少LED光源在光路中的过多损耗,在科勒照明系统中,视场光阑应设置得大一些,滤除掉较大的杂散光即可;而为了提高光源的空间相干性,需把孔径光阑设置得小一些。经科勒照明系统出射的质量均匀的平行光照射到物体上,后经物镜放大会聚,被镜筒透镜准直为一束平行光打在光栅上。光栅放置在4f系统的前焦面,CCD放置在4f系统的后焦面,以保证获取到良好的干涉条纹。在设置4f系统中用到的滤波器尺寸时,考虑到经普通光栅衍射后产生的0级光光强一般很强,而+1级光光强很弱,为了保证参物光光强均等,需让+1级光作物光,0级光作参考光。+1级滤波孔的设置较为容易,能够让+1级光完全通过而不让其邻近的0级光和+2级光进入即可,可将其设置为矩形孔径。考虑0级光作为参考光,一方面需要保证只有0级光的直流部分(不含物体信息)通过滤波孔,即对其进行低通滤波;另一方面,需保证最终参物光在CCD上进行干涉成像时,两束光的光强能够保持一致,因此0级滤波孔径的尺寸应设置得足够小。
图 4
 | 图 4 单色LED衍射相位显微系统实物图 |
根据上述理论分析,可最终确定实验中具体选用的元器件参数,如表 1所示。
表1
| 表 1 单色LED衍射相位显微系统参数表 |
我们选用油滴作为被观察的实验样品。取适量食用油与水混合,制备用来观察的油水混合物。图 5(a)和(b)为用手指沾取适量油水混合物后,轻按至载玻片上制成的样本全息图。图中较黑的地方,油滴分布较多。图 5(c)为用针尖沾取适量液体轻划到载玻片上制成的样本全息图,油滴分布较稀疏且较厚。为了便于分析,我们选取了这些全息图中的5处位置进行了重构,并采用了不同的渲染方式,很好地观察了油滴的三维形貌。
图 5
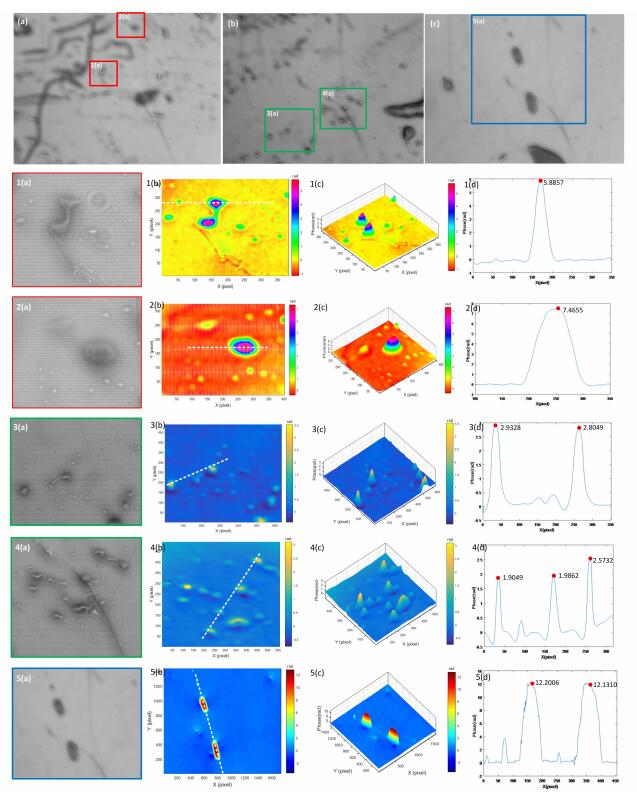 | 图 5 单色LED衍射相位显微系统实验结果(a)、(b)、(c)为本文系统获取到的全息图;*(a)重建的全息图的位置;*(b)重建得到的油滴的二维相位图;*(c)重建得到的油滴的三维相位图;*(d)图*(b)中白色虚线的油滴高度分布曲线(*代表 1,2,3,4,5) |
为验证该实验装置测量结果的准确性,我们选取了同一样本的相同位置,分别用本文的实验装置和实验室研制的离轴数字全息显微实验装置[24]进行对比,对比效果如图 6所示。该样品是用针尖划到载玻片上制成的,故油滴厚度较厚,分布也比较稀疏。从图 6 (c)和(d)组图中,可以看出MLED-DPM系统和激光全息系统得到的油滴横向宽度不一致,这是由于本文的MLED-DPM系统与激光全息系统CCD像素尺寸不一致造成的,激光全息系统的CCD像素尺寸为4.65 μm,MLED-DPM系统的CCD像素尺寸为2.2 μm,存在一个比例系数k=2.11。通过调整,将两个系统重建出的油滴最高高度所在行,即图 6(c)组图中白色虚线所示位置显示在同一图中便于对比,如图 6(e)所示。在图 6(e)中可以看到,MLED-DPM获取到油滴最高高度为1.0575 μm,激光离轴全息系统获取到的油滴最高高度为1.0699 μm,相对误差1.16%,测量结果准确度较高。
图 6
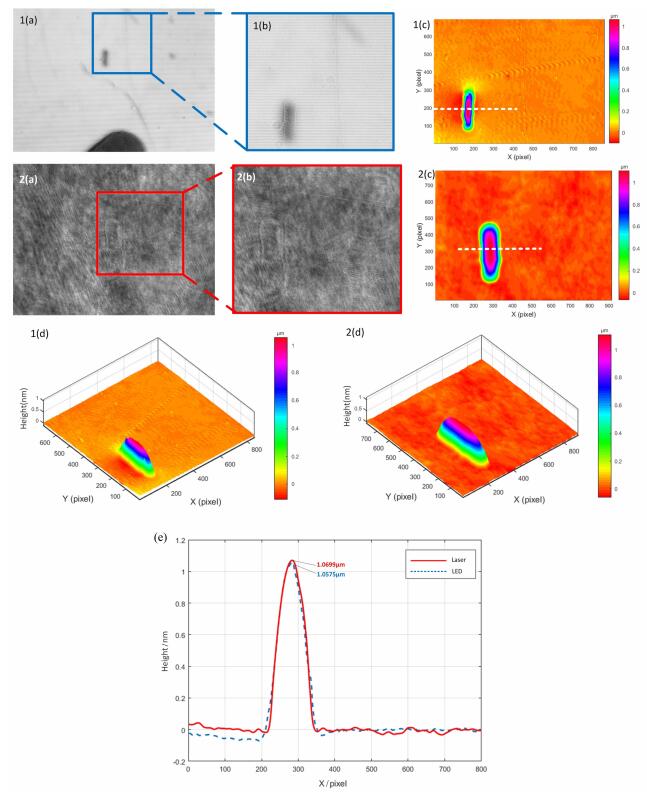 | 图 6 单色LED衍射相位显微系统与激光离轴全息显微系统实验结果对比图*(a) LED与激光系统分别获取到的全息图;*(b) LED与激光系统全息图的重建位置;*(c) LED与激光系统分别重建得到的油滴二维相位图;*(d) LED与激光系统分别重建得到的油滴三维相位图;(e) *(c)中白色虚线的油滴高度分布曲线(*代表 1和2) |
为验证系统的时空特性,我们在不放置任何样品的情况下,以1 frame/s的帧率采集了300张全息图。系统中CCD获取到的全息图尺寸大小为1944×2592。由于计算量太过庞大,因此我们截取了300张全息图相同位置尺寸大小为500×500的图像,用来计算该系统的时空噪声[11, 21]。
用相位重构算法求解出300张全息图的相位展开图。将第一张全息图重构出的相位图作为背景相位图φ0(x, y, 0),其余重构出的相位图φ(x, y, t)减去该背景图,即Δφ(x, y, t)=φ(x, y, t) - φ0(x, y, 0),得到299张去掉背景噪声后的相位图。根据相位差和光程差的关系Δδ=λ·Δφ/2π,其中Δδ为光程差,λ为照明光源光波长,计算得到系统的随机光程分布(optical path difference, OPD)。299张随机光程分布图中的任一张,代表该时刻的噪声分布,如图 7(a)所示。图 7(b)为图 7(a)的光程分布直方图。对该随机光程分布求均方差,即为系统的空间噪声σs=1.6851 nm。
图 7
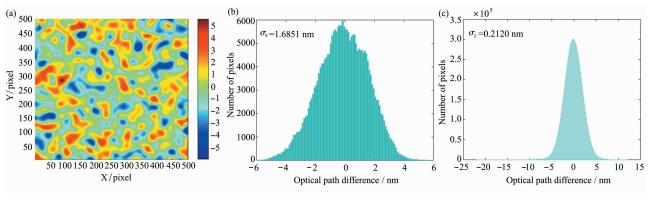 | 图 7 系统的时空噪声测量结果(a)随机光程分布图;(b)系统空间噪声分布图;(c)系统时间噪声分布图 |
系统的时间噪声计算方法为:先对光程分布图中每一个像素序列求均方差值,表示该像素的时间噪声,然后再对所有像素点的时间噪声求均方差值,即为系统的时间噪声,计算可得σt=0.2120 nm。图 7(c)为299张随机光程分布图所有像素的直方图,即系统的时间噪声分布图。
3 结论本文提出的单色LED衍射相位显微系统,一方面消除了激光照明源产生的激光散斑、相干寄生条纹噪声及白光照明源产生的光晕对系统精确度的影响;另一方面,该系统共路离轴的光路系统保证了低相干光源能够产生良好对比度的干涉条纹。实验结果表明,该系统测量准确度高,与标定的激光离轴数字全息显微系统相比,测量误差为1.16%;时空敏感性高,时间噪声σt=0.2120 nm,空间噪声σs=1.6851 nm,为相位型物体的定量测量提供了一种新的观测思路。目前的系统依旧存在轻微的光晕现象,为解决这方面的问题,后期可以从光路结构以及重构算法方面入手,以期进一步提高系统准确性。
参考文献
| [1] | Schnars U, Jüptner W P O. Digital recording and reconstruction of holograms in hologram interferometry and shearography[J]. Applied Optics, 1994, 33(20): 4373-4377. DOI:10.1364/AO.33.004373 |
| [2] | Cuche E, Marquet P, Depeursinge C. Simulataneous amplitude-contrast quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms[J]. Applied Optics, 1999, 38(34): 6994-7001. DOI:10.1364/AO.38.006994 |
| [3] | Brinkmann M, Dobner S, Fallnich C. Light source for narrow and broadband coherent Raman scattering microspectroscopy[J]. Optics Letters, 2015, 40(23): 5447-5450. DOI:10.1364/OL.40.005447 |
| [4] | Warnasooriya N, Kim M K. LED-based multi-wavelength phase imaging interference microscopy[J]. Virtual Journal for Biomedical Optics, 2007, 15(15): 9239-9247. |
| [5] | Kemper B, Stürwald S, Remmersmann C, et al. Characterisation of light emitting diodes(LEDs) for application in digital holographic microscopy for inspection of micro and nanostructured surfaces[J]. Optics and Lasers in Engineering, 2008, 46(7): 499-507. DOI:10.1016/j.optlaseng.2008.03.007 |
| [6] | Slaby T, Kolman P, Dostál Z, et al. Off-axis setup taking full advantage of incoherent illumination in coherence-controlled holographic microscope[J]. Optics Express, 2013, 21(12): 14747-14762. DOI:10.1364/OE.21.014747 |
| [7] | Guo R L, Yao B L, Min J W, et al. LED-based digital holographic microscopy with slightly off-axis interferometry[J]. Journal of Optics, 2014, 16(12): 125408. DOI:10.1088/2040-8978/16/12/125408 |
| [8] | 邓丽军, 杨勇, 石炳川, 等. 基于光程差扫描的低相干离轴数字全息术[J]. 光子学报, 2014, 43(10): 1011001. Deng L J, Yang Y, Shi B C, et al. Low coherence off-axis digital holography based on scanning the optical path difference[J]. Acta Photonica Sinica, 2014, 43(10): 1011001. |
| [9] | Popescu G, Ikeda T, Dasari R R, et al. Diffraction phase microscopy for quantifying cell structure and dynamics[J]. Optics Letters, 2006, 31(6): 775-777. DOI:10.1364/OL.31.000775 |
| [10] | Park Y K, Popescu G, Badizadegan K, et al. Diffraction phase and fluorescence microscopy[J]. Optics Express, 2006, 14(18): 8263-8268. DOI:10.1364/OE.14.008263 |
| [11] | Bhaduri B, Pham H, Mir M, et al. Diffraction phase microscopy with white light[J]. Optics Letters, 2012, 37(6): 1094-1096. DOI:10.1364/OL.37.001094 |
| [12] | Edwards C, Bhaduri B, Nguyen T, et al. Effects of spatial coherence in diffraction phase microscopy[J]. Optics Express, 2014, 22(5): 5133-5146. DOI:10.1364/OE.22.005133 |
| [13] | Popescu G, Deflores L P, Vaughan J C, et al. Fourier phase microscopy for investigation of biological structures and dynamics[J]. Optics Letters, 2004, 29(21): 2503-2505. DOI:10.1364/OL.29.002503 |
| [14] | Wang Z, Millet L, Mir M, et al. Spatial light interference microscopy (SLIM)[J]. Optics Express, 2011, 19(2): 1016-1026. DOI:10.1364/OE.19.001016 |
| [15] | Barty A, Nugent K A, Paganin D, et al. Quantitative optical phase microscopy[J]. Optics Letters, 1998, 23(11): 817-819. DOI:10.1364/OL.23.000817 |
| [16] | Ding H F, Popescu G. Instantaneous spatial light interference microscopy[J]. Optics Express, 2010, 18(2): 1569-1575. DOI:10.1364/OE.18.001569 |
| [17] | Wang Z, Marks D L, Carney P S, et al. Spatial light interference tomography(SLIT)[J]. Optics Express, 2011, 19(21): 19907-19918. DOI:10.1364/OE.19.019907 |
| [18] | 王华英, 王大勇, 谢建军, 等. 显微数字全息中物光波前重建方法研究和比较[J]. 光子学报, 2007, 36(6): 1023-1027. Wang H Y, Wang D Y, Xie J J, et al. Comparative studies for reconstruction algorithms of object wave front in microscopic digital holography[J]. Acta Photonica Sinica, 2007, 36(6): 1023-1027. |
| [19] | 葛宝臻, 崔鹏, 吕且妮, 等. 基于离散余弦变换最小二乘法实现数字全息再现像的相位解包裹[J]. 中国石油大学学报(自然科学版), 2008, 32(6): 169-173. Ge B Z, Cui P, Lyu Q N, et al. Implement of phase unwrapping of digital holographic reconstruction image by discrete cosine transform least square method[J]. Journal of China University of Petroleum, 2008, 32(6): 169-173. DOI:10.3321/j.issn:1673-5005.2008.06.036 |
| [20] | Arines J. Least-squares modal estimation of wrapped phases:application to phase unwrapping[J]. Applied Optics, 2003, 42(17): 3373-3378. DOI:10.1364/AO.42.003373 |
| [21] | Edwards C, Bhaduri B, Griffin B G, et al. Epi-illumination diffraction phase microscopy with white light[J]. Optics Letters, 2014, 39(21): 6162-6165. DOI:10.1364/OL.39.006162 |
| [22] | Hebling J. Derivation of the pulse front tilt caused by angular dispersion[J]. Optical and Quantum Electronics, 1996, 28(12): 1759-1763. DOI:10.1007/BF00698541 |
| [23] | 张家恒, 马利红, 李勇, 等. 卤素灯照明光栅衍射共路数字全息显微定量相位成像[J]. 中国激光, 2018, 45(6): 247-253. Zhang J H, Ma L H, Li Y, et al. Halogen-light quantitative phase imaging with common-path digital holographic microscopy based on grating diffraction[J]. Chinese Journal of Lasers, 2018, 45(6): 247-253. |
| [24] | Wen Y F, Cheng H B, Wu Y M, et al. Development of two user-friendly commercial digital holographic microscopes and applications[J]. Proceedings of SPIE-Sixth International Conference on Optical and Photonic Engineering, 2018, 10827. |
