任彦霖^*, 刘赵淼^,*,†,2), 逄燕^*,†, 王翔^**北京工业大学材料与制造学部, 北京 100124
^†北京工业大学先进制造重点实验室, 北京 100124

A LATTICE-BOLTZMANN METHOD SIMULATION OF THE HORIZONTAL OFFSET IN OBLIQUE COLUMN DEPOSITION OF ALUMINUM DROPLETS¹⁾

Ren Yanlin^*, Liu Zhaomiao^,*,†,2), Pang Yan^*,†, Wang Xiang^**College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China
^†Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100124, China

通讯作者: 2)刘赵淼, 教授, 主要研究方向: 微流控技术. E-mail:lzm@bjut.edu.cn

收稿日期:2021-01-14接受日期:2021-03-4网络出版日期:2021-06-18

基金资助:

1)装备预研领域基金资助项目.61409230309

Received:2021-01-14Accepted:2021-03-4Online:2021-06-18
作者简介 About authors


摘要
金属微滴沉积制造技术采用逐点堆砌方式成型, 为斜柱沉积提供无支撑制造方式, 具有高度灵活性. 本文针对铝液滴斜柱连续沉积过程, 建立格子玻尔兹曼模型进行数值模拟, 研究液滴在凝固表面上的水平偏移运动. 根据表面能充放过程, 沉积运动被划分为下落、快速扩张、慢速扩张、回弹4个阶段, 其受力状态由表面能、重力势能、动能和黏性耗散趋势得到. 液滴内部流动在扩张阶段中表现为滑动状态, 而在回弹阶段中表现为滚动状态. 液滴偏移运动的加速阶段主要发生在扩张阶段, 而偏移距离则在回弹阶段中产生. 扩张阶段的受力状态表明偏移运动的主要推动力为重力和毛细力. 随着液滴轴线距离的增大, 扩张阶段中的加速段时间缩短、速度峰值提高, 使水平偏移距离呈先增大后减小的趋势, 这种阶段化特征源于加速段时长和速度极大值的竞争关系. 不同沉积高度和固液浸润度下, 偏移距离均保持相同的演化趋势. 在相同的轴线距离下, 偏移距离随固液浸润度的增大而减小, 随沉积高度的增大而减小. 通过拟合水平偏移距离演化规律、优化扫描步距, 能够实现斜柱的均匀沉积, 并使倾角与理论结果一致.
关键词： 斜柱沉积;水平偏移;毛细力;铝微滴;格子玻尔兹曼方法

Abstract
The metal droplet deposition manufacturing technology adopts a point-by-point stacking method, which provide an unsupported manufacturing method for oblique column deposition with high flexibility. In this paper, a lattice Boltzmann model is established for simulating the continuous deposition process of the oblique column, and the horizontal displacement of the droplet on the solidification surface is studied. According to the charging and discharging process of surface energy, the deposition process is divided into four stages: falling, rapid expansion, slow expansion, and rebound. The forces on the deposited droplet are analyzed by the trend of surface energy, the gravitational potential energy, the kinetic energy, and the viscous dissipation. The internal flow of droplet is sliding in the expansion stage and rolling in the rebound stage. The internal flow of the droplet shows sliding state in the expansion stage and rolling state in the rebound stage. The acceleration of the deviation mainly occurs in the expansion stage, while the deviation distance occurs in the rebound stage. Combined with the forces in the expansion stage, it is concluded that the main driving forces of displacement are gravity and capillary force. With the increase of the droplet axial distance, the acceleration in expansion stage is shortened, and the peak of velocity is increased, so that the horizontal deviation is first increased and then decreased. This staged feature stems from the competitive relationship between the acceleration period and the maximum speed in the deviate motion. Under different deposition heights and solid-liquid wettability, the deviation distance maintains the same trend. Under a certain axial distance, the deviate distance decreases with the increasing solid-liquid wettability, or the increasing deposition height. The evolution tendency of the horizontal deviation distance is fitted, and the scanning step is optimized to realize the uniform deposition of the inclined column whose inclination angle is consistent with the theoretical result.
Keywords：oblique column deposition;horizontal offset;capillary force;aluminum droplets;lattice-Boltzmann method


PDF (3568KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
任彦霖, 刘赵淼, 逄燕, 王翔. 基于LBM的铝微滴斜柱沉积水平偏移研究¹⁾. 力学学报, 2021, 53(6): 1599-1608 DOI:10.6052/0459-1879-21-022
Ren Yanlin, Liu Zhaomiao, Pang Yan, Wang Xiang. A LATTICE-BOLTZMANN METHOD SIMULATION OF THE HORIZONTAL OFFSET IN OBLIQUE COLUMN DEPOSITION OF ALUMINUM DROPLETS¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1599-1608 DOI:10.6052/0459-1879-21-022

引言

在传统增材制造技术中, 微管结构^[1-2]、多孔结构^[3-4]因支撑材料难以去除而无法生产. 金属液滴沉积制造技术基于逐点成型原理, 通过按需喷射方式^[5-6], 进行无支撑斜柱沉积^[7], 实现空间网络结构的生产^[8-9]. 铝液滴是增材制造技术中常用的工质, 具有较好的界面张力和黏度等材料特性, 被广泛应用于液滴沉积制造技术的研究中^[10-11]. 然而, 先沉积液滴非受限表面凝固后的球帽形貌会影响后沉积液滴运动行为, 使液滴实际沉积位置与其生成位置存在偏差. 这种偏差使液滴沉积行为产生的偏移距离, 会降低斜柱沉积形貌精度. 精确分析影响水平偏移程度的控制因素, 成为斜柱沉积过程亟待解决的关键问题.

沉积液滴在球帽形凝固表面上的运动过程, 是一个复杂的流动、传热过程, 其实际沉积位置受到冲击^[12]、震荡^[13]、共同凝固过程^[14]等因素影响. Zhang等^[7]在液滴连续沉积实验中, 通过调整融合率引起实际沉积位置偏移, 并影响斜柱倾角; 进一步固定融合率, 却依然存在沉积位置偏移, 影响倾角的控制精度^[15]. Graham等^[16]和Dalili等^[17]实验观测了水滴的相互融合过程, 表明沉积位置的偏移由界面张力作用引起. Li等^[18]探究了石蜡滴水平连续沉积过程, 发现液滴间距会影响位置偏移程度. 这些研究多集中于液滴融合过程产生的偏移运动, 而缺少金属液滴凝固形成的球帽结构对偏移运动的影响. Ju等^[19]研究了液滴在球面上的沉积运动, 表明球面曲率影响液滴沉积运动, 但由于液滴与球面同轴, 而未产生滑落. Tian等^[20]实验研究了液滴在倾斜表面的沉积过程, 提出了沉积液滴动力学行为的能量分析法. 对于铝液滴在球帽形凝固表面上的偏移运动过程, 前、后液滴间轴线距离的影响及其受力机理尚未明确, 对斜柱沉积过程参数的优化设计有待研究.

为分析偏移运动和受力机理, 铝液滴的连续沉积过程需要采用格子玻尔兹曼方法(LBM), 进行数值模拟研究. LBM是一种介观尺度的模拟算法, 在两相流动方面采用S-C伪势模型统一处理离散相和分散相^[21], 并引入C-S状态方程计算分子碰撞有效质量使其满足热力学一致性^[22], 对平衡速度进行修正^[23]; 在传热相变方面采用焓的显式法求解传热过程, 通过双分布方程使其与流动耦合^[24], 并对固液相变前沿进行无滑移边界处理^[25-26]. LBM已经具备解决实际工程中传热、相变问题的能力^[27-31], 并应用于单液滴沉积过程的研究中^[32-34], 有助于实现金属液滴连续沉积过程的建模.

本文将基于LBM建立铝液滴斜柱沉积模型, 采用自编程序研究液滴水平偏移过程和受力机理. 根据液滴能量演化趋势, 对沉积过程进行阶段划分. 结合质心位移曲线, 分析水平偏移产生的主要阶段和主要推动力. 根据偏移距离的演化规律, 对扫描步距进行优化, 以实现斜柱的均匀沉积和倾角的精确控制.

1 物理模型

斜柱沉积制造是多个液滴按相同间距连续沉积的过程, 以其中两液滴先后下落的物理过程, 作为主要研究对象. 如图1所示, 密度、初始焓、直径分别为$\rho _H $, $H_A $, $D_d$的两个铝液滴, 从同一高度$h$, 水平相距$L$的位置先后下落. 先沉积的液滴接触温度为$T_B$的恒温基板后凝固, 后沉积的液滴接触前者表面后凝固. 外界环境气体密度为$\rho _{0} $, 初始温度为$T_{0}$ $(T_{0} = T_B )$. 铝液滴材料参数如表1所示.

图1

新窗口打开|下载原图ZIP|生成PPT
图1多液滴沉积物理过程简图

Fig.1Physical process of multi-droplet deposition



Table 1
表1
表1铝液滴材料参数
Table 1Material properties of the aluminum droplets

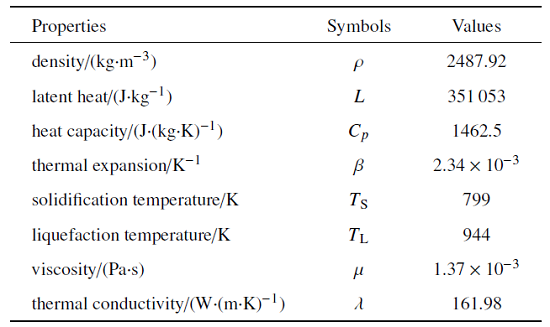新窗口打开|下载CSV

2 数值方法

2.1 两相流动方程

液滴沉积过程是一个两相流动过程, 需要准确追踪气液界面. 本文采用伪势模型, 通过流体粒子间相互作用力, 使其自发地形成两相界面, 以满足热力学一致性和第一性原理. 首先对流动过程建立密度的格子玻尔兹曼方程

(1)$f_{i} \left( {{ x}+{ e}_{i} \Delta t, t+\Delta t} \right)=f_{i} \left( {{ x}, t} \right)- \dfrac{1-B}{\tau_f }\left[ {f_{i} \left( {{ x}, t} \right)-f_{i}^eq \left( {{ x}, t} \right)} \right]+B\varOmega_{i}^S$
(2)$\rho =\sum_i f_{i}$
(3)$\rho u=\sum_i { e_{i} f_{i} }$
式中, $i$表示格子方向的索引编号, $ e_{i} $表示$i$方向上的单位格子速度, $\tau_f $表示密度松弛时间^[35]. 浸没边界法是LBM中处理曲面边界的常用方法^[36]. 本文采用Noble等^[26]提出的方法处理相变界面, 以$B$表示固体边界判别函数, $\varOmega_{i}^S $表示附加碰撞项.

在流动方程的基础上, 引入相邻位点间粒子的长程相互作用力, 实现流体的两相分离

(4)$F_int \left( {{ x}, t} \right)=-G\psi \left( {{ x}, t} \right)\sum_i {\omega_{i} \psi \left( {{ x}+{ e}_{i} \Delta t, t} \right){ e}_{i} }$
式中, $G$表示相互作用强度, $\psi $表示碰撞有效质量. 为了保证两相分离状态具有热力学一致性, 碰撞有效质量通过C-S状态方程计算^[22]

(5)$p=\rho RT\dfrac{1+{{b\rho }/4}+\left( {{{b\rho }/4}} \right)^{2}-\left( {{{b\rho }/4}} \right)^{3}}{\left( {1-{{b\rho }/4}} \right)^{3}}-a\rho ^{2}$
(6)$ \psi =\sqrt {\dfrac{2\left( {p-\rho c_s^{2} } \right)}{c_{0} g}}$
在流固界面上, 近壁面粒子所受作用力为

(7)$F_ads \left( {{ x}, t} \right)=-G\psi \left( {{ x}, t} \right)\sum_i {\omega_{i} \psi \left( {\rho _w } \right)s\left( {{ x}+{ e}_{i} \Delta t, t} \right){ e}_{i} }$
式中, $\rho _w $表示壁面粒子假想密度, 用于调节固液表面浸润度. 采用Shan-Doolen平衡态分布函数的速度校正法, 对平衡速度和物理速度进行修正^[23]

(8)${ u}^eq={ u}+\dfrac{\tau_f \left( {{ F}_int +{ F}_ads } \right)}{\rho }$
(9)${ u}^phy={ u}+\dfrac{ {{ F}_int +{ F}_ads }}{2\rho }$

2.2 传热相变方程

液滴在沉积过程中传热并发生凝固, 需要引入焓的格子玻尔兹曼方程求解

(10)$g_{i} \left( {x+e_{i} \Delta t, t+\Delta t} \right)=g_{i} \left( {x, t} \right)- \dfrac{1}{\tau_g }\left[ {g_{i} \left( {x, t} \right)-g_{i}^eq \left( {x, t} \right)} \right]$
(11)$H=\sum_i g_{i}$
式中, $\tau_g $表示焓的松弛时间, $g_{i}^eq $表示焓的平衡分布函数, 并采用Huang等^[34]提出的显式方程表示

(12)$\left. {\begin{array}{ll} g_{i}^eq =H-C_{p} T+\omega_{i} C_{p} T\left[ {1-\dfrac{\left( {{ u}^phy} \right)^{2}}{2{ c}_s^{2} }} \right], & i=0\\[5mm] g_{i}^eq =\omega_{i} C_{p} T\left[ 1+\dfrac{e_{i} \cdot { u}^phy}{{ c}_s^{2} }+ \dfrac{\left( {{ e}_{i} \cdot { u}^phy} \right)^{2}}{2{ c}_s^{4} }-\dfrac{\left( {{ u}^phy} \right)^{2}}{2{ c}_s^{2} } \right], & i\ne 0 \end{array}} \right\}$
式中, $\omega_{i} $表示$i$方向上的加权, $c_s $表示格子声速, $C_{p}$表示定压热容. 根据流体焓不仅可以计算出当地温度, 还可以追踪固液相变界面

(13)$\left. {\begin{array}{ll} T=T_S -\dfrac{H_S -H}{C_{p} }, & H\leqslant H_S \\ T=\dfrac{H_L -H}{H_L -H_S }T_S +\dfrac{H-H_S }{H_L -H_S }T_L, & H_S <H\leqslant H_L \\ T=T_L +\dfrac{H-H_L }{C_{p} }, & H>H_L \end{array}} \right\}$
(14)$\left. {\begin{array}{ll} f_L =0, & H\leqslant H_S \\ f_L =\dfrac{H-H_S }{H_L -H_S }, & H_S <H\leqslant H_L \\ f_L =1, & H>H_L \end{array}} \right\}$
式中, $H_S $表示流体固化焓, $H_L $表示流体液化焓, $T_S $表示固相线, $T_L $表示液相线. 对于相变界面上的无滑移边界条件, 采用Noble等^[26]提出的移动固体边界处理方法, 并通过固体判别函数和附加碰撞项修正流动方程

(15)$B=\dfrac{\left( {1-f_L } \right)\left( {\tau_f -0.5} \right)}{f_L+\tau_f -0.5}$
(16)$\varOmega_{i}^S =f_{k} \left( { x, t} \right)-f_{i} \left( { x, t} \right)+f_{i}^eq \left( {\rho , U_S } \right)- f_{k}^eq \left( {\rho , u}\right)$
式中, $k$表示运动方向与$ e_{i} $相反的分布函数索引, $ U_S$表示固体的运动速度.

2.3 网格独立性验证

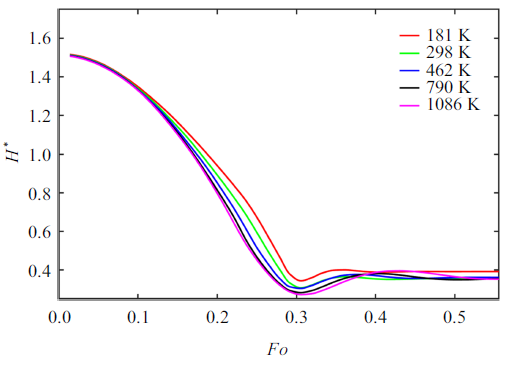
通过模拟单液滴下落过程中的形心高度变化, 对模型进行网格独立性验证. 计算域上下表面设为半步反弹及恒温边界条件, 四周设置为循环边界条件, 模拟单液滴下落过程. 如图2所示, 当液滴直径为$D_d =36$ lu时, 计算域总网格量超过$7.9\times 10^{5}$个单元, 液滴形心运动趋势不再有明显变化. 在LBM中, 计算域在无特殊格式处理时, 通常采用均匀网格划分, 网格精度由宏观尺寸在格子上的分辨率体现. 根据液滴实际直径$D_d =0.6$ mm, 和网格独立性验证得到的网格量大小, 得到宏观空间尺度的国际单位分辨率为1 m = $6.0\times 10^{4}$ lu, 并在保证计算收敛性的基础上, 进一步确定时间、温度、质量等基本单位在格子上的分辨率(如表2所示).

图2

新窗口打开|下载原图ZIP|生成PPT
图2网格独立性验证

Fig.2Grid independence verification



Table 2
表2
表2国际基本单位与格子单位的换算关系
Table 2Relationship between the SI units and the lattice units

新窗口打开|下载CSV

3 结果与讨论

对水平偏移距离的准确控制, 需要根据液滴沉积过程中的能量变化, 对液滴运动过程进行划分, 探寻水平偏移的主要产生阶段和主要推动力.

3.1 能量演化及运动阶段划分

沉积液滴与环境气体、凝固液滴形成三相接触, 其表面能直接反应液滴形态变化和运动过程. Tian等^[20]根据表面能的充放过程, 对液滴运动过程进行阶段划分, 并建立了表面能计算公式

(17)$SE=\sigma_gl \left( {S_gl -S_ls \cos \theta_e } \right)$
式中, $S_gl $表示气液界面面积, $S_ls $表示固液界面面积, $\theta_e$表示液滴静态接触角. 沉积液滴除了表面能外, 还具有重力势能$GP$和动能$KE$, 这两种能量的计算模型分别表示为

(18)$GP=\int_Droplet {\rho g\Delta z}$
(19)$KE=\int_Droplet {0.5\rho { u}^{2}}$
式中, $\rho $表示流体微元密度, $g$表示重力加速度, $\Delta z$表示流体微元运动的相对高度, ${ u}$表示流体微元速度. 沉积液滴接触凝固表面后, 由于壁面剪切作用产生黏性耗散$VD$, 使表面能、重力势能与动能之和降低. 因此, 液滴沉积过程中产生的黏性耗散可推算为

(20)$VD=-\Delta \left( {SE+KE+GP} \right)$
图3提取了浸润度为$\xi =0.42$、两液滴轴线距离为$L^{\ast }=0.33$下的液滴沉积能量变化. 其中$Fo$是无量纲时间尺度, 表示为

(21)$Fo=\dfrac{\upsilon t}{D_d^{2} }$
式中, $\upsilon $是铝的运动黏度, $t$表示时间, $D_d $为液滴的特征长度, 取液滴的初始直径. 根据$SE$的充放变化, 可以将沉积液滴运动过程分为下落阶段、快速扩张阶段、慢速扩张阶段、回弹阶段^[37] (如图3). 在下落阶段($Fo<0.17$), 液滴在界面张力作用下维持球状, $SE$不发生明显改变. 重力作用使势能下降$\left| {\Delta GP} \right|=2.32$ mu$\cdot$lu$^{2}$/ts$^{2}$, 并等额转化为动能$KE$, 形成接触凝固表面前的冲击速度.

图3

新窗口打开|下载原图ZIP|生成PPT
图3后沉积液滴运动过程中的能量演化曲线

Fig.3Tendency of energy in the motion of deposit droplet



液滴接触凝固表面后, 与气体、凝固表面形成三相接触, 进入快速扩张阶段($0.17<Fo\leqslant 0.22$). 表面能降低$\left| {\Delta SE}\right|=9.77$ mu$\cdot$lu$^{2}$/ts$^{2}$, 重力势能减小$\left|{\Delta GP} \right|=3.23$ mu$\cdot$lu$^{2}$/ts$^{2}$, 表明毛细力和重力在快速扩张运动中起推动作用. 此时液滴中央截面状态如图3(b)所示, 毛细力带动接触线扩张, 并使液滴质心下降. 过流断面的减小使黏性剪切作用增强, 使黏性耗散增大$\left| {\Delta VD} \right|=13.01$ mu$\cdot$lu$^{2}$/ts$^{2}$, 动能减小$\left| {\Delta KE}\right|=0.01$ mu$\cdot$lu$^{2}$/ts$^{2}$.

在慢速扩张阶段中($0.22<Fo\leqslant 0.28$). 表面能增大$\left| {\Delta SE}\right|=3.09$ mu$\cdot$lu$^{2}$/ts$^{2}$, 重力势能降低$\left|{\Delta GP} \right|=0.94$ mu$\cdot$lu$^{2}$/ts$^{2}$. 该结果表明毛细力在慢速扩张过程中起阻碍作用, 而重力起推动作用. 慢速扩张阶段的初始状态如图3(c)所示, 接触线达到毛细平衡状态, 并开始在重力和流动惯性作用下受迫扩张. 流速因气液界面阻碍而降低, 使壁面剪切强度降低, 黏性耗散仅为$\left| {\Delta VD}\right|=0.91$ mu$\cdot$lu$^{2}$/ts$^{2}$, 同时动能降低$\left| {\Delta KE} \right|=3.06$ mu$\cdot$lu$^{2}$/ts$^{2}$.

进入回弹阶段后($Fo>0.28$), 表面能下降$\left| {\Delta SE}\right|=4.44$ mu$\cdot$lu$^{2}$/ts$^{2}$, 同时重力势能提高$\left|{\Delta GP} \right|=0.13$ mu$\cdot$lu$^{2}$/ts$^{2}$, 表明毛细力在接触线回弹过程中起推动作用、重力起阻碍作用, 但二者作用效果均低于快速扩张阶段. 此时液滴中央截面状态如图3(d)所示, 毛细力带动接触线回缩, 并使质心位置升高. 过流断面的增大和流速的减小使黏性耗散增大$\left| {\Delta VD}\right|=4.43$ mu$\cdot$lu$^{2}$/ts$^{2}$, 并使动能降低$\left| {\Delta KE} \right|=0.12$ mu$\cdot$lu$^{2}$/ts$^{2}$.

尽管毛细力在扩张运动中, 先后起到推动作用和抑制作用, 但由于流动形式相似, 所以下文被统称为扩张阶段. 图4(a)表明扩张阶段中液滴内部流场以惯性力主导的下落运动为主, 而凝固表面上的流场表现为扩散运动. 如图4(b)所示的回弹阶段中, 上游接触点切线倾角较小, 重力与毛细力同向, 促使接触线进行回弹运动;下游接触点切线倾角较大, 重力与毛细力反向, 反而使接触线继续向下游运动. 由此导致液滴整体向下游运动, 形成了滚动流动状态.

图4

新窗口打开|下载原图ZIP|生成PPT
图4扩张和回弹阶段中的流场形式

Fig.4The flow field in spreading and rebound stage



由于前沉积液滴的凝固表面具有轴对称的球面形貌, 使后沉积液滴在各方向上的运动相同. 为分析水平偏移运动过程, 后文以偏移方向作为水平$x$轴正方向, 并提取三维结果中液滴质心运动距离和速度进行分析.

3.2 水平偏移主要阶段及推动力

图5展示了两液滴轴线距离为$L^{\ast }=0.33$的偏移运动过程. 其中$L^{\ast }$和$\Delta L^{\ast }$分别为无量纲轴线间距和无量纲偏移距离, 表示为

(22)$L^{\ast }=L/D_d$
(23)$\Delta L^{\ast }=\Delta L/D_d$

图5

新窗口打开|下载原图ZIP|生成PPT
图5冲击液滴偏移过程

Fig.5Horizontal displacements of the deposit droplets



$u_{x}^{\ast } $是液滴形心在水平方向的无量纲偏移速度

(24)$u_{x}^{\ast } =\dfrac{u_{x} D_d }{\upsilon }$
沉积液滴在扩张阶段中发生加速偏移, 并在$Fo=0.29$时偏移速度达到峰值$u_{x}^{\ast }=1.32$, 而偏移距离仅为$\Delta L^{\ast }=0.05$. 在随后的回弹阶段中, 偏移运动开始减速, 在$Fo=0.52$时偏移速度降低至$u_{x}^{\ast }=0.06$, 偏移距离增大至$\Delta L^{\ast }=0.21$. 由此可见, 水平偏移运动主要发生在回弹阶段, 而加速过程发生在扩张阶段. 根据3.1节对扩张阶段的受力分析, 表明重力、毛细力是水平偏移运动的主要推动力.

3.3 扫描步距优化

为实现对偏移距离的准确控制, 需要在实际工况中, 选择与主要推动力对应的控制条件, 并对其影响程度进行标定.

铝液滴与气体、凝固表面形成的三相接触过程中, 固液界面浸润度是控制毛细力作用的主要参数. 液滴间轴线距离决定了两液滴的接触点位置, 而在半球形凝固表面上, 接触点的位置与该点切线斜率直接相关, 并决定了切线方向上的重力分量. 液滴轴线距离和固液界面浸润度成为本文偏移距离研究的主要控制参数.

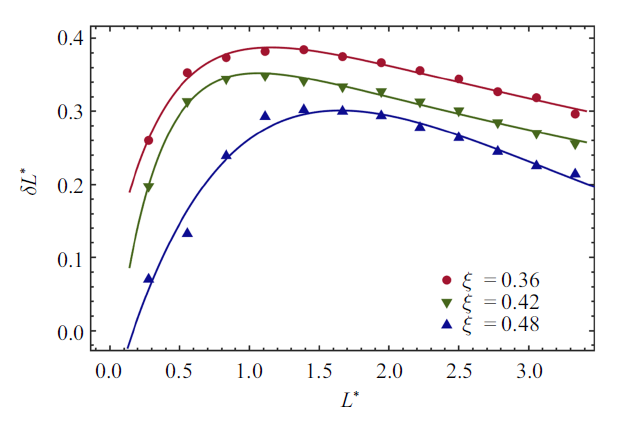
如图6所示, 水平偏移距离随轴线距离的演化趋势呈现阶段化特性: $L^{\ast }<0.10$时, 偏移距离随着轴线距离的增大而增大; 而$L^{\ast }>0.10$后, 偏移距离随着轴线距离的增大而减小. 在不同固液浸润度条件下对比, 表明偏移程度随着浸润度的增大而减小, 并且不影响偏移程度随轴线距离的演化趋势. 由于固液浸润度是材料属性, 需要根据材料浸润度以及所需的偏移距离$\Delta L$, 选择对应的轴线距离$L$. 以浸润度为$\xi =0.42$的材料工况为例, 对偏移距离进行数据拟合得到对勾函数关系

(25)$\Delta L^{\ast }=-0.62L^{\ast }-{{0.0067}/{L^{\ast }}}+0.46$

图6

新窗口打开|下载原图ZIP|生成PPT
图6液滴间轴线距离对水平偏移距离的影响

Fig.6Influence of axes distance between droplets on the horizontal deviation



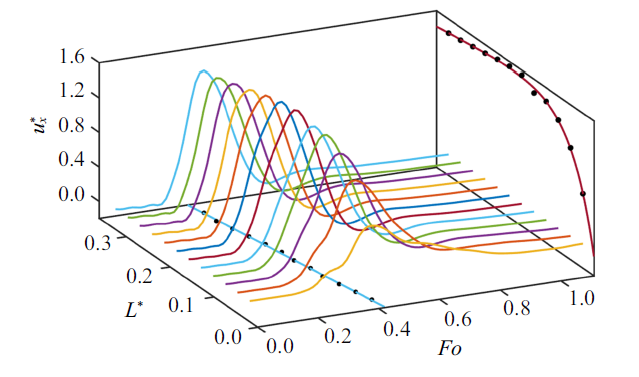
偏移程度随轴线间距演化的阶段化特征, 表明液滴的偏移运动过程存在竞争机制. 图7对比了不同轴线距离下, 液滴水平偏移速度的演化趋势: 在接触凝固表面后开始加速, 进入回弹阶段后减速, 并在表面能完全释放后速度趋于平缓. 演化趋势差异, 体现在加速段时长和速度极大值的变化.

图7

新窗口打开|下载原图ZIP|生成PPT
图7轴线间距对偏移运动的影响

Fig.7Influence of axis distance on deviate movement



如图7所示, 随着轴线间距由$L^{\ast }=0.03$增大到$L^{\ast }=0.14$, 速度极大值从$u_{x}^{\ast } =0.66$增大到$u_{x}^{\ast } =1.44$, 随后小幅减小. 液滴接触凝固表面后($Fo>Fo_{0} $), 速度达到极大值前的加速段时长$Fo_a=Fo-Fo_{0} $, 随倾角的增大而缩短. 随着轴线间距由$L^{\ast }=0.03$增大到$L^{\ast }=0.33$, 加速段时长从$Fo_a =0.25$减小到$Fo_a=0.17$. 对速度极大值和加速段时长的模拟结果进行数据拟合, 得到与轴线间距的关系式

(26)$u_{x, \max }^{\ast } =1.747e^{-0.566 3L^{\ast }}-1.825e^{-19.70L^{\ast }}$
(27)$Fo_a =-0.3619L^{\ast }+0.2562$
该结果表明加速段时长与轴线间距呈单调减小关系, 而速度极大值随轴线间距先增大后小幅减小. 二者对偏移程度起着相反的作用: 加速段时长的缩短会提高偏移程度, 而速度极大值的增大则与之相反. 这种竞争关系是导致偏移程度随轴线间距表现出阶段化特征的根本原因.

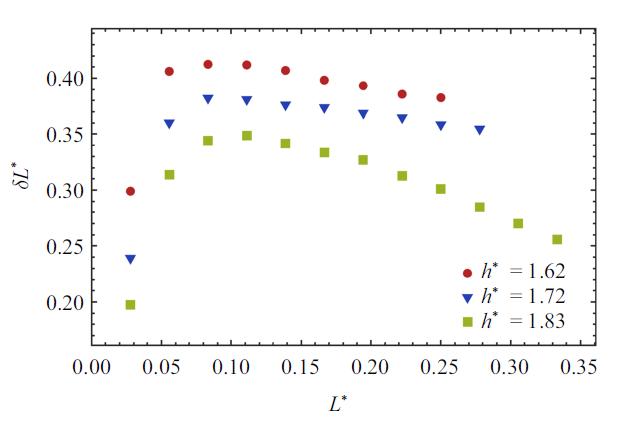
作为液滴沉积的控制参数之一, 沉积高度的增大会提高冲击速度, 也会使液滴温度提早降低, 所以该工况的研究范围被控制在$h^{\ast }=1.67\sim2.00$内. 图8展示了$h^{\ast }=1.67$, 1.72, 1.83三组工况的对比结果, 表明偏移程度随轴线间距具有相似的演化趋势, 最大偏移距离与沉积高度负相关, 分别为$\Delta L^{\ast }=0.41$, 0.38, 0.35.这是由于液滴接触凝固表面时, 内部流体以凝固表面上的扩散运动为主, 冲击速度的增大使流体克服重力作用产生的流量分配差异, 使液滴在扩张阶段中的偏移距离和速度减小. 该结果表明, 沉积高度的增大对偏移程度起抑制作用.

图8

新窗口打开|下载原图ZIP|生成PPT
图8轴线间距对水平偏移程度的影响

Fig.8Influence of axial distance on horizontal deviation



为实现斜柱的均匀沉积, 后续液滴沉积时的扫描步距既要包括液滴间的轴线距离, 还要考虑前沉积液滴的偏移距离

(28)$w^{\ast }=L^{\ast }+\Delta L^{\ast }$
在保证每个液滴扫描步距一致的基础上, 根据Zhang等^[7]提出的斜柱倾角理论公式, 可以得到

(29)$\theta =\arccos \left( {\dfrac{w^{\ast }}{\varepsilon }} \right)$
式中 $\varepsilon $表示液滴间的融合率, 是沉积后的液滴间形心距离与初始直径之比. 本文采用固液浸润度为$\xi=0.42$的铝液滴, 从高度为$h^{\ast }=1.5$下落. 通过测量液滴形心间距, 得到融合率为$\varepsilon =0.63$, 并将其代入式(29)、与式(25)和式(28)联立, 得到液滴轴线距离与倾角关系式为

(30)$L^{\ast }=0.83\cos \theta -0.61+ \\ \sqrt {\left( {0.83\cos \theta -0.61} \right)^{2}-0.0177}$
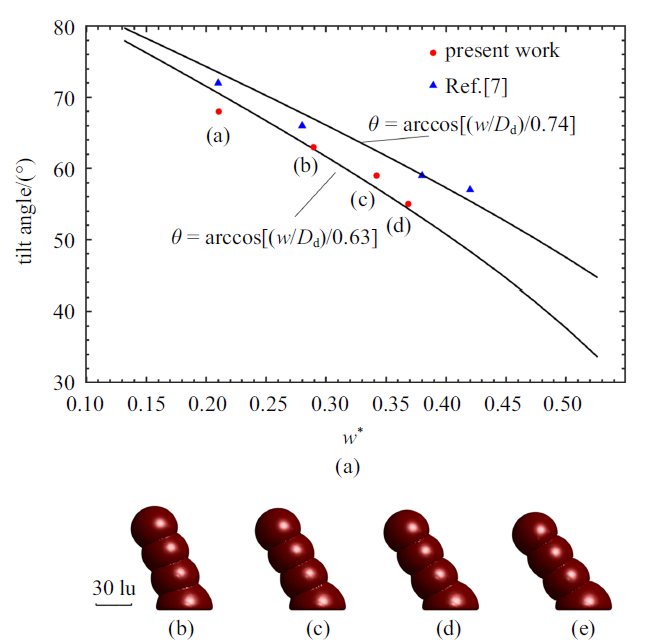
如图9所示, 根据式(28)计算得到扫描步距分别为$w^{\ast }=0.21$, 0.29, 0.34, 0.37的工况下, 多液滴斜柱沉积模拟结果具有均匀的形貌结构, 并且倾角与理论结果一致^[7].

图9

新窗口打开|下载原图ZIP|生成PPT
图9斜柱倾角与扫描步距关系及其沉积形貌

Fig.9Relationship between the tilt angle and the scanning step

4 结论

本文通过建立LBM液滴连续沉积模型, 探究了铝液滴沉积过程中水平偏移的主要发生阶段及其影响因素. 液滴沉积运动从能量角度被分为下落、快速扩张、慢速扩张和回弹4个阶段. 扩张阶段是偏移加速运动的主要阶段, 而回弹阶段产生了主要偏移距离. 偏移运动主要推动力源于毛细力、重力和黏性剪切力在扩张阶段中的共同作用. 此外, 偏移距离随轴线距离演化趋势呈阶段化特性, 拟合结果呈对勾函数关系. 这种阶段化特性是偏移运动中加速段时长和速度极大值间的竞争关系导致. 沉积高度和浸润度的减小均不影响该演化趋势, 但会使偏移程度增大. 结合斜柱几何特性, 扫描步距与斜柱倾角的关系式得到建立. 在该模型下选择扫描步距, 进行的多液滴连续沉积模拟, 具有均匀的斜柱形貌, 并且倾角与理论结果吻合程度较好. 本文所得结果有助于偏移距离的精确控制, 提高斜柱沉积制造的形貌质量.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 王强, 郑雄飞, 王赫然 等. 基于多喷头生物3D打印系统的管腔型结构构建
机械设计与制造, 2019, 11: 265-268
[本文引用: 1]

(Wang Qiang, Zheng Xiongfei, Wang Heran, et al. Fabrication of lumen structure based on multi-nozzle biological 3D printing system
Machinery Design & Manufacture, 2019, 11: 265-268 (in Chinese))
[本文引用: 1]

[2] 方健文, 朱佩文, 邵毅. 3D 打印在眼科血管性疾病的应用进展
国际眼科杂志, 2019, 19(9): 1499-1502
[本文引用: 1]

(Fang Jianwen, Zhu Peiwen, Shao Yi. Application progress of 3D printing technology in ophthalmic vascular disease
International Eye Science, 2019, 19(9): 1499-1502 (in Chinese))
[本文引用: 1]

[3] 芮敏, 郑欣, 张云庆 等. 3D打印多孔钛合金支架修复兔桡骨骨缺损
中国组织工程研究, 2019, 23(18): 2789-2793
[本文引用: 1]

(Rui Min, Zheng Xin, Zhang Yunqing, et al. Three-dimensional printing porous titanium alloy scaffold repairs radial bone defect in rabbits
Chinese Journal of Tissue Engineering Research, 2019, 23(18): 2789-2793 (in Chinese))
[本文引用: 1]

[4] 刘建恒, 李明, 刘鐘阳 等. 3D 打印多孔矿化胶原硫酸钙仿生组织工程骨修复兔股骨髁包容性骨缺损的实验研究
创伤外科杂志, 2020, 22(6): 408-413
[本文引用: 1]

(Liu Jianheng, Li Ming, Liu Zhongyang, et al. Experimental study on a new tissue engineering bone in repairing rabbit bone defect
Journal of Trauma Surgery, 2020, 22(6): 408-413 (in Chinese))
[本文引用: 1]

[5] 刘赵淼, 徐元迪, 逄燕. 压电式微滴按需喷射的过程控制和规律
力学学报, 2019, 51(4): 1031-1042
DOI [本文引用: 1]
微滴喷射增材制造技术中沉积微滴的大小与均匀性是影响成型件质量的关键因素.本文设计了一种用于生成均匀微滴的压电驱动式微滴喷射装置,通过压电材料带动柔性膜片振动,将液体从喷嘴中喷出生成微滴,采用数值模拟和实验相结合的方法,研究了不同控制参数下膜片振幅及其对生成微滴尺寸和均匀性的影响.研究结果表明：膜片振幅大小受到驱动电压和压电频率的共同影响,压电频率是导致膜片中心点振幅实验测量值小于理论计算值的主要原因,膜片振动会导致喷嘴内部压力发生变化从而影响微滴生成尺寸.在相同驱动电压条件下,压电频率为10 Hz时存在压电膜片振幅最大值.随着膜片振幅的增大,喷孔处液体速度和液柱长度增大到临界值时可以生成微滴,当喷孔处的液柱长度超过临界值时,会形成卫星液滴. 当膜片振幅区间在30 $\mu$m$\sim $42 $\mu $m可以稳定生成微滴,生成最小微滴尺寸为339.8$\mu$m,直径最大变化率为0.29%,相邻两微滴间距最大变化率为2.67%,生成微滴的尺寸及均匀性较好.研究结果有助于提高压电式微滴喷射装置的液滴生成质量.
(Liu Zhaomiao, Xu Yuandi, Pang Yan, et al. Study of process control on piezoelectric drop-on-demand ejection
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1031-1042 (in Chinese))
[本文引用: 1]

[6] 刘赵淼, 钟希祥, 杨刚 等. 气动式微滴喷射中液滴稳定生成的动力学特性研究
机械工程学报, 2020, 56(23): 203-211
[本文引用: 1]

(Liu Zhaomiao, Zhong Xixiang, Yang Gang, et al. Study on the kinetic characteristics of droplet formation in pneumatic microdroplet injection
Journal of Mechanical Engineering, 2020, 56(23): 203-211 (in Chinese))
[本文引用: 1]

[7] Zhang DC, Qi LH, Luo J, et al. Direct fabrication of unsupported inclined aluminum pillars based on uniform micro droplets deposition
International Journal of Machine Tools and Manufacture, 2017, 116: 18-24
DOIURL [本文引用: 4]

[8] Fang M, Chandra S, Park CB. Building three-dimensional objects by deposition of molten metal droplets
Rapid Prototyping Journal, 2008, 14(1): 44-52
DOIURL [本文引用: 1]

[9] Lee TK, Kang TG, Yang JS, et al. Drop-on-demand solder droplet jetting system for fabricating microstructure
IEEE Transactions on Electronics Packaging Manufacturing, 2008, 31(3): 202-210
DOIURL [本文引用: 1]

[10] 李素丽, 杨来侠, 卢秉恒. 基于金属液滴水平重叠沉积工艺对表面形貌和内部质量优化研究
稀有金属材料与工程, 2019, 8: 2460-2467
[本文引用: 1]

(Li Suli, Yang Laixia, Lu Bingheng. Process optimization of surface morphology and internal quality based on metal droplets horizontal lapped deposition
Rare Metal Materials and Engineering, 2019, 8: 2460-2467 (in Chinese))
[本文引用: 1]

[11] 李素丽, 杨来侠, 卢秉恒. 金属液滴垂直搭接成形工艺
稀有金属材料与工程, 2019, 48(9): 2773-3776
[本文引用: 1]

(Li Suli, Yang Laixia, Lu Bingheng. Vertically lapped deposition process of metal droplet
Rare Metal Materials and Engineering, 2019, 48(9): 2773-3776 (in Chinese))
[本文引用: 1]

[12] Wang CH, Tsai HL, Wu YC, et al. Investigation of molten metal droplet deposition and solidification for 3D printing techniques
Journal of Micromechanics & Microengineering, 2016, 26(9): 095012
[本文引用: 1]

[13] Du J, Wei ZY. Numerical analysis of pileup process in metal microdroplet deposition manufacture
International Journal of Thermal Sciences, 2015, 96: 35-44
DOIURL [本文引用: 1]

[14] Fang M, Chandra S, Park CB. Experiments on remelting and solidification of molten metal droplets deposited in vertical columns
Journal of Manufacturing & Engineering, 2007, 129(2): 461-466
[本文引用: 1]

[15] Zhang DC, Qi LH, Luo J, et al. Parametric mapping of linear deposition morphology in uniform metal droplet deposition technique
Journal of Materials Processing Technology, 2019, 264: 234-239
DOIURL [本文引用: 1]

[16] Graham PJ, Farhangi MM, Dolatabadi A. Dynamics of droplet coalescence in response to increasing hydrophobicity
Physics of Fluids, 2012, 24(11): 175-181
[本文引用: 1]

[17] Dalili A, Chandra S, Mostaghimi J, et al. Formation of liquid sheets by deposition of droplets on a surface
Journal of Colloid & Interface Science, 2014, 418: 292-299
[本文引用: 1]

[18] Li R, Ashgriz N, Chandra S, et al. Drawback during deposition of overlapping molten wax droplets
Journal of Manufacturing Science and Engineering, 2008, 130(4): 1188-1188
[本文引用: 1]

[19] Ju JJ, Jin ZY, Zhang HH, et al. The impact and freezing processes of a water droplet on different cold spherical surfaces
Experimental Thermal and Fluid Science, 2018, 96: 430-440
DOIURL [本文引用: 1]

[20] Tian DW, Tian YH, Wang CQ, et al. Modeling of an oblique impact of solder droplet onto a groove with the impact point to be offset from the groove surfaces interface
Journal of Materials Science, 2009, 44: 1772-1779
DOIURL [本文引用: 2]

[21] Shan X, Chen H. Lattice Boltzmann model for simulating flows with multiple phases and components
Physical Review E, 1993, 47(3): 1815-1820
DOIURL [本文引用: 1]

[22] He X, Doolen GD. Thermodynamic foundations of kinetic theory and lattice Boltzmann models for multiphase flows
Journal of Statistical Physics, 2002, 107(1-2): 309-328
DOIURL [本文引用: 2]

[23] Shan XW, Doolen G. Multicomponent Lattice- Boltzmann model with interparticle interaction
Journal of Statistical Physics, 1995, 81(1-2): 379-393
DOIURL [本文引用: 2]

[24] Huber C, Parmigiani A, Chopard B, et al. Lattice Boltzmann model for melting with natural convection
International Journal of Heat and Fluid Flow, 2008, 29(5): 1469-1480
DOIURL [本文引用: 1]

[25] Noble DR, Torczynski JR. A lattice-Boltzmann method for partially saturated computational cells
International Journal of Modern Physics C, 1998, 9(8): 1189-1201
DOIURL [本文引用: 1]

[26] Cook RK, Noble DR, Williams JR. A direct simulation method for particle-fluid systems
Engineering Computation, 2004, 21(2-4): 151-168
DOIURL [本文引用: 3]

[27] 张艳勇, 陈宝明, 李佳阳. 基于LBM 研究骨架对相变材料融化蓄热的影响
山东建筑大学学报, 2020, 35(2): 53-75
[本文引用: 1]

(Zhang Yanyong, Chen Baoming, Li Jiayang. Study on the influence of skeleton on the melting and heat storage of phase change materials based on LBM
Journal of Shandong Jianzhu University, 2020, 35(2): 53-75 (in Chinese))
[本文引用: 1]

[28] 高一倩, 柳毅, 李凌. 基于LBM的三角腔固液相变模拟
储能科学与技术, 2020, 9(6): 1798-1805


(Gao Yiqian, Liu Yi, Li Ling. Numerical simulation of natural convection melting inside a triangular cavity using lattice Boltzmann method
Energy Storage Science and Technology, 2020, 9(6): 1798-1805 (in Chinese))


[29] 周俊杰, 冯妍弁, 蔡峻杰 等. 等离子弧焊接熔池相变过程的LBM模拟与验证
工程热物理学报, 2019, 40(2): 442-449


(Zhou Junjie, Feng Yanhui, Cai Junjie, et al. Lattice Boltzmann simulation of phase transition process in a weld pool in plasma arc welding
Journal of Engineering Thermophysics, 2019, 40(2): 442-449 (in Chinese))


[30] Lu CL, Wang HN, Wang SY, et al. Effect of heating modes on melting performance of a solid-liquid phase change using lattice Boltzmann model
International Communications in Heat and Mass Transfer, 2019, 108: 104330
DOIURL

[31] Kasibhatla RR, Brüggemann D. Smoothed iterative enthalpy approach for solid-liquid phase change
International Journal of Thermal Sciences, 2020, 152: 106187
[本文引用: 1]

[32] Zhao J, Li X, Cheng P. Lattice Boltzmann simulation of a droplet impact and freezing on cold surfaces
International Communications in Heat and Mass Transfer, 2017, 87: 175-182
DOIURL [本文引用: 1]

[33] Sun JJ, Gong JY, Li GJ. A lattice Boltzmann model for solidification of water droplet on cold flat plate
International Journal of Refrigeration, 2015, 59: 53-64
DOIURL

[34] Huang RZ, Wu HY. Phase interface effects in the total enthalpy-based lattice Boltzmann model for solid-liquid phase change
Journal of Computational Physics, 2015, 294: 346-362
DOIURL [本文引用: 2]

[35] 霍元平, 王军锋, 左子文 等. 滴状模式下液桥形成及断裂的电流体动力学特性研究
力学学报, 2019, 51(2): 425-431
DOI [本文引用: 1]
对电场作用下微通道荷电液滴脱落过程中液桥形成及断裂的显微演变特征进行了可视化实验研究.借助时空分辨率较高的高速摄像技术精确捕捉了电场作用下液桥形成及断裂的界面演化过程,研究了液桥的界面结构变化及其断裂的动力学显微演变行为,获得了时间特征数、电邦德数及半月面形成角对液桥长度及断裂顺序的作用规律.实验结果显示,液桥断裂长度取决于黏度与表面张力之比,而受荷电弛豫时间的影响甚微,低电压工况下各实验介质液桥相对长度的变化并不明显,而在较高电压工况下相对液桥长度的增长速度加快.随着电邦德数的不断增加,液桥长度的变化在较高邦德数下更为明显且存在突变区,此时伴随着雾化模式的转变,表明液桥的突变恰恰是雾化模式过渡的信号.不同物性介质的射流过渡行为由于液桥上下游形成角的变化而存在较大差异.对于无水乙醇介质,电邦德数的增加使滴状模式首先过渡到纺锤模式,而对于生物柴油,滴状模式后会首先出现脉动模式而非纺锤模式.
(Huo Yuanping, Wang Junfeng, Zuo Ziwen, et al. Electrohydrodynamic characteristics of liquid bridge formation at the dripping mode of electrosprays
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 425-431 (in Chinese))
[本文引用: 1]

[36] 李桥忠, 陈木凤, 李游 等. 浸没边界-简化热格子Boltzmann方法研究及其应用
力学学报, 2019, 51(2): 392-404
DOI [本文引用: 1]
针对流固耦合传热问题,本文提出了一种基于浸没边界-简化热格子玻尔兹曼方法(immersed boundary method-simplified thermal lattice Boltzmann method,IB-STLBM)的耦合模型.不同于传统的格子玻尔兹曼方法使用分布函数演化流场和温度场,简化热格子玻尔兹曼方法(simplified thermal lattice Boltzmann method,STLBM)的演化过程不需要依赖分布函数,只涉及平衡态分布函数和非平衡态分布函数,能够直接演化宏观量,极大减小了计算过程中所占用的虚拟内存,简化了边界条件的实现方式,同时具有较高的稳定性.传统的浸没边界法对流场的计算采用欧拉网格,对固体边界采用拉格朗日网格,认为固体边界是对流场产生某种体积力.在应用浸没边界法时,汲取介观的思想,把固体的介入看作是对流场的干扰,打破了固体附近流体介观微团颗粒原始的平衡状态,这种干扰可以看作是在耦合边界上产生的一个非平衡项,可用非平衡态分布函数来表示.基于此,在模型中浸没边界法与简化热格子玻尔兹曼方法更紧密联系在一起,更大程度发挥二者的优点,整个计算过程更加简单直观,符合物理特性.通过对热圆柱绕流和内含热颗粒的封闭方腔自然对流问题的模拟以及对其结果的分析,验证了该算法在求解流固耦合传热问题的有效性和可行性.
(Li Qiaozhong, Chen Mufeng, Li You, et al. Immersed boundary-simplified thermal lattice Boltzmann method for fluid-structure interaction problem with heat transfer and its application
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 392-404 (in Chinese))
[本文引用: 1]

[37] 尚超, 阳倦成, 张杰 等. 镓铟锡液滴撞击泡沫金属表面的运动学特性研究
力学学报, 2019, 51(2): 380-391
DOI [本文引用: 1]
常温下为液态的镓铟锡合金以其优异的导热性能在具有特殊要求的传热领域有着重要的应用价值,与传统流动介质相比较大的表面张力使得其产生的流动现象必有所区别.本文研究镓铟锡所形成的液滴撞击泡沫金属表面后所产生的铺展、回缩及回弹现象.采用高速相机拍摄液滴投影轮廓随液滴运动的变化过程,并通过图像处理获得不同撞击速度、底板表面孔径下的液滴铺展系数、中心位置轮廓高度以及液滴回弹后在空中的振动特性.研究结果表明：具有较高表面张力的镓铟锡液滴的铺展系数随无量纲时间的变化在铺展初始阶段仍满足常规流体的1/2次幂关系,只在铺展后期与底板的无量纲孔径有关系;液滴的最大铺展系数在较小无量纲孔径底板大于在光滑镍板,且随底板无量纲孔径增大而逐渐减小;在回弹过程,由于底板孔隙结构的存在使得液滴回弹后在空中的振动呈现3种形态：规则的横向和纵向振动、带旋转的横向和纵向振动以及旋转振动;最后,通过对振动频率的拟合和分析,进一步拓展了传统振动频率理论公式在非规则振动过程预测中的应用.
(Shang Chao, Yang Juancheng, Zhang Jie, et al. Experimental study on the dynamic characteristics of Galinstan droplet impacting on the metal foam surface
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 380-391 (in Chinese))
[本文引用: 1]