崔竹轩, 丁举春, 司廷^,2)中国科学技术大学近代力学系, 合肥 230027

NUMERICAL STUDY ON THE EVOLUTION OF THREE-DIMENSIONAL CONCAVE CYLINDRICAL INTERFACE ACCELERATED BY REFLECTED SHOCK¹⁾

Cui Zhuxuan, Ding Juchun, Si Ting^,2)Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China

通讯作者: 2)司廷, 教授, 主要研究方向: 实验流体力学, 复杂界面流动. E-mail:tsi@ustc.edu.cn

收稿日期:2021-01-24接受日期:2021-02-28网络出版日期:2021-05-19

基金资助:

1)国家自然科学基金.12027801 国家自然科学基金.91952205 国家自然科学基金.11621202 中国科学院青年创新促进会.2018491

Received:2021-01-24Accepted:2021-02-28Online:2021-05-19
作者简介 About authors


摘要
激波与气柱相互作用是Richtmyer-Meshkov不稳定性研究的经典案例. 单次激波与二维气柱相互作用已得到广泛关注, 但是反射激波再次冲击气柱 (尤其是三维气柱) 的研究较少, 相关演化规律和机理尚不清楚. 反射激波再次冲击演化中的气柱界面会产生新的斜压涡量, 影响涡量的输运和分布, 从而影响界面的演化. 本文采用自主开发的HOWD (high-order WENO and double-flux methods) 程序, 研究了马赫数为1.29的平面激波冲击N$_{2}$气柱(气柱外为SF$_{6})$的演化过程, 并考察了反射激波对二维和三维凹气柱界面演化的影响规律. 在数值模拟中, 选取了不同的反射距离 (定义为气柱和反射边界的距离), 得到了二维和三维凹气柱在反射激波冲击前后的完整演化图像, 提取了气柱上特征点位置随时间变化的定量数据, 重点分析了不同演化阶段气柱几何特征及斜压涡量分布的变化趋势. 研究表明, 反射距离决定着反射激波作用气柱时的激波形状和气柱形态, 从而影响斜压涡量的生成和分布, 进而改变气柱的不稳定性演化过程. 对于三维气柱, 不同高度截面上的斜压涡量分布不同, 从而诱导出复杂的三维演化结构.
关键词： Richtmyer-Meshkov不稳定性;反射激波;气柱;数值计算

Abstract
The interaction of shock wave with cylindrical interface is fundamental in study of the Richtmyer-Meshkov (RM) instability. Although the RM instability of two-dimensional (2D) cylindrical interfaces under a single shock wave has been extensively studied previously, the interaction of reflected shock (short for reshock) with cylindrical interfaces, especially three-dimensional (3D) cylindrical interfaces has not been investigated thoroughly, with relevant development rules and underlying mechanisms unclear. When the shock wave interacts with the evolving interface after reshock, new baroclinic vorticity appears on the interface and this will have a major influence on the evolution of the interface. In this work, the HOWD (high order WENO and double-flux) solver developed in our group is used to numerically study the reshock effect on the evolution of 2D and 3D concave cylindrical N$_{2}$/SF$_{6}$ (inner/outer phases) interfaces with incident planar shock strength of $Ma=1.29$. This work will focus on the evolution of 2D and 3D concave cylindrical interfaces after the reshock under different reflected distances, which is defined as the distance between the end wall and the center of the gas cylinder. Series of data have been extracted both before and after the reshock, including the schlieren and vorticity images of the evolving gas cylinder and the quantitative data of the geometric position of the feature points on the gas cylinder. The geometrical characteristics of the distorted interface and the generation and distribution of baroclinic vorticity in different stages are analyzed. The results indicate that for different reflected distances, the shapes of the evolving interface and the reshock at the interaction instance affect the generation and distribution of the baroclinic vorticity, resulting in distinct evolution characteristics of the RM instability. For the 3D concave cylindrical interface, the baroclinic vorticity distributed in 3D space at different heights can induce complicated 3D structures of the evolving interface.
Keywords：Richtmyer-Meshkov instability;reflected shock;gas cylinder;numerical simulation


PDF (29981KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
崔竹轩, 丁举春, 司廷. 反射激波作用下三维凹气柱界面演化的数值研究¹⁾. 力学学报, 2021, 53(5): 1246-1256 DOI:10.6052/0459-1879-21-042
Cui Zhuxuan, Ding Juchun, Si Ting. NUMERICAL STUDY ON THE EVOLUTION OF THREE-DIMENSIONAL CONCAVE CYLINDRICAL INTERFACE ACCELERATED BY REFLECTED SHOCK¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1246-1256 DOI:10.6052/0459-1879-21-042

引言

Richtmyer-Meshkov (RM) 不稳定性是指一个具有初始扰动的流体分界面受到瞬时冲击力 (比如激波) 作用后, 界面上的初始小扰动随着时间不断增长, 在演化后期界面附近会生成许多小尺度涡, 并最终形成湍流混合的现象. 在1960年, Richmyer^[1]提出了激波加速下流体流动稳定性的理论推导和分析预测, Meshkov^[2]在1969年对这一问题开展了一系列激波管实验, 证实了Richtmyer的理论预测. 开展激波$\!-\!$界面相互作用研究不仅在流动不稳定性、旋涡动力学以及湍流形成机理等方面有着重要的学术价值, 而且在工程领域也有广泛的应用. 例如在惯性约束核聚变^[3-5]中, 氘氚靶丸外层为烧蚀材料, 内层为氘氚燃料. 当高能激光照射球形靶丸, 表面烧蚀层材料被高温烧蚀后形成向中心传播的汇聚激波. 受加工精度限制, 靶丸各层分界面存在初始小扰动, 这些小扰动在激波作用后发生RM不稳定性演化, 从而加剧了燃料和外层壳体材料的混合, 使得中心区压力和温度下降, 导致点火失败^[6]. 在超燃冲压发动机中^[7], 燃料和氧化剂在燃烧室的滞留时间在微秒量级, 激波和燃料/氧化剂界面相互作用可以促进燃料与氧化剂的混合, 提高燃烧和推进效率^[8]. 另外, RM不稳定性也被用来解释超新星爆发等天文现象^[9].

由于RM不稳定性在诸多科学和工程领域有重要价值, 自从其被发现以来, 科研工作者已经采用理论分析、数值计算、实验研究等手段开展了大量研究^[10-12]. 作为RM不稳定性的经典案例, 平面激波与气柱相互作用已被大量研究. Ding等^[13-14]利用肥皂膜技术生成三维柱形界面, 研究了三维性对重气柱和轻气柱的影响, 并将Haas和Sturtevant^[15]提出的理论模型拓展到三维情形. Ou等^[16]实验和数值研究了激波冲击椭圆重气柱的不稳定性发展, 重点关注了激波聚焦和射流现象, 并分析Atwood数($A_t =\left( {\rho_{2} -\rho_{1} } \right)/\left( {\rho_{2} +\rho_{1} } \right)$, 其中$\rho_{1} $和$\rho_{2} $分别为激波冲击前气柱外和气柱内气体密度)和椭圆气柱的长宽比^[17]对气柱演化的影响. Zou等^[18]利用粒子图像测速 (PIV) 方法研究了激波冲击不同长宽比椭圆气柱后的速度场, 分析了长宽比为0.25 $\sim$ 0.4的椭圆气柱, 得到了随着长宽比增大, 涡量和环量的最大值增大、涡心距缩短、气柱演化变快的结论.

激波冲击一道扰动界面后, 界面会持续变形, 同时激波也会变成一道扰动激波, 扰动激波到达反射壁面后形成一道反射激波, 二次冲击处于演化中的流体界面. 因此, 考察反射激波和变形界面相互作用的不稳定性演化至关重要^[19]. 二次作用之前, 激波和界面的形状会影响斜压涡量的生成和压力分布, 从而影响二次冲击之后的不稳定性演化. 反射激波二次冲击界面的不稳定性发展受到反射距离、激波强度等诸多参数的影响, 因此反射激波对界面演化造成的影响比单次激波冲击情形要更加复杂, 同时, 研究反射激波与界面相作用对于研究湍流混合有重要价值^[20-23].

目前, 反射激波诱导RM不稳定性的研究相对较少. 实验研究一直是研究激波作用下RM不稳定性发展的重要手段. Jacobs等^[24]利用振荡产生三维短波长扰动, 在竖直激波管中研究了反射激波冲击Air/SF$_{6}$界面的不稳定性发展, 获得了混合宽度增长的定量数据, 发现反射激波作用后, 不同初始条件下的混合宽度以相同增长率线性增长. Si等^[25]进行了不同反射距离27 $\sim$ 125 mm下反射激波冲击Air/SF$_{6}$气泡的实验研究, 发现了反射距离较小时会出现方向相反的射流以及界面振荡现象, 反射距离较长时则会出现小尺度的涡结构. Mohaghar等^[26]则在倾斜激波管中, 利用平面激光诱导荧光 (PLIF) 技术, 获得了单模及多模界面的浓度演化图. 此外, 已有的理论研究多关注适用于二维单模界面混合宽度增长率的模型, 例如, Brouillette和Strurtevant^[27]给出的广义Richtmyer模型. 鉴于RM不稳定性的实验研究对测量技术要求很高且理论分析很难获得大扰动界面演化的解析解, 数值模拟便成为一种广泛采用的有效研究方法^[28-30]. 数值计算方法近年来发展十分迅速. Hill等^[20]利用大涡模拟, 对不同马赫数下反射激波冲击平直Air/SF$_{6}$界面进行模拟, 得到反射激波作用后, 混合层宽度增长率随激波马赫数增大而变大的规律. Shankar和Lele^[31]通过数值模拟研究了反射激波冲击Air/SF$_{6}$气帘界面, 得到了反射距离越大, 反射激波作用后界面会以更快的速度混合并产生小尺寸结构的结论.

在已开展的反射激波冲击二维气柱研究中, 实验和数值计算均取得了一定进展. 实验方面, Zhang等^[32]利用PIV观测反射激波与SF$_{6}$无膜重气柱相互作用后的流场, 获得了相应的速度场和涡量场, He等^[33]利用无膜气柱研究了反射激波作用SF$_{6}$和Ar两种重气柱的演化, 分析了气柱几何尺寸的变化规律. 数值计算方面, Wang等^[34]使用VAS2D (2-Dimensional & Axisymmetric Vectorized Adaptive Solver) 程序研究了不同反射距离下Air/SF$_{6}$气柱的演化, 分析了界面几何尺寸, 特征点以及环量的变化规律, Sha等^[35]基于大涡模拟研究了反射激波作用Air/SF$_{6}$气柱后的波系以及射流的演化. 这些研究主要集中在二维重气柱方向, 三维性和Atwood数对气柱界面演化的影响还有待更深入研究.

虽然反射激波作用气柱的RM不稳定性已有一些研究, 但反射激波作用轻气柱以及反射激波作用三维气柱的研究尚未见报道, 其中涉及的物理规律和机理仍有待揭示. 鉴于上述讨论, 本文采用数值计算方法, 以三维凹气柱为研究对象, 选取反射距离以及凹气柱的三维性为变量, 对比研究不同反射距离时二维和三维凹气柱界面的演化过程, 从而进一步揭示反射激波与气柱界面相互作用的RM不稳定性演化规律和机理.

1 数值计算方法

1.1 控制方程与数值程序

激波与界面作用时间很短, 黏性、重力、气体扩散以及热传导等因素对气柱演化影响很小, 同时忽略化学反应过程, 这类流动可以用可压缩无黏欧拉方程来表示

(1)$\begin{eqnarray} \label{eq1} \frac{\partial { U}}{\partial t}+\frac{\partial { F}}{\partial x}+\frac{\partial {G}}{\partial y}+\frac{\partial {H}}{\partial z}={\bf0} \end{eqnarray}$
方程中$U$表示守恒变量, $F$, $G$, $H$分别表示$x$, $y$, $z$方向上的通量. 可以表示为

(2)$\left.\begin{array}\begin {U}=\left( {\begin{array}{c} \rho \\ \rho u \\ \rho v \\ \rho w \\ E \\ \rho_{i} \\ \end{array}} \right), \quad F=\left( {\begin{array}{c} \rho u \\ \rho u^{2}+p \\ \rho uv \\ \rho uw \\ \left( {E+p} \right)u \\ \rho_{i} u \\ \end{array}} \right) \\ G=\left( {\begin{array}{c} \rho v \\ \rho uv \\ \rho v^{2}+p \\ \rho vw \\ \left( {E+p} \right)v \\ \rho_{i} v \\ \end{array}} \right) ,\quad H=\left( {\begin{array}{c} \rho w \\ \rho uw \\ \rho vw \\ \rho w^{2}+p \\ \left( {E+p} \right)w \\ \rho_{i} w \\ \end{array}} \right)\end{array}\right\}$
其中, $u$, $v$, $w$表示流体在$x$, $y$, $z$各方向上的速度, $\rho $表示混合气体的密度, $\rho _{i} $表示界面内单种气体的密度, $p$表示混合气体的压力, $E$表示流体单位体积所包含的总能量. 为了使得方程组封闭, 还需增加气体的状态方程

(3)$\begin{eqnarray} \label{eq3} E=\frac{p}{r-1}, \ \ r=\frac{\rho_{1} C_{{\rm p1}} +\rho_{2} C_{{\rm p2}} }{\rho_{1} C_{{\rm v1}} -\rho_{2} C_{{\rm v2}} } \end{eqnarray}$
其中, $C_{{\rm p}i}$表示定压比热容, $C_{{\rm v}i}$表示定容比热容.

本文采用课题组自主开发的HOWD (high-order WENO and double-flux methods) 程序^[36]进行数值模拟, 该程序使用均匀网格, 能够实现五阶WENO (weighted essentially non-oscillatory)^[37]重构与双通量算法的耦合, 可以消除界面处的非物理震荡, 在准确模拟激波的同时, 还可以捕捉流场中的小涡结构. 由于小尺度的涡结构在RM不稳定性的研究中十分重要, 对数值格式提出了更高的要求, 而已有的数值结果证明, WENO格式对这些问题有更强的模拟能力^[21,37], 因此, 该程序选用WENO格式来离散方程.

1.2 计算模型和程序验证

在已有单次激波冲击气柱的实验中, 主要采取肥皂膜技术生成气柱^[38-39]. 由于肥皂膜存在表面张力, 气柱形状可以用Young-Laplace方程描述^[40], 即气柱界面上各处的主曲率之和为常数. 在柱坐标系中, 代入主曲率计算公式可以得到

(4)$\begin{eqnarray} \label{eq4} \frac{\Delta p}{\sigma }=-\frac{r_{zz} }{\left( {1+r_{z}^{2}} \right)^{{3}/{2}}}+\frac{1}{r\left( {1+r_{z}^{2}} \right)^{{1}/{2}}} \end{eqnarray}$
其中, $r=\sqrt {x^{2}+y^{2}} $表示在某一高度上气柱的半径, $r_{zz}$为半径关于高度的二阶导数, $r_{z}$为半径关于高度的一阶导数. 存在一个特殊情况即气柱内外压力差相等. 此时$\Delta p=0$, 此时为凹气柱, 气柱界面为极小曲面^[41], 此时气柱界面的表达式为

(5)$\begin{eqnarray} \label{eq5} \frac{r^{2}}{r_{{\rm 0}}^{2}}=\cosh^{2}\left( {\frac{z}{r_{{\rm 0}} }}\right) \end{eqnarray}$
其中, $r_{0}$表示$z=0$时对称面的气柱半径. 二维气柱半径取$r=17.5$ mm, 凹气柱边界面半径与二维气柱相同, 可计算得到$r_{0}=13.7$ mm.

计算模型如图1(a)所示, 模拟在方形截面激波管实验段中有一凹气柱界面, 实验段尾端封闭, 即为固壁边界. 反射距离定义为气柱圆心至右侧固壁端的距离. 整个计算域为200 mm$\times$140 mm$\times$20 mm. 为节省计算时间, 对于二维算例只计算半个气柱, 计算域为200 mm,$\times$70 mm$\times$20 mm; 对于三维算例计算对称的1/4个气柱, 计算域为200 mm$\times$70 mm$times$10 mm.

图1

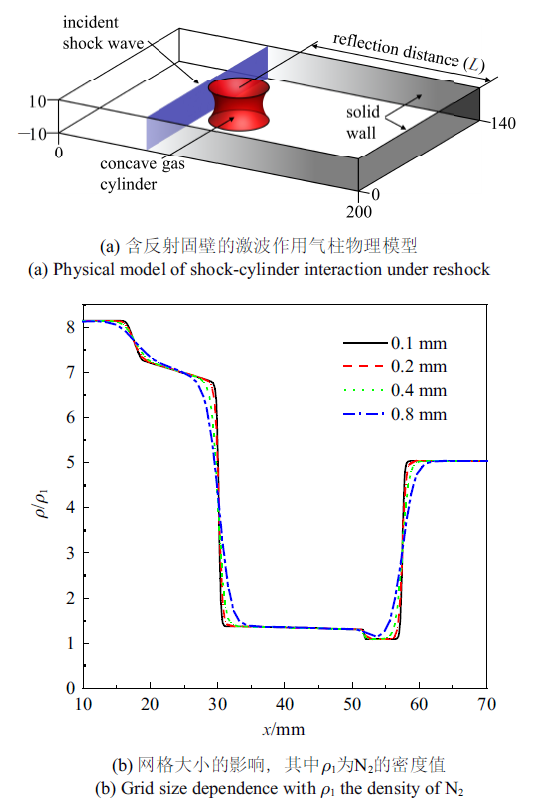新窗口打开|下载原图ZIP|生成PPT
图1计算模型和收敛性验证

Fig.1Computational domain and grid convergence validation



为了验证网格收敛性, 以平面激波与二维气柱作用作为参考. 为了便于对比, 本文计算初始条件与已开展的实验^[38-39]设置相同, 即激波马赫数$Ma=1.29$, $T_{0}=293.15$ K, $P_{0}=101 325$ Pa. 二维工况气柱内气体为97%的 N$_{2}$与3%的 SF$_{6}$混合气体, 气柱外则为纯SF$_{6}$, $T_{0}=293$ K, $P_{0}=101 325$ Pa, 凹气柱内气体为95%的 N$_{2}$与5%的 SF$_{6}$混合气体, 气柱外则为纯SF$_{6}$.

如图1(b)所示, 分别在网格大小为0.8 mm, 0.4 mm, 0.2 mm和0.1 mm时进行计算, 比较$t=80$ $\mu $s时对称轴上的密度分布, 可见网格大小为0.2 mm和网格大小为0.1 mm的计算结果已十分接近, 因此二维气柱算例采用尺寸为0.1 mm的均匀网格. 由于三维凹气柱算例计算量较大, 采用尺寸为0.2 mm的均匀网格.

已有研究已经对HOWD程序的准确性进行了验证^[13-14,16], 这里采用无反射激波作用二维轻气柱与三维凹气柱界面演化的数值计算结果与Ding^[36]的实验结果进行对比. 图2显示的是典型时刻的纹影结果, 可以观察到数值计算结果和实验结果吻合, 包括激波波系和界面结构都能一一对应. 证明了计算程序的可靠性和适用性.

图2

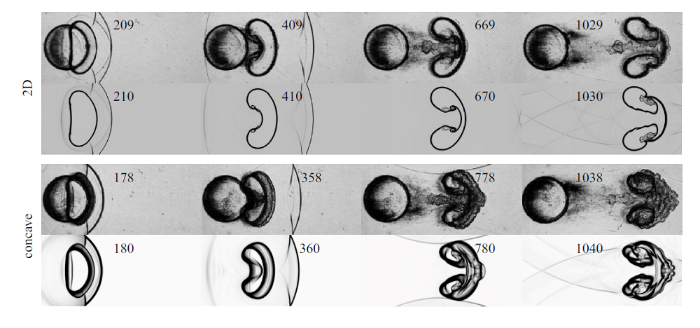新窗口打开|下载原图ZIP|生成PPT
图2无反射激波情况下二维气柱(上)和三维凹气柱(下)数值计算结果与相应的实验结果对比, 单位为$\mu $s. 对比图中上面是实验纹影结果, 下面是数值纹影结果

Fig.2Validation of the numerical results in comparison with experimental ones for 2D (top) and concave cylinders (bottom), respectively (time unit: $\mu $s). The experimental schlieren images are listed on top

2 反射激波对气柱界面演化的影响

2.1 二维气柱

图3展示了反射距离分别为40 mm, 80 mm, 120 mm时二维轻气柱演化的数值计算结果, 图的上半部分显示涡量分布 (其中深色为正涡量, 浅色为负涡量), 下半部分为纹影结果. 激波第一次冲击二维气柱界面后, 气柱界面上生成斜压涡量, 且距离对称面越远的界面上的涡量越大, 这是因为激波冲击气柱界面过程中压力梯度和密度梯度的夹角在逐渐变化.受到激波压缩以及斜压涡量的影响, 上游界面变得扁平, 随后从对称面附近开始, 上游气柱界面产生向下游的凹陷并生成射流结构, 随后向下游运动, 与下游界面距离缩短形成一个桥状结构. 下游界面在600 $\mu$s附近会因旋涡诱导^[36]产生负涡量.

图3

新窗口打开|下载原图ZIP|生成PPT
图3不同反射距离 (40 mm, 80 mm, 120 mm) 下二维轻气柱的演化图像, 并与无反射情况的结果进行对比. 入射激波从左往右运动,最右侧是固壁. 图中数字表示时刻, 单位为$\mu $s

Fig.3Evolution images of a two-dimensional light gas cylinder under reshock with reflected distance of 40 mm, 80 mm, 120 mm, respectively,in comparison with those without reshock (time unit: $mu$s)



当反射激波再次作用界面后, 下游界面的负涡量强度会更高. 以反射距离40 mm的工况为例, 如 图4所示, 320 $\mu$s时反射激波刚接触界面, 密度梯度与压力梯度几乎重合, 因此生成的斜压涡量强度较小. 随着激波与界面作用位置的变化, 生成的斜压涡量强度逐渐变大, 在360 $\mu$s时运动速度较快的透射激波再次运动到界面外形成前导激波, 并随着位置的变化密度梯度与压力梯度夹角逐渐变小, 斜压涡量强度变小. 总体来说, 斜压涡量的强度沿右侧界面从对称面到最外侧先变大再变小, 这与单一的入射激波作用气柱界面的情况完全不同.

图4

新窗口打开|下载原图ZIP|生成PPT
图4反射距离为40 mm时, 反射激波作用变形界面过程中的精细结构变化

Fig.4Variation of fine structures during the interaction of the reshock with distorted interface at reflected distance of 40 mm



如图5所示, 经过一段时间的输运, 负涡量形成一个顺时针旋转的涡, 并与第一次激波冲击形成的涡一起诱导气泡形成射流状结构, 将气泡分割成两个部分. 反射激波的作用使得右侧界面上的负涡量强度更大, 从而导致界面发展更快. 由于反射激波与入射激波方向相反, 为了描述方便, 用左侧 (L) 和右侧 (R) 来区分方向. 反射距离为40 mm时, 界面仍然处在发展前期, 弯曲程度较小, 因此生成的涡量强度较弱, 导致两个涡的强度并不均等, 生成的射流状结构在涡2的影响下方向逐渐偏转至指向右侧, 涡1本身也向右侧运动.

图5

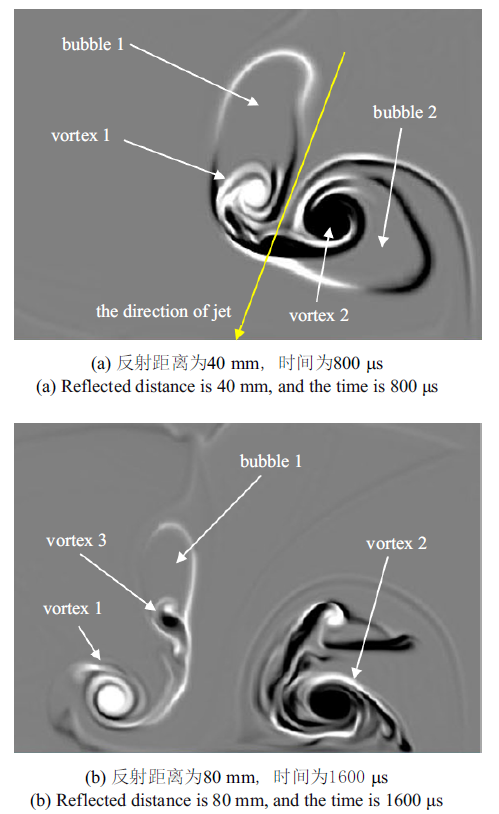新窗口打开|下载原图ZIP|生成PPT
图5气泡被射流分割

Fig.5Bubble is cut off by jet flow



不同反射距离下, 反射激波作用界面时的激波 形状和界面形态显著不同, 因此产生的涡结构也有所区别. 反射距离为80 mm时, 由于气泡弯曲程度较大导致生成涡量强度较大, 使得涡1和涡2强度相当, 生成的射流状结构将界面推向左侧, 导致气柱最左侧界面向左侧移动. 对于反射距离为120 mm的工况, 反射激波作用时气泡已经分裂, 因此反射激波作用后的演化更为复杂, 生成了数个旋转方向各异的小涡, 由于气泡最上部界面与激波几乎垂直, 生成的负涡量较大, 导致气泡1自身快速形成涡对. 整体上, 激波二次作用会使得气柱在演化后期有生成3个涡对的趋势: 激波第一次作用后由于正涡量输运形成的涡2, 反射激波作用后生成的负涡量输运形成的涡1, 以及气泡1在演化后期形成的涡3. 随着反射距离的变化, 这些涡的强度和生成时间会有所不同, 导致后期界面的发展演化也不同, 反射距离40 mm时生成的3个涡对均清晰可见, 反射距离为80 mm时可以看到在1600 $\mu$s尚未完成气泡1到涡3的演化 (如图5(b)所示), 而反射距离120 mm时则可以观察到涡3快速形成, 而涡1难以分辨 (如图3所示). 涡结构的演化决定了变形界面的结构形态, 进而直接改变气柱界面的演化规律.

2.2 三维凹气柱

三维凹气柱界面在入射激波及反射激波作用下的演化过程与二维情况有显著区别. 图6展示了三维凹气柱演化的纹影图, 对应反射距离为80 mm. 由于纹影图是由各个高度的纹影图俯视叠加而成, 因此可以观察到界面很厚. 由纹影图像可以辨识出由边界面生成的外层轮廓以及由对称面生成的内层轮廓. 随着时间的推移, 这两层轮廓间距开始加大, 并且在斜压涡量的影响下形成了向前的射流状结构. 与二维不同的是, 这个射流最终突破最前侧界面并在对称面附近破坏了桥状结构, 这使得气柱在宽度方向发展的更快. 反射距离为80 mm的工况, 从1000 $\mu$s就开始发生与固壁的相互作用, 这远早于二维的情况. 在反射激波冲击后, 桥状结构断裂开, 之前的射流部分分离并扩散成环. 为了便于分析, 图7给出了反射激波作用过程中较短时间内气柱的三维图像, 可以看出当激波刚穿过界面且未能恢复成平面激波时, 也具有很强的三维性, 而三维凹气柱界面的演化更加复杂.

图6

新窗口打开|下载原图ZIP|生成PPT
图6反射距离80 mm时凹气柱演化的纹影图, 单位为$\mu $s

Fig.6Sequence of schlieren frames showing the evolution of a concave light gas cylinder with reflected distance of 80 mm (time unit: $\mu$s)

图7

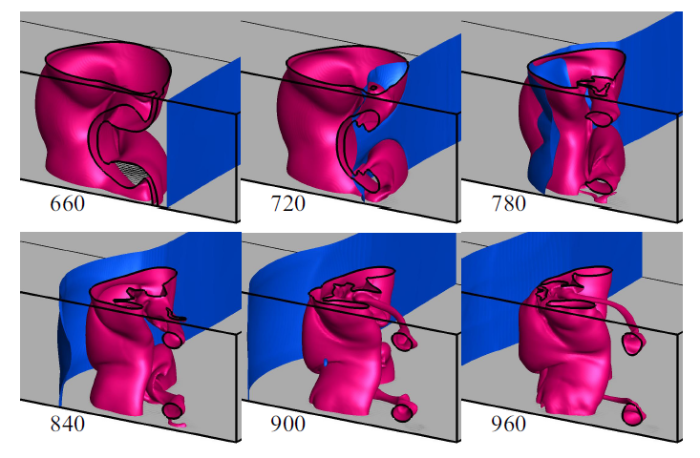新窗口打开|下载原图ZIP|生成PPT
图7反射距离80 mm时, 不同时刻反射激波作用凹气柱的三维图像, 单位为$\mu $s

Fig.7Three-dimensional frames during the interaction of a concave light gas cylinder with the reshock at reflected distance of 80 mm (time unit: $\mu $s)



为了更好地分析三维凹气柱在反射激波作用下的演化过程, 将凹气柱切片, 分层研究各自的演化情况. 如图8所示, 选取$z=0$, $z=10$ mm两处沿着$x$-$y$平面切片, 分别记为S1和S2平面, 选取$y=0$处沿$x$-$z$方向切片, 记为S3平面.

图8

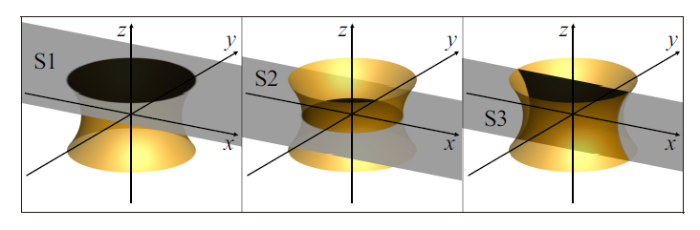新窗口打开|下载原图ZIP|生成PPT
图8三维凹气柱的截面示意图

Fig.8Schematics of the cross section of 3D concave cylinder



图9给出了不同反射距离下3个典型截面上的界面演化过程. 通过对比S1和S2两个截面可以发现, 射流突破桥状结构以及后期下游界面形成的环状结构都发生在S1截面, 与二维情况显著不同. 由S3截面可以看到, 由于凹气柱的三维性, 激波第一次作用后在截面的上半部分生成了负涡量. 在涡量诱导下, 边界面向右运动的速度增大, 而对称面向右的运动速度则减小, 并在S3截面形成了尖钉和气泡结构. 因此可以观察到S1截面上处于对称位置处的运动速度要高于S2截面上同位置的界面. 而处于非对称$x$-$z$截面上的界面会受到两个方向涡量 (对气柱$z>0$的部分来说, 为向$y$轴正方向和$z$轴正方向) 的叠加影响, 将气体向$y=0$及$z=\pm 10$ mm方向推动, 因此可以在S1截面上观察到桥状结构更短, 两个气泡离得更近, 以及600 $\mu$s后涌向边界面的气体在S1截面的气泡中形成了另一个小的气泡, 进一步推动S1截面上的气柱界面加速演化. 因此, S1截面上界面的演化速度高于S2截面且生成了更多复杂结构.

图9

新窗口打开|下载原图ZIP|生成PPT
图9不同反射距离 (40 mm, 80 mm, 120 mm) 下3个典型截面上的界面演化过程. 每个图的上半部分为涡量图, 下半部分为纹影图, 单位为$\mu $s.为便于观察, S3截面图放大至S1 (或S2)截面图的1.5倍(界面和激波位置看着略有不同)

Fig.9Evolution process of concave light gas cylinder under reshock along three typical cross section (time unit: $\mu$s). The plotting scale of the S3 cross section is 1.5 times larger than other frames in order to be observed clearly, thus the scale and the relative location of the deformed interface and shock waves shown in these frames seem different



对于S2截面, 在演化初期凹气柱界面的演化与二维气柱情况基本相同, 但是移动速度受S3截面涡量的影响减慢, 形态变化更快, 在600 $\mu$s时已经形成了厚度很薄的桥状结构, 而二维工况在800 $\mu$s后才出现类似结构. 更大的变化出现在反射激波与界面作用后. 气泡前部的涡 (即图5中二维气柱工况下的涡2) 在演化后期强度减小并被气泡所代替, 通过观察S3截面上界面的演化过程, 可以发现在演化后期受涡量影响, 界面发展有向$z=0$平面靠拢的趋势.

反射距离对界面演化过程有重要影响. 与二维情况类似, 反射激波以及反射距离的改变对界面演化的影响, 主要是由于反射激波作用界面时, 界面和激波的形态不同所造成的, 从而导致新生成的斜压涡量强度以及分布不同. 观察S1截面, 从涡量图中可以看到, 反射激波作用后生成的负涡量在气柱左侧界面诱导生成了涡对. 由于反射距离为40 mm时反射激波作用时间早且与固壁相互作用强烈, 因此涡对位置以及界面整体形状与其他工况不同. 对比反射距离为80 mm与反射距离120 mm的工况, 可以看到反射激波作用时界面的的整体形状相似, 因此反射激波作用后演化后期两个工况界面形状类似, 但80 mm工况反射激波作用更早, 因此环状结构演化更快, 扩散的更明显. 在S2截面上同样由于反射激波作用时界面的整体形状相似, 也满足反射距离越短, 界面扩散越明显的规律.

3 定量分析

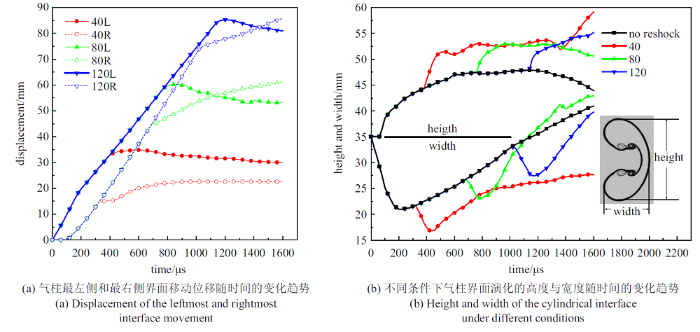
为了更好地分析气柱界面的演化情况, 提取二维和三维凹气柱的最左侧和最右侧界面位置以及高度与宽度数据, 分别如图10和图11所示. 由于对称性, 气柱高度的变化可以反映远离对称面气柱界面的位置变化.气柱高度的变化趋势总体上为: 激波第一次作用后, 由于激波的压缩效应, 气柱宽度减小的同时高度快速增长, 随后增长放缓, 激波第二次作用后再次快速增长, 随后增长趋于饱和, 开始出现下降趋势. 演化后期高度的不断震荡则是由于部分气柱界面跟随涡对整体旋转导致距离对称面最远处的界面不断变化.

图10

新窗口打开|下载原图ZIP|生成PPT
图10二维气柱界面位移和特征尺度随时间的变化情况

Fig.10Variation of displacements and characteristic scales of the 2D cylindrical interface with the time

图11

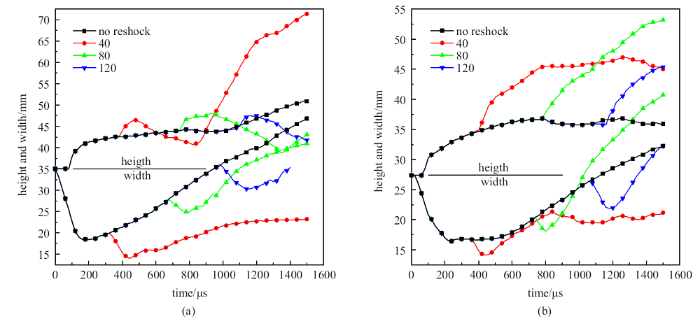
新窗口打开|下载原图ZIP|生成PPT
图11三维凹气柱不同截面上的特征尺度随时间的变化情况.边界面 (a) 和对称面 (b) 上气柱高度与宽度随时间的变化趋势

Fig.11Variation of characteristic scales of 3D concave cylindrical interface with the time along different cross sections. The height and width of the interface along (a) the boundary cross section and (b) the symmetry cross section



如图10所示, 与无反射激波的工况进行对比, 反射激波作用二维气柱界面后由于再次压缩使气柱的高度快速增长, 反射激波作用变形界面后生成负涡量, 气泡1的位置由左侧逐渐顺时针旋转, 先从左侧转向远离对称轴方向引起气柱高度的增长, 随后继续旋转并形成涡对使气柱高度增长趋于饱和. 而反射距离为40 mm的算例在1300 $\mu $s后气柱高度突然增大, 这是由于气柱下游界面到达固壁无法继续向前运动, 从而沿固壁向外围扩散. 此外, 在激波作用后, 气柱宽度迅速下降, 随后近似线性增长, 激波第二次作用后宽度再次迅速下降, 随后恢复线性增长, 最后增长速度有放缓趋势.

二维气柱的左侧界面在激波第一次作用后, 位于对称面附近的界面在激波和涡量诱导的双重作用下, 几乎以恒定速度快速向右侧运动, 而由于右侧界面受到激波冲击较晚, 开始运动后速度又小于左侧界面, 此时气柱宽度迅速减小. 200 $\mu$s后离对称面稍远的气泡结构取代了对称面成为气柱最左端界面, 因此界面运动速度有了突变, 运动速度减慢到小于右侧界面运动速度, 气柱宽度开始重新以线性增长. 反射激波首先作用右侧界面, 虽然并没有使右侧界面的增长停滞, 但仍可导致气柱宽度快速缩短. 除了受到固壁限制的反射距离为40 mm的工况外, 其他工况右侧界面均继续以近乎匀速向右侧缓慢运动. 反射激波作用左侧界面后, 左侧界面反向向左运动, 这是由于新生成的涡对诱导产生射流的结果, 气柱宽度由此恢复增长, 除反射距离120 mm的算例外, 其他工况在界面演化后期逐渐趋于饱和, 而反射距离为120 mm时由于距离固壁较远, 在1600 $\mu$s时仍处于增长阶段.

对于三维凹气柱, 边界面上气柱界面的运动速度较快, 而在对称面上较慢. 反射距离为40 mm时, 由于边界面比较贴近固壁, 将很快与固壁作用, 使气柱宽度的增长趋于停滞. 在边界面, 由于界面运动速度更快, 反射距离为80 mm时也出现了界面与固壁作用导致增长停滞的现象. 而在对称面截面上, 气柱界面的演化更接近二维情况.

如图11所示, 三维凹气柱界面的特征尺寸随时间的变化与二维情况显著不同, 主要在于三维性导致凹气柱演化过程中存在大量的沿$Z$轴方向的运动. 在测量时, 主要考察竖直方向上两端边界面 (最上或最下边界面) 和中心对称面两个截面, 且仅考虑始终在相应截面上的界面结构. 在边界面, 当反射激波作用后, 界面高度增长幅度不及二维情况, 并在短暂的增长后迅速下降, 在演化的后期才由于环状结构的快速扩张以及与固壁相互作用等因素快速反弹. 而在对称面, 由于此处界面形状演化更快而运动速度更慢, 因此更加接近于反射距离更长的二维工况.

需要强调的是, 由于三维凹气柱在竖直方向上出现了界面的负曲率效应, 导致界面的演化与二维气柱相比拥有更加复杂的结构, 从而使对称面以及边界面上的界面演化发生较大变化. 这种结构的变化与三维空间斜压涡量的产生密切相关, 也与反射激波带来的复杂波系结构密不可分, 不同现象及其演化机理仍需要进一步的深入研究.

4 结论

本文通过数值模拟研究了反射激波作用下二维气柱和三维凹气柱的演化过程, 考察了不同的反射距离对界面特征尺寸变化的影响规律. 首先, 不同反射距离下二维气柱的演化归因于反射激波作用于已变形气柱时激波与气柱的瞬时形态, 从而导致斜压涡量的生成和分布产生明显差异. 通过涡量分析, 发现反射激波作用界面时, 能够在上游界面产生反方向的斜压涡量, 促使气泡快速分裂成两部分, 并最终形成多个涡对, 以此来加速界面变形. 其次, 反射激波作用三维凹气柱的界面演化比二维情况更加复杂, 各个截面上的界面演化都存在三维性, 由此产生的涡量分布也具有三维性. 通过涡量诱导的界面运动揭示了各个截面上界面运动速度差异, 并得到了反射激波作用后的三维环状结构. 最后, 通过提取不同截面上界面几何尺寸的演化数据, 对比分析了三维气柱界面演化与二维气柱的不同之处. 本文的数值分析为进一步开展相关内容的实验研究奠定了基础, 也为揭示复杂界面三维性的影响机理提供了基础数据和有效手段.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Richtmyer RD. Taylor instability in shock acceleration of compressible fluids
Commun Pure Appl Math, 1960,13(2):297-319
DOIURL [本文引用: 1]

[2] Meshkov EE. Instability of the interface of two gases accelerated by a shock wave
Fluid Dyn, 1969,4(5):101-104
DOIURL [本文引用: 1]

[3] Lindl JD, McCrory RL, Campbell EM. Progress toward ignition and burn propagation in inertial confinement fusion
Phys Today, 1992,45(9):32-40
[本文引用: 1]

[4] Lindl JD, Amendt P, Berger RL, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility
Phys Plasmas, 2004,11:339-491
DOIURL

[5] 徐建于, 黄生洪. 圆柱形汇聚激波诱导Richtmyer-Meshkov不稳定的SPH模拟
力学学报, 2019,51(4):998-1011
[本文引用: 1]

(Xu Jianyu, Huang Shenghong. Numerical simulation of cylindrical converging shock induced Richtmyer-Meshkov instability with SPH
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):998-1011 (in Chinese))
[本文引用: 1]

[6] Robey HF, MacGowan BJ, Landen OL, et al. The effect of laser pulse shape variations on the adiabat of NIF capsule implosions
Phys Plasmas, 2013,20:052707
DOIURL [本文引用: 1]

[7] Yang J, Kubota T, Zukoski EE. Application of shock-induced mixing to supersonic combustion
AIAA J, 1993,31(5):854-862
DOIURL [本文引用: 1]

[8] 汪洋, 董刚. RM 不稳定过程中预混火焰界面演化及混合区增长预测
力学学报, 2020,52(6):1655-1665
[本文引用: 1]

(Wang Yang, Dong Gang. Interface evolutions and growth predictions of mixing zone on premixed flame interface during RM instability
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(6):1655-1665 (in Chinese))
[本文引用: 1]

[9] Arnett WD, Bahcall JN, Kirshner RP, et al. Supernova 1987A
Annu Rev Astron Astrophys, 2003,27(1):629-700
DOIURL [本文引用: 1]

[10] Luo XS, Liang Y, Si T, et al. Effects of non-periodic portions of interface on Richtmyer-Meshkov instability
Journal of Fluid Mechanics, 2019,861:309-327
DOIURL [本文引用: 1]

[11] Guo X, Zhai ZG, Si T, et al. Bubble merger in initial Richtmyer-Meshkov instability on inverse-chevron interface
Physical Review Fluids, 2019,4(9):092001
DOIURL

[12] 刘金宏, 邹立勇, 曹仁义 等. 绕射激波和反射激波作用下N$_{2}$/SF$_{6}$界面R-M不稳定性实验研究
力学学报, 2014,46(3):475-479
[本文引用: 1]

(Liu Jinhong, Zou Liyong, Cao Renyi, et al. Experimentally study of the Richtmyer-Meshkov instability at N$_{2}$/SF$_{6}$ flat interface by diffracted incident shock waves and reshock
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(3):475-479 (in Chinese))
[本文引用: 1]

[13] Ding JC, Liang Y, Chen MJ, et al. Interaction of planar shock wave with three-dimensional heavy cylindrical bubble
Physics of Fluids, 2018,30(10):106109
DOIURL [本文引用: 2]

[14] Ding JC, Si T, Chen MJ, et al. On the interaction of planar shock with three-dimensional light gas cylinder
Journal of Fluid Mechanics, 2017,828:289-317
DOIURL [本文引用: 2]

[15] Haas JF, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities
Journal of Fluid Mechanics, 1987,181:41-76
DOIURL [本文引用: 1]

[16] Ou JF, Ding JC, Luo XS, et al. Effects of Atwood number on shock focusing in shock-cylinder interaction
Experiments in Fluids, 2018,59(2):29-39
DOIURL [本文引用: 2]

[17] Ou JF, Zhai ZG. Effects of aspect ratio on shock-cylinder interaction
Acta Mechanica Sinica, 2019,35(1):61-69
DOIURL [本文引用: 1]

[18] Zou LY, Liao SF, Liu CL, et al. Aspect ratio effect on shock-accelerated elliptic gas cylinders
Physics of Fluids, 2016,28(3):036101
DOIURL [本文引用: 1]

[19] 丛洲洋, 郭旭, 司廷. 反射激波诱导界面不稳定性研究进展
中国科学: 物理学力学天文学, 2020,50:104703
[本文引用: 1]

(Cong Zhouyang, Guo Xu, Si Ting. Advances in interfacial instability induced by reshock
Sci Sin-Phys Mech Astron, 2020,50:104703 (in Chinese))
[本文引用: 1]

[20] Hill DJ, Pantano C, Pullin DI. Large-eddy simulation and multiscale modeling of a Richtmyer-Meshkov instability with reshock
Journal of Fluid Mechanics, 2006,557:29-61
DOIURL [本文引用: 2]

[21] Latini M, Schilling O, Don WS. Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer-Meshkov instability
Journal of Computational Physics, 2007,221(2):805-836
DOIURL [本文引用: 1]

[22] Schilling O, Latini M. High-order WENO simulations of three-dimensional reshocked Richtmyer-Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data
Acta Math Sci, 2010,30(2):595-620
DOIURL

[23] Haehn N, Weber C, Oakley J, et al. Experimental investigation of a twice-shocked spherical gas inhomogeneity with particle image velocimetry
Shock Waves, 2011,21(3):225-231
DOIURL [本文引用: 1]

[24] Jacobs JW, Krivets VV, Tsiklashvili V, et al. Experiments on the Richtmyer-Meshkov instability with an imposed, random initial perturbation
Shock Waves, 2013,23(4):407-413
DOIURL [本文引用: 1]

[25] Si T, Zhai ZG, Yang JM, et al. Experimental studies of reshocked spherical gas interfaces
Physics of Fluids, 2012,24(5):054101
DOIURL [本文引用: 1]

[26] Mohaghar M, Carter J, Musci B, et al. Evaluation of turbulent mixing transition in a shock-driven variable-density flow
Journal of Fluid Mechanics, 2017,831:779-825
DOIURL [本文引用: 1]

[27] Brouillette M, Sturtevant B. Growth induced by multiple shock waves normally incident on plane gaseous interfaces
Physica D, 1989,37(1-3):248-263
DOIURL [本文引用: 1]

[28] Shankar SK, Kawai S, Lele SK. Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder
Physics of Fluids, 2011,23(2):024102
DOIURL [本文引用: 1]

[29] Quirk JJ, Karni S. On the dynamics of a shock-bubble interaction
Journal of Fluid Mechanics, 1996,318:129-163
DOIURL

[30] Niederhaus JHJ, Greenough JA, Oakley JG, et al. A computational parameter study for the three-dimensional shock-bubble interaction
Journal of Fluid Mechanics, 2008,594:85-124
DOIURL [本文引用: 1]

[31] Shankar SK, Lele SK. Numerical investigation of turbulence in reshocked Richtmyer-Meshkov unstable curtain of dense gas
Shock Waves, 2014, 24(1): 79-95
DOIURL [本文引用: 1]

[32] 张赋, 翟志刚, 司廷 等. 反射激波作用下重气柱界面演化的PIV 研究
实验流体力学, 2014,28(5):13-17
[本文引用: 1]

(Zhang Bin, Zhai Zhigang, Si Ting, et al. Experimental study on the evolution of heavy gas cylinder under reshock condition by PIV method
Journal of Experiments in Fluid Mechanics, 2014,28(5):13-17 (in Chinese))
[本文引用: 1]

[33] 何惠琴, 翟志刚, 司廷 等. 反射激波作用下两种重气柱界面不稳定性实验研究
实验流体力学, 2014,28(6):56-60
[本文引用: 1]

(He Huiqin, Zhai Zhigang, Si Ting, et al. Experimental study on the reshocked RM instability of two kinds of heavy gas cylinder
Journal of Experiments in Fluid Mechanics, 2014,28(6):56-60 (in Chinese))
[本文引用: 1]

[34] 王显圣, 司廷, 罗喜胜 等. 反射激波冲击重气柱的RM不稳定性数值研究
力学学报, 2012,44(4):664-672
[本文引用: 1]

(Wang Xiansheng, Si Ting, Luo Xisheng, et al. Numerical study on the RM instability of a heavy-gas cylinder interacted with reshock
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(4):664-672 (in Chinese))
[本文引用: 1]

[35] 沙莎, 陈志华, 薛大文. 激波冲击R22重气柱所导致的射流与混合研究
物理学报, 2013,62(14):144701
[本文引用: 1]

(Sha Sha, Chen Zhihua, Xue Dawen. The generation of jet and mixing induced by the interaction of shock wave with R22 cylinder
Acta Phys Sin, 2013,62(14):144701 (in Chinese))
[本文引用: 1]

[36] 丁举春. 汇聚Richtmyer-Meshkov不稳定性的实验与数值研究. [博士论文]
合肥: 中国科学技术大学, 2016
[本文引用: 3]

(Ding Juchun. Experimental and numerical study on converging Richtmyer-Meshkov instability. [PhD Thesis]
Hefei: University of Science and Technology of China, 2016 (in Chinese))
[本文引用: 3]

[37] Liu XD, Osher S, Chan T. Weighted Essentially Non-oscillatory schemes
Journal of Computational Physics, 1994,115(1):200-212
DOIURL [本文引用: 2]

[38] Schilling O, Latini M, Don WS. Physics of reshock and mixing in single-mode Richtmyer-Meshkov instability
Phys Rev E, 2007,76(2):026319
DOIURL [本文引用: 2]

[39] Wang XS, Yang DG, Wu JQ, et al. Interaction of a weak shock wave with a discontinuous heavy-gas cylinder
Physics of Fluids, 27(6): 064104, 2015
[本文引用: 2]

[40] 王显圣. 极小曲面特征界面的Richtmyer-Meshkov不稳定性研究. [博士论文]
合肥: 中国科学技术大学, 2013
[本文引用: 1]

(Wang Xiansheng. The Richtmyer-Meshkov instability on minimum-surface featured interface. [PhD Thesis]
Hefei: University of Science and Technology of China, 2013 (in Chinese))
[本文引用: 1]

[41] Isenberg C. The Science of Soap Films and Soap Bubbles
New York: Dover Publications INC, 1992
[本文引用: 1]