李彬^,*,2), 徐海珏^,*,?,3), 白玉川^,*,?,4), 冀自青^*,?* 天津大学水利工程仿真与安全国家重点实验室, 天津 300350
? 天津大学建筑工程学院, 天津 300350

ANALYSIS OF HYDRODYNAMIC INSTABILITY AND NONLINEAR EVOLUTION CHARACTERISTICS OF TWO DIMENSIONAL FLOW IN CONSTANT CURVATURE BEND ¹⁾

Li Bin^,*,2), Xu Haijue^,*,?,3), Bai Yuchuan^,*,?,4), Ji Ziqing^*,?* The State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300350, China
? Institute of Sediment Research on River and Coastal Engineering, Tianjin University, Tianjin 300350, China

通讯作者: 2) 李彬, 博士研究生, 研究方向: 河流动力学. E-mail:Libin0425@tju.edu.cn3) 徐海珏, 副教授, 研究方向: 流体力学、泥沙运动力学. E-mail:xiaoxiaoxu_2004@163.com4) 白玉川, 教授, 研究方向: 河口海岸动力学. E-mail:ychbai@tju.edu.cn

收稿日期:2020-06-7接受日期:2020-11-21网络出版日期:2021-12-31

基金资助:

1)国家自然科学基金.51979185 1)国家自然科学基金.51879182 1)国家自然科学基金.51621092 天津市研究生科研创新项目资助.2019YJSB177

Received:2020-06-7Accepted:2020-11-21Online:2021-12-31
作者简介 About authors


摘要
国内外对弯曲河流的研究从线性特性转移到不稳定性与非线性特性上来, 弯曲河流作为一个不稳定的系统, 主要是受到水流和边界的不稳定性的影响.针对弯曲河流中存在的水流动力的不稳定性与非线性特征,利用弱非线性理论与摄动法进行展开, 在微弯条件下建立了时间模式下的常曲率 弯道二维水流扰动幅值与扰动幅角的非线性演化方程.研究了在不同弯曲度下的扰动发展特征,探讨了扰动流场在弯曲度影响下的时空分布的规律,分析了扰动流场中出现的扰动漩涡的运动过程, 阐述了弯曲度对弯曲边界内水流不稳定性的影响, 具体表现为在微弯的情况下, 弯道的弯曲度增大会提高河湾内水流的稳定性, 扰动振幅与扰动幅角会随弯曲度的增大其衰减速度更快, 并且扰动流速的对称性在弯曲度较大时减弱, 逐渐向弯道的凸岸偏斜, 在中性状态附近 的弯道水流动力具有对流不稳定性和非线性衰减的特征.本文的研究成果为构建水流动力非线性与床面形态几何非线性相互作用的模型提供了思路.
关键词： 常曲率弯道;不稳定性;弱非线性;弯曲度

Abstract
In recent years, the study of meandering river has shifted from linear characteristics to instability and nonlinear characteristics. Many researchers see the meandering river as an unstable system, for which they thought that the meandering river is mainly affected by the instability of the field flow and corresponding boundary. Aiming at the instability and nonlinear characteristics of the dynamics of the flow in meandering river, we make up the nonlinear evolution equations of flow disturbance amplitude and disturbance angle of constant curvature bend under the condition of weakly curve meandering, which were established by using the weakly nonlinear theory and perturbation method. In this paper we study the characteristics of disturbance development by considering different curvatures firstly, then discuss the spatial and temporal distribution characteristics of disturbed flow field under the influence of a series of curvatures, and expounds the influence of curvatures on the flow stability of curved river bend, in the end, we analyze the motion characteristics of disturbed vortex in disturbed flow field. We find that the increase of meandering bend curvature ratio will improve the stability of flow in the meandering bend, which is corresponding the others researchers' results. The disturbance amplitude and the disturbance angle of the flow decay faster with the increase of meandering curvature ratio, in the term of the symmetry of the disturbance velocity, which will become weaker with the increase of meandering curvature ratio and the incline to the convex bank of the bend when the meandering curvature ratio is larger. The flow dynamic of the meandering bend near the neutral state has the characteristics of convective instability and nonlinear attenuation. The research results in this paper provide a new idea for constructing a nonlinear interaction model of the nonlinear flow dynamics and the geometric nonlinearity of the meandering bed in the future research.
Keywords：constant curvature bend;instability;weak nonlinearity;curvature ratio


PDF (9078KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李彬, 徐海珏, 白玉川, 冀自青. 常曲率弯道二维流动稳定性与非线性演化规律分析 ¹⁾. 力学学报[J], 2021, 53(1): 168-183 DOI:10.6052/0459-1879-20-191
Li Bin, Xu Haijue, Bai Yuchuan, Ji Ziqing. ANALYSIS OF HYDRODYNAMIC INSTABILITY AND NONLINEAR EVOLUTION CHARACTERISTICS OF TWO DIMENSIONAL FLOW IN CONSTANT CURVATURE BEND ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(1): 168-183 DOI:10.6052/0459-1879-20-191

引言

弯曲河流的稳定性与非线性特征自20世纪80年代以来, 众多****都未停止对它的探究.Callander^[1]在对顺直河道中的水流线性稳定性分析中认为不稳定性是导致河流弯曲或辫状的原因,并指出所有的河流是不稳定的. Ikeda等^[2]基于浅水方程构建了在弯曲河流中的水流积深方程, 进行了弯道不稳定性分析时,假定河道宽度为恒定值, 弯曲度(河道半宽与曲率半径的比值)远小于1,在坐标转换过程中出现了与河道振幅相关的几何非线性项,但是在稳定性分析中却移除了几何非线性和与动力非线性项,他们在弯曲河流线性稳定性分析中认为最不稳定性波长是弯曲河流自身的有限振幅波长.Parker等^[3]对有限振幅弯道的非线性的处理是利用Stokes的水波摄动展开方法的修正进行非线性稳定性分析,忽略了高阶的动力非线性项, 仅保留了高阶的几何非线性项,他们分析弯道的形态特征是在正弦派生曲率的基础加上三次谐波的小振幅,其成果是基于水流与河床地形的线性模型,但是河岸侵蚀公式表明几何非线性是受到近岸流速在水流非线性作用下产生高次谐波的驱动而产生,即水流非线性产生了几何非线性. Seminara和Tubino^[4]在对弯曲河流的弱非线性分析中, 认为河流具有非线性动力系统的特性,利用弯曲度作为扰动参数,在较小曲率的河流中的共振状态附近进行几何弱非线性分析,揭示了响应的非唯一性以及非线性效应的抑制作用. Imran等^[5]建立了水下与地表的弯曲河道的水流的非线性模型,将曲率振幅的幂次进行展开并代入水深积分的控制方程中,在线性与非线性阶段进行求解, 研究了水流与河流几何参数的影响, 他指出对于Sun^[6]在长期的地质时间尺度上的弯曲河流演变的模拟存在基础性缺陷,原因是忽视了水流动力中的非线性的作用. Seminara^[7]指出在对弯曲河流的理论分析与室内试验,都表明弯曲河流的性质与不稳定机制有关,主要为水流自身不稳定性以及水流与可侵蚀边界的流动界面的不稳定性. Pittaluga等^[8]认为弯曲河流的线性理论说明了共振机理,然而仍未建立弯曲河流完全的非线性理论, 非线性作用对水流流场的影响不可忽略.Pittaluga和Seminara^[9]提出对于弯曲河流进一步研究的方向应集中在非线性与不稳定性,这与河流自身并不是一个稳定的系统相关,并指出之前对于弯曲河流的研究主要集中于线性稳定性模型的发展上面,非线性与不稳定性的作用被严重的忽略了. 徐海珏和白玉川^[10]针对顺直河道建立了水流与河床的扰动共振三波与床面泥沙作用的水流非线性理论模型,分析了顺直河道沙纹动力过程与演变特征. Bai等^[11-17]认为非线性流体动力学理论是探究河流在自然或者人为扰动下的演变的重要手段,并在弱非线性理论基础上建立了常曲率与变曲率河湾中的河湾控制方程与稳定性理论,探究了在小扰动情况下的河流响应以及涡量分布,认为在外部扰动影响下,河流类型可以发生短暂的变化,但能够回到原始平衡状态类型.Ail等^[18-21]对弯曲河流的水流不稳定分析中指出, 水流不稳定性与水流特性有关,其中流体黏滞系数在弯曲河流的紊流阻力的不稳定性中起到决定性作用,并且在微弯河道的水动力分析中考虑了水流的横向流动的不对称性,此外还指出河流的不稳定性源于水流与松散边界物质的相互作用,并从室内实验、现场观测及理论分析, 研究了近床水流动力特征.Tubino等^[22-25]研究了河曲弯道平面发育过程中河道宽度变化和曲率之间的相互作用,不同的河道曲率对水流流场、泥沙输移和平面演变过程具有显著的贡献,并分析了河流分叉时的不稳定性.Nelson等^[26-27]构建了一维与水深积分的正交曲线坐标系下的弯曲河流计算程序,包含水流、泥沙输移和河床演变, 但是在其计算程序中缺少对非线性影响的分析与讨论.

之前****们研究主要聚焦于弯曲河流平面形态的几何非线性、床面扰动的几何非线性、水流与床面的不稳定性,但对于水流自身动力的非线性及其演化特征的研究尚有不足, 本文通过构建弯道水流控制方程, 分析水流自身不稳定引起的非线性作用,在水流的小扰动情况下构建水流扰动的控制方程,构造了在时间模式下的Orr-Sommerfeld方程, 分析弯道水动力的稳定性特征,并利用流动稳定性的弱非线性理论 ^[28-29]构造考虑弯曲度的Landau-Stuart方程, 推导了在水流非线性作用下的常曲率弯道水动力的非线性演化方程, 暂不考虑河岸物质组成与床面形态对水流动力的影响. 在弯曲河流中, 往往存在对于河流的曲率半径沿程不变, 宽度受两侧岸壁限制的情况,如黑龙江第一弯、黄河晋陕峡谷段永和乾坤湾等常曲率河湾.在弯曲河流中, 水流动力为泥沙的输移提供了动力, 进而影响到河流形态与河床形态,因此研究常曲率弯道水动力结构以期为进一步探究河流稳定性与床面形态变化的完全非线性提供水动力非线性基础.

图1

新窗口打开|下载原图ZIP|生成PPT
图1黑龙江第一湾

Fig.1The first bend of Heilongjiang

1 理论模型

1.1 坐标变换

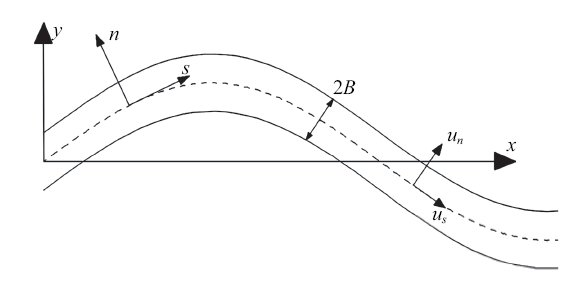
本文研究对象为常曲率河湾, 为了反映出河湾的流动情况, 首先建立适用于一般蜿蜒河湾的正交曲线坐标系, 其中$s$为河道中轴线,指向下游流动方向, n为垂直于s方向. 取B为半河宽; $x_{0} $和$y_{0}$分别为河道中心线的坐标值, 如图2所示.

图2

新窗口打开|下载原图ZIP|生成PPT
图2河湾正交曲线坐标系

Fig.2Orthogonal curvilinear coordinate system in meandering river



正交曲线坐标系与直角坐标系的转换关系为

(1a)$\begin{eqnarray} x=x_{0} +\Delta x=x_{0} -n\frac{{d}y_{0} }{{d}s} \end{eqnarray}$

(1b)$\begin{eqnarray} y=y_{0} +\Delta y=y_{0} +n\frac{{d}x_{0} }{{d}s} \end{eqnarray}$

曲率半径为

(2)$\begin{eqnarray} R\left( s \right)=\left( {\frac{{d}x_{0} }{{d}s}\frac{{d}^{2}y_{0} }{{d}s^{2}}-\frac{{d}y_{0} }{{d}s}\frac{{d}^{2}x_{0} }{{d}s^{2}}} \right)^{-1} \end{eqnarray}$
拉梅系数为

(3)$\begin{eqnarray} h_{s} =1-\frac{n}{R\left( s \right)}=1-N,\\ h_{n} =1,\\ h_{z} =1 \end{eqnarray}$

1.2 常曲率河湾控制方程

在二维情况下, 对连续性方程与水流运动方程进行无量纲化. 在正交曲线坐标下, 取$B_{r}^{\ast}$为半河宽; $R_{m}^{\ast}$为河道最小曲率半径; $U_{m}^{\ast}$为基本流的流速峰值, "$\ast $"表示有量纲, 因此长度、速度和时间尺度分别为: $B_{r}^{\ast}$, $U_{m}^{\ast}$, ${{B_{r}^{\ast } }/{U_{m}^{\ast } }}$, 即有

$\begin{eqnarray*} &&\left( {s^{\ast },n^{\ast }} \right)=B_{r}^{\ast } \left( {s,n} \right), \\ R^{\ast }=R_{m}^{\ast } R, \\ \left( {u_{s}^{\ast } ,u_{n}^{\ast } } \right)=U_{m}^{\ast } \left( {u_{s} ,u_{n} } \right)\\ &&p^{\ast }=\rho U_{m}^{\ast2}p, \\ t^{\ast }=\frac{B_{r}^{\ast } }{U_{m}^{\ast } }t, \\ N=\frac{B_{r}^{\ast } }{R_{m}^{\ast } }\frac{n}{R}, \\ \psi =\frac{B_{r}^{\ast } }{R_{m}^{\ast } } \end{eqnarray*}$

上式中, $p^{\ast }$为压强, $\rho $为流体密度, $t^{\ast }$为时间, $\psi$为河流弯曲度, 为河流重要的弯曲特征参数, 其值越小则弯道越平缓. 在常曲率情况下无量纲曲率半径$R=1$, 故$h_{s} =1-\psi n$, 得到的常曲率弯曲河流无量纲控制方程为

(4)$\begin{eqnarray} &&\frac{1}{h_{s} }\frac{\partial u_{s} }{\partial s}+\frac{\partial u_{n} }{\partial n}-\frac{\psi u_{n} }{h_{s} }=0 \end{eqnarray}$
(5)$\begin{eqnarray} && \frac{\partial u_{s} }{\partial t}+\frac{u_{s} }{h_{s} }\frac{\partial u_{s} }{\partial s}+u_{n} \frac{\partial u_{s} }{\partial n}-\frac{\psi u_{s} u_{n} }{h_{s} }=-\frac{1}{h_{s} }\frac{\partial p}{\partial s} + \frac{1}{Re}\bar{{\Delta }}u_{s} -\frac{\psi }{Re}\left( {\frac{2}{h_{s} ^{2}}\frac{\partial u_{n} }{\partial s}+\frac{1}{h_{s} }\frac{\partial u_{s} }{\partial n}+\frac{\psi u_{s} }{h_{s}^{2}}} \right) \end{eqnarray}$
(6)$\begin{eqnarray} && \frac{\partial u_{n} }{\partial t}+\frac{u_{s} }{h_{s} }\frac{\partial u_{n} }{\partial s}+u_{n} \frac{\partial u_{n} }{\partial n}+\frac{\psi u_{s}^{2}}{h_{s} }=-\frac{\partial p}{\partial n} + \frac{1}{Re}\bar{{\Delta }}u_{n} +\frac{\psi }{Re}\left( {\frac{2}{h_{s} ^{2}}\frac{\partial u_{s} }{\partial s}+\frac{1}{h_{s} }\frac{\partial u_{n} }{\partial n}+\frac{\psi u_{n} }{h_{s}^{2}}} \right) \end{eqnarray}$
式中$Re={B_{r}^{\ast } U_{m}^{\ast } }/{\upsilon }$为雷诺数, $\upsilon$为运动黏滞系数, $\bar{{\Delta }}=({1}/{h_{s}^{2}})(\partial^{2}/\partial s^{2})+{\partial ^{2}}/{\partial n^{2}}$.

图3

新窗口打开|下载原图ZIP|生成PPT
图3常曲率河湾

Fig.3Sketch illustrating the constant curve river

1.3 摄动分析

因为弯曲度$\psi $为一小参数, 按照流体力学中对拟序结构的处理方法, 对式(4) ~式(6)采用摄动方法求解, 将速度与压强分解为

(7)$\begin{eqnarray} \label{eq7} \left[ {\begin{array}{c} u_{s} \\ u_{n} \\ p \\ \end{array}} \right]=\left[ {\begin{array}{c} u_{s\psi_{0} } \\ u_{n\psi_{0} } \\ p_{\psi_{0} } \\ \end{array}} \right]+\sum\limits_{i=1}^\infty {\psi^{i}\left[ {\begin{array}{c} u_{s\psi_{i} } \\ u_{n\psi_{i} } \\ p_{\psi_{i} } \\ \end{array}} \right]} +\sum\limits_{i=1}^\infty {\varepsilon^{i}\left[ {\begin{array}{c} u_{s_{i} } \\ u_{n_{i} } \\ p_{_{i} } \\ \end{array}} \right]} \end{eqnarray}$
式中, 右端第一项为明渠基本流, 即$\psi =0$时的水流分布, 第二项为弯曲修正项,第三部分为水流扰动项, $\varepsilon $与$\psi $皆为小量. Seminara^[7]在对接近共振时的弯曲河流的弱非线性分析中,水流速度解的形式采用微小的弯曲度的幂次展开.本研究中的解的形式包含基本流、微小弯曲度的扰动与水流自身扰动, 主要考虑了水流自身扰动在弯曲河流中的非线性效应. 在基本流与弯曲修正项分析中,依据Lagasse等^[30]的报告, 天然河湾的$\psi$值大多在0.05~0.20之内,在微弯下由弯曲引起的影响仅考虑其一阶弯曲度的作用, 忽略高阶弯曲度的影响.

在明渠中$\psi =0$, $u_{n\psi_{0}} =0$, $\partial/\partial s=\partial / \partial t=0$, 边界条件为$u_{n\psi_{0} } =u_{s\psi_{0} } =0$ $(n=\pm 1)$, 故流速及压强的形式为

(8)$\begin{eqnarray} u_{n\psi_{0} }=0,\\ u_{s\psi_{0} } =1-n^{2}, \\ p_{\psi_{0} } =0 \end{eqnarray}$
由弯曲引起的修正项$u_{s\psi_{1}}, u_{n\psi_{1}}, p_{\psi_{1}}$在常曲率河湾的分布为

(9)$\begin{eqnarray} \label{eq9} u_{n\psi_{1} } =0, u_{s\psi_{1} } =\frac{-1}{3}\left( {n-n^{3}} \right), p_{\psi_{1} } =-n-\frac{1}{5}n^{5}+\frac{2}{3}n^{3}\quad \end{eqnarray}$
将基本流与一阶弯曲修正项作为常曲率弯道基本流,

与水流扰动项带到常曲率河湾控制方程中, 即

(10)$\begin{eqnarray} \label{eq10} \left[ {\begin{array}{c} u_{s} \\ u_{n} \\ p \\ \end{array}} \right]=\left[ {\begin{array}{c} \bar{u}_{s} \\ \bar{u}_{n} \\ \bar{{p}} \\ \end{array}} \right]+\sum\limits_{i=1}^\infty {\varepsilon^{i}\left[ {\begin{array}{c} u_{s_{i} } \\ u_{n_{i} } \\ p_{_{i} } \\ \end{array}} \right]} \end{eqnarray}$
将上式代入控制方程式(4)~式(6)有

(11)$\begin{eqnarray} \label{eq11} \sum\limits_{i=1}^\infty {\left( {\frac{1}{h_{s} }\frac{\partial u_{s_{i} } }{\partial s}+\frac{\partial u_{n_{i} } }{\partial n}-\frac{\psi u_{n_{i} } }{h_{s} }} \right)} =0\end{eqnarray}$
(12)$\begin{eqnarray} \sum\limits_{i=1}^\infty \Bigg[\frac{\partial u_{s_{i} } }{\partial t}+{L}u_{s_{i} } +u_{n_{i} } \frac{\partial \bar{u}_{s} }{\partial n}+\frac{1}{h_{s} }\frac{\partial p_{i} }{\partial s}-\frac{\psi \bar{u}_{s} u_{n_{i} } }{h_{s} }+ \frac{\psi }{Re}\Bigg[ \frac{2}{h_{s}^{2}}\frac{\partial u_{n_{i} } }{\partial s}+\frac{1}{h_{s} }\frac{\partial u_{s_{i} } }{\partial n}+\frac{\psi u_{s_{i} } }{h_{s}^{2}} \Bigg)\Bigg] \varepsilon^{i} =-\varepsilon \sum\limits_{i=1}^\infty \sum\limits_{j,k\geqslant 1}^{j+k=i+1} {\left( {\frac{1}{h_{s} }u_{s_{j} } \frac{\partial u_{s_{k} } }{\partial n}+u_{n_{j} } \frac{\partial u_{s_{k} } }{\partial n}-\frac{\psi u_{s_{j} } u_{n_{k} } }{h_{s} }} \right)} \varepsilon^{i}\end{eqnarray}$
(13)$\begin{eqnarray} \sum\limits_{i=1}^\infty \Bigg[ \frac{\partial u_{n_{i} } }{\partial t}+{L}u_{n_{i} } +\frac{\partial p_{i} }{\partial n}+2\frac{\psi \bar{u}_{s} u_{s_{i} } }{h_{s} }+\frac{\psi }{Re}\Bigg( \frac{-2}{h_{s}^{2}}\frac{\partial u_{s_{i} }}{\partial s}+\frac{1}{h_{s} }\frac{\partial u_{n_{i} } }{\partial n}+\frac{\psi u_{n_{i} } }{h_{s}^{2}} \Bigg)\Bigg] \varepsilon^{i} =-\varepsilon \sum\limits_{i=1}^\infty \sum\limits_{j,k\geqslant 1}^{j+k=i+1} \left( \frac{1}{h_{s} }u_{s_{j} } \frac{\partial u_{n_{k} } }{\partial n}+u_{n_{j} } \frac{\partial u_{n_{k} } }{\partial n}+\frac{\psi u_{s_{j} } u_{s_{k} } }{h_{s}} \right) \varepsilon^{i} \end{eqnarray}$
上式中

$\begin{eqnarray*} {L}=\frac{\bar{u}_{s} }{h_{s} }\frac{\partial }{\partial s}-\frac{1}{Re}\left( {\frac{1}{h_{s}^{2}}\frac{\partial^{2}}{\partial s^{2}}+\frac{\partial^{2}}{\partial n^{2}}} \right). \end{eqnarray*}$

1.4 一阶扰动量稳定性的线性方程

由于式(10)中$\bar{u}_{s} $, $\bar{{p}}$仅为$n$的函数, 因此将一阶扰动量$u_{s_{1} } ,u_{n_{1} } ,p_{1} $可以利用分离变量而写成

(14)$\begin{eqnarray} \left[ {\begin{array}{c} u_{s_{1} } \\ u_{n_{1} } \\ p_{_{1} } \\ \end{array}} \right]=\left[ {\begin{array}{c} \hat{u}_{s_{1} (n)} \\ \hat{u}_{n_{1} (n)} \\ \hat{p}_{1(n)} \\ \end{array}} \right]\exp \left[ {{i}\left( {\alpha s-\omega t} \right)} \right]+c.c \end{eqnarray}$
式中, $\hat{u}_{s_{1} (n)}$, $\hat{u}_{n_{1} (n)}$, $\hat{p}_{1(n)} $为关于$n$的形状函数, $\alpha $为扰动波数, $\omega $为扰动频率, $c.c$为共轭复数, 将式(14)代入式(11) ~式(13)中, 得到一阶扰动的控制方程(见附录A).

本文探究的问题是在时间模式中的水流稳定性与非线性演化过程, 即$\omega =\omega_{r} +{i}\omega_{i} $, 其中虚部$\omega_{i}$为与扰动的增长情况相关, 即扰动振幅为$a=\exp ( \omega_{i} t)$, 扰动幅角$\theta =-\omega_{r} t$, 其满足的关系式为

(15)$\begin{eqnarray} F\left( {\alpha ,\omega ,Re,\psi } \right)=0 \end{eqnarray}$
上式为常曲率弯道水流动力特征的Orr-Sommerfeld方程(简称O-S方程, 具体过程与形式参见附录A), 利用O-S方程可求出在弯曲度影响下的中性曲线分布以及相应的扰动波数与雷诺数的变化情况.

1.5 常曲率河湾时间模式弱非线性演化理论

利用Landau-Stuart方程的弱非线性理论, 在时间模式下利用$a$表示线性理论某一扰动模式的幅值, 考虑非线性的影响,

扰动幅值与扰动幅角的演化方程为

(16)$\begin{eqnarray} \lt.\begin{array}{l} \dfrac{{d}a}{{d}t}=\omega_{i} a+\sum\limits_{s=1}^\infty A_{s} a^{s} =A\\\dfrac{{d}\theta }{{d}t}=-\omega_{r} +\sum\limits_{s=1}^\infty B_{s}a^{s} =B \end{array}\rt\} \end{eqnarray}$
其中$A_{0} =\omega_{i} a$, $B_{0} =-\omega_{r}$, $a={e}^{\omega_{i} t}$, $\theta=-\omega_{r} t$, 根据链式法则有

(17)$\begin{eqnarray} \hspace{-5mm}\frac{\partial u_{i} }{{d}t}=\frac{\partial u_{i} }{\partial a}\left( {\omega _{i} a+\sum\limits_{s=1}^\infty {A_{s} a^{s}} } \right)+\frac{\partial u_{i} }{\partial \theta }\left( {-\omega_{r} +\sum\limits_{s=1}^\infty {B_{s} a^{s}} } \right) \end{eqnarray}$
式(17)中$u_{i} $为任意阶扰动速度或扰动速度分量($i=1,2,\cdots$), 将式(17)代回式(12)和式(13), 则可得到任一阶数下常曲率弯道时间模式弱非线性演化方程. Pittaluga和Seminara^[9]建立的考虑了水流非线性与不稳定性作用影响的弯曲河流地貌动力过程的模型中忽略了侧壁边界层作用,但是他们指出对弯曲河流的分析需要完全的非线性控制方程进行模拟, 对于侧壁边界层的作用不可忽略, 本文中相应的水流扰动的侧壁上边界条件为

(18)$\begin{eqnarray} u_{n_{i} } =u_{s_{i} } =0\\ \left(n=\pm 1,i=1,2,\cdots\right) \end{eqnarray}$
本文将扰动控制方程展开至五阶, 即得到了一阶至五阶的常曲率弯道时间模式下弱非线性演化下的扰动控制方程,在附录B给出了二阶扰动控制方程的展开形式.

2 结果与讨论

2.1 稳定性理论模型验

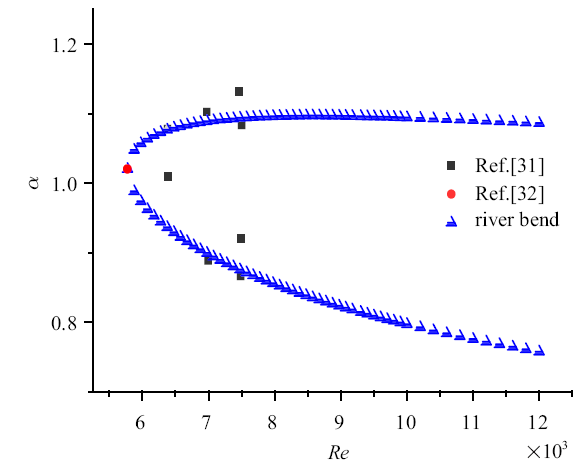
利用中心差分与Muller法, 可以计算出在特定的$Re$, $\alpha$下的$\omega_{r}$, $\omega_{i}$变化, 其中$\omega_{i} =0$时, 即为中性状态. 本次的验证过程采用$\psi=0$时计算得到的临界雷诺数与中性曲线与Nishioka等^[31]所做的平面Poiseuille流实验结果进行验证, 临界雷诺数采用Orszag^[32]论文中的$Re_{cr}=5 772.22$, $\alpha =1.020 59$. 本文常曲率弯道模型得出对应的临界雷诺数$Re_{cr} =5772.222 2,\alpha =1.020 59$其结果与国际上公认的理论与实验模型相一致, 如图4所示.

图4

新窗口打开|下载原图ZIP|生成PPT
图4中性曲线结果验证($Re\mbox{-}\alpha )$

Fig.4Verification of neutral curve ($Re\mbox{-}\alpha )$

2.2 河湾弯曲度对中性曲线特征影响

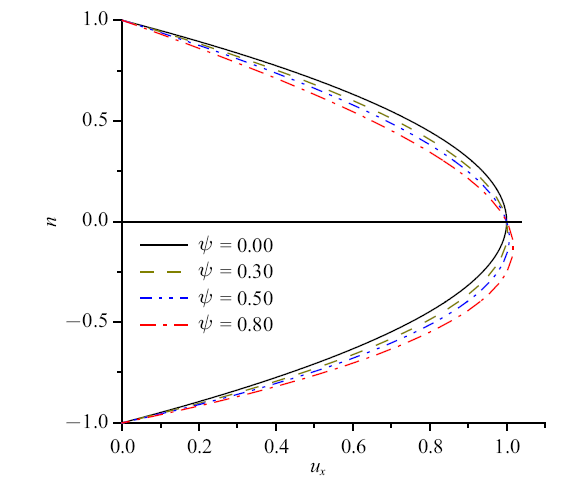
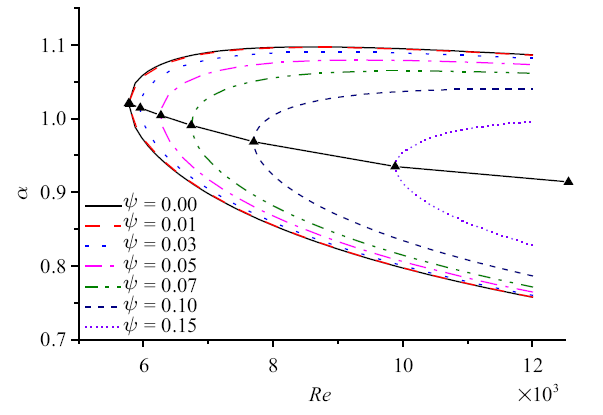
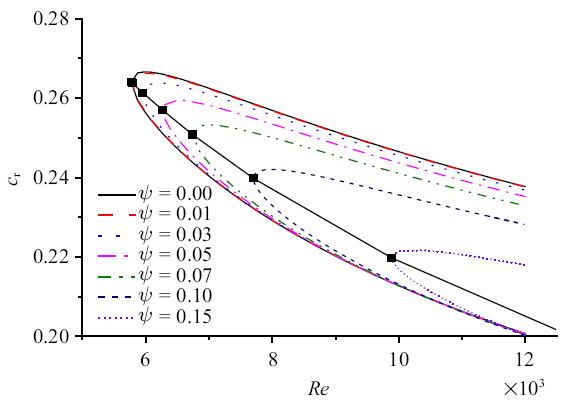
与顺直河道不同, 常曲率河湾中弯曲边界会对基本流以及相应的对河湾水流动力稳定性有影响, 随着弯曲度逐渐增大, 基本流分布向$n<0$方向移动, 即水流向凹岸移动, 使得微弯弯道逐渐向有限弯曲的弯道演变.

图6与图7中黑色点线为不同弯曲度下的临界雷诺数分布曲线, 图7中$c_{r} ={{\omega_{r} }/\alpha }$为扰动波速的实数部分. $\psi $对$\alpha$, $c_{r}$, $Re$的影响主要表现在$\psi$的增大使中性曲线向$Re$增大方向迁移,中性曲线外侧区域为稳定区域, 内侧为失稳区域, 即随着$\psi $的增大,常曲率弯道的临界失稳雷诺数增大, 弯道趋于稳定. 在中性曲线上对于同一个雷诺数(除临界雷诺数$Re_{cr}$外)存在两个中性点, 即上支点与下支点, 随着$\psi $的增大, 下支点的$\alpha$, $c_{r} $相互趋近, 上支点$\alpha$, $c_{r}$相差较大,失稳区域缩窄(中性曲线内侧为失稳区、外侧为稳定区), 稳定性区域增大,与文献[33]描述的在弯曲度影响下的中性曲线趋势相一致,即弯道的弯曲度的存在使得流动趋于在更大雷诺数下失稳.

图5

新窗口打开|下载原图ZIP|生成PPT
图5弯曲度$\psi $对基本流的影响

Fig.5Effect of curvature ratio $\psi $ on basic flow

图6

新窗口打开|下载原图ZIP|生成PPT
图6弯曲度对$Re\mbox{-}\alpha $的中性曲线影响

Fig.6Effect of curvature on neutral curve of $Re\mbox{-}\alpha $

图7

新窗口打开|下载原图ZIP|生成PPT
图7弯曲度对$Re\mbox{-}c_{r} $的中性曲线影响

Fig.7Effect of curvature on neutral curve of $Re\mbox{-}c_{r} $



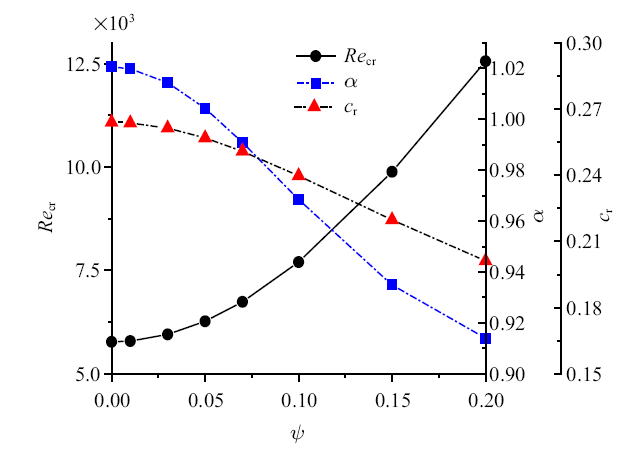
在弯曲度逐渐增大的过程中, 临界雷诺数、扰动波数与扰动波速表现出一定的规律,

在图8中, 在微弯的限制下, 弯曲度从0增大至0.20过程中, 中性状态下的$Re_{cr}$呈现指数型增长, $\alpha $与$c_{r}$呈现单调下降的趋势.

图8

新窗口打开|下载原图ZIP|生成PPT
图8不同弯曲度下稳定性特征

Fig.8Stability characteristics under different curvature ratio

2.3 非线性幅值与幅角的演化特征分析

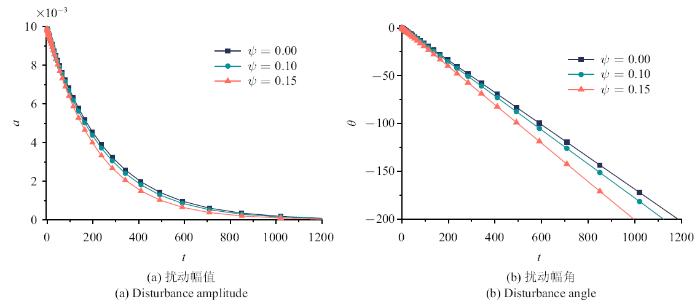
在利用可解条件在求得Landau系数$A$, $B$后, 设初始扰动幅$a_{0}=0.01$. 取图6与图7中的中性曲线附近的值进行分析不同弯曲度对扰动幅值与扰动幅角演化的影响. 以下分析中对扰动波速的虚部取$c_{i}=-0.005$, $\alpha$与$c_{r}$的均取中性曲线上的值.

由弯曲度影响下的扰动幅值演化曲线可知, 在同一雷诺数下, 随着弯曲的增大,其$a$随时间的衰减速度增大, $a$随时间的变化率$A$在$\psi $为0.15时,衰减率大于$\psi $为0.10与0.00的变化率, 但当时间增大到一定程度时,其变化率$A$为0, 相应的扰动幅值也降为0, 即在初始扰动在经历了一定的时间后扰动会逐渐消失,这种效应可以被称为"非线性衰减". 扰动幅角随时间呈现单调下降的趋势, 扰动幅角的衰减率$B$基本保持不变, 在雷诺数相同时,弯曲度越大, 扰动幅角的衰减率$B$更大, 即扰动幅角随时间下降的更快, 如图9与图10所示.

图9

新窗口打开|下载原图ZIP|生成PPT
图9不同弯曲度下扰动幅值与扰动幅角演化图 ($Re=10 000$, $c_{i}=-0.005$)

Fig.9Evolution diagram of disturbance amplitude and angle under different curvature ratio $Re$ ($Re=10 000$, $c_{i}=-0.005$)

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同弯曲度下扰动幅值与扰动幅角变化率曲线图 ($Re=10 000$, $c_{i}=-0.005$)

Fig.10Curve chart of amplitude and angle change rate of disturbance under different curvature ratio ($Re=10 000$, $c_{i}=-0.005$)

2.4 扰动速度分布与变化

2.4.1 扰动幅角对扰动速度变化分析

扰动速度的分量$u_{s_{i} } ,u_{n_{i}}$可表示为

(19)$\begin{eqnarray} \left.\begin{array}{l} u_{sr} ={Re}\left( {\sum\limits_{i=1}^5 {\varepsilon^{i}u_{s_{i} } } } \right),u_{si} ={Im}\left( {\sum\limits_{i=1}^5 {\varepsilon^{i}u_{s_{i}} } } \right) \\ u_{nr} ={Re}\left( {\sum\limits_{i=1}^5 {\varepsilon^{i}u_{n_{i} } } } \right),u_{ni} ={Im}\left( {\sum\limits_{i=1}^5 {\varepsilon^{i}u_{n_{i}} } } \right) \\ \end{array}\right\} \end{eqnarray}$
上式中, Re为取实部, Im为取虚部, $u_{sr} ,u_{si} $分别为一阶至五阶扰动流速$u_{s_{i} }$ (i=1,2,3,4,5)累和的实部与虚部分量, $u_{nr},u_{ni} $分别为一阶至五阶扰动流速$u_{n_{i} }$ (i=1,2,3,4,5)累和的实部与虚部分量. 考虑到$\varepsilon $为小量, 故以扰动振幅$a$取代, 令$k=\alpha s+\theta $, 将欧拉变化式(${e}^{{i}k}=\cos k+{i}\sin k)$代入式(19), 在此将对基本流的修正项略去, 仅仅分析扰动速度的分布.

在Seminara和Tubino^[4]的分析中, 弯曲河道频率高阶谐波的产生是与水流动力非线性相关,即空间上的扰动与水流的弱非线性相互作用产生高次谐波过程,这一点与文献[2,3]研究的几何非线性相区别, 并且认为高阶谐波不可忽略.本文研究中各阶扰动量的高次谐波的产生是源于弯道中的基本流与水流弱非线性相互作用,这一点与以上****的研究相区别. 为了探讨弯曲度在不同幅角下对扰动速度的影响, 选取$\psi =0.03$, 0.05, 0.10, 0.15, $Re=10 000$, 在初始位置$s=0$, 分析在$\theta=-4\pi $, $-4\pi -{\pi /2}$, $-4\pi -2{\pi /3}$, $-5\pi $, $-6\pi$下各个弯曲度下的扰动速度变化特征.

在图11中, 受弯曲度与扰动幅角影响下的扰动流速中,沿水流流向的$u_{sr}$与$u_{si}$的在横断面上都呈现"S"形分布,这与白玉川和冀自青^[11]所得到的不同弯曲程度河流中扰动流速的形状函数分布相似. 当弯曲度较大时,在$n=-1$端附近(凹岸)$u_{sr}$的扰动速度, 如$\psi =0.15$时存在一个速度转折点,使得在凹岸近壁处的速度与在$n=1$端(凸岸)的速度方向相同, 但远小于凸岸的速度,在此转折点之前, 即在稍微远离$n=-1$处,存在一个速度的极大值, 该速度与在$n=1$端的速度极大值相对应,但在弯曲度逐渐增大的过程中, 该速度极大值大小逐渐减小, 如在$\theta =-4\pi $时, $\psi =0.03$的$u_{sr}$两个速度极大值的大小几乎相等, $\psi=0.15$时, 在$n=-1$端的$u_{sr}$速度极大值约为$n=1$端的一半(图11(a)).随着$\psi $增大, 沿着河道轴线方向的$u_{sr}$与$u_{si}$对称性逐渐减弱, 即在$\psi=0$时, $u_{sr}$与$u_{si}$的两个极大值点呈现关于$n=0$对称的特点, 在$\psi$逐渐增加到0.15时, 在$n=1$端的极大值位置点不发生改变,但在$n=-1$端对应的极大值点向$n=0$移动(图11(a)).此外在$n=1$端的$u_{sr}$与$u_{si}$的极大值随着$\theta $的减小(负向增大),如当$\theta =-4\pi $与$\theta =-6\pi $, 该点处的$u_{sr}$与$u_{si}$在$\psi $较大时衰减较慢,即弯曲度的增大使得扰动流速对扰动幅角的反应减弱(图11(a), 图11(i)).

在横断面方向的扰动速度分布中, $u_{nr}$与$u_{ni}$主要呈现"抛物线"形分布,但$u_{nr}$在扰动幅角在$\theta =-4\pi $, $-5\pi $时(图11(b), 图11(h)), 弯曲度较大, 即$\psi =0.10$, 0.15, $u_{nr}$的分布呈现"S"形分布, 即两侧速度方向相反, 但在$n< 0$一侧的速度明显小于$n > 0$一侧,这种现象在$u_{ni}$的速度分布中同样出现, 如$\theta =-4\pi-{\pi/2}$ (图11(d)).

图11

新窗口打开|下载原图ZIP|生成PPT
图11扰动幅角影响下多弯曲度的扰动速度变化特征(左侧: $u_{sr}$与$u_{si}$; 右侧: $u_{nr}$与$u_{ni}$. 实线为实部, 虚线为虚部)

Fig.11Characteristics of disturbance velocity variation of multi curvature ratio under the influence of disturbance amplitude (left side: $u_{sr}$ and $u_{si}$; right side: $u_{nr}$ and $u_{ni}$. Solid line is real part, dotted line is imaginary part)

图11

新窗口打开|下载原图ZIP|生成PPT
图11扰动幅角影响下多弯曲度的扰动速度变化特征(左侧: $u_{sr}$与$u_{si}$; 右侧: $u_{nr}$与$u_{ni}$. 实线为实部, 虚线为虚部) (续)

Fig.11Characteristics of disturbance velocity variation of multi curvature ratio under the influence of disturbance amplitude (left side: $u_{sr}$ and $u_{si}$; right side: $u_{nr}$ and $u_{ni}$. Solid line is real part, dotted line is imaginary part) (continued)



此外, 在不同的弯曲度下, $ u_{nr}$与$u_{ni}$的分布都会随弯曲度的增大而向$n=1$端(凸岸)偏移,扰动流速的对称性减弱. 因此弯曲度的增大, 对于$u_{sr}$与$u_{si}$来说其扰动速度分布的对称性则越弱, 即在$n>0$侧速度加强, 在$n<0$侧速度减弱, 对于$u_{nr}$与$u_{ni}$的扰动速度分布逐渐向$n=1$端偏移,并且弯曲度的存在使得扰动速度对扰动幅角的变化反应减弱.

2.4.2 扰动速度空间分布变化特征

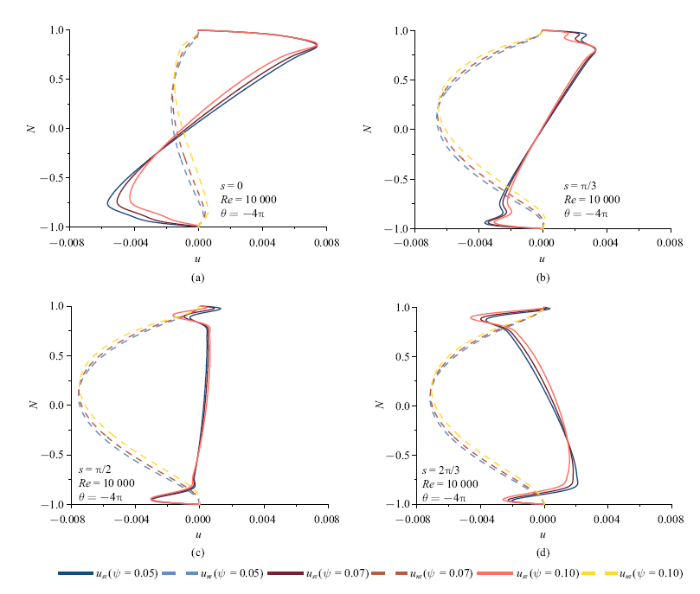
对于弯曲度对扰动速度的沿程分布的影响, 主要分析$\theta =-4\pi $, $Re=10 000$时, $\psi =0.05$, 0.07, 0.10, 在$s=0$, ${\pi /3}$, ${\pi/2}$, $2{\pi /3}$, $5{\pi /6}$, $\pi$位置上$u_{sr}$与$u_{nr}$变化特征.

在一个弯道内, 在入口端与出口端的$u_{sr}$呈现对称分布, 即在入口端($s=0$)正向流速出现在凸岸区域($n> 0$),负向流速出现在凹岸区域($n<0$), 在出口端($s=\pi )$则相反, 出口端的流速大小在靠近凹岸区域略小于入口端, 而在靠近凸岸区域则相反.

从入口到出口, 扰动流速在空间分布上具有周期性, 本次分析中($Re=10 000$,$\theta =-4\pi )$, 在$s={\pi /3}$处靠近两岸$u_{sr}$出现双峰结构(图12(b)), 在$s={\pi /2}$处$u_{sr}$的大小达到最小值(图12(c)), 随着$s$的增大, $u_{sr}$在$n> 0$侧流速向负向增大, $n<0$侧向正向增大, 呈现出扰动水流分离的情况, 分离点在$s={\pi /2}$附近. 在弯曲度较大时, $u_{sr}$的扰动速度曲线向$n> 0$方向偏斜,在$n<0$侧的最大值逐渐减小, 在$n> 0$侧的最大值则稍微加强.

$u_{nr}$在弯曲度逐渐增大的过程中, 流速向$n > 0$方向偏斜, 其速度抛物线顶点也随弯曲度的增大而向$n> 0$方向移动.可以看出在不同弯曲度下$u_{nr}$并不发生较大的变化, 但在$s={{5\pi}/6}$至$s=\pi $的区域内(图12(e), 图12(f)), 随着弯曲度的增大, $u_{nr}$逐渐减小, 其扰动速度曲线不断向内移动. 从$s=0$到$s=\pi $, $u_{nr}$经历了从增长至峰值再衰减, 其峰值的位置为$s={\pi /2}$附近, 这与$u_{sr}$的分离点一致.

图12

新窗口打开|下载原图ZIP|生成PPT
图12不同弯曲度下的扰动速度在空间位置上的变化特征(实线: $u_{sr}$; 虚线: $u_{nr})$

Fig.12Change characteristics of the disturbance velocity in spatial position under different curvature (Solid line: $u_{sr}$, dotted line: $ u_{nr})$}

图12

新窗口打开|下载原图ZIP|生成PPT
图12不同弯曲度下的扰动速度在空间位置上的变化特征(实线: $u_{sr}$; 虚线: $u_{nr})$ (续)

Fig.12Change characteristics of the disturbance velocity in spatial position under different curvature (Solid line: $u_{sr}$, dotted line: $ u_{nr})$ (continued)



2.4.3 扰动速度空间全域分布特征

在阐明了在不同的扰动幅角以及在不同空间位置上的扰动速度随弯曲度变化特征后, 对常曲率弯道中的全域扰动流速的分布特征进行分析, 取$\psi =0.10$, $\theta =-4\pi $至$-5\pi-{\pi /3}$中的多个特征扰动幅角进行分析, $\theta =-5\pi-{\pi /3}$作为$-4\pi -{\pi /3}$相差半个周期进行对比分析, $Re=10 000$, 结果如图13, 图中UXRAO为扰动速度矢量在$x$方向的分量.在全域中的常曲率弯道中的扰动速度分布具有明显的特点, 半个周期内, $\theta$在减小(负向增大)过程中, 在常曲率弯道内的扰动漩涡的位置也逐渐改变, 主要是在$\theta $从$-4\pi $至$-5\pi $中,扰动漩涡开始出现并逐渐从$s=0$的位置逐渐向$s=\pi $移动并消失的过程, 计算各个漩涡中心所在的位置,发现在一个周期内扰动幅角的大小与扰动漩涡的位置有一定的相关性, 如在$=\theta -4\pi-{\pi /3}$时,相应的扰动漩涡中心所在位置为$s=0.338\pi $ (图13(b)). 在$\theta $相差半个周期时, 如$\theta $为$-4\pi-{\pi/3}$与$-5\pi -{\pi /3}$时(图13(b)与图13(c)), 扰动速度和扰动漩涡的方向相反, 即$\theta =-4\pi-{\pi /3}$时, 在凸岸附近的流速方向指向下游, 在凹岸附近的流速则指向上游, 扰动漩涡呈现顺时针旋转, 当$\theta =-5\pi-{\pi /3}$时, 在凸岸附近的流速方向指向上游, 在凹岸附近的流速则指向下游, 扰动漩涡呈现逆时针旋转.

扰动漩涡随着扰动幅角周期性变化而变化, 表现在: (1)在扰动幅角减小(负向增大)过程中, 即$\theta =-4\pi $至$-5\pi-{\pi /3}$, 扰动漩涡的位置和方向也会出现周期性变化, 扰动漩涡总是从上游产生并逐渐向下游移动; (2)随着扰动幅角的减小(负向增大), 扰动流场的水流大小逐渐减小, 相应的扰动漩涡的强度也会逐渐衰减并最终消亡.Seminara^[7]在弯曲河流失稳的性质分析中指出, 如果一个初始小扰动产生时, 当时间趋于无穷大整个流场不受干扰,则这种不稳定是对流不稳定; 反之, 当初始小扰动同时向上游与下游两个方向传播, 随着时间的增长, 最终影响个水流区域, 则这种不稳定是绝对不稳定. 在上述分析中, $ u_{sr}$与$u_{nr}$随着时间延长而衰减, 扰动漩涡逐渐消亡,因此本次进行的分析属于扰动传播的对流不稳定性.

为分析$\psi =0.05$, 0.07, 0.10时的扰动速度的全域分布特征, 取$\theta =-4\pi -{\pi /3}$, $Re=10 000$进行分析, 结果如图14所示. 在同一扰动幅角下对于不同的弯曲度, 扰动漩涡中心的位置大致相同, 扰动漩涡边缘的速度在弯曲度较小时大于弯曲度为较大值时, 相应大的速度梯度更大.在相同弯曲度下的不同扰动幅角以及相同幅角下的不同弯曲度下的扰动速度空间分布可知,在全域中扰动流速最大值出现在扰动漩涡所在的侧壁处,并且随着扰动漩涡的移动而发生迁移.

3 结论

(1) 弯曲度的增大使中性曲线向雷诺数增大方向迁移, 即在微弯情况下,随着弯曲度的增大, 常曲率河湾的临界失稳雷诺数增大, 河湾趋于稳定.

图13

新窗口打开|下载原图ZIP|生成PPT
图13不同扰动幅角下的弯道全域扰动流速分布(2)在相同雷诺数下, 随着弯曲度的增大, 扰动幅值随时间的衰减速度增大, 即在初始扰动在经历了一定的时间后会逐渐消失,扰动流场具有非线性衰减效应. 扰动幅角随时间呈现单调下降的趋势, 弯曲度越大,扰动幅角随时间下降的更快.

Fig.13Disturbance velocity distribution in the whole bend under different disturbance angles



(3)在不同的弯曲度下, 沿流向的扰动速度呈现"S"形分布. 随弯曲度增大,沿着流动方向的扰动速度对称性逐渐减弱, 向凸岸偏斜, 弯曲度越大,扰动流速对扰动幅角的反应减弱.在垂直于流动方向的扰动速度呈现"抛物线"形分布,扰动流速$u_{nr}$会随弯曲度的增大而向凸岸偏移.

图14

新窗口打开|下载原图ZIP|生成PPT
图14不同弯曲度下的弯道全域扰动流速分布

Fig.14Disturbance velocity distribution in the whole bend under different disturbance angles



(4)在全域中常曲率弯道中的扰动速度分布具有明显的特点, (1)在扰动幅角减小(负向增大)过程中, 扰动漩涡的位置和方向呈出现周期性变化, 在一个周期内, 扰动漩涡总是从上游产生并逐渐向下游移动;

(2)随着扰动幅角的减小(负向增大), 扰动流场的水流大小逐渐衰减, 相应的扰动漩涡的强度也会逐渐衰减并最终消亡, 这种衰减效应属于对流不稳定性. 在相同扰动幅角下的不同弯曲度扰动漩涡中心位置大致相同, 但侧壁速度在弯曲度较小的时候要大于弯曲度较大的情况. 在全域中扰动流速最大值出现在扰动漩涡所在的侧壁处,并且随着扰动漩涡的移动而发生迁移.

(5)对于未来的探究应该构建三维完全非线性的河湾控制方程, 应考虑泥沙输移和床面形态特征的影响,构建水流动力非线性与床面形态几何非线性相互作用模型.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Callander RA . Instability and river channels
Journal of Fluid Mechanics, 1969,36(3):465-480
[本文引用: 1]

[2] Ikeda S, Parker G, Sawai K . Bend theory of river meanders. Part 1. Linear development
Journal of Fluid Mechanics, 1981,112(1):363-377
[本文引用: 2]

[3] Parker G, Sawai K, Ikeda S . Bend theory of river meanders. Part 2. Nonlinear deformation of finite-amplitude bends
Journal of Fluid Mechanics, 1982,115(1):303-314
[本文引用: 2]

[4] Seminara G, Tubino M . Weakly nonlinear theory of regular meanders
Journal of Fluid Mechanics, 1992,244(1):257-288
[本文引用: 2]

[5] Imran J, Parker G, Pirmez C . A nonlinear model of flow in meandering submarine and subaerial channels
Journal of Fluid Mechanics, 1999,400:295-331
[本文引用: 1]

[6] Sun T, Meakin P, J$\phi$ssang T, et al. A simulation model for meandering rivers
Water Resour Research, 1996,32:2937-2954
[本文引用: 1]

[7] Seminara G . Meanders
Journal of Fluid Mechanics, 2006,554(1):271-297
[本文引用: 3]

[8] Pittaluga MB, Nobile G, Seminara G . A nonlinear model for river meandering
Water Resources Research, 2009,45(4):546-550
[本文引用: 1]

[9] Pittaluga MB, Seminara G . Nonlinearity and unsteadiness in river meandering: A review of progress in theory and modelling
Earth Surface Processes & Landforms, 2011,36(1):20-38
[本文引用: 2]

[10] Xu HJ, Bai YC . The nonlinear theory for sediment ripple dynamic process of straight river
Science China, 2012(3):177-195
[本文引用: 1]

[11] Bai YC, Wang ZY . Theory and application of nonlinear river dynamics
International Journal of Sediment Research, 2014,29(3):285-303
[本文引用: 2]

[12] Xu HJ, Bai YC . Theoretical analyses on hydrodynamic instability in narrow deep river with variable curvature
Applied Mathematics and Mechanics, 2015,36(9):1147-1168


[13] 白玉川, 冀自青, 徐海珏 . 摆动河槽水动力稳定性特征分析
力学学报, 2017,49(2):274-288.


( Bai Yuchuan, Ji Ziqing, Xu Haijue . Hydrodynamic instability characteristics of laminar flow in a meandering channel with moving boundary
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(2):274-288 (in Chinese))


[14] 宋晓龙, 白玉川 . 基于河流阻力规律的河型统计与分类
水力发电学报, 2018,186(1):52-64.


( Song Xiaolong, Bai Yuchuan . Statistics and classification of river patterns based on river resistance law
Journal of Hydroelectric Engineering, 2018,186(1):52-64 (in Chinese))


[15] Xu HJ, Bai YC, Chen . Hydro-instability characteristics of bingham fluid flow as in the Yellow River
Journal of Hydro Environment Research, 2018,20:22-30


[16] Gao SX, Xu HJ, Bai YC . Theoretical analyses on bed topography responses in large depth-to-width ratio river bends with constant curvatures
Applied Mathematics and Mechanics, 2018,39(05):747-766


[17] 曹玉芬, 高术仙, 白玉川 . 正弦派生曲线弯道水流结构特征实验研究
水力发电学报, 2020,39(4):21-32.
[本文引用: 1]

( Cao Yufen, Gao Shuxian, Bai Yuchuan . Experimental study on flow structures in sine-generated meandering channel
Journal of Hydroelectric Engineering, 2020,39(4):21-32 (in Chinese))
[本文引用: 1]

[18] Ali SZ, Dey S . Hydrodynamic instability of meandering channels
Physics of Fluids, 2017,29(12):1-20
[本文引用: 1]

[19] Ali SZ, Dey S . Hydrodynamics of a weakly curved channel
Physics of Fluids, 2019,31(5):1-18


[20] Dey S, Ali SZ . Fluvial instabilities
Physics of Fluids, 2020,32(6):1-21


[21] Dey S, Ali SZ, Padhi E . Hydrodynamic lift on sediment particles at entrainment: Present status and its prospect
Journal of Hydraulic Engineering, 2020,146(6):1-9
[本文引用: 1]

[22] Monegaglia F, Tubino M, Zolezzi G . Interaction between curvature-driven width oscillations and channel curvature in evolving meander bends
Journal of Fluid Mechanics, 2019,876:985-1017
[本文引用: 1]

[23] Redolfi M, Zolezzi G, Tubino M . Free and forced morphodynamics of river bifurcations
Earth Surface Processes and Landforms, 2019(44):973-987


[24] Monegaglia F, Tubino M . The hydraulic geometry of evolving meandering rivers
Journal of Geophysical Research: Earth Surface, 2019,124(11):2723-2748


[25] Monegaglia F, Zolezzi G, G$\ddot{u}$neralp I, et al. Automated extraction of meandering river morphodynamics from multitemporal remotely sensed data
Environmental Modelling & Software, 2018,105:171-186
[本文引用: 1]

[26] Nelson JM, Mcdonald RR, Shimizu Y , et al. Modelling flow, sediment transport and morphodynamics in rivers//Kondolf GM, Herv$\acute{e}$ P. Tools in Fluvial Geomorphology.
Chichester, UK: John Wiley & Sons, 2016. 412-441
[本文引用: 1]

[27] Shimizu Y, Nelson J, Kattia AF , et al. Advances in computational morphodynamics using the international river interface cooperative (iRIC) software
Earth Surface Processes and Landforms, 2020,45(1):11-37
[本文引用: 1]

[28] Stuart JT . On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane poiseuille flow
Journal of Fluid Mechanics Digital Archive, 1960,9(3):353-370
[本文引用: 1]

[29] Heng Z, Fujimura K . Further improvement of weakly nonlinear theory of hydrodynamic stability
Science in China, 1998,41(1):84-92
[本文引用: 1]

[30] Lagasse P, Spitz W, Zevenbergen L , et al. Handbook for Predicting Stream Meander Migration. Washington,
DC: Transportation Research Board, 2004: 1-65
[本文引用: 1]

[31] Nishioka M, Iid AS, Ichikawa Y . An experimental investigation of the stability of plane poiseuille flow
Journal of Fluid Mechanics, 1975,72(4):731-751
[本文引用: 1]

[32] Orszag SA . Accurate solution of the orr-sommerfeld stability equation
Journal of Fluid Mechanics, 1971,50(4):689-703
[本文引用: 1]

[33] 白玉川, 冀自青, 徐海珏 . 窄深型河湾多尺度紊流拟序结构动力稳定与自适应特征研究
中国科学, 2012,42(11):1264-1273.
[本文引用: 1]

( Bai Yuchuan, Ji Ziqing, Xu Haijue . Instability and self-adaption character of turbulence coherent structure in narrow-deep river bend
Science China: Technology Science, 2012,42(11):1264-1273 (in Chinese))
[本文引用: 1]