李朝鑫^*, 武晓刚^,?,2,**, 孙玉琴^?, 秦迎泽^**, 段王平^**, 张美珍^??, 王艳芹^?, 陈维毅^,?,3), 卫小春^*** 太原理工大学机械与运载工程学院, 太原 030024
? 太原理工大学生物医学工程学院, 太原 030024
** 骨与软组织损伤修复山西省重点实验室, 太原 030001
?? 太原理工大学体育学院, 太原 030024

MECHANOTRANSDUCTION OF THE CELL AND ITS PRIMARY CILIUM IN THE MICROFLUIDIC CHANNEL ¹⁾

Li Chaoxin^*, Wu Xiaogang^,?,2,**, Sun Yuqin^?, Qin Yingze^**, Duan Wangping^**, Zhang Meizhen^??, Wang Yanqin^?, Chen Weiyi^,?,3), Wei Xiaochun^*** College of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China
? College of Biomedical Engineering, Taiyuan University of Technology, Taiyuan 030024, China
** Shanxi Provincial Key Laboratory for Repair of Bone and Soft Tissue Injury, Taiyuan 030001, China
?? Physical Education College of Taiyuan University of Technology, Taiyuan 030024, China

通讯作者: 2)武晓刚, 教授, 主要研究方向: 生物力学. E-mail:wuxiaogangtyut@163.com3)陈维毅, 教授, 主要研究方向: 生物力学. E-mail:chenweiyi211@163.com

收稿日期:2020-08-13接受日期:2020-10-19网络出版日期:2020-12-31

基金资助:

1)国家自然科学基金.11972242 国家自然科学基金.11702183 国家自然科学基金.11632013 国家自然科学基金.11572213 山西省高等学校科技创新项目.2017135 哲学社会科学研究项目.2017313 太原理工大学学科经费资助项目

Received:2020-08-13Accepted:2020-10-19Online:2020-12-31
作者简介 About authors


摘要
细胞处于复杂的生理环境之下,附着在细胞表面的初级纤毛被认为是重要的力学信号传感器,其与细胞的代谢、发育、分裂和增殖等生理活动密切相关.为了研究细胞及其初级纤毛在微流体环境下的力传导行为,本文建立了力-电协同驱动下的矩形微流控通道和含有多孔黏弹性属性的贴壁细胞有限元模型系统.考察了细胞的细胞质和细胞核在振荡层流下的应力、应变、孔隙压力和孔隙流速等力学信号响应,量化研究了初级纤毛作为细胞独特的力学感受器的生物力学行为. 结果表明:细胞在振荡层流下的力学响应表现出和外加力-电驱动载荷相同的震荡规律.渗透率是细胞多孔弹性力学行为的主要影响因素. 初级纤毛是细胞主要的力学感受器,细胞可以通过纤毛长度和直径调节其力学感受敏感性(应力影响区域),随着初级纤毛长度的增大, 其纤毛挠曲刚度减小, 但是敏感性增大.模型的建立为进一步研究微流体剪切作用下的细胞生长、分化等微观机理提供基础,同时也为检测细胞微结构器(纤毛等蛋白链)的力学性能提供了理论技术支持.
关键词： 细胞;初级纤毛;微流控;多孔黏弹性;力传导

Abstract
Cells usually live in a complex physiological environment. The primary cilium, which is a an important organelle of the cell, is attached to the cell surface and is regard as an important mechanical signal sensor to help living cell receive various external mechanical signals, the primary cilium is considered to be closely related to physiological activities such as metabolism, development, division and proliferation of the living cell. In order to study the mechanotransduction behavior of the living cell and the primary cilium growing on its surface in a microfluidic environment, this paper established the adherent cells within a rectangular microfluidic control channel model system, cells with poroviscoelastic properties are in a culture solution driven by the pressure gradient and electric field driven loads. The mechanical signal responses of cytoplasm and nucleus of cells such as the stress, strain, pore fluid pressure and pore fluid velocity under oscillatory laminar flow were investigated, as the mechanical signal's receptors of the living cell, the primary cilium's biomechanical behavior was quantitatively investigated. The results show that the mechanical response of the living cell under an oscillating laminar flow field has the same oscillating law as the synchronous external the pressure gradient and electric field driven loads. The permeability of the living cell is one of the most important physical parameters affecting the cell's poroviscoelastic behavior. Primary cilium is the main mechanoreceptor organelle. The living cell can adjust their mechanical sensitivity (stress-affected zone) by changing the length and diameter of its primary cilium. With the increase of the length of the primary cilium, the flexural rigidity of the primary cilium decreases, but the sensitivity increases. The establishment of the model provides a basis for further research on the microscopic mechanisms of cell growth and differentiation under the loading of microfluidic shear stress, and also provides theoretical technical support for testing the microstructure mechanical properties of the cell anticipates (protein chains such as primary cilium).
Keywords：cell;primary cilium;microfluidic control;poroviscoelasticity;mechanotransduction


PDF (2670KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李朝鑫, 武晓刚, 孙玉琴, 秦迎泽, 段王平, 张美珍, 王艳芹, 陈维毅, 卫小春. 微流控通道内细胞及其初级纤毛的力传导行为 ¹⁾. 力学学报[J], 2020, 53(1): 260-277 DOI:10.6052/0459-1879-20-283
Li Chaoxin, Wu Xiaogang, Sun Yuqin, Qin Yingze, Duan Wangping, Zhang Meizhen, Wang Yanqin, Chen Weiyi, Wei Xiaochun. MECHANOTRANSDUCTION OF THE CELL AND ITS PRIMARY CILIUM IN THE MICROFLUIDIC CHANNEL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 53(1): 260-277 DOI:10.6052/0459-1879-20-283

引言

微流控芯片^[1]可以实现细胞的体外培养, 广泛应用于细胞的检测研究中.微流控腔中培养液的动力流动方式从原理上主要分两类: 第一类为被动式,如表面张力和毛细作用, 第二类为主动式,包括压力驱动、离心力驱动、磁流体动力和电渗流驱动等^[2].生物体内的细胞生长、分化、粘附、迁移等活动受到力学微环境的影响,而微流控芯片培养细胞可以模拟实现特定的力学微环境,并完成细胞的生物力学研究^[3-4].电渗流^[2]是一种重要的微流体系统,它可以在不需要机械运动部件的情况下通过微通道输送流体, 当施加轴向电场时,带电表面会影响溶液中离子的运动状态, 从而带动溶液流动.为了研究生物组织的逆向力-电效应^[5],微流控技术可以实现力-电协同驱动培养液流动刺激贴壁细胞的生物力学技术微环境^[6].人工配置的无血清培养液可以简化为理想的牛顿型流体,而生理流体和细胞培养液一般被视为不可压缩的非牛顿型流体(Maxwell流)^[7-8], 忽略惯性力后可视为蠕动流. 在之前的工作中,建立含有细胞的牛顿型流体和非牛顿型流体的二维有限元模型被用于研究两种流体模型下线弹性细胞的动态响应^[9].

现有的细胞模型有线弹性、黏弹性、多孔弹性和多孔黏弹性模型等^[10-12].细胞组织的力学性质主要通过实验的方法探究, 裘钧^[13]研究发现细胞存在滞后,蠕变和松弛等黏弹性材料才有的力学行为并测定了标准线性固体黏弹性骨细胞模型的三参数$k_{1}$ (黏弹性材料的平衡态模量)、$k_{2}$ (黏性系数)和$\eta $ (黏滞系数), 在此基础上可以进一步推导出松弛时间$\tau =\eta /k_{2}$和剪切模量$G=k_{1}/3$. 研究表明, 水在人体体重的比重在一半以上, 从宏观生物器官组织到微观的各类细胞,均可以被视为同时具有固相和液相的多孔弹性材料^[14-16]. 近年来,原子力显微镜通过测量微悬臂梁探针与样品表面之间的相互作用, 提供了评估细胞力学性能的新技术,原子力显微镜实验数据和有限元模拟结合的方法被用于估算了两种细胞的孔隙弹性和黏弹性参数^[17-18]. 最初, 为了简化, 细胞被视为线弹性体而不足以考察细胞的生物力学特性, 随着细胞力学的发展, 建立更精确的多孔黏弹性细胞模型来考察复杂的力学行为是必要的.

初级纤毛是生长在细胞表面的毛发状细胞器, 它可以通过改变长度和抗弯性,以调节其力学敏感性, 适应微观力学环境^[19-23].初级纤毛已被观察与多种细胞途径的活动相结合,但是作为化学和力学信号的重要感受器还未被充分认识. 在很多情况下,初级纤毛充当调节细胞与细胞通信的信号传导中心^[24],它充当力学传感器并执行高度专业化的感知功能.初级纤毛的力学行为在细胞的体外培养技术和相关疾病中研究发现,软骨祖细胞(osteochondroprogenitors)独特地感知流体剪切并且参与成骨细胞的分化现象,但去除初级纤毛后这种现象基本消失,这个结果表明初级纤毛充当了具有力学信号传导功能的成骨分化细胞器^[25].在医学上, 初级纤毛与认知障碍、耳蜗听觉丧失、视网膜变性、嗅觉缺失症、颅面畸形、肺癌和呼吸 道异常、骨骼异常等疾病都具有相关性^[26].最近的研究表明骨细胞初级纤毛不仅可以作为感知外部力学刺激的"天线",还可以作为信号转导中各种信号分子的受体和吸收剂^[27].血管内衬内皮细胞上的初级纤毛起着钙依赖性力学传感器的作用,通过感应血流刺激来调节血管系统内的血液动力学参数^[28].内皮初级纤毛的缺陷会导致不适当的血流诱导反应,并导致血管功能障碍如动脉粥样硬化、高血压和动脉瘤^[29].肾初级纤毛在暴露于血流中时发生弯曲, 并在血流停止后发生恢复,类似于材料力学中的悬臂梁,其周期性弯曲可以激活钙离子通道的开关^[30].在发现初级纤毛的力学行为的重要性之后,从理论方面探讨初级纤毛的力学机制也就成为了一项重要工作.初级纤毛最初被简化为圆柱截面悬臂梁,并结合实验中观察到的弯曲情况得到初级纤毛的刚度范围^[29].结合实验观察研究初级纤毛尖端的摆动对其轴突和基底的力学响应,初级纤毛被更细化的建模为微管集合体计算初级纤毛在轴向和半径方向的弹性模量,发现长初级纤毛刚度比短初级纤毛更高^[31].培养腔内的细胞的流-固耦合有限元模型的建立证明了定常流中初级纤毛可以通过调节长度和刚度来改变线弹性细胞的力学敏感性^[24].

至今为止, 对于初级纤毛力学行为的理论研究大多数都是在稳定流场中进行的. 那么,有初级纤毛附着的细胞在振荡流中有怎样的周期性力学行为以及初级纤毛又如何对细胞体造成动态的影响就成为了重要的问题.本文通过有限元建模的方法研究振荡层流中多孔黏弹性细胞的力学响应,得到了初级纤毛在微流控腔内液体流动中的力学行为.具体研究了细胞质渗透率变化对细胞多孔弹性力学行为的影响,以及初级纤毛的几何(长度、直径)和力学(弹性模量)特性对自身及其他细胞器(细胞质、细胞核)的力学信号感受能力的影响.

1 材料和方法

1.1 矩形截面通道振荡层流理论

微流控腔体内的液体流动可以用Navier-Stokes方程来描述, 图1所示,流动为充分发展的矩形截面($a \times b)$层流体系. 并且假设:流体为不可压缩的牛顿流体, 压力在管道截面上均匀分布

(1)$\begin{eqnarray} \rho \left(\frac{\partial {u}}{\partial t}+{u}\cdot \nabla {u}\right)=-\nabla {P}+{f}+\mu \Delta {u} \end{eqnarray}$

图1

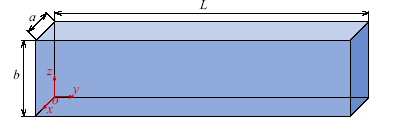新窗口打开|下载原图ZIP|生成PPT
图1微流控通道中的流场示意图

Fig.1Schematic diagram of flow field in microfluidic channel



不可压缩流体的连续性方程为

(2)$\begin{eqnarray} \nabla \cdot {u}=0 \end{eqnarray}$
式中, $\mu =\nu \rho $是流体的动力黏度, $\nu $是流体的运动黏度, $\rho$为流体密度, $u$为流体在矩形截面上的速度, $f$是流体所受的体力, $\Delta$为Laplace算子, $\nabla $为梯度算子. 若微管$x$和$z$方向的流速为0, 设$y$方向的速度为$u$, 压强$P$仅是关于$y$和时间$t$的函数, 忽略体力的影响, 则$x-z$截面上的方程(1)可简化为

(3)$\begin{eqnarray} \label{eq3} \nu \lt(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial z^{2}}\rt)-\frac{\partial u}{\partial t}=\frac{1}{\rho }\frac{\partial P(y,t)}{\partial y} \end{eqnarray}$
$\partial P(y,t)/\partial y$是$y$轴方向的压力梯度. 为便于数学计算,原点$o$设置在通道的左下角, 使$0≤ x≤ a$和$0≤ z≤ b$, 则初始和边界条件为

(4)$\begin{eqnarray} \label{eq4} \left.\begin{array}{l} \left. {\dfrac{\partial u}{\partial x}} \right|_{x=0} =\left. {\dfrac{\partial u}{\partial z}} \right|_{z=0} =0 \\ \left. u \right|_{t=0} =0 \\ \left. u \right|_{x=0} =\left. u \right|_{x=a} =0 \\ \left. u \right|_{z=0} =\left. u \right|_{z=b} =0 \\ \end{array} \right\} \end{eqnarray}$
方程(3)的解写成$u=u_{s}(y,z)+u_{t}(x,z,t)$, 其中$u_{s}$为稳态速度分量,$u_{t}$为振荡瞬时速度分量. 由于各种周期性函数均能通过傅里叶变换分解为三角函数的叠加,Blythman等^[32]用格林函数求解了在压力分别为 $\partial P(y,t)/\partial y=\nabla P_{os}$ $(\nabla P_{os}$是定常流的常数项压力梯度值)和$\partial P(y,t)/\partial y=\nabla P_{ot}\cos(\omega t)(\nabla P_{ot}$是三角函数压力梯度幅值)振荡层流的解析解, $\omega $为振荡角速度,当压力梯度为常数时, 稳态速度的解析解为

(5)$\begin{eqnarray} \label{eq5} u_{s} \left( {x,z} \right)=-\frac{16\nabla P_{{0S}} }{\mu \pi ^{2}}\sum\limits_{m odd}^\infty {\sum\limits_{n odd}^\infty {\frac{\varPhi }{mn\beta }} } \end{eqnarray}$
式中$m$, $n$为求和指数, odd表示$m$和$n$从1 $\sim$ $\infty $取奇数, 其中$\varPhi$和$\beta$是由式(6)确定的函数

(6)$\begin{eqnarray} \label{eq6} \varPhi =\sin \frac{m\pi x}{a}\sin \frac{n\pi z}{b},\\ \beta =\pi^{2}\left( {\frac{m^{2}}{a^{2}}+\frac{n^{2}}{b^{2}}} \right) \end{eqnarray}$
当压力梯度为振荡层流时, 速度的解析解为

(7)$\begin{eqnarray} \label{eq7} && u_{t} \left( {x,z,t} \right)=-\frac{16\nabla P_{0t} }{\rho \pi ^{2}}\left[ \left( {\sum\limits_{m odd}^\infty {\sum\limits_{n odd}^\infty {\frac{\varPhi }{mn}\frac{\omega }{\nu^{2}\beta^{2}+\omega^{2}}} } } \right)^{2} + \right. \left. \left( {\sum\limits_{m odd}^\infty {\sum\limits_{n odd}^\infty {\frac{\varPhi }{mn}\frac{\nu \beta }{\nu^{2}\beta^{2}+\omega^{2}}} } } \right)^{2} \right]^{{1}/{2}}\sin \left( {\omega t+\phi_{u} } \right) \end{eqnarray}$
其中$\varphi_{u}$为初相

(8)$\begin{eqnarray} \label{eq8} \phi_{u} \left( {x,z} \right)=\tan^{-1}\left( {\frac{\sum\limits_{m odd}^\infty {\sum\limits_{n odd}^\infty {\dfrac{\varPhi }{mn}\dfrac{\nu \beta }{\nu^{2}\beta^{2}+\omega^{2}}} } }{\sum\limits_{m odd}^\infty {\sum\limits_{n odd}^\infty {\dfrac{\varPhi }{mn}\dfrac{\omega }{\nu^{2}\beta ^{2}+\omega^{2}}} } }} \right) \end{eqnarray}$

1.2 有限元建模

1.2.1 几何模型

根据先前的细胞培养微流控芯片装置模型^[33], 将其扩展为三维有限元模型,如图2(a)所示. 根据先前工作, 液体压力沿流动方向$y$线性分布^[32],截取其中包含第40个单细胞进行分析, 如图2(c)所示, 培养腔全长$L=35$ mm,宽$a=150$ $\mu$m, 高$b=150$ $\mu$m, 割离出的培养腔长$l=350$ $\mu$m.建立的三维微流控通道流场模型中, 细化出了细胞的初级纤毛,细胞质和细胞核三维结构(忽略了细胞膜). 如图2(b)和图2(d)所示,细胞质呈半椭球状, 长轴$Y_{cytoplasm}=20$ $\mu$m, 长轴方向沿通道$y$轴方向,短轴$X_{cytoplasm}=14$ $\mu$m, 高度$H_{cytoplasm}=4$ $\mu$m.将细胞核建模为椭球体, 长轴$X_{nucleus}=5$ $\mu$m, 长轴方向沿通道$x$轴方向,短轴$Y_{nucleus}=4$ $\mu$m, 高度$H_{nucleus}=2.5$ $\mu$m,初级纤毛建立为圆柱截面悬臂梁嵌入细胞表面下0.05 $\mu$m,初始直径为$D_{pc}=0.2$ $\mu$m, 初始长度为$L_{pc}=2.5$ $\mu$m^[24],模型的尺寸参数总结为表1.

图2

新窗口打开|下载原图ZIP|生成PPT
图2微流体培养腔和单细胞的模型和网格: (a)矩形截面培养腔和其中等间隔的细胞;(b)由初级纤毛、细胞质和细胞核组成的细胞; (c)分离的单细胞培养腔有限元网格;(d)单细胞的有限元网格

Fig.2Models and mesh of microfluidic culture chamber and single cell: (a) Rectangular cross-section culture chamber and equidistantly distributed cells; (b) cell diagram composed of primary cilium, cytoplasm and nucleus; (c) finite element mesh of separated single cell culture chamber; (d) finite element mesh of single cell




Table 1
Table 1Sizes of rectangular channel and cell model

新窗口打开|下载CSV

1.2.2 边界条件和载荷施加

半椭球细胞的椭圆形底面贴在细胞腔壁上故施加固定约束, 细胞流体接触面和培养腔壁设定无滑移边界,细胞和液体的边界设定结构上的流体载荷流固耦合边界. 细胞模型属于多孔弹性模型,是建立在流体-结构耦合有限元模型中的: (1)细胞的固相成分是均匀的,各向同性和不可压缩黏弹性连续体; (2)在不考虑任何主动力的情况下,只分析骨细胞在流场中的被动变形; (3)为防止初级纤毛底部旋转过大,便于将初级纤毛视为悬臂梁分析, 对初级纤毛的底面施加刚性连接并限制其旋转.

载荷驱动^[33]设置: 全培养腔入出口处分别设置正弦压力驱动$P_{inlet}$和 $P_{outlet}$,分离出的单细胞培养腔压力梯度频率$f=1$ Hz, $\partial P(y, t)/\partial y=\partial P_{0t} \sin(2\pi ft)$, 并施加频率$f=1$ Hz, 电场强度为$\partial E(y, t)/\partial y=\partial E_{0t} \sin(2\pi ft)$的电场力, 压力梯度和电场强度变化见表2和图3.


Table 2
Table 2Load parameters of pressure and electric field

新窗口打开|下载CSV

图3

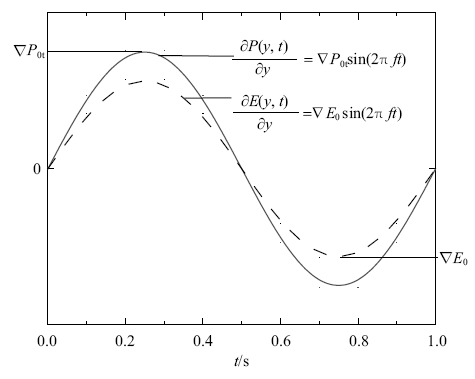新窗口打开|下载原图ZIP|生成PPT
图3通道中$y$轴方向的压力梯度和电场梯度

Fig.3Pressure gradient and electric field gradient in the $y$-axis direction in the channel



1.2.3 材料参数

细胞培养液的参数设置见表3, 其中$C$为电解质的摩尔浓度, $\psi_{0}$为腔壁的Zeta电势, $z_{0} $为离子所带电荷数, $k_{b}$为玻尔兹曼常数, $N_{A}$为阿伏伽德罗常数, $e$为单位电荷电量, $\varepsilon_{0} $为真空介电常数, $\varepsilon_{r} $为相对介电常数, $t_{0}$为摄氏温度, $\rho $和$\mu$为细胞培养液的密度和动力黏度.


Table 3
Table 3Fluid parameters^[33]

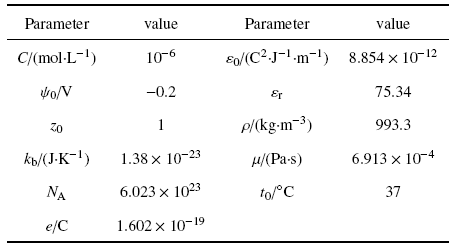新窗口打开|下载CSV

多孔黏弹性细胞的参数设置见表4和表5, 其中$E$为弹性模量,$v_{s}$为泊松比, $\rho_{S} $为固相密度, $\kappa $为渗透率,$\varepsilon_{p} $为孔隙率, $\alpha_{B}$为Biot-Wills系数, $\rho_{l}$为液相密度, $\mu$为动力黏度, $\chi_{f} $为压缩系数, $\tau_{v}$为松弛时间, $G_{v}$为剪切模量, 初级纤毛^[24]的初始弹性模量为$E_{0}=178$ kPa, 泊松比为0.3.


Table 4
Table 4Cytoplasmic parameters^[13,34,35]

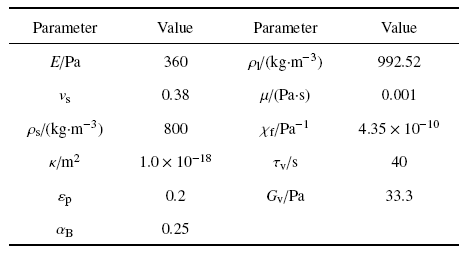新窗口打开|下载CSV


Table 5
Table 5Nuclear parameters^[13,34,35]

新窗口打开|下载CSV

2 结果

2.1 不含细胞矩形通道层流的有限元有效性验证

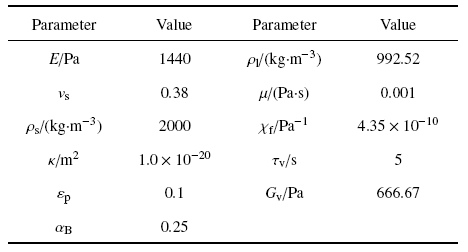
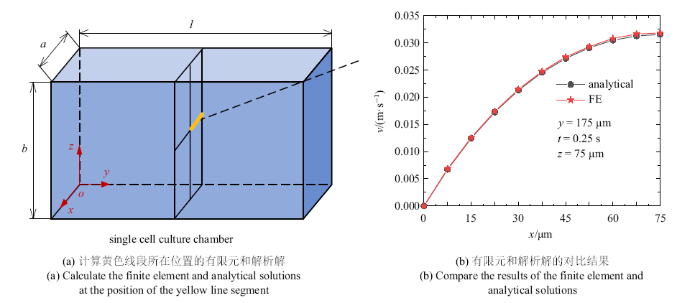
为了验证有限元结果的可靠性, 如图4(a)为分离出单细胞所在培养腔,腔体的宽和高$a=b=150$ $\mu$m, 长$l=350$ $\mu$m, 压力梯度为$\partial P(y,t)/\partial y=4.6 \sin (2\pi ft)/3.5\times 10^{-4}$ Pa/m. 由于矩形通道的对称性,选取流速幅值时刻$t=0.25$ s, 将$x\in (0$ $\mu$m, 75 $\mu$m), 通道的中轴线$z=75$ $\mu$m 的有限元流速结果与式(7)计算的解析解进行对比, 计算过程中公式中$m$和$n$从1, 2, $\cdots$, 999取奇数, 对比结果如下图4(b)所示, 为不含细胞矩形通道层流的有限元分析和解析解对比结果,可以看出从管道中心到管道壁面流速呈抛物线式逐渐减小.从图中可以看出有限元模拟的结果与解析解吻合,矩形通道层流的有限元有效性得以验证.

图4

新窗口打开|下载原图ZIP|生成PPT
图4流速$v$的有限元结果与解析解的对比: (a)计算黄色线段所在位置的有限元和解析解;(b)有限元和解析解的对比结果

Fig.4Comparison of finite element results and analytical solutions of velocity $v$: (a) Calculate the finite element and analytical solutions at the position of the yellow line segment; (b) compare the results of the finite element and analytical solutions

2.2 多孔黏弹性细胞的力学响应

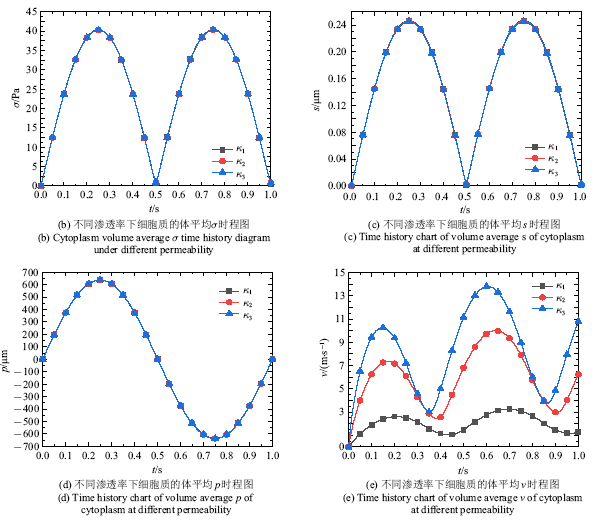
图5(a)表明除孔隙流速的幅值时刻较外加载荷提前, 其他三种力学信号幅值时刻与外加载荷相同, 图5(b) ~图5(e)依次为0~1 s内细胞质在不同渗透率下的体平均Mises应力$\sigma$ (Pa), 总位移$s$ ($\mu$m), 孔隙压力$p$ (Pa)和孔隙流速$v$ (nm/s)四种力学信号的时程曲线, 体平均应力值由网格节点应力求和除以节点数求得, 其中 $\kappa_{1} $, $\kappa_{2} $和$\kappa_{3} $依次为$1.0\times10^{-19}$ m$^{2}$, $5.0\times10^{-19}$ m$^{2}$和$1.0\times10^{-18}$ m$^{2}$.

可以看出四种力学信号表现为与流场外加驱动同周期的发展规律.

细胞质渗透率为$\kappa_{1} $, $\kappa_{2} $和$\kappa_{3} $时, 体平均Mises应力在$t=0.25$ s达到最大值为41.25 Pa, 41.09 Pa和41.04 Pa, 体平均位移达到最大值均为0.24 $\mu$m, 体平均孔隙压力达到最大值为729.64 Pa, 661.03 Pa和654.53 Pa, 其中渗透率$\kappa_{1} $, $\kappa_{2} $和$\kappa_{3}$的体平均孔隙流速值的最大值依次出现在0.70 s, 0.64 s和0.61 s, 为3.31 nm/s, 9.79 nm/s和13.42 nm/s.

图5

新窗口打开|下载原图ZIP|生成PPT
图5力学信号时程曲线

Fig.5Mechanical signal time history curve

图5

新窗口打开|下载原图ZIP|生成PPT
图5力学信号时程曲线(续)

Fig.5Mechanical signal time history curve (continued)



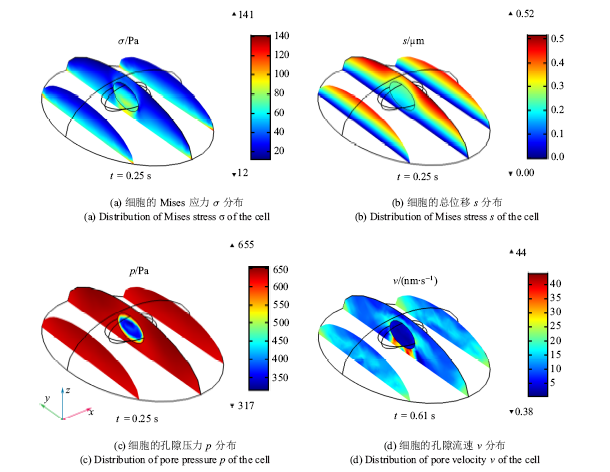
如图6(a) ~图6(d)为渗透率为$\kappa_{3} $的细胞在$t=0.25$ s时细胞的$\sigma $, s, p云图和$t=0.61$ s时细胞的云图. 从图6(a)中可以看出细胞贴壁侧的受力较大, 细胞受力较大的位置处于细胞的贴壁边界, 细胞核的Mises应力大于细胞质. 图6(b)为细胞在$t=0.25$ s时细胞的总位移云图, 可以看出细胞远离贴壁侧位移较大,细胞位移最大的位置处于细胞核与贴壁边界中间的细胞质表面, 细胞质的总位移大于细胞核. 图6(c)为细胞的孔隙压力云图, 可以看出细胞质和细胞核的孔隙压力分布均匀, 细胞质的孔隙压力大于细胞核, 且细胞质中位移越大的位置孔隙压力越大. 图6(d)为细胞的孔隙流速云图, 可以看出贴壁边界和细胞核附近的孔隙流速较大, 细胞孔隙流速最大的点位于细胞核下方的细胞质贴壁处, 细胞质的孔隙流速大于细胞核.

2.3 初级纤毛的研究

2.3.1 有无初级纤毛的细胞对比

图7(a) ~图7(d)依次为不含初级纤毛的细胞在$t=0.25$ s (细胞变形和纤毛挠度达到最大值时刻)的$\sigma $, $s$, $p$和$v$云图, 图7(e) ~图7(h)依次为含初级纤毛的细胞在$t=0.25$ s的$\sigma $, $s$, $p$和$v$云图. 从中可以看出,初级纤毛的存在使纤毛基部(纤毛嵌入细胞内的部分)所在的局部细胞质应力增大和孔隙流速降低,但并不对整体应力、位移和孔隙压力和孔隙流速分布产生影响. 不含初级纤毛和2.5 $\mu$m长的初级纤毛基部所在区域的局部平均Mises应力分别为36.02 Pa和94.51 Pa,平均总位移分别为0.73 $\mu$m和0.76 $\mu$m, 平均孔隙压力分别为654.61 Pa和648.15 Pa, 平均孔隙流速分别为7.62 nm/s和4.80 nm/s.

图6

新窗口打开|下载原图ZIP|生成PPT
图6无初级纤毛细胞的力学信号云图

Fig.6Mechanical signals contours of cell without primary cilium

图7

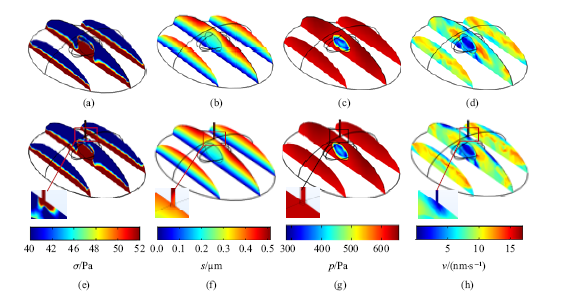新窗口打开|下载原图ZIP|生成PPT
图7无初级纤毛细胞Mises应力$\sigma $(a), 总位移$s$(b), 孔隙压力$p$(c)和孔隙流速$v$(d)和有初级纤毛细胞的Mises应力$\sigma $(e), 总位移$s$(f), 孔隙压力$p$(g)和孔隙流速$v$(h)的对比

Fig.7Comparison of Mises stress $\sigma $(a), total displacement $s$(b), pore pressure $p$(c) and pore flow velocity $v$(d) \quad of cell without primary cilium and Mises stress $\sigma $(e), total displacement $s$(f), pore pressure $p$(g) and pore flow velocity $v$(h) of cell with primary cilium



图8为初级纤毛、细胞质和细胞核的体平均Mises应力和第一主应变对比图, 结果表明初级纤毛的平均应力和应变大于细胞核大于细胞质.

图8

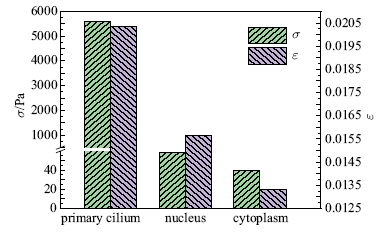新窗口打开|下载原图ZIP|生成PPT
图8$t=0.25$ s时初级纤毛, 细胞质和细胞核的应力和应变对比

Fig.8Comparison of stress and strain of primary cilium, cytoplasm and nucleus at $t=0.25$ s



此外, 如图9(a)的红色区域为初级纤毛的影响区域图, 图中红色区域应力大于40 Pa. 为了总结初级纤毛的存在对初级纤毛基部局部细胞质的影响, 进行如图9(b)的局部选点分析, 点与点间隔5 nm, $t=0.25$ s时左侧(Zone 1)在初级纤毛向右侧弯曲时受拉, 右侧(Zone 3)受压.

研究表明, 初级纤毛的形状和力学参数受细胞外界生理环境、细胞生命活动、药物干预等多种因素影响.

所以进一步研究了初级纤毛在不同长度($L_{pc})$、不同直径($D_{pc})$、不同弹性模量($E_{pc})$下的力学行为.

图9

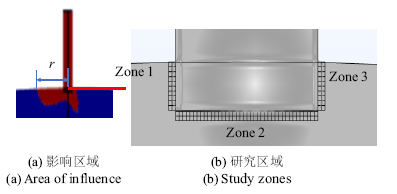新窗口打开|下载原图ZIP|生成PPT
图9初级纤毛的影响区域尺寸$r$和研究区域

Fig.9Primary cilium's affected area size $r$ and the study zones



2.3.2 初级纤毛长度的影响

如图10(a)为$t=0.25$ s时带有不同长度初级纤毛($L_{pc})$的Mises应力和变形云图,从图中可以看出, 初级纤毛的长度越长弯曲和拉伸程度越大, 初级纤毛中下方的应力也越大. 当初级纤毛的长度分别为1.5 $\mu$m, 2 $\mu$m, 2.5 $\mu$m, 3 $\mu$m, 3.5 $\mu$m时^[29], 初级纤毛顶端的挠度依次为0.34 $\mu$m, 1.25 $\mu$m, 3.38 $\mu$m, 7.74 $\mu$m, 15.34 $\mu$m, 初级纤毛基部的最大Mises应力依次为9.41 kPa, 19.69 kPa, 34.42 kPa, 55.15 kPa, 81.13 kPa. 从中可以看出初级纤毛长度的变化对初级纤毛的弯曲程度和初级纤毛基部的应力将产生很大的影响.

如图10(b) ~图10(e)所示, 统计了$t=0.25$ s初级纤毛基部局部细胞质的力学信号的平均值和标准差, 取点方式见图9(b).随着初级纤毛长度的增大, 从图10(b)中可以看出,纤毛基部局部细胞质总体上应力提升, 拉伸侧、压缩侧和底部应力大小相近;从图10(c)中可以看出, 总位移随着长度的增大而小幅增大,拉伸侧、压缩侧和底部总位移大小相近; 从图10(d)中可以看出,孔隙压力随着长度的增大而保持

图10

新窗口打开|下载原图ZIP|生成PPT
图10初级纤毛长度变化的影响

Fig.10The influence of primary cilium's length changes

图10

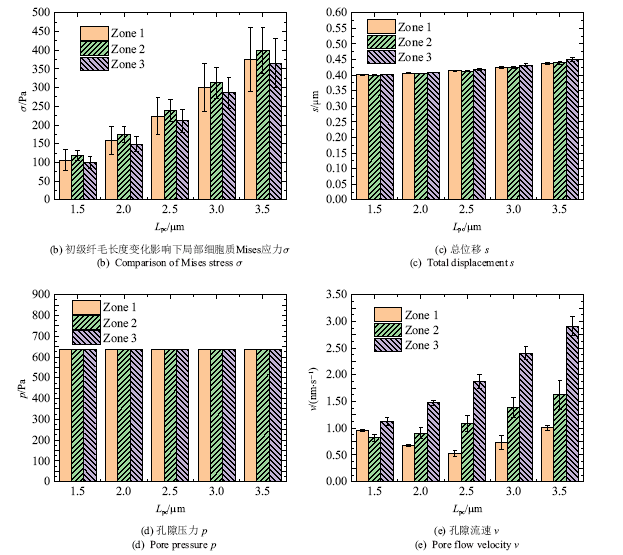新窗口打开|下载原图ZIP|生成PPT
图10初级纤毛长度变化的影响(续)

Fig.10The influence of primary cilium's length changes (continued)



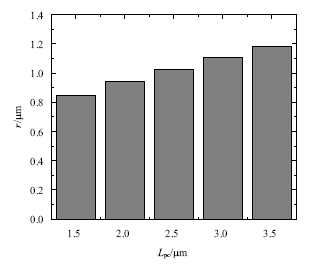
不变, 拉伸侧、压缩侧和底部孔隙压力大小相同;从图10(e)中可以看出, 孔隙流速随着长度的增大而增大, 长度较低时,压缩侧流速大于拉伸侧大于底部, 当长度大于2 $\mu$m后,压缩侧流速大于底部大于拉伸侧. 此外, 从图11可以看出, 初级纤毛长度越长,纤毛基部的局部细胞质受影响范围越大.

图11

新窗口打开|下载原图ZIP|生成PPT
图11不同长度初级纤毛影响区域

Fig.11Influence area of primary cilium of different lengths



2.3.3 初级纤毛直径的影响

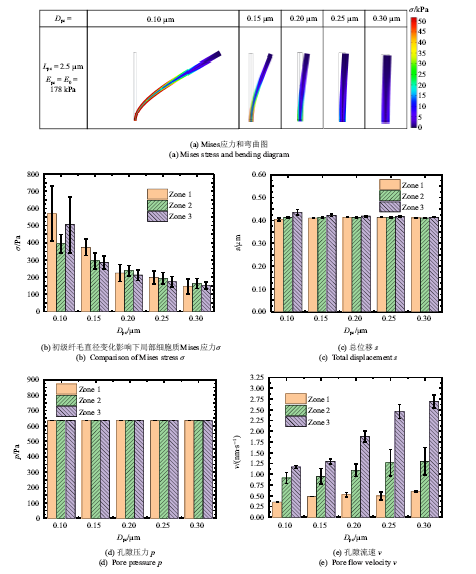
对于悬臂梁模型来说, 初级纤毛的直径是影响初级纤毛抗弯行为的主要因素,因此研究了初级纤毛的直径($D_{pe})$在0.1~0.3 $\mu$m范围变化^[36-37]对细胞感受外界生物力学因素的影响.如图12(a)为$t=0.25$ s时带有不同直径初级纤毛的Mises应力和变形云图,当直径分别为0.10 $\mu$m, 0.15 $\mu$m, 0.20 $\mu$m, 0.25 $\mu$m, 0.3 $\mu$m时, 初级纤毛顶端的挠度分别为40.44 $\mu$m, 9.65 $\mu$m, 3.38 $\mu$m, 1.56 $\mu$m, 0.79 $\mu$m, 初级纤毛基部的最大Mises依次为202.88 kPa, 75.49 kPa, 34.42 kPa, 19.06 kPa, 12.00 kPa.从图中可以看出, 初级纤毛直径的变化对初级纤毛的弯曲变形程度和初级纤毛基部的应力将产生很大的影响,初级纤毛的直径越小其弯曲和拉伸程度越大, 应力也越大.

图12

新窗口打开|下载原图ZIP|生成PPT
图12初级纤毛直径变化的影响

Fig.12The influence of primary cilium's diameter changes



如图12(b) ~图12(e)所示, 统计了$t=0.25$ s初级纤毛基部局部细胞质的力学信号的平均值和标准差, 取点方式见图9(b).随着初级纤毛直径的增大, 从图12(b)中可以看出, 纤毛基部局部细胞质总体上应力降低, 直径$D_{pc}=0.1$ $\mu$m时,拉伸侧、压缩侧的应力明显大于底部, 随着直径的增大, 拉伸侧、压缩侧和底部应力大小相近; 从图12(c)中可以看出, 直径的增大仅仅引起压缩侧位移的小幅减小; 从图12(d)中可以看出, 孔隙压力随着直径的增大而保持不变, 拉伸侧、压缩侧和底部孔隙压力大小相同; 从图12(e)中可以看出, 孔隙流速随着长度的增大而增大, 压缩侧流速大于底部大于拉伸侧. 此外, 从图13可以看出, 初级纤毛直径越大, 纤毛基部的局部细胞质受影响范围越大.

图13

新窗口打开|下载原图ZIP|生成PPT
图13不同直径初级纤毛影响区域

Fig.13Influence area of primary cilium with different diameters



2.3.4 初级纤毛弹性模量的影响

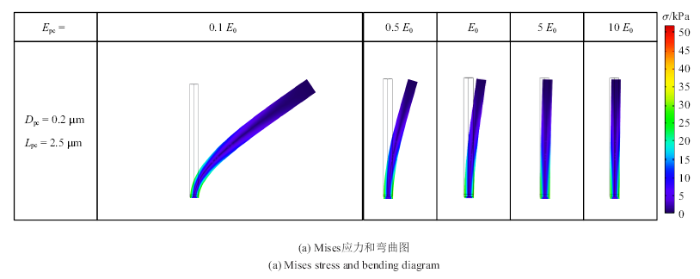
影响初级纤毛刚度的因素包括初级纤毛直径和弹性模量,研究了弹性模量($E_{pe})$在$E_{0}=178$ kPa的0.1, 0.5, 1, 5,10倍范围内变化对于细胞的力学响应的影响. 研究发现,从弹性模量和直径两方面改变初级纤毛的刚度, 对初级纤毛的影响并不相同,弹性模量越大, 初级纤毛弯曲程度越小, 如图14(a)所示, $t=0.25$ s弹性模量分别为$E_{0}$的0.1, 0.5, 1, 5, 10倍时,初级纤毛顶部的挠度依次为33.73 $\mu$m, 6.69 $\mu$m, 3.78 $\mu$m, 0.68 $\mu$m, 0.34 $\mu$m, 初级纤毛底部的Mises应力依次为33.40 kPa, 34.04 kPa, 34.42 kPa, 34.50 kPa, 34.53 kPa, 初级纤毛的弹性模量越高,初级纤毛的弯曲变形程度越低, 初级纤毛弹性模量的变化对纤毛基部应力无明显影响.

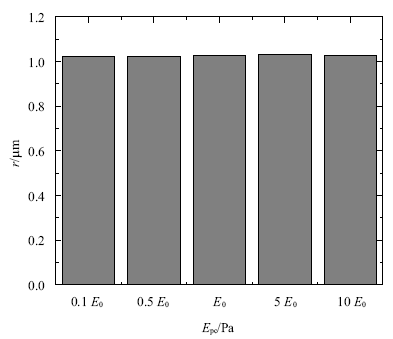
如图14(b) ~图14(e)所示, 统计了$t=0.25$ s初级纤毛基部局部细胞质的力学信号的平均值和标准差, 取点方式见图9(b).从图14(b)中可以看出弹性模量很小(0.1$E_{0})$的纤毛弯曲时拉伸侧的应力大于压缩侧大于底部,弹性模量大于0.5$E_{0}$后, 应力变化不再显著.从图14(c)中可以看出随着初级纤毛弹性模量的增大, 压缩侧总位移小幅降低,拉伸侧和底部总位移不变, 从图14(d)中可以看出初级纤毛附近的孔隙压力恒定,从图14(e)中可以看出纤毛基部局部细胞质孔隙流速无明显变化,压缩侧流速大于底部大于拉伸侧, 从图15知随着初级纤毛弹性模量的增大,基部细胞质的受影响范围保持1 $\mu$m左右不变.

图14

新窗口打开|下载原图ZIP|生成PPT
图14初级纤毛弹性模量变化的影响

Fig.14Influence of primary cilium's elastic modulu changes

图14

新窗口打开|下载原图ZIP|生成PPT
图14初级纤毛弹性模量变化的影响(续)

Fig.14Influence of primary cilium's elastic modulu changes (continued)

图15

新窗口打开|下载原图ZIP|生成PPT
图15不同弹性模量初级纤毛影响区域

Fig.15Influence area of primary cilium with different elastic modulus



2.3.5 初级纤毛的受力分析

如图16(a)所示, 假设初级纤毛是一个底部埋在细胞质中的圆柱形杆件,由于矩形微流体通道中流体的压力沿长轴线性变化, 而初级纤毛的尺度相对于通道很小, 因此初级纤毛附近的流体压力值近似恒定,杆件在流体压力均匀作用下弯曲, 用$q$来表示杆件所受的均布载荷, $w$来表示弯曲挠度,根据材料力学的悬臂梁知识, 则可以通过初级纤毛的挠度$w$计算初级纤毛所受到的均布载荷$q$大小.初级纤毛在均布载荷$q$作用下悬臂端的挠度$w$大小为

(9)$\begin{eqnarray} w=-\frac{1}{E_{pc} I}\frac{qL_{pc}^{4}}{8} \end{eqnarray}$
式中, $L_{pc}$表示纤毛长度, $E_{pc}$表示弹性模量和$I=\pi D_{pc}^{4} /$64表示圆形截面惯性矩, $D_{pc}$表示直径. 通过计算得到不同长度初级纤毛在流场中受到的均布载荷为

(10)$\begin{eqnarray} q=-\frac{8E_{pc} Iw}{L_{pc}^{4}}=-\frac{E_{pc} \pi D_{pc}^{4} w}{8L_{pc}^{4}} \end{eqnarray}$

图16

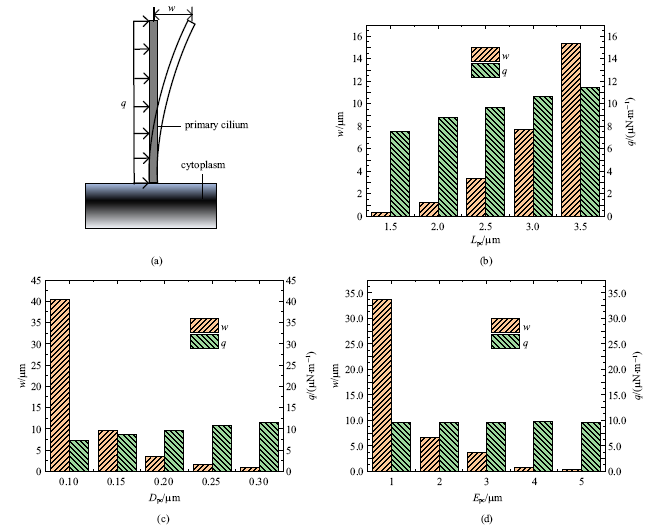新窗口打开|下载原图ZIP|生成PPT
图16根据悬臂梁受均布载荷理论(a)和不同长度$L_{pc}$ (b)、直径$D_{pc}$ (c)和弹性模量$E_{pc}$ (d)初级纤毛的挠度$w$计算均布载荷$q$

Fig.16Calculate the uniform load $q$ based on the cantilever beam subjected touniform load theory (a) and the deflection $w$ of primary cilium of different lengths $L_{pc}$ (b), diameter $D_{pc}$ (c) and elastic modulus $E_{pc}$ (d)}



图16(b)为通过式(10)和$t=0.25$ s不同长度$L_{pc}$的初级纤毛的挠度$w$算出的均布载荷$q$.图16(c)为通过式(10)和$t=0.25$ s不同直径$D_{pc}$的初级纤毛的挠度$w$算出的均布载荷$q$.图16(d)为通过式(10)和$t=0.25$ s不同弹性模量$E_{pc}$的初级纤毛的挠度$w$算出的均布载荷$q$. 图16(b) ~图16(d)中左轴对应$t=0.25$ s时不同初级纤毛的挠度$w$的有限元结果,右轴对应根据挠度$w$的有限元结果和式(10)得出的均布载荷$q$.从图中可以看出挠度$w$的有限元结果随着其长度$L_{pc}$,直径$D_{pc}$和长度$L_{pc}$的增大而非线性变化,初级纤毛的均布载荷$q$的结果随着其长度$L_{pc}$,直径$D_{pc}$的增大而线性增大却不受弹性模量$E_{pc}$变化的影响.

3 讨论

本文建立了矩形通道中压力和电场同频驱动微流体流动刺激细胞的三维有限元模型,该模型将细胞外界流场与多孔黏弹性细胞内部各细胞器的应力、位移、孔隙压力和孔隙流速联系起来,考察了初级纤毛, 细胞质和细胞核三种细胞器的力学信号传导能力,为细胞如何通过调节渗透率和初级纤毛的几何和力学特性改善自身的力学敏感性和感知力学信号的能力提供了理论参考,并提供了一种通过有限元方法结合细胞体外微流控实验测试初级纤毛弹性模量的方法.

在前期工作中, 王兆伟等^[33]建立了二维振荡层流理论,先前的工作主要讨论了压力驱动(pressure gradient driven)、电场驱动(electric filed driven)、力-电协同驱动(pressure-electricity synergic driven)三种驱动方式液体流场的不同, 17为根据该理论还原的三种驱动力学信号图, 图17(a)为力-电协同培养腔简化图; 图17(b)描述了三种驱动方式下的流率随时间变化规律,力电协同驱动的流率是压力和电场驱动的叠加; 图17(c)和图17(d)描述了流速幅值时刻三种驱动方式的流速和切应力分布,力电协同驱动的流速和切应力是压力和电场驱动的叠加,压力驱动下腔壁附近即细胞所在位置($y/h=\pm1$)的流速和切应力很小,而电场驱动大幅加大了腔壁附近的流速和切应力,电场驱动能提供较大的切应力幅值而压力梯度驱动则能提供较大的流率幅值,力-电协同作用时,可以联合压力梯度和电场驱动的调控优势.但二维的理论仅仅适用于宽度远大于高度的矩形通道并且只能研究二维细胞的力学响应.本文首次建立三维有限元模型并通过理论计算验证其有效性,进一步研究了流场中细胞的力学响应机制.而本文的工作具体细化出了细胞等实体结构进行建模计算.本三维模型不局限于腔宽远大于腔高的情况,可以考察流体的流速压力等在腔宽方向的变化,还可以进一步研究流体的压力梯度场、电场、流体力学参数以及通道尺寸变化对细胞流体刺激的影响.与细胞的线弹性模型相比, 多孔黏弹性模型可以考察细胞中的孔隙液体压力,流速和相应黏弹性行为.可以通过进一步细化细胞结构的初级纤毛、细胞质和细胞核三种细胞器来评估三种细胞器的力学传导及其感受功效.因此在流场分析和细胞属性方面较以前的工作有了很大的进展.

图17

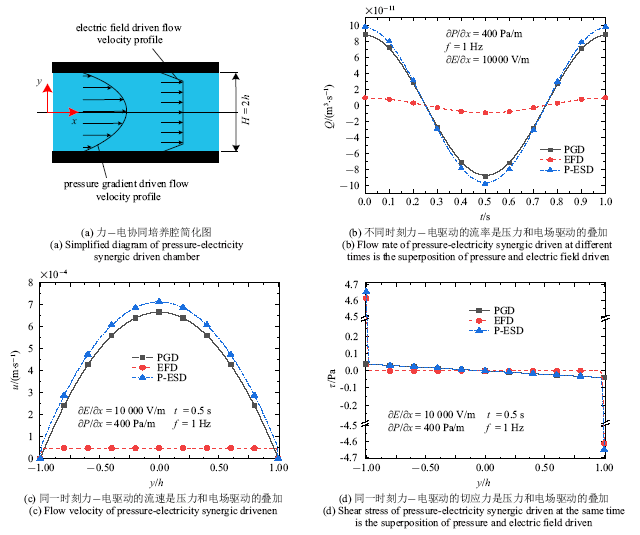新窗口打开|下载原图ZIP|生成PPT
图17力-电协同驱动

Fig.17Pressure-electricity synergic driven



渗透率^[38]是多孔弹性材料力学性能的主要影响因素.

骨陷窝-骨小管系统的渗透率范围大致在$5.0\times10^{-25}$~$7.172\times10^{-17}$ m$^{2}$范围内, 渗透率从大到小依次为: 骨细胞 $>$ 骨小管 $>$ 骨陷窝 $>$ 骨单元基质,本文选择的细胞质渗透率变化范围在$1.0\times10^{-19}$~$1.0\times10^{-18}$ m$^{2}$内^[35]. 在周期性流场下的瞬态行为中, 细胞质的应力、位移和孔隙压力与培养液的发展周期和幅值时刻相同(均在$t=0.25$ s达到最大值),但如图5所示细胞的液相流速响应速度快于固相, 渗透率越高, 细胞的液相孔隙流速的响应越快, 流速幅值越大(图5), 分析认为:细胞内液体的流动主要起因是细胞固相的挤压和膨胀变形, 细胞的液相流速幅值应该发生在细胞变形最快的时刻左右, 并与细胞的液相参数有关, 而不是发生在细胞的变形最大的时刻, 因为细胞变形最大的时刻反而是细胞变形速度最慢的时刻. 结合这一结论, 在之后的模型中, 可以进一步开发细胞核与细胞质间的物质运输通道, 也可以进一步研究细胞核的物质交换能力. 如图6所示, 细胞质贴壁侧应力较大, 细胞贴壁侧的细胞膜存在大量的整合蛋白发挥一定的粘附固定以及力学感知的作用^[39],而细胞核被认为是细胞的信号处理中心并且细胞核的应力和应变大于细胞质^[40]; 细胞质的渗透率、总位移、孔隙压力和孔隙流速和体积比均大于细胞核, 证明了细胞质具有比细胞核更好的变形能力和物质运输水平.

初级纤毛被认为是主要的力学信号传感器, 如图8所示,初级纤毛的应力和应变远大于细胞质和细胞核,这个研究结果进一步说明了初级纤毛在细胞器中力学信号感知能力最强.初级纤毛的弯曲和拉伸是细胞感知外界流体环境的方式, 那么在感受到外界信号后,初级纤毛如何将信号传递到细胞内部的细胞核等细胞器就是一个重要的问题.研究表明, 细胞信号的传递主要通过信号因子的运动来实现,纤毛基部、纤毛膜和纤毛内部的偶联微管广泛分布着多种相关蛋白等作为信号因子,这些蛋白参与不同的信号通路, 具有不同的功能,比如初级纤毛在流体力学条件下发生弯曲变形时,通过调节初级纤毛基底体LKB1-AMPK-mTOR反应, 可以阻断信号mTORC1,从而影响细胞体积^[41]. 在Notch通路中, Notch3受体被锚定在初级纤毛膜上,可以通过与位于初级纤毛基底体的presenilin-2相互作用而激活;血小板源生长因子受体(PDGFR)是一种蛋白受体, 位于初级纤毛膜,PDGFR通路可以通过与受体结合的PDGF配体激活,并通过激活下游MEK/ERK级联来诱导细胞反应^[42].而本文的研究发现纤毛基部附近的局部细胞质的孔隙流速因为纤毛的弯曲而加大,这可能更有利于初级纤毛影响区域信号因子的运输, 而且从图10(e)可以看出长度超过2$\mu$m的初级纤毛影响区域的孔隙流速压缩侧(Zone 3)$>$底部(Zone 2)$>$拉伸侧(Zone 1), 说明足够长的初级纤毛弯曲时纤毛基部对局部细胞质的压缩行为是局部孔隙流速提升的主要原因.所以, 研究影响初级纤毛长度, 刚度的因素有利于预防相关疾病,而研究调控其长度和刚度的方法也成为重要的生物医学问题.

可以通过调节初级纤毛自身的几何(长度, 直径)和力学(弹性模量)特性来调整其力学敏感性. 本研究在$t=0.25$s时初级纤毛的摆动挠度达到最大值.(1)初级纤毛的长度是影响细胞力学信号传导的主要因素, 且越长的初级纤毛受流体力、自身弯曲、应力和对基部的刺激都越大, 具有更好的力学敏感性. 初级纤毛的周期性摆动行为是一种非常重要的细胞行为, 初级纤毛的长度不足与相关疾病有充分的联系,比如癌细胞中初级纤毛长度的退化和减小^[43], 因此可以利用初级纤毛的力学敏感性来检测相关疾病. 在骨节炎软骨中,随着等级的严重程度, 侵蚀关节从表面到潮汐线的初级纤毛的发生率和长度增大.这些结果提示初级纤毛参与了骨关节炎的发病机制^[44]. (2)初级纤毛的弯曲刚度是影响细胞力学信号传导的主要因素,而弯曲刚度主要受直径和弹性模量影响, 且弹性模量和直径越小的初级纤毛拥有更好的弯曲能力.力学和化学刺激被证明都能改变纤毛的刚度, 乙酰化导致了HDAC6 mRNA表达的抑制导致纤毛刚度增加, 导致细胞对力学刺激的反应减弱^[45]. 最近的研究表明通过药物等方法来调节初级纤毛来治疗相关疾病已经成为可能^[45].细胞的初级纤毛会调节自身长度和刚度来适应生理环境的变化, 当初级纤毛的弯曲和拉伸程度过大, 初级纤毛会发生解体,将不能继续发挥力学感知的作用, 如图12(e)初级纤毛的直径越小, 对影响区域的流速刺激越小,所以初级纤毛的刚度和长度应在合理的范围内变化以保证其在流场中保持一定的结构稳定性.

此外, 本文的研究为初级纤毛在流场中的承载大小和刚度计算提供了一种简易的评估方法,计算结果表明初级纤毛的长度和直径越大, 在流场中所受的载荷也越大,这是初级纤毛通过自身变化来感受外界流场力学信号的机制,这也提供了一种在通过观察初级纤毛在特定流场中的弯曲情况并结合相关理论或者有限元模拟来测定初级纤毛刚度的一种方法.初级纤毛所受的挠度与自身长度、直径和弹性模量呈非线性关系,初级纤毛所受的载荷与自身长度和直径呈线性关系, 且不受自身弹性模量变化的影响,结合绕圆柱层流流体阻力公式$q=4\pi \rho v^{2}D_{pc} /Re[2.002-\ln (Re)]$和悬臂梁自由端斜率$k=qL_{pc}^{3} /6E_{pc} I$测定的初级纤毛的弯曲刚度$E_{pc}I$在$1.4\times10^{-23}$~$1.6\times10^{-23}$ N$\cdot$m$^{2}$之间,式中$Re$为雷诺数^[46], 这也为本文初级纤毛的受载随长度和直径的增大而增大的结论提供了理论依据.

本模型将细胞与其微流体环境有机结合, 考察了多孔黏弹性属性细胞及其初级纤毛对流体环境的力学响应. 模型存在以下不足:

(1)细胞是具有主动意识形态的生命体,忽略了细胞内力(如组成细胞骨架的肌动蛋白束主观运动)对其力传导行为的影响;

(2)在本文的研究中并没有给细胞赋予带电的特性,不能考察包括初级纤毛在内的细胞器在电场中自身受到的电场力的影响;

(3)各细胞器为理想化规则的几何体, 并且将细胞假设为各向同性材料体,并未建立更精细的细胞器(细胞骨架, 细胞膜, 初级纤毛囊,高尔基体等)及初级纤毛偶联微管等系统结构模型将有利于研究工作的深入开展;(4)在估算初级纤毛的受力时, 将初级纤毛在流体中的复杂受力简化为均布载荷.

4 结论

本文建立了力-电驱动下含有多孔黏弹性细胞的微流控腔的有限元模型,研究了微流控通道内的细胞及其纤毛的力学行为.

具体建立了外界物理场与细胞内部受力之间的关系,进一步量化了细胞的重要力学感受器——初级纤毛摆动力学行为.本文的工作为进一步研究微流体剪切对细胞的生长、分化等作用机理奠定了基础,同时也为检测细胞微结构(纤毛等蛋白链)的力学性能提供了理论技术基础.尽管模型有其局限性, 但可以得出以下参考结论.

(1) 渗透率对细胞结构的孔隙压力和流速有明显的影响, 是细胞多孔弹性力学响应的主要物理影响参数. 细胞质渗透率的提高加快了细胞质的液相响应速度并加大了液相流速大小.

(2) 相对于细胞质、细胞核, 初级纤毛所受到的应力刺激最大, 它是细胞主要的力学感受器, 细胞核所受到的应力刺激大于细胞质.

(3) 初级纤毛长度和抗弯刚度可以调节细胞的力学感受敏感性, 从纤毛的挠度和应力, 影响区域的应力大小来衡量初级纤毛的敏感性, 长度越大, 刚度越小, 敏感性越大.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 吕永钢, 詹世革 . 第三届全国生物力学青年****学术研讨会报告综述
力学学报, 2019,51(1):306-311.
[本文引用: 1]

( L$\ddot{u}$ Yonggang, Zhan Shige . Review of the third national symposium on biomechanic
Chinese Journal of Theoretical and Applied Mechanics 2019,51(1):306-311 (in Chinese))
[本文引用: 1]

[2] 林金明 . 微流控芯片细胞分析. 北京: 科学出版社, 2018.
[本文引用: 2]

( Lin Jinming. Microfluidic Chip Cell Analysis. Beijing: Science Press, 2018 (in Chinese))
[本文引用: 2]

[3] Du J, Liu X, Xu X . Advances in isolation and enrichment of circulating tumor cells in microfluidic chips
Chinese Journal of Chromatography 2014,32(1):7-12
[本文引用: 1]

[4] Hung PJ, Lee PJ, Sabounchi P , et al. Continuous perfusion microfluidic cell culture array for high-throughput cell-based assays
Biotechnology & Bioengineering 2005,89(1):1-8
[本文引用: 1]

[5] Singh S, Melnik R . Coupled thermo-electro-mechanical models for thermal ablation of biological tissues and heat relaxation time effects
Physics in Medicine and Biology 2019,64(24):245008
[本文引用: 1]

[6] Visone R, Giuseppe , Occhetta P , et al. A microscale biomimetic platform for generation and electro-mechanical stimulation of 3D cardiac microtissues
Apl Bioengineering 2018,2(4):046102
[本文引用: 1]

[7] Qi H, Xu M . Unsteady flow of viscoelastic fluid with fractional Maxwell model in a channel
Mechanics Research Communications 2007,34(2):210-212
[本文引用: 1]

[8] Chaube MK, Tripathi D, Anwar BO , et al. Peristaltic creeping flow of power law physiological fluids through a nonuniform channel with slip effect
Applied Bionics and Biomechanics 2015,64(24):152802-152802
[本文引用: 1]

[9] 王兆伟 . 力-电协同驱动细胞培养腔内微液流动的理论模拟研究. [硕士论文]
太原: 太原理工大学, 2018.
[本文引用: 1]

( Wang Zhaowei . Theoretical simulation study of force-electricity cooperation driving the micro-liquid flow in the cell culture cavity. [Master thesis]
Taiyuan: Taiyuan University of Technology, 2018 (in Chinese))
[本文引用: 1]

[10] Guilak F, Haider MA, Setton LA , et al. Multiphasic models of cell mechanics
Cytoskeletal Mechanics 2006,5:84-102
[本文引用: 1]

[11] Liu Y, Mollaeian K, Ren JJM , et al. Finite element modeling of living cells for afm indentation-based biomechanical characterization
Micron (Oxford, England: 1993) 2018,116:108-115


[12] Hoang MT, Bonnet G, Perrot C . Multi-scale acoustics of partially open cell poroelastic foams
Journal of the Acoustical Society of America 2013,133(5):3289
[本文引用: 1]

[13] 裘钧 . 骨细胞力学的实验和数值研究. [博士论文]
北京: 清华大学, 2011.
[本文引用: 5]

( Qiu Jun . Experimental and numerical research on bone cell mechanics. [PhD Thesis]
Beijing: Tsinghua University, 2011 (in Chinese))
[本文引用: 5]

[14] Islam MD, Raffaella R . An analytical poroelastic model of a spherical tumor embedded in normal tissue under creep compression
Journal of Biomechanics 2019,89:48-56
[本文引用: 1]

[15] Zhang D . Oscillatory pressurization of an animal cell as a poroelastic spherical body
Annals of Biomedical Engineering 2005,33(9):1249


[16] 武晓刚, 于纬伦, 王兆伟 等. 一种骨小管中液体流动产生的流量及切应力模型
力学学报, 2016,48(5):1208-1216.
[本文引用: 1]

( Wu Xiaogang, Yu Weilun, Wang Zhaowei , et al. A model of flow and shear stress generated by fluid flow in bone tubules
Chinese Journal of Theoretical and Applied Mechanics 2016,48(5):1208-1216 (in Chinese))
[本文引用: 1]

[17] Mollaeian K, Liu Y, Bi S , et al. Atomic force microscopy study revealed velocity-dependence and nonlinearity of nanoscale poroelasticity of eukaryotic cells
J Mech Behav Biomed Mater 2018,78:65-73
[本文引用: 1]

[18] Wei F, Lan F, Liu B , et al. Poroelasticity of cell nuclei revealed through atomic force microscopy characterization
Applied Physics Letters 2016,109(21):7159
[本文引用: 1]

[19] Bangs F, Anderson KV . Primary cilia and mammalian hedgehog signaling
Cold Spring Harbor Perspectives in Biology 2016,9(5):a028175
[本文引用: 1]

[20] Berbari NF, Connor AK, Haycraft CJ , et al. The primary cilium as a complex signaling center
Current Biology 2009,19(13):R526-R535


[21] Eichholz KF, Hoey DA . The Role of the Primary Cilium in Cellular Mechanotransduction
Mechanobiology 2016: 61-73


[22] Lim YC, Cooling MT, Long DS . Computational models of the primary cilium and endothelial mechanotransmission
Biomechanics and Modeling in Mechanobiology 2015,14(3):665-678


[23] Spasic M, Jacobs CR . Primary cilia: Cell and molecular mechanosensors directing whole tissue function
Seminars in Cell & Developmental Biology 2017,71:42-52
[本文引用: 1]

[24] Khayyeri H, Barreto S, Lacroix D . Primary cilia mechanics affects cell mechanosensation: a computational study
Journal of Theoretical Biology 2015,379:38-46
[本文引用: 4]

[25] Moore ER, Xing ZY, Seul RH , et al. Periosteal progenitors contribute to load-induced bone formation in adult mice and require primary cilia to sense mechanical stimulation
Stem Cell Research & Therapy 2018,9(1):190
[本文引用: 1]

[26] Goetz SC, Anderson KV . The primary cilium: A signalling centre during vertebrate development
Nature Reviews Genetics 2010,11(5):331-344
[本文引用: 1]

[27] Temiyasathit S, Jacobs CR . Osteocyte primary cilium and its role in bone mechanotransduction
Chemistry of Life 2010,1192(1):422-428
[本文引用: 1]

[28] Luu VZ, Biswajit C, Mohammed AO , et al. Role of endothelial primary cilia as fluid mechanosensors on vascular health
Atherosclerosis 2018,275:196
[本文引用: 1]

[29] Ahern DP, Thompson CL, Duffy MP , et al. Primary Cilia Mechanobiology
Mechanobiology 2020: 99-115
[本文引用: 3]

[30] Buljan VA, Graeber MB, Holsinger RM , et al. Calcium--axonemal microtubuli interactions underlie mechanism(s) of primary cilia morphological changes
Journal of Biological Physics 2017,44:53-80
[本文引用: 1]

[31] Flaherty J, Feng Z, Peng Z , et al. Primary cilia have a length-dependent persistence length
Biomechanics and Modeling in Mechanobiology 2020,19(2):445-460
[本文引用: 1]

[32] Blythman R, Persoons T, Jeffers N , et al. Localised dynamics of laminar pulsatile flow in a rectangular channel
International Journal of Heat & Fluid Flow 2017,66(8):8-17
[本文引用: 2]

[33] 王兆伟, 武晓刚, 陈魁俊 等. 一种力-电协同驱动的细胞微流控培养腔理论模型
力学学报, 2018,50(1):124-137.
[本文引用: 5]

( Wang Zhaowei, Wu Xiaogang, Chen Kuijun , et al. A theoretical microfluidic flow model for the cell culture chamber under the pressure gradient and electric field driven loads
Chinese Journal of Theoretical and Applied Mechanics 2018,50(1):124-137 (in Chinese))
[本文引用: 5]

[34] Miller AD, Chama A, Louw TM , et al. Frequency sensitive mechanism in low-intensity ultrasound enhanced bioeffects
PloS One 2017,12(8):e0181717
[本文引用: 4]

[35] 陈魁俊 . 骨单元到骨细胞尺度的多孔弹性力学信号传导. [硕士论文]
太原: 太原理工大学, 2019.
[本文引用: 5]

( Chen Kuijun . Signal transduction of poroelasticity from bone unit to bone cell scale. [Master Thesis]
Taiyuan: Taiyuan University of Technology, 2019 (in Chinese))
[本文引用: 5]

[36] Rydholm S, Zwartz G, Kowalewski J , et al. Mechanical properties of primary cilia regulate the response to fluid flow. American Journal of Physiology-renal
Physiology 2010,298(5):1096-1102
[本文引用: 1]

[37] Molla-Herman A, Ghossoub R, Blisnick T , et al. The ciliary pocket: An endocytic membrane domain at the base of primary and motile cilia
Journal of Cell Science 2010,123(10):1785-1795
[本文引用: 1]

[38] 于纬伦, 武晓刚, 李朝鑫 等. 骨陷窝-骨细胞形状和方向对骨单元内液体流动行为的影响
力学学报, 2020,52(3):244-254.
[本文引用: 1]

( Yu Weilun, Wu Xiaogang, Li Chaoxin , et al. Effect of osteocyte-lacunae shape and direction on the fluid flow behavior in osteon
Chinese Journal of Theoretical and Applied Mechanics 2020,52(3):244-254 (in Chinese))
[本文引用: 1]

[39] 冯世亮, 周吕文, 吕守芹 等. 悬浮态上皮细胞粘附的力学-化学耦合模型及数值模拟
力学学报, 2020,52(3):255-264.
[本文引用: 1]

( Feng Shiliang, Zhou Lvwen , L$\ddot{u}$ Shouqin, et al. Mechanochemical coupling model and numerical simulation for cell-cell adhesion in suspended epithelial cells
Chinese Journal of Theoretical and Applied Mechanics 2020,52(3):255-264 (in Chinese))
[本文引用: 1]

[40] Vaughan TJ, Mullen CA, Verbruggen SW , et al. Bone cell mechanosensation of fluid flow stimulation: A fluid--structure interaction model characterising the role integrin attachments and primary cilia
Biomechanics & Modeling in Mechanobiology 2015,14(4):703-718
[本文引用: 1]

[41] Boehlke C, Kotsis F, Patel V , et al. Primary cilia regulate mtorc1 activity and cell size through lkb1
Nature Cell Biology 2010,12(11):1115-1122
[本文引用: 1]

[42] Tao F, Jiang T, Tao H , et al. Primary cilia: versatile regulator in cartilage development
Cell Proliferation 2020,2:1-12
[本文引用: 1]

[43] Jamal MH, Nauli SM , The effect of primary cilia restoration on cancer cells
The FASEB Journal. 2020,34(S1):1-1
[本文引用: 1]

[44] Mcglashan SR, Cluett EC, Jensen CG , et al. Primary cilia in osteoarthritic chondrocytes: from chondrons to clusters
Developmental Dynamics An Official Publication of the American Association of Anatomists 2008,237(8):2013-2020
[本文引用: 1]

[45] Jacobs C, Spasic M. Regulation of gene expression by modulating primary cilia length
US: US20190015423, 2019 -01-17
[本文引用: 2]

[46] Schwartz EA, Leonard ML, Bizios R , et al. Analysis and modeling of the primary cilium bending response to fluid shear
American Journal of Physiology 1997,272(2):132-138
[本文引用: 1]