马航空, 周晨阳, 李世荣^,2)扬州大学建筑科学与工程学院,江苏扬州 225127

ANLYTICAL SOLUTION OF THERMOELASTIC DAMPING IN RECTANGULAR MINDLIN MICRO PLATES ¹⁾

Ma Hangkong, Zhou Chenyang, Li Shirong^,2)School of Civil Science and Engineering,Yangzhou University,Yangzhou 225127, Jiangsu, China

通讯作者: 2)李世荣,教授,主要研究方向：结构非线性分析及新型材料结构力学行为. E-mail:srli@yzu.edu.cn

收稿日期:2020-05-26接受日期:2020-05-26网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金资助项目.11672260

Received:2020-05-26Accepted:2020-05-26Online:2020-09-18
作者简介 About authors


摘要
首次给出了四边简支的 Mindlin 矩形微板热弹性阻尼的解析解. 基于考虑一阶剪切变形的 Mindlin 板理论和单向耦合热传导理论建立了微板热弹性耦合自由振动控制微分方程. 忽略温度梯度在面内的变化,在上下表面绝热边界条件下求得了用变形几何量表示的温度场的解析解. 进一步将包含热弯曲内力的结构振动方程转化为只包含挠度振幅的四阶偏微分方程. 利用特征值问题之间在数学上的相似性,在四边简支条件下给出了用无阻尼 Kirchhoff 微板的固有频率表示的 Mindlin 矩形微板的复频率解析解,从而利用复频率法求得了反映热弹性阻尼水平的逆品质因子. 最后,通过数值结果定量地分析了剪切变形、材料以及几何参数对热弹性阻尼的影响 规律. 结果表明,Mindlin 板理论预测的热弹性阻尼小于 Kirchhoff 板理论预测的热弹性阻尼. 两种理论预测的热弹性阻尼之间的差值在临界厚度附近十分显著. 另外,随着微板的边/厚比增大,Mindlin 微板的热弹性阻尼最大值单调增大,而 Kirchhoff 微板的热弹性阻尼最大值却保持不变.
关键词： 热弹性阻尼;微板谐振器;Mindlin 板理论;热弹性耦合振动;复频率

Abstract
Analytical solution of thermoelastic damping for rectangular Mindlin micro plate with the four edges simply supported is presented for the first time. Based on the Mindlin plate theory and the one-way coupled heat conduct theory, governing differential equations for thermo-elastically coupled free vibration of the micro plate are formulated. Ignoring the in-plane variation of the temperature gradient, analytical solution of temperature field in terms of the kinematic parameters is obtained under the adiabatic boundary conditions at the top and bottom surfaces. Furthermore, the equations of structural vibration including the thermal bending moment are transformed into a fourth-order partial differential equation only in terms of the deflection. By using the mathematical similarity between the eigenvalue problems under the simply supported boundary conditions, analytical solution of the complex natural frequency of the Mindlin plate is expressed in terms of the frequency of isothermal Kirchhoff plate. Then the inverse quality factor which represents the level of the thermoelastic damping is obtained. Finally, the effects of the shear deformation, the material and the geometry parameters on the thermoelastic damping are examined in detail by the numerical results. The numerical results show that thermoelastic damping estimated by Mindlin plate theory is less than that by Kirchhoff plate theory. The difference between the values evaluated by the two plate theories becomes very significant near the critical thickness. Moreover, along with the increase of the side-to-thickness aspect ratio,the maximum of the thermoelastic damping in micro Mindlin plate increase monotonically, however, that of micro Kirchhoff plate keeps constant.
Keywords：thermoelastic damping;micro plate resonator;Mindlin plate theory;thermoelastic coupling vibration;complex frequency


PDF (5474KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
马航空, 周晨阳, 李世荣. Mindlin 矩形微板的热弹性阻尼解析解 ¹⁾. 力学学报[J], 2020, 52(5): 1383-1393 DOI:10.6052/0459-1879-20-175
Ma Hangkong, Zhou Chenyang, Li Shirong. ANLYTICAL SOLUTION OF THERMOELASTIC DAMPING IN RECTANGULAR MINDLIN MICRO PLATES ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1383-1393 DOI:10.6052/0459-1879-20-175

引言

微/纳谐振器作为微/纳电机系统 (MEMS/NEMS) 中的基本器件被广泛用作频率控制器件、逻辑开关、传感器、驱动器、陀螺仪、能量收集器等,在生物医学、自动控制、航空电子设备、国防科技等众多领域有着十分广泛的应用. 为了设计和制造高性能的微/纳电机系统, 需要谐振器在工作时耗能越小越好,即具有更高的品质因子. 然而,在微/纳电机系统中不可避免地存在各种耗能机制. 除了空气阻尼、支撑阻尼、挤压模阻尼等外部能量耗散外还存在内部能量耗散,例如热弹性阻尼 (thermoelastic damping, TED),或内摩擦^[1]. 实践证明,可以通过完美的设计和制造工艺最大限度地降低或消除外阻尼引起的耗量能散. 但是,TED 是系统所固有的能耗机制,是在结构周期振动时材料内部的热弹性耦合变形引起的内部阻尼,它不能通过改善外部条件而消除. 因此,TED 有时会成为微电机系统的主要能耗形式,或影响品质因子的重要因素. 要在理论上分析微/纳结构在振动中的热弹性阻尼,就需要基于热-弹耦合动力学理论建立结构振动的数学模型,通过联立求解热-弹耦合的运动方程和热传导方程获得系统的动力响应,从而求得表征热弹性阻尼的品质因子. TED 与微结构的材料性质、几何尺寸、支承条件以及环境温度等诸多因素密切相关. 因此,定量地分析和预测 TED 对高品质微/纳谐振器的研究和设计具有重要意义.

大多数谐振器力学模型可以简化为弹性梁或 弹性板. 最早关于谐振器热弹性阻尼的理论研究当属 Zener 的工作^[1]. 早在 1938 年,Zener 首先基于 Euler-Bernoulli (E-B) 梁理论和单相耦合的准一维热传导方程求得了矩形截面微梁谐振器的TED近似解析解^[1],被称为著名的 Zener 公式. 2000 年,在 Zener 工作的基础上 Lifshitz 和 Roukes (L-R)^[2]首次给出了 E-B 微梁的准一维热传导方程的解析解,进而求解振动方程的特征值问题,获得了更为精确的矩形截面微/纳梁谐振器逆品质因子和频移的解析解,被称为著名的 L-R 公式. Zener 和 L-R 的杰出工作对后来关于微结构的 TED 的进一步研究具有重要的参考和借鉴作用,他们的成果在后来研究者的论文中被高频次引用. 研究者采用不同的结构变形理论、热传导理论和分析方法开展了关于微/纳梁板谐振器的热弹性阻尼研究. 关于逆品质因子的计算主要采用能量法^[1]和复频率法^[2].

基于经典板理论,文献^{[3,4,5,6,7,8,9,10,11,12,13,14,15]} 报道了均匀各 向同性材料弹性薄板谐振器的 TED $^{[3\hbox{-}15]}$. Nayfeh 和 Youns^[3]采用摄动法求解了引入刚度阻尼的振动方程,获得了受静电载荷和残余面内应力共同作用的矩形微板 TED 的近似解析解. Sun 等 $^{[3\hbox{-}5]}$、Ali 和 Mohammadi^[6]采用复频率法分别研究了微圆/环板的 TED,给出了 L-R 形式的解析解. Salajeghe 等^[7]在运动方程的建立中考虑了变形的几何非线性,定量 分析了轴对称振动微圆板谐振器的振幅对热弹性阻尼的影响规律. Li 等^[8]采用准一维热传导方程,通过计算一个周期内弹性板损失的能量与结构内存储的最大弹性势能之比求得了矩形和圆形薄板谐振器 L-R 形式的逆品质因子解析解. 在此基础上 Fang 等$^{[9\hbox{-}10]}$分别采用二维和三维热传导方程研究了轴对称自由振动的圆板和矩形板谐振器的 TED, 分析了热传导方程的简化对热弹性阻尼值的预测精度的影响. 考虑热传导过程中温度热流运动的延滞效应 (或波动效应), 文献^{[11,12,13,14]} 利用广义热传导理论 (或非傅里叶热传导理论) 研究了微/纳板谐振器的热弹性耦合振动响应. Sharma 等^[11]基于 Lord-Shulman 广义热传导理论和经典板理论研究了非轴对称自由振动圆板谐振器的热弹性阻尼,分析了延滞时间参数对热弹性阻尼 的影响. 在此基础上,Sharma 和 Grover^[12]还进一步研究了由于空隙率变化而引起的延滞效应对板式 谐振器的影响. Guo 等^[13]采用双向延滞广义热传导模型研究了圆板谐振器的热弹性阻尼,采用复频率法获得逆品质因子的 L-R 形式解析解. 数值结果发现,在广义热传导理论下逆品质因子随着厚度的减小出现极 小值. Grover 等^[14]基于 Kelvin-Voigt 材料模型下的广义热黏弹性理论研究了均匀微圆板谐振器的阻尼特性,定量地分析了机械松弛时间和热松弛时间对逆品质因子的影响.

考虑材料性质沿单轴方向阶梯变化,Bishop 和 Kinra$^{[15\hbox{-}16]}$最早采用能量法开展了关于复合材料层合微/纳谐振器的热弹性阻尼研究. 在表面边绝热条件和内部界面处的非完善协调条件下,求得了准一维热传导方程的解析解,并通过计算一个振动周期内由不可逆传热产生的总热量与弹性总弹性势能之比给出了谐振器的逆品质因子^[15]. 并定量地分析了对称铺设的三层矩形微板的弹性热动阻尼特性^[16]. Sun 等^[17]基于准一维热传导方程,采用复频率法研究了对称铺设的三层微圆板在轴对称自由振动下的热弹性阻尼. 采用与文献^[16] 中相同的能量方法,忽略温度梯度在面内的变化,Zuo 等^[18]研究了双层微板的热弹性阻尼,给出了周边夹紧矩形板和圆板的逆品质因子解析解. 考虑温度梯度在面内的变化,Liu 等$^{[19\hbox{-}20]}$采用格林函数法分别求解了二维和三维热传导方程,利用能量法获得了双层圆板和非对称铺设三层矩形板在给定边界条件下的逆品质因子的级数形式解析解. 这里需要说明的是,文献^[18,19,20] 通过引入物理中面的概念消去了几何中面的面内位移,简化了几何方程. 但是,当材料性质变化关于几何中面非对称时板内将会产生热薄膜力,而热薄膜力对热弹性阻尼具有 贡献^[29]. 显然,在上述文献中忽略了热薄膜力对热弹性阻尼的影响.

近年来,亦有少量的文献 研究了材料性质沿厚度连续变化的功能梯度材料 (functionally graded material, FGM) 微/纳梁板结构的热弹性阻尼. Azizi 等^[21]研究了由硅和压电材料为组分材料复合而成的两端夹紧的矩形截面FGM微梁横向自由振动时的 TED. 采用 Galerkin 法求得了 FGM 微梁的复频率进而获得反映热弹性阻尼的逆品质因子. 数据结果表明可以通过压电材料组分的合理调节来降低系统的 TED. 基于一阶剪切变形理论和单向耦合的准一维热传导方程,Emami 和 Alibeigloo^[22]研究了材料性质沿横向幂函数变化的 FGM 微梁的 TED. 将热传导方程的系数和温度场同时展开成关于横向坐标的泰勒级数形式,获得了变系数热传导方程的级数形式的解析解,进而获得了两端简支FGM 微梁的 TED. 在此基础上,文献^[22] 的作者中又基于一阶剪切变形板理论和修正的应变梯度理论,研究了四边简支功能梯度中厚度矩形板的热弹性阻尼^[23]. 但是,通过 研究发现其中给出的关于均匀材料方板的热弹性阻尼的计算结果是错误的. 由此无法肯定其中关于功能梯度材料微板热弹性阻尼数值结果的可靠性. 考虑材料性质在厚度方向按指数函数分布特殊情形,Zhong 等^[24]采用解析方法获得了功能梯度 E-B 微梁的热弹性阻尼解析解. 但是,作者在应变的计算中却直接忽略了由于材料性质在横向的非均匀性而导致的拉-弯耦合变形. 许新等$^{[25\hbox{-}26]}$基于单向耦合的准一维热传导方程研究了材料性质在横向任意连续变化的 FGM E-B 微梁的热弹性阻尼. 发展了求解横向非均匀微梁的复杂变系数热传导方程的分层均匀化方法,从而获得 FGM 微梁热弹性阻尼的半解析解, 其中精确地考虑了热轴力对 TED 的影响. 最近又将分层均匀化方法成功地应用于功能梯度微板的热弹性阻尼的求解$^{[27\hbox{-}28]}$. 研究了材料梯度指数、环境温度、边厚比、振动模态等对热弹性阻尼的影响规律,首次定量地分析了热薄膜力对热弹性阻尼的影响程度.

文献调研表明,截至目前关于均匀微板热弹性阻尼的解析解是基于 Kirchhoff 经典弹性板理论推导出的,其中忽略了横向剪切变形对振动响应的影响. 本文基于考虑一阶剪切变形效应的 Mindlin 中厚板理论和单向耦合热传导理论建立四边简支均匀材料微板的热-弹耦合自由振动的控制微分方程. 消去两个独立的转角变量将振动方程转化为只包含挠度函数和热弯矩的四阶偏微分方程. 忽略温度梯度在面内的变化,在上下表面绝热边界条件下求得了用挠度函数表示的热传导方程的解析解. 从而将包含热弯曲内力的结构振动方程转化为只包含挠度振幅的偏微分方程. 利用特征值问题的数学相似性,在四边简支条件下获得了用均匀无阻尼 Kirchhoff 微板的固有频率表示的 Mindlin 矩形微板的复频率,从而由复频率法给出了反映热弹性阻尼水平的逆品质因子解析解. 通过数值结果定量地分析了剪切变形对热弹性阻尼值的影响程度.

1 问题的控制方程

1.1 运动方程

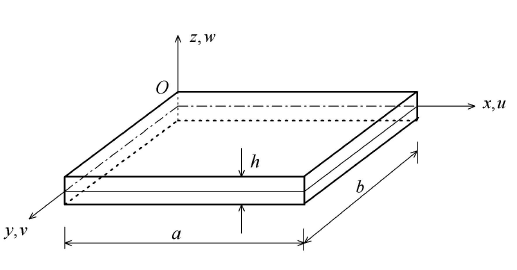
考虑长度 $a$、宽度为 $b$、厚度为 $h$ 的等厚度矩形微/纳板. 选取直角坐标系,板在空间的区域定义为：$0 < x < a$,$0 < y < b$,$ - h / 2 < z < h / 2$ (见图 1). 基于 Mindlin 板理论$^{[29\hbox{-}33]}$,板内任意一点的位移分量可表示为

(1a)$u(x,y,z,t) = z\varphi _x (x,y,t) $
(1b)$v(x,y,z,t) = z\varphi _y (x,y,t) $
(1c)$w(x,y,z,t) = w_0 (x,y,t) $

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1微板的几何尺寸和坐标示意图

Fig. 1Schematic illustration of a micro plate and the coordinate system



其中,$t$ 为时间;$u$,$v$ 和 $w$ 分别为板内任意一点沿 $x$,$y$ 和 $z$ 轴方向的位移分量;$\varphi_x $ 和 $\varphi_y $ 为中面法线分别绕 $y$ 轴和 $x$ 轴的转角.

将式 (1) 代入弹性力学的几何方程可得板的应变场

(2a)$ \varepsilon _x = z\dfrac{\partial \varphi _x }{\partial x} , \ \ \varepsilon _y = z\dfrac{\partial \varphi _y }{\partial y} , \ \ \gamma _{xy} = z\left( {\dfrac{\partial \varphi _x }{\partial y} + \dfrac{\partial \varphi _y }{\partial x}} \right) $

(2b)$ \gamma _{xz} = \varphi _x + \dfrac{\partial w_0 }{\partial x} , \ \ \gamma _{yz} = \varphi _y + \dfrac{\partial w_0 }{\partial y} $

根据胡克定律得到应力场

(3a)$ \sigma _x = \dfrac{E}{1 - v^2}\left[ {\varepsilon _x + v\varepsilon _y - \left( {1 + v} \right)\alpha \theta } \right] $

(3b)$ \sigma _y = \dfrac{E}{1 - v^2}\left[ {\varepsilon _y + v\varepsilon _x - \left( {1 + v} \right)\alpha \theta } \right] $

(3c)$ (\tau _{xy} ,\tau _{xz} ,\tau _{yz} ) = \dfrac{E}{2\left( {1 + \nu } \right)}(\gamma _{xy} ,\gamma _{xz} ,\gamma _{yz} ) $

其中,$\theta \left( {x,y,z,t} \right) = T\left( {x,y,z,t} \right) - T_0 $ 为变温场,$T$ 为瞬态温度,$T_{0}$ 为初始温度. $E$,$v$ 和 $\alpha $ 分别为弹性模量、泊松比和热膨胀系数. 这里的温度场是由热-弹耦合振动引起的.

将弹性力学空间问题应力形式的运动方程在厚度进行静力等效,并利用上下表面的应力边界条件可得用等效内力和内力矩表示的 Mindlin 板$^{[29\hbox{-}33]}$自由振动微分方程

(4) $ \dfrac{\partial M_x }{\partial x} + \dfrac{\partial M_{xy} }{\partial y} - Q_x = I_2 \dfrac{\partial ^2\varphi _x }{\partial t^2} $
(5) $ \dfrac{\partial M_{xy} }{\partial x} + \dfrac{\partial M_y }{\partial y} - Q_y = I_2 \dfrac{\partial ^2\varphi _y }{\partial t^2} $
(6) $ \dfrac{\partial Q_x }{\partial x} + \dfrac{\partial Q_y }{\partial y} = I_0 \dfrac{\partial ^2w_0 }{\partial t^2} $
其中 $I_i $ 为等效惯性参数,具体表示为

(7) $ I_0 = \rho h,I_2 = \rho h^3 / 12 $
$\rho$ 为板的质量密度. 式 (4) $\sim$ 式 (6) 中的等效内力和内力矩可分别表示为

(8a)$ M_x = D\left( {\dfrac{\partial \phi _x }{\partial x} + \nu \dfrac{\partial \varphi _y }{\partial y}} \right) - M_{\rm T} $

(8b)$ M_y = D\left( {\nu \dfrac{\partial \phi _x }{\partial x} + \dfrac{\partial \varphi _y }{\partial y}} \right) - M_{\rm T} $

(8c)$ M_{xy} = \dfrac{1 - \nu }{2}D\left( {\dfrac{\partial \varphi _y }{\partial x} + \dfrac{\partial \varphi _x }{\partial y}} \right) $

(8d)$ Q_x = k_{\rm s} S_0 \left( {\varphi _x + \dfrac{\partial w_0 }{\partial x}} \right) $

(8e)$ Q_y = k_{\rm s} S_0 \left( {\varphi _y + \dfrac{\partial w_0 }{\partial y}} \right) $

其中 $D = Eh^3 / [12(1 - \nu ^2)]$,$S_0 = Eh / [2(1 + \nu )]$ 为抗弯刚度和抗剪切刚度;$M_{\rm T} = \int_{ - h / 2}^{h / 2} \dfrac{\alpha E\theta z}{1 - \nu } d z $ 为热弯矩, $k_s = 5 / 6$ 为剪切修正系数.

将式(8)代入式(4)和式(5),分别关于坐标$x$和$y$求导后相加,利用 式(6)可得

(9) $ D\nabla ^2\kappa _0 - \nabla ^2M_T = \dfrac{\partial ^2}{\partial t^2}(I_0 w_0 + I_2 \kappa _0 ) $
其中

(10) $ \nabla ^2 = \dfrac{\partial ^2}{\partial x^2} + \dfrac{\partial ^2}{\partial y^2} , \ \ \kappa _0 = \dfrac{\partial \varphi _x }{\partial x} + \dfrac{\partial \varphi _y }{\partial y} $
将式 (8d) 和式 (8e) 代入 式 (6) 可得

(11) $ \kappa _0 + \nabla ^2w_0 = \dfrac{I_0 }{k_{\rm s} S_0 }\dfrac{\partial ^2w_0 }{\partial t^2} $
最后,将式 (11) 代入式 (9), 可得只用横向位移 $w_0 $ 表示的运动方程

(12) $ D\nabla ^4w_0 + \nabla ^2M_T = - I_0 \dfrac{\partial ^2}{\partial t^2} \cdot \\ \qquad \left[ {w_0 - \left( {\dfrac{I_2 }{I_0 } + \dfrac{D}{k_{\rm s} S_0 }} \right) \nabla ^2w_0 + \dfrac{I_2 }{k_{\rm s} S_0 }\dfrac{\partial ^2w_0 }{\partial t^2}} \right] $
上式中热弯矩由热-弹耦合产生的变温场确定.

1.2 热传导方程

根据单向耦合的热弹性动力学理论,可给出微/纳板的准一维热传导方程$^{[3\hbox{-}8]}$

(13) $ \kappa \dfrac{\partial ^2\theta }{\partial z^2} = \rho C\dfrac{\partial \theta }{\partial t} + \dfrac{\alpha ET_0 }{1 - 2v}\dfrac{\partial e}{\partial t} $
其中,$\kappa $,$C$ 分别是热传导系数和比热,$e$ 是体积应变. Mindlin 板的体积应变可表示为

(14) $ e = \varepsilon _x + \varepsilon _y + \varepsilon _z = \dfrac{1 - 2v}{1 - v}z\kappa _0 + \dfrac{1 + v}{1 - v}\alpha \theta $
将 式 (14) 代入式 (13),可得单向耦合的准一维热传导方程

(15) $ \kappa \dfrac{\partial ^2\theta }{\partial z^2} = \left( {1 + \varsigma } \right)\rho C\dfrac{\partial \theta }{\partial t} + \dfrac{\alpha ET_0 z}{1 - v}\dfrac{\partial \kappa _0 }{\partial t} $
其中 $\varsigma = \dfrac{(1 + v)E\alpha ^2T_0 }{(1 - v)\left( {1 - 2v} \right)\rho C} \ll 1$. 对于金属镍 (Ni),$\varsigma = 4.044\times 10^{ - 5}$;对于氮化硅 (Si$_{3}$N$_{4}$),$\varsigma = 3.48\times 10^{ - 7}$. 因此,在后面的求解中方程 (15) 中的这一微量被忽略$^{[3\hbox{-}8,22\hbox{-}28]}$.

2 热弹性阻尼的求解

2.1 自由振动响应

假设位移场合温度场的动态响应同步,则系统的热-弹耦合自由振动响应可假设为调和形式

(16) $ \left( \begin{matrix} w_0 \\ \varphi _x \\ \varphi _y \\ \theta \end{matrix} \right)= \left( \begin{matrix} \bar {w}(x,y) \\ \bar {\varphi }_x (x,y) \\ \bar {\varphi }_y (x,y) \\ \bar {\theta }(x,y,z) \end{matrix} \right) {\rm e}^{{\rm i}\omega t} $
其中,$\omega $ 为固有频率;$\bar {w}$,$\bar {\varphi }_x $,$\bar {\varphi }_y $ 和 $\bar {\theta }$ 分别为对应位移分量、转角和变温场的振幅;$ {\rm i} = \sqrt { - 1} $. 将式 (16) 分别代入式 (12) 和 式 (15) 可消去时间变量,并利用下列无量纲变换

(17) $ \left.\begin{array}{l} \xi = \dfrac{x}{a} , \ \ \eta = \dfrac{y}{b} , \ \ \zeta = \dfrac{z}{h} , \ \ \lambda = \dfrac{a}{h} , \ \ \varTheta = \alpha \bar {\theta } \\ (U,V,W,\delta ) = \dfrac{1}{a}(\bar {u},\bar {v},\bar {w},b) , \ \ K = a\bar {\kappa }_0 \end{array}\!\!\right\} $
(18) $ \left.\begin{array}{l} m_{\rm T} = \dfrac{a}{D}\bar {M}_{\rm T} , \ \ \varOmega = a^2\omega \sqrt {\dfrac{\rho h}{D}} , \ \ p = \sqrt { - {\rm i}\dfrac{\varOmega }{g}} \\ g = \dfrac{\lambda ^2\kappa }{\rho C}\sqrt {\dfrac{\rho h}{D}} , \ \ q = \dfrac{E\alpha ^2T_0 }{\lambda \rho C(1 - \nu )} \end{array} \right\} $
可得无量纲控制方程

(19) $ \tilde {\nabla }^4W + \mu _2 \varOmega ^2\tilde {\nabla }^2W + (\mu _{00} + \mu _{02} \varOmega ^2)\varOmega ^2W +\\ \qquad \tilde {\nabla }^2m_{\rm T} = 0 ,\quad 0 < \xi < 1,0 < \eta < 1 $
(20) $ \dfrac{\partial ^2\varTheta }{\partial \zeta ^2} + p^2\varTheta = - p^2q\zeta K , \ \ - 1 / 2 < \zeta < 1 / 2 $
其中

(21) $ \left. \mu _{00} = - 1 , \ \ \mu _{02} = \dfrac{c_{\rm s} }{12\lambda ^2} \\ \mu _2 = c_{\rm s} + \dfrac{1}{12\lambda ^2} , \ \ c_{\rm s} = \dfrac{1}{6k_{\rm s} \lambda ^2(1 - \nu )} \right\} $
(22) $ K = \dfrac{\partial \varphi _x }{\partial \xi } + \dfrac{1}{\delta }\dfrac{\partial \varphi _y }{\partial \eta } , \ \ \tilde {\nabla }^2 = \dfrac{\partial ^2}{\partial \xi ^2} + \dfrac{1}{\delta ^2}\dfrac{\partial ^2}{\partial \eta ^2} $
其中结构振动方程通过无量纲的热弯矩振幅 $m_{\rm T} $ 与热传导方程耦合.

2.2 热传导方程的求解

方程 (20) 的通解为

(23) $ \varTheta = A\sin p\zeta + B\cos p\zeta - q\zeta K $
微谐振器一般在恒温真空环境内工作, 可认为没有外界的热流输入. 而由于热-力耦合振动在谐振器内部产生的变温场幅度很小, 因而热流强度也很低. 于是可假设在微板的上下表面没有热流通过. 这样,在微板的上下表面通常给出绝热边界条件$^{[2\hbox{-}28]}$

(24) $ \left. {\dfrac{\partial \varTheta }{\partial \zeta }} \right|_{\zeta = - 1/2} = \left. {\dfrac{\partial \varTheta }{\partial \zeta }} \right|_{\zeta = 1/2} = 0 $
利用边界条件 (24) 可确定系数 $A = qK / [ p\cos (p / 2)]$ 和 $B = 0$. 于是得到特解

(25) $ \varTheta = - q\left( {\zeta - \dfrac{\sin (p\zeta )}{p\cos (p / 2)}} \right)K $

2.3 热弹性阻尼

将 式 (25) 代入热弯矩的计算公式可得

(26) $ m_{\rm T} = 12(1 + \nu )\lambda \int_{ - 1 / 2}^{1 / 2} \varTheta \zeta d \zeta = - f(\varOmega )K $
其中

(27) $ f(\varOmega ) = (1+ \nu )\lambda q\left\{ {1 + \dfrac{24}{p^3}\left[ {\dfrac{p}{2} - \tan \left( {\dfrac{p}{2}} \right)} \right]} \right\} $
将 式 (26) 代入 式 (19), 并利用 式 (11) 的无量纲形式

(28) $ K = - \tilde {\nabla }^2W - c_{\rm s} \varOmega ^2W $
可得只用无量纲挠度表示的结构振动微分方程

(29) $ (1 + f)\tilde {\nabla }^4W + \left( {\mu _2 + c_{\rm s} f} \right)\varOmega ^2\tilde {\nabla }^2W +\\ \qquad (\mu _{00} + \mu _{02} \varOmega ^2)\varOmega ^2W = 0 $
微分方程 (29) 可记为标准形式

(30) $ (\tilde {\nabla }^2 + \varLambda _1 )(\tilde {\nabla }^2 + \varLambda _2 )W = 0 $
其中

(31) $ \varLambda _1 ,\varLambda _2 = \dfrac{(\mu _2 + c_{\rm s} f)\varOmega ^2\pm \varOmega \sqrt {(\mu _2 + c_{\rm s} f)^2\varOmega ^2 - 4(1 \!+\! f)(\mu _{00} + \mu _{02} \varOmega ^2)} }{2(1 + f)} $
另外,由弹性薄板理论可得不考虑热弹性阻尼的 Kirchhoff 板的振动微分方程^[29]

(32) $ (\tilde {\nabla }^2 + \varOmega _0^\ast )(\tilde {\nabla }^2 - \varOmega _0^\ast )W_0^\ast = 0 $
其中$\varOmega _0^\ast $ 为无阻尼 Kirchhoff 板的无量纲固有频率.

对于四边简支矩形板,Kirchhoff 薄板理论下方程(32)的边界条件可表示为

(33) $ W_0^\ast = 0 , \ \ \tilde {\nabla }^2W_0^\ast = 0 , \ \ {\rm on \ the \ boundary} $
可以证明 (具体证明见附录),对于四边简支 Mindlin 矩形板,振动微分方程 (30) 的边界条件亦可表示为

(34) $ W = 0 , \ \ \tilde {\nabla }^2W = 0 , \ \ {\rm on \ the \ boundary} $
由微分方程边值问题 (30),(34) 与问题 (32),(33) 之间的相似性,可得它们的特征值之间的关系

(35) $ \varLambda _1 = \varOmega _0^\ast , \ \ \varLambda _2 = - \varOmega _0^\ast $
于是,将式 (31) 代入式 (35),可得特征方程

(36) $ \mu _{02} \varOmega ^4 + R\varOmega ^2 + (1 + f)\varOmega _0^{\ast 2} = 0 $
其中 $R = \mu _{00} - (\mu _2 + c_{\rm s} f)\varOmega _0^\ast $. 由 式 (27) 知 $f(\varOmega )$ 是关于频率 $\varOmega $ 的超越函数,因此方程 (36) 具有很强非线性. 为了简化求解, 可近 似地令 $f(\varOmega ) = f(\varOmega _0 )$$^{[2\hbox{-}14]}$,其中 $\varOmega _0 $ 为等温 (不考虑热弹性阻尼) Mindlin 微板的固有频率. 于是,由式 (36) 可容易求得用无阻尼 Kirchhoff 板的 频率 $\varOmega_0^\ast $ 表示的具有热弹性阻尼的 Mindlin 微板的复频率

(37) $ \varOmega = \Bigg( \dfrac{ - R\pm \sqrt {R^2 - 4\mu _{02} (1 + f)\varOmega _0^{\ast 2} }}{2\mu _{02} } \Bigg)^{1 / 2} $
其中,四边简支等温 Kirchhoff 矩形微板的固有频率的解析解为

(38) $ \varOmega _0^\ast = \left( {r^2 + \dfrac{s^2}{\delta ^2}} \right)\pi ^2 , \ \ r,s = 1,2,\cdots $
在式 (37) 中令 $f = 0$ 可得

(39) $ \varOmega _{0} = \Bigg( \dfrac{ - \mu _{00} + \mu _2 \varOmega _0^\ast \pm \sqrt {[ - \mu _{00} + \mu _2 \varOmega _0^\ast ]^2 - 4\mu _{02} \varOmega _0^{\ast 2} }}{2\mu _{02} } \Bigg )^{1 / 2} $
式 (39) 给出了等温 Mindlin 微板的固有频率与相应的 Kirchhoff 板的固有频率之间的解析关系. 将 文献^[29] 中的式 (12.2.16) 进行无量纲运算后所得结果与 式 (39) 完全相同.

先由 式 (39) 求得 $\varOmega _0 $,然后代入 式 (27) 可得到 $f = f(\varOmega _0 )$, 最后将其代入 式 (37) 即可得到热-弹耦 合自由振动 Mindlin 微板的复频率. 根据复频率法$^{[2\hbox{-}8]}$即可得 到用逆品质因子表示的 Mindlin 微板的热弹性阻尼解析解

(40) $ Q_{\rm M}^{ - 1} = 2\left| {\dfrac{ {\rm Im}\left( \varOmega \right)} {{\rm Re}\left( \varOmega \right)}} \right| $
其中 ${\rm Re}(\varOmega )$ 和 ${\rm Im}(\varOmega )$ 分别是复频率的实部和虚部.

可以证明,对于简支多边形微板式 (33) 和式 (34) 仍然成立^[29]. 因此,式 (37) 和式 (40) 也可以计算直边多边形中厚度微板的复频率和热弹性阻尼.

如果在式 (36) 中令 $\mu _2 = c_{\rm s} = 0$,$f = f(\varOmega _0^\ast)$,则可得到 Kirchhoff 微板的复频率$^{[3\hbox{-}8]}$

(41) $ Q_{\rm K} = \varOmega _0^\ast \sqrt {1 + f(\varOmega _0^\ast )} \approx \varOmega _0^\ast (1 + f(\varOmega _0^\ast ) / 2) $
利用式 (27) 和式 (41) 可得文献^[8] 中 Kirchhoff 微板热弹性阻尼 L-R^[2] 形式的解析解

(42) $ Q_{\rm K}^{ - 1} = 2\left| {\dfrac{{\rm Im}\left( {\varOmega _{\rm K} } \right)}{{\rm Re} \left( {\varOmega _{\rm K} } \right)}} \right| = \dfrac{1 + \nu }{1 - \nu }\dfrac{6\Delta _{\rm E} } {\psi ^2}\left( {1 - \dfrac{1}{\psi }\dfrac{\sinh \psi + \sin \psi }{\cosh \psi +\cos \psi }} \right) $
其中,$\Delta _{\rm E} = \dfrac{E\alpha ^2T_0 }{\rho C}$ 为松弛强度, $\psi = [\varOmega _0^\ast / (2g)]^{ 1 / 2}$.

3 数值结果与讨论

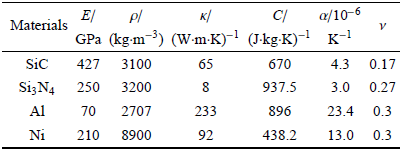
数值计算时微板的材料分别选取碳化硅 (SiC)、氮化硅 (Si$_{3}$N$_{4})$、金属铝 (Al) 和金属镍 (Ni) ^[23,29], 具体材料参数见表 1. 环境温度为 $T_0 = 300$ K.

Table 1
表1
表1微板的材料性质 ($T_0 = 300$ K)^{[23, 25]}
Table 1Material properties of the micro plate ($T_0 = 300$ K)^{[23, 25]}

新窗口打开|下载CSV

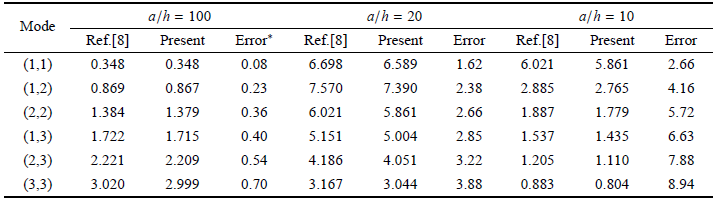
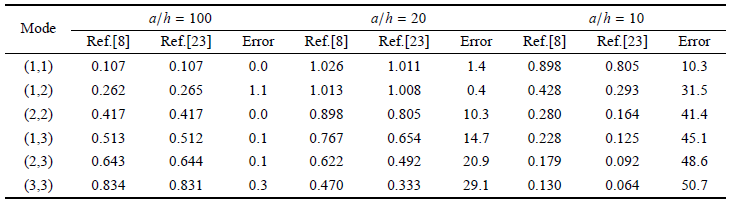
首先,针对碳化硅 (SiC) 方板,在表 2 中给出了在不同振动模态下,基于 Mindlin 板理论得到的热弹性阻尼 (40) 与文献^[8] 中采用经典理论所得到的解析解 (42) 的比较. 由表中的数据可见,随着微板的边/厚 比的减小 (或边长的减小) 以及模态阶数的增大 Mindlin 微板的逆品质因子与 Kirchhoff 微板的逆品质因子 之间的相对误差 ${\rm Error }= 100\% (Q_{\rm K}^{ - 1} - Q_{\rm M}^{ - 1} ) / Q_{\rm K}^{ - 1} $ 逐渐 增大. 在 $a / h = 10$ 和基频振动下,两种理论预测结果之间的相对误差仅为 2.66%, 而当微板以高阶模 态 $(r, s)=(3,3)$ 振动时,相对误差却达到了 8.94%. 对应同样的几何参数、材料性质参数和振 动模态,在表 3 中给出了文献^[23] 中的数值结果. 与表 2 对比后可见,文献^[23] 中的结果与 本文结果相差甚远. 而且在表 3 中利用文献^[8] 中的 Kirchhoff 微板的解析公式 (42) 计算得到 的数值结果与本文利用同样公式计算结果亦有很大差别. 特别是在边厚比 $a / h = 10$、振动 模态为 (3, 3) 的条件下,本文所得 Mindlin 板和 Kirchhoff 板的 TED 分别为 $8.04\times 10^{ - 5}$ 和 $8.83\times 10^{ - 5}$,相对误差为 8.94%;而在文献^[23] 中的相应结果 则分别为 $6.4\times 10^{ - 5}$ 和 $1.30\times 10^{ - 4}$,两种理论的预测值之间 的相对误差竟然达到了 50.7%. 而对于长厚比 $a / h = 5$ 的正方形微板, 在振动模态为 (3, 3) 的条件下,本文预测的两种理论下的热弹性阻尼之间的相对误差也仅为 28.4%.

Table 2
表2
表2两种板理论下正方形形陶瓷 (SiC) 微板的热弹性阻尼 ($Q^{ - 1}\times 10^4)$ 比较 ($a = b, h = 1 \mu$m)
Table 2Comparison of TED ($Q^{ - 1}\times 10^{4}$) of the square micro plate of ceramic (SiC) based on both of the Kirchhoff and Mindlin plate theories ($a = b, h = 1 \mu$m)

新窗口打开|下载CSV

Table 3
表3
表3具有不同边/厚比的正方形微板在前六阶模态下的热弹性阻尼比较 TED ($Q^{- 1}\times 10^{3}$) ($h = 1 \mu$m)^[23]
Table 3Comparison of TED ($Q^{-1}\times 10^{3}$) of square microplate with different side-to-thickness ratios for the first six modes ($h = 1 \mu$m)^[23]

新窗口打开|下载CSV

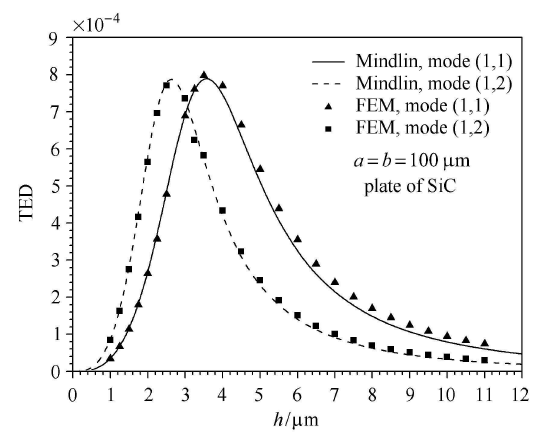
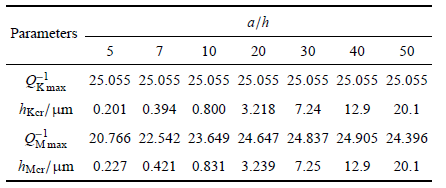
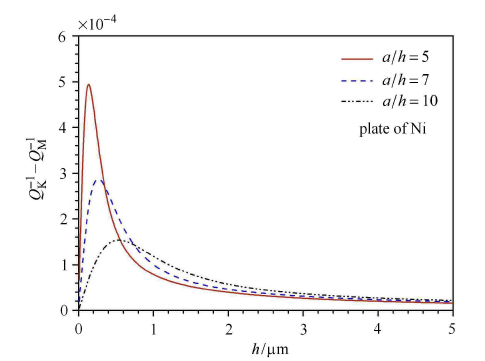
为了进一步验证本文解析解的可靠性,选择 $a = b = 100 \mu$m 的陶瓷 (SiC) 微板,在图 2 中分别给出了由式 (34) 和式 (40) 预测的 TED 和采用有限元法得到数值结果的比较. 有限元法是基于全耦合热弹性动力学理论、采用空间六面体单元获得的. 由图中结果可见,在板厚较小时二者吻合很好. 随着厚度的增大,有限元解答与本文 解析解稍有偏离. 这是因为在板理论中,将侧面上的应力边界条件沿着厚度静力等效为几何中面周边上的合力矩边界条件,根据圣维南原理随着厚度的增大板的自然边界条件与空间弹性力学的应力边界条件的差别将会增大. 实际上,位移边界条件的差别也在增大为了定量地分析剪切变形对热弹性阻尼预测值的影响,给定不同边/厚比 $a / h$,在图 2 中绘出了正方形金属 (Ni) 板谐振器在基频振动时的热弹性阻尼随板厚的连续变化曲线. 并在表 4 中列出 了图 2 中热弹性阻尼的最大值 $Q_{\max }^{ - 1} $ 和对应的临界厚度 $h_{\rm cr} $. 数值结果表明,Kirchhoff 板理论的热弹性阻尼预测 值始终大于 Mindlin 板理论的预测值. 两种理论预测的热弹性阻尼之间的差值在临界厚度附近十分显著. 另外,随着微板的边/厚比的增大,Mindlin 微板的热弹性阻尼最大值单调增加,而 Kirchhoff 微板的热弹性阻尼最大值却保 持不变. 从表 4 中数据可见,Mindlin 微板的临界厚度大于 Kirchhoff 微板的临界厚度. 为了更加清晰地反映两种理论预测值的差值的变化,在图 3 中绘出了差值 $Q_{\rm K}^{ - 1} - Q_{\rm M}^{ - 1}$ 随厚度的连续变化曲线. 图中结果 再次清楚地表明在临界厚度附近差值变化最大. 但是,在不考虑热弹性阻尼的情况下由式 (39) 可知 Mindlin 板的无量纲固 有频率只与边厚比有关. 在给定边厚比后无量纲频率为常数. 因此,两种理论预测的等温板的无量纲故有频率差值为常数.

图 2

新窗口打开|下载原图ZIP|生成PPT
图 2分别由本文方法和有限元法预测的正方形陶瓷 (SiC) 微板的热弹性阻尼值的比较

Fig. 2Comparison between the values of TED of square ceramic micro plate by FEM and present approach, respectively



Table 4
表4
表4具有不同边/厚比正方形微板 (Ni) 的最大热弹性阻尼和相应的临界厚度 (一阶模态)
Table 4The maximum TED and related critical thickness of square micro plate (Ni) for different side-to-thickness ratios (the first mode)

新窗口打开|下载CSV

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3两种板理论下正方形金属 (Ni) 微板的热弹性阻尼随厚度的变化曲线 (一阶模态)

Fig. 3Curves of the TED versus the plate thickness of a square micro metal plate (Ni) based on the two plate theories (in the first mode)



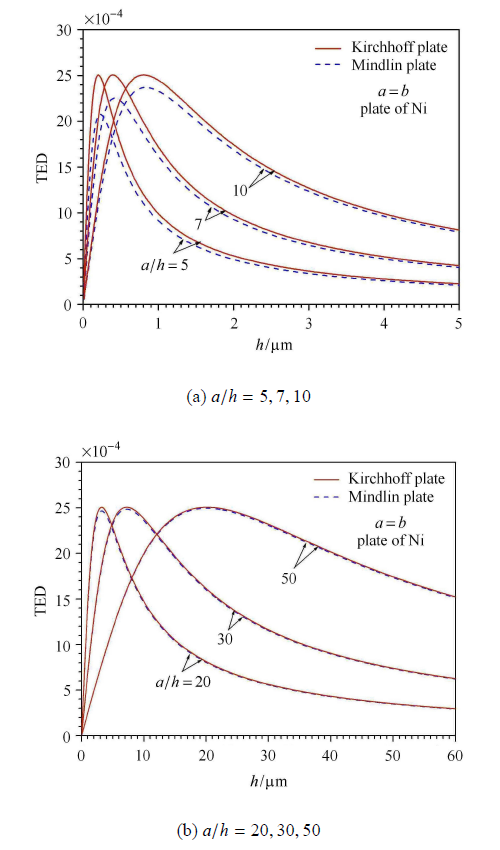
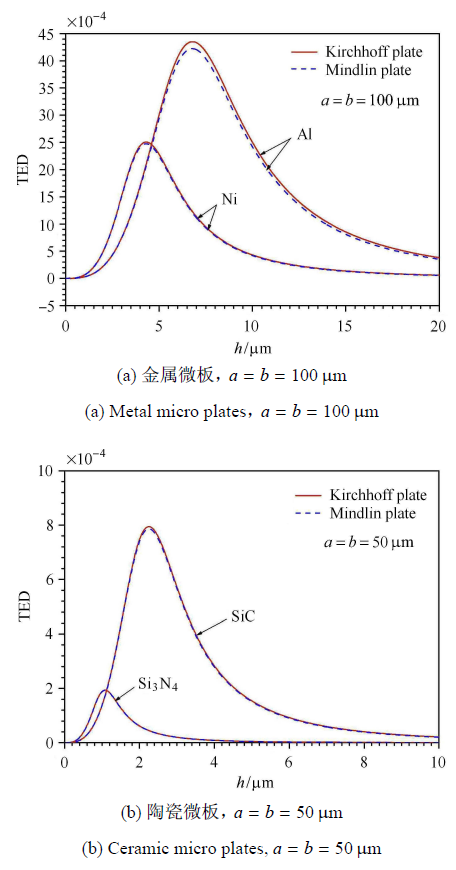
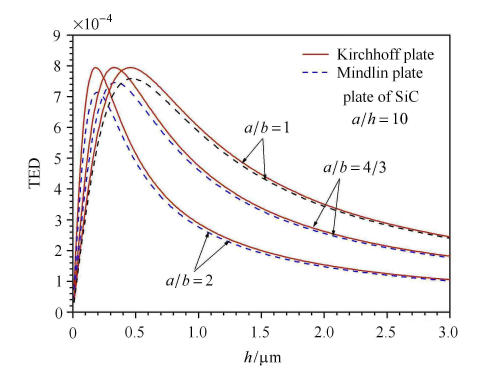
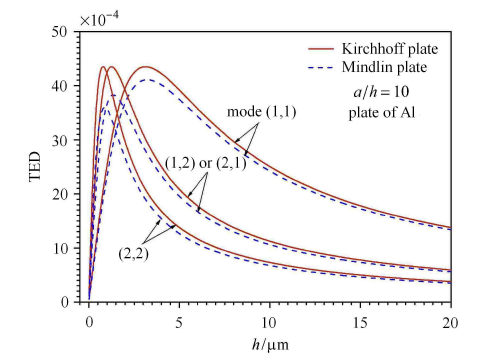
图 4 中绘出了表 1 中所列 4 种材料的正方形微板在一阶模态振动时的热弹性阻尼随厚度的连续变化曲线. 其中给出了 两种板理论预测结果的对比. 从图中可见,金属微板的热弹性阻尼明显大于陶瓷微板的热弹性阻尼. 并且两种理论下金属微 板的最大热弹性阻尼之间的差值比陶瓷微板显著. 图 5 给出了 $a / h = 10$ 时,具有不同长宽比的矩形陶瓷 (SiC) 微板 在基频振动下的 TED 与厚度的关系曲线. 结果表明,随着长宽比的增大 (相当于弯曲刚度增大) 两种板理论预测的热弹性阻尼的最大值之间的差值显著增大,而经典理论下的最大值却保持不变. 图 6 则为 $a / h = 10$ 的中等厚度板金属 (Al) 微板在前四阶振动模态下的热弹性阻尼随厚度的变化曲线. 其中的变化规律与图 5 相似. 随着振动模态阶数的增大,板的固有频率增大. 这相当于弯曲刚度在增加,从而导致剪切变形对热弹性阻尼的影响加大.

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4给定不同边厚比时,两种板理论预测的正方形金属 (Ni) 微板的热弹性阻尼差值随厚度的变化曲线 (一阶模态)

Fig. 4Difference between the values of TED of a square metal (Ni) micro plate evaluated by the two plate theories varying with the thickness for some specified values of $ a/h$ (in the first mode)

图 5

新窗口打开|下载原图ZIP|生成PPT
图 5一阶模态下不同材料正方形微板的热弹性阻尼与板厚之间的关系曲线

Fig. 5Relationship curves of TED versus the plate thickness of the square micro plates of different materials in the first mode

图 6

新窗口打开|下载原图ZIP|生成PPT
图 6具有不同长宽比 $(a/b)$ 的矩形陶瓷 (SiC) 微板的热弹性阻尼与板厚之间的关系曲线 (一阶模态)

Fig. 6TED versus the plate thickness in ceramic (SiC) micro rectangular plate with different length to width ratio(in the first mode)

图 7

新窗口打开|下载原图ZIP|生成PPT
图 7不同振动模态下金属 (Al) 微板的热弹性阻尼随厚度的关系曲线 ($a/h =10$)

Fig. 7TED versus the plate thickness in a square metal (Al) micro plate in different vibration modes ($a/h =10$)

4 结论

基于一阶剪切变形理论和单向耦合准一维热传导理论,采用解析方法研究了四边简支中厚度矩形微板谐振 器的热弹性阻尼. 利用微分方程边值问题之间的相似性,推导出了用无阻尼 Kirchhoff 微板的固有频率表示的 Mindlin 微板热-弹耦合自由振动复频率的解析解,从而采用复频率法给出了表征 Mindlin 微板热弹性阻尼的逆品质因子解析解. 分别选定两种金属和两种陶瓷材料微板,通过参数变化的数值结果定量地分析了剪切变形对热弹性阻尼预测值的影响规律. 数值结果表明,经典板理论预测的热弹性阻尼值大于一阶剪切变形板理论的预测值. 通过研究还发现,两种理论的预测的热弹性阻尼值的差别在微板的临界厚度附近最为显著.

致谢

根据审稿专家的建议, 在修改稿中增加了本文解析解与有限元法所得数值结果的比较. 扬州大学建筑 科学与工程学院的张志超博士和他指导的硕士研究生曹静同学在有限元数值计算中给予作者重要的技术帮助. 在此表示感谢.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Zener C, Internal fraction in solids. I. Theory of internal fraction in reeds
Physical Review, 1937,53:90-99
DOIURLPMID [本文引用: 4]

[2] Lifshitz R, Roukes ML, Thermoelastic dampinginmicro--and nanomechanical systems
Physical Review B, 2000,61:5600-5609
DOIURL [本文引用: 3]

[3] Nayfeh AH, Younis MI. Modeling and simulations of thermoelastic damping in microplates
Journal of Micromechanics and Microengineering, 2004,14:1711-1717
DOIURL [本文引用: 2]

[4] Sun YX, Tohmyoh H. Thermoelastic damping of the axisymmetric vibration of circular plate resonators
Journal of Sound and Vibration, 2009,319:392-405
[本文引用: 1]

[5] Sun YX, Saka M. Thermoelastic damping in micro-scale circular plate resonators
Journal of Sound and Vibration, 2010,329:328-337
[本文引用: 1]

[6] Ali NA, Mohammadi AK. Thermoelastic damping in clamped-clamped annular microplate
Applied Mechanics and Materials, 2012, 110-116:1870-1878
[本文引用: 2]

[7] Salajeghe S, Khadem SE, Rasekh M. Nonlinear analysis of thermoelastic damping in axisymmetric vibration of micro circular thin-plate resonators
Applied Mathematical Modelling, 2012,36:5991-6000
[本文引用: 2]

[8] Li P, Fang YM, Hu RF. Thermoelastic damping in rectangular and circular microplate resonators
Journal of Sound and Vibration, 2012,331:721-733
[本文引用: 5]

[9] Fang YM, Li P, Wang ZL. Thermoelastic damping in the axisymmetric vibration of circular micro plate resonators with two-dimensional heat conduction
Journal of Thermal Stresses, 2013,36:830-850
[本文引用: 1]

[10] Fang YM, Li P, Zhou HY, et al. Thermoelastic damping in rectangular microplate resonators with three-dimensional heat conduction
International Journal of Mechanical Sciences, 2017,133:578-589
[本文引用: 1]

[11] Sharma JN, Sharma R. Damping in micro-scale generalized thermoelastic circular plate resonators
Ultrasonics, 2011,51:352-358
DOIURLPMID [本文引用: 3]
The out-of-plane vibrations of a generalized thermoelastic circular plate are studied under different environmental temperature, plate dimensions and boundary conditions. The analytical expressions for thermoelastic damping of vibration and phase velocity of circumferential surface wave modes are obtained. It is noticed that the damping of vibrations and phase velocities of circumferential surface wave modes significantly depend on thermal relaxation time in addition to thermoelastic coupling in circular plates under resonance conditions. The surface conditions also impose significant effects on the vibrations of such resonators. The expressions for displacement and temperature fields in the plate resonator are also derived and obtained. Some numerical results have also been presented for illustration purpose in case of silicon material plate.

[12] Sharma JN, Grover D. Thermoelastic vibration analysis of MEMS/NEMS plate resonators with voids
Acta Mechanics, 2012,223:167-187
[本文引用: 3]

[13] Guo FL, Song J, Wang GQ, et al. Analysis of thermoelastic dissipation in circular micro-plate resonators using the generalized thermoelasticity theory
Journal of Sound and Vibration, 2014 ( 333):2465-2474
[本文引用: 3]

[14] Grover D. Damping in thin circular viscothermoelastic plate resonators
Canadian Journal of Physics, 2015,93:1597-1605
[本文引用: 3]

[15] Mohammadi AK, Ali NA. Effect of high electrostatic actuation on thermoelastic damping in thin rectangular microplate resonators
Journal of Theoretical and Applied Mechanics, 2015,53:317-329
[本文引用: 2]

[16] Bishop GE, Kinra V. Equivalence of the mechanical and entropic description of elastothermodynamics in composite materials
Mechanics of Composite Materials and Structures, 1996,3:83-95
DOIURL [本文引用: 2]

[17] Bishop GE, Kinra V. Elastothermaldynamic damping in laminated composites
International Journal of Solids and Structures, 1997,34:1075-1092
DOIURL [本文引用: 1]

[18] Sun YX, Jiang Y, Yang JL. Thermoelastic damping of the axisymmetric vibration of laminated trilayered circular plate resonators
Canada Journal of Physics, 2014,92:1026-1032
[本文引用: 2]

[19] Liu SB, Ma JX, Yang XF, et al. Theoretical analysis of thermoelastic damping in bilayered circular plate resonators with two-dimensional heat conduction
International Journal of Mechanical Sciences, 2018,135:114-123
[本文引用: 1]

[20] Liu SB, Ma JX, Yang XF, et al. Theoretical 3D model of thermoelastic damping in laminated rectangular plate resonators
International Journal of Structural Stability and Dynamics, 2018,18:1850158
[本文引用: 1]

[21] Azizi S, Ghazavi MR, Rezazadeh G, et al. Thermo-elastic damping in a functionally graded piezoelectric micro-resonator
International Journal of Mechanics and Materials in Design, 2015,11:357-369
DOIURL [本文引用: 1]

[22] Emami AA, Alibeigloo A. Exact solution for thermal damping of functionally graded Timoshenko microbeams
Journal of Thermal Stresses, 2016,39:231-243
[本文引用: 2]

[23] Emami AA, Alibeigloo A. Thermoelastic damping analysis of FG Mindlin microplates using strain gradient theory
Journal of Thermal Stresses, 2016,39:1499-1522
[本文引用: 9]

[24] Zhang ZY, Zhou JP, Zhang HL. Thermoelastic damping in functionally graded microbeam resonators
IEEE Sensors Journal, 2017,17:3381-3390
DOIURL [本文引用: 1]

[25] Li SR, Xu X, Chen S. Analysis of thermoelastic damping of functionally graded material beam resonators
Composite Structures, 2017,182:728-736
DOIURL [本文引用: 2]

[26] 许新, 李世荣. 功能梯度材料微梁的热弹性阻尼研究
力学学报, 2017,49(2):308-316


( Xu Xin, Li Shirong, Analysis of thermoelastic damping for functionally graded material micro-beam
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(2):308-316 (in Chinese))


[27] 陈顺, 李世荣. 轴对称自由振动功能梯度材料微圆板中的热弹性阻尼
力学季刊, 2018,39(4):719-730


( Chen Shun, Li Shirong. Thermoelastic damping in functionally graded material micro circular plates vibrating axisymmetrically
Chines Quarterly of Mechanics, 2018,39(4):719-730 (in Chinese))


[28] Li SR, Ma HK. Analysis of free vibration of functionally graded material micro-plates with thermoelastic damping
Archive Applied Mechanics, 2020,90:1285-1304
DOIURL

[29] Reddy JN, Wang CM, Lee KH. Shear Deformable Beams and Plates-Relationship with Classical Solutions
Elsevier Science Ltd, 2000
[本文引用: 5]

[30] 李世荣, 张靖华, 徐华. 功能梯度与均匀圆板弯曲解的线性转换关系
力学学报, 2011,43(5):871-877


( Li Shirong, Zhang Jinghua, Xu Hua. Linear transformation between the bending solutions of functionally graded and homogenous circular plats
Chinese Journal of Theoretical and Applied Mechanics, 2011,43(5):871-877 (in Chinese))


[31] 李尧臣, 亓峰, 仲政. 功能梯度矩形板的近似理论与解析解
力学学报, 2010,42(4):670-681


( Li Yaochen, Qi Feng, Zhong Zheng. Approximate theory and analytical solution for functionally graded piezoelectric rectangular plates
Chinese Journal of Theoretical and Applied Mechanics, 2010,42(4):670-681 (in Chinese))


[32] 李尧臣, 聂国隽, 杨昌锦. 面内功能梯度矩形板的近似理论与解答
力学学报, 2013,45(4):560-567


( Li Yaochen, Nie Guojun, Yang Changjin. Approximate theory and analytical solution for rectangular plates with in-plane stiffness gradient
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(4):560-567 (in Chinese))


[33] 刘璟泽, 姜东, 韩晓林 等. 曲线加筋Kirchhoff-Mindlin 板自由振动分析
力学学报, 2017,49(4):929-939


( Liu Jingze, Jiang Dong, Han Xiaolin, et al. Free vibration analysis of curvilinearly stiffend Kirchhoff-Mindlin plates
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(4):929-939 (in Chinese))