,2), 姜潮湖南大学机械与运载工程学院, 长沙410006AN INTERVAL FINITE ELEMENT METHOD BASED ON THE NEUMANN SERIES EXPANSION 1)
Wu Pengge, Ni Bingyu,2), Jiang ChaoCollege of Mechanical and Vehicle Engineering, Hunan University, Changsha 410006, China通讯作者: 2)倪冰雨, 博士后, 主要研究方向: 结构不确定性分析. E-mail:nby@hnu.edu.cn
收稿日期:2020-05-8接受日期:2020-05-8网络出版日期:2020-09-18
| 基金资助: |
Received:2020-05-8Accepted:2020-05-8Online:2020-09-18
作者简介 About authors
摘要
实际工程问题中通常存在大量的不确定参数, 区间有限元方法是一种结合有限元数值计算工具对结构进行不确定性分析的区间方法. 区间有限元的目的是获得在含有区间不确定性参数条件下的结构响应上下边界, 其关键问题在于区间平衡方程组的求解, 而这属于一类往往很难求解的NP-hard问题. 本文归纳了一类工程实际中常见的结构不确定性问题, 即可线性分解式区间有限元问题, 并针对此提出一种基于Neumann级数的区间有限元方法. 在区间有限元分析中, 当区间不确定参数表示为一组独立区间变量线性叠加时, 若结构的刚度矩阵也可表示为这些独立区间变量的线性叠加形式, 则称此类区间有限元问题为可线性分解式区间有限元问题. 对于此类问题, 采用Neumann级数对其刚度矩阵的逆矩阵进行表示, 可获得结构响应关于区间变量的显式表达式, 从而可高效求解结构响应的上下边界. 最后通过两个算例验证了本文所提方法的有效性.
关键词：
Abstract
Uncertainty is common in the practical engineering. The interval finite element method is an interval method which introduces the numerical computational method of finite element to structural uncertainty analysis. The aim of the interval finite element analysis is to obtain the upper and lower response bounds of the structure with interval uncertain parameters, where solving the interval finite element equilibrium equations is the key issue. But the solution of interval linear equations belongs to a class of NP-hard problems which are often difficult to solve. This paper classifies and defines a type of linearly decomposable interval finite element problems, which exist commonly in practical engineering. To solve this type of problems, an interval finite element method based on Neumann series is proposed. It is named as the linearly decomposable interval finite element problem if the stiffness matrix in the interval finite element analysis formulation can be expressed as a linear superposition of a set of independent interval variables when the interval uncertain parameter is expressed as a linear superposition form of the independent interval variables. For this kind of problems, the inverse of the stiffness matrix can be represented by its Neumann series expansion. Thus the explicit expressions of structural responses with interval variables can be then obtained, with which the upper and lower bounds of the structural response can be solved efficiently. Finally, two numerical examples show the effectiveness and accuracy of the proposed method.
Keywords：
PDF (1126KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
伍鹏革, 倪冰雨, 姜潮. 一种基于Neumann级数的区间有限元方法 1). 力学学报[J], 2020, 52(5): 1431-1442 DOI:10.6052/0459-1879-20-152
Wu Pengge, Ni Bingyu, Jiang Chao.
引言
不确定性广泛存在于实际工程中, 如结构的材料属性、几何尺寸及结构所受载荷等. 传统方法主要基于概率模型对上述不确定性参数进行描述, 并使用概率方法对其进行分析[1-5]. 使用概率方法进行不确定性分析通常需要大量的实验样本以获得精确的概率分布信息. 然而在许多工程实际问题中, 由于测试成本或测试技术等原因往往造成样本数据缺乏, 很难获得足够的样本信息以构建上述参数的精确概率分布函数. 为此, 一系列非概率分析方法及非精确概率分析方法得以发展, 包括证据理论[6-8]、P-box模型[9-10]、凸模型方法[11-12]、模糊集理论[13-14]和区间方法[15-17]等. 其中区间方法于20世纪50年代末由Moore[17]提出, 最早用于处理计算机内浮点运算问题, 后来被引入到工程结构领域的不确定性问题中[18-20]. 在使用区间方法进行不确定性分析时, 参数的不确定性由上下边界表示, 不仅有效适用于小样本条件下的不确定性度量, 而且易于工程人员理解和方便使用, 近年来在理论研究和实际应用方面获得了广泛关注[21-25].20世纪90年代中期, 为解决在小样本条件下工程结构问题中的不确定性, 将区间分析与有限元方法[26-27]相结合, 发展出了区间有限元方法[28-30]. 区间有限元是一种考虑区间不确定性的有限元分析方法, 其主要目的在于借助有限元分析这一有力数值分析工具, 对含区间不确定参数的结构进行响应边界求解. 而获得有限元结构响应边界的关键在于区间平衡方程组的求解, 该平衡方程组属于一类区间线性方程组, 其中的刚度矩阵或载荷向量为区间矩阵或区间向量. 区间线性方程组的求解被认为是一类NP-hard问题[31-33], 一般情况下很难获得其解析结果. 因此, 不少****发展了区间有限元分析的近似方法以求解实际响应集合的最小区间包络. Rao和Berke[34]提出了顶点组合方法, 在区间参数波动范围较小的情况下能够得到较为精确的解. Neumaier和Pownuk[35]针对桁架结构这一典型结构力学问题提出了一种关于区间线性系统的迭代解法, 能够得到较准确的桁架结构响应包络解. Muhanna和Mullen[36]提出了element-by-element (EBE)列式技术, 在一定程度上避免了响应区间的过保守估计问题. Rao等[37]和Xiao等[38]将EBE技术与迭代解法相结合应用于结构响应静态以及动态分析中. Muscolino等[39]对具有不确定性参数结构的频率响应提出了比例多项式的近似求解方法. Sofi和Romeo[40]基于比例多项式建立了适用于含区间变量及随机变量的结构有限元分析方法. Qiu和Elishakoff[41]、Chen和Yang[29]、Qiu等[42]应用区间摄动方法求解了含有有界不确定参数的结构响应区间, 对于小扰动问题有较好的求解精度. Degrauwe等[43]将仿射运算引入至区间变量的表示中, 改善了区间运算中的区间扩张问题.
现有大多数区间有限元方法计算得到的响应区间包络往往过为保守, 或只对于参数波动范围较小的区间有限元问题能够得到较准确的响应区间, 或计算效率较低等. 因而, 如何高效求解区间有限元中结构响应的最小包络解仍是有待解决的难点问题. 本文归纳了一类在工程实际中常见的区间有限元问题, 其中刚度矩阵可以表示为一系列独立区间变量线性叠加的形式, 称之为可线性分解式区间有限元问题. 如弹性模量或横截面积等为区间参数的桁架结构, 弹性模量或厚度尺寸等为区间参数的混凝土板连续体结构等, 对其进行区间有限元分析时均可处理为可线性分解式区间有限元问题. 针对此类可线性分解式区间有限元问题, 采用Neumann级数展开方法对其刚度矩阵的逆矩阵进行表示, 可获得结构响应关于区间变量的显式表达式, 从而便于高效求解结构响应的上下边界. 本文剩余部分内容安排如下: 第1节首先简要介绍区间有限元分析的概念, 并归纳出一类工程中广泛存在的可线性分解式区间有限元问题; 第2节针对可线性分解式区间有限元问题, 提出了基于Neumann级数的区间有限元方法; 第3节通过2个算例验证了本文方法的有效性; 第4节给出了全文结论.
1 区间有限元问题描述
在区间有限元分析中, 通过区间模型等度量参数的有界不确定性, 通常适用于样本信息不足以构建参数概率分布但参数上下边界可知的结构不确定性问题中. 由于区间不确定性的存在, 通常区间有限元平衡方程中的刚度矩阵为一区间矩阵或节点力向量为一区间向量, 从而导致其平衡方程组为一区间线性方程组. 本节简要介绍区间有限元平衡方程组的构成, 并归纳出一类可线性分解式区间有限元问题.1.1 区间有限元平衡方程
在有限元方法中, 首先将结构离散为由多个单元组成的有限单元模型, 计算各个单元的单元刚度矩阵, 进而将离散后的单元按照单元与单元之间的共同节点相互连接起来, 从而组建全局刚度矩阵${ K}$式中, $N_{\rm e} $为结构的离散单元总数目; ${ K}^{{\rm e}(i)}$为第$i$个单元的单元刚度矩阵; ${ T}_i$是对应的单元刚度矩阵的变换矩阵, 将单元刚度矩阵从单元局部坐标变换到全局坐标. 结构的平衡方程则可表示为
式中, ${ K}\in {\bf R}^{N_{\rm d} \times N_{\rm d}}$是结构的全局刚度矩阵; ${ u}\in {\bf R}^{N_{\rm d} \times 1}$表示节点位移向量, 为待求量; ${ p}\in {\bf R}^{N_{\rm d} \times 1}$是结构的节点等效载荷向量; $N_{\rm d}$为整个结构的自由度数目. 当给定边界约束条件后, 式(2)中节点位移向量${ u}$便可求出, 进而可获得结构的应力和应变响应.
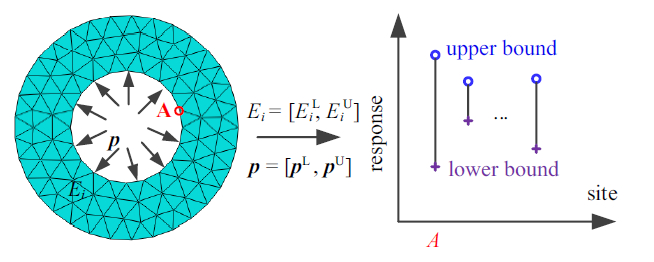
在上述通过有限元方法求解结构在外力作用下的力学响应信息时, 结构参数均假设为确定性量. 对于工程中普遍存在的不确定性结构, 如材料属性、几何尺寸、载荷等具有不确定性的情况, 通过引入区间变量描述参数的不确定性, 并结合有限元分析方法, 即可通过构建区间有限元分析列式对含区间不确定性的结构进行响应边界分析, 结构不确定性分析的示意图如图1所示. 结构材料属性或几何尺寸等参数的不确定性将导致结构刚度矩阵${ K}$的不确定性, 而外加载荷的不确定性会引起载荷向量${ p}$的不确定性. 设结构中存在不确定性参数${ \alpha}=\left[ {\alpha _{\rm 1} ,\alpha _{\rm 2} ,\cdots ,\alpha _k } \right]^{\rm T}$, 其上、下边界分别为${ \alpha }^{\rm U}=\left[ {\alpha _1^{\rm U},\alpha _2^{\rm U},\cdots ,\alpha _k^{\rm U}} \right]^{\rm T}$, $ \alpha ^{\rm L}=\left[ {\alpha _1^{\rm L},\alpha _2^{\rm L},\cdots ,\alpha _k^{\rm L}} \right]^{\rm T}$, 通过区间模型[17]可表示为
图 1
新窗口打开|下载原图ZIP|生成PPT图 1结构不确定性分析
Fig. 1Structural uncertainty analysis
且称$\alpha _l^{\rm C} =\left( {\alpha _l^{\rm L} +\alpha _l^{\rm U} } \right)/2$为区间$\alpha_l^{\rm I} $的中值, 称$\alpha _l^{\rm W} =\left( {\alpha _l^{\rm U} -\alpha _l^{\rm L} } \right)/2$为区间$\alpha _l^{\rm I}$的半径. 此时适用于含区间参数的结构有限元平衡方程可表示为
式中, ${ \alpha }^{\rm I}=\left[ {\alpha _1^{\rm I} ,\alpha _2^{\rm I} ,\cdots ,\alpha _k^{\rm I} } \right]^{\rm T}$为区间向量. 式(4)即为区间有限元平衡方程组, 该方程组的解集$\varGamma $为包含所有满足条件的位移响应的集合, 即
式(4)所表示的平衡方程组属于一区间线性方程组, 其求解结果$ \varGamma $通常较为复杂, 难以解析获得. 实际上, 通常寻求的是包络真实解$ \varGamma $尽可能小的区间边界${ u}^{\rm I}$. ${ u}^{\rm I}$为一区间向量, 每个分量描述了对应位移响应量的变化范围, 而不考虑各分量之间的相关性, 因此${ u}^{\rm I}$又称为最小的超立方体近似解[44]. 目前求解上述区间有限元问题的方法主要包含三类, 即基于区间运算的方法[32, 45], 基于级数展开的方法[41, 46]和全局优化方法[47-48].
1.2 一类可线性分解式区间有限元问题
本小节归纳了在工程结构中常见的一类区间有限元问题, 该类问题的刚度矩阵可分解为一系列独立区间变量的线性叠加形式, 称之为可线性分解式区间有限元问题.设式(4)中区间参数$\alpha _l^{\rm I} $可表示为
式中, $a_{l,0} $为常数项, 一般取作区间参数$\alpha _l^{\rm I} $的中值; $\zeta _j^{\rm I}=[-1,1]$, $j=1,2,\cdots ,m$为相互独立的标准区间变量; $a_{l,j} $为实数, 是标准区间变量$\zeta _j^{\rm I} $对应的系数; $m$为标准区间变量$\zeta _j^{\rm I} $的个数. 区间向量${ \alpha }^{\rm I}$则可表示为
本文仅考虑结构材料属性或几何尺寸参数具有不确定性, 而载荷确定的情况, 此时式(4)退化为
若参数${ \alpha }^{\rm I}$与结构刚度矩阵${ K}$中的每个元素呈线性关系, 且${ \alpha }^{\rm I}$可如式(7)表示为一组独立区间变量$\zeta _j^{\rm I} $线性叠加的形式, 则区间刚度矩阵${ K}({ \alpha }^{\rm I})$也具有关于区间变量$\zeta _j^{\rm I} $的线性叠加表达式
式中, ${ K}_j$ $(0,1,2,\cdots ,m)$为对称的确定性矩阵. 对于不同的区间有限元问题, ${ K}_j $的具体形式有所不同. 形如式(9)的可线性分解式区间刚度矩阵在工程实际问题中较为常见, 如弹性模量或横截面积等为区间参数的桁架结构, 具有区间弹性模量或区间厚度尺寸等参数的混凝土板连续体结构等, 对其进行数值分析时, 相应的区间刚度矩阵均具有上述叠加形式. 下面以含区间弹性模量的连续体结构为例, 通过推导给出其区间刚度矩阵的线性分解形式.
考虑一由线弹性各向同性材料构成的连续体结构, 其有限元模型包含$N_{\rm e} $个单元, $N_{\rm n} $个节点, $N_{\rm d} $个自由度, 受到节点载荷${ p}$的作用. 为便于理解, 这里仅考虑弹性模量具有不确定性的情况, 且由区间变量描述. 设区间弹性模量$E^{\rm I}$可表示为式(6)的形式, 即
式中, $E_0 $为弹性模量$E^{\rm I}$的中值.
根据有限元理论[26], 连续体的单元刚度矩阵${ K}^{{\rm e}(i)}$有如下形式
式中, $A^{{\rm e}(i)}$为第$i$个单元的单元积分域, $t$为厚度, ${ B}$为几何矩阵, $ D$为弹性系数矩阵, 与弹性模量$E$呈线性关系
式中, $ M=\dfrac{1}{1-\mu }\left[ {{\begin{array}{c@{\quad }c@{\quad }c} 1 & \mu & 0 \\ \mu & 1 & 0 \\ 0 & 0 & {\dfrac{1-\mu }{2}} \\ \end{array} }} \right]$, $\mu $为泊松比. 式(10)代入式(12)中得
式中, $ D_0 =E_0 { M}$, $ D_j =E_j { M}$. 将式(13)代入式(11)中, 此时单元刚度矩阵也为一区间矩阵
式中, ${ K}_{\rm 0}^{{\rm e}(i)} =\int_{A^{{\rm e}(i)}} { B}^{\rm T} D_0 { B}{\rm d}A\cdot t $, ${ K}_j^{{\rm e}(i)} =\int_{A^{{\rm e}(i)}} {{ B}^{\rm T} D_j { B}{\rm d}A\cdot t} $. 根据式(1)将单元刚度矩阵组装为全局刚度矩阵, 可得到全局刚度矩阵关于标准区间变量的线性叠加形式
式中, ${ K}_0 = \sum\limits_{i=1}^{N_{\rm e} } {{ T}_{^i} { K}_0^{{\rm e}(i)} { T}_i^{\rm T} } $和${ K}_j = \sum\limits_{i=1}^{N_{\rm e} } {{ T}_{^i} { K}_j^{{\rm e}(i)} { T}_i^{\rm T} } $为组装构成的确定性矩阵, 且称${ K}_0 $为名义矩阵. 从而该结构的区间有限元平衡方程式可表示为
由式(16)可发现, 上述问题的区间平衡方程中区间刚度矩阵可表示为关于区间变量的线性叠加形式, 因此此类问题即属于一类线性可分解式区间有限元问题.
2 基于Neumann级数的区间有限元分析方法
区间平衡方程组的求解是区间有限元分析的关键. 与确定性的有限元求解相比, 在区间有限元分析中最大的不同也是难点即区间平衡方程组中区间矩阵的逆运算难以求解. 现有区间有限元分析方法在进行结构响应边界分析时, 通常采用一系列数值手段避免对上述区间刚度矩阵进行求逆. 本节针对在上一节中归纳的可线性分解式区间有限元问题提出基于Neumann级数的区间有限元方法, 利用Neumann级数展开方法对区间刚度矩阵进行求逆运算, 从而便于后续求解结构响应的上下边界.2.1 基于Neumann级数的区间刚度矩阵求逆
Neumann级数是一种适用于算子求逆的级数展开方法. 设有任意矩阵${ A}$, 则该矩阵的逆矩阵${ A}^{-{\rm 1}}$可表示为关于矩阵${ A}_{\rm 0} $的逆矩阵及两者差值矩阵$\Delta { A}={ A}-{ A}_0 $的Neumann级数展开[49], 即式中, ${ I}$为单位矩阵, $n$为展开式的阶数. Neumann级数的收敛条件为矩阵${ A}_0^{-1} \Delta { A}$的谱半径小于1, 即$\rho \left( {{ A}_0^{-1} \Delta { A}} \right)<1$[50].
根据式(17), 对于可线性分解式区间有限元刚度矩阵的逆矩阵, 其Neumann级数展开式可表示为
由式(18)可以看出, 在区间有限元分析中引入Neumann级数表示可线性分解式刚度矩阵的逆, 可将原非确定性刚度矩阵的逆运算转换为确定性名义矩阵${ K}_0 $的逆运算及矩阵加、减法和乘法运算, 避免了区间矩阵的直接逆变换. 通过上述展开方法, 式(18)给出了刚度矩阵逆矩阵关于区间变量的显式表达式, 从而很大程度上方便了后续对结构响应进行不确定性分析与求解.
2.2 位移边界分析
由式(8)可知位移向量可表示为将式(18)代入式(19)中, 位移响应向量可表示为
令
$$\begin{eqnarray*} &&\Delta { u}({ \zeta })=-\sum\limits_{j=1}^m {{ K}_0^{-1} { K}_j\zeta _j^{\rm I} } { K}_0^{-1} { p}+\cdots+ \\&&\qquad\left( {-1} \right)^n\left({\sum\limits_{j=1}^m {{ K}_0^{-1} { K}_j \zeta _j^{\rm I} } } \right)^n{ K}_0^{-1} { p} \end{eqnarray*}$$
${ u}_0 ={ K}_0^{-1} { p}$, 则式(20)可表示为
计算第$s$ ($s=1,2,\ldots ,N_{\rm d} $)个自由度位移响应的上边界$u_s^{\rm U}$和下边界$u_s^{\rm L}$从而可转换为对如下两个优化问题的求解
式中, $u_{0,s} $表示向量${ u}_0 $的第$s$个元素, $\Delta u_s $表示向量$\Delta { u}$的第$s$个元素. 通过求解式(22)和式(23)得到结构在每一自由度上的位移响应区间, 从而可获得整个结构的位移响应边界.
对于常见的不确定参数扰动较小的问题, 通常保留Neumann展式中的低阶部分即可使结果满足精度要求. 进行一阶截断时可得
考虑到标准区间变量$\zeta _j^{\rm I} =[-1,1]$, $j=1,2,\cdots ,m$, 则一阶截断时位移响应的上、下边界可解析表示为
此时, 式(25)和式(26)即为整个结构位移响应一阶截断时的上下边界矢量.
2.3 应力边界分析
通过Neumann级数展开, 不确定性结构的应力也可表示为关于区间变量$\zeta _j^{\rm I} $的显式表达式. 单元的应力场表达式为式中, ${ \sigma }^{{\rm e}(i)}=\lt[ \sigma _{xx}^{(i)} \ \ {\sigma _{yy}^{(i)} } \ \ {\tau _{xy}^{(i)} } ]^{\rm T}$(对于平面问题)或${ \sigma }^{{\rm e}(i)}=\lt[{\sigma _{xx}^{(i)} } \ \ {\sigma _{yy}^{(i)} } \ \ {\sigma _{zz}^{(i)} } \ \ {\tau _{xy}^{(i)} } \ \ {\tau _{yz}^{(i)} } \ \ {\tau _{zx}^{(i)} } ]^{\rm T}$ (对于空间问题); ${ u}^{{\rm e}(i)}$表示对应单元的节点位移向量, 可表示为
因此单元应力场也可表示为
当位移响应${ u}$取前一阶截断时, ${ \sigma }^{{\rm e}(i)}$表示为
式中
$$\begin{eqnarray*} \varDelta _{\zeta \zeta } =-\left( {\sum\limits_{j=1}^m { D_j \zeta _j^{\rm I} } } \right){ B T}_i \left( {\sum\limits_{j=1}^m {{ K}_0^{-1} { K}_j { K}_0^{-1} { p}\zeta _j^{\rm I} } } \right). \end{eqnarray*}$$
若进一步忽略二阶项$\varDelta _{\zeta \zeta } $, 则应力矢量也是关于区间变量$\zeta _j^{\rm I} $的线性函数, 其上下边界可表示为
通过式(31)和式(32)得到每个单元的应力响应区间, 整个结构的应力响应边界即可获得.
2.4 收敛条件与误差分析
根据Neumann展式(17)的收敛条件可知, 区间刚度矩阵逆矩阵的Neumann级数展开式的收敛条件为式中, $\rho (\cdot )$表示矩阵的谱半径.
根据矩阵谱半径的性质有
由于$\zeta _j^{\rm I} =[-1,1]$, $\max (| {\zeta _j^{\rm I} }|)=1$, 区间刚度矩阵逆矩阵的Neumann级数展开式收敛的充分不必要条件为
考虑位移响应向量表达式(20)取前$n$阶时, 位移响应的绝对误差可表示为
位移响应的相对误差为
$$\begin{eqnarray*} e_{\rm r} \leqslant \left\| \left( \sum\limits_{j=1}^m { K}_0^{-1} { K}_j \zeta _j^{\rm I} \right)^{n+1} \right\|_2 \leqslant \left\| {\sum\limits_{j=1}^m {{ K}_0^{-1} { K}_j \zeta _j^{\rm I} } } \right\|_2^{n+1} \end{eqnarray*}$$
满足$\left\| {\sum\limits_{j=1}^m {{ K}_0^{-1} { K}_j \zeta _j^{\rm I} } } \right\|_2 <1$的条件, 位移响应的相对误差$e_{\rm r} <1$, 且随着展开项数$n$的增大而减小, 当$n\to \infty $时, 相对误差$e_{\rm r} \to 0$. 同理, 应力矢量相对误差也可类似获得.
3 算例分析
本节通过两个算例验证了本文所提基于Neumann级数展开区间有限元法的可行性和有效性. 第1个算例是横截面积为区间变量的平面四杆桁架结构在节点力作用下的位移响应分析; 第2个算例是弹性模量为区间变量的汽车驾驶室受到集中载荷的形变分析.3.1 平面四杆桁架结构
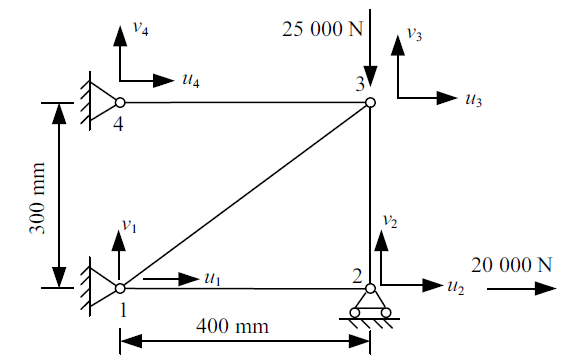
考虑如图2所示的平面桁架结构[51], 由4个杆件单元构成, 其整体宽为400 mm, 高为300 mm. 该桁架在节点2处受到沿$x$轴方向的节点力20 000 N, 节点3处受到沿$y$轴方向的节点力$-$25 000 N. 节点1和节点4固定, 节点2和节点3为铰接点. 各杆的弹性模量均为$E=2.95\times 10^5$ N/mm$^{2}$, 各杆的横截面积为不确定性区间参数, 可表示为$A_i^{\rm I} =A_i^{\rm C} +A_i^{\rm W} \zeta _i^{\rm I}\zeta _i^{\rm I} =[-1,1]=1,2,3,4$. 4个杆单元的横截面积的中值分别为: $A_1^{\rm C} =150$ mm$^{2}$, $A_2^{\rm C} =120$ mm$^{2}$, $A_3^{\rm C} =100$ mm$^{2}$, $A_{\rm 4}^{\rm C} =100$ mm$^{2}$. 区间半径分别考虑(1)$A_i^{\rm W} =0.1A_i^{\rm C}$,(2) $A_i^{\rm W} =0.15A_i^{\rm C}$, (3) $A_i^{\rm W} =0.2A_i^{\rm C}$, $i=1$, 2, 3, 4三种情形.图 2
新窗口打开|下载原图ZIP|生成PPT图 2平面四杆桁架[51]
Fig. 2Four bar truss in the plane[51]
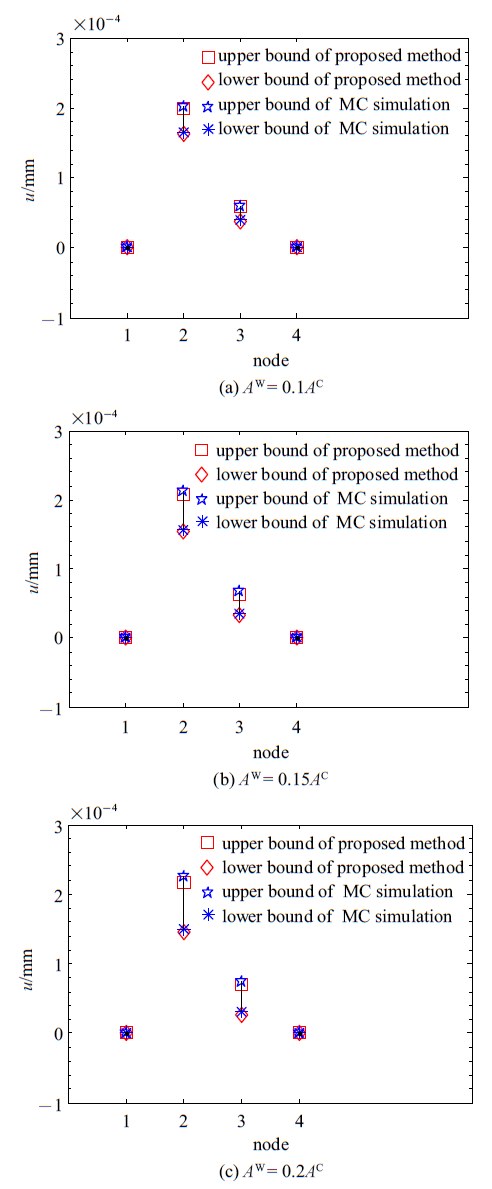
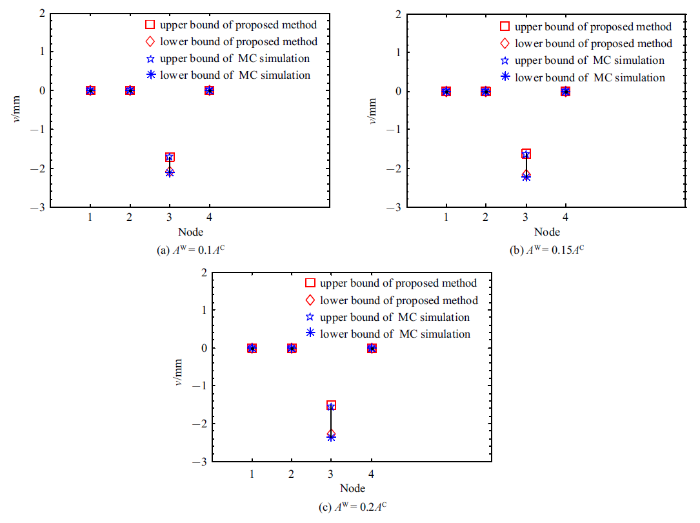
由于在$A_i^{\rm C} =0.1A_i^{\rm W}$, $0.15A_i^{\rm W}$, $0.2A_i^{\rm W}$三种情况下都有$\sum\limits_{j=1}^m {\left\| {{ K}_0^{-1} { K}_j }\right\|_2 } <1$, 满足本文方法的收敛性要求, 因此可采用本文方法求解各节点位移响应的上下边界. 为验证本文方法的精度, 使用Monte Carlo 模拟(MCS)作为参考标准, MCS的具体步骤在附录中给出. 3种不同区间半径情况下, 基于Neumann级数区间有限元方法的前一阶截断和MCS抽样100 000次得到结构各节点位移响应上下边界的对比如图3和图4所示. 从图中可看出, 两种方法得到的结果基本一致, 随着参数区间范围的增大结构响应位移的区间范围也增大, 但与MCS对比的误差也稍有增大. 为了验证本文所提方法的精确度以及Neumann级数截断阶数对结果的影响, 本文选择了沿$x$, $y$轴方向上位移相对较大的自由度进行相对误差分析, 即节点2沿$x$轴方向的位移响应$u_2$和节点3沿$y$轴方向的位移响应$v_3 $. 表1列出了基于Neumann级数区间有限元方法的前一阶截断、前二阶截断及MCS方法计算出的$u_2$和$v_3 $具体上下边界值及相对误差, 可发现在$A_i^{\rm C} =0.1A_i^{\rm W}$, $0.15A_i^{\rm W}$, $0.2A_i^{\rm W}$三种情况下, 采用Neumann级数前一阶截断计算结果的相对误差分别约为1%, 2%, 4%, 而采用Neumann级数前二阶截断计算结果的相对误差均在1%以内, 证明了本文所提方法的计算结果是可信的, 也说明了Neumann级数的阶数越高精度越好, 且对于比较简单的问题或不确定性较小时保留Neumann展式中的低阶部分即可使结果满足精度要求.
图 3
新窗口打开|下载原图ZIP|生成PPT图 3沿$x$轴方向位移响应上下边界
Fig. 3Displacement bounds in the direction of $x$
图 4
新窗口打开|下载原图ZIP|生成PPT图 4沿$y$轴方向位移响应上下边界
Fig. 4Displacement bounds in the direction of $y$
Table 1
表1
表1节点位移上下边界值相对误差
Table 1
 |
新窗口打开|下载CSV
3.2 汽车驾驶室
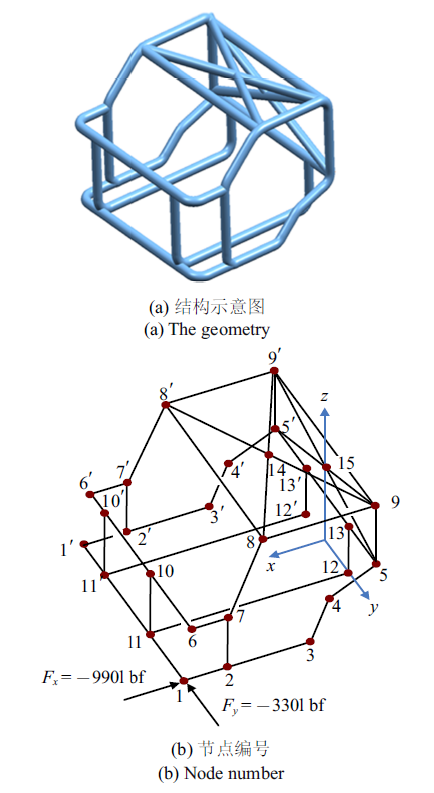
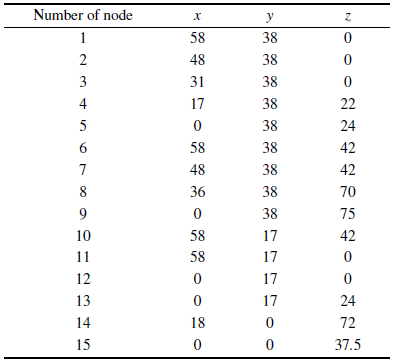
汽车驾驶室结构设计是汽车设计中的重要环节, 驾驶室结构的静动态分析有助于评估设计性能并进行结构改进使其满足设计要求. 图5所示是一个简化的汽车驾驶室车身有限元模型[26,52], 该模型包括28个节点和43个单元, 且节点1$'$-13$'$与节点1-13具有对应相同的和坐标及相反的坐标. 驾驶室有限元模型详细的节点坐标信息由表2给出. 每一根梁的横截面积为$A=0.2$ in$^{\rm 2}$ (1~in = 25.4 mm), 惯性矩为$I_{y'} =I_{z'} =0.003$ in$^{4}$, 极坐标矩$J=0.006$ in$^{4}$, 泊松比为$\mu =0.3$. 节点11, 11$'$, 12和12$'$的所有自由度均被约束, 仅仅在节点1处施加集中载荷, 大小为$F_x =-990.0$ lbf和$F_y=-330.0$ lbf (1~lbf = 4.45N). 由于缺乏足够的实验数据, 将梁的弹性模量考虑为不确定区间参数, 由于该结构为对称结构, 假设对称位置的梁的弹性模量为同一区间参数, 各单元的弹性模量区间值具体如表3所示(以psi为单位, 1 psi = 6.894 757 kPa), 共有24个相互独立的区间参数.图 5
新窗口打开|下载原图ZIP|生成PPT图 5汽车驾驶室模型[26,52]
Fig. 5A model of auto cab[26,52]
Table 2
表2
表2汽车驾驶室模型节点坐标 (单位: in)
Table 2
 |
新窗口打开|下载CSV
Table 3
表3
表3单元弹性模量的中值和半径(单位: psi)
Table 3
 |
新窗口打开|下载CSV
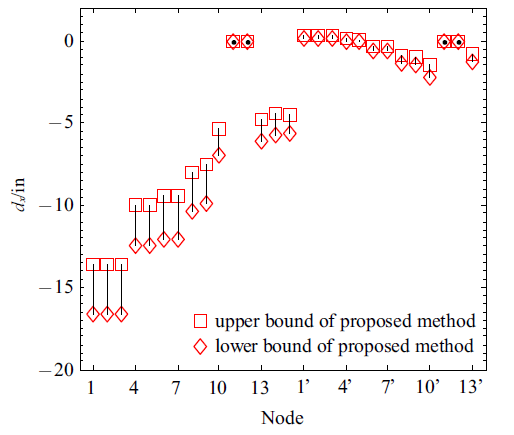
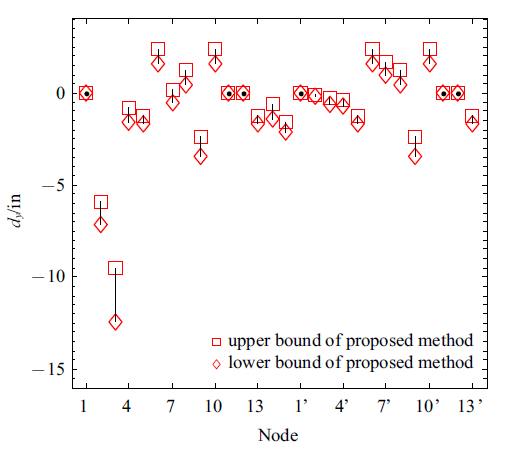
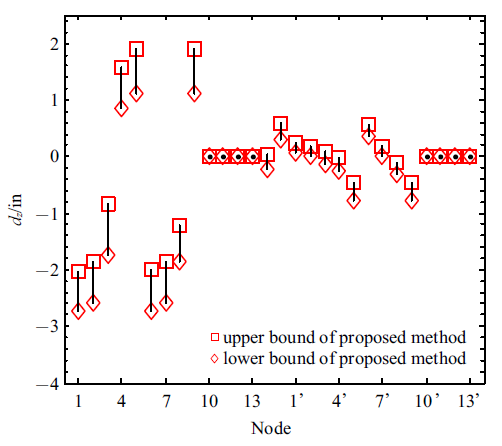
利用本文所提基于Neumann级数展开前一阶截断计算出的各节点在载荷作用下沿、和轴方向位移响应的上下边界值如图6~图8所示. 图9~图11分别表示3个方向上的节点位移响应与MCS及GA结果相对比, 该算例中区间变量为24个, MCS抽取样本点数为. 从图中可看出3种方法得到的结果基本一致, 沿轴方向上的节点位移响应较大, 尤其是1, 2, 3这3个节点位移响应最大, 可达17 in, 且第3节点在轴方向的位移响应也较大. 故而在设计阶段应考虑在这些节点单元处做出优化改进以提升安全性能.
图 6
新窗口打开|下载原图ZIP|生成PPT图 6沿$x$轴方向位移的上下边界
Fig. 6Displacement bounds in the direction of $x$
图 7
新窗口打开|下载原图ZIP|生成PPT图 7沿$y$轴方向位移的上下边界
Fig. 7Displacement bounds in the direction of $y$
图 8
新窗口打开|下载原图ZIP|生成PPT图 8沿$z$轴方向位移的上下边界
Fig. 8Displacement bounds in the direction of $z$
图 9
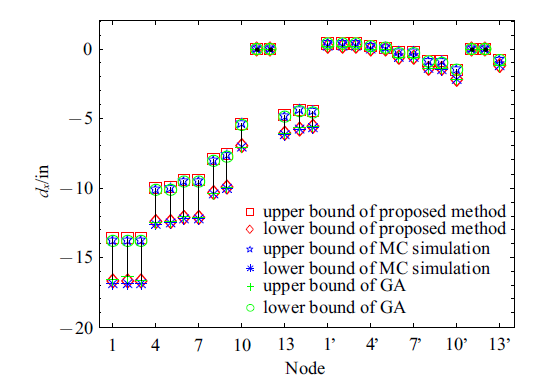新窗口打开|下载原图ZIP|生成PPT图 9沿$x$轴方向位移的上下边界值
Fig. 9Displacement bounds in the direction $x$
图 10
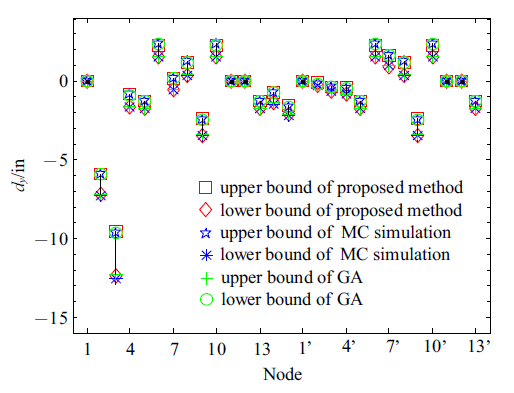新窗口打开|下载原图ZIP|生成PPT图 10沿$y$轴方向位移的上下边界值
Fig. 10Displacement bounds in the direction $y$
图 11
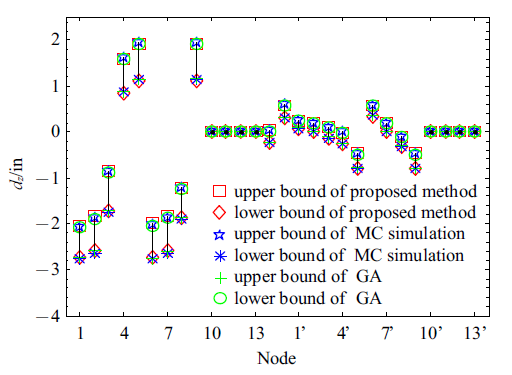新窗口打开|下载原图ZIP|生成PPT图 11沿$z$轴方向位移的上下边界值
Fig. 11Displacement bounds in the direction $z$
4 结论
本文针对可线性分解式区间有限元问题, 提出了一种基于Neumann级数的区间有限元方法. 通过对弹性模量不确定情况下的连续体结构进行举例分析, 推导得到了其可线性分解式区间有限元的具体形式. 对于工程实际中普遍存在的此类可线性分解式区间有限元问题, 采用Neumann级数对区间刚度矩阵的逆矩阵进行表示, 可获得结构响应关于区间变量的显式表达式, 从而便于后续对结构响应上下边界的求解. 根据Neumann级数的收敛条件给出了区间有限元求解方法收敛的充分不必要条件, 并给出了所求结构响应的相对误差. 通过两个算例对所本文方法的可行性与有效性进行了验证. 结果表明, 本文基于Neumann级数的区间有限元方法在进行结构响应边界分析时具有较好的求解效率和求解精度.附录
区间有限元的Monte Carlo 模拟(MCS)方法借助于Monte Carlo模拟方法的思想, 通过对区间参数进行大量抽样并进行确定性有限元分析, 并根据响应集合的极值确定响应边界. 其具体步骤如下:(1) 获取结构区间参数的上下边界;
(2) 在$m$维超立方体中按均匀分布抽取区间变量样本, 共抽取$N_s$组样本点;
(3) 根据所抽取的样本点确定结构的全局刚度矩阵, 进行确定性有限元分析求解平衡方程(2)获得结构位移响应; 重复该过程, 遍历所有样本变量, 获得结构位移响应的集合;
(4) 根据结构位移响应的集合判断出各单元节点位移响应的最大值与最小值, 从而构成结构位移响应的上边界和下边界.
注: 由上述步骤2中抽取的样本将均匀分布在$m$维超立方体范围内. 实际上, 也可以在抽样中使用任何其他分布形式获得样本, 唯一的要求是要确保可以获得$m$维超立方体范围内的任何点.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
DOIURL
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
The objective of this paper is to give a general overview of recent research activities on non-probabilistic finite element analysis and its application for the representation of parametric uncertainty in applied mechanics. The overview focuses on interval as well as fuzzy uncertainty treatment in finite element analysis. Since the interval finite element problem forms the core of a fuzzy analysis, the paper first discusses the problem of finding output ranges of classical deterministic finite element problems where uncertain physical parameters are described by interval quantities. Different finite element analysis types will be considered. The paper gives an overview of the current state-of-the-art of interval techniques available from literature, focussing on methodological as well as practical aspects of the presented methods when their application in an industrial context is envisaged. Their possible value in the framework of applied mechanics is discussed as well. The paper then gives an overview of recent developments in the extension of the interval methods towards fuzzy finite element analysis. Recent developments in the framework of the transformation method as well as optimisation-based procedures are discussed, Finally, the paper concentrates specifically on implementation strategies for the application of the interval and fuzzy finite element method to large FE problems. (C) 2010 Elsevier B.V.
[本文引用: 1]
[本文引用: 1]
[本文引用: 5]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
//
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 3]
DOIURL [本文引用: 3]
Evidence theory has a strong ability to deal with epistemic uncertainty, based on which the imprecise parameters with limited information can be conveniently treated. In this paper, a numerical method is developed to compute the linear elastic static and dynamic responses of structures with epistemic uncertainty based on evidence theory. Inspired by the moment concept in probability theory, the Raw Moments, Central Moments and Mixed Central Moments are proposed to describe the distribution characteristics of evidence variables, and the corresponding moments of functions with evidence variables are also defined. By integrating the moment concept and finite element method, a linear elastic static and dynamic response analysis technique is formulated to compute the moments of uncertain structural responses. To reduce the computational cost, the interval analysis techniqueis adopted to obtain the approximate response bounds for each focal element. Three numerical examples are investigated to demonstrate the effectiveness of the present method. (C) 2013 Elsevier B.V.
