,*,2)天津大学化工学院, 化学工程联合国家重点实验室, 天津 300072SELF-ASSEMBLY OF BUBBLE SWARM IN LARGE CAVITIES IN STEP-TYPE PARALLELIZED MICROCHANNELS AND ITS FEEDBACK ON BUBBLE FORMATION 1)
Zhang Zhiwei, Yin Xiangyu, Zhu Chunying, Ma Youguang, Fu Taotao,*,2)State Key Laboratory of Chemical Engineering, School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China通讯作者: 2)付涛涛，副教授，主要研究方向：微流体与界面现象、多相流、复杂流体. E-mail:ttfu@tju.edu.cn.
收稿日期:2019-09-6接受日期:2020-01-17网络出版日期:2020-03-18
| 基金资助: |
Received:2019-09-6Accepted:2020-01-17Online:2020-03-18
作者简介 About authors
摘要
台阶式微通道乳化装置因易于高通量生产均一性的气泡及液滴而受到关注.本文利用高速摄像仪研究了台阶式并行微通道装置空腔内的气泡群复杂行为及其对气泡生成的反馈效应.实验设计的操作变量为气液相进出口位置、气相流速和液相流速. 在实验操作范围内,共发现了气泡的单管生成模式和多管生成模式.研究了空腔内气泡群复杂行为随操作条件的变化趋势. 发现在受限空间内,气泡在水平面内发生挤压堵塞能够自组装成具有特定几何特点的二维晶格,分别为有序的行三角晶格、有序的竖三角晶格和无序的三角晶格.晶格结构与气相压力密切相关; 同时, 气泡界面能量随着气相压力的增大而增大.运用介尺度、能量和活化等概念分析了气泡群复杂行为对气泡生成方式的影响,充分阐释了受限空间内气泡群的介尺度效应.以变异系数CV来表示气泡的均匀性特征, 考察了气泡晶格自组装行为的控制因素.结果表明: 气泡的自组装路径由气泡尺寸及其分布决定,有序的三角晶格变异系数小于5%, 无序的三角晶格变异系数大于5%.
关键词：
Abstract
Step-emulsification microfluidic devices attract attentions due to the ability for the high-throughput production of bubbles and droplets. In this study, the bubble behavior of the bubble swarm in the cavity in a step-type parallelized microchannel and its feedback effect on bubble formation were studied by using a high-speed camera. The operating variables were the position of gas/liquid phase inlet, gas flow rate and liquid flow rate. Two bubble generation modes were observed: single-tube generation mode and multi-tube generation mode. The variation trend of the complex behavior of bubble swarm in the cavity with operating conditions was studied. It is found that in the confined space, the bubble can be self-assembled into a two-dimensional lattice with geometric features in the horizontal plane: including an ordered row triangular lattice, an ordered vertical triangular lattice, and a disordered triangular lattice. As the gas pressure changes, the crystal lattice changes, the bubble surface area becomes larger, and the interfacial energy becomes larger. Then, the effects of complex behavior of bubble swarm on bubble generation were analyzed by using the concepts of mesoscale, energy and activation. These fully explain the mesoscale characteristics of bubble behavior in confined spaces. The determinants of the bubble self-assembly path are revealed. It is indicated that the self-assembly path of bubbles is determined by the size and distribution of bubbles. The coefficient of variation of CV is used to represent the crystal structure of bubbles, and the coefficient of variation for the ordered triangular lattice is less than 5%, while that for the disordered triangular lattice is greater than 5%.
Keywords：
PDF (26827KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张志伟, 殷翔宇, 朱春英, 马友光, 付涛涛. 台阶式并行微通道内气泡群自组装行为及其对气泡生成的反馈效应 1). 力学学报[J], 2020, 52(2): 420-430 DOI:10.6052/0459-1879-19-251
Zhang Zhiwei, Yin Xiangyu, Zhu Chunying, Ma Youguang, Fu Taotao.
引言
近年来, 微化工技术逐渐成为化学工程新的发展方向[1-5].由于设备尺寸显著减小, 相比于传统的化工技术,微化工系统具有放大效应小、集成度高、安全性高、可控性强、以及节能环保等优点[6-10].微通道内两相流中的典型应用包括微颗粒合成[11-12]、液相氧化[13]、加氢[14]、直接氟化[15]以及液-液萃取[16]等.气液两相流中分散体系的形成、演化与构型对于传热传质以及反应过程具有重要的作用.目前,对于单微通道内气泡生成、流动、破裂及聚并规律有了较为良好的工作基础[17-19],人们希望通过微通道数目放大使微化工技术走向工业化,期待并行多通道内多相流特性彼此一致且无放大效应[20].其中最常用的微通道为T形结构和聚焦结构, 这两种结构可用于生成尺寸为10 $\mu$m数量级的均匀分散体系[21]. 然而,这两种微通道装置构型都属于二维平面结构,其内生成的气泡或液滴尺寸受流体物性参数影响较大,不能独立控制气泡尺寸和生产频率. 另一种台阶型的2.5D结构打破了二维结构的限制,实现了分散体系的尺寸和生产频率的独立控制[22].Alessandro等[23]设计的台阶式乳化装置实现了液滴尺寸仅由台阶尺寸控制,而不受其他操作变量的控制.Stoffel等[24]设计了具有256个可并联工作的台阶式微通道组装成的微流控气泡制造装置,对于单个微通道, 生产频率高达4 kHz、变异系数小于1%,但气泡尺寸受气液相物性参数的影响较大, 并不完全由台阶尺寸控制. 研究发现,在台阶式并行放大系统中, 不同微通道间的流体动力学相互影响和耦合. 因此,台阶式并行微通道内气泡生成机理较为复杂.
国内外****探索了微通道受限空间内气泡群的自组装行为及动力学反馈效应.研究发现, 具有几何排列特点的微气泡/液滴群通过固化措施,可组装成新的固体超材料[25-26],在声子晶体、光子学、和过滤等领域具有潜在的应用价值.自组装液滴和气泡作为研究非平衡自组装和多相系统的简单平台,引起了人们的广泛关注[27-28].Raven等[29]发现泡沫的形成过程是具有记忆的,可用于生成具有可控和潜在可调多分散性的泡沫聚集体.Pravien等[30]研究了微流体液滴在轴向高度梯度微通道引导下可调谐自组装成三维有序阵列的过程,适用于具有三维形貌的复杂材料的连续合成.赵等[31]利用微通道技术进行多晶型的调控方法.Sharon等[32]研制出具有广泛应用背景的泡沫或乳液结构的设计标准.对于台阶式微通道而言,下游空腔内气泡群的复杂行为势必对气泡生成的产生反馈效应. 因此,亟需阐释并行微通道主通道中气泡群动力学及其对气泡生成的反馈机制.
本文研究了台阶式并行微通道装置中空腔内气泡群的自组装规律以及气泡群复杂行为对气泡生成的反馈机制,以期为台阶式微通道内多相流的研究及化工领域的并行放大过程提供一定的理论指导.
1 实验材料和方法
1.1 实验材料
气相采用氮气, 液相采用重量百分浓度0.3%的十二烷基硫酸钠(SDS)溶液.液相由固体十二烷基硫酸钠(SDS)(Aladdin, China)和纯净水(WAHAHA,China)配置而成. 加入表面活性剂, 目的是改变液、固之间的润湿程度,防止气泡黏壁, 并通过吸附于气液界面而改变界面特性, 在一定程度上阻碍气泡聚并.流体的物性参数如表1所示, 其中黏度由乌式毛细管黏度计测量,表面张力通过悬滴法由表面张力仪(KINO Industry Co., Ltd, SL200KB, USA)测得.Table 1
表1
表1实验所用流体的物性参数
Table 1
 |
新窗口打开|下载CSV
1.2 实验方法
实验装置分为流体控制设备、微通道芯片、图像采集设备3部分. 实验流程如图1所示. 氮气由钢瓶供给, 通过不锈钢管输送, 气相流量通过高精度的配气装置 (Gas distribution device, AZ-S/E-2-201805-05, China)控制. 在微通道装置的气体入口处连接差压变送器(Honeywell, STD800, America, 0$\sim$200 kPa $\times $ 0.025%), 测量气相入口与通道出口间的压差, 并采用无纸记录仪(SIN-R9600, China)实时记录压差变化. 液相用蠕动泵(Lander, BT100-1F/YZ1515X, Baoding, 0.27 $\pm$ 0.002 ml/min$\sim$162 $\pm$ 0.002 ml/min)通过聚乙烯胶管注入微通道. 微通道内气泡的生成过程以及流动状况通过连接显微放大镜(Tamron, SP AF90mmF/2.8 Di, Japan)的高速摄像仪(Photonfoucs MV2-1280-640-CL-8, Switzerland)记录, 本实验过程中拍摄帧率设为500 fps, 采集视窗大小为1280 $\times$ 1024, 数据采集过程中采用冷光源(FJI, FJI-AS100100-W, China)进行照明. 实验在常温常压条件下进行.图1
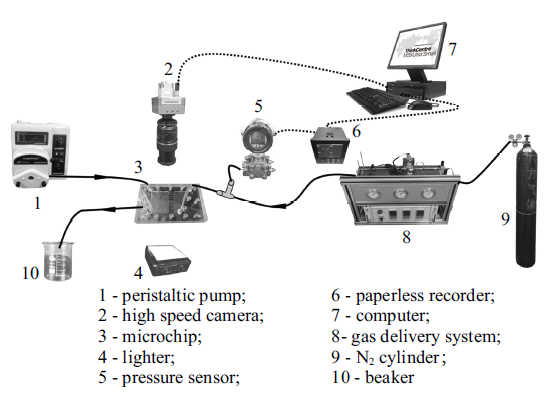新窗口打开|下载原图ZIP|生成PPT图1实验流程图
Fig. 1Diagram of experimental procedure
本实验采用的微通道由两块大小相同的聚甲基丙烯酸甲酯(PMMA)平板组成,其中下板使用精密铣床加工出通道及台阶结构, 上下板使用螺钉进行固定.图2为装置结构示意图, 分为气相缓冲腔、微通道、台阶结构、气泡收集腔、气液进出口共5个部分.气相缓冲区设置斜边的目的是优化气相分配, 当气相入口为尖端口时,可以有效防止气相缓冲区内出现死区. 其中微通道宽0.6 mm, 深0.4 mm, 间隔3.0 mm,共10条通道; 台阶宽1.2 mm, 深2.0 mm; 气体缓冲区深度为1 mm; 气泡收集区深度为2 mm;气液进口均为1.2 mm. 微通道装置组装完成后的实物为图2(d).
图2
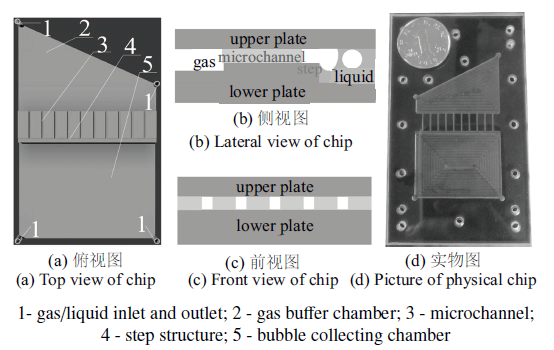新窗口打开|下载原图ZIP|生成PPT图2微通道装置图
Fig. 2Microchannel device diagram
根据气相进样位置以及气液相相对方向, 本装置共有4种进样方式, 如图3所示.对于每种进样方式, 需要保留一个气相入口并使用止水夹夹住另一个气相入口,以防漏气. 实验过程中未出现漏液等现象.本文对4种进样方式分别进行实验采集数据, 通过比较进行分析.
图3
新窗口打开|下载原图ZIP|生成PPT图34种进样方式示意图
Fig. 3Schematic diagram of four injection modes
2 实验结果与讨论
2.1 气泡生成方式
在本文采用的并行微通道体系中, 出现了两种气泡生成方式,分别为单管生成系统和多管生成系统. 如图4(a)所示,单管生成系统并不是仅有一个固定位置的通道生成气泡,而是当气泡的生成位置由一个通道转换为另一个通道的时间间隔大于2 s时,可以认为气泡能够在一个通道稳定的生成. 如图4(b)所示, 在多管生成系统中,很难实现在多个通道中共同生成气泡, 气泡是由两个或是多个通道交替生成,通道之间转化的时间间隔小于2 s.如图5所示, 随液相流率增大, 气泡依次出现单管生成模式和多管生成模式.由图5(a)和图5(c)可知, 当气相进样位置为装置尖端时,气泡的单管生成方式和近似双管生成方式之间存在一条线性转变线;由图5(b)和图5(d)可知, 当气相进样位置不是装置尖端时,两种生成方式之间不存在线性转变规律. 由此可知,气相的进样位置决定了生成方式之间的转化特点, 当气相缓冲区内无死区时,气相生成方式的转化规律更具可控性. 由图5(b)和图5(d)可知,单管生成模式与多管生成模式之间没有明显的转化规律,故气相缓冲腔内的气相分配不均匀性使得调控性能变差.
图4
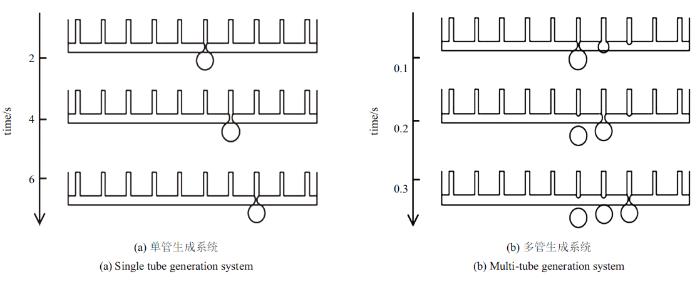新窗口打开|下载原图ZIP|生成PPT图4气泡生成方式示意图
Fig. 4Schematic diagram of four bubble generation modes
图5
新窗口打开|下载原图ZIP|生成PPT图5不同进样方式下气泡生成方式随操作变量的变化趋势图
Fig. 5Dependence of bubble generation type with operating variables under different injection modes
图5
新窗口打开|下载原图ZIP|生成PPT图5不同进样方式下气泡生成方式随操作变量的变化趋势图(续)
Fig. 5Dependence of bubble generation type with operating variables under different injection modes (continued)
2.2 空腔内气泡自组装行为
2.2.1 气泡二维晶格的自组装由于气泡或液滴大小近似相同, 它们可自发地自组装成有序的晶格,称为微流体晶体[33-36]. 在本实验中, 当分散相体积分数较高时,气泡在水平面内发生挤压堵塞并自组装成二维晶格[29],Whitesides等[33]在非稳态泡沫的流动晶体时发现,气泡群多数自组装为一种独特的结构: 菱形或六边形. 在本文中,这种特殊的结构可以进一步拆分为多个三角形. 如图6(a)所示,根据气泡的结构特点和排列方式可以将晶格分为3种,分别为有序的竖三角晶格、行三角晶格和无序的三角晶格.
Parthiban等[30]在三维空间的液滴自组装行为的实验中得到自组装结构由液滴大小、液滴体积分数、微通道尺寸和液滴组装方式等共同决定.在本实验中, 通过改变气液相流量观察气泡收集腔内晶体结构的变化. 如图6(b)所示, 空腔内气泡群排列紧密, 从通道的气泡生成位置到空腔的气泡出口位置这段紧密相连气泡, 可以近似看作是连续的整体, 定义为气泡进--出段,则气泡进--出段压降近似等于气相测得的表压.
当调节液相流量时, 晶体结构也会发生变化, 据实验观察得到,类型1和类型2晶格变化趋势相同, 类型3和类型4晶格变化趋势相同.如图6(b)所示, 当进样方式为类型1时, 随着液相流量的增大,气泡流区的晶格变化分为两个阶段: 第一阶段, 与上述的气相流量的变化相类似,气泡流区内有序的行三角晶格随着液相流量的增大而减小,当气泡流区内不存在死区时, 有序的行三角晶格消失,气泡流区内主要为有序的竖三角晶格和无序的三角晶格, 此阶段气泡都呈现紧密排列;第二阶段, 随着液相流量的进一步增大, 气泡流区内的有序竖三角晶格逐渐消失,无序的三角晶格占据整个空腔, 气泡流区由紧密排列方式转化为杂乱松散的排列.纯液相区域的面积随着液相流量的增大而增大,气泡的生成位置一直集中在气泡流区内,进一步佐证了气泡流区内的阻力要远小于纯液相区的阻力. 气相压力的增大,气泡流区由多种晶格共存转变为竖三角晶格和无序的三角晶格.气泡排列的规律性与气泡在空腔内的体积分率$\varPhi$成正相关. $\varPhi$越大, 气泡排列的越规律; $\varPhi$越小, 气泡填充的越杂乱[33]. 如图6(c)所示, 当进样方式为类型3时, 随着液相流量的增大, 气泡流区气泡由相互挤压转变为杂乱松散, 由多种晶格共存转变为无序的晶格;随着气相压力的增大, 气泡体积增大, 气泡无法随着液相流动及时排出,气泡由多种晶格共存转变为无序的三角晶格.
图6
新窗口打开|下载原图ZIP|生成PPT图6气泡流区的晶格随操作变量的变化趋势
Fig. 6The change of the lattice in the bubble flow region with the operating variables
图6
新窗口打开|下载原图ZIP|生成PPT图6气泡流区的晶格随操作变量的变化趋势(续)
Fig. 6The change of the lattice in the bubble flow region with the operating variables (continued)
利用图像分析方法, 得到气泡进-出段气泡上界面的椭圆率在0.6$\sim$0.7之间,所以气泡形状不能近似看作圆柱, 空腔内气泡上下表面的形状近似为椭圆[32]. 气泡的表面积$A$ 为可由式(1)计算, 表达式如下
式中, $a$为气泡上下椭圆面长轴, $b$为气泡上下椭圆面短轴, $h$为空腔高度.
如图6(b)所示, 随着气相压力的增大, 气泡进--出段压降变大, 气泡特征尺寸变大,即$A$变大, 气泡流区内的死区面积减小, 有序的行三角晶格区域减小;当压降升至4 kPa时, 有序的行三角晶格消失, 气泡流区内主要为有序的竖三角晶格.由式(2)求得气泡界面能$E$[37]
式中, $\sigma $为表面张力, $A$为气泡表面积. 如图7(a)所示, 当进样方式为类型一时,随着气泡进-出段压降的增大, 气泡体积增大, 界面能随之增大,当界面能$E$增大到一定数值时, 气泡流区内无行三角晶格. 当压降相同时,界面能随着液相流量的增大而降低,气泡流区内达到稳定的三角晶格界面能也随之降低. 如图7(b)所示,当进样方式为类型3时, 随着气泡进--出段压降的增大, 气泡体积增大,界面能随之增大, 当界面能$E$增大到一定数值时, 气泡流区内为无序的三角晶格.当压降相同时, 界面能随着液相流量的增大而降低,气泡流区内转变为无序的三角晶格的界面能也随之降低.
图7
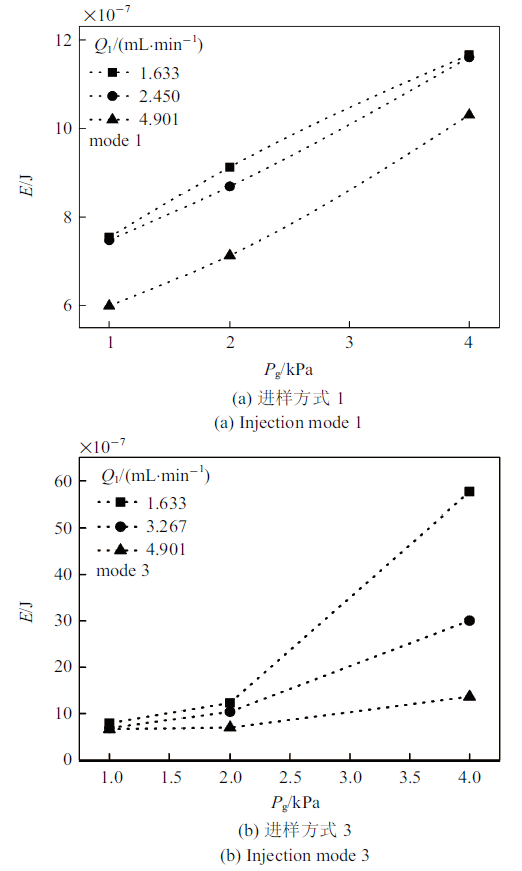新窗口打开|下载原图ZIP|生成PPT图7气泡界面能随操作变量的变化规律
Fig. 7The change of interfacial energy of bubble with operating variables
Raven等[29]在探究两相流稳定性的实验中发现,通道内的气泡晶格会随着气相流量的波动而出现周期震荡,这种震荡取决于下游的气泡体积和泡沫结构演变产生的阻力. 因此,新泡沫的体积与其前身有关, 泡沫的形成过程是有记忆的. 在本实验中,在固定操作变量的情况下, 随着时间的推移, 三种晶体结构呈现出此消彼长的趋势.但在气泡流动区域, 气泡群呈现出有序的竖三角晶格, 简称竖三角晶格;在气泡稳定区域, 气泡自组装成有序的行三角晶格, 简称行三角晶格;在这两种晶格之间存在一无序的三角晶格的过渡区域, 如图8(a)所示.以气泡1为示踪气泡来观察行三角晶格随时间的变化趋势, 0$\sim$7.85 s这段时间内,气泡1未发生移动, 从而可以得到在低气液相流速的情况下,远离气泡出口的行三角晶格区域不随着时间的变化而移动, 为气泡流区域的死区.以气泡2, 3, 4三个气泡来示踪有序的行三角晶格的自组装过程, 在0 s时,三个气泡贴着台阶壁排列, 在受限空间内受液相推动力和气泡群的挤压力的影响,贴着行三角晶格区域的边缘移动. 在7.85 s时, 气泡2、气泡3和气泡4依次补足空位,呈现出有序的行三角晶格排列.
图8
新窗口打开|下载原图ZIP|生成PPT图8气泡收集腔内晶体结构随时间的变化趋势(进样方式一)
Fig. 8Evolution of crystal structure in bubble collection cavity (mode 1 of injection)
图8(b)为竖三角晶格占气泡收集腔的比例随时间的变化趋势图, 竖三角晶格的占比数随着时间的推移呈现出上下波动的趋势, 具有一定的周期性,晶格流动变化过程中会由一个最大值波动至另一个最大值, 取两个最大峰值之间的时间段为一个周期, 如图8(b)所示, 0.167$\sim$5.167 s可以看作一个周期, 其中一个周期内竖三角晶格占比的最大值稳定在0.27$\sim$0.30之间. 由此可知, 气泡群在有限空间内的变化组装过程并不是无序的, 而具有一定的周期性变化. 从界面能量的角度来讲, 空腔内晶格演化的周期性特征也是系统不断调整变化以降低自身能量的过程[33].
2.2.2 气泡的自组装行为的决定因素
Raven等[29]在研究不平衡泡沫结构的流动晶体时发现, 不同晶格中的气泡尺寸不同. 在本实验中, 当空腔内气泡群紧密排列时, 气泡尺寸是决定气泡自组装路径的关键因素. 如图9所示, 气泡I的尺寸大于其受力两侧的气泡, 气泡的前端超出两侧气泡,使得气泡I在气泡群挤压运动的过程中, 前后两端受到不平衡的挤压力, 后端的挤压力远大于前端的挤压力, 气泡I被挤出. 气泡II在0.63 s时受到与I气泡相同的不平衡力, 开始重复气泡I的过程, 到0.79 s时被挤出. 当气泡受力两侧的气泡尺寸差异不大时, 气泡呈现出有序的排列方式, 即有序的行、列三角晶格; 当气泡与受力两侧的气泡尺寸差别较大时, 气泡受周边不平衡的挤压力, 使其找寻能够与自身形成局部最小界面能的位置, 即受力两侧气泡尺寸相近的位置. 气泡在非平衡力作用下移动过程使其周围呈现出无序的三角晶格.
图9
新窗口打开|下载原图ZIP|生成PPT图9气泡收集腔内气泡路径演化图
Fig. 9Diagram of bubble path in bubble collection cavity (mode 3): ($P_{\rm g}=1$ kPa, $Q_{\rm l}=1.633$ mL/min)
由上述可知, 气泡尺寸的均一性能有效的预测晶体结构,将上述有序的行三角晶格和有序的列三角晶格定义为有序的三角晶格.引入变异系数$CV$ [37], 定量分析不同晶体结构下气泡尺寸的分散性.选取有序三角晶格和无序三角晶格进行变异系数$CV$的计算. 其中,行三角晶格选取单行气泡进行计算, 列三角晶格选取单列进行计算,无序三角晶格选取无序排列的区域进行变异系数$CV$的计算.$CV$定义为气泡二维平面直径的标准差与平均值之比
式中, $\bar{D}$为气泡平均直径. 一般认为, 变异系数$CV\leqslant5$%时, 气泡的均匀性好.将$CV=5$%作为气泡单分散性较好的基准线, 如图10(a)所示,将各个操作变量下的有序晶格和无序晶格进行数据处理, 结果表明:在实验操作变量区间内, 当变异系数$CV>5$%时, 气泡自组装成无序的三角晶格;变异系数$CV<5$%时, 气泡呈现出有序的三角晶格.进一步佐证了气泡的尺寸是决定大空腔内气泡自组装路径的关键因素.
图10
新窗口打开|下载原图ZIP|生成PPT图10不同操作变量下的晶格转变图
Fig. 10Diagram of lattice transition with different operating variables
在本实验中, 为确定不同晶格的界面能量波动趋势, 将气泡表面积简化$A\propto D^{2}$, 此时, 波动界面能量为
如图10(b)所示, $\Delta E=4.72\times 10^{-8}$ J为有序晶格与无序晶格的分界线, 当$\Delta E>4.72\times 10^{-8}$ J时,气泡自组装为无序的三角晶格, 当$\Delta E<4.72\times 10^{-8}$ J时,气泡自组装为有序的三角晶格.
气泡/液滴属于软物质的范畴, 其晶格排列机制与固体颗粒之间的排列机制不甚相同.软物质的动力学效应和熵效应不容忽视,故软物质自组装行为通常比硬物质的自组装行为更为复杂[38]. 然而,软/硬物质的自组装晶格的变化规律由微粒间的排斥力、吸引力以及外力的共同作用决定[39]. 因此, 软物质可发挥可视化优势, 在一定程度上揭示自组装机制.固体微粒的形状不易受外力的影响而发生变化. 故在固体晶格的形成过程中,固体微粒的形状以及尺寸的均一性也是影响自组装变化规律的一个关键因素.
在本文中, 当空腔内液含率较高时, 气泡在二维平面内呈现出圆形的湿泡沫;当空腔内液含率极低时, 气泡彼此挤压相连, 呈现出不规则多边形的干泡沫.干泡沫的泡沫边界遵循Plateau定律,即相邻的三个气泡膜总以相同的角度交于一点[29]. 值得一提的是,表面活性剂的种类会影响泡沫的晶格排列方式. 泡沫晶格的自组装行为,可以理解为外加应力与屈服应力共同作用的结果[40]. 在湿泡沫中,局部宏观应力受气相压力、气泡体积、气泡总数以及表面张力的控制,不同的表面活性剂会导致局部宏观应力发生变化, 进而影响泡沫的排列方式.而在干泡沫中, 泡沫之间的排水效应会造成的气泡液膜破裂并发生聚并,这种现象的边界流动条件主要取决于表面活性剂的种类以及浓度. 因此,表面活性剂的种类会影响到气泡自组装的变化规律[40].目前对台阶式微流控装置内气泡生成的研究较少,未涉及到表面活性剂种类对气泡生成尺寸及晶格的作用机制.探索表面活性剂对气泡均一性的作用机制, 是一个亟需解决的问题.
2.2.3 空腔内气泡群复杂行为的影响因素
对于台阶式并行微通道系统,影响台阶处气泡生成过程的因素不仅包括气相与液相的单相流体特性以及并行微通道内流体均匀性问题,还包括管道之间多相流的耦合效应以及下游多相流对上游的反馈效应[24].本实验中, 发现了空腔内气泡群的复杂行为在很大程度上影响气泡的生成方式.实验中多相流体系表现为液相中分散的气泡, 称为气泡流. 对于气泡流,存在着液相对气相的分散作用, 也存在气泡群内部的相互作用,这两种作用在系统中呈现动态竞争及协调关系, 具有动态时空的介尺度特征.
如图11(a)和图11(b)所示, 当进样方式为类型1和类型2时,气泡收集腔内因液相的滞留形成无气泡的液相区和气液两相区. 当液相流量较小时,气泡排列紧密为多种晶格, 此时可发现气泡主要由两相区最边缘的单个微通道生成,称作活化单空隙[41], 气泡的生成方式为单管生成系统.此时气泡流两相区形成了一个相对独立的体系,液相区的压力需要通过气泡的接触挤压传递至两相区. 由于气泡具有较好的压缩性,压力的传递具有损耗, 因此从与液相接触的最外层气泡至内层气泡, 压力逐渐降低,在最边缘处的通道出口处气液两相流的压力达到最低,故气泡更倾向于在该阻力最小位置生成. 当液相流量逐渐增大,空腔内气泡排列松散杂乱, 随着气泡群内部结构的动态演化过程,使得台阶处最小阻力点呈现动态特征, 导致活化单孔隙增多, 且位置随机变化,气泡的生成方式转化为多管生成模式.
如图11(c)和图11(d)所示, 当进样方式为类型3和类型4时, 气泡收集腔内为气液两相区.当液相流量较低时, 液相推动力较低, 气泡无法快速移出, 气泡群排列紧密,气泡群之间的相互所用占据优势, 此时气泡的生成方式主要为单管生成系统;当液相流量增大时, 液相推动力变大, 气泡移出速度较快, 气泡排列松散杂乱,空腔内液相推动力占据主要作用, 气泡的生成方式转化为多管生成模式.生成方式的转化原因与类型1和类型2相同.
图11
新窗口打开|下载原图ZIP|生成PPT图11操作变量对气泡群的影响
Fig. 11Effects of operating variables on bubble swarm
3 结论
本文研究了台阶式微通道装置大空腔内气泡群自组装规律及其对气泡生成的反馈效应,探究了气泡自组装晶格随操作条件的变化规律, 获得了如下主要结论:
(1)实验发现了两种气泡生成方式, 分别为单管生成模式和多管生成模式.发现了气泡生成方式的类型由气相缓冲腔内的气相流动性能决定的机制:进样方式1、方式3在生成方式转化过程中具有明显的线性转化分界线,气泡的生成方式转化更具可控性; 进样方式2、方式4无线性转化分界线.
(2)发现了液相进样位置决定了空腔内气泡群晶格随操作变量转化的特点.在受限空间内, 气泡在水平面内发生挤压堵塞能够自组装成具有几何特点的二维晶格,分别为有序的行三角晶格、有序的竖三角晶格和无序的三角晶格.竖三角晶格只存在于流动区域; 行三角晶格在进样方式1、方式2中存在于稳定区域,在进样方式1、方式4中无此规律;无序三角晶格分布在竖三角晶格和行三角晶格之间以及气泡流区的边界区域.气泡群的排列方式与液相流量有关: 在较低液相流量下, 气泡群排列紧密;而在较大液相流量下, 气泡群排列松散杂乱. 随着气相压力的改变, 晶格会发生变化,气泡表面积和界面能量会随着气相压力的变大而变大.
(3)研究了气泡自组装路径的决定性因素.发现气泡的自组装路径由气泡尺寸及其分布决定.以变异系数 CV 表示气泡的晶体结构特征, 发现有序的三角晶格情况下,变异系数小于5%; 而无序的三角晶格情况下, 变异系数大于5%.分析了空腔内复杂界面的介尺度行为对气泡生成的反馈效应.本文结果对台阶式微通道内多相流动力学及其并行放大规律具有重要的参考价值和指导意义.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 5]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 4]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
