颗粒毛细效应影响因素的离散元分析 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

张华腾, 凡凤仙^,²⁾, 王志强上海理工大学上海市动力工程多相流动与传热重点实验室, 上海 200093

DEM ANALYSIS OF FACTORS INFLUENCING THE GRANULAR CAPILLARITY ¹⁾

Zhang Huateng, Fan Fengxian^,²⁾, Wang ZhiqiangShanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China

通讯作者: 2)凡凤仙, 副教授, 主要研究方向: 多相流与颗粒流. E-mail:fanfengxian@usst.edu.cn

收稿日期:2019-10-30接受日期:2020-03-4网络出版日期:2020-03-18

基金资助:

1)国家自然科学基金.51976130
上海市科委科研计划.13DZ2260900

Received:2019-10-30Accepted:2020-03-4Online:2020-03-18
作者简介 About authors

摘要
颗粒毛细效应是指将一根细管插入填充有颗粒物质的容器中并对管施加竖直振动时颗粒在管内上升并最终达到一个稳定的高度的现象, 该现象为颗粒物料的逆重力输运提供了一种潜在的技术途径. 为探究颗粒毛细效应的影响因素, 采用离散元方法, 模拟再现了颗粒毛细效应过程,展示了不同管径下颗粒竖直方向速度演变特性, 考察了不同容器宽度和振动条件下颗粒最终毛细上升高度随管径的演变规律. 结果表明, 在容器宽度与粒径比为40、管振幅与粒径比为14.33、管振动频率为12 Hz情况下, 管径与粒径比$D/d = 3.33$时, 管内颗粒堵塞严重, 使得颗粒上升缓慢,并造成颗粒柱中断; $D/d = 8.33$时, 起初毛细上升高度增加迅速, 随后毛细上升高度的增大逐渐减缓, 管内颗粒在管径方向几乎不存在速度梯度; $D/d =15$时, 随着颗粒毛细上升高度的增大, 管内颗粒柱分离为速度截然不同的两层, 上层颗粒在管径方向几乎不存在速度梯度, 而下层颗粒存在明显的速度梯度.研究还发现, 在毛细效应能够发生的管径范围内, 存在一个对应于颗粒最终毛细上升高度最大值的临界管径, 当管径小于临界管径时, 颗粒最终毛细上升高度随管径的增大而增大, 当管径大于临界管径时, 颗粒最终毛细上升高度随管径的增大而趋于减小; 增大容器宽度,临界管径有所增大; 增大振幅、适当提高频率能够有效促进临界管径的增大.
关键词： 颗粒物质;毛细效应;竖直振动;离散元方法;颗粒输运

Abstract
Granular capillarity refers to the phenomenon that when a narrow tube is vertically inserted into a container filled with particles and then set into vertical vibration, the particles rise up along the tube and eventually reach a certain height. This provides a potential technical method for the transportation of granular materials against gravity. To explore the factors influencing the granular capillarity, the processes of granular capillarity were numerically investigated using the discrete element method (DEM). On this basis, the evolutions of vertical velocities of particles at different tube diameters were shown, and the dependences of the final capillary height of the particles on the tube diameter at different container widths and vibrational parameters were examined. The results obtained under the conditions with the container-width-to-particle-diameter ratio of 40, vibration-amplitude-to-particle-diameter ratio of 14.33 and vibration frequency of 12 Hz show that at the tube-to-particle diameter ratio $D/d = 3.33$ severe jamming occurs for the particles in the tube, which makes the particles rise slowly and leads to a discontinuous granular column within the tube. At $D/d = 8.33$, the granular capillary height rises rapidly at the beginning, and then the increasing rate of the capillary height decreases gradually. In this case, there is almost no particle velocity gradient along the tube radius. However, at $D/d=15$, as the granular column height within the tube increases, the particles in the tube separated into two layers. In the upper layer, almost no particle velocity gradient along the tube radius is observed, whereas in the lower layer obvious velocity gradient can be found. It is also found that for the tube diameter range in which the granular capillarity can occur, there exists a critical tube diameter that corresponds to the maximal final capillary height. When the tube diameter is less than the critical tube diameter, the final capillary height increases with the tube diameter, whereas when the tube size is greater than the critical tube diameter, the final capillary height tends to decrease with the tube diameter. Moreover, increasing the container width leads to an increase in the critical tube diameter, while increasing the vibration amplitude of the tube and appropriately increasing the vibration frequency can effectively promote the increase of the critical tube diameter.
Keywords：granular matter;capillary effect;vertical vibration;discrete element method;particle transportation

PDF (7664KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
张华腾, 凡凤仙, 王志强. 颗粒毛细效应影响因素的离散元分析 ¹⁾. 力学学报[J], 2020, 52(2): 442-450 DOI:10.6052/0459-1879-19-301
Zhang Huateng, Fan Fengxian, Wang Zhiqiang. DEM ANALYSIS OF FACTORS INFLUENCING THE GRANULAR CAPILLARITY ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(2): 442-450 DOI:10.6052/0459-1879-19-301

引言

在外加扰动作用下颗粒物质的敏感性和非线性响应等使得颗粒物质表现出复杂而奇特的动力学行为, 日益吸引着不同领域科研工作者的兴趣^[1-6]. 近几年, 文献报道了颗粒的毛细效应^[4-6], 即将一根细管插入填充有颗粒物质的容器中并对管施加竖直振动时, 颗粒物质在管内迅速上升并最终达到一个稳定的高度的现象. 该现象为实现颗粒物料的逆重力输送提供了一种潜在的技术途径, 引起了研究者的高度关注.

自Liu等^[7]对颗粒毛细效应进行实验报道以来, 研究者迅速开展了针对颗粒毛细效应的实验、理论和数值模拟研究. 首先, 在实验研究方面,获得了管振动强度、振幅、频率、管插入深度、管口形状、管内颗粒填充高度、间隙气体、管内径、管截面形状、颗粒直径对颗粒上升高度的影响^[7-11]; 对比了管顶开口与封闭两种情况下颗粒的上升过程, 发现管顶封闭对颗粒上升起促进作用, 分析了管径及管长对这种促进作用的影响^[12]. 其次, 在理论研究方面, 将管内颗粒视为一个整体, 建立了颗粒受力模型, 对颗粒的上升高度和速度进行了理论分析, 并提出了颗粒上升的"空穴填充"机理^[7]; 建立了颗粒上升高度随时间变化的半经验关系式, 进一步分析了颗粒上升的"空穴填充"机理, 并且基于能量平衡假设, 推导出颗粒最终毛细上升高度的理论表达式^[13]; 基于一个振动周期内管内颗粒的流进和流出特性, 建立了颗粒毛细上升高度的理论模型, 该模型能够在一定程度上解释振幅、频率和管径对颗粒最终毛细上升高度的影响, 但无法解释较大振动频率下颗粒最终毛细上升高度随频率下降的现象, 以及较小管径下颗粒最终毛细上升高度随管径增加的现象^[14]. 再者,在数值模拟方面, 利用离散元方法, 获得了颗粒毛细效应全过程^[15]; 揭示了颗粒毛细效应的对流机理, 并发现了颗粒最终毛细上升高度随管径的变化特性^[4]; 展现了颗粒在竖直方向的运动规律^[5]; 获得了颗粒填充率的变化特性,以及振幅、振动强度、恢复系数对颗粒上升过程的影响规律^[16]; 展示了不同初始填充高度下颗粒毛细效应的过程,探讨了颗粒毛细上升过程中管内颗粒柱高度、颗粒速度场和填充率分布随时间的演变特性,获得了颗粒毛细效应过程中由容器传输到管内的颗粒的占比分布^[6].

虽然已有研究在颗粒毛细效应的宏观效果、动力学过程和内在机理上取得了诸多进展. 然而, 由于颗粒系统参数的复杂性和多样性, 目前颗粒毛细效应研究尚处于起步阶段, 宏观的实验研究仍不系统, 尚缺乏对不同操作参数下管径影响的探讨, 而这方面研究对推动颗粒毛细效应在颗粒逆重力输运上的应用具有重要意义. 此外, 已有研究中提出的颗粒毛细上升高度的理论模型都是建立在把大量颗粒视为整体的基础之上, 事实上管内不同高度和径向位置颗粒的运动速度往往不同, 因此现有理论模型无法对颗粒的输运提供有效的定量指导. 离散元方法通过跟踪每一个离散单元(颗粒)的运动以实现对整个颗粒系统的模拟, 是从颗粒尺度探究颗粒动力学行为的行之有效的方法^[17-19]. 本文将在课题组前期工作的基础上^{[4-6, 15]}, 利用离散元方法, 开展颗粒毛细效应过程数值模拟, 获得不同容器宽度、管振幅和频率下颗粒毛细上升高度随管径的变化规律, 以探明颗粒毛细效应的影响因素, 并为颗粒物料逆重力输运方案的优化提供科学依据.

1 离散元模型与计算方法

1.1 离散元模型

在离散元模型中, 颗粒系中任意颗粒$i$的平动与转动方程由牛顿第二定律给出, 即

(1)$ \begin{eqnarray} m_i \frac{{\rm d}v_i }{{\rm d}t}=\sum_{j=1}^n\left( {F_{ij,{\rm n}} +F_{ij,{\rm t}}} \right)+ m_i g \end{eqnarray}$

(2)$ \begin{eqnarray} I_i \frac{{\rm d} \omega _i }{{\rm d}t}=\sum_{j=1}^n {\left( {M_{ij,{\rm t}} +M_{ij,{\rm r}} } \right)} \end{eqnarray}$

式中, $m_{i}$和$I_{i}$分别为颗粒$i$的质量和转动惯量; $v_{i}$和$ \omega _{i}$分别为颗粒$i$的速度和角速度; $t$为时间; $n$为与颗粒$i$相接触的颗粒的个数; $F_{ij,{\rm n}}$和$F_{ij,{\rm t}}$分别为颗粒$i$和与它相接触的颗粒$j$之间的法向作用力和切向作用力; $M_{ij,{\rm t}}$为颗粒$j$对颗粒$i$的切向作用力产生的力矩; $M_{ij,{\rm r}}$为颗粒$j$对颗粒$i$的滚动摩擦力产生的力矩; $g$为重力加速度.

采用黏弹性接触模型^[20]描述法向作用力, 采用修正的Cundall-Strack模型^[21]描述切向作用力, 则

(3)$ \begin{eqnarray} \label{eq3} &&F_{ij,{\rm n}} =\min \left(0, \rho \delta _{ij,{\rm n}}^{3/2} -\dfrac{3}{2}A_{\rm n} \rho \sqrt{\delta _{ij,{\rm n}} } \dot{{\delta }}_{ij,{\rm n}}\right)e_{\rm n} \end{eqnarray}$

(4)$ \begin{eqnarray} \label{eq4} &&F_{ij,{\rm t}} =-\min \Bigg[\mu _{\rm s} \vert F_{ij,{\rm n}}\vert,\int_{\rm path} \frac{4G}{2-\upsilon }\sqrt {R_{\rm eff} \delta _{ij,{\rm n}} } {\rm d}s+\\&&\qquad A_{\rm t} \sqrt {R_{\rm eff} \delta _{ij,{\rm n}} } v_{ij,{\rm t}} \Bigg]e_{\rm t} \end{eqnarray}$

式中, $\rho $为弹性参数, 其是杨氏模量$Y$、泊松比$\upsilon $、有效半径$R_{\rm eff}=R_{i}R_{j}/(R_{i}+R_{j})$的函数; $R_{i}$和$R_{j}$分别为颗粒$i$和$j$的半径; $\delta_{ij,{\rm n}}$为颗粒$i$与$j$之间的法向重叠量, $\delta_{ij,{\rm n}}=R_{i}+R_{j}-\vert r_{i}-r_{j}\vert $; $r_{i}$和$r_{j}$分别为颗粒$i$和$j$的位置矢量; $A_{\rm n}$为法向耗散系数, 根据其与恢复系数$\varepsilon$之间的关系^[22-24], 可采用Padé}近似方法进行计算^[25]; $e_{\rm n}$为法向单位矢量,$e_{\rm n}=(r_{j}-r_{i})/\vert r_{j}-r_{i}\vert $; $\mu_{\rm s}$为滑动摩擦系数; $G$为剪切模量,$G=Y/[2(1+\upsilon)]$; $A_{\rm t}$为切向耗散系数, $A_{\rm t}=A_{\rm n}Y/(1-\upsilon ^{2})$^[26]; $v_{ij,{\rm t}}$为接触点上颗粒$i$与$j$的切向相对速度; $e_{\rm t}$为切向单位矢量. 此外, 式(4)中的积分路径为两颗粒接触期间在接触点的相对位移.

弹性参数$\rho$的计算式为

(5)$ \begin{eqnarray} \label{eq5} \rho =\frac{2Y}{3(1-\upsilon^2)}\sqrt {R_{\rm eff} } \end{eqnarray}$

根据定向恒转矩模型^[27], $M_{ij,{\rm r}}$可写为

(6)$ \begin{eqnarray} M_{ij,{\rm r}} =-\mu _{\rm r} \rho \delta _{ij,{\rm n}}^{3/2} \frac{ \omega _{ij} }{\vert \omega _{ij} \vert }R_{\rm eff} \end{eqnarray}$

式中, $\mu_{\rm r}$为滚动摩擦系数; $ \omega_{ij}$为颗粒$i$和$j$的相对角速度, $ \omega_{ij}= \omega _{i}- \omega _{j}$.

对于颗粒$i$与管壁面及容器壁面之间的相互作用, 将壁面视为半径无限大的颗粒, 利用上述模型进行处理^[28-30].

1.2 计算方法

基于DEM模型, 借助开源颗粒系统数值模拟软件LIGGGHTS^[31]对颗粒毛细效应动力学行为开展数值模拟. 本文数值模拟采用的颗粒系统示意图如图1所示. 其中, 容器的横截面为正方形, 其边长为$w$; 容器底面位于$z=-18$ mm处, 容器高度足够高; 管竖直插入容器中心, 管底面中心位于坐标原点, 管内径为$D$, 管壁厚为0.3 mm, 管长度足够长; 颗粒直径$d = 0.6$ mm. 数值模拟采用的颗粒物性参数见表1. 数值模拟过程为:首先将一定数目的颗粒随机加入容器内(含管内区域), 颗粒在重力作用下发生沉降, 由于重力作用、颗粒与壁面以及颗粒与颗粒之间的相互作用, 系统内颗粒总动能先增大后减小, 趋于总动能为0的松弛状态; 待颗粒达到松弛状态后, 对管施加竖直方向的周期性正弦振动, 使得管底面位置$z_{\rm b}$随管振动时间$t$的变化规律为

(7)$ z_{\rm b} =a sin (2\pi ft)$

式中, $a$为振幅, $f$为频率.

数值模拟时, 时间步长的选择非常重要, 时间步长越小, 计算精度越高, 但计算时间成本也越高. 因而, 在选择时间步长时, 应兼顾计算精度和计算成本.在离散元模拟中, 通常选择颗粒碰撞时间的1/50$\sim $1/10作为时间步长^[32-33]. 为确定时间步长,采用无阻尼、无黏性碰撞模型估算颗粒碰撞时间^[34]

图1

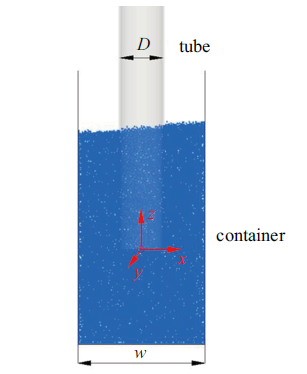新窗口打开|下载原图ZIP|生成PPT
图1数值模拟采用的颗粒系统示意图

Fig. 1Schematic of the granular system used in numerical simulations

Table 1
表1
表1数值模拟采用的颗粒物性参数
Table 1Physical properties of the particles used in numerical simulations

新窗口打开|下载CSV

(8)$ \begin{eqnarray} t_{\rm col} \approx 3.21\left(\frac{m_{\rm eff} }{\rho }\right)^{2/5}v_{\rm imp}^{-1/5} \end{eqnarray}$

式中, $m_{\rm eff}$为颗粒对的有效质量, $m_{\rm eff}=m_{i}m_{j}/(m_{i}+m_{j})$; $v_{\rm imp}$为碰撞速度. 取$v_{\rm imp}=1$ m/s 作为碰撞速度参考值, 则有$t_{\rm col}\approx 6.0\times 10^{-5}$ s. 因此, 选择时间步长$\Delta t=t_{\rm col}/30\approx 2.0\times 10^{-6}$ s. 在数值模拟时, 发现采用更小的时间步长, 数值模拟结果不发生改变, 这表明时间步长的选择是合理的.

2 结果与讨论

2.1 不同管径下颗粒毛细效应过程

在容器宽度与粒径比$w/d = 40$、管振幅与粒径比$a/d = 14.33$、管振动频率$f = 12$ Hz时, 得到的典型管径与粒径比($D/d)$下, 颗粒毛细效应过程快照如图2所示. 图2(a) $\sim\!$图2(c)分别为$D/d = 3.33$, 8.33, 15时的结果. 图中, $T$为管振动周期, $T =1/f$; $H_{\rm c}$为毛细上升高度; 竖直方向速度接近0 ($\vert v_{z}\vert < 0.05$ m$\cdot$s$^{-1}$)的颗粒用蓝色表示, 其余颗粒中, 向上运动的用红色、向下运动的用绿色表示. 由图2(a)可见, 在$D/d$很小时, 由于堵塞严重, 毛细上升速度较慢, 且管内颗粒发生结团现象, 使得颗粒柱出现中断. 需要说明的是: 图中给出的是振动周期整数倍时刻的结果, 此时管内颗粒处于最密堆积状态^[4,6], 为结团和中断最弱的时刻,非整数倍周期时刻结团和中断更为严重. 由图2(b)可以看出, $D/d$增大到8.33时,起初毛细上升高度增大迅速, 随后毛细上升高度的增大逐渐减缓,直至达到一个稳定的最终毛细上升高度; 由于$D/d$仍较小, 受堵塞影响,管径方向几乎不存在速度梯度; 在12$T$时刻, 颗粒柱顶部的少量颗粒因相互作用较弱,自由程较大, 运动行为不同于管内其余颗粒而向下运动,管内其余颗粒间频繁的摩擦与非弹性碰撞不断消耗颗粒系统的动能,使得颗粒聚集在一起, 颗粒自由程较小,颗粒呈现随管向上运动的状态; 图中$24T\sim 108T$各时刻, 管内颗粒均向上运动,这与颗粒体系的能量耗散有关, 经过更多振动周期,颗粒间的摩擦与非弹性碰撞使得颗粒柱顶部颗粒呈密堆积状态,管内颗粒柱顶部与下部的颗粒运动协同起来, 因而颗粒柱整体向上运动.由图2(c)可知, 在$D/d = 15$条件下, 颗粒毛细上升高度先迅速增大, 而后在$t \geqslant 24T$时出现起伏, 这与图2(b)差异显著. 由图2(c)还可以看出, $t \geqslant 24T$时, 管内颗粒柱分离为速度截然不同的两层: 管以最大速度向上运动时,管内上层颗粒向下运动, 与管的运动方向相反; 管内下层颗粒随管向上运动,且管壁附近颗粒的速度大于管中心区域颗粒的速度, 在管径方向存在明显的速度梯度.

为定量描述颗粒毛细上升高度(即管内颗粒表面高度和容器内颗粒表面高度之差)随时间的演变,将管内$z >0$区域沿$z$轴划分为高度为5$d$的连续的单元, 计算各单元内颗粒填充率$\phi $, 并定义满足$\phi >0.1$的单元的最大高度为管内颗粒表面高度. 类似地, 将容器内$z > 0$, $r>D/2$区域沿$z$轴划分为高度为$d$的连续的单元, 计算各单元内颗粒填充率,采用相同的方法确定容器内颗粒表面高度. 在此基础上, 即可获得颗粒毛细上升高度. 不同$D/d$条件下颗粒毛细上升高度随时间的演变如图3所示. 其中, 图3(a)给出了$D/d = 5$, 6.67, 8.33时的结果, 图3(b)给出了$D/d = 10$, 15, 20, 30时的结果. 从图3可以清楚地看到, 颗粒毛细效应过程中伴随着颗粒毛细上升高度的波动, 且颗粒毛细上升速度和最终毛细上升高度受到管径的影响. 由图3(a)可知, 管径较小时, 随着管径的增加, 颗粒毛细上升速度更快, 所能达到的最终毛细上升高度也更大. 总体看来, 管径较大时, 随着管径的增加,颗粒毛细上升速度减小, 所能达到的最终毛细上升高度也更小, 如图3(b)所示. 同时, 需要指出的是: $D/d = 15$时, 颗粒毛细上升高度呈现出反复波动的非稳定特征, 这一特征产生的原因可能是竖直振动过程中颗粒的填充率分布和堆积结构、颗粒与颗粒以及颗粒与壁面之间的碰撞等因素影响了颗粒的自组织行为.复杂体系中颗粒物质的行为模式对其内部结构及扰动具有高敏感性,其物理机制十分复杂, 有待进一步深入研究.

图2

新窗口打开|下载原图ZIP|生成PPT
图2数值模拟得到的颗粒毛细效应过程快照

Fig. 2Snapshots of the granular capillarity process obtained by numerical simulations

图3

新窗口打开|下载原图ZIP|生成PPT
图3不同管径下颗粒毛细上升高度随时间的演变

Fig. 3Evolution of capillary height of the granular materials with time at different tube diameters

2.2 临界管径的影响因素分析

Fan等^[4]在仅改变管径而保持其他参数不变时, 发现在毛细效应能够发生的管径范围内, 颗粒最终毛细上升高度随管径的增大, 先增大后减小. 为了叙述的方便, 本文将颗粒最终毛细上升高度随管径增大而增大的管径区间的上限称为临界管径. 基于此, 临界管径下颗粒最终毛细上升高度达到最大, 一旦管径大于临界管径, 颗粒最终毛细上升高度下降. 临界管径影响因素研究对于利用颗粒毛细效应输运颗粒物料的效果优化具有重要意义.

2.2.1 容器宽度的影响

为探究容器宽度对临界管径的影响, 在$a/d = 14.33$, $f = 12$ Hz条件下, 对容器宽度与粒径比$w/d = 40$, 60时颗粒毛细效应过程开展数值模拟,获得颗粒最终毛细上升高度$H^\infty_{\rm c}$随$D/d$的变化关系, 如图4所示. 为体现颗粒最终毛细上升高度随管的振动而上下波动的特性,图中利用点表示颗粒最终毛细上升高度的平均值, 利用误差条表示标准差. 由图可知, $w/d = 40$情况下, 临界管径对应的$D/d = 9.17$, 在$D/d \geqslant 10$时, 颗粒表现出液体的性质, 由于管内颗粒的流化, 阻碍了颗粒的上升, 使得在临界管径附近颗粒最终毛细上升高度急剧下降. 确切地说, $w/d = 40$情况下, 在$D/d = 9.17$时, $H^\infty_{\rm c}= 133.5$ mm; 在$D/d = 10$时, $H^\infty_{\rm c}= 65.9$ mm, 两者相比颗粒最终毛细上升高度下降了67.6 mm. 在$w/d = 60$情况下, 颗粒最终毛细上升高度随着$D/d$的增大, 同样呈现出先增大后减小的特征,并且在管径超出临界管径时颗粒最终毛细上升高度急剧下降. 然而, 两种容器宽度下, 临界管径并不相同, 在$w/d = 60$情况下, 临界管径对应的$D/d = 10$,相应的颗粒最终毛细上升高度为138.1 mm; 在$D/d = 11.67$时, 颗粒最终毛细上升高度为60.7 mm, 与$D/d = 10$时相比下降了77.4 mm. 究其原因是: 有摩擦的容器侧壁边界的存在对于诱导容器内颗粒的对流起到了不可缺少的作用^[4], 随着容器宽度的增大, 容器侧壁的边界效应降低, 容器内颗粒的对流强度随之减小, 这造成了由颗粒对流传输至管口的颗粒的质量通量的减小, 从而削弱了管内颗粒的流化, 因此, 颗粒由堵塞到流化的转折点延后, 表现为临界管径随容器宽度的增大而增大.

图4

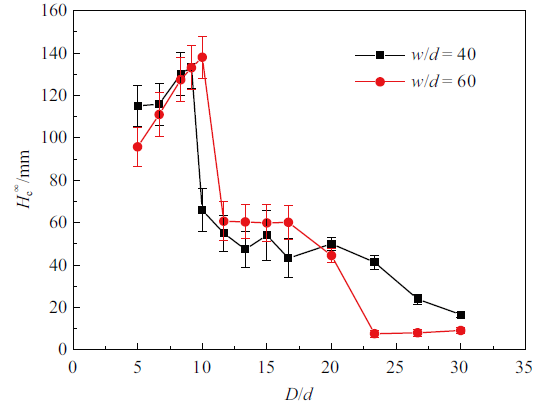新窗口打开|下载原图ZIP|生成PPT
图4容器宽度对临界管径的影响

Fig. 4Effect of container width on critical tube diameter

2.2.2 振幅的影响

为探究振幅对临界管径的影响, 在$w/d = 40$的条件下对振幅与粒径比$a/d = 14.33$与20两种情况下颗粒毛细效应开展数值模拟,得到颗粒最终毛细上升高度$H^\infty_{\rm c}$随管径与粒径比$D/d$的变化情况, 如图5所示. 在$a/d = 20$情况下, 临界管径对应的$D/d = 11.67$, 对比显示, 该情况下的临界管径明显大于$a/d = 14.33$时的临界管径; 同时, 颗粒最终毛细上升高度$H^\infty_{\rm c}$的最大值可达到203.2 mm, 也明显大于$a/d = 14.33$时$H^\infty_{\rm c}$的最大值133.5 mm. 振幅增大引起临界管径增大的原因是: 振幅增大, 管的振动强度增大, 管内壁附近的颗粒受到了更大的壁面剪切力作用, 使得更多颗粒能够跟随管运动, 减小了管内颗粒自由流动的区域, 相当于减少了有效管径, 因而增强了管内颗粒的堵塞效应, 使得颗粒堵塞能够在更大的管径下影响颗粒毛细效应. 在$D/d = 5$时, $a/d =20$情况下颗粒最终毛细上升高度比$a/d = 14.33$情况下略低, 这同样能够通过颗粒堵塞进行解释. 由于振幅较大时, 更易出现堵塞, 管径很小时,管内颗粒堵塞严重抑制了颗粒的上升, 使得最终颗粒毛细上升高度下降, 特别是当管径过小时, 颗粒出现完全堵塞, 颗粒毛细效应将无法发生^[4]. 此外, $D/d > 5$时, $a/d = 20$情况下的颗粒最终毛细上升高度均大于$a/d = 14.33$时的值, 这与文献中实验报道的颗粒最终上升高度随振幅的增加而增加的现象一致^[11], 该现象可解释为振幅增加引起管的振动强度增大, 使得管外壁对容器内的颗粒产生了更大的剪切力作用, 促进了容器内颗粒的对流, 增强了容器内颗粒向管口的传输, 有效地提高了颗粒毛细上升高度.

图5

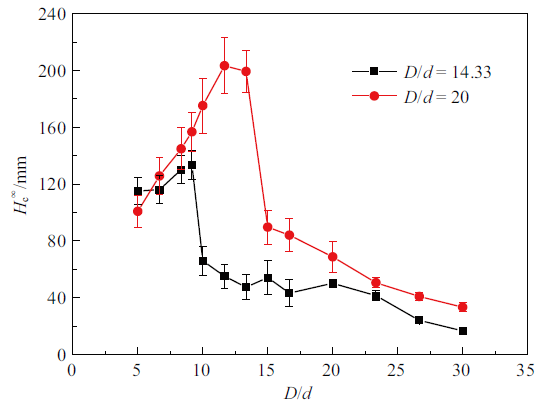新窗口打开|下载原图ZIP|生成PPT
图5振幅对临界管径的影响

Fig. 5Effect of vibration amplitude on critical tube diameter

2.2.3 频率的影响

在$w/d = 40$, $a/d = 14.33$条件下, 考察$f = 12$ Hz与$f = 15$ Hz时最终稳定毛细上升高度$H^\infty_{\rm c}$随$D/d$的变化情况, 结果如图6所示. 对比发现, $D/d\leqslant 8.33$时, 在较高频率下, $H^\infty_{\rm c}$略低; $D/d \geqslant 9.17$时, 在较高频率下, $H^\infty_{\rm c}$也较高. 特别是当$10\leqslant D/d \leqslant15$时, 两种频率下颗粒最终毛细上升高度差异显著: $f= 15$ Hz条件下, 颗粒毛细效应动力学处于受堵塞影响的区域, $H^\infty_{\rm c}$保持很高的值; $f = 12$ Hz条件下, 颗粒毛细效应动力学处于不受颗粒堵塞影响的流化区域, $H^\infty_{\rm c}$较低. 与振幅相比, 频率对颗粒毛细效应的影响更为复杂,频率升高引起振动强度增大、振动周期减小. 由于本文研究中采用的两种频率相差不大, 振动强度的增大对颗粒毛细效应动力学的影响起主导作用. 较高频率下, 振动强度也较大, 靠近管内壁的颗粒因受到更大的壁面剪切力作用更难以与管壁分离, 导致管内颗粒的有效流动区域变小, 使得管内颗粒更容易发生堵塞. 频率较高时, 更为严重的堵塞效应造成较小管径($D/d\leqslant 8.33$)下颗粒更难以上升, 从而产生更小的最终毛细上升高度. 同时, 频率较高时, 堵塞效应能够在更大的管径($D/d \leqslant 15$)下发挥作用, 使得临界管径增大. 此外, 由于频率增大, 增加了管的振动强度,因而增强了管外颗粒在对流机制作用下向管口的传输, 导致$D/d > 15$时, 较高频率下, 颗粒最终毛细上升高度较大. 然而, 需要说明的是: 若振动频率在很大的范围内变化, 则管振动周期的改变将可能对颗粒动力学行为起主导作用. 来自文献的实验结果表明, 保持振幅不变时, 随着频率的增大, 颗粒最终上升高度先增加后减小, 存在一个使得$H^\infty_{\rm c}$最大的最佳频率值^[11]. 更大的频率变化范围内, 临界管径的变化特性, 有待进一步研究.

图6

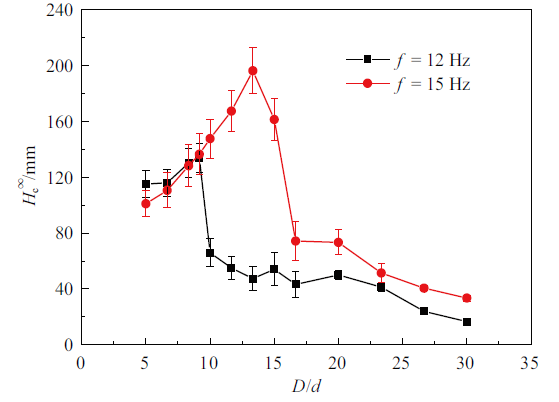新窗口打开|下载原图ZIP|生成PPT
图6频率对临界管径的影响

Fig. 6Effect of vibration frequency on critical tube diameter

3 结论

基于离散元方法, 对颗粒毛细效应动力学行为开展数值模拟研究, 给出了不同管径下颗粒毛细效应过程中颗粒竖直方向速度和毛细上升高度随时间的演变规律,

分析了容器宽度、管的振幅和频率对颗粒最终毛细上升高度随管径变化的影响特性. 通过本文研究, 得到如下结论:

(1)在容器宽度与粒径比为40、管振幅与粒径比为14.33、管振动频率为12 Hz情况下, 管径与粒径比$D/d = 3.33$时, 管内颗粒堵塞严重, 使得颗粒上升缓慢, 并造成颗粒柱中断; $D/d = 8.33$时, 起初颗粒毛细上升高度迅速增加, 随后颗粒毛细上升高度增速减缓, 管内颗粒在管径方向几乎不存在速度梯度; $D/d= 15$时, 随着颗粒毛细上升高度的增大, 管内颗粒柱分离为速度截然不同的两层.

(2)在颗粒毛细效应能够发生的管径范围内, 存在一个对应于颗粒最终毛细上升高度最大值的临界管径, 当管径小于临界管径时, 颗粒最终毛细上升高度随管径的增加而增加,当管径大于临界管径时, 颗粒最终毛细上升高度随管径的增大而减小; 临界管径受到容器宽度和振动参数的影响.

(3)临界管径随着容器宽度的增加而有所增大; 增加振幅和适当增大频率能够有效促进临界管径的增大, 从而将更多的颗粒输运到更高的高度,这对于利用颗粒毛细效应实现颗粒物料的逆重力输运具有重要意义.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Gerner

HJV

, Hoef

MAVD

, Meer

DVD

, et al. Interplay of air and sand: Faraday heaping unravelled
Physical Review E, 2007,76(5):051305

[本文引用: 1]

[2]

Darias

, Sánchez

, Gutiérrez

. Experimental study on the vertical motion of grains in a vibrated U-tube
Granular Matter, 2011,13(1):13-17

[3]

Eshuis

, Ko

VDW

, Devaraj

VDM

, et al. Phase diagram of vertically shaken granular matter
Physics of Fluids, 2007,19(12):123301

[4]

Fan

, Parteli

EJR

, P?schel

. Origin of granular capillarity revealed by particle-based simulations
Physical Review Letters, 2017,118(21):218001

[本文引用: 7]

[5]

Fan

, Liu

, Parteli

EJR

, et al. Vertical motion of particles in vibration-induced granular capillarity
EPJ Web of Conferences, 2017,140:16008

[本文引用: 1]

[6]

凡凤仙, 王志强, 刘举等. 竖直振动管中颗粒毛细效应的离散元模拟
力学学报, 2019,51(2):415-424

[本文引用: 5]

( Fan

Fengxian

, Wang

Zhiqiang

, Liu

, et al. DEM simulation of granular capillarity in vertically vibrating tube
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):415-424 (in Chinese))

[本文引用: 5]

[7]

Liu

, Wu

, Wang

. Particle climbing along a vibrating tube: A vibrating tube that acts as a pump for lifting granular materials from a silo
Soft Matter, 2013,9(19):4762-4766

[本文引用: 3]

[8]

Liu

, Zhang

, Wu

, et al. Effect of hoisting tube shape on particle climbing
Powder Technology, 2014,259:137-143

[9]

张富翁, 王立, 刘传平等. 竖直振动管中颗粒的上升运动
物理学报, 2014,63(1):014501

( Zhang

Fuweng

, Wang

, Liu

Chuanping

, et al. The rising motion of grains in a vibrating pipe
Acta Physica Sinica, 2014,63(1):014501 (in Chinese))

[10]

Zhang

, Wang

, Liu

, et al. Climbing motion of grains in vibrating tubes with different geometries
Advanced Powder Technology, 2017,28(2):356-362

[11]

Zhang

, Cronin

, Lin

, et al. Effects of vibration parameters and pipe insertion depth on the motion of particles induced by vertical vibration
Powder Technology, 2018,333:421-428

[本文引用: 3]

[12]

Zhang

, Cronin

, Lin

, et al. Sealing pipe top enhancing transportation of particulate solids inside a vertically vibrating pipe
Powder Technology, 2019,343:383-391

[本文引用: 1]

[13]

Liu

, Zhao

. Experimental study and analysis on the rising motion of grains in a vertically-vibrated pipe
Chinese Physics B, 2015,24(3):034502

[本文引用: 1]

[14]

Zhang

, Cheng

, Baoyin

. A new physical model on the capillary phenomenon of granular particles.
Applied Mathematics and Mechanics (English Edition), 2019,40(1):127-138

[本文引用: 1]

[15]

刘举, 白鹏博, 凡凤仙等. 竖直振动下颗粒物质的行为模式研究进展
化工进展, 2016,35(7):1956-1962

[本文引用: 2]

( Liu

, Bai

Pengbo

, Fan

Fengxian

, et al. Research progress on behavior mode of granular matter under vertical vibration
Chemical Industry & Engineering Progress, 2016,35(7):1956-1962 (in Chinese))

[本文引用: 2]

[16]

, Musser

, Li

, et al. Particles climbing along a vertically vibrating tube: Numerical simulation using the discrete element method (DEM)
Powder Technology, 2017,320:304-312

[本文引用: 1]

[17]

谭援强, 肖湘武, 张江涛等. 尼龙粉末在SLS预热温度下的离散元模型参数确定及其流动特性分析
力学学报, 2019,51(1):56-63

[本文引用: 1]

( Tan

Yuanqiang

, Xiao

Xiangwu

, Zhang

Jiangtao

, et al. Determination of discrete element model contact parameters of nylon powder at SLS preheating temperature and its flow characteristics
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):56-63 (in Chinese))

[本文引用: 1]

[18]

钱劲松, 陈康为, 张磊 . 粒料固有各向异性的离散元模拟与细观分析
力学学报, 2018,50(5):1041-1050

( Qian

Jinsong

, Chen

Kangwei

, Zhang

Lei

. Simulation and micro-mechanics analysis of inherent anisotropy of granular by distinct element method
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(5):1041-1050 (in Chinese))

[19]

熊迅, 李天密, 马棋棋等. 石英玻璃圆环高速膨胀碎裂过程的离散元模拟
力学学报, 2018,50(3):622-632

[本文引用: 1]

( Xiong

Xun

, Li

Tianmi

, Ma

Qiqi

, et al. Discrete element simulations of the high velocity expansion and fragmentation of quartz glass rings
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):622-632 (in Chinese))

[本文引用: 1]

[20]

Brilliantov

, Spahn

, Hertzsch

, et al. Model for collisions in granular gases
Physical Review E, 1996,53(5):5382-5392

[本文引用: 1]

[21]

Cundall

, Strack

. A discrete numerical model for granular assemblies
Geotechnique, 1979,29(1):47-65

[本文引用: 1]

[22]

Schwager

, P?schel

. Coefficient of restitution for viscoelastic spheres: The effect of delayed recovery
Physical Review E, 2008,78(5):051304

[本文引用: 1]

[23]

Schwager

, P?schel

. Coefficient of normal restitution of viscous particles and cooling rate of granular gases
Physical Review E, 1998,57(1):650-654

[24]

Ramírez

, P?Schel

, Brilliantov

, et al. Coefficient of restitution of colliding viscoelastic spheres
Physical Review E, 1999,60(4):4465-4472

[本文引用: 1]

[25]

Müller

, P?schel

. Collision of viscoelastic spheres: Compact expressions for the coefficient of normal restitution
Physical Review E, 2011,84:021302

[本文引用: 1]

[26]

Rycroft

, Orpe

, Kudrolli

. Physical test of a particle simulation model in a sheared granular system
Physical Review E, 2009,80(3):031305

[本文引用: 1]

[27]

, Chen

, Rotter

, et al. Assessment of rolling resistance models in discrete element simulations
Powder Technology, 2011,206:269-282

[本文引用: 1]

[28]

Parteli

EJR

, Schmidt

, Blümel

, et al. Attractive particle interaction forces and packing density of fine glass powders
Scientific Reports, 2014,4:6227

[本文引用: 1]

[29]

Verbücheln

, Parteli

EJR

, P?schel

. Helical inner-wall texture prevents jamming in granular pipe flows
Soft Matter, 2015,11(21):4295-4305

[30]

Parteli

EJR

, P?schel

. Particle-based simulation of powder application in additive manufacturing
Powder Technology, 2015,288:96-102

[本文引用: 1]

[31]

Kloss

, Goniva

, Hager

, et al. Models, algorithms and validation for opensource DEM and CFD-DEM
Progress in Computational Fluid Dynamics, 2012,12(2/3):140-152

[本文引用: 1]

[32]

赵永志, 程易, 郑津洋 . 三方程线性弹性-阻尼 DEM 模型及碰撞参数确定
计算力学学报, 2009,26(2):239-244

[本文引用: 1]

( Zhao

Yongzhi

, Cheng

, Zheng

Jinyang

. Three-equation linear spring-dashpot DEM model and the determination of contact parameters
Chinese Journal of Computational Mechanics, 2009,26(2):239-244 (in Chinese))

[本文引用: 1]

[33]

, Zhou

, Ma

, et al. Damping and particle mass in DEM simulations under gravity
Journal of Engineering Mechanics, 2015,141(6):04014167

[本文引用: 1]

[34]

Sch?fer

, Dippel

, Wolf

. Force schemes in simulations of granular materials
Journal de Physique I France, 1996,6(1):5-20

[本文引用: 1]