占旺龙^,*,2), 李卫^?, 黄平^?* 深圳技术大学中德智能制造学院, 深圳 518118
? 华南理工大学机械与汽车工程学院, 广州 510640

TANGENTIAL RESPONSE MODELING OF JOINT SURFACE BASED ON IWAN MODEL ¹⁾

Zhan Wanglong^,*,2), Li Wei^?, Huang Ping^? * Sino-German College of Intelligent Manufacturing, Shenzhen Technology University, Shenzhen 518118, China
? School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China

通讯作者: 2)占旺龙, 讲师, 主要研究方向: 润滑设计、摩擦建模与仿真. E-mail：zhanwl1992@foxmail.com

收稿日期:2019-12-4接受日期:2020-02-9网络出版日期:2020-03-18

基金资助:

1)国家自然科学基金资助项目.51575190

Received:2019-12-4Accepted:2020-02-9Online:2020-03-18
作者简介 About authors


摘要
针对工程中常见预紧力作用下的搭接接头,研究其在小幅切向位移激励时的切向位移响应问题,为此提出一种新的基于实际表面形貌和材料性能参数的滑移力密度分布函数.应用该分布函数得到搭接接头切向响应本构模型,并获得单位加载周期内的迟滞曲线和能量耗散值, 通过与已出版的实验结果相对比,发现得到的模拟值与实验结果吻合, 证明该模型的合理性.在此基础上利用该分布函数研究了接合面切向位移与切向力、切向接触刚度及能量耗散之间的关系,结果表明: 建立的模型能很好地描述接合面间切向力与切向位移之间的关系,临界滑移力函数开始迅速上升, 到达最大值后迅速收敛到零;切线力与切向位移之间表现出非线性特性, 随着切向位移的增大,切向接触刚度表现出"软化"现象;初始切向刚度与法向载荷、粗糙度参数及塑性指数有关, 对于确定的接触表面,法向力越大, 初始切向刚度越大; 初始切向刚度同样也随着塑性指数的增大而增大.
关键词： 搭接接头;粗糙面接触;切向接触刚度;能量耗散;Iwan模型

Abstract
Aiming at the problems of tangential displacement response of common used pre-tightening lap joints under tangential displacement excitation in engineering, a new slip force density distribution function based on actual morphological parameters and material performance parameters was proposed. The tangential response constitutive model of lap joint was obtained by using the distribution function, and the hysteresis curve and energy dissipation value per loading cycle were obtained. Compared with the published experimental results, it is found that the simulation value was consistent with the experimental, which proves the rationality of the model. Based on this, the relationship between the tangential displacement of the joint surface and the tangential force, tangential contact stiffness, and energy dissipation was studied. The results showed that the model could well describe the relationship between tangential force and tangential displacement. The trend of critical slip force function rise rapidly and then converges to zero after reaching its maximum value. The tangential force and tangential displacement show a non-linear characteristic, and with the increase of tangential displacement, the tangential contact stiffness shows softening phenomenon; the initial tangential stiffness is related to normal load, roughness parameters and plastic index. For a given contact surface, the greater normal force is given, the greater initial tangential stiffness is observed; the initial tangential stiffness also increases with the increase of plastic index.
Keywords：lap-type joints;rough surface contact;tangential contact stiffness;energy dissipation;Iwan model


PDF (4609KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
占旺龙, 李卫, 黄平. 基于Iwan模型的接合面切向响应建模 ¹⁾. 力学学报[J], 2020, 52(2): 462-471 DOI:10.6052/0459-1879-19-343
Zhan Wanglong, Li Wei, Huang Ping. TANGENTIAL RESPONSE MODELING OF JOINT SURFACE BASED ON IWAN MODEL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(2): 462-471 DOI:10.6052/0459-1879-19-343

引言

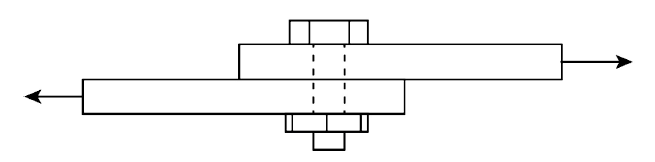
机械工程结构中广泛存在着以螺纹连接、法兰盘和铆接为代表的搭接接头形式, 如图1所示. 搭接连接的典型特征是接合面在法向预紧力作用下发生接触,由于表面粗糙度的存在使得接触界面上承受着非均匀的压力分布. 当连接件受到切向力作用时, 接触面间的摩擦力会阻碍界面间的宏观相对运动. 假设接触界面上摩擦系数处处相等, 则显然接触界面上各处抵抗切向相对运动的能力各不相同, 法向接触压力大的区域抵抗切向相对运动的能力强, 而法向接触压力小的区域则抵抗切向相对运动的能力弱. 由于界面接触压力大小与粗糙峰高度正相关, 因此在切向力作用下微凸体高度小的先发生滑移, 而高度大的粗糙峰后发生滑移, 当切向力增大到一定程度时, 滑移区将覆盖整个接触界面从而导致连接失效. 在往复振荡切向载荷作用下, 接触界面上的黏着区与滑移区会交替变化, 力与位移关系在笛卡尔坐标系中形成迟滞曲线, 迟滞曲线所围成的面积即为振荡加载过程中的能量耗散^[1-2].

图1

新窗口打开|下载原图ZIP|生成PPT
图1螺栓搭接接头

Fig. 1Bolted lap joint



在传统的机械动力学研究中, 一般都采用等效的弹簧阻尼元件来模拟连接界面间的接触力学行为而忽略接合面的非线性特征^[3], 模型中的参数需要通过实验进行标定. 然而, 由于连接界面间的非线性特征, 在某种条件下标定得到的模型参数并不一定适用于其他实验条件^[4]. 有限元方法也被广泛应用于简单装配结构的建模分析工作中,但是若想要准确地了解接合面的滑移行为则需要更加细密的网格, 这将大大增大计算时间. 与此同时, 对于由随机粗糙面组成的接合面, 要建立精确的有限元模型还存在很大的困难, 因此开展搭接接头非线性特性研究并建立基于实际可测物理参数的理论模型具有重要的意义^[5-7].

目前用于描述接合面非线性力学行为的代表模型有: Iwan模型^[8]、LuGre模型^[9]和Valanis模型^[10]等. 但是这些模型大部分都是唯象的, 模型中的参数靠实验标定而往往缺少明确的物理含义, 因此也就无法反应出接合面粗糙程度对宏观力学行为的影响. Iwan模型^[11]最早用来描述土木结构的弹塑性迟滞行为, 而后Segalman^[8]通过定义连接界面临界滑移力密度分布函数, 将该模型推广至连接界面黏滑行为建模. 在小幅振荡周期性载荷作用下, 单个加载周期内的能量耗散值$D$与切应力幅值$F_{0}$之间的关系可以表示为

(1)$ \begin{eqnarray} \label{eq1} D\left( {F_0 } \right)=\nu F_0^{3+\chi } \end{eqnarray}$
式中, $\nu$和$\chi $通过实验数据拟合得到, $\chi $范围在$-1$到0之间^[12]. 利用该关系, Segalman定义的临界滑移力分布函数为

(2)$ \begin{eqnarray} \rho \left( \phi \right)=R\phi ^\chi \left[ {H\left( \phi \right)-H\left( {\phi -\phi _{\max } } \right)} \right]+S\delta \left( {\phi -\phi _{\max } } \right) \end{eqnarray}$
式中, $H(\cdot )$为Heaviside单位阶跃函数; $\phi_{\max}$为发生宏观滑移时的位移; $S$为界面开始发生宏观滑移时力-位移曲线斜率不连续程度, $R$和$S$的具体计算方法见文献^[8].

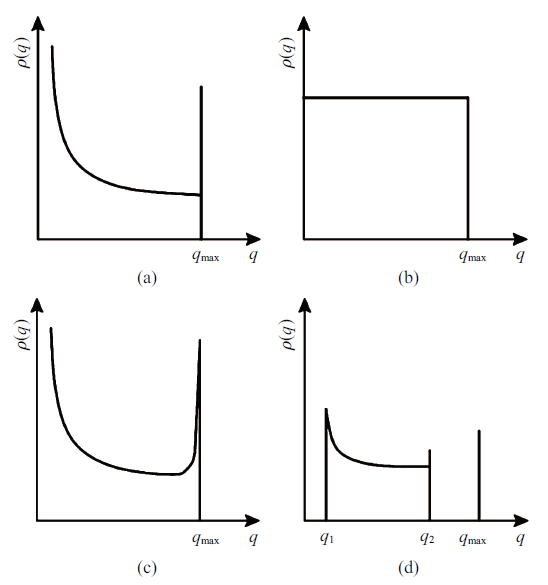
从式(2)可以看出, 当$\phi$增大时, $\rho(\phi$)会逐渐减小; 当$\phi= \phi_{\max}$时, $\rho(\phi$)会发生突变; 而当$\phi >\phi_{\max}$时, $\rho(\phi) = 0$,其对应的图像形式如图2(a)所示, 其为含截断幂律分布和单脉冲的四参数非均匀密度函数^[8]. Song等^[13] 和张相盟等^[14]基于均匀密度函数建立起摩擦接头Iwan模型(如图2(b)所示). 其他一些比较常见的临界滑移力分布函数如图2(c)和图2(d)所示, 具体解释可参阅文献^[15]. 而后Argatov等^[16]、王东等^[17]利用Kragelsky-Demkin粗糙面接触理论求解了螺栓连接接合面间的非线性力学行为. Brake^[15]还将Iwan模型扩展到连接界面发生宏观滑移后的阶段. 另外李一堃等^[18-19]提出一种含截断幂律分布和双脉冲的非均匀密度函数的六参数Iwan模型.

图2

新窗口打开|下载原图ZIP|生成PPT
图2临界滑移力密度分布函数图^[20]

Fig. 2Density distribution function of critical slip force^[20]



本文针对前人研究中临界滑移力分布函数需要进行参数标定的缺陷, 从接触面统计接触模型出发, 推导出新的临界滑移力分布函数, 在此基础上对典型工程摩擦副表面进行数值计算并对结果进行分析, 最后还将推导出的函数用于与已发表的实验结果进行对比, 结果表明理论推导出的分布函数与实验结果具有很好的一致性, 该研究成果可为搭接接头的切向响应研究提供参考.

1 Iwan模型

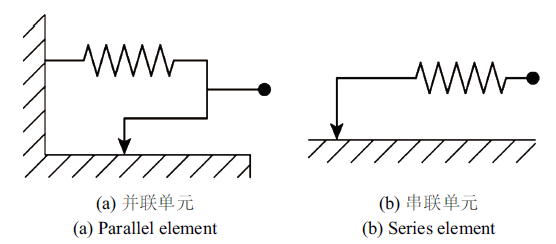
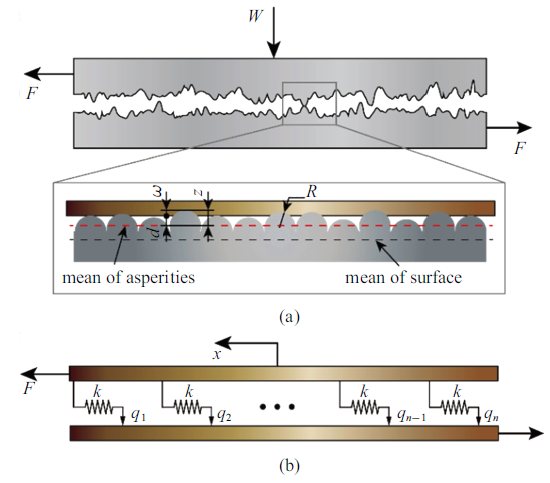
组成Iwan模型的两种基本单元如图3所示, 每个基本单元由一个线性弹簧元件和一个库仑摩阻片按照串联或者并联方式组成. 并联单元允许在位移不发生改变的情况下改变力的大小; 而串联模型允许位移发生改变而力不发生变化.

一般可以将随机粗糙面的接触问题简化成刚性平面与球体高度随机分布的弹性体之间的接触, 如图4(a)所示. 由于球体高度随机分布, 那么每个球体所受到的法向力则会是球体高度的函数. 根据库仑摩擦定律, 即摩擦副间的摩擦力与法向力成正比, 这样由于每个微凸体所承受的法向载荷不同而使得其所能承受的最大切应力也各不相同. 与Iwan模型对比发现^[16], 可以将摩擦面间的切向接触问题用串-并联单元来描述, 如图4(b)所示. 该模型由若干个Jenkins单元并联组成, 而每个Jenkins单元又是由弹性常数为$k$的弹簧和阈值为$q_{i}$的库仑摩阻片串联而成. 通过类比可以将图4(a)中每个微凸体的接触行为用图4(b)中的一个Jenkins单元进行描述.

图3

新窗口打开|下载原图ZIP|生成PPT
图3Iwan模型基本单元

Fig. 3Basic element of Iwan model

图4

新窗口打开|下载原图ZIP|生成PPT
图4(a)粗糙面接触模型; (b)简化并-串联Iwan模型

Fig. 4(a) Rough surface contact model; (b) Simplified parallel-series Iwan model



Iwan模型的工作原理如下: 当单个Jenkins单元所受到的切向力$F_{i}$小于摩阻片滑动阈值$q_{i}$时, 弹簧将会发生弹性形变从而承受切向力作用;而当切向力$F_{i}$大于摩阻片滑动阈值$q_{i}$时, 摩阻片将会发生滑动, 此时该单元所能承受的最大切向力为$q_{i}$. 假设在力$F$作用下, 上表面相对于下表面切向相对位移为$x$, 根据上述描述的Jenkins切向滑动行为, 可以用数学关系表示为

(3)$ \begin{eqnarray} \label{eq3} \left. \begin{array}{ll} F_i =kx, &\ \dot{{x}}>0,\ 0\leqslant x\leqslant q_i/k \\ F_i =q_i, &\ \dot{{x}}>0,\ x\geqslant q_i / k \\ \end{array}\right\} \end{eqnarray}$
式中, $\dot{{x}}$为滑移速度, $k$为弹簧的弹性常数, $q_{i}$为摩阻片临界滑移力阈值.

由于微凸体高度随机分布, 根据类比可以假定摩阻片滑动力阈值也随机分布. 假设其摩阻片临界滑移力密度分布函数为$\rho(q)$, 这样当$\dot{{x}}>0$时,整个体系切向力与相对位移之间的关系可以表示为

(4)$ \begin{eqnarray} \label{eq4} F\left( x \right)=\int_0^{kx} {q \rho \left( q \right)\mbox{d}q} +kx\int_{kx}^{+\infty } {\rho \left( q \right)\mbox{d}{\kern 1pt}q} \end{eqnarray}$
式中, $\rho(q){\rm d}q$为滑动力阈值在($q$, $q+{\rm d}q)$之间的Jenkins单元数. 式(4)中等号右边第一项为处于滑动状态下Jenkins单元所产生的总切向力, 此时所对应的微凸体发生滑动; 第二项为处于弹性变形状态下Jenkins单元所产生的总切向力, 此时微凸体处于黏着状态. 若式(4)等号右端第二项为零, 此时界面发生宏观滑移; 而若该项不为零, 此时接触界面部分微凸体处于滑移状态. 因此摩擦副界面间的运动可以分为两个阶段:

(1) 微滑移阶段: 当外界施加的切向载荷较小时, 接触面承受法向载荷较小的局部会发生滑动, 而其他部分处于黏着状态;

(2) 宏观滑移阶段: 当外界施加的切向载荷大到一定值的时候, 接触面间会发生明显的宏观滑动, 此时整个接触面都发生相对滑动.

利用以下变量关系式对式(4)进行变换

(5)$ \begin{eqnarray} \label{eq5} \left.\begin{array}{l} x=\sigma \tilde{{x}} \\ q=k\sigma \phi \\ k^2\sigma ^2\rho \left( q \right)=\tilde{{\rho }}\left( \phi \right) \\ \end{array}\right\} \end{eqnarray}$
式中, $\sigma$为微凸体高度分布方均根. 经过上述变量代换后, 式(4)中变量的量纲将发生变化, 由于$\sigma$量纲为长度, 因此$\tilde{x}$和$\phi$为无量纲量, 同理$\tilde{\rho}(\phi$)的量纲为力. 代入式(4)后可得

(6)$ \begin{eqnarray} \label{eq6} F\left( {\tilde{{x}}} \right)=\int_0^{\tilde{{x}}} {\phi \tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } +\tilde{{x}}\int_{\tilde{{x}}}^{+\infty } {\tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } \end{eqnarray}$
对上式求一阶导数, 可以得到摩擦副间的切向刚度$k_{t}$为

(7)$ \begin{eqnarray} \label{eq7} k_t =\frac{1}{\sigma }\cdot \frac{\mbox{d}\:F\left( {\tilde{{x}}} \right)}{\mbox{d}\:\tilde{{x}}}=\frac{1}{\sigma }\int_{\tilde{{x}}}^{+\infty } {\tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } \end{eqnarray}$
由上式可知分布函数$\tilde{\rho}(\phi$)的尾部分布函数为摩擦副间切向刚度的度量. 根据实际经验, 随着切向位移的增加, 切向刚度逐渐减小, 也就意味着界面连接刚度出现明显的"软化"现象, 直至摩擦界面发生宏观滑移时, 此时切向刚度为零, 即: $\tilde{x}\to \infty $时, $k_{t}\to 0$, 表明$\tilde{\rho}(\phi$)函数有水平渐近线, 渐近线为$\tilde{\rho}(\phi) = 0$. 另外分布函数$\tilde{\rho}(\phi$)还应满足始终大于或等于零的条件.

对式(6)求二阶导数可得

(8)$ \begin{eqnarray} \label{eq8} \frac{\mbox{d}^2F\left( {\tilde{{x}}} \right)}{\mbox{d}\tilde{{x}}^2}=-\tilde{{\rho }}\left( {\tilde{{x}}} \right) \end{eqnarray}$
由于$\tilde{\rho}(\phi$)恒大于零, 因此由上式可知切向力与切向位移之间满足凸函数关系.

当摩擦副上下表面间发生宏观滑移, 即$\tilde{x}\to\infty $时, 式(6)等号右端第二项会消失, 这样摩擦副间最大切应力$F_{\max}$为

(9)$ \begin{eqnarray} \label{eq9} F_{\max } =\int_0^{+\infty } {\phi \tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } \end{eqnarray}$
对于一般的摩擦副而言, 其上下表面间能承受的最大切向力为摩擦力, 即$F_{\max} = \mu W$. 从上式可以看出变量$\phi$的期望为滑动摩擦力, 并且当$\phi\to \infty $时, 有$\tilde{\rho}\to 0$. 若将式(9)两端同时除以摩擦力可得

(10)$ \begin{eqnarray} \label{eq10} \int_0^{+\infty } {\phi \cdot \frac{\tilde{{\rho }}\left( \phi \right)}{\mu W}\mbox{d}\phi } =1 \end{eqnarray}$
从上述分析可知, 若要将Iwan模型成功地应用于粗糙表面之间的切向接触问题研究, 首先要解决的问题应该是推导出正确的分布函数$\tilde{\rho}(\phi)$, 该分布函数要满足恒大于或等于零及式(7) $\sim\!$式(9)的条件.

2 周期性加载力-位移曲线

将求得的临界滑移力密度分布函数代入式(6)便可得到切向力与切向位移之间的关系. 一般来说, 分布函数为分段函数, 因此在计算加载曲线时要考虑$\phi$成立的区间范围,例如, 当$\phi_{1}\leqslant \tilde{x}\leqslant\phi_{2}$时, 切向力计算式为

(11)$ \begin{eqnarray} && F\left( {\tilde{{x}}} \right)=\int_0^{\phi _1 } {\phi \tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } +\int_{\phi _1 }^{\tilde{{x}}} {\phi \tilde{{\rho }}\left( \phi \right)\mbox{d}\phi }+ \\&&\qquad\tilde{{x}}\int_{\tilde{{x}}}^{\phi _2 } {\tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } +\tilde{{x}}\int_{\phi _2 }^\infty {\tilde{{\rho }}\left( \phi \right)\mbox{d}\phi } \end{eqnarray}$
对于其他区间范围也同样可以用上述方法求出. 由于式(11)形式较为复杂, 特别是当表面粗糙峰处于非高斯分布时, 为得到切向力与切向位移之间的关系, 可以用Simpson数值积分方法进行求解.

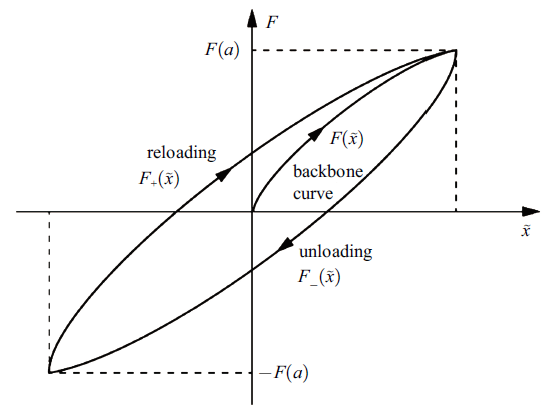
当摩擦副承受位移幅值为$a$的周期性位移激励时, 在位移-力图上可以得到如图5所示的迟滞曲线. 其中脊线函数可以根据式(6)得出, 而正、反向加载曲线可以通过Masing模型^[21]求出. 当体系由图5所示的$F(\cdot )$的$(a,F(a))$位置反向加载到$(-a, F(-a))$位置时, 反向加载力-位移曲线方程$F_-(\tilde{x})$为

(12)$ \begin{eqnarray} \label{eq12} F_- \left( {\tilde{{x}}} \right)=F\left( a \right)-2F\left( {\frac{a-\tilde{{x}}}{2}} \right) \end{eqnarray}$
式中, $-a\leqslant \tilde{x}\leqslant a$; $F(\cdot )$函数在式(6)中给出. 当对体系从$-a$到$a$重新加载时, 重新加载力-位移曲线方程$F_{+}(\tilde{x})$为 $ \begin{eqnarray} \label{eq13} F_+ \left( {\tilde{{x}}} \right)=-F_- \left( {\tilde{{x}}} \right) \end{eqnarray} $(13)

图5

新窗口打开|下载原图ZIP|生成PPT
图5力-位移迟滞曲线

Fig. 5Force-displacement hysteresis curve



反向加载曲线$F_-(\tilde{x})$与重新加载曲线$F_{+}(\tilde{x})$所围成的面积即为单个加载周期内的能量耗散量, 用积分的方式表示为

(14)$ \begin{eqnarray} \label{eq14} D\left( a \right)=\sigma \int_{-a}^a {\left[ {F_+ \left( {\tilde{{x}}} \right)-F_- \left( {\tilde{{x}}} \right)} \right]\mbox{d}\tilde{{x}}} \end{eqnarray}$
将式(12)和式(13)代入式(14), 即可得到不同位移幅值下单个加载周期内的能量耗散值.

3 临界滑移力分布函数推导

如图4(a)所示, 粗糙面之间的接触问题可以等价成刚性平面与覆盖球体但高度随机分布的弹性面之间的接触. 一般用轮廓仪测量得到的是$\sigma$, 但在现有的统计学模型中用到的是$\sigma_{a}$, 两者存在如下关系^[22]

(15)$ \begin{eqnarray} \label{eq15} \frac{\sigma _a }{\sigma }=\sqrt {1-\frac{3.717\times 10^{-4}}{\beta ^2}} \end{eqnarray}$
其中, $\beta = \sigma R\eta$, $R$为微凸体曲率半径, $\eta$为微凸体分布密度, 对一般工程表面来说, $\beta$范围为0.02$\sim$0.06. 当微凸体高度服从正态分布$N(0, \sigma_{a}^{2})$时, 分布函数可以写成

(16)$ \begin{eqnarray} \label{eq16} \varphi \left( z \right)=\frac{1}{\sqrt {2\pi } \sigma _a }\exp \left({-\frac{z^2}{2\sigma _a^2 }} \right) \end{eqnarray}$
对$z$进行无量纲化, 令$z^{\ast }=z/\sigma$, 则分布函数可以写成

(17)$ \begin{eqnarray} \label{eq17} \varphi ^\ast \left( {z^\ast } \right)=\frac{\sigma }{\sqrt {2\pi } \sigma _a }\exp \left[ {-\frac{z^{\ast2}}{2}\cdot \left( {\frac{\sigma }{\sigma _a }}\right)^2} \right] \end{eqnarray}$
塑性指数$\psi$为^[23]

(18)$ \begin{eqnarray} \label{eq18} \psi =\frac{E}{\pi KH}\left( {\frac{\sigma }{R}} \right)^{1/2}\left( {1-\frac{3.717\times 10^{-4}}{\beta ^2}} \right)^{1/4} \end{eqnarray}$
式中, $E$为综合弹性模量, $2 / E={\left( {1-\nu _1^2 } \right)} / {E_1 }+{\left({1-\nu _2^2 } \right)} / {E_2 }$, $E_{1,2}$为摩擦副材料的弹性模量, $\nu_{1,2}$为摩擦副材料的泊松比, $H$为较软材料硬度值, $K$最大应力接触系数.

根据粗糙表面ZMC弹塑性接触模型^[23], 当微凸体法向干涉量$\omega <\omega_{1}$ ($\omega = z-d$, $d$为摩擦面间的法向接触间距)时, 微凸体发生完全弹性变形, 此时法向载荷$W_{e}$与微凸体法向形变量$\omega$的关系为

(19)$ \begin{eqnarray} \label{eq19} W_e =\frac{2}{3}ER^{1/2}\omega ^{3/2} \end{eqnarray}$
当$\omega >\omega _{2}$时, 微凸体发生完全塑性变形, 此时法向载荷$W_{p}$与微凸体法向形变量$\omega$ 的关系为

(20)$ \begin{eqnarray} \label{eq20} W_p =2\pi RH\omega \end{eqnarray}$
当$\omega \in [\omega _{1}$, $\omega _{2}$]时, 微凸体间既有弹性变形, 又存在塑性变形, 利用样板函数插值方法可到法向载荷$W_{ep}$与微凸体法向形变量$\omega$ 的关系为

(21)$ \begin{eqnarray} &&W_{ep} =\pi HR\omega \left[ {1-k_a \frac{\ln \omega _2 -\ln \omega }{\ln \omega _2 -\ln \omega _1 }} \right] \cdot \\&&\qquad \left[ {1-2\left( {\frac{\omega -\omega _1 }{\omega _2 -\omega _1 }} \right)^3+3\left( {\frac{\omega -\omega _1 }{\omega _2 -\omega _1 }} \right)^2} \right] \end{eqnarray}$
式中, $k_{a} = 1 - 2K/3$, 其中$K$为最大接触应力系数, $K = 0.454 + 0.41\nu$ $(\nu$为材料泊松比). $\omega _{1}$为微凸体开始发生弹塑性变形时的法向临界干涉量, $\omega _{1} = (\pi KH/E)^{2}R$; $\omega_{2}$为开始发生完全塑性变形时的法向干涉量阈值, $\omega _{2} = 54\omega_{1}$^[24].

利用统计学方法对式(19) $\sim\!$式(21)进行积分可以得到粗糙表面接触时的法向载荷与变形量的关系为

(22)$ \begin{eqnarray} \label{eq22} && W=A_n E \cdot \Bigg\{ \frac{2}{3}\eta R^{1/2}\int_d^{d+\omega _1} \omega^{3/2}\varphi \left( z \right)\mbox{d}z+ \\&&\qquad \frac{\eta \pi R}{E}\int_{d+\omega _1}^{d+\omega _2 } \left(H-k_a H\frac{\ln \omega _2 -\ln \omega }{\ln \omega _2 -\ln \omega _1 } \right) \cdot \\&&\qquad\left[ {1-2\left( {\frac{\omega -\omega _1 }{\omega _2 -\omega _1 }} \right)^3+3\left( {\frac{\omega -\omega _1 }{\omega _2 -\omega _1 }} \right)^2} \right]\cdot \\&&\qquad \omega \varphi \left( z \right)\mbox{d}z + \frac{2\eta \pi RH}{E}\int_{d+\omega _2 }^{+\infty } {\omega \varphi \left( z \right)\mbox{d}z}\Bigg\} \end{eqnarray}$
式中, $\varphi(z)$为微凸体高度分布函数, $A_{n}$为名义接触面积, 具体推导过程可以参见文献^[23,24]. 由于法向载荷$W$与法向接触距离$d$之间为单调关系, 即接触间距越小, 接触面间的法向载荷越大. 因此在给定法向载荷的条件下, 可以通过二分法计算得到给定条件下的法向接触间距$d$.

根据库仑摩擦定律, 摩擦界面间的摩擦力为

(23)$ \begin{eqnarray} \label{eq23} && F=\mu A_n E\beta \cdot \Bigg\{ \frac{2}{3}\left( {\frac{\sigma }{R}} \right)^{1/2}\int_0^{\omega _1^\ast } {\omega ^{\ast 3/2}\varphi ^\ast \left( {\omega ^\ast +d^\ast } \right)\mbox{d}\omega ^{\ast }} + \\&&\qquad \frac{\pi H}{E}\int_{\omega _1^\ast }^{\omega _2^\ast } {\left( {1-k_a \frac{\ln \omega _2^\ast -\ln \omega ^\ast }{\ln \omega _2^\ast -\ln \omega _1^\ast }} \right)} \cdot \\&&\qquad\left[ {1-2\left( {\frac{\omega ^\ast -\omega _1^\ast }{\omega _2^\ast -\omega _1^\ast }} \right)^3+3\left( {\frac{\omega ^\ast -\omega _1^\ast }{\omega _2^\ast -\omega _1^\ast }} \right)^2} \right] \cdot \\&&\qquad \omega ^\ast \varphi ^\ast \left( {\omega ^\ast +d^\ast } \right)\mbox{d}\omega ^{\ast} + \\&&\qquad\frac{2\pi H}{E}\int_{\omega _2^\ast }^{+\infty } {\omega ^\ast \varphi ^\ast \left( {\omega ^\ast +d^\ast } \right)\mbox{d}\omega ^{\ast }}\Bigg\} \end{eqnarray}$
式中所有带星号(*)的变量都是用高度分布均方根$\sigma$进行无量纲化后的变量, $\mu$为滑动摩擦系数. 对比式(23)与式(9), 由于积分计算与积分变量无关, 因此将$\omega ^{\ast}$替换为$\phi$便可得到分布函数$\tilde{\rho}(\phi$), 为

(24)$ \begin{eqnarray} \label{eq24} && \tilde{{\rho }}\left( \phi \right)=\mu A_n E\beta \cdot \\ &&\qquad \left\{\begin{array}{l} \dfrac{2}{3}\left( {\dfrac{\sigma }{R}} \right)^{1/2}\phi ^{1/2}\varphi ^\ast\left( {\phi +d^\ast } \right),\quad 0\leqslant \phi<\phi _1 \dfrac{\pi H}{E}\left( {1-k_a \dfrac{\ln \phi _2 -\ln \phi }{\ln \phi _2 -\ln \phi _1 }} \right)\cdot \\ \qquad \left[ {1-2\left( {\dfrac{\phi -\phi _1 }{\phi _2 -\phi _1 }} \right)^3+3\left( {\dfrac{\phi -\phi _1 }{\phi _2 -\phi _1 }} \right)^2} \right] \\ \cdot\qquad \varphi ^\ast \left( {\phi +d^\ast } \right),\quad \phi _1 \leqslant \phi \leqslant \phi _2 \\ \dfrac{2\pi H}{E}\varphi^\ast \left( {\phi +d^\ast } \right),\quad \phi >\phi _2 \\ \end{array}\right. \end{eqnarray}$
式中$\phi_{1} = \omega_1^\ast$, $\phi_{2} = \omega_2^\ast$. 由上式可以看出, $\tilde{\rho}(\phi)$与$d^{\ast }$和粗糙面参数有关, 而$d^{\ast}$是法向载荷$W$的函数, 因此可以看出对于不同的法向载荷, $\tilde{\rho}(\phi)$分布也有所差异.另外上式中所有的变量都与接触面的粗糙度参数有关, 从而使得分布函数$\tilde{\rho}(\phi)$有实际的物理含义,解决了Segalman^[8]提出的四参数方程中需要通过实验进行参数标定的缺陷.

4 实验结果验证

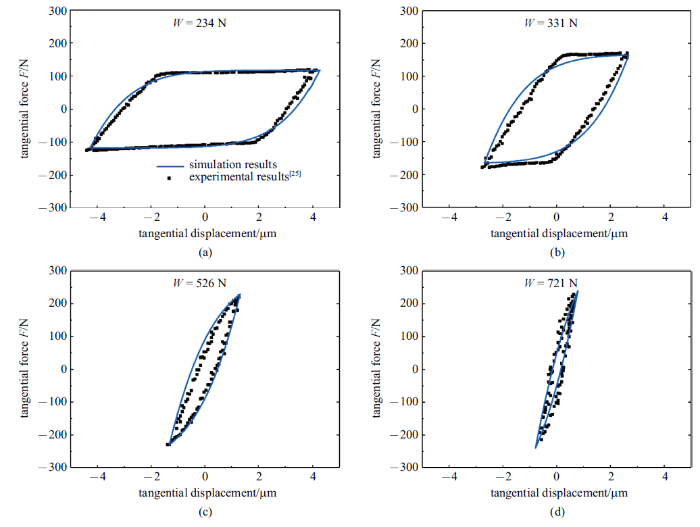
Eriten等^[25]对不同预紧力作用下螺栓搭接接头的切向行为进行了实验研究, 组成摩擦副的材料为420型不锈钢, 接触表面经铣削加工而成. 材料参数为:弹性模量$E = 200$ GPa, 泊松比$\nu = 0.24$, 硬度$H = 5.825$ GPa, 名义接触面积$A_{n} = 156$ mm$^{2}$, 表面粗糙度参数$\sigma/R = 0.088 8$, $\beta = 0.023$, $\sigma = 2.677 \mu $m, $\psi = 4.725$, 摩擦系数$\mu = 0.5$, 具体实验装置及过程可以参考文献^[25]. 需要注意的是, 在文献^[25]中摩擦系数为一与法向载荷有关的参数,但在本文中设定摩擦系数为发生宏观滑动时摩擦力与法向载荷的比值, 认为其为一恒定量, 本文取摩擦副发生宏观滑动时摩擦系数为计算值, 约为0.5.

图6给出了不同法向载荷下对摩擦副进行切向循环位移加载得到的迟滞曲线图. 其中实线为用本文中模型计算得到的迟滞曲线, 点状线的为文献^[25]中实验得到的曲线. 从图中可以看出理论计算值与实验结果很吻合, 从而证明了本文模型的可行性.

图6

新窗口打开|下载原图ZIP|生成PPT
图6不同法向载荷及位移幅值下的迟滞曲线实验与数值结果对比

Fig. 6Experimental and numerical results comparision of hysteresis curves under different normal loads and displacement amplitudes



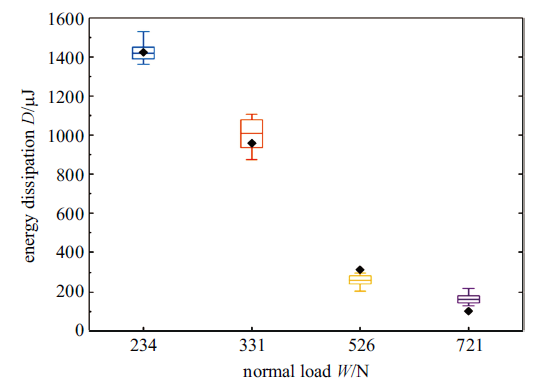
图7给出了不同法向载荷下单个加载周期内的能量耗散实验值与理论计算结果图, 其中实验值是统计10个加载周期内得到的统计箱式图, 黑色菱形为计算结果. 从图中可以看出计算结果与实验结构很吻合, 进一步证明了本文提出模型的有效性.

图7

新窗口打开|下载原图ZIP|生成PPT
图7单个周期内的能量耗散值实验与数值结果对比(箱图为实验值, 黑色菱形为计算值)

Fig. 7Experimental and numerical results comparision of energy dissipation per cycle (the box shows the experimental value, and the black diamond is the numerical value)

5 数值计算结果与讨论

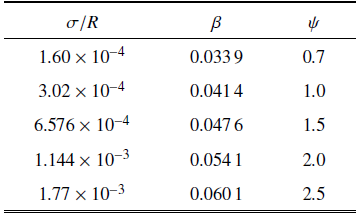
下面以钢-钢接触为例, 计算中所用到的材料物理参数为^[23]: 弹性模量$E_{1} = E_{2} = 207$ GPa, 泊松比$\nu_{1} = \nu _{2} = 0.29$, 硬度$H_{1}=H_{2} = 1.96$ GPa, 名义接触面积$A_{n} = 100$ mm$^{2}$, 摩擦系数$\mu = 0.5$. 由式(24)可知滑移力密度分布函数与形貌参数$\sigma$和$R$都有关,根据McCool^[22]的研究, 曲率半径$R$、粗糙峰分布密度$\eta$及方均根$\sigma$与测量的表面形貌高度$z(x)$之间为耦合关系. 因此对于一般的工程应用表面, 形貌参数可以用两个参数描述, 即: $\beta$和$\sigma/R$. 而这两个参数直接决定塑性指数$\psi$的大小,所以下面仅讨论不同塑性指数$\psi$对本构关系的影响.表1给出典型工程表面的形貌参数及对应的塑性指数值.

Table 1
表1
表1典型工程表面参数及塑性指数
Table 1Typical engineering surface parameters and plasticity index

新窗口打开|下载CSV

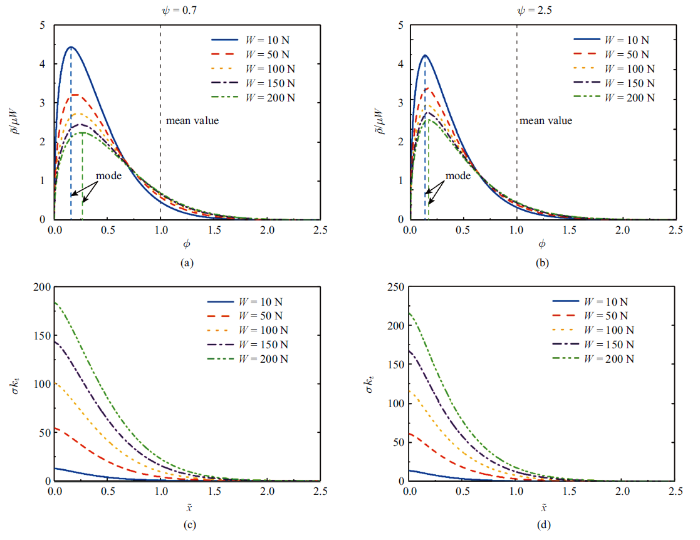
假设微凸体高度满足正态分布, 根据上述推导公式得出如图8所示的在不同塑性指数和不同法向载荷下的摩阻片滑动阈值分布函数和切向刚度图. 其中图8(a)和图8(b)分别为塑性指数为0.7和2.5时的临界滑移力分布函数图. 由式(5)中第二式可知, 对于给定的粗糙表面, $\phi$是摩阻片滑动阈值$q$的度量值, $\phi$越大即摩阻片滑动阈值$q$越大. 另外由式(10)可知, $\tilde{\rho}/\mu W$ 的数学期望为1, 即图8(a)和图8(b)图所示分布曲线的期望值为1.对比图8(a)和图8(b)图中不同法向载荷下的分布函数可以发现, 随着法向载荷的减小, 出现概率最大的摩阻片滑动阈值也随之减小, 这主要是因为法向载荷越小, 表面间接触间距$d$变小, 此时单个微凸体承担的法向载荷减小从而使其发生相对滑动所需的切向力也随之减小, 即摩阻片滑动阈值减小. 对于给定的法向载荷, 虽然$\phi$的取值范围为$[0, +\infty]$, 但当$\phi>1$时, $\tilde{\rho}/\mu W$迅速趋于零, 这是因为为了保证期望为恒定值, $\tilde{\rho}/\mu W$必须在达到一定程度后迅速减小到零, 法向载荷越小, 衰减速度越快. 从微凸体高度分布函数也可以进行解释, 因为虽然正态分布中自变量的取值范围为$[-\infty , +\infty]$, 但在$\pm 3\sigma$范围内的微凸体高度所占比例达到99.73%, 在该范围以外的可以忽略不计, 另外实际工程表面亦不存在无穷高度的微凸体, 这些因素都保证了$\tilde{\rho}(\phi$)具有水平渐近线. 对比相同载荷下不同塑性指数时的分布曲线可以看出, 塑性指数越大, $\phi$的众数越小,众数出现的概率越大. 这主要是因为随着塑性指数的增大, 高度较高的微凸体将发生塑性变形, 该状态下法向干涉量增大但法向载荷保持不变, 这样就会导致更多其他的微凸体发生接触但实际承担的法向载荷较小, 从而导致随着塑性指数的增大而众数减小, 同时出现的概率增大. 图8(c)和图8(d)为不同法向载荷下的切向刚度随切向位移的变化关系图, 由式(7)可知图中单条曲线为在给定载荷下临界滑移力分布函数的尾部分布积分值. 从图中可以看出随着$\phi$的增大, 切向刚度迅速减小到零, 此时摩擦副间将发生宏观滑动. $\phi = 0$所对应的量即为初始切向刚度, 从图中可以看出随着法向载荷的增大, 初始切向刚度也随之增大, 这也与文献^[26]中的结论相一致. 同时塑性指数越大, 初始切向接触刚度也越大.

图8

新窗口打开|下载原图ZIP|生成PPT
图8不同法向载荷及塑性指数下的分布函数及切向刚度

Fig. 8Distribution function and tangential stiffness under different normal load and plasticity index



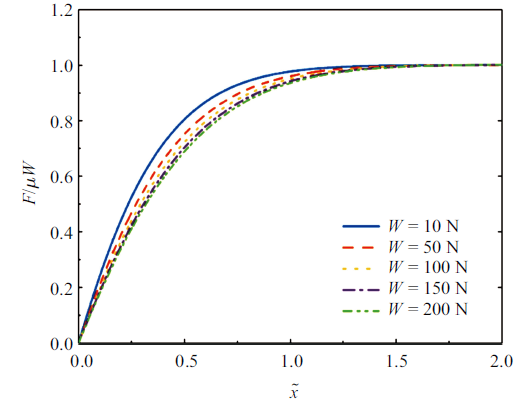
图9为在塑性指数$\psi=0.7$时无量纲切向力与切向位移关系图, 从图中可以看出加载曲线为凸函数, 随着切向位移的增大, 切向力也同样随之增大, 切向力增大速率逐渐减小并趋于零, 表明切向力逐渐趋于滑动摩擦力, 此时摩擦副发生宏观滑动. 法向载荷越大, 发生宏观滑动所需的切向位移越大.

图9

新窗口打开|下载原图ZIP|生成PPT
图9无量纲化切向力-位移曲线 ($\psi = 0.7$)

Fig. 9Dimensionless tangential force-displacement curve ($\psi = 0.7$)



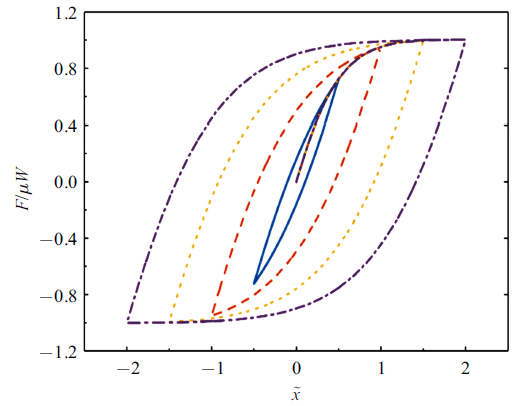
图10为当塑性指数$\psi = 0.7$及法向载荷$W = 100$ N条件下对摩擦副进行周期性加载时不同位移幅值下用Masing准则求解的力-位移迟滞曲线,

由图中可以看出不同的位移幅值下, 脊线曲线都相同. 随着位移幅值的增大, 迟滞曲线所围成的面积增大, 表明单个周期内能量耗散值随位移幅值的增大而增大.

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同切向位移幅值下的迟滞曲线($\psi = 0.7$, $W = 100$ N)

Fig. 10Hysteresis curves under different tangential displacement amplitudes ($\psi = 0.7$, $W = 100$ N)

6 总结

本文对以螺栓连接为代表的搭接接头为例, 对在法向预紧力作用下的粗糙面接触问题进行研究. 基于Iwan模型研究界面接触的非线性力学性质, 重点推导了Iwan模型中摩阻片临界滑移力密度分布函数. 相比于前人研究, 本文推导出的分布函数不再是唯象描述, 而是从材料性能参数和表面粗糙度参数推导得出. 在求出临界滑移力密度分布函数的基础上, 进而求解出接触面间的切向接触响应和在周期性位移加载条件下的迟滞曲线及能量耗散.主要结论如下:

(1) 临界滑移力函数开始迅速上升, 到达最高点后迅速收敛到零. 收敛速度和最大值出现位置与法向载荷、塑性指数及粗糙度参数有关.

(2) 界面切向接触刚度是滑移力分布函数的尾部分布. 刚开始时切向刚度最大, 进一步增大切向位移时, 切向刚度逐渐减小到零, 此时界面发生宏观滑动. 初始切向刚度与法向载荷、粗糙度参数及塑性指数有关. 对于确定的接触表面, 法向力越大, 初始切向刚度越大; 初始切向刚度同样也随着塑性指数的增大而增大.

(3) 使用本文推导出的函数计算得到的单位加载周期内的迟滞曲线与实验结果很吻合, 计算出的单个周期内的能量耗散也与实验结果吻合, 证明模型的正确性.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Ouyang H, Oldfield MJ, Mottershead JE . Experimental and theoretical studies of a bolted joint excited by a torsional dynamic load
International Journal of Mechanical Sciences, 2006,48(12):1447-1455
[本文引用: 1]

[2] Xiao H, Shao Y, Xu J . Investigation into the energy dissipation of a lap joint using the one-dimensional microslip friction model.
European Journal of Mechanics A/Solids, 2014,43:1-8
[本文引用: 1]

[3] 刘兴天, 陈树海, 王嘉登 等. 几何非线性摩擦阻尼隔振系统动力学行为研究
力学学报, 2019,51(2):371-379
[本文引用: 1]

( Liu Xingtian, Chen Shuhai, Wang Jiadeng , et al. Anlysis of the dynamic behavior and performance of a vibration isolation system with geometric nonlinear friction damping
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):371-379 (in Chinese))
[本文引用: 1]

[4] 徐超, 王东 . 考虑粗糙表面接触的连接面黏滑摩擦建模
西安交通大学学报, 2014,48(7):131-135
[本文引用: 1]

( Xu Chao, Wang Dong . Stick-slip friction modeling of structural joint interface considering rough contact. Journal of Xi'an
Jiaotong University, 2014,48(7):131-135 (in Chinese))
[本文引用: 1]

[5] 邓佳东, 程耿东 . 基于局部插值的结构动力模型降阶方法
力学学报, 2012,44(2):342-350
[本文引用: 1]

( Deng Jiadong, Cheng Gengdong . Structure dynamic model reduction technique based on local interpolation
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(2):342-350 (in Chinese))
[本文引用: 1]

[6] Li W, Zhan W, Huang P . Modeling for microslip behavior of lap joints based on non-Gaussian rough surfaces
Journal of Tribology, 2020,142(1):011501


[7] Bograd S, Reuss P, Schmidt A , et al. Modeling the dynamics of mechanical joints
Mechanical Systems and Signal Processing, 2011,25(8):2801-2826
[本文引用: 1]

[8] Segalman DJ . A four-parameter Iwan model for lap-type joints
Journal of Applied Mechanics, 2005,72(5):752-760
[本文引用: 5]

[9] Pikunov D, Stefanski A . Numerical analysis of the friction-induced oscillator of Duffing's type with modified LuGre friction model
Journal of Sound and Vibration, 2019,440:23-33
[本文引用: 1]

[10] Abad J, Medel FJ, Franco JM . Determination of Valanis model parameters in a bolted lap joint: Experimental and numerical analyses of frictional dissipation
International Journal of Mechanical Sciences, 2014,89:289-298
[本文引用: 1]

[11] Iwan WD . A distributed-element model for hysteresis and its steady-state dynamic response
Journal of Applied Mechanics, 1966,33(4):893-900
[本文引用: 1]

[12] Segalman DJ, Gregory DL, Starr MJ , et al. SAND2009-4164.
Albuquerque, Mexico: Sandia National Laboratories, 2009
[本文引用: 1]

[13] Song Y, Hartwigsen CJ, McFarland DM , et al. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements
Journal of Sound and Vibration, 2004,273(1-2):249-276
[本文引用: 1]

[14] 张相盟, 王本利, 卫洪涛 . Iwan模型非线性恢复力及能量耗散计算研究
工程力学, 2012,29(11):33-39
[本文引用: 1]

( Zhang Xiangmeng, Wang Benli, Wei Hongtao . Calculation of nonlinear restoring forces and energy dissipation of Iwan model
Engineering Mechanics, 2012,29(11):33-39 (in Chinese))
[本文引用: 1]

[15] Brake MRW . A reduced Iwan model that includes pinning for bolted joint mechanics
Nonlinear Dynamics, 2017,87(2):1335-1349
[本文引用: 2]

[16] Argatov II, Butcher EA . On the Iwan models for lap-type bolted joints.
International Journal of Non-Linear Mechanics, 2011,46(2):347-356
[本文引用: 2]

[17] 王东, 徐超 . 一种考虑粗糙结合面切向黏滑摩擦模型
机械工程学报, 2014,50(13):129-134
[本文引用: 1]

( Wang Dong, Xu Chao . A tangential stick-slip friction model for rough interface
Chinese Journal of Mechanical Engineering, 2014,50(13):129-134 (in Chinese))
[本文引用: 1]

[18] 李一堃, 郝志明, 章定国 . 基于六参数非均匀密度函数的伊万模型研究
力学学报, 2015,47(3):513-520
[本文引用: 1]

( Li Yikun, Hao Zhiming, Zhang Dingguo . Investigation into Iwan model based on the six-parameter non-uniform density function
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(3):513-520 (in Chinese))
[本文引用: 1]

[19] Li Y, Hao Z . A six-parameter Iwan model and its application
Mechanical Systems and Signal Processing, 2016, 68-69:354-365
[本文引用: 1]

[20] Zhan W, Huang P . Physics-based modeling for lap-type joints based on the Iwan model
Journal of Tribology, 2018,140(5):051401
[本文引用: 2]

[21] Segalman DJ, Starr MJ . Inversion of masing models via continuous Iwan systems.
International Journal of Non-Linear Mechanics, 2008,43(1):74-80
[本文引用: 1]

[22] McCool JI . Predicting microfracture in ceramics via a microcontact model
Journal of Tribology, 1986,108(3):380-385
[本文引用: 2]

[23] Zhao Y, Maietta DM, Chang L . An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow
Journal of Tribology, 2000,122(1):86-93
[本文引用: 4]

[24] 赵永武, 吕彦明, 蒋建忠 . 新的粗糙表面弹塑性接触模型
机械工程学报, 2007,43(3):95-101
[本文引用: 2]

( Zhao Yongwu, Lü Yanming, Jiang Jianzhong . New elastic-plastic model for the contact of rough surfaces
Chinese Journal of Mechanical Engineering, 2007,43(3):95-101 (in Chinese))
[本文引用: 2]

[25] Eriten M, Polycarpou AA, Bergman LA . Physics-based modeling for fretting behavior of nominally flat rough surfaces
International Journal of Solids and Structures, 2011,48(10):1436-1450
[本文引用: 4]

[26] Zhan W, Huang P . Modeling tangential contact based on non-Gaussian rough surfaces.
Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2019,233(1):51-60
[本文引用: 1]