,2), 杜修力北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124AN ABSORBING BOUNDARY CONDITION FOR SH WAVE PROPAGATION IN VISCOELASTIC MULTILAYERED MEDIA 1)
Wu Lihua, Zhao Mi,2), Du XiuliKey Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China通讯作者: 2)赵密, 教授, 主要研究方向: 土-结动力相互作用. E-mail:zhaomi@bjut.edu.cn.
收稿日期:2019-11-14接受日期:2020-02-20网络出版日期:2020-03-18
| 基金资助: |
Received:2019-11-14Accepted:2020-02-20Online:2020-03-18
作者简介 About authors
摘要
提出一种高精度时域吸收边界条件,与有限元法结合用于模拟瞬态标量SH波在达朗贝尔黏弹性多层介质中传播问题.建立时域吸收边界条件的过程是:首先将半无限域沿着竖向半离散得到半离散的位移方程以及人工边界处的力-位移关系,再通过引入模态分解, 将物理空间下的量转化到模态空间,从而获得半无限域模态空间下的频域动力刚度;其次采用一种在全频范围内收敛的连分式精确逼近单层介质模态空间下标量形式的频域动力刚度,将标量连分式扩展为矩阵形式用来表示多层介质的频域动力刚度;最后通过引入辅助变量技术,将模态空间下基于连分式的频域动力刚度关系转化为时域吸收边界条件,进一步转换到物理空间后得到物理空间下的时域吸收边界条件.单层介质和五层介质的数值算例表明,建立的高精度时域吸收边界条件对于达朗贝尔黏弹性单层介质是精确且稳定的;对于达朗贝尔黏弹性多层介质, 为了保证其高精度特性,需要将人工边界放置在距离感兴趣区域约为0.5倍无限域高度的位置处.
关键词：
Abstract
A high-accuracy absorbing boundary condition in the time domain is proposed, which can be coupled with the finite element method seamlessly to simulate the propagation of the transient scalar wave in the D'Alembert viscoelastic multilayered media. First, a semi-discrete displacement equation of the semi-infinite domain and the force-displacement relationship in the artificial boundary are obtained by semi-discretizing the semi-infinite domain along the vertical depth. Modal decomposition is utilized to convert the field of the semi-infinite domain in the physical space into the modal space. Then the dynamic stiffness of the semi-infinite domain in the frequency domain in the modal space is obtained according to both the displacement equation and the force-displacement relationship in the modal space. Second, a scalar continued fraction, which is convergent over the whole frequency domain, is proposed to describe the scalar dynamic stiffness in the modal space of the D'Alembert viscoelastic single-layered medium. The scalar continued fraction is extended to the matrix form to represent the dynamic stiffness in the modal space of the D'Alembert viscoelastic multilayered media. Last, by introducing auxiliary variables, a time-domain absorbing boundary condition in the modal space is constructed based on the proposed continued fraction. Subsequently, considering the relationship of the field in the modal space and in the physical space, a time-domain absorbing boundary condition in the physical space is obtained by converting the absorbing boundary condition in the modal space into the physical space. Two numerical examples of a single-layered medium and a five-layered media verify that the proposed method is accurate and stable for the D'Alembert viscoelastic single-layered medium, and for the D'Alembert viscoelastic multilayered media, in order to ensure the proposed method's property of high-accuracy, the distance from artificial boundary to the region of interest needs to be about 0.5 times of the total layer height of the infinite domain.
Keywords：
PDF (1580KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
吴利华, 赵密, 杜修力. 黏弹性多层介质中SH波动的一种吸收边界条件 1). 力学学报[J], 2020, 52(2): 480-490 DOI:10.6052/0459-1879-19-315
Wu Lihua, Zhao Mi, Du Xiuli.
引言
刚性基岩上卧成层土是工程结构地基的普遍存在形式[1].由于工程结构尺寸远小于场地尺寸, 从数学建模的角度可以把场地看作是无限域.采用如有限元法、有限差分法等数值方法分析工程结构动力响应时,通常人为引入人工边界将无限域截掉, 取包含感兴趣区域的有限域作为数值分析对象.吸收边界条件应该被施加在有限域的人工边界上来反映被截掉的无限域和有限域间的动力相互作用[2].对结构进行非线性分析等情况下, 需要吸收边界条件是时域方法.已有的时域吸收边界条件大多是基于线弹性介质建立的,如局部吸收边界条件[3-11]和高精度吸收边界条件[12-20].但是波在土中的传播总是伴随着能量的衰减, 因此相比于把无限域看作线弹性介质,将其考虑为黏弹性介质更接近工程实际[21].特征线法[22]、传递矩阵法[23]、高阶薄层法[24]以及阻尼层法[25-29]等方法被用来建立黏弹性成层介质的频域吸收边界条件.但是频域吸收边界条件有两点局限性,一是将频域结果转化为时域结果需要复杂耗时的卷积计算[30],二是频域方法不适用于非线性时程分析.针对黏弹性介质建立的时域吸收边界条件目前主要有两类: 局部吸收边界条件[31-32]和阻尼层形式的吸收边界条件[33-39].王振宇和刘晶波[31]基于黏弹性理论构造了局部吸收边界条件的一维形式,证明了在弱阻尼时其近似等效于弹性一维吸收边界条件,并将其推广得到二维吸收边界条件[31]. 但是对于强阻尼介质,将基于线弹性介质建立的吸收边界条件未加修正地应用于黏弹性情形会导致数值失稳或模拟精度降低等问题[33].Badry等[32]建立了半空间黏弹性介质的局部吸收边界条件,其中黏性考虑为与质量成正比的瑞利阻尼形式.上述两种局部时域吸收边界条件都是基于半空间模型建立的,将其用于刚性基岩上卧成层介质模型时模拟精度较低.阻尼层形式的时域吸收边界条件是近年的研究热点,其通过在人工边界外设置具有耗能作用的缓冲区来吸收透射波.黏弹性介质的阻尼层吸收边界条件有: 完美匹配层[34-35]、Caughey吸收层[36]、增加阻尼吸收层[37]以及阻尼溶剂抽取法[38]等.阻尼层的层厚度和耗能参数选择不当时, 会导致模拟精度低或出现数值失稳问题.
为了提高计算的精度和效率, 高精度时域吸收边界条件被广泛研究,它是针对具体的无限域定解问题, 基于解析或者半解析方法建立的,因而具有精度高的特点.目前该类方法主要被用于建立线弹性介质的时域吸收边界条件. 但是,线弹性成层介质的时域高精度吸收边界条件的构建方法可以被借鉴用来建立黏弹性成层介质的时域高精度吸收边界条件.线弹性成层介质的高精度时域吸收边界条件的构建方法主要有两类,一类是对时域下的场方程运用算子分离法得到时域吸收边界条件.Liu等利用该方法建立了相关时域吸收边界条件来模拟瞬态标量波[12]和矢量波[14]在成层介质中的传播.然而该方法得到的时域吸收边界条件一般会存在稳定性问题[39].另一类是通过如薄层法[40]和比例边界有限元法[41]等半离散方法得到成层介质的频域动力刚度,再通过时域化方法[13, 15, 19]建立时域吸收边界条件.单层介质的频域动力刚度是标量形式, 多层介质的频域动力刚度是矩阵形式.为了将频域动力刚度时域化, 可以通过优化方法将标量动力刚度表示为有理函数近似,进一步有理函数近似可以等价为时域集中参数模型[15];也可以通过数学计算将标量动力刚度表示为连分式展开,再结合辅助变量技术将连分式展开转化为时域吸收边界条件[13, 19-20].由于优化方法对于矩阵问题很难收敛,一般有理函数近似不能用来描述多层介质的动力刚度.但是标量连分式可以被扩展为矩阵形式用来描述多层介质的动力刚度[19].基于连分式的时域吸收边界条件对于单层介质是精确且稳定的,对于多层介质是高精度且不易失稳的[19].
本文将无限土看作达朗贝尔线性黏弹性介质[21,42], 它是通过在运动方程中增加阻尼项来描述介质的黏性. 尽管达朗贝尔模型相对简单, 没有从本构层面描述介质, 但由于它包含很少的物理参数, 在实际应用中具有优势. 考虑到连分式用于构建高精度吸收边界条件的优越性, 本文将达朗贝尔单层介质动力刚度表示为连分式展开, 类似文献[19]的做法, 再将连分式扩展为矩阵形式, 建立基于连分式的达朗贝尔黏弹性单层和多层介质稳定的时域高精度吸收边界条件.
1 问题描述
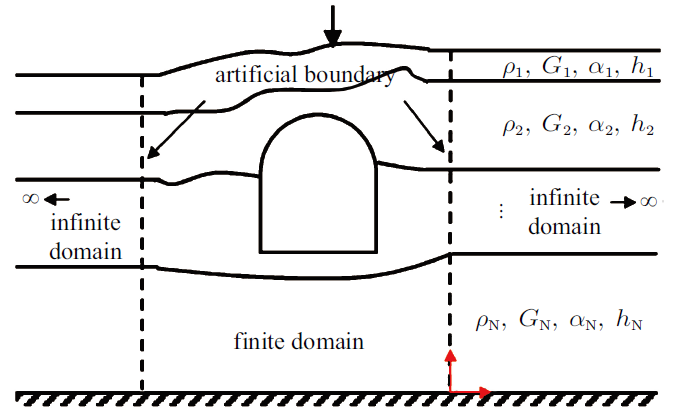
如图1所示, 工程结构的地基为刚性基岩上卧达朗贝尔线性黏弹性成层介质.用有限元法分析工程结构的二维出平面SH波动响应,需要人为引入两条直线型人工边界将整个域分为有限域和左右两个半无限域.有限域可以包含非线性,时域吸收边界条件应该被施加在有限域的人工边界上来表示被截掉的无限域和有限域间的动力相互作用.吸收边界条件根据无限域推导获得.达朗贝尔黏弹性介质和线弹性介质两者控制方程的区别是达朗贝尔黏弹性介质比线弹性介质的运动方程多了一项耗散项$\eta \dot{{u}}$, 其余控制方程两者相同. 达朗贝尔黏弹性介质的波动方程为
图1
新窗口打开|下载原图ZIP|生成PPT图1刚性基岩上卧达朗贝尔黏弹性成层介质
Fig. 1D'Alembert viscoelastic multilayered media overlying rigid bedrock
无限域的上下表面物理边界条件分别为
其中, ($x$, $y)$ 表示笛卡尔坐标, $u$ 表示出平面位移, $\tau _y $是应力, $G$是剪切模量, $\rho $是质量密度, $\eta =\alpha \rho $, $\alpha $ 和 $\eta $ 是阻尼参数, 变量上方的点表示对时间求导. 假定每一层的材料参数是常量, 不同层的材料参数可不同. 另外, 位移u 在不同土层的分界面以及人工边界处是连续的. 土层的初始状态为静止.变量上方的点表示对时间求导. 假定每一层的材料参数是常量, 不同层的材料参数可不同. 另外, 位移 $u$ 在不同土层的分界面以及人工边界处是连续的. 土层的初始状态为静止.
2 半无限域的频域动力刚度
本节结合半离散法和模态分解法获得模态空间下半无限域的频域动力刚度,并显式表示出单层介质的频域动力刚度.2.1 物理空间下的频域动力刚度
将半无限域沿着土层$y$方向离散,同时考虑式(2)的物理边界条件及介质交界面的连续条件, 得到半离散的有限元方程以及人工边界上的等效结点载荷
其中, ${E}_1 =\int_0^H {{N}^{\rm T}G{N}{\rm d}y} $, ${E}_2=\int_0^H {\frac{\partial {N}^{\rm T}}{\partial y}G\frac{\partial {N}}{\partial y}{\rm d}y} $, ${E}_3 =\int_0^H {{N}^{\rm T}\rho {N}{\rm d}y}$和${E}_4 =\int_0^H {{N}^{\rm T}\eta {N}{\rm d}y} $, $u_{\rm b}$ 表示人工边界上的结点位移向量, $H$表示无限域的总高度, $N$ 是线性形函数, T表示矩阵转置, $m=1$ 和$m=-1$分别表示被截掉的左、右无限域的外法线方向. 值得注意的是, 对于每个单元, 式(3)中的阻尼矩阵$E_{4}$是质量矩阵$E_{3}$的$\alpha$倍. 所以达朗贝尔黏弹性介质相当于与质量成正比的瑞利阻尼形式[32 ,43].
半无限域人工边界的结点力-位移关系为
顶标$\sim $表示频域下的值, ${S}^\infty$表示物理空间下半无限域的频域动力刚度.
2.2 模态空间下的频域动力刚度
为了将物理空间下半离散的有限元方程变换到模态空间下, 引入广义特征值分解其中, ${ \varPhi }$是特征向量矩阵, ${ \varLambda }^2$是对角形式的特征值矩阵, 其对角线上的元素为$\omega _n^2 $. 考虑半无限域模态缩减, 有: ${ \varPhi }_n^{\rm T} {E}_3 { \varPhi }_n ={I}$和${ \varPhi }_n^{\rm T} {E}_2 { \varPhi}_n ={ \varLambda }_n^2 $. ${ \varPhi }_n$表示包含前$n$阶特征向量的矩阵, ${ \varLambda }_n^2$表示由前$n$阶特征值组成的对角阵, $I$表示单位阵.
根据模态分解法, 得到人工边界上结点力、位移在模态空间下和物理空间下的关系为
其中, $q$和$p$分别表示模态空间下的位移和力.
将式(7)和式(8)分别代入式(3)和式(4), 得
其中${e}_1 ={ \varPhi }_n^{\rm T} {E}_1 { \varPhi }_n$, ${e}_4 ={ \varPhi }_n^{\rm T} {E}_4 { \varPhi }_n$.
将式(7)和式(8)代入式(5), 得到模态空间下人工边界的结点力-位移关系为
其中${S}={ \varPhi }_n^{\rm T} {S}^\infty { \varPhi }_n$为模态空间下半无限域的频域动力刚度.
当半无限域是单层介质时, ${E}_1 =c^2{E}_3 $, $c=\sqrt {G/\rho } $; ${E}_4 =\alpha {E}_3 $; 所以$e_1 =c^2{I}$, ${e}_4 =\alpha I$. 合式(9) $\sim\!$式(11),
得到对角形式的动力刚度矩阵$S$对角线上的元素为
其中, i是虚数单位, $\omega $表示圆频率.
3 频域动力刚度的连分式展开
本节提出一种新的连分式精确逼近单层介质模态空间下的频域动力刚度, 并将连分式扩展用于表示多层介质的动力刚度.3.1 标量连分式
式(12)表示的动力刚度系数还可以将其表达为其中, $z={\rm i}\omega /\omega _n $, $\beta =\alpha /\omega _n $.
函数$\sqrt {1+z^2+\beta z} $有如下恒等式
\begin{eqnarray*} &&\sqrt {1+z^2+\beta z} -(1+z)=\\&&\qquad\frac{(\beta-2)z}{2(1+z)+\left[ {\sqrt {1+z^2+\beta z} -(1+z)}\right]} \end{eqnarray*}
可以将其写成连分式
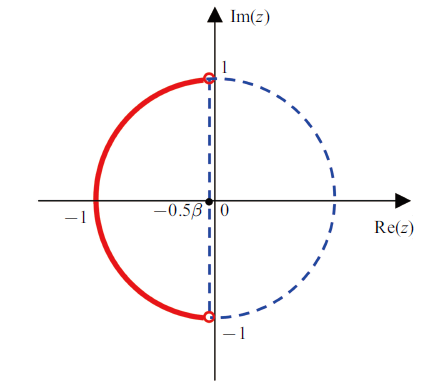
显然, $\sqrt {1+z^2+\beta z} $可以等价为若干种连分式,但不是所有的连分式都能保证在整个频率域都收敛[19].本文提出的连分式(14)在整个频率域都是收敛的.经推导得到式(14)的非收敛域为$\left| z \right|=1$, Re$(z)<-0.5\beta $,Re($z)$表示$z$的实部. 图2中左复平面的红线为连分式的非收敛域.可以看出在整个频率域$\omega =[0, \infty )$, $z$坐落在收敛域的虚轴上,所以连分式(14)对整个频率域都是收敛的.
图2
新窗口打开|下载原图ZIP|生成PPT图2连分式的收敛域
Fig. 2The convergence domain of the continued fraction
为了直观看出连分式的收敛率, 定义总绝对误差
\begin{eqnarray*} \varepsilon =\frac{\sum\limits_{l=0}^N {\left(\left| {CF-\sqrt {1+z^2+\beta z} } \right|\right)} }{N+1} \end{eqnarray*}
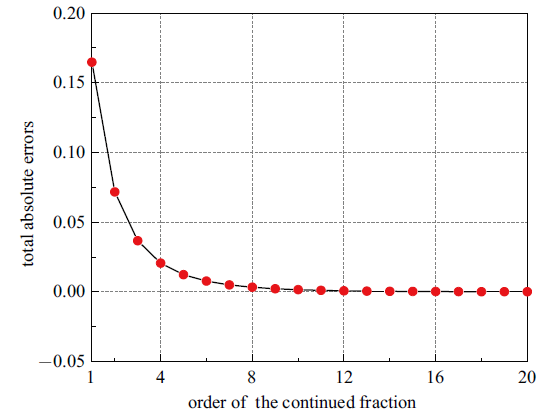
其中, $CF$表示式(14)的连分式, $N$表示频率步数. 总绝对误差与连分式阶数的关系如图3所示, 其中, 步距为0.1, $N$为10, $\beta$为0.05, 可以看出连分式是呈指数收敛的.
图3
新窗口打开|下载原图ZIP|生成PPT图3连分式的收敛率
Fig. 3The convergence rate of the continued fraction
式(14)的连分式可以写为如下形式
其中, $S_{J+1}^{-1} =0$, $g_0 =c\omega _n$, $h_0 =c$.
当$j$是奇数时
\begin{eqnarray*} g_j =\frac{1}{h_0 -0.5\alpha /\omega _n h_0}, \ \ h_j =\frac{1}{g_0 -0.5\alpha /\omega _n g_0} \end{eqnarray*}
当$j$是偶数时
\begin{eqnarray*} g_j =2g_0, \ \ h_j =2h_0 \end{eqnarray*}
3.2 矩阵连分式
由式(15)可得出单层介质的模态动力刚度为当$j$是奇数时
当$j$是偶数时
其中, 上标$-1$表示矩阵求逆.
连分式(16)可以被扩展应用于多层介质. 需要注意的是, 单层介质的$g_{0}$ 和$h_{0}$的值不适用于多层介质. 多层介质的$g_{0}$ 和$h_{0}$可以参考文献[19]的做法得到.
根据式(9) $\sim\!$式(11), 得到模态动力刚度方程
将式(16)代入式(22), 并令i$\omega $的零次项和二次项分别为0, 得到关于$g_{0}$ 和$h_{0}$的如下方程
式(23)是黎卡提方程, 可利用Matlab内置函数care直接求出$g_{0}$ 和$h_{0}$. 显然, 式(23)的解包含单层介质的解式(19).
式(16) $\sim\!$式(21)表示的连分式对于单层介质是精确且无条件收敛的. 将式(23)替换式(19)后, 连分式可以用于表示多层介质的动力刚度.
4 基于连分式的时域吸收边界条件
本节通过引入辅助变量的方式将连分式时域化, 建立能与有限元法无缝耦合的时域吸收边界条件.4.1 模态空间下的时域吸收边界条件
将式(16) $\sim\!$式(21)代入式(11), 同时引进辅助变${S}_j {\tilde{{q}}}_j ={\tilde{{q}}}_{j-1} $, $j=1$, 2, ${\cdots}$, $J$, 得到将式(24)和式(25)变换到时域, 得
其中,
\begin{eqnarray*} &&\left[ {{\begin{array}{cc} {{c}_{\rm bb}^\infty } & {{c}_{\rm bc}^\infty } \\ {{c}_{\rm cb}^\infty } & {{c}_{\rm cc}^\infty } \\ \end{array} }} \right]=\left[ {{\begin{array}{c;{2pt/2pt}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {\ \ {h}_0\ \ } & {\ \ -I\ \ } & {{\bf 0}} & \cdots & {{\bf 0}} & {{\bf 0}} \\ \hdashline[2pt/2pt] {{\bf 0}} & {{h}_1 } & {-I} & \cdots & {{\bf 0}} & {{\bf 0}} \\ {{\bf 0}} & {{\bf 0}} & {{h}_2 } & \cdots & {{\bf 0}} & {{\bf 0}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{h}_{J-1} } & {-I} \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{h}_J } \\ \end{array} }} \right] \\&& \left[ {{\begin{array}{cc} {{k}_{\rm bb}^\infty } & {{k}_{\rm bc}^\infty } \\ {{k}_{\rm cb}^\infty } & {{k}_{\rm cc}^\infty } \\ \end{array} }} \right]=\left[ {{\begin{array}{c;{2pt/2pt}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {\ \ {g}_0 \ \ } & {\ \ {\bf 0}\ \ } & {{\bf 0}} & \cdots & {{\bf 0}} & {{\bf 0}} \\ \hdashline[2pt/2pt] {-I} & {{g}_1 } & {{\bf 0}} & \cdots & {{\bf 0}} & {{\bf 0}} \\ {{\bf 0}} & {-I} & {{g}_2 } & \cdots & {{\bf 0}} & {{\bf 0}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {-I} & {{g}_{J-1} } & {{\bf 0}} \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {-I} & {{g}_J } \\ \end{array} }} \right] \\&& {q}_{\rm c} =\left\{ {{\begin{array}{*{20}c} {{q}_1^{\rm T} } & {{q}_2^{\rm T} } & \ldots & {{q}_{J-1}^{\rm T} } & {{q}_J^{\rm T} } \\ \end{array} }} \right\}^{\rm T} \end{eqnarray*}
式(26)即为模态空间下的时域吸收边界条件. 5.1和5.2节分别通过稳定性理论说明吸收边界条件在单层和多层介质中的稳定性.
4.2 物理空间下的时域吸收边界条件
将式(7)和式(8)代入式(26), 得到物理空间下的吸收边界条件$ \begin{eqnarray}\left[ {{\begin{array}{*{20}c} {{C}_{\rm bb}^\infty } & {{C}_{\rm bc}^\infty } \\ {{C}_{\rm cb}^\infty } & {{C}_{\rm cc}^\infty } \\\end{array} }} \right]=\left[ {{\begin{array}{c;{2pt/2pt}c@{\ }c@{\ }c@{\ }c@{\ }c} {\ \ {E}_3 { \varPhi }_n {h}_0 { \varPhi }_n^{\rm T} {E}_3\ \ } &{\ \ -{E}_3 { \varPhi }_n\ \ } & {{\bf 0}} & \cdots & {{\bf 0}} & {{\bf 0}} \\\hdashline[2pt/2pt] {{\bf 0}} & {{h}_1 } & {-I} & \cdots & {{\bf 0}} & {{\bf 0}} \\ {{\bf 0}} & {{\bf 0}} & {{h}_2 } & \cdots &{{\bf 0}} & {{\bf 0}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{h}_{J-1} } & {-I} \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{h}_J } \\\end{array} }} \right] \end{eqnarray} $
$ \begin{eqnarray} &&\left[ {{\begin{array}{*{20}c} {{K}_{\rm bb}^\infty } & {{K}_{\rm bc}^\infty } \\ {{K}_{\rm cb}^\infty } & {{K}_{\rm cc}^\infty } \\\end{array} }} \right]=\left[ {{\begin{array}{c;{2pt/2pt}c@{\ }c@{\ }c@{\ }c@{\ }c} {\ \ {E}_3 { \varPhi }_n {g}_0 { \varPhi }_n^{\rm T} {E}_3\ \ } &{\ \ {\bf 0}\ \ } & {{\bf 0}} & \cdots & {{\bf 0}} & {{\bf 0}} \\\hdashline[2pt/2pt] {-{ \varPhi }_n^{\rm T} {E}_3 } & {{g}_1 } & {{\bf 0}}& \cdots & {{\bf 0}} & {{\bf 0}} \\ {{\bf 0}} & {-I} & {{g}_2 } & \cdots & {{\bf 0}} & {{\bf 0}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {-I} & {{g}_{J-1} } & {{\bf 0}} \\ {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {{\bf 0}} & {-I} & {{g}_J } \\\end{array} }} \right]\end{eqnarray} $
4.3 有限元法和吸收边界条件的耦合
式(27)表示的时域吸收边界条件可以和有限元法无缝耦合.图1所示的有限域的有限元方程为其中, 下标i表示除了人工边界的有限域部分, 下标b表示人工边界部分, $f_{\rm i}$是施加在有限域的动力载荷, $K$, $C$, $M$分别是通过标准四边形等参元、双线性形函数以及四结点高斯积分得到的刚度阵、阻尼阵和质量阵.
组装式(27)和式(28), 得
式(29)可以通过标准的时间积分算法求解. 需要说明的是, 本文提出方法的精度不受有限域材料特性的影响, 有限域的介质和结构可以考虑其真实的非线性效应.
5 数值算例
通过单层介质和五层介质的数值算例来考察本文建立的吸收边界条件的精度和稳定性.5.1 单层介质
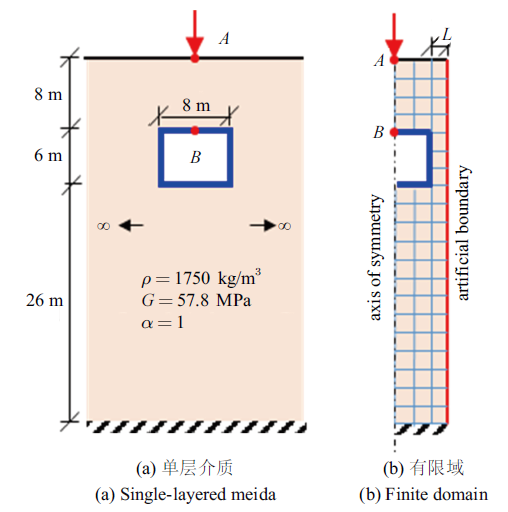
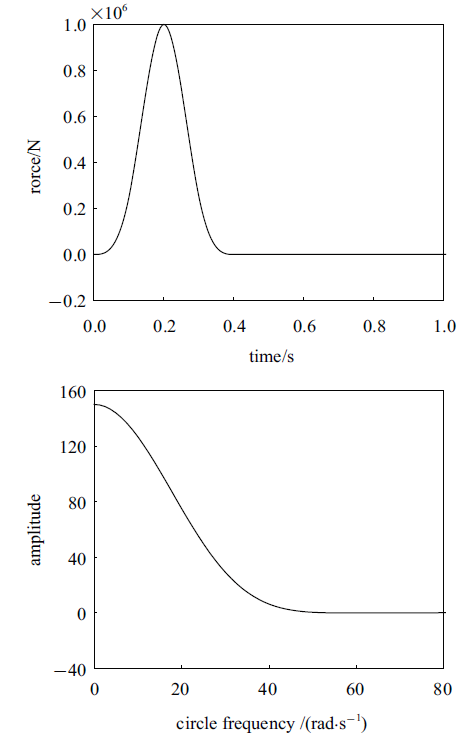
如图4(a)所示, 总高为40 m的刚性基岩上卧达朗贝尔黏弹性单层介质的场地内嵌一个矩形孔洞,其位于地表以下8 m, 尺寸为6 m $\times $ 8 m. 均匀场地的材料参数如图4(a)中所示.$A$点施加如图5所示的狄拉克脉冲点载荷, 载荷的频谱范围约为0$\sim $55 rad/s,其表达式为其中, $t$表示时间, $Z(x)=x^{3}H(x)$, $H(x)$表示Heaviside函数. 输出$B$点的位移时程.
图4
新窗口打开|下载原图ZIP|生成PPT图4单层数值算例
Fig. 4The numerical example of the single-layered medium
图5
新窗口打开|下载原图ZIP|生成PPT图5狄拉克脉冲
Fig. 5Dirac pulse
如图4(b)所示, 引入人工边界, 截取有限域用有限元法计算, 网格尺寸为2 m $\times$ 2 m.在有限域的人工边界上施加本文提出的时域吸收边界条件.由于本文的时域吸收边界条件对于单层介质是精确的,将人工边界紧靠感兴趣区域放置, 取人工边界到孔洞的距离$L$为一个网格尺寸即2 m.将只用有限元法计算足够大的计算域得出的结果作为参考解.采用Newmark常平均加速度法进行时间积分计算, 时步为0.01 s.
(1)方法的精度
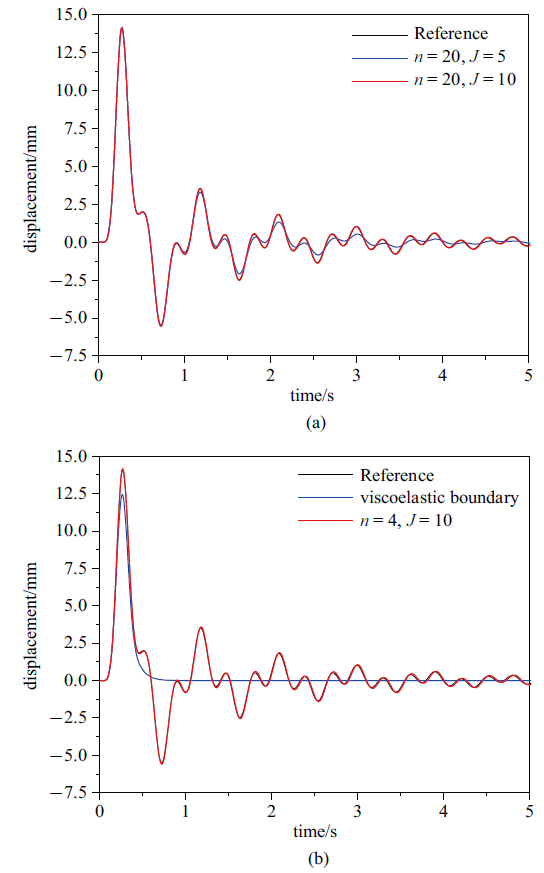
考察单层介质时本文提出的吸收边界条件的精度. $B$点的位移时程如图6所示(注: $n$表示无限域的模态数, $J$表示吸收边界条件的阶数).图6(a)是无限域取满模态时, 吸收边界条件的阶数分别为5和10时的结果.可以看出与参考解相比, $J=5$时, 1.5 s之后结果的精度降低, 当$J$提高到10时,在整个分析时间内其结果和参考解一致.以上分析说明了当吸收边条件的阶数达到要求, 吸收边界条件具有很高的精度.
图6
新窗口打开|下载原图ZIP|生成PPT图6单层介质的吸收边界条件的精度
Fig. 6Accuracy of proposed absorbing boundary condition for the single-layered medium
无限域为线弹性介质的前5阶固有圆频率分别为7.16, 21.48, 35.92, 50.55和65.31 rad/s, 为了减少计算量, 将无限域模态缩减, 取载荷能激起的前4阶模态参与计算,其结果与参考解的比较如图6(b)所示. 可以看出, 缩减模态的结果和参考解重合,说明缩减模态, 即只取载荷能激起的土层模态数能够不影响精度的同时减少计算量.图6(b)也展示了同样的边界位置处黏弹性边界的计算结果, 可以看出,黏弹性边界精度较低.
(2)方法的稳定性
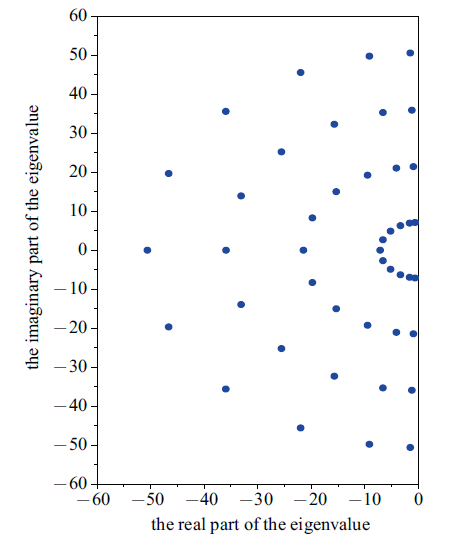
通过考察式(26)表示的模态空间下吸收边界条件的特征值分布说明吸收边界条件的稳定性,即特征值全部分布在复平面左侧, 说明吸收边界条件是稳定的.图7是吸收边界条件取模态数$n=4$和阶数$J=10$时特征值的分布. 可以看出,特征值全部分布在复平面左侧, 且特征值的分布规律是:特征值分布在一族位于复平面左侧的同心半圆上, 半圆的数目是模态数$n$,每个半圆上特征值的数目是$J+1$. 以上分析说明, 吸收边界条件对于单层介质是稳定的.
图7
新窗口打开|下载原图ZIP|生成PPT图7单层介质的吸收边界条件的稳定性
Fig. 7Stability of proposed absorbing boundary condition for the single-layered medium
5.2 多层介质
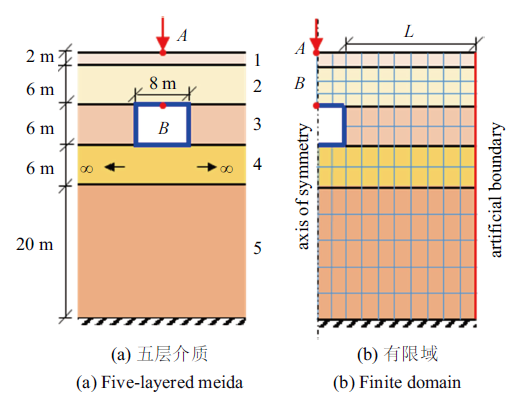
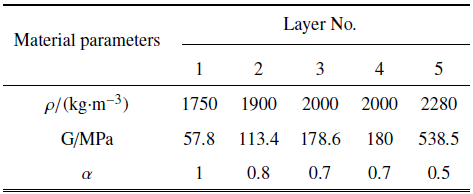
如图8(a)所示, 总高$H$为40 m的刚性基岩上卧达朗贝尔黏弹性五层介质的场地内嵌一个矩形孔洞,其位于地表以下8 m, 尺寸为6 m $\times $ 8 m. 场地每层的高度如图中所示,每层的材料参数如表1所示. $A$点施加如图5所示的狄拉克脉冲点载荷,输出$B$点的位移时程.图8
新窗口打开|下载原图ZIP|生成PPT图8五层数值算例
Fig. 8The numerical example of the five-layered media
Table 1
表1
表1五层介质的材料参数
Table 1
 |
新窗口打开|下载CSV
分析方法与5.1节单层介质算例类似. 因为表示多层介质动力刚度的连分式是通过简单扩展单层介质的连分式获得的,必然会有误差引进. 为了使吸收边界条件对于多层介质具有高精度的特性,人工边界的位置到感兴趣区域的距离$L$需要被讨论, 分别取$L=0.5$ $H$和$L=0.75$ $H$.从上到下每层竖向网格的尺寸为2 m, 2 m, 3 m, 3 m和4 m, 横向网格尺寸为2.5 m,如图8(b)所示. 时步为0.004 s.
(1)方法的精度
考察多层介质时本文提出的吸收边界条件的精度. 无限域为线弹性五层介质的前3阶固有圆频率分别为17.21, 41.39, 67.20 rad/s,取载荷能激起的前2阶模态参与计算, $J$取10. 两种人工边界位置$L=0.5$ $H$, $L=0.75$ $H$的结果如图9所示(注:$L$表示人工边界到感兴趣区域的距离). 可以看出两种边界位置的结果几乎完全重合,说明$L=0.5$ $H$时所提出的吸收边界条件已具有很高的精度. 图9还展示了$L=0.5$ $H$边界位置处黏弹性边界的结果, 可以看出黏弹性边界精度较低.
图9
新窗口打开|下载原图ZIP|生成PPT图9五层介质的吸收边界条件的精度
Fig. 9Accuracy of proposed absorbing boundary condition for the five-layered media
(2)方法的稳定性
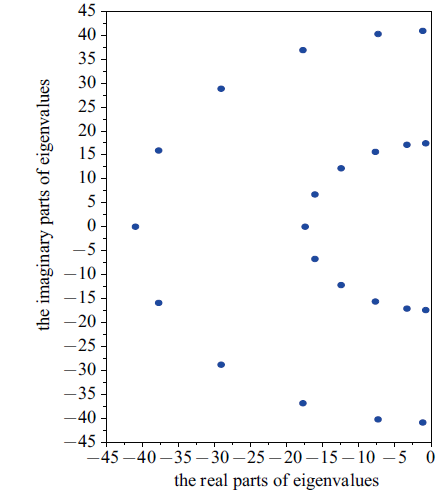
对于上述五层介质, 其吸收边界条件取$n=2$, $J=10$时特征值的分布如图10所示.特征值都分布在复平面左侧, 且特征值的分布规律与单层介质相同,即特征值分布在一族位于复平面左侧的同心半圆上, 半圆的数目是模态数$n$,每个半圆上特征值的数目是$J+1$. 以上分析说明, 吸收边界条件对于五层介质是稳定的.
图10
新窗口打开|下载原图ZIP|生成PPT图10五层介质的吸收边界条件的稳定性
Fig. 10Stability of proposed absorbing boundary condition for the five-layered media
6 结论
本文建立了一个高精度的时域吸收边界条件,与有限元法结合用于分析达朗贝尔黏弹性成层介质中出平面SH波动响应.结合半离散和模态分解获得半无限域模态空间下的频域动力刚度,并显式地表示出了达朗贝尔黏弹性单层介质模态空间下的频域动力刚度.为了将频域动力刚度时域化,采用一种全频域收敛的连分式精确逼近单层介质模态空间下标量形式的频域动力刚度;将标量连分式扩展为矩阵形式用来表示多层介质的频域动力刚度. 通过引进辅助变量,将模态空间下基于连分式的动力刚度关系转化为时域吸收边界条件,进一步转换到物理空间后得到物理空间下的时域吸收边界条件.
数值算例表明,本文建立的吸收边界条件对于达朗贝尔黏弹性单层介质是精确且稳定的;对于达朗贝尔黏弹性多层介质, 为了保证精度,需要将人工边界放置在距离感兴趣区域约为0.5倍无限域高度的位置处.吸收边界条件仅用能被载荷激起的无限域模态数参与计算, 不但能减少计算量,同时还不影响精度.
下一步工作可以通过等效线性化方法[31, 44]考虑被截掉的无限域的非线性效应. 另外, 本文的工作还可以被扩展用于模拟矢量波在无限成层介质中的传播问题.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 7]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 4]
[本文引用: 3]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
