, 吕爱钟华北电力大学可再生能源学院,北京102206
ANALYTICAL STRESS SOLUTION RESEARCH ON AN INFINTE PLATE CONTIANING TWO NON-CIRCULAR HOLES1)
ZengXiangtai, 中图分类号:O343.1
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1437KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
不同载荷作用下的带有不同形状孔的各向同性板,在航空航天、船舶、汽车、机械等工程领域有着广泛的应用.对于不同的工程需求,在板中有不同的开孔结构.其中最普遍的是圆孔,还有椭圆孔,多边形孔以及键槽孔等复杂孔形.由于几何形状以及施加的载荷不同,孔边的应力分布不可能是均匀的,在某些地方可能产生很大的应力集中[1].由于在应力集中的地方容易出现脆性断裂和塑性变形等失效现象[2-5],因此在工程中,对于带孔板的设计,都需要准确了解孔边应力集中的大小.
对于无限大平板中含有一个圆孔的问题,当远处的载荷为均匀分布时,早在1898年Kirsch就给出了它的应力解析解[6].对于无限平板中含有一个椭圆孔,矩形孔和其他多边形孔的问题,许多****运用复变函数法研究了其在不同外载荷下孔边应力集中情况[7- 11]. 朱大勇和蔡永祥[12 -13]将无限域中含有单个孔的问题化为半无限域问题,获得了逼近的解析解.求解无限平板中含一个任意形状孔的问题,都可以使用复变函数法中的保角变换方法进行求解[14-15].使用保角变换的方法,可以将板中含有单个椭圆,正方形及其他复杂形状孔映射到象平面上的单位圆外域或圆内域,从而利用复变函数方法获得问题的解析解.
如果两孔之间的距离远大于孔的尺寸,它们之间应力场的相互影响就可以不用考虑.但是很多情况下两孔的间距不大,其相互影响便不能忽略.相对于只含有单个孔的问题,求解平板中含有两个或两个以上孔问题的难度将大大增加.对于无限平板中含有两个圆孔的问题,许多****运用不同的解析方法获得了该问题的解.利用Jeffery[16]提出的双极坐标法,Ling[17],Iwaki 和Miyao[18],以及Kumari等[19]分别解决了无限板中含有两个等圆和不等圆孔受不同载荷的问题.Green[20]使用双调和分析的方法获得了两个圆孔在无穷远处受力但孔边不受力情况下的解,2008年Hoang和Abousleiman[21]推广了Green的解,使其可以解决孔边受力的情况.利用Muskhelishvili提出的复变函数方法,Haddon[22]和王林江等[23]也获得了两个圆孔问题的解,吕爱钟等[24]获得了一个圆孔和一个椭圆孔问题的解,曾祥太等[25]同样使用复变函数法解决了两个椭圆孔的问题.但是对于形状更加复杂的双孔问题目前只能使用迭代逼近的方法,张路青等[26-27]使用Schwartz交替法对两个相邻任意形状孔进行了求解,朱大勇和蔡永祥[28]则使用化为半无限域问题的迭代方法进行了求解.
在实际工程中有时会遇到板内含有一个正方形孔和一个椭圆形孔的问题,这个问题早在1968年以前就被研究过[29],但是由于问题的复杂性,仅仅使用Schwartz交替法给出了它的一阶近似解,而此方法要经过多次迭代才能得到较高的精度,因此其解存在很大的误差.本文将使用保角变换方法对该问题进行求解,拟解决板在远处受有均布载荷和孔边受有垂直均布压力的应力计算问题,一次性获得了具有高精度的解析解.
1 映射函数的解法
根据黎曼映射定理,物理平面上的任意双连通域,只要域的边界为光滑的曲线,则都能保角映射到象平面上的一个圆环,且映射函数是唯一的[30].当讨论的区域为有限双连通域时,已有一些数值方法确定映射函数[31-35],但当讨论的区域为无限双连通域,即无限域内含有两个孔洞的问题,目前所见到的只是简单孔形映射函数的确定方法[24-25],对于复杂的一般孔形目前尚未见到确定映射函数的一般性方法.本文利用具有一般形式的映射函数,结合Korn等[36]提出的映射函数,分两步把带有一个正方形孔和一个椭圆孔的无限域映射成了一个圆环,且这种方法对于任意两个关于同轴对称的孔都适用.先把$z$平面上的一个正方形和一个椭圆(图1所示)映射到{$\zeta$}$_{1}$平面上的两个圆(图2(a)所示),再映射为{$\zeta$}平面上的一个圆环(图2(b)所示).图1中的$A$,$B$,$C$,$D$为孔边界与$x$轴的交点,它们在{$\zeta$}$_{1}$平面和{$\zeta $}平面上的象点分别为$A'$,$B'$,$C'$,$D' $和$A",B",C",D"$.
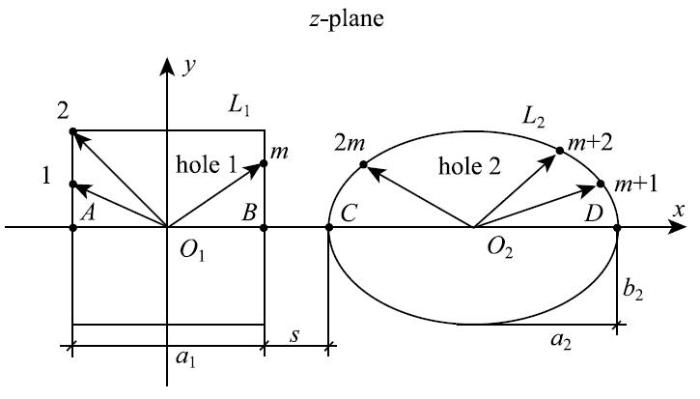显示原图|下载原图ZIP|生成PPT图1$z$平面中的一个正方形孔和一个椭圆孔...
-->Fig. 1A square hole and an elliptical hole in $z$-plane
-->
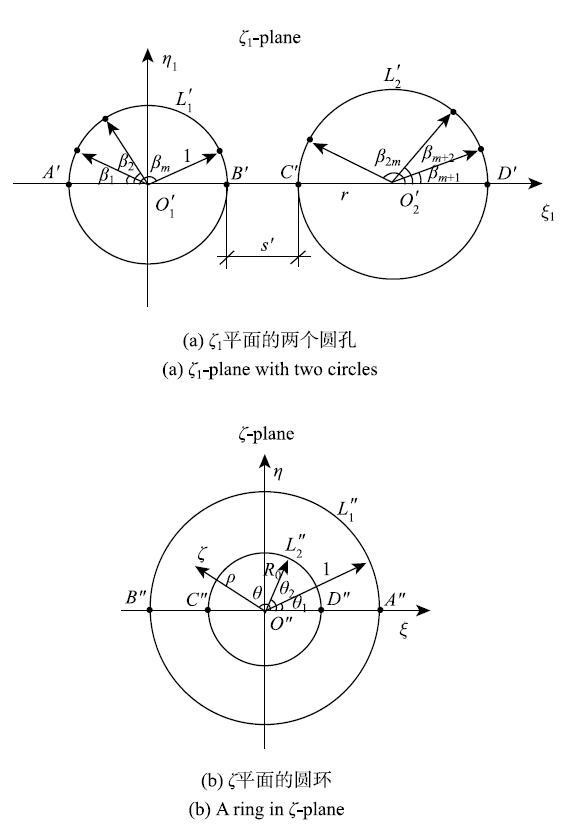显示原图|下载原图ZIP|生成PPT图2映射成的区域...
-->Fig. 2Mapped region
-->
本文令将$z$平面映射到{$\zeta$}$_{1}$平面的映射函数一般形式如下
\begin{equation}\label{eq1} \begin{array}{ll} z = \omega _1 (\zeta _1 ) = R\bigg[\zeta _1 + c_0 +\sum\limits_{j = 1}^{k_1 } {\lambda _j \zeta _1 ^{-j} + }\\[4mm]\qquad \sum\limits_{j = 1}^{k_2 } {\lambda _{-j} \left({\zeta _1-s_3 } \right)^{-j}} \bigg]\tag{1}\end{array}\end{equation}
图2(a)中的左圆的半径为1,孔距$s'$和右圆的半径$r$未知,式(1)中的$s_{3}$=1+$s'+r$.取$k$={${k}$}$_{1}=k_{2}$,则$R$,$c_{0}$,{$\lambda$}$_{1}$,$\cdots$,{$\lambda$}$_{k}$和$\lambda_{-1},\cdots,$ {$\lambda$}$_{-k}$也是待确定的未知量,但由于孔形关于$x$轴对称,这些都是实数.如何确定上面的2$k$+4个未知量是非常重要的一步,本文根据两个孔边有限个点的坐标对应关系,利用最优化方法获得这些参数.图1中孔1和孔2都取$m$个点,映射后对应于图2的2$m$个未知点,得到关于$x$-\!轴坐标和$y$-\!轴坐标的4$m$个等式约束,以及$A, B, C, D$对应于图2的 $A' $,$B' $,$C'$,$D'$,得到关于$x$轴坐标的4个等式约束.加上2$m$个关于角度大小的不等式约束,以及角度,孔距和半径的4个非零约束,共6$m$+8个约束.
优化问题的数学模型为
\begin{equation}\label{eq1} \left. {\begin{array}{ll} \min F(X)&\left( {X \in E\subset R^n} \right)\\[2mm] E:\;\;G_{j_1 } \left( X \right) > 0&\left( {j_1 = 1,2,\;\cdots,k_3 } \right) \\[2mm]H_{j_2 } \left( X \right) = 0&\left( {j_2 =1,2,\cdots ,k_4 } \right) \\ \end{array}} \right\}\tag{2}\end{equation}
本文运用混合罚函数法求解未知参数.罚函数法就是将等式和不等式约束函数分别构成惩罚项,加到目标函数$F(X)$上,构成一个新的无约束目标函数$P(X$,$r_{f})$,把有约束问题化为求罚函数$P(X$,$r_{f})$的无约束极小值问题.
对于本文问题,$k_{3}$=2$m$+4,$k_{4}$=4$m$+4.因为没有目标函数$F(X)$,只要满足不等式和等式约束即可.其具体约束以及罚函数如下所示
$$E:G_{j_1 } (X) = \beta _{j_1 + 1}-\beta _{j_1 } > 0,\;j_1 =1,2,\cdots,m-1 \\ \ G_{m + j_1 } (X) = \beta _{m + j_1 + 1}-\beta _{m + j_1 } >0,\;j_1 = 1,2,\cdots,m-1 \\ \ G_{j_1 } (X) = \pi-\beta _{j_1 } > 0, \;j_1 = m,2m \\ \ G_{2m + 1} (X) = \beta _1 > 0 \\ \ G_{2m + 2} (X) = \beta _{m + 1} > 0 \\ \ G_{2m + 3} (X) = {s}' > 0 \\ \ G_{2m + 4} (X) = r > 0 \\ \ H_{j_2 } (X) = x_{j_2 }-{ Re}\left[ {\omega _1 \left( {{e}^{{ i}(\pi -\beta _{j_2 } )}} \right)} \right] = 0,j_2 = 1,2,\cdots,m \\ \ H_{m + j_2 } (X) = y_{j_2 }-{ Im}\left[ {\omega _1 \left({{ e}^{{ i}(\pi-\beta _{j_2 } )}} \right)} \right] = 0,j_2 = 1,2,\cdots,m \\ \ H_{2m + j_2 } (X) = x_{m + j_2 }-{ Re}\left[ {\omega _1\left( {1+ {s}' + r + r{ e}^{{ i}\beta _{m + j_2 } }} \right)} \right]=\ \\ \qquad 0,j_2 =1,2,\cdots,m \\ \ H_{3m + j_2 } (X) = y_{m + j_2 }-{ Im}\left[ {\omega _1\left( {1+ {s}' + r + r{ e}^{{ i}\beta _{m + j_2 } }} \right)} \right]= \\ \qquad 0,j_2 =1,2,\cdots,m \\ \ H_{4m + 1} (X) = x_A-{ Re}\left[ {\omega _1 \left( {-1}\right)} \right] = 0 \\\ H_{4m + 2} (X) = x_B-{ Re}\left[ {\omega _1 \left( 1\right)}\right] = 0 \\ \ H_{4m + 3} (X) = x_C-{ Re}\left[ {\omega _1 \left( {1 +{s}'}\right)} \right] = 0 \\ \ H_{4m + 4} (X) = x_D-{ Re}\left[ {\omega _1 \left( {1 + {s}'+ 2r} \right)} \right] = 0$$
$$P(X,\;r_{ f} ) = r_{ f} \sum\limits_{j_1 \in I_1 }{\ln \frac{1}{G_{j_1 } (X)}} + \sum\limits_{j_1 \in I_2 }\frac{1}{r_{ f} }\ \qquad \left\{ {\min [0,G_{j_1 } (X)]} \right\} ^2+ \frac{1}{r_{ f} }\sum\limits_1^{4m + 4} {H_{j_2 }^2 (X)}\tag{3}$$
这里$I_1 = \left\{ {\left. {j_1 } \right|G_{j_1 } (X) >0;1 \le j_1 \le 2m + 4} \right\}$,$I_2 = \left\{ {\left. {j_1 }\right|G_{j_1 } (X) \le 0;1 \le j_1 \le 2m + 4} \right\}$,$r_{f}$是罚因子,$X$为设计变量,$X = \bigg[ R,c_0 ,{s}',r,\lambda _1,\cdots, \lambda _k ,\lambda _{-1}, \cdots, \lambda _{-k},$ $\beta _1, \cdots,\beta _{2m} \bigg]^{T}$,符号Re[ ]为取实部,Im[ ]为取虚部.
求解过程为：先给定$X$的一组计算初始点$X^{(0)}$以及控制精度{$\varepsilon$}. 罚因子$r_{f}$为一系列确定的单调递减的正值,每改变一次$r_{f}$就构造一个新的罚函数$P(X$,$r_{ f})$.若到第$k$个$r_{f}$时,由式(3)求解无约束最小值问题,得到的$X^{(k)}$使得$P(X$,$r_{f})<${$\varepsilon $},则$X^{(k)}$即为问题的解.其中使用变尺度法(DFP)求解无约束最小值问题.
根据函数的连续性,只要有限个点满足约束条件,映射图形和实际图形就很相似了.从本质上说,这就是一个根据不等式和等式求未知数的过程,所以等式个数要大于或等于未知数个数,即$k\le m$.一般来说$m$,$k$越大,优化结果和原图形吻合得越好,不过我们发现对于本文的问题,在$k$=8时,映射结果就很好了.
取正方形边长$a_{1}$=4,椭圆长半轴$a_{2}$=3,短半轴$b_{2}$=2,孔距$s$=4.取$m$=10,$k$=8. 初值设为
$$\left. {\begin{array}{ll} R = c_0 = {s}' = r = 1.0 \\[2mm] \lambda _j = \lambda _{-j} = 0,&j = 1,2,\cdots,8 \\[3mm] \beta _j = \beta _{10 + j} = \dfrac{3.14j}{11}\;,&j = 1,2,\cdots,10 \\ \end{array}} \right\}$$
经过11 866次搜索,达到精度1.0$\times $10$^{ -6}$,所得到的映射函数系数为
$$\begin{array}{l} \left[ {{s}',r,R,c_0 ,\lambda _1 ,\cdots, \lambda _8,\lambda _{-1}, \cdots, \lambda _{-8} } \right] = [1.640,1.033,\\\qquad 2.414, 6.217\times 10^{-2}, 0.559~2\times 10^{-3}, -0.189~3\times 10^{-2},\\\qquad -0.170~5, 0.226~6\times 10^{-2}, 0.281~1\times10^{-3}, 0.655~8\times \\\qquad 10^{-3}, 0.168~9\times 10^{-1}, -0.495~1\times10^{-3}, 0.213~1, \\\qquad -0.132~0\times 10^{-4}, 0.335~9\times 10^{-4},-0.212~2\times 10^{-4}, \\\qquad 0.102~1\times 10^{-4}, -0.617~4\times 10^{-5}, 0.253~89\times 10^{-5}, \\\qquad -0.110~2\times 10^{-5}]\end{array}$$
映射函数描绘的实际形状见图3.
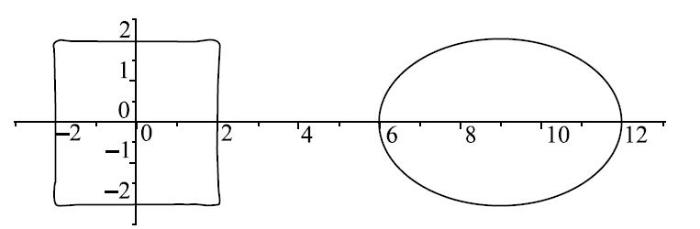显示原图|下载原图ZIP|生成PPT图3映射成的正方形和椭圆...
-->Fig. 3Mapped square and ellipse
-->
再根据Korn提出的映射函数将{$\zeta$}$_{1}$平面的两个圆映射成{$\zeta $}平面的圆环
\begin{equation}\label{eq3} \zeta _1 = \omega _2 (\zeta ) = \frac{\zeta -d}{d\zeta-1}\tag{4}\end{equation}
其中
$$d = \frac{1 + \xi _{F'} \xi _{D'} + \sqrt {\left( {\xi _{F'}^2 -1} \right)\left( {\xi _{D'}^2-1} \right)} }{\xi _{F'} + \xi_{D'} }\ R_0 = \frac{\xi _{F'} \xi _{D'}-1-\sqrt {\left( {\xi _{F'}^2- 1} \right)\left( {\xi _{D'}^2-1} \right)} }{\xi _{F'}-\xi_{D'} }\ \xi _{F'} = s_3 + r,~\xi _{D'} = s_3-r$$
图2(b)中$\zeta = \rho { e}^{{ i}\theta },{ i} = \sqrt{-1}.$ 边界{$\rho$}=1对应于图1中的$L_{1}$边界,边界{$\rho$}=$R_{0}$对应于图1中的$L_{2}$边界.
那么最终把一个正方形孔和一个椭圆形孔映射成圆环的映射函数应该具有如下一般形式
$$z = \omega (\zeta ) = R \left[\dfrac{\zeta-d}{{d}\zeta-1} +c_0 + \sum\limits_{j = 1}^{k_1 } {\lambda _j \left(\dfrac{\zeta- d}{d\zeta-1}\right)^{-j}}+ \right.\\ \qquad\left.\sum\limits_{j = 1}^{k_2 } {\lambda _{-j}\left(\dfrac{\zeta-d}{d\zeta-1}-s_3 \right)^{-j}}\right]\tag{5} $$
$\zeta$}平面的圆环在极坐标系下的极径和极角等于常数的坐标线(图4(a)),经$z= \omega (\zeta)$共形映射后,对应于$z$平面的正交的曲线,部分对应曲线如图4(b)所示.
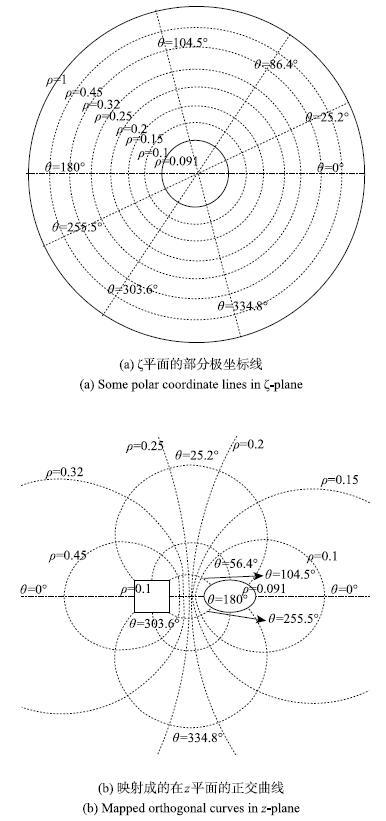显示原图|下载原图ZIP|生成PPT图4圆环极坐标线映射成的线簇...
-->Fig. 4Cluster mapped from polar coordinate curves of the ring
-->
2 解析函数表示的应力边界条件
对于本文所讨论的问题(如图5所示),正方形边长为$a_{1}$,椭圆长半轴为$a_{2}$,短半轴为$b_{2}$,孔距$s$.假设无穷远处受均布的水平应力$\sigma _x^\infty $、垂直应力$\sigma_y^\infty $和剪力$\tau _{xy}^\infty$,孔1和孔2边界分别作用垂直边界的均布压力$P_{1}$,$P_{2}$.本文规定正应力都以压为正,以拉为负.对于复变函数方法,二维平面弹性问题涉及两个解析函数,本文用$\phi _1 \left( z \right)$和$\psi _1\left( z \right)$表示. 这里$z = x + { i}y$是复变量.于是应力边界条件可以表示为
\begin{equation}\label{eq1} \phi _1 \left( z \right) + z\overline {{\phi }'_1\left( z \right)} + \overline {\psi _1 \left( z \right)} = {i}\int_L {\left( {X_M + { i}Y_M } \right){ d}s + c_A}\tag{6}\end{equation}
式中,$X_{M}$和$Y_{M}$分别是作用在孔边界上沿$x$轴及$y$轴的面力分量;$M$=1,2分别对应孔1和孔2; $L$为孔的边界,$c_{A}$为复常数.
显示原图|下载原图ZIP|生成PPT图5含有一个正方形孔和一个椭圆孔的无限平板受均布力...
-->Fig. 5A square hole and an elliptical hole in an infinite plate with uniform stress
-->
对于无限域问题,两个解析函数$\phi _1 \left( z \right)$和$\psi _1\left( z \right)$具有如下形式
\begin{equation}\label{eq2} \varphi _1 \left( z \right) =-\frac{1}{2\pi \left({1 + \kappa } \right)}\sum\limits_{j = 1}^M {\left( {X_j + {i}Y_j } \right)} \ln z + \left( {b + { i}c} \right)z + \varphi_0 \left( z \right)\tag{7}\end{equation}
\begin{equation}\label{eq3} \psi _1 \left( z \right) = \frac{\kappa }{2\pi\left( {1 + \kappa } \right)}\sum\limits_{j = 1}^M {\left( {X_j- { i}Y_j } \right)} \ln z + \left( {{b}' + { i}{c}'}\right)z + \psi _0 \left( z \right)\tag{8}\end{equation}
其中,{$\kappa$}与材料性质有关,平面应变问题{$\kappa$}=$3-4${$\upsilon$},平面应力问题$\kappa=(3-\upsilon)/(1+\upsilon)$,{$\upsilon $}是材料的泊松比.$b = \left( {\sigma _x^\infty + \sigma _y^\infty } \right) /4$,${b}' = \left( {\sigma _y^\infty-\sigma _x^\infty } \right)/ 2$,${c}' = \tau _{xy}^\infty$,$c$反映无穷远处的刚体转动,不考虑刚体转动则$c=$0,$\varphi _0\left( z \right)$和$\psi _0 \left( z\right)$为区域内的单值解析函数.
对于本文的问题$\sum\limits_{j = 1}^M {X_j } = \sum\limits_{j= 1}^M {Y_j } = 0$,则式(7)和式(8)可简化为
$$\phi _1 \left( z \right) = \left( {b + { i}c} \right)z + \phi_0\left( z \right)\tag{9}\\ \psi _1 \left( z \right) = \left( {{b}' + { i}{c}'} \right)z +\psi _0 \left( z \right)\tag{10}$$
由${ i}\int_{L_1 } {\left( {X_1 + { i}Y_1 }\right)} { d}s = P_1 z$和${ i}\int_{L_2 } {\left( {X_2 +{ i}Y_2 } \right)} { d}s = P_2 z$,则孔1和孔2边界条件可以写为
$$\varphi _1 \left( z \right) + z\overline {{\varphi }'_1 \left( z\right)} + \overline {\psi _1 \left( z \right)} = P_1 z,\;\;z \inL_1\tag{11}\\ \varphi _1 \left( z \right) + z\overline{{\varphi }'_1 \left( z \right)} + \overline {\psi _1 \left( z\right)} = P_2 z + c_A ,\;\;z \in L_2\tag{12}$$
不失一般性,这里已令孔1边界条件的$c_{A}$等于零,将孔2边的$c_{A}$视为待求复常数.
由$z = \omega \left( \zeta \right)$,$\varphi _0 \left( z\right)$和$\psi _0 \left( z\right)$单值解析,则它们在圆环域内可写成关于{$\zeta$}的洛朗级数形式
$$\varphi _0 \left( z \right) = \phi _0 \left( \zeta \right) =\sum\limits_{j = 0}^\infty {a_j } \zeta ^j + \sum\limits_{j= 1}^\infty {b_j } \zeta ^{-j}\tag{13}$$
$$\psi _0\left( z \right) = \psi _0 \left( \zeta \right) =\sum\limits_{j = 0}^\infty {c_j } \zeta ^j + \sum\limits_{j= 1}^\infty {d_j } \zeta ^{-j}\tag{14} $$
式中,$a_{j}$,$b_{j}$,$c_{j}$和$d_{j}$为待求的复数.
从式(6)到式(14),令孔1边界$\zeta = \sigma $,孔2边界$\zeta = R_0\sigma $,这里$\sigma = { e}^{{ i}\theta}$,应力边界条件可以写成
$$\varphi _0 \left( \sigma \right) + \frac{\omega \left( \sigma\right)}{\overline {{\omega }'\left( \sigma \right)} }\overline{{\varphi }'_0 \left( \sigma \right)} + \overline {\psi _0 \left(\sigma \right)}=\\ \qquad -\left( {2b-P_1 } \right)\omega \left( \sigma \right)- \left( {{b}'-{ i}{c}'} \right)\overline {\omega \left(\sigma \right)}\tag{15}$$
$$\varphi _0 \left( {R_0 \sigma} \right) + \frac{\omega \left( {R_0 \sigma } \right)}{\overline{{\omega }'\left( {R_0 \sigma } \right)} }\overline {{\varphi }'_0\left( {R_0 \sigma } \right)} + \overline {\psi _0 \left( {R_0\sigma } \right)-} c_A= \\ \qquad-\left( {2b -P_2 } \right)\omega \left( {R_0 \sigma } \right)\;-\left( {{b}'- { i}{c}'} \right)\overline {\omega \left( {R_0 \sigma }\right)}\tag{16}$$
3 求解的基本方程组
式(15)和式(16)对于任意$\sigma \left( {\sigma = { e}^{{i}\theta }} \right)$都成立,则等式左右两边{$\sigma$}的所有同幂次项系数必须相等.为了形成关于$a_{j}$,$b_{j}$,$c_{j}$和$d_{j}$的方程组,需将式(15)和式(16)写成不带分式的{$\sigma$}的幂级数形式. 但是其中的$\omega (\sigma )$,$\omega (R_0 \sigma)$,$\omega (\sigma ) / \overline {{\omega }'(\sigma )} $和$\omega(R_0 \sigma ) / \overline {{\omega }'(R_0 \sigma )}$都是分式函数且相当复杂,难以通过解析方法直接展开为幂级数,所以本文将使用数值方法直接将它们展开[37].以$\omega (\sigma )$为例,由$\sigma = { e}^{{ i}\theta}$可知$\omega (\sigma )$是变量{$\theta$}的函数,且以2{$\pi$}为周期,则可将它展开为周期为2{$\pi $}的傅里叶级数
\begin{equation}\label{eq12} \omega (\sigma ) = \sum\limits_{j = 1}^{n_1 } {e_j} \sigma ^{-j} + \sum\limits_{j = 0}^{n_1 } {f_j } \sigma^j\tag{17}\end{equation}
其中,$e_{j}$和$f_{j}$只与映射函数的系数$R$,$c_{0}$,$\lambda_{1}$,$\cdots$,$\lambda _{k}$和$\lambda _{ -1}$,$\cdots$,$\lambda _{-k}$相关. 式(17)对任意的$\theta \in[0,2\pi ]$都应成立,于是在区间$[0,2\pi ]$内取有限个$\theta _j$,式(17)右边级数取有限项来建立求解$e_{j}$和$f_{j}$的复线性方程组.具体求解过程如下.
式(17)右边的最高正负幂次都取为$n$,则$\theta _j $取为
$$\theta _j = \frac{2\pi (j-1)}{2n + 1},\mbox{ }j = 1,2, \cdots,2n + 1$$
即区间$[0,2\pi]$被2$n$+1等分,边界上得到2$n$+1个点.对于不同的$\theta _j $,$\omega (\sigma ) = \omega ({ e}^{{i}\theta _j })$. 从而得到复数线性方程组
\begin{equation}\label{eq13} U = WV\tag{18}\end{equation}
其中
$$W = \left[ {{\begin{array}{*{20}c} {{ e}^{ -{ i}(2n + 1)\theta _1 }} & {{ e}^{ -{ i}(2n)\theta _1 }} &\cdots & {{ e}^{ -{ i}\theta _1 }} & 1 & {{ e}^{{i}\theta _1 }} & \cdots & {{ e}^{{ i}(2n)\theta _1 }} &{{ e}^{{ i}(2n + 1)\theta_1 }} \\ {{ e}^{ -{ i}(2n + 1)\theta _2 }} & {{ e}^{ -{ i}(2n)\theta _2 }} &\cdots & {{ e}^{ -{ i}\theta _2 }} & 1 & {{ e}^{{i}\theta _2 }} & \cdots & {{ e}^{(2n)\theta _2 }} & {{e}^{{ i}(2n + 1)\theta_2 }} \\ \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\ {{ e}^{ -{ i}(2n + 1)\theta _{2n + 1} }} & {{ e}^{ -{ i}(2n)\theta _{2n + 1}}} & \cdots & {{ e}^{ -{ i}\theta _{2n + 1} }} & 1 &{{ e}^{{ i}\theta _{2n + 1} }} & \cdots & {{e}^{(2n)\theta _{2n + 1} }} & {{ e}^{{ i}(2n + 1)\theta_{2n + 1} }}\end{array} }} \right]$$
$$\begin{array}{ll} U = \left[ {\omega ({ e}^{{ i}\theta _1 })~\mbox{}\omega ({ e}^{{ i}\theta _2 })\mbox{ } \cdots \mbox{}\omega ({e}^{{ i}\theta _{2n + 1} })} \right]^{ T}\\[3mm] V = \left[ {e_n \mbox{ }e_{n-1} \cdots \mbox{ }e_k \cdots\mbox{ }e_1 \mbox{ }f_0 \mbox{ }f_1 \cdots f_{n-1} \mbox{ }f_n }\right]^{ T}\end{array}$$
因${ W}$和${ U}$都是复常数,所以式(18)是关于${V}$的复数线性方程组. 但对于本文的问题,所求出的${V}$都是实常数.通过算例发现,$n$取150项以上时,所求得的$e_{j}$和$f_{j}$的绝对值就非常小了,接近$1\times 10^{-8}$.
$\omega (R_0 \sigma )$,$\omega (\sigma ) / \overline {{\omega}'(\sigma )} $和$\omega (R_0 \sigma ) / \overline {{\omega }'(R_0\sigma )} $也可以以同样的方式展开成
$$\omega (R_0 \sigma ) = \sum\limits_{j = 1}^{n_1 } {g_j }\sigma ^{-j} + \sum\limits_{j = 0}^{n_1 } {h_j } \sigma ^j\tag{19}$$
$$\dfrac{~~ \omega (\sigma )~~ }{\overline {{\omega }'(\sigma )} }= \sum\limits_{j = 1}^{n_2 } {l_j } \sigma ^{-j} +\sum\limits_{j = 0}^{n_2 } {m_j } \sigma ^j\tag{20}$$
$$\dfrac{~~\omega (R_0 \sigma )~~}{\overline {{\omega }'(R_0 \sigma)} } = \sum\limits_{j = 1}^{n_2 } {s_j } \sigma ^{-j} +\sum\limits_{j = 0}^{n_2 } {t_j } \sigma ^j\tag{21}$$
代入式(17)和式(20),式(15)的左边为
$$\varphi _0 \left( \sigma \right) + \dfrac{~~\omega \left( \sigma\right)~~}{\overline {{\omega }'\left( \sigma \right)} }\overline{{\varphi }'_0\left( \sigma \right)} + \overline {\psi _0 \left( \sigma \right)} = \\ \qquad \sum\limits_{j = 0}^\infty {a_j \sigma ^j} +\sum\limits_{j = 1}^\infty {b_j \sigma ^{-j}} +\sum\limits_{j = 0}^\infty {\overline c _j \sigma ^{- j}} + \\ \qquad \sum\limits_{j = 1}^\infty {\overline d _j \sigma ^j}+\left( {\sum\limits_{j = 1}^{n_2 } {l_j } \sigma ^{-j} +\sum\limits_{j = 0}^{n_2 } {m_j } \sigma ^j} \right)\;\cdot \\ \qquad \left( {\sum\limits_{j = 1}^\infty {j\overline a _j }\sigma ^{-j + 1}-\sum\limits_{j = 1}^\infty {j\overline b_j } \sigma ^{j + 1}} \right) \tag{22}$$
右边为
$$-\left( {2{b}'-P_1 } \right)\omega \left( \sigma \right) -\left( {{b}'- { i}{c}'} \right)\overline {\omega \left( \sigma \right)} = \\ \qquad-\left( {2b-P_1 + {b}'-{ i}{c}'} \right)f_0 -\\ \qquad \sum\limits_{j = 1}^{n_1 } {\left[ {\left( {2b-P_1 }\right)e_j + \left( {{b}'-{ i}{c}'} \right)f_j }\right]} \sigma ^{-j}- \\ \qquad \sum\limits_{j = 1}^{n_1 } {\left[ {\left( {2b-P_1 }\right)f_j + \left( {{b}'-{ i}{c}'} \right)e_j } \right]}\sigma ^j\tag{23}$$
同理,式(16)的左边为
$$\varphi _0 \left( {R_0 \sigma } \right) + \dfrac{~~\omega \left({R_0 \sigma } \right)~~}{\overline {{\omega }'\left( {R_0 \sigma }\right)} }\overline {{\varphi }'_0 \left( {R_0 \sigma } \right)} +\overline {\psi _0 \left( {R_0\sigma } \right)}-c_A = \\ \qquad \left( {\sum\limits_{j = 1}^{n_2 } {s_j } \sigma ^{ -j} + \sum\limits_{j = 0}^{n_2 } {t_j } \sigma ^j} \right)\cdot\bigg( \sum\limits_{j = 1}^\infty {j\overline a _j R_0^{j-1}} \sigma ^{-j + 1} -\\ \qquad \sum\limits_{j =1}^\infty {j\overline b _j R_0^{-j-1} } \sigma ^{j + 1} \bigg)+\sum\limits_{j = 0}^\infty {a_j R_0^j \sigma ^j} + \\ \qquad \sum\limits_{j = 1}^\infty {b_j R_0^{-j} \sigma ^{ -j}} + \sum\limits_{j = 0}^\infty {\overline c _j R_0^j \sigma^{-j}} + \sum\limits_{j = 1}^\infty {\overline d _j R_0^{ -j} \sigma ^j} \tag{24}$$
右边为
$$\left( {2b-P_2 } \right)\omega \left( {R_0 \sigma } \right) +\left({{b}'-{ i}{c}'} \right)\overline {\omega \left( {R_0 \sigma } \right)} =\\ \qquad -\left( {2b-P_2 + {b}'-{ i}{c}'} \right)h_0 -\\ \qquad \sum\limits_{j = 1}^{n_1 } {\left[ {\left( {2b-P_2 }\right)g_j + \left( {{b}'-i{c}'} \right)h_j }\right]} \sigma ^{- j}-\\ \qquad \sum\limits_{j = 1}^{n_1 } {\left[ {\left( {2b-P_2 }\right)h_j + \left( {{b}'-{ i}{c}'} \right)g_j } \right]}\sigma ^j \tag{25}$$
式(23)和式(25)中$\sigma ^j$和$\sigma ^{ -j}$前面的系数可直接写出,而式(22)和式(24)要通过一些数学运算才能求出.
比较等式(15)和式(16)左右两边{$\sigma$}的所有同幂次项系数可得无限个线性方程,但求解时只能取有限个方程.由于$\varphi _0 \left( \zeta \right)$和$\psi _0 \left( \zeta\right)$都是收敛的级数,意味着{$\sigma$}正负幂次很大的项,系数接近于零.具体计算时可取有限项,所取项数越多,孔边应力边界条件满足得越好.于是对未知的系数$a_{j}$,$b_{j}$,$c_{j}$和$d_{j}$都取{${N}$}项.对于$j>${${N}$}认为$a_{j}$=0,$b_{j}$=0,$c_{j}$=0 和$d_{j}$=0.
根据式(22)和式(24)可知方程组的未知系数为$a_0 + \overline c _0 -c_A $,$a_0 + \overline c _0 $,$a_1 \sim a_N $,$b_1 \sim b_N$,$c_1 \sim c_N $和$d_1 \sim d_N $. 其中的$a_0 + \overline c _0 -c_A $和$a_0 + \overline c _0$只在常数项中存在,对于应力无影响,可以不参于计算.根据等式(15)和式(16)左右两边的$\sigma ^1 \sim \sigma ^N$和$\sigma^{-1} \sim \sigma ^{-N}$的系数相等分别得到2$N$个方程.4$N$个方程对应于未知系数$a_1 \sim a_N $,$b_1 \sim b_N $,$c_1\sim c_N $和$d_1 \sim d_N $,未知数个数和方程个数相等,方程可解.
由于复数线性方程组含有未知数的共轭,求解时我们把它拆开实部和虚部分别求解
$$ { P_{ R} X_{ R}} = { Q_{ R}}\tag{26}$$
$${ P_{ I} X_{ I}} = { Q_{ I}}\tag{27}$$
其中
$$\begin{array}{l} X_{ R} = \big[ { Re}\left( {a_1 } \right), \cdots ,{Re}\left( {a_N } \right),{ Re}\left( {b_1 }\right), \cdots ,{ Re}\left( {b_N } \right), \\\qquad~ { Re}\left( {c_1 } \right), \cdots ,{ Re}\left( {c_N} \right),{ Re}\left( {d_1 } \right), \cdots ,{ Re}\left({d_N } \right)]^{ T} \end{array}$$
$$\begin{array}{l} X_I = [ { Im}\left( {a_1 } \right), \cdots ,{ Im}\left({a_N } \right),{ Im}\left( {b_1 }\right), \cdots ,{ Im}\left( {b_N } \right),\; \\\qquad~{ Im}\left( {c_1 } \right), \cdots ,{ Im}\left( {c_N} \right),{ Im}\left( {d_1 } \right), \cdots ,{ Im}\left({d_N } \right)]^{ T}\end{array}$$
根据平面弹性复变函数方法,两个解析函数求出之后,区域的任一点应力就可以直接求得.下面给出正交曲线坐标系中应力的求解公式
$$\sigma _\rho + \sigma _\theta = 4{ Re}\left({\frac{{\phi }'(\zeta )}{{\omega }'(\zeta )}} \right)\tag{28}$$
$$\sigma _\theta-\sigma _\rho + 2{ i}\tau _{\rho \theta } = \frac{2\zeta^2}{\rho^2\overline{\omega'(\zeta)}}\cdot\\ \qquad \left( \overline{\omega(\zeta)}\frac{\varphi"(\zeta)\omega'(\zeta)- \omega"(\zeta)\varphi'(\zeta)}{\left(\omega'(\zeta) \right)^2} + \psi'(\zeta) \right) \tag{29}$$
式中,$\sigma _\rho ,\sigma _\theta$ 和$ \tau _{\rho \theta }$是在$z$平面正交曲线坐标系下的应力分量.
4 与ANSYS解的对比
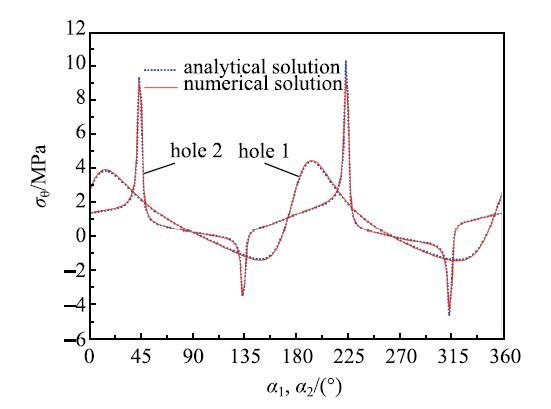
有限单元法是用来解决复杂结构问题的一种有效数值方法.本文将把解析解的结果与有限单元法的计算结果进行比对.对比使用模型为: 正方形边长$a_{1}$=4 m,椭圆长半轴$a_{2}$=3m,短半轴$b_{2}$=2 m,孔距$s$=4 m. 外载荷为：$\sigma _x^\infty=0.5$ MPa,$\sigma _y^\infty $=1 MPa, $\tau_{xy}^\infty $=0.5 MPa,$P_{1}=P_{2}$=0.5 MPa.为模拟无限平板,模型大小取为80 m$\times $80 m.使用三角形单元Plane2将模型划分成642 662个单元,得到1 287293个节点. 为消除刚体位移,板的左下角$x$,$y$方向固定,右下角$y$方向固定(见图6). 图7为两孔边界$[0,360^ \circ]$范围切向应力数值解和本文解析解的对比. 在正方形孔两个顶点$\alpha_1 = 45^ \circ $和$\alpha _1 = 225^ \circ$应力集中较大处切向应力有差异,其余点的结果吻合得很好.对于椭圆孔边界,两种方法的结果基本一样.
显示原图|下载原图ZIP|生成PPT图6ANSYS使用模型...
-->Fig. 6Model of ANSYS
-->
显示原图|下载原图ZIP|生成PPT图7本文方法和ANSYS方法孔边切向应力结果对比...
-->Fig. 7Tangential stress on the boundaries compared between methods of this paper and ANSYS
-->
5 算例分析
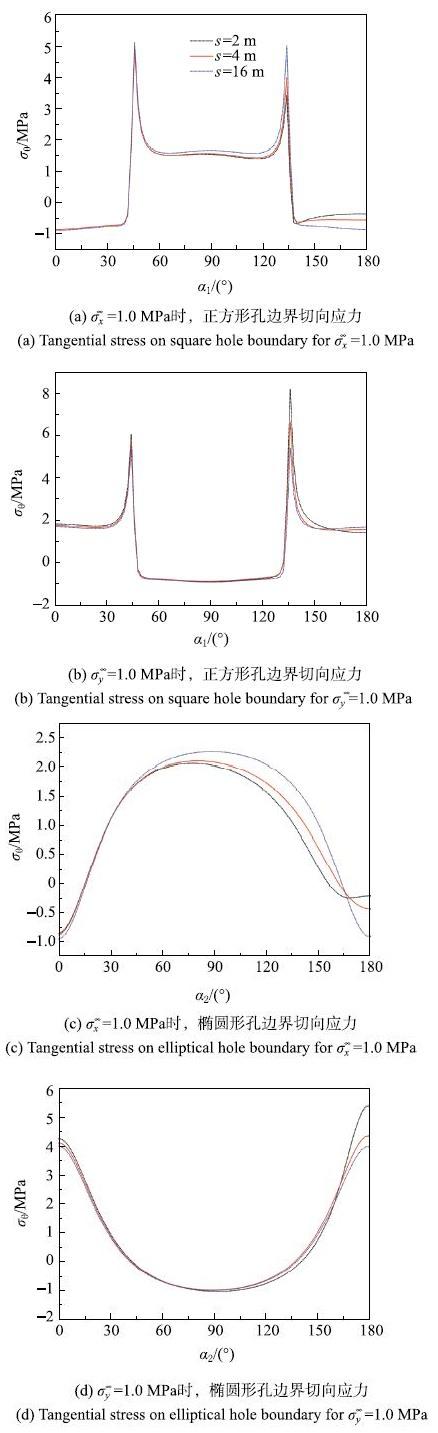
为了便于分析,下文的应力,位移和角度单位分别为MPa,m和度($^\circ$).5.1 孔距对应力的影响
考虑$a_{1}=4$ m, $a_{2}=3$ m和$b_{2}$=2 m,在3个不同孔距2 m,4m和16 m下计算了受单向压力的应力分布.由于对称性,给出了孔边$[0^\circ,180^ \circ ]$范围的切向应力.图8(a)和图8(b)分别为正方形孔在$\sigma _x^\infty $=1.0 MPa和$\sigma_y^\infty $=1.0 MPa作用时,不同孔距下的孔边切向应力分布.受$x$方向单压时,在$[0^\circ ,42^\circ ) \cup (138^ \circ ,180^\circ ]$范围产生拉应力,其余边界产生压应力. 随着孔距增大,在$(58^\circ ,136^ \circ )$范围的切向压应力增大,且顶点$\alpha _1 = 135^\circ $处增大尤为明显;在$(144^ \circ ,180^ \circ]$范围的切向拉应力增大. 受$y$方向单压时,在$(47^ \circ ,132^ \circ)$范围产生拉应力,其余边界产生压应力.随着孔距增大,顶点处压应力减小,且顶点$\alpha _1 = 135^ \circ$处减小得最快.
图8(c)和图8(d)分别为椭圆形孔在$\sigma _x^\infty $=1.0 MPa和$\sigma_y^\infty $=1.0 MPa作用时,不同孔距下的孔边切向应力分布.受$x$方向单压时,随着孔距增大,在$(39^ \circ ,165^ \circ)$范围的切向应力增大,在$(165^ \circ ,180^ \circ]$范围的切向应力减小.受$y$方向单压时,随着孔距增大,椭圆与$x$轴交点附近切向应力减小,其余部分变化不大.
当孔距很大($s>$16m)时,正方形孔和椭圆孔上的切向应力大致关于$\alpha _1 = 90^ \circ$对称,这也意味者两孔的相互影响很小了,可以看成单孔情况.
显示原图|下载原图ZIP|生成PPT图8孔距对应力的影响...
-->Fig. 8Effect of separation distance on stress
-->
5.2 椭圆大小对正方形孔边应力的影响
保持正方形边长$a_{1}$=4 m和椭圆短轴长轴比值${b_2 }/ {a_2 } = 2/3$不变,考虑椭圆大小对左侧正方形孔边界切向应力分布的影响.图9(a)和图9(b)显示的分别为正方形孔在$\sigma _x^\infty $=1.0MPa和$\sigma _y^\infty $=1.0MPa时,在椭圆大小不同的孔边切向应力分布. 当只有$\sigma _x^\infty$作用时,椭圆越大,正方形孔边界$[45^ \circ ,135^ \circ]$范围的切向应力越小,顶点$\alpha _1 = 135^ \circ$处应力减小最大;$(135^ \circ ,180^ \circ ]$范围的切向拉应力减小.只有$\sigma _y^\infty $作用时,椭圆越大,两个顶点$\alpha _1 = 45^\circ $和$\alpha _1 = 135^ \circ$处压应力越大,其余边界部分切向应力变化较小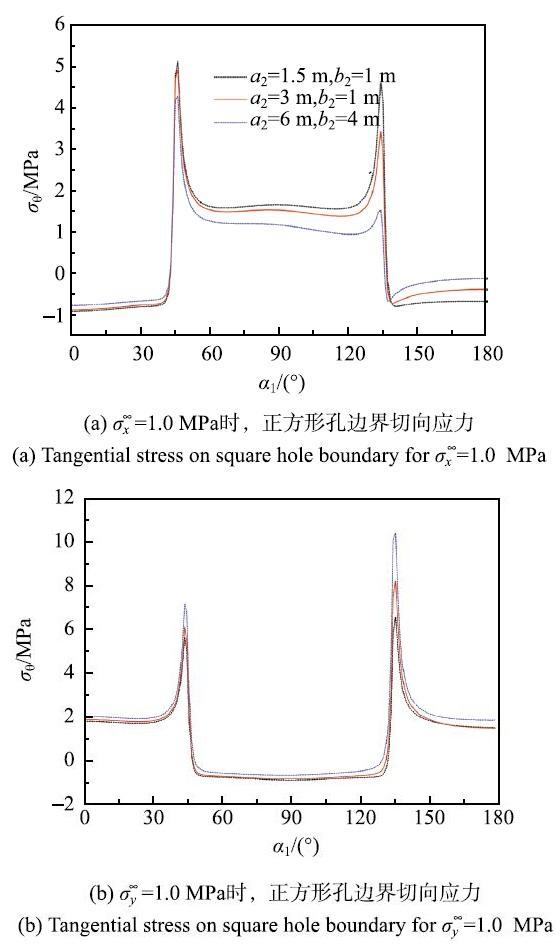
显示原图|下载原图ZIP|生成PPT图9椭圆大小对正方形孔边界应力的影响...
-->Fig. 9effect of size of elliptical hole on stress on square Hole boundary
-->
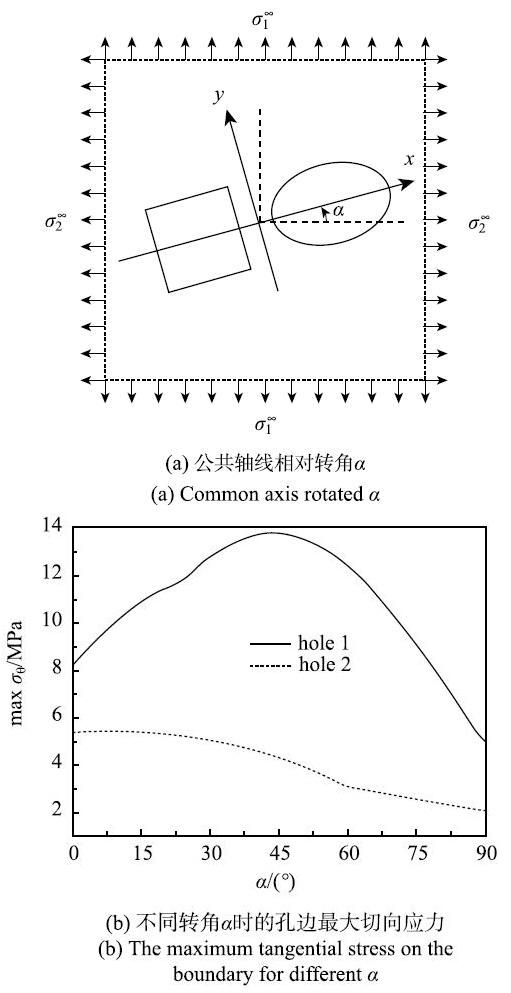
5.3 孔的布置方位对孔边应力的影响
如图10(a)所示,$\alpha $表示两孔的公共轴线与$\sigma _2^\infty$方向的相对转角.那么根据应力转轴公式,沿$x$轴和$y$轴的均布正应力和剪应力为$$\sigma _x^\infty = \sigma _1^\infty \sin ^2\alpha + \sigma_2^\infty \cos ^2\alpha\ \sigma _y^\infty = \sigma _1^\infty \cos ^2\alpha +\sigma _2^\infty \sin ^2\alpha \tau _{xy}^\infty = \frac{\sigma _1^\infty-\sigma _2^\infty}{2}\sin 2\alpha$$
其中$\sigma _1^\infty $和$\sigma _2^\infty$是两个主应力.
图10(b)表示的是不同相对转角{$\alpha $}时,孔边最大切向应力的大小. 随着{$\alpha$}增大,正方形孔孔边的最大切向应力先增大后减小,当$\alpha = 45^\circ $时最大,为13.77 MPa,当$\alpha = 90^ \circ $时最小,为4.95MPa;椭圆孔孔边最大切向应力减小.正方形孔边界上的最大切向应力总是大于椭圆形孔边界上的最大切向应力.
显示原图|下载原图ZIP|生成PPT图10布置方位对应力的影响...
-->Fig. 10Effect of the orientation of holes on stress
-->
5.4 两孔中心线BC上的应力
考虑$a_{1}$=4 m,$a_{2}$=3 m,$b_{2}$=2 m和$s$=2 m. 图10(a)、 图10(b)、图10(c)和图10(d)分别为受$\sigma _x^\infty $=1.0MPa,$\sigma _y^\infty $=1.0 MPa,$\tau _{xy}^\infty $=1.0MPa和$P_{1}=P_{2}$=1.0 MPa时中心线{BC}上的应力分布. $\sigma_x^\infty $,$\sigma _y^\infty$和孔边压力$P_{1}$和$P_{2}$作用时,中心线上只有$\sigma _x$和$\sigma _y $. 受$x$方向单压时,中心线上的$\sigma _x $和$\sigma_y $为拉应力,$\sigma _x $很小,$\sigma _y $在$B$点处拉应力最大.受$y$方向单压时,中心线上的$\sigma _x $和$\sigma _y$为压应力,$\sigma _x $很小,$\sigma _y$在$C$点处最大,是所加力的5.4倍大小. 孔边作用均布压力时,$\sigma_x $约等于压力大小,$\sigma _y $为拉应力,在$C$点处最大. $\tau_{xy}^\infty $作用时,中心线上只存在剪应力$\tau _{xy}$,在距$B$点1.3 m的地方最大.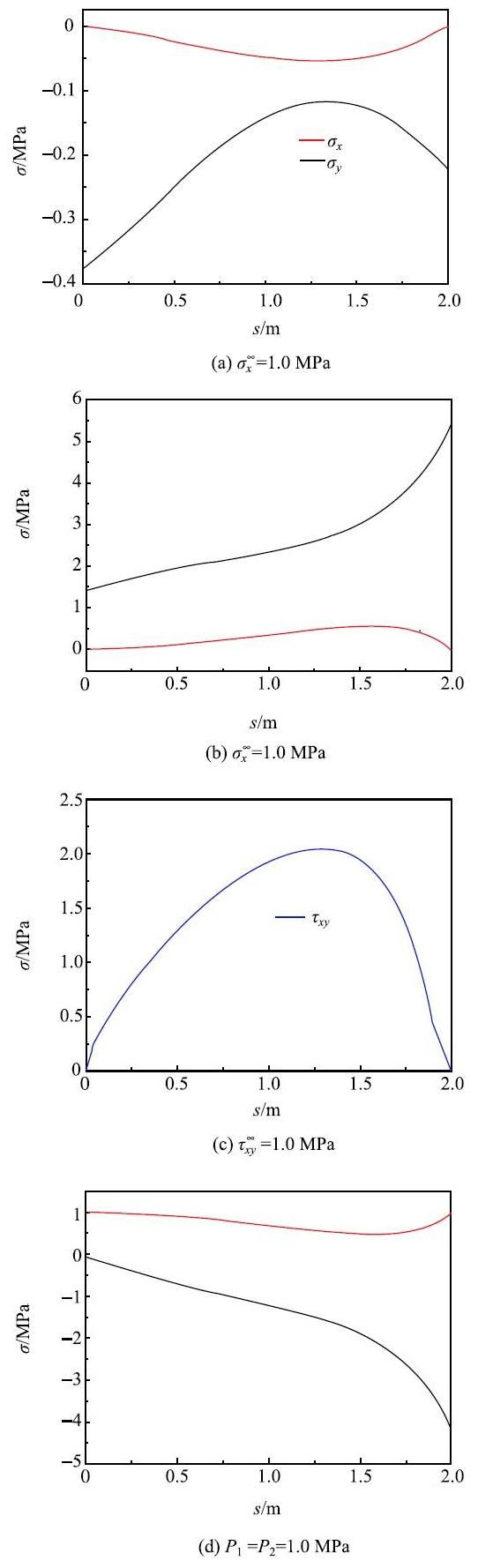
显示原图|下载原图ZIP|生成PPT图11不同外力作用下中心线{BC}上的应力...
-->Fig. 11Stress distribution on the line {BC }under different loads
-->
6 结论
本文利用保角变换,将无限平板中的一个正方形孔和一个椭圆形孔映射成了一个圆环,这个方法具有一般性.基于本文提出的映射函数一般形式,可以将无限域中两个关于同轴对称的任意形状孔映射成一个圆环.利用最优化方法,可以找到具体问题的映射函数.映射函数已知后,可以通过应力边界条件建立求解两个解析函数的基本方程,从而可以获得在板远处受有压应力、剪应力和孔边受有均布压力的应力解析解,并用ANSYS有限单元法数值解与结果进行了对比.
利用解析解分析了孔距、椭圆大小和两孔布置方位对孔边应力分布的影响,以及不同载荷下两孔中心线上的应力分布规律.受平行于公共轴线的单向压力时,孔距越大,正方形孔边右侧顶点的应力越大;椭圆孔越大,正方形孔孔边顶点附近的应力越小.受垂直于公共轴线的单向压力时,孔距越大,正方形孔孔边右侧顶点的应力越小;椭圆孔越大,正方形孔顶点附近的应力越大.在板只受到剪力作用时,两孔中线上才存在剪应力.在公共轴线与单向载荷方向成$45^ \circ$时,正方形孔边最大切向应力最大,工程中应尽量避免这种情况.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | |
| [2] | |
| [3] | . . |
| [4] | . . |
| [5] | . . |
| [6] | |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | . . |
| [13] | . . |
| [14] | . |
| [15] | |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . . |
| [29] | . |
| [30] | |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | |
| [37] | . . |
