, 谭文长THERMAL INSTABILITY OF VISCOELASTIC FLUIDS IN POROUS MEDIA1)
KangJianhong, TanWenchang中图分类号:O357.3
文献标识码:A
收稿日期:2018-09-17
接受日期:2018-09-17
网络出版日期:2018-11-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
3) 谭文长,教授,主要从事生物力学、非牛顿流体力学等研究. E-mail: tanwch@pku.edu.cn
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (22392KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
流动稳定性是流体力学的一个经典研究方向, 自雷诺实验起至今已有百余年的历史.热对流的不稳定性是由流体内部存在温度差导致流体中密度分布不均匀所引起的,是流动稳定性研究领域的一个重要分支.1900年Bénard[1]首次在实验中观测到热对流不稳定性现象(Bénardcells), 1916年Rayleigh理论解释了Bénard实验[2]. 此后,越来越多的****开始研究经典的Rayleigh-Bénard问题[3-4],考虑双扩散[5-7]、旋转效应[8-10]、磁性流体[11-12]以及不同的流动边界条件和加热边界条件等[13-14]在实际应用可能出现的情况.Horton和Rogers[15]以及Lapwood[16]分别于1945年和1948年将经典的Raleigh-Bénard 问题引入多孔介质中.在达西定律的基础上, 他们运用线性稳定性方法得到了水平多孔介质层底部等温加热热对流失稳的临界温度梯度.1967年Katto 和 Masuoka[17] 对底部加热多孔介质层内的热对流进行了实验研究, 分析了达西数对热对流发生的影响.此后, 关于多孔介质内热对流的研究逐渐发展起来. 对于无界的水平多孔介质层, Rayleigh数作为波数的函数是连续的正值,且Rayleigh数临界值等于4$\pi ^{2}$, 这是经典的结论[15-16]. 但是,对于有界的多孔介质结构, 比如多孔圆柱或者多孔方腔, Rayleigh 数仅可能是某些离散的值.Beck[18]研究了等温加热边界条件下方腔多孔介质内的热对流不稳定性, 计算了热对流启动的临界Rayleigh数和最优模态随多孔介质几何尺度的变化, 给出了热对流发生对应的优先模态图. Wang[19]研究了类似的问题,但边界条件为顶部等温加热、底部等热流加热, 后来又研究了上端开口底部等热流加热的情况[20], 也给出了热对流发生的优先模态图. Zebib[21]对等温加热多孔圆柱内牛顿流体的热对流进行研究,考虑了不可渗透壁面和绝热侧壁的边界条件, 这个问题又被拓展到侧壁是完美导热的情况[22]. Bau 和Torrance[23]考虑了更加普遍的模型, 即侧壁绝热多孔同轴圆环柱, 在内圆柱半径等于零的极限情况下,圆环柱模型就简化为圆柱模型;进一步, 在外圆柱半径趋于无穷大的极限情况下, 圆环柱模型退化为无穷大平行平板模型.最近, 利用高精度直接数值模拟的方法, Otero等[24]研究了高Rayleigh 数下底部加热水平多孔介质层的热对流问题,分析了对流从静态到复杂流动的演化过程, 发现了不同流动状态下Nusselt 数随Rleiaygh数的变化存在标度率. Cherkaoui和Wilcock[25]对底部加热上端开口的方腔多孔介质内的高Rayleigh 数热对流进行了数值模拟,计算结果显示随着Rleiaygh 数的增大流动会出现不同的分叉, 同时他们也发现了Nusselt 数随Rleiaygh数变化的标度率.
近年来, 随着生物流变学、地球物理学、化学和石油工业等学科的不断发展,多孔介质内黏弹性流体的热对流问题越来越受到人们的重视. 例如,目前世界范围内主要使用常规热采法进行稠油油藏的开发, 如蒸汽吞吐、蒸汽驱和热水驱等.蒸汽驱是向一口生产井短期内连续注入一定数量的蒸汽, 然后关井(焖井)数天,使热量得以扩散之后再开井生产, 这一过程将引起油气藏内的热对流产生[26].又如, 在研究地幔对流运动中, 地幔本身的加热作用使地幔产生热对流,其中上地幔小尺度对流就是与Rayleigh-Bénard对流或与其变化形式相似的对流,因此在对其进行物理模拟实验的时候就可以利用Rayleigh-Bénard对流原理进行研究[27]. 1989年Rudraiah 等[28]首次利用修正的Oldroyd模型对底部加热水平多孔层内黏弹性流体的热对流进行了线性稳定性分析, 结果发现黏弹性流体的热对流有静态对流和振荡两种不同的失稳模态, 而牛顿流体只有静态对流一种失稳模态.Bertola等[29]利用Maxwell-Jeffrey模型研究了类似的问题,发现了流体的黏弹性可以促进热对流的产生, 并得到了对流换热的Nusselt数.Kim等[30]使用修正的Darcy-Jeffrey模型, 对多孔介质内的Rayleigh-Bénard问题进行了线性和弱非线性分析, 发现只要黏弹性参数满足一定的条件,超稳态对流总是优先发生的, 在临界点附近流动分叉是超临界稳定的,而且与黏弹性参数的取值无关. 最近, 谭文长教授团队在多孔介质内黏弹性流体热对流方面取得了一系列研究成果[31-46]. 谭文长和Masuoka[31]提出修正的Darcy-Brinkman-Maxwell模型, 研究了多孔介质内黏弹性流体的线性稳定性.符策基等[32]数值模拟了底部加热多孔方腔内黏弹性流体的高Rayleigh 数热对流,揭示了流动从静态到混沌的分叉过程以及对流换热的幂律标度率.牛骏等[33-37]研究了底部为第三类热边界加热条件下多孔方腔内黏弹性流体的热对流稳定性, 分析了Biot 数对热对流的影响.张志勇等[38]分析了多孔圆柱内黏弹性流体热对流的稳定性,比较了底部等温加热和等热流加热两种边界条件对热对流启动的影响,得到了静态对流和振荡对流情况下Nusselt数随Rayleigh数的变化规律[39].王少伟等[40-41]研究了Maxwell流体的双扩散热对流, 分析了Soret效应和流体的黏弹性对振荡对流稳定性以及换热速率的影响. 康建宏等[42]考虑在旋转Coriolis离心力作用下底部加热水平多孔介质层和多孔圆柱内的黏弹性流体热对流问题, 发现黏弹性的不稳定效应和旋转的稳定性效应之间存在竞争关系, 确立了热对流失稳的优先模态与多孔介质几何尺度关系的模态图[43]. 尹晨等[44-46]研究了流体-多孔介质双层系统中黏弹性流体的热对流稳定性问题, 发现稳态对流和振荡对流都有可能出现双模曲线. 此外, Malashetty等[47-49]研究了热非平衡、各向异性多孔介质层内黏弹性流体的双扩散热对流稳定性, 分析了各向异性参数、Prandtl数以及溶质Rayleigh 数对热对流产生的影响.
在研究多孔介质热对流问题时, 确定热对流发生的临界Rayleigh数具有非常重要的实际意义[50],如果Rayleigh数超过临界值, 那么多孔介质内的流体将失稳继而产生对流, 此时热流量远大于热传导的热流量,换热效率明显提高. 一般来说,黏弹性流体热对流的临界Rayleigh数依赖于多孔介质的几何形状、流体动力学和热边界条件、流体的流变属性以及外部约束条件等[51].本文着重介绍多孔介质黏弹性流体热对流研究的几个常用数学模型以及稳定性分析的一般方法,给出热对流临界Rayleigh数和对流换热Nusselt数的一些主要结果,分析黏弹性流体的黏弹性参数、多孔介质的几何形状以及边界条件等因素对热对流稳定性和对流换热的影响.谨以此文纪念著名流体力学专家郭永怀教授为国牺牲50周年.
1 水平多孔介质层内黏弹性流体的热对流稳定性研究
1.1 底部等温加热情形
考虑一个厚度为$d$ 的无穷大水平多孔介质层, 内部充满了不可压缩黏弹性的流体,上下表面都是不可渗透的, 其上表面温度为$T_{0}$, 下表面的温度为$T_{0}+\Delta T$, 且$\Delta T > 0$, 如图1 所示. 在热对流启动前, 多孔介质内的流体处于静止状态,温度沿垂直平板的方向线性均匀分布, 该基本状态可表示为$${\pmb V}_{\rm b} = {\bf 0} , \ \ T_{\rm b}= T_0 + \dfrac{\Delta T}{d}(d - z) (1)$$
流体密度随温度变化满足如下状态方程
$$\rho = \rho _0 [1 - \alpha (T - T_0 )] (2)$$
其中, $\alpha $表示热膨胀系数, $\rho_{0}$表示温度为$T_{0}$时的参考密度.由于靠近底部的流体温度较高、密度较小, 靠近顶部的流体温度较低、密度较大,热流体层位于冷流体层之下产生浮力, 流体有向上运动的趋势,且如果温度梯度足够大, 系统就会变得不稳定.
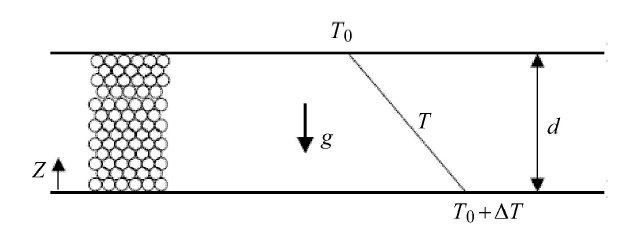显示原图|下载原图ZIP|生成PPT图1底部等温加热水平多孔介质系统示意图[
-->Fig.1The schematic diagram of horizontal porous layer heated from below[
-->
黏弹性流体热对流的连续性方程和能量方程与牛顿流体热对流并无区别,其表达式可以写为
$$\nabla \cdot {\pmb V} = 0 (3)$$
$$\dfrac{\partial T}{\partial t} + {\pmb V} \cdot \nabla T = \kappa \nabla ^2T (4)$$
其中, $\kappa $表示流体的热扩散系数, ${\pmb V}$表示流体的达西渗流速度,但刻画牛顿流体的达西定律并不能刻画黏弹性流体在多孔介质内的流动.和牛顿流体相比, 黏弹性流体在多孔介质内流动的模型相对较少,目前使用最广泛的一个模型是修正的Darcy-Jeffrey模型[52-56]
$$\dfrac{\mu }{K}\left( {\varepsilon ^\ast \dfrac{\partial }{\partial t} + 1}\right) {\pmb V} = \left( {\lambda ^\ast \dfrac{\partial }{\partial t} + 1} \right)(-\nabla p + \rho {\pmb g} ) (5)$$
其中, $\varepsilon^{\ast }$和$\lambda^{\ast }$是黏弹性参数,分别表示弛豫时间和松弛时间;$K$表示渗透率;$\mu $表示流体黏度;$p$表示流体压力;${\pmb g}$是重力加速度;$\rho $是流体密度, 随温度的变化满足状态方程.
为了研究该系统的稳定性问题, 在基本态(1)上叠加无穷小扰动来观察其发展情况.令${\pmb V} = {\pmb V}_{\rm b} +{\pmb V}'$, $T = T_{\rm b} + \theta $, 代入方程(3)$\sim $(5), 并选取$\kappa / H$, $\Delta T$, $\mu \kappa / H^2$以及$H^2 / \kappa$作为速度、温度、压力和时间的特征物理量进行无量纲化,可以得到如下无量纲控制方程
$$\dfrac 1{Da} \Big ( \varepsilon \dfrac{\delta}{\delta t}+1 \Big ) {\pm b V}=\Big ( \lambda \dfrac{\delta }{\delta t}+1\Big ) (-\nabla p+Ra\theta {\pmb k} ) (6)$$
$$\dfrac{ \theta}{\delta t}+{\pm b V} \cdot \nabla \theta=\nabla^2 \theta (7)$$
$$\nabla \cdot {\pm b V} = 0 (8)$$
其中, $\varepsilon $是无量纲弛豫时间, $\lambda $是无量纲松弛时间,${Da}$是达西数, ${Ra}$是Rayleigh数. 这4个无量纲数是研究热对流稳定性最重要的参数, 他们的定义分别为
$$\left. \varepsilon = \dfrac{\varepsilon ^\ast \kappa }{d^2} ,\quad \lambda = \dfrac{\lambda ^\ast \kappa }{d^2} \\ Da = \dfrac{K}{d^2} , \quad Ra = \dfrac{\rho g\alpha \Delta Td^3}{\mu \kappa } \right\} (9)$$
这里为简便起见省略扰动量的上标" $'$ ", 且用相同的符号表示无量纲量, 即方程(6)$\sim $(8)中${\pmb V}$和$\theta $分别表示无量纲的扰动速度和扰动温度.
微分方程组(6)$\sim $(8)的边界条件为： (1) $\theta=0$, $z=\{ 0, 1\}$ (等温加热边界条件);(2) $w=0$, $z=\{ 0, 1\}$ (不可渗透边界条件). 这里$w$表示竖直方向无量纲扰动速度. 当$\lambda=\varepsilon =0$ 时, 方程(6)$\sim$(8)就是牛顿流体热对流的控制方程, 所研究问题就是经典的Horton-Rogers-Lapwood问题[57].
流动方程(5) 是根据现象学上的相似性, 类比Oldroyd-B本构关系推测出来的经验公式, 适用于孔隙度较小的致密多孔介质,但忽略了黏性剪切效应, 不能预测边界层附近的流动,不适用于孔隙度较大的疏松多孔介质. 为了考虑边界效应,有****提出了修正的Darcy-Brinkman-Jeffrey模型[58-59],并研究了黏弹性流体的热对流稳定性. 但在这些研究存在一个问题,黏弹性流体的流动阻力是根据经典的Darcy定律来估算的. 最近,谭文长等[60]利用体积平均法且根据力的平衡的思想,提出了黏弹性流体在多孔介质中流动的修正Darcy-Brinkman-Oldroyd模型,改进了使用多年的经验公式, 克服了以前利用牛顿流体的Darcy定律来估计黏弹性流体阻力的缺点. 该模型可以表示为
$$\rho _0 \left[ {\dfrac{\partial {\pmb V}}{\partial t} + ({\pmb V}\cdot \nabla ) {\pmb V}} \right]= - \nabla p + \nabla \cdot {\pmb\tau} +{\pmb r} + \rho {\pmb g} (10)$$
$${\pmb\tau} + \lambda ^\ast \left[ {\dfrac{\partial {\pmb\tau} }{\partial t} + ({\pmb V} \cdot \nabla ){\pmb\tau} - (\nabla {\pmb V})^{\rm T}{\pmb\tau} - {\pmb\tau} (\nabla {\pmb V})} \right] = $$
$$\mu \left\{ { {\pmb A} + \varepsilon ^\ast \left[ {\dfrac{\partial {\pmb A}}{\partial t} + ({\pmb V} \cdot \nabla ) {\pmb A} - (\nabla {\pmb V})^{\rm T}{\pmb A} - {\pmb A} (\nabla {\pmb V})}\right]} \right\} (11) $$
$$\left( {1 + \lambda ^\ast \dfrac{\partial }{\partial t}} \right){\pmb r} = -\dfrac{\mu }{K}\left( {1 + \varepsilon ^\ast \dfrac{\partial }{\partial t}}\right) {\pmb V} (12)$$
其中, ${\pmb r}$表示流动阻力, ${\pmb\tau }$表示体积平均应力张量, ${\pmb A}$表示剪切速率张量. 进一步将方程(12)无量纲化可得[39]
$$ \left( {1 + \lambda \dfrac{\partial }{\partial t}} \right)\Bigg\{ Pr ^{ - 1}\left[ {\dfrac{\partial{\pmb V}}{\partial t} + ({\pmb V} \cdot \nabla ) {\pmb V}} \right] + \nabla p - \\ \qquad \nabla \cdot{\pmb\tau} - Ra\theta {\pmb k} \Bigg \}{\pmb r} = - \dfrac{1}{Da}\left( {1 + \varepsilon \dfrac{\partial}{\partial t}} \right) {\pmb V} (13)$$
其中, ${Pr} =\mu /\rho_{0} \kappa $表示Prandtl数, $Da = K / d^2$表示Darcy数. 当$\varepsilon =0$时, Darcy-Brinkman-Oldroyd模型就简化为Darcy-Brinkman-Maxwell模型$^{[31,44]}$. 此外, 当$Da \to \infty $时, 该模型退化为纯黏弹性流体模型[61].
Rudraiah等[28]研究致密多孔介质内黏弹性流体振荡热对流时,在Darcy-Jeffrey模型(5)中保留了时间导数项, 其形式为
$$\dfrac{\mu }{K}\left( {\varepsilon ^\ast \dfrac{\partial }{\partial t} + 1} \right){\pmb V}+ \left( {\lambda^\ast \dfrac{\partial }{\partial t} + 1} \right)\left( {\rho _0 \dfrac{\partial {\pmb V}}{\partial t} +\nabla p - \rho {\pmb g}} \right) = {\bf 0} (14)$$
1.1.1 线性稳定性分析
基于修正Darcy-Jeffrey模型, Kim等$^{[30,54]}$运用线性稳定性理论分析了多孔介质黏弹性流体热对流发生的临界Rayleigh数. 在热对流启动阶段对流的扰动振幅很小, 线性项相比非线性项是高阶小量. 因此, 可以忽略方程(6)$\sim$(8)中的高阶非线性小量,得到温度和速度扰动量的无量纲控制方程
$$\left.\begin{array}{l} \dfrac{1}{Da}\left( {\varepsilon \dfrac{\partial }{\partial t} + 1}\right)\nabla ^2w = Ra\left( {\lambda \dfrac{\partial }{\partial t} + 1}\right)\nabla _1^2 \theta \\ \dfrac{\partial \theta }{\partial t} - w = \nabla ^2\theta \end{array}\!\!\right\} (15)$$
其中,$\nabla _1^2 = \partial ^2 / \partial x^2 + \partial ^2 / \partial y^2 +\partial ^2 / \partial z^2$.
按照简正模态分析方法, 在热对流启动阶段多孔介质内小扰动温度和速度在水平方向呈周期性变化. 考虑到边界条件, 可假设温度和速度有如下的形式
$$\left[ {w(x,y,z,t),\theta (x,y,z,t)} \right] = \left[ {\hat {w}(z),\hat{\theta }(z)} \right]{\rm e}^{{\rm i}(lx + my) + \sigma t} (16)$$
其中, ${\rm i} = \sqrt { - 1} $, 表示单位纯虚数, $l$和$m$分别为水平面上$x$和$y$方向的波数, $\sigma $为时间增长率. 一般来说, $\sigma $是一个复数, 可以表示为
$$\sigma = \sigma _r + {\rm i}\omega$$
当$\sigma_{r} < 0$ 时, 小扰动的振幅随着时间的增长趋于零,线性系统总是稳定的;当$\sigma _{r} > 0$ 时, 小扰动的振幅随着时间的增长趋于无穷,线性系统会变得不稳定;特别地, 当$\sigma_{r} = 0$时, 线性系统是中性稳定的.
黏弹性流体热对流的失稳有两种方式：如果$\omega = 0$, 而$\sigma _{r}$随着Rayleigh的增大由负数变为正数, 那么稳定性交换原则(exchange of stabilities)成立,静态对流(stationary convection)发生;如果$\omega \ne 0$, 而$\sigma_{r}$随着Rayleigh 的增大由负数变为正数, 那么超稳态是优先模态(overstability),振荡对流发生(oscillatory convection). 对于牛顿流体而言,热对流失稳的优先模态总是静态对流.
将$\sigma _{\rm r} = \omega = 0$和方程(16)代入方程(15),得到静态对流的Rayleigh数
$$Ra_{\rm D}^{\rm s} = \dfrac{\pi ^4 + 2a^2\pi ^2 + a^4}{a^2} (17)$$
其中,$Ra_{\rm D} = Ra \cdot Da$表示Darcy-Rayleigh数, $a = \sqrt {l^2 + m^2}$表示水平面上的波数. 由此式可得临界Darcy-Rayleigh数和临界波数为
$$Ra_{\rm D,c}^{\rm s} = 4\pi ^2 , \ \ a_{\rm c} = \pi (18)$$
可以看出, 静态对流的临界Rayleigh数就等于牛顿流体热对流的临界值, 而与流体 黏弹性 无关[15-16].Bertola等[29]基于Darcy-Jeffrey模型(5)、Rudraiah \linebreak 等[28]基于模型(14)得到了相同的结果.
张志勇等[39]基于Darcy-Brinkman-Oldroyd模型(13)得到静态对流的Rayleigh数表达式为
$$Ra^{\rm s} = \dfrac{(\pi ^2 + a^2)^2 / Da + (\pi ^2 + a^2)^3}{a^2} (19)$$
由此给出静态对流临界Rayleigh为
$$Ra_{\rm c}^{\rm s} = \dfrac{(\pi ^2 + a_{\rm c}^2 )^3 + (\pi ^2 + a_{\rm c}^2 )^2 / Da}{a_{\rm c}^2 } (20)$$
其中临界波数$a_{\rm c}$满足方程
$$6(\pi ^2 + a_{\rm c}^2 ) - \dfrac{2}{a_{\rm c}^2 }(\pi ^2 + a_{\rm c}^2 )^2 - \\ \qquad \dfrac{2}{a_{\rm c}^2 Da}(\pi ^2 + a_{\rm c}^2 ) + \dfrac{4}{Da} = 0 (21)$$
当$Da \to \infty $时,系统简化为非多孔介质内纯黏弹性流体的热对流问题, 方程(20)和(21)退化为$Ra_{\rm c}^{\rm s} = 27\pi ^4 / 4$,$a_{\rm c} = \pi / \sqrt 2 $, 与Kolkka和Ierley[62]的结果一致. 当$Da \to 0$时,方程(20)和(21)退化为方程(18), 与Kim等[30]的结果一致.
将$\sigma _r = 0$, $\omega \ne 0$和方程(16)代入方程(15),得到振荡对流的Rayleigh数的表达式为
$$Ra_{\rm D}^{\rm o} = \dfrac{\varepsilon (\pi^2 + a^2 )^2 + (\pi ^2 + a^2 )}{\lambda a^2 } (22)$$
相应的临界Rayleigh数、临界波数和振荡对流的频率为
$Ra_{\rm D,c}^{\rm o} = \dfrac{1 + 2\varepsilon \pi \left( {\pi + \sqrt {\pi ^2 + 1 /\varepsilon } } \right)}{\lambda } , \ \ a_c^2 = \pi \sqrt {\pi ^2 + 1 / \varepsilon } $ (23)
$\omega ^2 = \dfrac{(\pi ^2 + a^2)(\lambda - \varepsilon ) - 1}{\varepsilon \lambda } (24)$
由方程(24)可以看出, 产生超稳态对流的条件为
$$\lambda - \varepsilon > \dfrac{1}{\pi ^2 + a^2} (25)$$
张志勇等[39]基于Darcy-Brinkman-Oldroyd模型(13)得到振荡对流的Rayleigh数和振荡频率表达式为
$Ra^{\rm o} =\Big [( 1 / Pr + \varepsilon / Da + \varepsilon c + c\lambda / Pr)(c / Da + c^2 +$
$\qquad c^2 / Pr + \varepsilon c^2 / Da + \varepsilon c^3) -\lambda (c^2 / Da + c^3) / Pr \Big] \Big / $
$\qquad \Big[ \lambda (\varepsilon / Da + \varepsilon c +\lambda c / Pr )a^2 (26)$
$\omega ^2 = \dfrac{(\lambda - \varepsilon )(c / Da + c^2) - (1 / Da + c + c /Pr )}{\lambda (\varepsilon / Da + \varepsilon c + \lambda c / Pr )} (27)$
其中,$c = a^2 + \pi ^2$. 由方程(27)可以看出,对于Darcy-Brinkman-Oldroyd模型, 超稳态对流发生的条件为
$$\lambda - \varepsilon > \dfrac{1 / Da + c + c / Pr }{c / Da + c^2} (28)$$
特别地, 当$Da \to 0$时, 方程(26)退化为方程(22),与Darcy-Jeffrey模型的结果一致;当$\varepsilon \to 0$时,方程(26)与Darcy-Brinkman-Maxwell模型的结果一致[31].
随着松弛时间$\lambda $的延长, 振荡对流的临界Rayleigh数不断减小, 如图2所示,即意味着流体的黏弹性能够促进振荡对流的的发生;相反, 随着弛豫时间$\varepsilon$的延长, 振荡对流的临界Rayleigh数不断增大,即流体的黏性阻尼能够抑制振荡对流的发生.
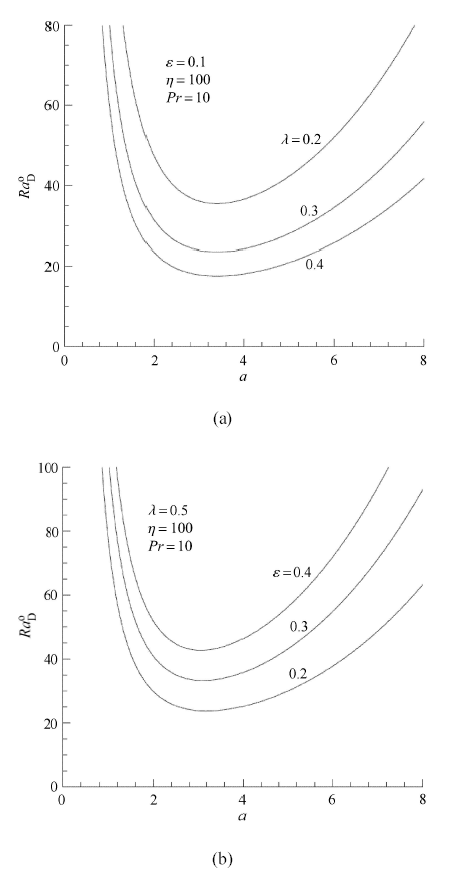显示原图|下载原图ZIP|生成PPT图2不同黏弹性参数下振荡对流Rayleigh数随波数的变化曲线[
-->Fig.2The variations of Rayleigh number for oscillatory convection with the wavenumber for different viscoelastic parameters[
-->
1.1.2 弱非线性稳定性分析
线性稳定性分析能够决定热对流发生的临界条件,但是不能预测热对流运动的振幅以及在临界点附近的分叉情况.Gupta等[63]和Rosenbalt等[64]提出一种摄动法来计算热对流在临界点附近基本态分叉的有限振幅解. 首先, 假设在临界点附近热对流发生的优先模态是二维涡胞结构的形式, 速度可以用流函数$\psi $来表示
$$u = \dfrac{\partial \psi }{\partial z} , \ \ w = - \dfrac{\partial \psi}{\partial x} (29)$$
能量方程和修正的Darcy-Jeffrey流动方程有如下形式
$L(\theta ) + \dfrac{\partial \psi }{\partial x} - \Delta ^2\theta = 0 (30)$
$\left( {\varepsilon \dfrac{\partial }{\partial t} + 1} \right)\Delta ^2\psi +Ra_{\rm D} \left( {\lambda \dfrac{\partial }{\partial t} + 1} \right)\dfrac{\partial\theta }{\partial x} = 0 (31)$
其中, 算子${\rm L} = \dfrac{\partial }{\partial t} - \dfrac{\partial \psi }{\partial x}\dfrac{\partial }{\partial z} + \dfrac{\partial \psi }{\partial z}\dfrac{\partial }{\partial x}$, 算子$\Delta ^2 = \dfrac{\partial ^2}{\partial x^2} + \dfrac{\partial ^2}{\partial z^2}$.
相应地, 修正Darcy-Brinkman-Oldroyd流动方程用流函数表示为
$$\left( {\lambda \dfrac{\partial }{\partial t} + 1} \right)\left[ { Pr ^{ -1} {\rm L}(\Delta ^2\psi ) - N + Ra\dfrac{\partial \theta }{\partial x}} \right] + \\ \qquad \dfrac{1}{Da}\left( {\varepsilon \dfrac{\partial }{\partial t} + 1}\right)\Delta ^2\psi = 0 (32)$$
其中$N = \dfrac{\partial ^2(\tau _{11} - \tau _{33} )}{\partial x\partial z}+ \dfrac{\partial ^2\tau _{13} }{\partial z^2} - \dfrac{\partial ^2\tau _{13}}{\partial x^2}$由方程(11)确定.
为了确定静态对流临界点($Ra_{\rm c}^{\rm s}$)附近的有限振幅分叉解, 引入一个摄动小参数$\chi $,并将Rayleigh数、扰动温度以及流函数按照$\chi $展开
$$\left.\begin{array}{l} Ra = Ra_{\rm c}^{\rm s} + \chi ^2Ra_2 + \cdots \\ \theta = \chi \theta _1 + \chi ^2\theta _2 + \cdots \\ \psi = \chi \psi _1 + \chi ^2\psi _2 + \cdots \end{array}\right\} (33)$$
其中, $Ra_{2} \cdots , \theta_{1} \cdots , \psi_{1} \cdots $等是待定未知函数.${Ra}_{2}>0$对应于超临界分叉, 而$Ra_{2}<0$对应于亚临界分叉. 对于静态对流,时间变量以慢尺度$s = \chi ^2t$变化, $\dfrac{\partial }{\partial t} = \chi^2\dfrac{\partial }{\partial s}$.
按照摄动法的一般原理, 将方程(33)代入方程(30)和(31),Kim等[28]得到$\theta _1 = A_1 \cos ax\sin \pi z$, $\psi _1 = B_1\sin ax\cos \pi z$, 且
$$\left. \left( {1 + \varepsilon c - \dfrac{\lambda a^2Ra_{\rm D,c}^{\rm s} }{c}}\right)\dfrac{\partial A_1 }{\partial t} = \left( {\dfrac{a^2}{c}Ra_{\rm D,2} -\dfrac{c^2}{8}A_1^2 } \right)A_1 \\ B_1 = - \dfrac{c}{a}A_1 \!\!\right\} (34)$$
这是一个经典Laudau方程, 非平凡振幅稳态解为
$$Ra_{\rm D,2} = \dfrac{c^3}{8a^2}A_1^2 (35)$$
显然$Ra_{\rm D,2}>0$, 所以从静态对流临界点的分叉解是超临界稳定的.
基于有限振幅解, 静态对流换热的Nusselt数可以表示为
$$ Nu = 1 - \left\langle {\left. {\dfrac{\partial \theta }{\partial z}} \right|_{z = 0} } \right\rangle = 1 + \dfrac{2a^2}{c^2}\left( {Ra_{\rm D} - Ra_{\rm D,c}^{\rm s} } \right) = \\ \qquad 1 +\dfrac{1}{2\pi ^2}\left( {Ra_D - 4\pi ^2} \right) (36)$$
利用相同的弱非线性分析方法, 基于Darcy-Brinkman-Oldroyd模型得到静态对流分叉解同样是超临界稳定的, 并且在$Da \to0$的极限情况下, 结果与Kim等[30]的结果完全一致[31].
对于振荡对流临界点($Ra_{\rm c}^{\rm o}$)附近的有限振幅分叉解,计算方法与静态对流基本相同, 主要的区别在于振荡对流分叉同时存在两种不同的时间尺度：慢时间尺度$s = \chi ^2t$和快时间尺度$t$, 用算子$\partial / \partial t + \chi ^2\partial / \partial s$替换方程(32)中的时间算子$\partial / \partial t$. 此外,${Ra}$需要在临界点${Ra}_{\rm c}^{\rm o}$附近按小参数展开.
一阶问题解的形式可以写为
$$\left. \theta _1 = \left\{ {A_1 (s){\rm e}^{{\rm i}\omega t} + \bar {A}_1 (s){\rm e}^{ - {\rm i}\omega t}} \right\} \cos (ax)\sin (\pi z) \\ \psi _1 = \left\{ {B_1 (s) {\rm e}^{{\rm i}\omega t} + \bar {B}_1 (s) {\rm e}^{ - {\rm i}\omega t}} \right\} \sin (ax)\sin (\pi z) \!\!\right\} (37)$$
式中, $A_1 $和$\bar {A}_1 $, $B_1 $和$\bar {B}_1 $互为共轭复数,且满足[30,39]
$$\dfrac{\partial \left| {A_1 } \right|^2}{\partial s} = 2\left( {p_{\rm r} Ra_{\rm D,2} - l_{\rm r} \left|{A_1 } \right|^2} \right)\left| {A_1 } \right|^2 (38)$$
其中
$$p_{\rm r} + {\rm i} p_i = \dfrac{a^2\gamma ^{ - 1}}{(1 + {\rm i}\omega \varepsilon )c} , \ \ l_{\rm r}+ {\rm i}l_i = \gamma ^{ - 1}k \\ \gamma = \dfrac{ 1 + \varepsilon (c +{\rm i}\omega ) - Ra_{\rm D,c}^{\rm o} \lambda a^2 / c }{1 + {\rm i}\omega \varepsilon } \\ k = \pi ^2\Big[ (c^2 + \omega ^2) / 8\pi ^2 + (c +{\rm i}\omega )^2 / 8\pi ^2 + \\ \qquad (c^2 + \omega ^2) / (8\pi ^2 + 4{\rm i}\omega ) \Big ]$$
令$Q=p_{\rm r}/l_{\rm r}$, 则当$Q>0$时, 振荡对流在临界点附近的分叉是超临界稳定的;若$Q<0$,振荡对流在临界点附近的分叉是亚临界不稳定的. 因此可以通过$Q$值的符号判断分叉方向[66].
振荡对流的非平凡振幅稳态解为
$$\left| { A_1 } \right|^2 = \dfrac{p_{\rm r} }{l_{\rm r} }Ra_{\rm D,2} (39)$$
基于有限振幅解, 振荡对流换热的Nusselt数可以表示为
$$Nu = 1 - \left\langle {\chi ^2\left. {\dfrac{\partial \theta _2 }{\partial z}} \right|_{z = 0} } \right\rangle = \\ \qquad 1 + \left[ {\dfrac{c}{2} + \dfrac{\pi^2\sqrt {c^2 + \omega ^2} }{\sqrt {4\pi ^4 + \omega ^2} }\cos (\phi ^\ast +2\omega t)} \right]\cdot \\ \qquad \dfrac{p_{\rm r} }{l_{\rm r} }\left( {Ra - Ra_{\rm D,c}^{\rm o} }\right) (40)$$
可以看出, 与静态对流 Nusselt数不同, 振荡对流的Nusselt数随时间周期性变化,这一结果与纯黏弹性流体的Rayleigh--Benard热对流结果定性一致[67]. 对式(40)作时间$\!$-$\!$-$\!$面积平均,则得到如下时间$\!$-$\!$-$\!$面积平均Nusselt数[39]
$$\overline {Nu} = 1 + \dfrac{c}{2}\dfrac{p_{\rm r} }{l_{\rm r} }\left( {Ra - Ra_{\rm D,c}^{\rm o} } \right) (41)$$
由图3可以看出, 随着黏弹性流体松弛时间的延长, 振荡对流传热速率变大,而随着弛豫时间的延长, 振荡对流传热速率降低.这说明黏弹性能够促进振荡对流的换热能力,这一结论与非多孔介质纯黏弹性的结果一致[67].
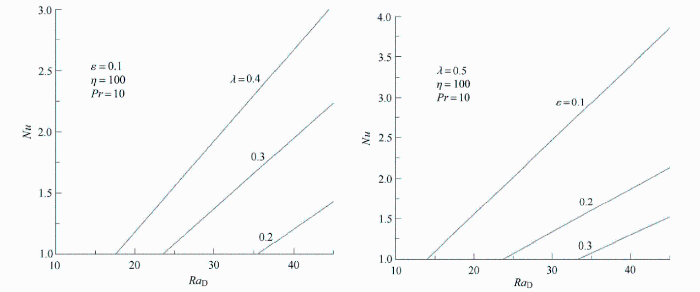显示原图|下载原图ZIP|生成PPT图3不同黏弹性参数下振荡对流平均Nusselt数随Rayleigh数的变化[
-->Fig.3The variations of average Nusselt number for oscillatory convection with Rayleigh number for different viscoelastic parameters[
-->
在临界点附近振荡对流的分叉情况依赖于流体的黏弹性参数、Prandtl数以及Darcy数.如图4所示, 实线右下方参数区域对应于静态对流,实线左上方区域对应于于振荡对流;虚线左上方区域是超临界分叉,虚线与实线之间区域是亚临界分叉. 同时可以看出, 随着Prandtl数的增大,超临界分叉区域变大.
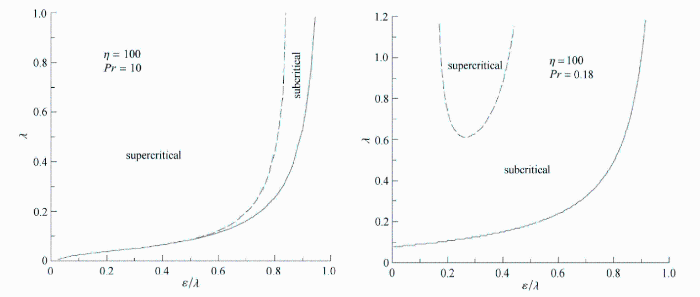显示原图|下载原图ZIP|生成PPT图4振荡对流超临界分叉与亚临界分叉的参数区域划分[
-->Fig.4Regions of subcritical and supercritical oscillatory bifurcations[
-->
1.2 底部等热流加热情形
尽管大部分关于热对流的研究是基于等温加热的情况,等热流加热的情况在诸如电子设备等实际应用中也很常见. 例如,随着半导体技术以及集成电路技术的发展, 电子器件的热流密度也越来越高,已有芯片的热流密度超过500 W/cm$^{2}$.季爱林等[68]介绍了热管及微通道冷板散热方法来解决电子设备的过热问题,将电子器件安装在热管或冷板上, 在热管或冷板内形成热对流并将热量带走. 然而,等热流加热引起的多孔介质内黏弹性流体的热对流问题的研究非常有限.尹晨等[44]应用修正的Darcy-Brinkman-Maxwell模型研究了多孔介质内由底部等热流加热的Maxwell流体的热对流稳定性问题. 在Darcy-$\!$-Brinkman-$\!$-Oldroyd模型(10)和(11)中,令$\varepsilon \to 0$, 就得到Darcy-$\!$-Brinkman-$\!$-Maxwell模型.考虑一个水平无穷大多孔介质层内的流动, 其上表面与下表面之间的高度为$d$,假设上表面为恒定温度$T_{0}$, 如图1所示,但下表面被一个数值为$q$的恒定热流加热.与1.1节底部等温加热情形的基本态(1)不同, 底部等热流加热情形的基本态为
$$V_{\rm b} = 0 , \ \ T_{\rm b} = \dfrac{q}{k}(d - z) + T_0 (42)$$
线性稳定性分析方法与1.1节的类似, 可以得到温度和速度扰动量的无量纲控制方程如下
$$\left.\!\!\begin{array}{l} \left[ {\dfrac{1}{Pr}\left( {1 + \lambda \dfrac{\partial }{\partial t}}\right)\dfrac{\partial }{\partial t} - \nabla ^2 + \dfrac{1}{Da}}\right]\nabla ^2w = \\ \qquad Ra\left( {1 + \lambda \dfrac{\partial }{\partial t}}\right)\nabla _1^2 \theta \\ \dfrac{\partial \theta }{\partial t} - w = \nabla ^2\theta \end{array}\!\!\right\} (43)$$
其中, $\nabla _1^2 = \partial ^2 / \partial x^2 + \partial ^2 / \partial y^2$, $Ra$是用热流量定义的Rayleigh数
$$Ra = \dfrac{\rho _0 g\alpha d^4q}{k\mu \kappa } (44)$$
其中, $k $是多孔介质内的热传导系数, $\kappa $是流体的热扩散系数.
微分方程组(43)的边界条件为
$$\left. z = 0 , \ \ w = \theta = 0 \\ z = 1 , \ \ w = \dfrac{\partial \theta }{\partial z} = 0 \!\!\right\} (45)$$
按照简正模态假设(16)代入控制方程(43),可以得到一个关于Rayleigh数的热对流扰动温度幅值函数的特征值方程[44]
$$ \left( { {\rm D}^2 - a^2 - \gamma } \right)\left( {{\rm D}^2 - a^2} \right)\left( {{\rm D}^2 - a^2 -\sigma } \right)\hat {\theta } = \\ \qquad - a^2Ra(1 + \lambda \sigma )\hat {\theta } (46)$$
其中算子${\rm D} = \partial / \partial z$, $\gamma = (1 + \lambda \sigma )\sigma /Pr + 1 / Da$. 对应的边界条件为
$$\left.\!\!\begin{array}{l} z = 0 , \ \ {\rm D} \hat {\theta } = \left( {{\rm D}^2 - a^2 - \sigma } \right)\hat{\theta } = \left( {{\rm D}^2 - a^2 - \sigma } \right){\rm D}\hat {\theta } = 0 \\ z = 1 , \ \ \hat {\theta } = {\rm D}^2\hat {\theta } = {\rm D}^4\hat {\theta } = 0 \end{array} \!\!\right\} (47)$$
在这个复杂边界条件的问题中, 简单的正弦和余弦函数并不能满足边界条件(47),只能使用数值计算得到Rayleigh数随着水平波数$a$变化曲线, 找到其临界值,分析各参数对热对流稳定性的影响, 详细过程参考文献[44].
由图5可以看出, 系统的临界Rayleigh数都是随着$Da$数的减小而增大的,说明越是致密的多孔介质, 热对流越是稳定. 特别地, 当$Da \to \infty $时,临界Rayleigh数是816.7, 相应的临界波数为2.21,这个结果和非多孔介质内纯Maxwell流体的文结果是一致[69]. 当Maxwell流体的应力松弛时间$\lambda $增大时, 临界Rayleigh数减小,说明流体的弹性增大会促进热对流的不稳定性, 这一结论与底部等温加热情形类似.还可以看出Prandtl数越小, 热对流越不容易失稳.
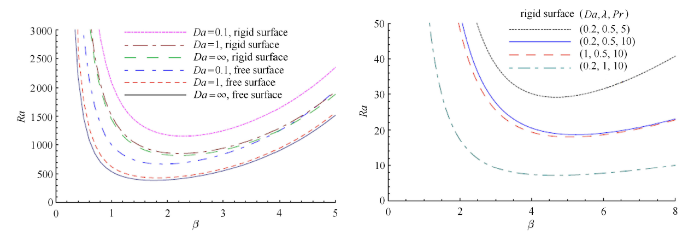显示原图|下载原图ZIP|生成PPT图5静态对流(左图)和振荡对流(右图)的Rayleigh数随波数的变化曲线[
-->Fig.5The variations of Rayleigh number with wavenumber for stationary convection (left) and oscillatory convecton (right)[
-->
2 多孔圆柱内黏弹性流体的热对流稳定性
2.1 底部等温加热情形
张志勇等[38]考虑一个高度为$d$、半径为$a$的有界多孔圆柱, 如图6所示,内部充满了不可压缩流体, 上下表面都是不可渗透的,其上表面($z=0$)温度为$T_{0}$, 下表面($z =- d$)的温度为$T_{0}+\Delta T$, 且$\Delta T > 0$, 侧壁绝热. 黏弹性流体用修正的Darcy-Jeffrey模型(5)刻画,那么该问题的基本状态形式与方程(1)相同, 控制方程的形式与方程(15)完全一致,但其中的坐标系采用柱坐标系, 即$$\nabla _1^2 = \dfrac{\partial ^2}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial }{\partial r} + \dfrac{1}{r^2}\dfrac{\partial ^2}{\partial \varphi ^2}$$
边界条件可以表示为
$$\left.\!\!\begin{array}{l} T = T_0 , \ \ w = 0 , \ \ z = 0 \\ \qquad {\rm (impermeable \ top \ with \ constant \ temperature)} \\ T = T_0 + \Delta T , \ \ w = 0 , \ \ z = - d \\ \qquad{\rm (impermeable \ bottom \ with \ constant \ temperature)} \\ \dfrac{\partial T}{\partial r} = 0 , \ \ v_r = 0 , \ \ r = a \\ \qquad { \rm (impermeable \ and \ adiabatic \ sidewall)} \end{array}\!\!\right\} (48)$$
其中, ($v_{r}$, $v_{\theta }$, $w$)分别表示$r$, $\theta $, $z$三个方向的扰动速度.
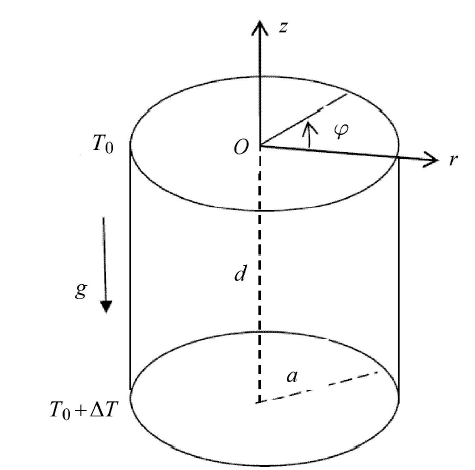显示原图|下载原图ZIP|生成PPT图6底部等温加热多孔圆柱系统示意图
-->Fig.6The schematic diagram of porous cylinder heated from below
-->
按照简正模态分析方法和分离变量法, 扰动速度和温度具有下列形式的解
$$\left.\begin{array}{l} \theta ={\rm J}_n (\gamma _{n,m} r)\cos (n\varphi )\hat {\theta }(z){\rm e}^{\sigma t} \\ w = {\rm J}_n (\gamma _{n,m} r)\cos (n\varphi )\hat {w}(z){\rm e}^{\sigma t} \end{array}\!\!\right\} (49)$$
其中, ${\rm J}_{\rm n}(.)$表示$n$阶Bessel函数. 为了满足侧壁绝热的边界条件, $\gamma _{n,m}$是下列方程代数方程的第$m$个根
$${\rm J}'_n (\gamma a) = 0 (50)$$
关于未知数$\gamma $的方程(50) 有无穷多个正解, 将第$n$个解记作$\gamma _{n,m} $.值得指出的是, 和无穷大多孔介质的情况有所不同, 对于有界多孔介质热对流,波数$\gamma _{n,m} $仅是一些不连续的离散值.
将方程(49)代入控制方程(15)和边界条件(48)得到
$$\left[ {{\rm D}^4 - (2\gamma _{n,m}^2 + \sigma ){\rm D}^2 + \gamma _{n,m}^4 + \gamma _{n,m}^2\sigma - }\right.$$
$$\qquad \left.{Ra_{\rm D} \gamma _{n,m}^2 \dfrac{1 + \lambda \sigma }{1 + \varepsilon \sigma }}\right]\hat {\theta } = 0 (51)$$
$$\hat {\theta }=0 , \ {\rm D}^2\hat {\theta } + (\gamma _{n,m}^2 +\sigma )\hat {\theta } = 0 , \ z = \{0, - 1\} (52)$$
静态对流与黏弹性流变属性无关, 因此只考虑振荡对流. 考虑到边界条件的形式,可以假设$\hat {\theta } = C\sin (l\pi z)$, 由此得到振荡对流Rayleigh的表达式
$Ra_{\rm D}^{\rm o} = \dfrac{\varepsilon (\pi ^2 + \gamma _{n,m}^2 )^2 + (\pi ^2 +\gamma _{n,m}^2 )}{\gamma _{n,m}^2 \lambda } (53)$
$Ra_{\rm D,c}^{\rm o} = \sum_{(m,n) \in N}^{m > 0,n > 0} {Ra_{\rm D}^{\rm o} } (54)$
对于一给定的圆环半径$a$, 确定临界Rayleigh数($Ra_{\rm D,c}^{\rm o}$)的算法实际上等价于寻找一个整数对($n, m)$, 在这一整数对下的波数$\gamma _{n,m} $使得$Ra_{\rm D}^{\rm o}$取极小值. 所以, 我们可以把一个优先对流模态和一对整数$(n, m)$关联起来, 并且把这个优先对流模态叫作$(n, m)$模态.
图7给出了三组黏弹性参数下临界$Ra_{\rm D,c}^{\rm o} $随圆柱半径的变化曲线.可以看出临界Rayleigh数随圆柱半径振荡变化, 但振幅越来越小, 热对流更容易失稳,说明圆柱的侧壁具有抑制热对流的作用. 圆柱内黏弹性流体的松弛时间和弛豫时间对热对流稳定性的影响与前面水平多孔介质的情况类似.图中还给出了优先模态($n, m$)的空间分布情况. 优先模态($n,m$)与松弛时间$\lambda $无关, 但依赖于弛豫时间$\varepsilon $;圆柱半径越大,越容易产生高阶模态, 速度与温度变化周期更小.相邻两个模态的间距随着弛豫时间$\varepsilon $的减小而增大,但不依赖于松弛时间$\lambda $.
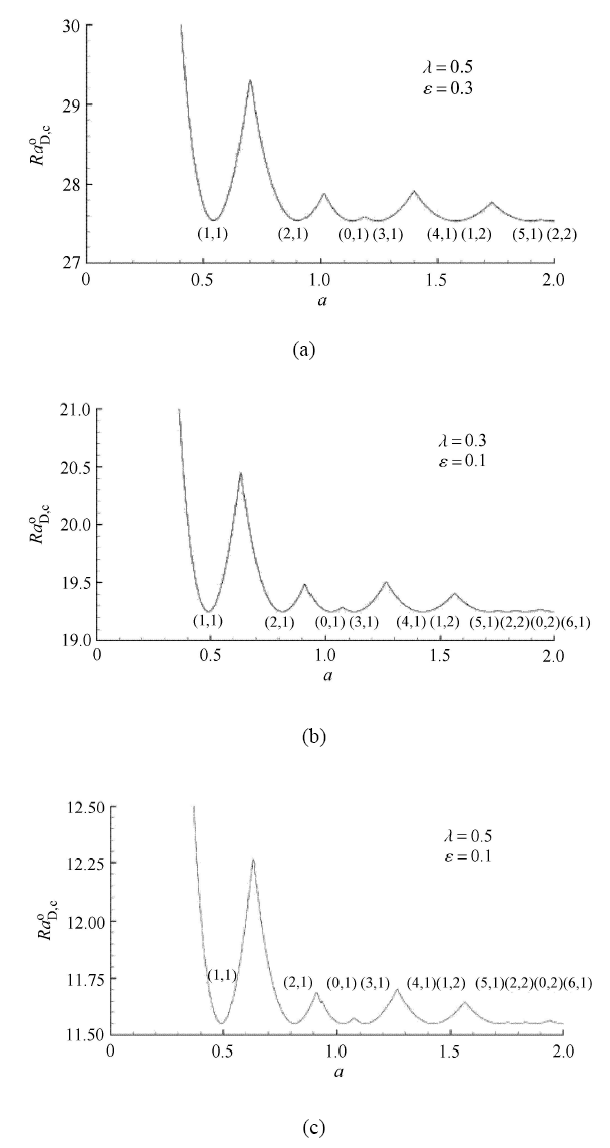显示原图|下载原图ZIP|生成PPT图7等温加热下临界Rayleigh数随圆柱半径变化曲线及优先模态$(n, m)$[
-->Fig.7The variations of Rayleigh number and preferred mode $(n, m)$ with the radius of cylinder heated with constant temperature[
-->
图7中曲线的最低点值为
$$\left[ {1 + 2\varepsilon \pi \left( {\pi + \sqrt {\pi ^2 + 1 / \varepsilon } } \right)} \right]\big /\lambda$$
对应的波长为$\pi \sqrt {\pi ^2 + 1 / \varepsilon } $. 特别地, 当$a \to \infty $时,底部等温加热多孔圆柱内黏弹性流体的热对流问题退化为水平多孔介质层内黏弹性流体的热对流问题, 所得结果与方程(23)相吻合.
2.2 底部等热流加热情形
底部等热流加热与底部等温加热的控制方程相同, Rayleigh数的定义与(44)相同,区别在于$z = -d$处的边界条件不同$$ - k\dfrac{\partial T}{\partial z} = q , \ \ w = 0 , \ \ z = - d \\ \quad {\rm (impermeable \ bottom \ with \ constant \ temperature)} (55)$$
对应于式(52), 等热流加热的无量纲扰动温度的边界条件为
微分方程(51)和(56)有非平凡解的条件是
$$k_1 ( - k_3^2 + \gamma _{n,m}^2 + \sigma )\cosh k_1 \sinh k_3 - \\ \qquad k_3 ( -k_1^2 + \gamma _{n,m}^2 + \sigma )\cosh k_3 \sinh k_1 = 0 (57)$$
其中
$$k_1^2 = \dfrac{1}{2}\left[ {2\gamma _{n,m}^2 + \sigma + \sqrt {\sigma ^2 +4Ra_D \gamma _{n,m}^2 \dfrac{1 + \lambda \sigma }{1 + \varepsilon \sigma }} }\right] \\ k_3^2 = \dfrac{1}{2}\left[ {2\gamma _{n,m}^2 + \sigma - \sqrt {\sigma ^2 +4Ra_D \gamma _{n,m}^2 \dfrac{1 + \lambda \sigma }{1 + \varepsilon \sigma }} }\right] $$
通过等式(57)可以数值求解临界Rayleigh数, 分析各参数对流动稳定性的影响.特别地, 当$a \to \infty $时,底部等热流加热多孔圆柱内黏弹性流体的热对流问题退化为无穷大水平多孔介质层内黏弹性流体的热对流问题.
张志勇等[38]发现底部等热流加热的临界Rayleigh数比等温加热的要小,等热流加热时黏弹性流体更容易发生振荡对流, 并给出了不同圆柱半径下扰动温度场分布, 如图8所示.扰动温度场依赖于圆柱半径$a$和($n$, $m$)值. 一般地, 一个($n$, $m)$优先模态的对流在圆周方向存在2$n$个对流单元结构. 如果$n \ne 0$, 那么对流流动是非轴对称的, 并且在沿半径方向有$m-1$个对流单元;如果$n = 0$, 那么对流流动是轴对称的, 并且在沿半径方向会形成$m$个对流单元.
显示原图|下载原图ZIP|生成PPT图8等热流加热下扰动温度在圆柱底部的分布[
-->Fig.8Temperature disturbance on the bottom wall for constant heat flux heating with $\lambda = 0.5,\varepsilon = 0.1$[
-->
3 多孔方腔内黏弹性流体的热对流稳定性研究
3.1 底部等温加热情形
符策基等[32]考虑一个高度为$d$的二维有界多孔方腔,内部充满Oldroyd型黏弹性流体, 所有边界是不可渗透的, 垂直边界绝热,上下边界等温加热, 且保持温差为$\Delta T$, 如图9所示.该热对流问题可用控制方程(3)$\sim$(5)描述. 引入流函数$\psi $使$u = -\dfrac{\partial \psi }{\partial z}$, $w = \dfrac{\partial \psi }{\partial x}$, 则无量纲控制方程可表示为$\left( {1 + \varepsilon \dfrac{\partial }{\partial t}} \right)\nabla ^2\psi = Ra\left({1 + \lambda \dfrac{\partial }{\partial t}} \right)\dfrac{\partial T}{\partial x} (58)$
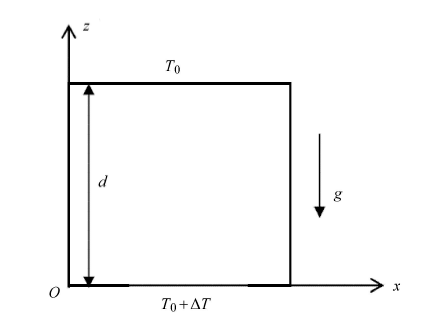显示原图|下载原图ZIP|生成PPT图9底部等温加热多孔有界方腔系统示意图
-->Fig.9The schematic diagram of porous cavity heated from below
-->
$\dfrac{\partial T}{\partial t} - \dfrac{\partial \psi }{\partial z}\dfrac{\partial T}{\partial x} + \dfrac{\partial \psi }{\partial x}\dfrac{\partial T}{\partial z} = \nabla ^2T (59)$
相应的边界条件为
$$ \psi (x,0) = 0 , \ \ T(x,0) = 1 \\ \psi (x,1) = 0 , \ \ T(x,1) = 0 \\ \psi (0,z) = 0 , \ \ \dfrac{\partial T(0,z)}{\partial x} = 0 \\ \psi (1,z) = 0 , \ \ \dfrac{\partial T(1,z)}{\partial x} = 0 $$
对流换热体积平均Nusselt数定义为
$$Nu = - \left\langle {\int_0^1 {\left.{\dfrac{\partial T}{\partial z}} \right|} _{z = 0} d x} \right\rangle$$
符策基等[32]选择三组黏弹性参数：(1) $\lambda = 0.3$, $\varepsilon = 0.2$;(2) $\lambda = 0.2$,$\varepsilon = 0.1$; (3) $\lambda = 0.3$, $\varepsilon = 0.1$,计算了Nusselt数随Rayleigh的变化规律以及流函数和扰动温度场的分布.三组参数对应的振荡对流临界Rayleigh数分别为33.0, 29.7和19.8, 静态对流的临界Rayleigh数都是39.5($ \approx 4\pi^2$), 数值计算Rayleigh数最大直到400.
当Rayleigh数从零开始逐渐增大直至39.5时, 多孔方腔内将首先产生周期性震荡流动, Nusselt数也随时间周期性变化,如图10(a)所示. 此时, 振荡对流的主导频率为$f_{1} =3.1$, 完全由流体的黏弹性所致, 如图10(b)中的能谱所示.当Rayleigh数高于39.5时, 多孔介质内将同时产生振荡对流和静态对流.图11(a)给出了${Ra}=50$时Nusselt数随时间的演化, 与${Ra}=39.5$时的情形相比,Nusselt数变化的振荡波形变得更加复杂, 起主导频率降低为$f_{1}=2.5$, 黏弹性流体在方腔内形成一个单元涡胞结构,如图11(d)所示, 这一结果与牛顿流体基本类似, 但这个涡胞是周期性变化和非对称分布[70]. 若Rayleigh数继续增大,静态对流将逐渐占据主导地位,在传热过程中发挥越来越重要的作用. 当从65增 大75时, 换热速率有明显的增加,因为此时流场从一个单元涡胞变为两个单元涡胞, 如图12(d)所示. 此时,在方腔顶部的热边界层内能观察到明显的热羽流现象, 如图12(c)所示. 由于振荡对流和静态对流的相互作用,以及Rayleigh数的增大, 热流能可能会出现更复杂的流态[32].
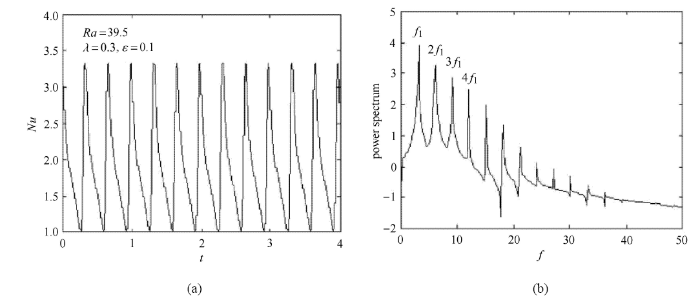显示原图|下载原图ZIP|生成PPT图10(a) Nusselt数随时间的演化;(b)能谱曲线, 其中$\lambda = 0.3$,$\varepsilon = 0.1$, $Ra =39.5$[
-->Fig.10(a) Evolution of the Nusselt number with time and (b) power spectrum of the Nusselt number for a viscoelastic fluid with $\lambda = 0.3$, $\varepsilon = 0.1$ at $Ra =39.5$[
-->
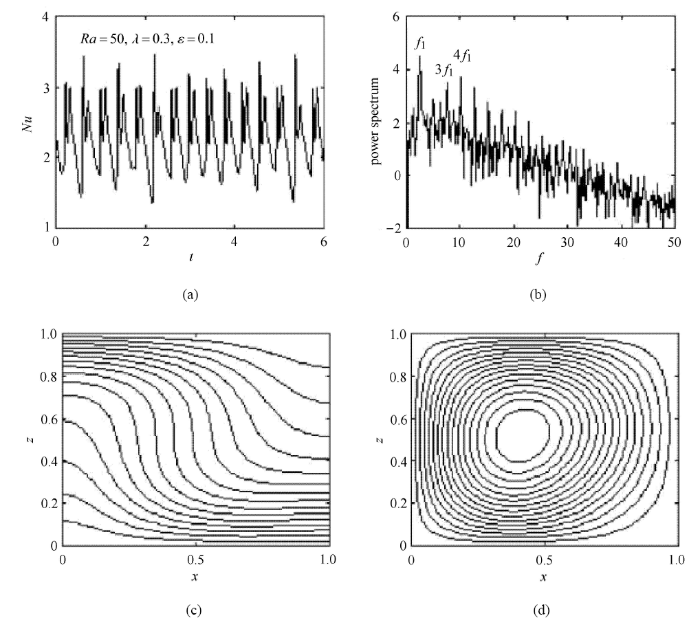显示原图|下载原图ZIP|生成PPT图11(a)Nusselt数随时间的演化;(b)能谱曲线;(c)扰动温度分布;(d)流函数分布, 其中$\lambda = 0.3$, $\varepsilon = 0.1$, $Ra =50$[
-->Fig.11(a) Evolution of the Nusselt number with time and (b) power spectrum of the Nusselt number for a viscoelastic fluid with $\lambda = 0.3$, $\varepsilon = 0.1$ at $Ra=50$. (c) and (d) Snapshots of temperature and stream function distributions, respectively[
-->
显示原图|下载原图ZIP|生成PPT图12(a) Nusselt数随时间的演化;(b)能谱曲线;(c)扰动温度分布;(d)流函数分布, 其中$\lambda = 0.3$, $\varepsilon = 0.1$, $Ra=75$[
-->Fig.12(a) Evolution of the Nusselt number with time and (b) power spectrumof the Nusselt number for a viscoelastic fluid with $\lambda = 0.3$, $\varepsilon = 0.1$ at $Ra=75$. Snapshots of (c) temperature distribution and (d) streamfunction show that the flow is in a two-cell pattern[
-->
3.2 底部对流换热情形
牛骏等[34]考虑了一个高度为$H$、长为$a$、宽为$b$的三维有界矩形多孔方腔,内部充满Oldroyd型黏弹性流体, 所有边界是不可渗透的, 垂直边界绝热,顶部保持常温$T_{1}$, 底部按照牛顿对流换热加热, 对流换热系数为$h$,周围环境温度为$T_\infty $. 该热对流问题可用控制方程(15)描述,相应的边界条件可表示为$$\left.\!\!\begin{array}{l} u = 0 , \ \ \dfrac{\partial T}{\partial x} = 0 , \ \ x = \{0,a\} \\ v = 0 , \ \ \dfrac{\partial T}{\partial y} = 0 , \ \ y = \{0,b\} \\ w = 0 , \ \ T = T_1 , \ \ z = 0 \\ w = 0 , \ \ h(T_\infty - T) = - k\dfrac{\partial T}{\partial z} , \ \ z= - H \end{array}\!\!\right\} (60)$$
其中, $h$表示对流换热系数, $k$表示流体的导热系数, $T_{\infty }$表示外部环境温度.
引入一个热流量$q$使得$q = \dfrac{Bi}{Bi + 1}\dfrac{k(T_\infty - T_1 )}{H}$,其中${Bi}$表示Biot数, 定义为${Bi = hH/k}$. 同时, 以$H$为特征长度, $H^2 / k$为特征时间, $qH / k$为特征温度, $k / H$为特征速度,得到无量纲扰动速度和温度的控制方程在形式上与方程(15)完全一致,但其中${Ra}$为Biot数修正的Rayleigh数
$$Ra = \dfrac{qK\rho _0 \alpha gH^2}{\mu k\kappa } = \dfrac{Bi}{Bi +1}\dfrac{K\rho _0 \alpha gH}{\mu \kappa } = \dfrac{Bi}{Bi + 1}\overline {Ra} (61)$$
无量纲扰动量对应的边界条件为
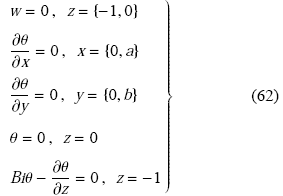
按照稳定性线性分析方法的简正模态, 扰动温度具有下列形式的周期解
$\theta = \cos \left( {\dfrac{m\pi }{a}} \right)\cos \left( {\dfrac{n\pi }{b}}\right)\hat {\theta }(z){\rm e}^{\sigma t} (63)$
$\hat {\theta }(z) = A_1 {\rm e}^{k_1 z} + A_2 {\rm e}^{k_2 z} + A_3 {\rm e}^{k_3 z} +A_4 {\rm e}^{k_4 z} (64)$
其中$A_{1}$, $A_{2}$, $A_{3}$, $A_{4}$是未知常数;$k_{1}$, $k_{2}$, $k_{3}$,$k_{4}$是以下方程的根
$$k^4 - (2L^2 + \sigma )k^2 + L^4 + \sigma L^2 - L^2Ra\dfrac{1 + \lambda \sigma}{1 + \varepsilon \sigma } = 0$$
其中, $L^2 = \pi ^2\left( {m^2 / a^2 + n^2 / b^2} \right)$.
考虑到边界条件(62), 方程(64)有非零解的条件为
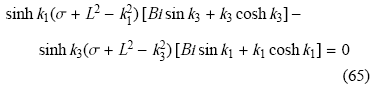
采用数值求解的方法, 由方程(65)可以得到静态对流和振荡对流的临界Rayleigh数. 特别地, 当$b \gg 1$时, 可取$n = 0$,则该三维问题简化为二维问题. 牛骏等研究了7种黏弹性参数组合：(1) $\lambda = 0.003$, $\varepsilon = 0.001$;(2)$\lambda = 0.3$, $\varepsilon = 0.1$;(3)$\lambda = 15$, $\varepsilon = 5$;\linebreak (4) $\lambda = 5$,$\varepsilon = 0.1$;(5) $\lambda = 5$, $\varepsilon = 0.5$; (6) $\lambda = 5$, $\varepsilon = 3$;(7)$\lambda = 0.5$, $\varepsilon = 0.1$. 前三组保持$\lambda / \varepsilon $不变, (4)$\sim$(6)保持松弛时间不变,(2), (4)和(7)保持弛豫时间不变, 以此分析各参数对稳定性的影响.
图13给出了不同多孔方腔尺寸下热对流发生的临界Rayleigh数及其对应的优先模态$m$.对于三组黏弹性参数下的全局最小Rayleigh数(即$Ra_{\min } = \min Ra_{\rm c} $)分别为36.5, 18.2和12.3. 因此,尽管$\lambda / \varepsilon $保持不变, 但全局最小Rayleigh数随着$\lambda $和$\varepsilon $幅值的增大而减小.此外,还发现第一组黏弹性参数下的${Ra}_{\min}$与相同边界条件下的牛顿流体热对流的${Ra}_{\min}$完全相等[71].正如前面所述, 牛顿流体只有静态对流, 不会发生振荡对流, 所以推断对于$\lambda = 0.003$和$\varepsilon =0.001$这样的弱黏弹性流体, 黏弹性效应可以忽略, 热对流只有静态对流一种失稳方式. 此外, 多孔方腔的尺寸越大,黏弹性流体热对流优先模态的$m$值也越大.
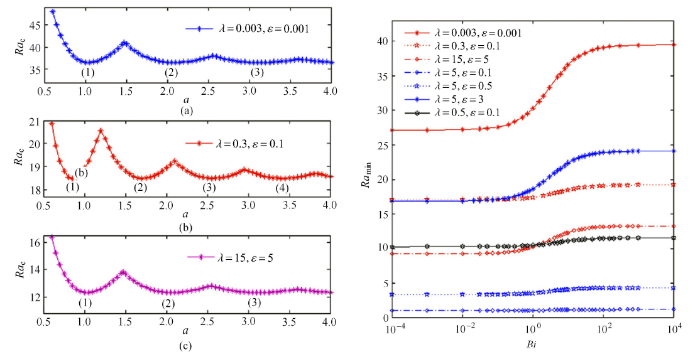显示原图|下载原图ZIP|生成PPT图13临界Rayleigh数随多孔方腔尺寸的变化,其中${Bi}=10$ (左图);全局最小Rayleigh数随Biot数的变化(右图)[
-->Fig.13Variation of the critical Rayleigh number with rectangular dimension $a$ at $Bi = 10$ (left), and variation of the global minimum Rayleigh number with the Biot number (right) [
-->
当$Bi \to 0$时, 底部牛顿加热就退化为底部等温加热情形;当$Bi \to \infty $时,底部牛顿加热就退化为底部等热流加热情形. 从图13可以看出,底部等温加热的全局最小Rayleigh数比相同情况下底部等热流加热时的小. 对于所有黏弹性参数, Biot数越大,全局最小Rayleigh数越大, 特别是在$10^{ - 2} \leqslant Bi \leqslant 10^3$的范围内, ${Ra}_{\min}$有明显的增大.
3.3 顶部自由开口边界情形
牛骏等[33]考虑了一个边长$d$的二维方形多孔腔体,内部充满Oldroyd型黏弹性流体, 顶部和底部保持常温,底部不可渗透加热且与顶部的温差为$\Delta T$, 垂直边界绝热且不可渗透,而顶部是一个开口的自由边界, 保持常压.这样问题的控制方程仍然可用方程(3)$\sim$(5), (58)和(59)描述,相应的边界条件为$$\left. \psi = 0 , \ \ \dfrac{\partial T}{\partial x} = 0 , \ \ x = \{0,1\} \\ \psi = 0 , \ \ T = 1 , \ \ z = 0 \\ \left( {1 + \varepsilon \dfrac{\partial }{\partial t}} \right)\dfrac{\partial \psi }{\partial z} = 0 , \ \ T = 0 , \ \ z = 1 \!\!\right\} (66)$$
采用与3.2节类似的方法, 可以得到决定Rayleigh数和振荡频率的代数方程
$$k_1 (\sigma + \pi ^2 - k_1^2 )\cosh (k_1 )\sinh (k_3 ) - \\ \qquad k_3 (\sigma + \pi ^2 - k_3^2 )\cosh (k_3 )\sinh (k_1 ) = 0 (67)$$
其中$A_{1}$, $A_{2}$, $A_{3}$, $A_{4}$是未知常数;$k_{1}$, $k_{2}$, $k_{3}$,$k_{4}$是下列方程的根
$$k^4 - (2\pi ^2 + \sigma )k^2 + \pi ^4 + \sigma \pi ^2 - \pi ^2Ra\dfrac{1 + \lambda \sigma }{1 +\varepsilon \sigma } = 0$$
牛骏等研究了6种黏弹性参数组合：(1) $\lambda = 0.01$, $\varepsilon = 0.005$;(2) $\lambda = 0.2,\varepsilon =0.1$;(3) $\lambda = 10$, $\varepsilon = 5$;(4) $\lambda = 5$, $\varepsilon = 0.1$;(5) $\lambda = 5$,$\varepsilon = 0.5$;(6) $\lambda = 5$, $\varepsilon = 1$. 基于方程(67),计算得出6种情形下的黏弹性流体振荡对流临界Rayleigh数分别为29.21, 25.58, 14.83, 1.04, 3.38和6.30,而在相同边界条件下, 牛顿流体静态对流的临界Rayleigh数为29.3[25] (也是黏弹性流体静态对流的临界值).
采用有限差分算法, 牛骏等计算了高Rayleigh数下的对流换热速率以及扰动流场分布. 由图14知, 对于情形(1),黏弹性流体的Nusselt曲线几乎与牛顿流体的重合;对于情形(3),黏弹性流体的Nusselt数完全比牛顿流体的高;对于情形(2), 黏弹性流体的Nusselt曲线与牛顿流体的部分重合,这是由振荡对流和静态对流相互作用导致的结果. 图15画出了${Ra}=150$时Nusselt数随时间的演化过程. 对于3种情形,Nusselt曲线均呈现准周期变化趋势, 且$\lambda / \varepsilon $越大, 振荡的频率越高. 对于强黏弹性情形(4),当${Ra}=50$时在流场在方腔内形成4个明显的涡胞结构. 当${Ra}$增大到150时, 顶部和底部的黏性边界变得不稳定,在底部生成更多小涡胞, 而当${Ra}$增加到250时, 流场发展为混沌状态, 如图16(c)所示. 当$\varepsilon $增大时,流场将变得更简单, 起到稳定热对流的作用.
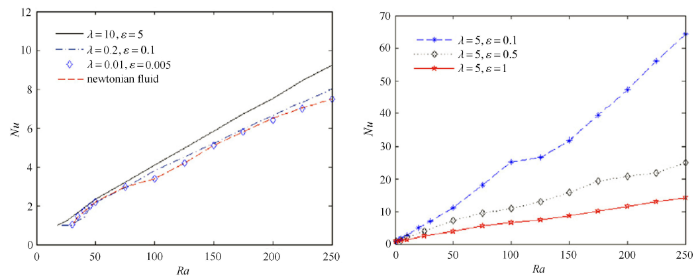显示原图|下载原图ZIP|生成PPT图146组不同黏弹性参数下对流换热曲线的比较[
-->Fig.14Comparison of the heat transfer curves for different cases of viscoelastic parameters[
-->
显示原图|下载原图ZIP|生成PPT图 15当${Ra}=150$时(4)$\sim$(6)情形下Nusselt数随时间的演化[
-->Fig.15The time history of the Nusselt number for Cases (4)$\sim$(6) at ${Ra} = 150$[
-->
显示原图|下载原图ZIP|生成PPT图 16${Ra}=50$, 150和250时热对流流场分布[
-->Fig.16Snapshots of flow patterns at $Ra = 50$, 150 and 250[
-->
除了上面讨论的底部等温加热、底部牛顿加热、顶部自由开口边界情形,文献[35,36,37]中还研究了其他边界条件下方腔多孔介质内黏弹性流体的热对流问题.
4 局部热非平衡效应和旋转效应对黏弹性流体热对流稳定性的影响
4.1 局部热非平衡效应对黏弹性流体的热对流稳定性
前面讨论的热对流问题均假设流体和多孔介质处于局部热平衡状态,系统的能量方程可以合并为一个, 但是若流体和多孔介质的导热系数相差较大,局部热平衡假设不成立, 这时要考虑局部热非平衡模型(local thermal non-equilibrium model, LTNE), 分别给出流体和多孔介质的能量方程.Malashetty等[47]考虑类似1.1节的热对流问题,区别在于流体和多孔介质处于热非平衡状态.流体在多孔介质内的流动方程采用式(14)刻画, 而能量方程为
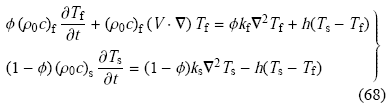
其中, 下标"f"和"s"分别表示流体和多孔基质参数, $\phi $表示孔隙度, $h$表示对流换热系数,$k$表示导热系数, $c$表示热容. 选取$d$作为长度特征量, $\left( {\rho _0 c} \right)_{\rm f} d^2 / k_{\rm f}$作为特征时间, $\varphi k_{\rm f} / \left( {\rho _0 c} \right)_ {\rm f} d$作为特征速度, $\Delta T$作为特征温度, 则无量纲扰动速度与温度的控制方程为
$$\left.\!\!\begin{array}{l} \left( {1 + \varGamma \dfrac{\partial }{\partial t}} \right)\left[{\dfrac{1}{ Pr }\dfrac{\partial }{\partial t}\left( {\nabla ^2w} \right) - R_{\rm D} \nabla _1^2 \theta _f }\right] + \\ \qquad \left( {1 + \varGamma \varLambda \dfrac{\partial }{\partial t}} \right)\nabla ^2w = 0 \\ \left( {\dfrac{\partial }{\partial t} - \nabla ^2} \right)\theta _{\rm f} = w +H(\theta _{\rm s}- \theta _{\rm f} ) \\ \left( {\alpha \dfrac{\partial }{\partial t} - \nabla ^2} \right)\theta _{\rm s} = \gamma H(\theta _{\rm f} - \theta _{\rm s} ) \end{array} \!\!\right\} (69)$$
其中, $\varGamma = \lambda k_{\rm f}/ d$表示无量纲松弛时间, $\varLambda = \lambda/ \varepsilon $表示松弛时间与弛豫时间之比, $H = hd^2 / \phi k_{\rm f} $表示无量纲换热系数, $ Pr = \upsilon d^2 / \varphi k_{\rm f} K$表示Darcy-Prandtl数, $\alpha = k_{\rm f} / k_{\rm s} $表示流固导热系数之比, $\gamma = \phi k_{\rm f} / (1 - \phi )k_{\rm s} $, $R_{\rm D} = g\beta d K\Delta T / \phi \upsilon k_{\rm f}$表示Darcy-Rayleigh数.
按照线性稳定性的简正模态分析方法, 方程(69)的特征解和特征值为
$(w,\theta _{\rm f},\theta _{\rm s} ) = [\hat {w}(z),\hat {\theta }_{\rm f} (z),\hat {\theta }_{\rm s} (z)]{\rm e}^{{\rm i}(lx + my) + \sigma t} $ (70)
$R_{\rm D} = \dfrac{\delta ^2}{a^2}\left( {\dfrac{\sigma }{Pr } + \dfrac{1 + \varGamma \varLambda \sigma }{1 + \varGamma \sigma }} \right)\left( {\sigma + \delta ^2 + \dfrac{H(\alpha \sigma + \delta ^2)}{\alpha \sigma + \delta ^2 + \gamma H}}\right) (71)$
其中, $\delta ^2 = a^2 + \pi ^2$, $a = \sqrt {l^2 + m^2} $表示水平面上的波数.
令$\sigma = 0$, 得到静态对流的Rayleigh数表达式如下
$$R_{\rm D}^{\rm St} = \dfrac{\delta ^4(\delta ^2 + \gamma H + H)}{a^2(\delta ^2 + \gamma H)} (72)$$
可以看出, 静态对流Rayleigh数与流体的黏弹性性质无关,与相同条件下牛顿流体的结果一致[72].
令$\sigma ={\rm i}\omega \ (\omega \ne 0)$,得到振荡对流的Rayleigh数表达式如下
$ R_{\rm D}^{\rm Osc} = \dfrac{\delta ^2(1 + \varGamma ^2\varLambda \omega ^2)}{a^2(1 +\varGamma ^2\omega ^2) } \cdot $
$ \qquad \left\{ {\delta ^2 + \dfrac{H\left[ {\alpha ^2\omega ^2 + \delta ^2\left( {\delta ^2 +\gamma H} \right)} \right]}{\alpha ^2\omega ^2 + \left( {\delta ^2 + \gamma H} \right)^2}} \right\} -$
$ \qquad \omega ^2\left[ {\dfrac{1}{ Pr } + \dfrac{\varGamma (\varLambda - 1)}{1 + \varGamma^2\omega ^2}} \right]\left[ {1 + \dfrac{\alpha \gamma H^2}{\alpha \omega ^2 + \left( {\delta ^2 + \gamma H}\right)^2}} \right] (73)$
由图17可以看出, 当$H$值较小时, 流体和固体之间几乎没有传热, 所以振荡对流的$R_{\rm D}^{\rm Osc}$不受参数$\gamma $和$\alpha $的影响;随着$H$的增大, 振荡对 流$R_{\rm D}^{\rm Osc}$也变大,即流体与固体间的传热具有抑制热对流失稳的作用.
显示原图|下载原图ZIP|生成PPT图17不同参数$\gamma $, $\alpha $, $\varGamma $和$\varLambda$下对流换热系数$H$对振荡对流$R_{\rm D}^{\rm Osc} $的影响[
-->Fig.17The effect of convective heat transfer coefficient $H$ on the critical Rayleigh number $R_{\rm D}^{\rm Osc}$ for oscillatory convection with different values of $\gamma, \alpha , \varGamma $ and $\varLambda$[
-->
4.2 旋转效应对多孔介质内黏弹性流体热对流的影响
旋转多孔介质内黏弹性流体的热对流现象自然界和工业生产中非常普遍,例如在食品加工和化工行业的间歇式生产工艺中, 填充床作为机械搅拌容器,通常由固体颗粒或纤维材料组成, 而流体在这些多孔材料内流动.制糖工业中通过离心结晶分离工艺提取糖浆和从海带中提取海藻酸钠就是这种工艺的两个例子[73].因此, 研究旋转效应对多孔介质内热对流的影响具有重要意义[50].康建宏等[43]考虑一个竖直的同轴圆环柱模型, 圆环柱高为$h$,内外半径分别为$r_{i}$和$r_{o}$, 整个多孔介质充满Oldroyd型黏弹性流体,如图18所示. 同时, 整个圆环柱多孔介质框架连同其内的黏弹性流体以角速度 $\varOmega $沿圆环柱的轴匀速旋转.多孔介质的侧壁完全绝热, 上下底面分别保持恒定温度差$T_0 - T_1 = \Delta T$,其中下底面温度较高, 并且所有壁面都是不可渗透的.该系统受到3个质量力：重力、离心力和Coriolis力, 如果圆柱外径满足$r\ll g /\varOmega ^2$, 那么离心力可以忽略,则描述黏弹性流体流动的无量纲修正Darcy-Jeffrey模型可以表示为
$$ \left( {1 + \lambda \dfrac{\partial }{\partial t}} \right)\left( { - \nabla p -Ta^{1 / 2}{\pmb k}\times{\pmb V} +RaT {\pmb k} } \right) = \\ \qquad \left( {1 + \varepsilon \dfrac{\partial }{\partial t}}\right) {\pmb V} (74)$$
其中, ${Ta}$表示Taylor数, 定义为$Ta = \left( {\dfrac{2\varOmega K}{\upsilon \phi }}\right)^2$ , $\upsilon $表示流体的运动黏度, $K$表示多孔介质的渗透率, $\phi $表示多孔介质的孔隙度.
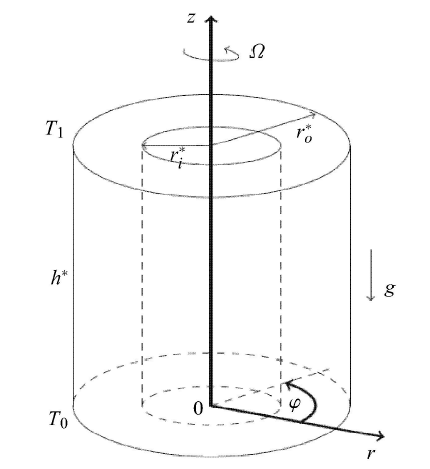显示原图|下载原图ZIP|生成PPT图18底部等温加热旋转圆环柱多孔介质系统示意图[
-->Fig.18The schematic diagram of rotating porous cylindrical annulus heated from below[
-->
扰动速度和温度的无量纲线性控制方程组为
$$\left.\begin{array}{l} \left( {1 + \varepsilon \dfrac{\partial }{\partial t}} \right)^2\nabla ^2w -Ra\left( {1 + \varepsilon \dfrac{\partial }{\partial t}} \right)\left( {1 +\lambda \dfrac{\partial }{\partial t}} \right)\nabla _1^2 \theta + \\ \qquad Ta\left( {1 + \lambda \dfrac{\partial }{\partial t}} \right)^2\dfrac{\partial ^2w}{\partial z^2} = 0 \\ \dfrac{\partial \theta }{\partial t} - w = \nabla ^2\theta \end{array}\!\!\right\} (75)$$
其相应的边界条件为：$w = 0$, $\theta = 0$, $z = \{0,1\}$;$v_{\rm r} = 0$, $\partial \theta / \partial r =0$, $r = \{r_{\rm i}, r_{\rm o} \}$.
按照简正模态分析方法, 特征值问题(75)的特征解可假设为
$$(\theta ,w) = C\left[ {\dfrac{ {\rm J}_m (\gamma _{m,n} r)}{ {\rm J}'_m (\gamma_{m,n} r_i )} - \dfrac{{\rm Y}_m (\gamma _{m,n} r)}{ {\rm Y}'_m (\gamma _{m,n} r_i)}} \right]\cdot \\ \qquad {\rm e}^{\sigma t}\cos (m\phi )\sin (l\pi z) (76)$$
其中, J$_m ( \cdot )$和Y$_m ( \cdot )$分别表示$m$阶第一类和第二类Bessel函数,
$\gamma _{mn} $是下列代数方程的第$n$个根
$${\rm J}'_m (\gamma r_o ) {\rm Y}'_m (\gamma r_i ) - {\rm J}'_m (\gamma r_i ) {\rm Y}'_m (\gamma r_o ) = 0 (77)$$
将方程(76)代入方程(75), 能够得到Rayleigh数的如下表达式
$$Ra = \dfrac{l^2\pi ^2 + \gamma _{m,n}^2 + \sigma }{\gamma _{m,n}^2 }\cdot \\ \qquad \left[{\dfrac{\left( {l^2\pi ^2 + \gamma _{m,n}^2 } \right)\left( {1 + \varepsilon\sigma } \right)}{1 + \lambda \sigma } + \dfrac{l^2\pi ^2Ta\left( {1 +\lambda \sigma } \right)}{1 + \varepsilon \sigma }} \right] (78)$$
令$\sigma = 0$, 得到静态对流的Rayleigh数表达式如下
$$R_{\rm a}^{\rm S} = \gamma _{m,n}^2 + \dfrac{\pi ^4\left( {1 + Ta} \right)}{\gamma_{m,n}^2 } + \pi ^2\left( {2 + Ta} \right) (79)$$
令$\sigma = {\rm i}\omega \ (\omega \ne 0)$,得到振荡对流的Rayleigh数表达式如下
$ R_{\rm a}^{\rm O} = \dfrac{1}{\gamma _{m,n}^2 }\left\{ {\dfrac{\left( {\pi ^2 + \gamma_{m,n}^2 } \right)\left[ {\left( {\pi ^2 + \gamma _{m,n}^2 } \right)\left({1 + \varepsilon \lambda \omega ^2} \right) + \left( {\lambda - \varepsilon} \right)\omega ^2} \right]}{1 + \varepsilon ^2\lambda ^2}} \right. + \left. {\dfrac{\pi ^2Ta\left[ {\left( {\pi ^2 + \gamma _{m,n}^2 }\right)\left( {1 + \varepsilon \lambda \omega ^2} \right) - \left( {\lambda- \varepsilon } \right)\omega ^2} \right]}{1 + \varepsilon ^2\lambda ^2}}\right\} (80)$
当$Ta \to 0$且$r_{\rm i} \to 0$时, 与非旋转多孔圆柱内黏弹性流体热对流的结果相吻合[36].
图19给出了热对流临界Rayleigh 数${Ra}_{\rm c}$随外圆柱半径$r_{\rm o}$的变化. 在低速旋转的小Taylor 数(${Ta} =1$) 情形下, 对于任何的圆环柱半径, 振荡对流总是优先模态. 但是, 对于较高转速下的大Taylor 数(${Ta }= 2$) 情况,振荡对流并不总是优先模态. 当$r_{\rm o}$逐渐增大的时候, 振荡对流模态仅仅间歇性地是热对流的优先模态. 也就是说,振荡对流和静态对流交替作为热对流不稳定性的优先模态.振荡对流这种间歇性地作为热对流优先模态的现象主要是由于黏弹性效应、多孔介质的有界侧壁效应和Coriolis效应三者之间的相互制约和竞争关系引起的.
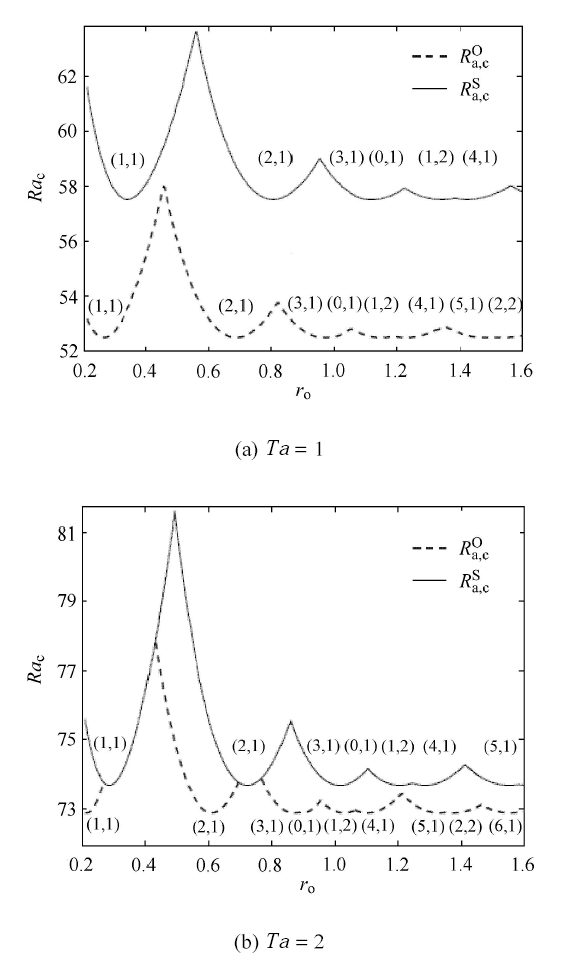显示原图|下载原图ZIP|生成PPT图19临界Rayleigh数与相应的优先模态($m, n)$随圆环柱外径$r_{\rm o} $的变化规律,其中$\varepsilon = 0.3$, $\lambda = 0.5$, $r_{\rm i} = 0.2$[
-->Fig.19The critical Rayleigh number and corresponding mode ($m, n)$ as a function of $r_{\rm o}$ for different Taylor numbers with $\varepsilon = 0.3$, $\lambda =0.5$ and $r_{\rm i} = 0.2$[
-->
此外, Malashetty等[74]和康建宏等[42]还研究了旋转效应对水平多孔介质内黏弹性流体热对流稳定性的影响,同样发现旋转能够抑制热对流失稳.
5 结论与展望
流体热对流失稳主要取决于Rayleigh数的大小, 只要Rayleigh数大于某一临界值,就会产生热对流. 若Rayleigh数从零开始不断增大,牛顿流体的热对流失稳只有静态对流一种模态,而黏弹性流体的热对流失稳先后经历振荡对流和静态对流两种模态.对于Oldroyd型黏弹性流体, 静态对流与流体的黏弹性无关,而振荡对流与流体的黏弹性有密切关系. 一般来说, 流体的黏弹性越强,越容易产生振荡对流.除了流体的流变属性,黏弹性流体热对流的临界Rayleigh数依赖于多孔介质的几何形状、流体动力学和热边界条件以及外部约束条件等因素.和无穷大水平多孔介质的情况相比,有界多孔介质(如多孔圆柱、多孔方腔)内黏弹性流体热对流的波数仅是某些不连续的离散值,有界侧壁具有抑制热对流的作用. 与底部等温加热情况相比,底部等热流加热时黏弹性流体更容易发生振荡对流,而底部采用牛顿加热的临界Rayleigh数介于二者之间;与顶端封闭情况相比,顶端开口自由边界条件下的热对流更加剧烈, 换热速率更高.与流体和多孔介质处于局部热平衡状态相比,黏弹性流体和多孔介质处于局部非热平衡状态时, 更容易发生振荡对流失稳. 此外,Coriolis旋转效应能够抑制黏弹性流体的热对流, 若Taylor数足够大,则可能不发生振荡对流.
随着研究的不断深入, 黏弹性流体热对流稳定性研究在广度上不断延伸,考虑诸如多孔介质各向异性、流体$\!$-$\!$-$\!$多孔介质双层系统、Soret效应双扩散以及磁流体等因素[40-41,45-46,48-49]. 在深度上, 除了热对流失稳的临界Rayleigh数外,缺少关于静态对流和振荡对流相互作用机制以及高Rayleigh数下的混沌和湍流热对流的相关研究. 此外,当前大多数研究集中于理论分析和数值模拟, 热对流的实验研究较少, 非常有必要开展此方面研究.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . [硕士论文]. . |
| [27] | . . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | |
| [43] | . |
| [44] | . |
| [45] | . |
| [46] | . |
| [47] | . |
| [48] | . |
| [49] | . |
| [50] | . . |
| [51] | . . |
| [52] | . |
| [53] | . |
| [54] | . |
| [55] | |
| [56] | . |
| [57] | . |
| [58] | . |
| [59] | . |
| [60] | . |
| [61] | . |
| [62] | |
| [63] | . |
| [64] | |
| [65] | . |
| [66] | |
| [67] | . |
| [68] | . . |
| [69] | . |
| [70] | . |
| [71] | . |
| [72] | . |
| [73] | . |
| [74] | . |
