, 李法新INVESTIGATION ON TRANSITION BETWEEN TIP-SAMPLE INTERACTION REGIMES IN BIMODAL AMPLITUDE MODULATION ATOMIC FORCE MICROSCOPY1)
ZhouXilong, LiFaxi中图分类号:TH742.9
文献标识码:A
通讯作者:
收稿日期:2018-04-22
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (12176KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
原子力显微镜(atomic force microscope, AFM)[1]是扫描探针显微镜家族中应用最为广泛的一种. 作为材料微纳米尺度形貌、物理和化学等性能测试及成像的重要技术和平台, 原子力显微镜在不同学科的前沿领域均得到了深入和广泛应用[2-7]. 在原子力显微镜众多应用模式中, 以动态的振幅调制(amplitude modulation, AM)模式应用最为普遍[8-10], 也常被称为轻敲模式. 近些年来, 原子力显微镜朝着多频、高速和定量化方向发展[11-16]. 多模态振幅调制原子力显微术是多频原子力显微术中应用最广泛的模式之一, 通过同时激励和检测探针的多个振动模态进行测试或成像, 可以获得更多的样品信息, 具有高分辨率、高灵敏度、定量化、无损及成像速度快等典型优势. 应用多模态振幅调制原子力显微术, 一次扫描就能同时获得样品的形貌、弹性、损耗等性能, 适合低维材料和软物质, 如二维材料、薄膜、细胞等的纳米力学性能成像, 也是目前基于原子力显微镜的纳米力学测试技术发展的主要方向之一.双模态振幅调制原子力显微术由于操作简单、可定量化以及对硬件要求相对较低, 在纳米力学测试领域得到了广泛应用. 双模态振幅调制原子力显微术同时激励探针的两阶模态, 通常以一阶模态的响应振幅作为反馈实现对样品形貌成像, 高阶模态的振幅和相位则在针尖样品相互作用力影响下自由变化. Garcia等[8-9]最早通过数值模拟发现, 同时激励探针前两阶模态, 二阶模态相位对吸引力中的Hamaker常数的灵敏度远高于一阶模态[17]. 他们随后通过实验发现在引力区成像时, 二阶模态对于样品不同组分的相位差比一阶模态高一个数量级[18]. Proksch发现在斥力区成像时, 探针二阶模态振幅比一阶模态具有更高的灵敏度[19]. Garcia等[20]建立了双模态振幅调制原子力显微术的理论基础, 并分析了探针在吸引力作用下的动力学特性.
Stark[21]研究了不同模态振幅比情况下, 双模态振幅调制原子力显微术的动力学响应及相应的时域和频域特性. Solares等[22]研究了不同成像参数设置和样品性能对双模态和三模态原子力显微术频响特性的影响. Shi等[23-24]研究了参数设置对探针引力区和斥力区对比度的影响以及前三阶模态在单模态或双模态组合成像时的最优对比度. 部分****从能量角度对探针动力学特性进行研究. Kiracofe 等[25]发现相位对比度的反转与不同模态的动能相对大小相关, 并给出了3个不同的成像区域. Chakraborty等[26]发现振幅和相位对比度反转分别取决于在样品不同区域探针的模态动能比和模态输入能量比.
****们在研究双模态激励下探针的动力学特性时, 通常将探针在引力区或斥力区的动力学行为分开讨论[27-29], 对于引力区和斥力区之间的转变以及成像条件对作用区转变影响的研究却很少开展. 然而, 相互作用区转变及其控制对于双模态振幅调制原子力显微术的成像尤为重要. 在成像过程中如果发生相互作用区转变, 会不可避免地引入伪像, 产生难以理解和解释的图像, 影响对样品力学性能的定量化成像, 甚至定性解释也非常困难. 通常, 探针在斥力区成像时比较稳定, 操作也相对简单, 缺点是针尖施加压力较大, 容易对样品造成损坏, 适用于较硬样品的测试和表征. 在引力区对生物软样品进行成像, 与斥力区相比可以很大程度减小对样品的损害.
本文研究双模态振幅调制原子力显微术引力区和斥力区之间的转变. 研究探针模态自由振幅大小设置、样品力学性能以及激励频率设置对引力区向斥力区转变的影响. 研究结果对于控制作用区范围、避免成像过程中发生作用区转变以及对成像结果的正确分析均具有指导意义.
1 计算模型
采用Euler-Bernoulli梁模型描述原子力显微镜探针微悬臂弯曲振动的动力学特性, 其控制方程为[8]\begin{equation*}\begin{split}&EI\dfrac{\partial^4 q(x,t)}{\partial x^4}+\kappa\dfrac{\partial q(x,t)}{\partial t}+\rho A\dfrac{\partial^2q(x,t)}{\partial t^2}=\\&\quad\quad\delta(x-L)\Big[F_{\text{ ts}}(d)+F_{\text{ext}}\Big]\end{split}\tag*{(1)}\end{equation*}
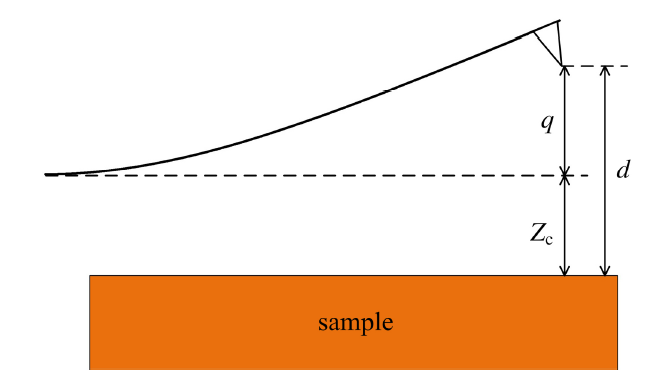
式中, $q$为探针瞬时挠度, $E$为探针弹性模量, $I$为截面惯性矩, $\kappa$为流体介质阻尼系数, $\rho$, $A$ 和$L$分别为探针密度、横截面面积和探针长度. $d$为针尖样品瞬时距离, 与探针样品间距$Z_\text c$以及针尖瞬时挠度$q$之间满足关系式$d=q+Z_\text c$, 如图1 所示. $F_{\text {ts}}$ 为针尖样品相互作用力, $F_{\rm ext}$ 为施加在探针上的外激励力. $\delta(x-L)$ 指针尖样品相互作用力和外激励力施加在探针微悬臂的末端. 由于针尖质量相对悬臂质量可以忽略, 以上方程中略去了针尖质量的影响, 只在分析针尖样品接触力学行为时考虑针尖的曲率半径[8]. 采用振型叠加法表示探针微悬臂的瞬时挠度, 并利用悬臂梁振型的正交性, 将探针多模态振动的控制方程简化为一常微分方程组[25]
\begin{equation*}\dfrac{\ddot{q}_i(t)}{\omega^2_{0i}}+\dfrac{\dot{q}(t)}{Q_i\omega_{0i}}+\dot{q}_i(t)=\dfrac{1}{k_i}\Big[F_{\rm ts}(d)+F_{\rm ext}\Big]\tag*{(2)}\end{equation*}
显示原图|下载原图ZIP|生成PPT图1双模态振幅调制原子力显微术针尖样品之间的三种距离示意图. 三种距离之间满足关系式$d=q+Z_\text c$
-->Fig.1Schematic diagram of three kinds of distances in bimodal AM-AFM. The three distances satisfies $d=q+Z_\text c$
-->
式中, $q_i$为探针第$i$阶模态的瞬时挠度. $\omega_{0i}$, $Q_i$, $k_i$分别为探针第$i$ 阶模态的自由共振圆频率、品质因子和力常数. 其中, $\omega_{0i}=\lambda_i^2(EI/\rho A)^{1/2}$, $\lambda_i$ 满足特征方程$1+{\rm cos}\lambda_i L {\rm cosh}\lambda_iL=0$. 探针各阶模态力常数为$k_i=(\lambda_iL)^4EI/(4L^3)$. 从探针振动的控制方程可知, 不同模态之间的振动通过针尖样品相互作用力和外激励力相互耦合在一起. 采用Derjaguin-Muller-Toporov (DMT) 模型描述针尖样品之间的接触力学行为[8,30], 同时增加针尖样品之间的黏弹性相互作用[31], 则$F_{\rm ts}$ 的表达式为
\begin{equation*}F_{\rm ts}(d)=\begin{cases}-\dfrac{HR}{6d^2},d>a_0\\-\dfrac{HR}{6a^2_0}+\dfrac{4}{3}E^*\sqrt{R}(a_0-d)^{3/2}-\eta\sqrt{R(a_0-d)}\dfrac{\text{d}q}{\text{d}t},\\\quad\quad\quad\quad\quad~~ d\leqslant a_0\end{cases}\tag*{(3)}\end{equation*}
式中, $H$为Hamaker常数, $a_0$为分子间距, $R$为针尖曲率半径, $\eta$为黏度系数. $E^*$ 为折合弹性模量, 其表达式为
\begin{equation*}\dfrac{1}{E^*}=\dfrac{1-v^2_\text t}{E_\text t}+\dfrac{1-v^2_\text s}{E_\text s}\tag*{(4)}\end{equation*}
式中, $E_\text t$, $v_\text t$ 和$E_\text s$, $v_\text s$分别为针尖和样品的弹性模量和泊松比.
采用单一频率激励探针时, 针尖样品相互作用的平均力定义为单个响应周期内相互作用力的平均值[8], 即
\begin{equation*}F_\text a=\langle F_{\rm ts} \rangle=\dfrac{1}{T}\int^T_0F_{\rm ts}(t)\text d t\tag*{(5)}\end{equation*}
式中, $T$为探针的响应周期. 若平均力为负值, 则称探针位于引力区; 若平均力为正值, 则称其位于斥力区. 对于双模态原子力显微术而言, 所选取的两个模态激励频率$\omega_{\text d1}$ 和$\omega_{\text d2}$ 的比值决定了探针响应的周期性[32]. Santos[29]指出当两个激励频率之间存在如下关系时
\begin{equation*}\omega_{\text F}=\dfrac{\omega_\text {d1}}{r}=\dfrac{\omega_\text {d2}}{s}\tag*{(6)}\end{equation*}
式中, $r$和$s$为不可约的整数, $\omega_\text F$称为基本频率, 则探针响应的周期为$rT_1$(或$sT_2$)[32]. 其中, $T_1$和$T_2$分别为一阶和二阶模态的响应周期. 对于双模态振幅调制原子力显微术, 通常将两个激励频率设置为模态自由共振频率. 在计算探针振幅、相位和平均力等物理量时通常是选取探针稳定振动后的几十到几百个周期进行平均[21-22,33]. 本文对于探针动态响应曲线计算中的每一个探针样品间距$Z_\text c$, 计算探针一阶模态1500个周期的响应使其达到稳定振动, 再选取之后的100 个周期进行平均. 采用有限差分方法[34]求解式(2)所构成的常微分方程组, 获得每个模态的时域响应, 并基于同相正交(in-phase and quadrature) 方法计算各阶模态的振幅和相位[22], 同时计算探针的平均力、峰值力以及接触时间. 通过计算探针在接近样品表面过程中平均力的变化, 确定作用区转变的位置. 需要说明的是, 由于成像过程一般是探针从自由状态逐渐接近样品表面, 通常只涉及引力区向斥力区转变的过程, 因此计算过程只考虑引力区向斥力区转变的情况. 分别讨论探针前两阶模态自由振幅大小、样品力学性能变化以及激励频率的设置对相互作用区转变的影响. 数值计算过程中采用的探针和样品参数如表1所示. 其中, 探针一阶模态力常数$k_1$由Euler-Bernoulli梁模型计算获得. 为使二阶模态力常数$k_2$更接近实际情况, $k_2$ 由Labuda等给出的高阶模态力常数幂律模型校准公式确定[35].
Table 1
表1
表1数值计算过程中采用的探针和样品参数
Table 1The parameters of the probe and the sample used in the simulation
| parameters | Value | |
|---|---|---|
| length/μm | 225 | |
| width/μm | 28 | |
| thickness/μm | 3 | |
| density/(kg • m-3) | 2.33 x i03 | |
| R/nm | 20 | |
| H/J | 7.i x i0-20 | |
| a0 /nm | 0.165 | |
| Et/GPa | 160 | |
| Vt | 0.3 | |
| Vs | 0.3 | |
| natural frequency/kHz | 79.327 C/0i) | 497.131 (/02) |
| force constant/(N • m-i) | 2.73(ki) | 61.94(k2) |
| quality factor | 200(Gi) | 450(^2) |
新窗口打开
2 结果与讨论
2.1 模态自由振幅大小对相互作用区转变的影响
双模态振幅调制原子力显微术一般以一阶模态振幅作为反馈进行形貌成像. 成像前需要预先设定一阶模态归一化振幅$A_1/A_{01}$的数值, 通常称为设定点(setpoint). 其中, $A_{01}$为探针一阶模态自由振幅, $A_1$为存在针尖样品相互作用力时一阶模态的响应振幅. 因此, 将引力区向斥力区转变时$A_1/A_{01}$的值作为特征量, 即为作用区转变时的临界设定点. 分析探针前两阶模态自由振幅$A_{0i} (i=1, 2)$对引力区向斥力区转变时临界设定点$A_1/A_{01}$ 的影响. 双模态振幅调制原子力显微术成像时, 一阶模态自由振幅通常远高于二阶模态. 设定一阶模态自由振幅范围$A_{01}=1\sim50$ nm, 二阶模态自由振幅范围$A_{02}=0.1\sim5$ nm, 计算数据点阵列为$50\times 50$, 临界设定点$A_1/A_{01}$与模态自由振幅大小之间的关系如图2 所示. 由图可知, 由于$A_{01}$ 相对较大, 作用区转变时$A_1/A_{01}$的大小主要由$A_{01}$ 控制. 临界设定点$A_1/A_{01}$ 变化较快的区域集中在模态自由振幅的某一范围内. 当$A_{01}\geqslant 40$ nm 时, 引力区向斥力区转变时$A_1/A_{01}\geqslant 0.845$, 使探针位于引力区的设定点范围为$0.845<A_1/A_{01}<1$. 当$A_{01}\leqslant 10$ nm 时, 探针在接近样品的整个过程中平均力始终为负值. 需要说明的是, 虽然平均力始终为负值, 模态相位却在$Z_\text c$ 较小时(通常$<2.5$ nm) 由高于$90^\circ$ 突降为很小的值(一阶模态相位为$0.8^\circ$左右, 二阶模态相位为$5^\circ$ 左右), 对应平均力也发生跳变降低(平均力为负, 其幅值增大), 且转变过程中发生多次跳变振荡. $A_{01}$ 中等大小时, $A_1/A_{01}$ 随着$A_{02}$ 的增加逐渐增大, 即引力区的设定点范围减小. 同样, $A_{02}$ 不变时, $A_1/A_{01}$ 亦随$A_{01}$ 的增加而增大. 这主要是由于模态自由振幅增大,导致样品的压入深度增大, 针尖样品之间相互作用排斥力峰值增大, 使其更易占主导地位. 结果表明, 探针前两阶模态自由振幅之和越大, 引力区向斥力区转变时$A_1/A_{01}$越大, 与单一模态点质量模型给出的结果类似[36].
显示原图|下载原图ZIP|生成PPT图2引力区向斥力区转变时$A_1/A_{01}$与前两阶模态自由振幅之间的关系. 样品弹性模量$E_{\rm s}=1.0$ GPa, 黏度系数$\eta=50~\text{Pa}\cdot \text s$
-->Fig.2Dependence of $A_1/A_{01}$ on the free resonance amplitudes of the first two modes when the transition from attractive to repulsive regime occurs. The elastic modulus is $E_\text s=1.0$ GPa and the viscosity coefficient is $\eta=50~ \text{Pa}\cdot \text s$
-->
代表性自由振幅值对应的平均力、振幅和相位曲线如图3所示. 图中, 左列对应$A_{01}=50$ nm和$A_{02}=1$ nm(振幅组合1), 右列对应$A_{01}=20$ nm和$A_{02}=2$ nm(振幅组合2). 对于振幅组合1, 平均力曲线给出在$Z_{\text c}=45.3$ nm平均力由负值突变为正值,对应$A_1/A_{01}=0.90$. 引力区向斥力区转变时, 振幅和相位亦发生突变. 其中, 一阶模态振幅突增, 二阶模态振幅亦发生微幅突增. 之后,一阶模态振幅随$Z_\text c$减小而线性减小. 前两阶模态的相位值由高于$90^{\circ}$突变为低于$90^\circ$. 引力区范围内二阶模态振幅和相位对于$Z_\text c$ 变化的灵敏度远大于一阶模态, 在斥力区则相反, 与实验结果相一致[23]. 对于接触时间的计算表明, 引力区向斥力区转变时接触时间突然增大, 之后随着$Z_\text c$ 的降低单调增大, 并在$Z_\text c$ 趋于零时再次发生跳变, 针尖样品一直保持接触状态[37].
显示原图|下载原图ZIP|生成PPT图3前两阶模态自由振幅分别为$A_{01}=50$ nm, $A_{02}=1$ nm和$A_{01}=20$ nm, $A_{02}=2$ nm 时的平均力((a) 和(b))、振幅((c)和(d))和相位((e)和(f))曲线
-->Fig.3The average force ((a) and (b)), amplitude ((c) and (d)) and phase curves ((e) and (f)) with the free resonance amplitudes of $A_{01}=50$ nm,$A_{02}=1$ nm and $A_{01}=20$ nm, $A_{02}=2$ nm respectively
-->
对于振幅组合2, 平均力曲线在$Z_\text c=13.6$ nm由负值突变为正值, 对应$A_1/A_{01}=0.61$. 引力区向斥力区转变时, 一阶模态振幅跳变增大, 二阶模态振幅则突然减小.作用区转变后, 随着$Z_\text c$ 逐渐降低, 某些位置处探针在高振幅解和低振幅解之间跳变, 说明不同模态之间振动的相互耦合导致系统并不稳定.
2.2 样品力学性能对相互作用区转变的影响
对非均质材料进行双模态振幅调制原子力显微术成像, 不同组分力学性能的差异会导致作用区转变时$A_1/A_{01}$值的不同. 不同组分力学性能差异较大时, 成像过程中可能发生作用区转变, 产生难以理解的图像. 图4为样品的弹性模量和黏度系数不同时, 引力区向斥力区转变时对应$A_1/A_{01}$ 的变化趋势. 其中, 弹性模量$E_\text s=0.1 \sim 10$ GPa, 黏度系数$\eta =0 \sim 200~\text{Pa} \cdot\text s$, 数据点阵列为$51 \times 51$.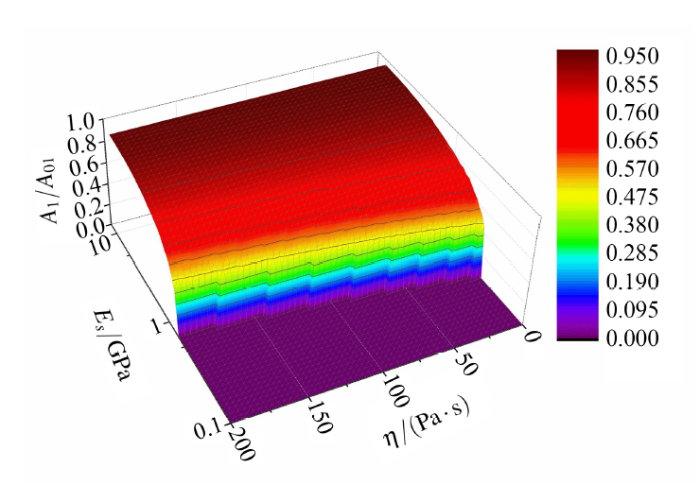
显示原图|下载原图ZIP|生成PPT图4引力区向斥力区转变时$A_1/A_{01}$与样品弹性模量和黏度系数之间的关系. 模态自由振幅$A_{01}=30$ nm, $A_{02}=1$ nm
-->Fig.4Dependence of $A_1/A_{01}$ on the elastic modulus and viscosity coefficient of the sample when the transition from attractive to repulsive regime occurs. The free resonance amplitudes are\\ $A_{01}=30$ nm and $A_{02}=1$ nm
-->
从图4可以看到, 当激励一定时($A_{01}$ 和$A_{02}$ 保持不变), 样品的弹性模量越大、黏度系数越小, 引力区向斥力区转变时$A_1/A_{01}$ 的值越大, 即引力区的设定点范围越小. 这是因为样品弹性模量较高时针尖样品间的相互作用排斥力较大, 排斥力更易占主导地位, 使探针更快进入斥力区. 黏性力的存在则会耗散部分探针动能, 使探针振幅降低, 对样品的压入深度减小[22], 针尖样品排斥力减小, 使探针更晚进入斥力区. 在以上给定的样品模量和黏度系数范围内, 引力区向斥力区转变时$A_1/A_{01}$的值主要由弹性模量决定, 且变化较快的区域主要集中在弹性模量的某一范围内. 弹性模量为中等大小时, 随着黏度系数的增大, 引力区向斥力区转变时$A_1/A_{01}$ 逐渐减小, 引力区的设定点范围增大. 对于生物材料等软样品, 其弹性模量较小且黏度系数较大, 成像时引力区的范围较大, 可在引力区实现对软样品的成像, 并能较好地保护样品免受损害.
图5给出样品力学性能分别为$E_\text s=0.8$ GPa, $\eta=100$ Pa$\cdot$s(情况1)和$E_\text s=1.0$ GPa, $\eta=50~\text{Pa}\cdot$s(情况2)时探针的平均力、振幅和相位曲线. 情况1的平均力曲线显示, 在$Z_\text c=19.6$ nm引力区转变为斥力区, 对应$A_1/A_{01}=0.64$. 对于情况2, 在$Z_\text c=23.3~\text{nm}$ 引力区转变为斥力区, 对应$A_1/A_{01}=0.76$. 可以看到, 由于弹性模量和黏度系数的差异, 情况2 引力区向斥力区转变发生更早. 振幅和相位在作用区转变时亦发生突变. 同样, 探针二阶模态在引力区变化的灵敏度远大于一阶模态, 在斥力区则相反.
显示原图|下载原图ZIP|生成PPT图5样品力学性能分别为$E_\text s=0.8$ GPa, $\eta=100$ Pa$\cdot$s和$E_\text s=1.0~\text{GPa}$, $\eta=50~\text{Pa}\cdot$s 时的 平均力((a)和(b)), 振幅((c) 和(d)) 和相位((e) 和(f))曲线
-->Fig.5Average force ((a) and (b)), amplitude ((c) and (d)) and phase ((e) and (f)) curves with the sample properties of $E_\text s=0.8$ GPa, $\eta=100~\text{Pa}\cdot$s and $E_\text s=1.0$ GPa, $\eta=50$ Pa$\cdot$s respectively
-->
2.3 激励频率设置对相互作用区转变的影响
双模态振幅调制原子力显微术成像时通常将激励频率设置为探针的模态自由共振频率. 图6为探针自由状态下一阶和二阶模态振幅和相位频响曲线. 其中, 前两阶阶模态自由共振频率分别为$f_{01}=79.327$ kHz和$f_{02}=497.131$ kHz. 激励频率低于或高于自由共振频率会影响探针的动力学特性. 为了提高计算精度, 选取激励频率时, 设置两个激励频率满足一定比例关系(式(6)), 在计算探针响应时, 可选取用来平均的周期数为$rT_1$的整数倍[32]. 考虑前两阶模态的激励频率$f_{\text di} (i=1, 2)$同时低于、同时高于以及其中一个低于, 另一个高于相应自由共振频率总共4种激励频率设置情况, 在大约$70\%\sim80\%$ 峰值大小所对应的左右两侧的频率带范围内选取激励频率, 并采用相应周期数进行振幅和相位的计算, 具体设置如表2所示. 需要说明的是, 激励频率处的模态响应振幅设置为等于以自由共振频率激励时的模态自由振幅值.
显示原图|下载原图ZIP|生成PPT图6探针自由状态下前两阶模态振幅和相位频响曲线
-->Fig.6Amplitude and phase response curves when the tip is far away from the surface
-->
Table 2
表2
表2探针前两阶模态激励频率设置
Table 2Excitation frequencies setting for the first two modes of the cantilever
| fdi/kHz | fd2/kHz | Number of periods | |
|---|---|---|---|
| both below | 79.155 | 6.275 fdi | 40 T1 |
| 1st below,2nd above | 79.155 | 6.285 fdi | 200 T1 |
| 1st above,2nd below | 79.490 | 6.248 fdi | 125 T1 |
| both above | 79.490 | 6.260fdi | 50 T1 |
新窗口打开
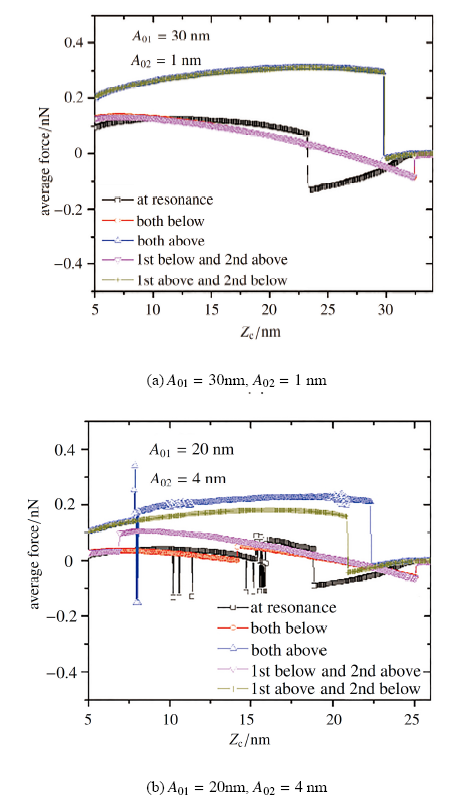
不同激励频率设置情况下针尖样品平均力随$Z_\text c$变化的曲线如图7所示. 可以看到, 两种自由振幅组合情况下, 采用以上任一种激励频率设置方案, 引力区范围均小于以自由共振频率激励时引力区的范围. 对于$A_{01}=30$ nm, $A_{02}=1$ nm (图7(a)), 由于$A_{01}$远大于$A_{02}$, 一阶模态动能远大于二阶模态动能, 其平均力变化趋势主要由一阶模态主导[21]. 当$f_{\text d1}<f_{01}$ 时, 平均力在$Z_\text c=32.4$ nm突然向下发生微幅跳变, 仍为负值, 并未发生相互作用区转变. 此时, 接触时间亦从零发生跳变, 一阶模态单个振荡周期内平均接触时间为0.097$T_1$. 平均力由负值到正值为一连续过程, 在$Z_\text c=26.3$ nm 时平均力开始变为正值. 当$f_{\text d1}>f_{01}$ 时, 平均力在$Z_\text c=29.8$ nm 由负值突变为正值, 针尖样品之间由纯吸引力非接触模式转变为轻敲模式. 斥力区平均力幅值高于以自由共振频率激励时的平均力. 对于峰值力的计算表明, 探针接近样品的整个过程中斥力区排斥力的峰值为13.8 nN, 高于以自由共振频率激励时的排斥力峰值9.8 nN. 这是由于在斥力区探针的共振频率增大, 更加接近激励频率, 相对于以自由共振频率激励时样品的变形量增加, 从而引起峰值力以及平均力的增加. 在对生物软样品进行测试时, 可能对样品造成损害. 对于$A_{01}=20$ nm, $A_{02}=4$ nm (图7(b)), 探针前两阶模态的动能在同一量级, 模态间的相互耦合影响较大, 探针运动有时并不稳定, 会发生运动状态的突变, 导致平均力曲线出现振荡和突变. 因此, 实际测试并不建议选取较大的二阶模态自由振幅[38]. 以上结果表明, 可以通过设置激励频率, 减小引力区的范围, 实现对相互作用区范围的控制.
显示原图|下载原图ZIP|生成PPT图7不同激励频率设置时的平均力曲线. 样品力学性能为$E_\text s=1.0$ GPa, $\eta=50~\text{Pa}\cdot$s
-->Fig.7Average force curves for different excitation frequencies setting. The mechanical properties of the sample are $E_\text s=1.0$ GPa and $\eta=50~\text{Pa}\cdot$s
-->
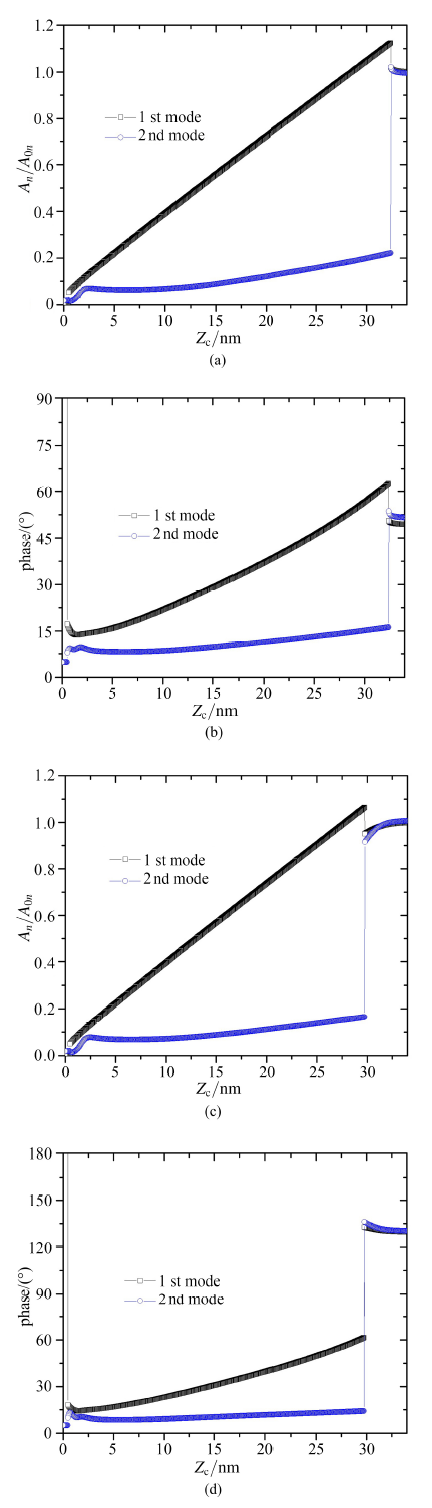
对于$A_{01}=30$ nm, $A_{02}=1$ nm, 前两阶模态激励频率同时低于和高于相应自由共振频率时的振幅和相位曲线如图8所示(模态激励频率等于自由共振频率时的振幅和相位曲线如图5 右列所示). 当$f_{\text di}<f_{\text 0i}$时, 在初始阶段振幅随$Z_\text c$减小而缓慢增加. 这是由于此阶段针尖样品之间的吸引力占主导, 使共振频率向左偏移, 激励频率更加接近共振频率, 从而引起振幅逐渐增加. 前两阶模态的初始相位均小于$90^\circ$. 在$Z_\text c=32.4$ nm 一阶模态振幅突然增大, 其值高于一阶模态自由振幅, 二阶模态振幅则突然减小; 一阶模态相位突然增大(仍小于$90^\circ$), 二阶模态相位突然降低. 此时, 振幅和相位的跳变仅仅是探针运动状态的突变, 平均力仍为负值. 当激励频率偏离自由共振频率时, 不能通过相位值高于或低于$90^\circ$判断探针位于引力区或斥力区. $Z_\text c$ 趋近零时, 一阶模态振幅突然降低, 其值近似为零; 一阶模态相位亦发生突变, 其值略低于360°. 对于$f_{\text di}>f_{\text 0i}$ 的情况, 在初始阶段, 前两阶模态振幅随着$Z_\text c$降低而逐渐减小, 前两阶模态相位均大于$90^\circ$, 且随着$Z_\text c$ 降低略有增加. 这是由于在引力区范围内共振频率左移, 激励频率逐渐远离共振频率. 随着$Z_\text c$ 继续减小, 在$Z_\text c=29.8$ nm时一阶模态振幅突然增大, 二阶模态振幅突然降低, 引力区转变为斥力区.
显示原图|下载原图ZIP|生成PPT图8不同激励频率设置时前两阶模态的振幅和相位曲线. (a)和(b)为激励频率同时低于模态自由共振频率的振幅和相位, (c)和(d)为激励频率同时高于模态自由共振频率时的振幅和相位
-->Fig.8Amplitude and phase curves in bimodal AM-AFM for different excitation frequencies setting. (a) and (b) are the amplitude and phase when excitation frequencies are both below the free resonance frequencies; (c) and (d) are the amplitude and phase when excitation frequencies are both above the free resonance frequencies
-->
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | . . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
