北京理工大学爆炸科学与技术国家重点实验室, 北京 100081
MECHANISM OF EXPLOSION-INDUCED DISTURBANCE IN NATURAL MAGNETIC FIELD1)
LiJianqiao, MaTianbao, NingJianguo中图分类号:O383.1,P318.1,O361.3
文献标识码:A
通讯作者:
收稿日期:2018-03-19
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (16964KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
众所周知, 核爆过程中会产生非常强烈的电磁脉冲. 事实上, 常规爆炸同样会引起自然磁场的扰动, 从而在一定范围内产生电磁干扰, 有时候产生的电磁场会干扰到附近的电子设备, 甚至导致设备停机[1].常规炸药爆炸产生电磁信号最早发现于1954年, 由Kolsky发表于$Nature$[2], 他采用探针测量了1g PETN炸药爆炸产生的信号, 发现所有工况下测量得到的最大电压值都出现在50 $\textrm{μ}$s时刻. 之后不断有****进行相关的实验研究, 获得了不同工况的实验数据. 1958年, Cook[3]针对常规炸药爆炸产生电磁效应提出了一种机理解释, 认为是导电的爆轰产物在地球背景电场中产生极化, 接地之后放电产生了电磁场. 针对这一解释, Boronin等[4-5]进行了有针对性的实验验证, 他们分别进行了有外加电场和无外加电场下爆炸产生电磁辐射的信号采集, 发现虽然冲击波接触地面时会出现一个电磁信号的脉冲, 但是这个脉冲出现在导电区域接地之前. 对此他们提出了Cook的机理不能用于爆炸产生电磁辐射的解释, 常规炸药爆炸产生电磁辐射是由于双极辐射引起的, 并给出了理论描述. Boronin等的工作非常有意义, 首次提出了详尽的理论描述, 给出了一种具体解释机理, 这些都是之前研究所不具备的, 这也为后续的理论研究指引了一个方向, 但其所提出的理论模型中并没有清晰直观的物理机理说明. 在这之后仍然有大量的研究开展, 但并没有新的理论完善, 都集中在爆炸产生电磁信号数据测量, 丰富已有实验结果[6-10]. 2001年Fine[11]提出了更为直观的理论解释, 他认为爆炸产生的等离子体在激波前沿冲击波厚度内被加速引起了电磁辐射, 给出了详细的计算公式, 可以用来估算爆炸产生电磁场强度的量级, 并给出了大量的实验数据. 在Fine以及之前的理论中, 始终认为产生电磁场的原因在于导电气体中电荷分离产生电场, 而后电场变化产生磁场, 这与Boronin的理论基础[5]是一致的, 针对这一点, Fine同样没有给出明确的物理机理. 2014年Kuhl等[12]提出了一种新的理论模型, 事实上这与超高速碰撞过程产生电磁场问题的理论描述较为一致[13]. Kuhl 等认为等离子体在背景磁场中的集群运动会产生电流, 而这个电流会导致周围空间电磁场的变化, 他们根据这一理论模型建立了一维爆炸问题模型, 模拟了球形爆轰产生的电磁辐射现象. 这一理论模型是较为合理的, 物理机理清晰直观. 不过Kuhl的理论模型相对过于简单, 没有形成完整的理论体系, 没有考虑流场对磁场的扰动, 也没有考虑磁场的扩散, 所提出的理论描述只能用于球形爆轰情况.
国内在这方面同样开展了一系列的研究, 但相比国外研究来说起步较晚, 相对研究较少. 陈生玉等[14]在1997年报道了带壳装药爆炸产生的电磁辐射现象, 并且根据量纲分析给出了电场强度与爆炸动力学参数之间的关系, 在这项工作中并没有深入讨论机理等问题, 相对比较初步. 在随后的十几年中再没有相关报道, 直到最近十年相继出现了一些实验研究. 曹景阳等[15]测量了航天火工品爆炸引起的电磁干扰, 分析了主要频率的范围在兆赫兹量级, 为航天器电子设备抗干扰设计提供了一些依据. 王长利等[16]利用天线测量系统对爆炸产生的电磁辐射进行了实验研究, 认为辐射信号强度与炸药当量的1/3次方呈正比, 信号主要频率在100 MHz以内, 并且只与炸药种类有关. 陈鸿等[17]针对含铝炸药爆炸产生电磁辐射问题进行了实验研究, 结果表明铝含量越高电磁辐射强度也越高, 并且给出了主要辐射频率在1 MHz以内, 而且只与组分有关.
从国内外的研究进展可以看出, 爆炸产生电磁效应的问题从发现到现在几十年间持续不断地得到关注, 并且近几年逐步得到国内相关领域****的重视, 开展了一系列实验研究. 这个领域的研究目前以实验为主, 这是因为爆炸产生电磁效应是一个非常复杂的多物理场耦合问题, 尽管可以对问题进行非常多的简化, 最终的结果仍然是相当复杂的. 国外在这方面较为领先, 提出了相对合理的理论模型和机理解释, 但是这些机理和模型仍然非常不完善, 忽略了很多重要的影响因素, 而国内在这一方面的研究完全基于实验研究, 基本没有理论机理方面的进展. 目前国内外的研究中, 对爆炸产生磁场扰动的机理没有清晰的认识, 对影响磁场扰动的因素缺乏全面深入的了解. 研究爆炸引起自然磁场扰动问题不仅具有深刻的科学意义, 同时也具有重要的应用前景.
本文针对爆炸过程引起的自然磁场扰动机理, 开展了理论和数值模拟相结合的研究, 提出了非理想磁流体运动中的磁场压缩和扩散是产生磁场扰动的一方面原因. 针对这一机理, 基于热平衡电离模型开展了数值模拟研究, 首先根据热平衡电离假设给出了爆炸过程中热电离产生等离子体的电导率; 然后根据无磁扩散的磁流体力学方程对爆炸过程中产生的磁场压缩现象进行模拟; 最后将电导率引入磁场扩散方程, 对压缩后磁场在不同电导率气体中的扩散问题进行计算, 最终获得了爆炸产生自然磁场扰动的数值模拟结果. 针对装药几何不对称性开展数值模拟研究, 给出了不同自然磁场方向对磁场扰动的影响.
1 理论模型
1.1 爆炸过程热电离模型
从Eichhorn[18]和Lee等[19]的研究可以看出, 超高速碰撞过程产生的等离子体基本处于热平衡状态, 唐恩凌等[20]的研究也可以证明这一点, 而爆炸与高速冲击问题相似, 也是一种能量沉积很快的动态过程, 并且炸药以及冲击波前沿的物质密度也较高, 因此我们采用了热平衡电离模型, 具体的过程如下:考虑单一电离情况, 这是因为多电离的发生条件很苛刻, 在常规爆炸下基本不可能发生. 元素A电离反应的过程可以描述为
\begin{equation*}\text A\rightleftharpoons \text A^++\text e^-\tag*{(1)}\end{equation*}
其中, $\text A^{+}$表示电离产生的正离子, $\text e^-$表示产生的电子.
对于一个反应平衡的系统, 体系的自由能应处于最低状态, 即自由能$F$的变分为零
\begin{equation*}\delta F=\dfrac{\partial F \partial N_0}\delta N_0+\dfrac{\partial F}{\partial N_1}\delta N_1+\dfrac{\partial F}{\partial N_{\text e}}\delta N_{\text e}=0\tag*{(2)}\end{equation*}
式中, $N$ 表示系统中各种粒子数量, 下标1表示正离子, 下标0表示中性原子, 下标e表示电子. 由单一电离的关系(1) 可以看出各种粒子数之间的变化符合关系
\begin{equation*}\delta N_0=-\delta N_1=-\delta N_{\text e}\tag*{(3)}\end{equation*}
这样一来, 就可以得到一个体系自由能应当满足的关系
\begin{equation*}\dfrac{\partial F}{\partial N_0}-\dfrac{\partial F}{\partial N_1}-\dfrac{\partial F}{\partial N_{\text e}}=0\tag*{(4)}\end{equation*}
体系自由能与能量配分函数$Z$具有如下关系
\begin{equation*}F=-kT\text{ln}Z\tag*{(5)}\end{equation*}
其中$k$为玻尔兹曼常数, $T$为温度, 而配分函数可以表示为位形积分的函数
\begin{equation*}\left.\begin{split}&Z=\dfrac{Q}{\lambda^{3N}N!}\\&Q=\int\cdots\int\text{exp}\left(-\dfrac{U_{\text p}(r_1,\cdots,r_N)}{kT}\right) &\quad\quad\quad\text dr_1~\text dr_2\cdots\text dr_N\end{split}\right\}\tag*{(6)}\end{equation*}
其中$Q$表示位形积分, 是一个与体系势能$U_\text p(r_1,r_2,\cdots,r_N)$相关的量, 如果我们忽略体系的势能, 就得到了描述理想气体热电离的Saha方程, 因为炸药爆炸电离过程的气体密度很高, 所以需要考虑势能的作用, 但是可以假定势能是均匀分布在气体中的, 电子是理想气体, 电子与离子之间的作用以离子的势能代替, 并且离子与原子具有相同的势能, 于是可以将势能表示为
\begin{equation*}\left.\begin{split}&U_{\text p0}\left(r_1,r_2,\cdots,r_{N_0}\right)=N_0E_{\text p}\\&U_{\text p1}\left(r_1,r_2,\cdots,r_{N_1}\right)=N_1\left(E_{\text p}+I_1\right)\end{split}\right\}\tag*{(7)}\end{equation*}
$E_\text p$表示一个原子或离子所具有的势能.
位形积分就表示为
\begin{equation*}\begin{split}&Q_N=\text{exp}\left(-\dfrac{NE_{\text p}}{kT}\right)\int\cdots\int\text dr_1~\text dr_2\cdots\text dr_N=\\&\quad\quad~\text{exp}\left(-\dfrac{NE_{\text p}}{kT}\right)V^N\end{split}\tag*{(8)}\end{equation*}
式中$V$表示体系的体积.
体系总体自由能可以描述为中性原子自由能、离子自由能和电子自由能之和
\begin{equation*}\left.\begin{split}&F=-kT\text{ln}\dfrac{Q_{N_0}Q_{N_1}Q_{N_\text e}}{\lambda^{3(N_1+N_0)}\lambda^{3N_\text e}_\text e N_0!N_1!N_\text e!}\\&\lambda^3=\left\lgroup \dfrac{2\pi \hbar^2}{m_\text akT}\right\rgroup^{\tfrac{3}{2}}\\&\lambda^3_\text e=\left\lgroup \dfrac{2\pi \hbar^2}{m_\text ekT}\right\rgroup^{\tfrac{3}{2}}\end{split}\right\}\tag*{(9)}\end{equation*}
其中$m_\text e$为电子质量, $m_\text a$为气体原子质量, 最终自由能描述为
\begin{equation*}\begin{split}&F=kTN\text{ln}\dfrac{\lambda^3_T}{V}+kTN_0\text{ln}N_0-kTN+\\&kTN_1\text{ln}N_1+E_\text pN+I_1N_1+\\&kTN_\text e\text{ln}\dfrac{\lambda^3_{T_e}}{V}+kTN_\text e\text{ln}N_\text e-kTN_{\text e}\end{split}\tag*{(10)}\end{equation*}
可以得到真实气体热平衡电离中各组分的粒子数密度关系
\begin{equation*}\left\lgroup\dfrac{m_{\text e}kT}{2\pi h^2} \right\rgroup^{\tfrac{3}{2}}\text{exp}\left\lgroup -\dfrac{I_1}{kT}\right\rgroup=\dfrac{n_{\text e}n_1}{n_0}\tag*{(11)}\end{equation*}
式(11)与Saha方程具有相同的表述, 表明在假设势能均匀分布在每个粒子情况下, 势能对电离过程没有影响, 仅对相同内能下的温度有影响.
定义电离度并将热电离关系写成电离度形式, 其中$n$是中性原子和离子的数密度之和
\begin{equation*}\dfrac{\alpha^2}{1-\alpha}=\dfrac{1}{n}\left\lgroup\dfrac{m_\text ekT}{2\pi h^2}\right\rgroup^{\tfrac{3}{2}}\text{exp}\left\lgroup-\dfrac{I_1}{kT}\right\rgroup\tag*{(12)}\end{equation*}
这样根据文献[20,21]给出的电导率模型, 可以获得电离气体的电导率$\sigma$描述为
\begin{equation*}\sigma=\dfrac{e^2n_\text e}{\bar{Z}m_\text e},~\bar{Z}=\sqrt{2}\pi d^2n\bar{v},~\bar{v}=\sqrt{\dfrac{3kT}{\pi m_{\text e}}}\tag*{(13)}\end{equation*}
式中$e$为元电荷数, $d$为原子的有效直径.
接下来需要将等离子体模型和电导率模型结合到磁流体力学方程中.
1.2 MHD模型
分析认为炸药爆炸过程中产生的磁场扰动是由导电气体在自然磁场中运动产生的磁场压缩和扩散造成的, 因此采用MHD模型来描述导电气体的运动和磁场的演化, 单流体全MHD控制方程如下\begin{equation*}\left.\begin{split}&\dfrac{\partial\rho \partial t}+\nabla\cdot\left(\rho U\right)=0\\&\dfrac{\partial(\rho U)}{\partial t}+\nabla\cdot(\rho {UU})+\nabla\cdot\left\lgroup p_{\text{MHD}} I-\dfrac{{BB}}{\mu_\text e} \right\rgroup-\\&\quad\quad\quad\nabla\cdot{\tau}=\rho F\\&\dfrac{\partial B}{\partial t}+\nabla\cdot\left({UB}-{BU}\right)+\nabla\cdot\left(-v_\text e\nabla B\right)=\text{\textbf{0}}\\&\dfrac{\partial(\rho e_{\text{MHD}})}{\partial t}+\nabla\cdot((\rho e_{\text{MHD}}+p_{\text{MHD}}) U)-\\&\quad\quad\quad\nabla\cdot\left\lgroup\dfrac{ B}{\mu_\text e}( U\cdot B)\right\rgroup=\\&\quad\quad\quad\rho F\cdot U+\dot{q}+v_\text e\dfrac{(\nabla\times B)^2}{\mu_\text e}+\\&\quad\quad\quad\nabla\cdot({\tau}\cdot U+ q) &p_{\text{MHD}}=p+\dfrac{ B\cdot B}{2\mu_\text e}\\&\rho e_{\text {MHD}}=\rho e+\dfrac{1}{2}\rho U\cdot U+\dfrac{ B\cdot B}{2\mu_\text e}\end{split}\right\}\tag*{(14)}\end{equation*}
其中, $ q$为热流, $ \dot q$为热源的热生成速率, $p$为压力, $e$为比内能, $\rho$为密度, $ U$ 为流场速度矢量, $ B$为磁感应强度矢量, $ F$为体力矢量, $v_\text e=1/(\sigma\mu_\text e)$为磁扩散率, $\mu_\text e$为绝对磁导率, $ I$为单位张量, $\tau$为流体黏性力张量.
一般来说常规爆炸问题中的电离效应相对较弱, 电离和磁场扰动过程主要发生在爆炸的初期, 爆轰产物和冲击波区域气体密度相对较高, 整体上等离子体的电中性条件保持很好, 并没有显著的电荷分离, 电子和重粒子的运动是一致的, 因此采用单流体模型也可以很好描述常规爆炸产生的磁流体问题. 因为考虑地磁场的强度很低, 磁场的扰动对流体的影响不大, 因此可以忽略能量源项中的焦耳热, 又因为冲击波前沿流场速度很高, 因此近场仿真中可以忽略热对流, 而且问题中并没有热源和体积载荷, 所以可以忽略上述方程的源项, 同时采用八波方程形式, 增加一个源项矢量, 最终的MHD方程以张量形式表示为
\begin{equation*}\dfrac{\partial}{\partial t}\begin{bmatrix}\rho\\\rho U\\ B\\\rho e_{\text{MHD}}\end{bmatrix}+\nabla\cdot\begin{bmatrix}\rho U\\\rho{UU}+p_{\text{MHD}} I-\dfrac{{BB}}{\mu_\text e}\\{UB}-{BU}\\(\rho e_{\text{MHD}}+p_{\text{MHD}}) U-\dfrac{ B}{\mu_{\text e}}( U\cdot B)-{\tau}\cdot U\end{bmatrix}+\nabla\cdot\begin{bmatrix}0\\-{\tau}\\-v_\text e\nabla B\\0\end{bmatrix}=-(\nabla\cdot B)\begin{bmatrix}0\\\dfrac{ B}{\mu_\text e}\\ U\\ U\cdot\dfrac{ B}{\mu_\text e}\end{bmatrix}\tag*{(15)}\end{equation*}
方程(15)左边第一项为时间变化项, 第二项为对流项, 第三项为扩散项, 全MHD方程是一个对流扩散方程, 在进行数值计算的时候, 扩散项的存在对时间步长提出了限制, 要满足稳定性条件, 这与扩散系数有关, 一般情况下流体的动力黏度较低, 因此对方程时间步长没有要求, 但是磁场的扩散率与电导率和磁导率有关, 而一般情况下电导率和磁导率都很小, 这导致磁场扩散很快, 所以在低磁雷诺数的情况下不进行磁场计算, 因为磁场的扰动瞬间就在全场扩散达到平衡. 但是对于爆炸一类问题来说, 全场大部分空间的磁扩散率很高, 然而在近场冲击波位置由于高温高压导致气体电离度较高, 导致磁扩散率相对较低, 磁场的对流和扩散同时起作用, 不能忽视磁场的演化和扩散, 所以需要将求解过程分为两步:
(1)在不考虑磁扩散的情况下进行对流问题的求解, 这时方程化为
\begin{equation*}\dfrac{\partial}{\partial t}\begin{bmatrix}\rho\\\rho U\\ B\\\rho e_{\text{MHD}}\end{bmatrix}+\nabla\cdot\begin{bmatrix}\rho U\\\rho{UU}+p_{\text{MHD}} I-\dfrac{{BB}}{\mu_\text e}\\{UB}-{BU}\\(\rho e_{\text{MHD}}+p_{\text{MHD}}) U-\dfrac{ B}{\mu_{\text e}}( U\cdot B)\end{bmatrix}+\nabla\cdot\begin{bmatrix}0\\-{\tau}\\\text{\textbf{0}}\\-{\tau}\cdot U\end{bmatrix}=-(\nabla\cdot B)\begin{bmatrix}0\\\dfrac{ B}{\mu_\text e}\\ U\\ U\cdot\dfrac{ B}{\mu_\text e}\end{bmatrix}\tag*{(16)}\end{equation*}
针对这个非线性问题可以采用显式求解技术, 采用AUSM类格式分裂对流通量, 黏性项的单元界面值取两侧单元的平均[22], 完成一次时间步的计算, 并且演化求解的自由度, 这时候得到一个对流过程之后的磁场. 这个过程中源项的影响很小, 因为磁场的散度在理论上应该为零, 然而数值计算过程中很难保证散度为零, 不过散度误差一般会很小, 所以计算的稳定性不会受到影响.
(2)仅考虑磁场的扩散过程, 磁扩散是由于电流密度表达式中电场项引起的, 磁扩散方程原始形式为
\begin{equation*}\dfrac{\partial B}{\partial t}=-\nabla\times(v_\text e\nabla\times B)\tag*{(17)}\end{equation*}
旋度的计算有如下的变换关系
\begin{equation*}\nabla\times(\nabla\times B)=\nabla(\nabla\cdot B)-\nabla\cdot(\nabla B)\tag*{(18)}\end{equation*}
所以磁扩散方程改写为
\begin{equation*}\dfrac{\partial B}{\partial t}=-v_\text e(\nabla(\nabla\cdot B)-\nabla\cdot(\nabla B))\tag*{(19)}\end{equation*}
由于磁场是无源场, 其散度为零, 式(19)变化为
\begin{equation*}\dfrac{\partial B}{\partial t}-\nabla\cdot(v_{\text e}\nabla B)=\text{\textbf{0}}\tag*{(20)}\end{equation*}
大部分空间磁扩散率较高, 这导致显式计算扩散问题的时间步长很小, 因此在以对流问题的时间步长作为扩散问题的时间步长, 采用隐式格式来处理磁场扩散问题, 得到扩散后的磁场, 作为一个时间步后最终磁场的演化结果. 整个过程的模拟采用有限体积方法, 结合自主开发的可压缩流体力学程序和磁流体力学程序完成的.
上述全MHD方程并没有考虑电磁波的传播问题, 在导入Maxwell方程组的时候忽略了电位移矢量部分, 同时也没有考虑相对论效应和霍尔效应.
2 数值模拟
爆炸是一类强间断强非线性问题, 随着仿真技术发展, 出现了很多解决这类问题的方法[23-26], 这里采用有限体积法, 基于AUSM+-up格式[27-37]实现对爆炸产生磁场扰动的数值模拟. 数值模拟的目的是探索炸药几何不对称时不同放置方向对产生磁场扰动的影响, 所以并没有针对特定炸药进行模拟, 模拟过程中炸药的参数采用了固体炸药常见的性能参数. 而改变磁场方向与改变炸药放置的方向是等效的, 为了方便起见, 采用了改变初始磁场和磁场边界条件方向, 则不同工况模拟可以采用同一套仿真模型.以自然磁场作为背景磁场, 针对不同背景磁场方向对爆炸产生电磁扰动的影响开展数值模拟研究, 进行背景磁场水平方向($x$方向)以及竖直方向($y$方向)两种工况的模拟计算, 磁场采用高斯单位制(磁感应强度单位为Gs), 取自然磁场磁感应强度为0.5 Gs, 其余变量取国际单位制, 计算物理时间为0.5 ms.
炸药采用瞬时起爆模型, 状态方程采用理想气体状态方程
\begin{equation*}p=(\gamma-1)\rho e\tag*{(21)}\end{equation*}
炸药和空气的模型参数如表1所示, 其中$\rho_0$为初始密度, $e_0$为初始比内能, $\gamma$为比热容比, $T_0$ 为初始温度, $\mu_\text e$为磁导率.
Table 1
表1
表1数值模拟材料参数
Table 1Material properties in numerical simulation
| Material | ρ0/(kg • m-3) | E0/(J • kg-1) | γ | T0/K | μe/(T • m • A-1) |
|---|---|---|---|---|---|
| explosive | 1640 | 7.0 x 106 | 1.4 | 300.0 | 1.257 x 10-6 |
| air | 1.29 | 196 366 | 1.4 | 300.0 | 1.257 x 0-6 |
新窗口打开
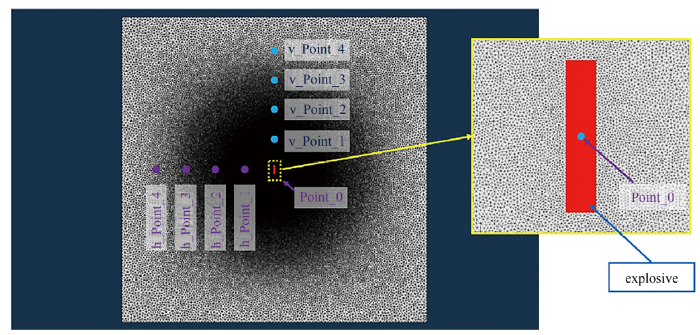
二维计算的模型网格如图1所示, 计算域为边长10 m的正方形, 中心位置放置炸药片, 炸药厚0.06 m, 边长0.3 m. 网格中心密集, 边界稀疏, 保证爆炸初始阶段物理量变化率较大的时候计算的准确性, 整体采用非结构网格. 在边界处约束磁场强度为初始值, 对于流体流动过程设置为流出边界. 计算过程中保存了图1中各关键点的时间历程曲线, 各关键点等间距给出, 间隔1 m.
显示原图|下载原图ZIP|生成PPT图1数值模拟模型网格
-->Fig.1The model and mesh used in numerical simulation
-->
除了炸药之外的计算域填充空气, 计算过程实际为单物质计算, 炸药与空气从组分上认为是相同的, 相当于状态不同的同种介质, 因此在计算电导率的时候爆轰产物和空气的电导率计算方法相同, 因为初始状态下空气电导率较低, 为了防止计算磁扩散系数时分母的电导率为零, 为计算域设置了背景电导率, 其值为大气常温下海平面高度电导率[38], 约为$5.0\times 10^{-15}~\text S / \text m$. 计算域内所有网格计算电导率之后, 需要加上背景电导率, 作为最后参与磁场计算的电导率.
两种工况数值模拟的初始磁场条件如表2所示. 其中$B_{x0}$表示初始磁场$x$方向分量, $B_{y0}$表示初始磁场$y$ 方向分量. 工况1 表示背景磁场沿$x$方向, 工况2表示背景磁场沿$y$方向.
Table 2
表2
表2磁场初始条件
Table 2Initial condition of magnetic field
| Simulation case | Bx0/Gs | By0 /Gs |
|---|---|---|
| 1 | 0.5 | 0 |
| 2 | 0 | 0.5 |
新窗口打开
2.1 数值计算格式
控制方程组的时间积分采用二阶的预估-矫正格式, 作为一种经典的二阶精度时间积分数值格式, 其具体形式本文不再赘述. 控制方程组的空间离散采用有限体积法, 对于空气和爆轰产物我们采用无黏流动来描述, 因此式(15)中唯一的黏性通量来自于磁扩散项, 无论是哪一种通量, 其有限体积离散的形式是一样的, 将式(15)以求解自由度矢量形式表示\begin{equation*}\dfrac{\partial X \partial t}+\nabla\cdot F+\nabla\cdot G= 0\tag*{(22)} \end{equation*}
其中$ X=[\rho,\rho U^\text T, B^\text T,\rho e_{\rm MHD}]$为求解矢量的转置, 上标T表示转置, $ F$ 为对流通量张量, 表示为
\begin{equation*}\begin{split}&F=\Bigg\lbrack \rho U,\rho {UU}+p_{\text{MHD}}I-\dfrac{ {BB}}{\mu_\text e}, {UB}- {BU},\\&\quad\quad(\rho e_{\text{MHD}}+p_{\text{MHD}}) U-\dfrac{ B}{\mu_\text e}( U\cdot B)\Bigg\rbrack\end{split}\tag*{(23)}\end{equation*}
$ G=[ 0,0\cdot I,-v_\text e\nabla B, 0]$与$ F$同阶, 表示黏性通量, 梯度算符$\nabla$ 为行向量, 这样控制方程由式(22) 表示, 将散度进行空间降维, 式(22) 表示为式(24)
\begin{equation*}\iiint\limits_{\varOmega}\dfrac{\partial X}{\partial t}\text d\varOmega+\iint\limits_S n^\text T\cdot F\text dS+\iint\limits_S n^\text T\cdot G\text d S= 0\tag*{(24)}\end{equation*}
$ n^\text T$表示微元面的外法向量转置, 有限体积法对于具有$m$个面的单元$i$来说, 其离散的格心格式为
\begin{equation*}\dfrac{\partial X_i}{\partial t}=-\dfrac{1}{\varOmega}\sum\limits^m_{o=1} n^\text T_o\cdot( F_o+ G_o)\cdot S_o\tag*{(25)}\end{equation*}
其中$S_o$表示$i$单元中第$o$个面的面积, $\varOmega_i$表示$i$单元的体积. 针对对流通量和黏性通量采用不同的数值格式. 实际的计算过程可以概括为%\vskip 0.5mm
\begin{align}&\dfrac{\partial X_{i1}}{\partial t}=-\dfrac{1}{\varOmega_i}\sum\limits^{m}_{o=1} n^\text T_o\cdot F_o\cdot S_o\tag*{(26)}\\&\dfrac{\partial X_i}{\partial t}=-\dfrac{1}{\varOmega_i}\sum\limits^m_{o=1} n^\text T_o\cdot G_o\left( X_{i1}\right)\cdot S_o\tag*{(27)}\end{align}
即先完成一次对流通量计算, 更新后做一次磁扩散的黏性通量计算. 对于黏性通量, 考虑界面$o$两侧单元$i$和$j$, 界面$o$上的黏性通量可以表示为两侧单元黏性通量的平均值: $ G_o=0.5( G_i+ G_j)$, 对所有单元面循环, 可以组装总体矩阵, 采用隐式格式求解.
对于对流通量, 采用AUSM+-up格式通过马赫数分裂计算单元界面的通量值, 需要将对流通量张量分开写成守恒量项和压力项
\begin{align*}& F= F^\text c+ F^\text p+ F_\text{MHD}\tag*{(28)}\\& F^\text c=[\rho U,\rho {UU}, {UB},\rho e_\text{MHD} U]\tag*{(29)}\\& F^\text p=[ 0,p_\text{MHD} I, 0,p_\text{MHD} U]\tag*{(30)}\\& F^\text {MHD}=\Bigg[ 0,-\dfrac{ {BB}}{\mu_\text e},- {BU},-\dfrac{ B}{\mu_\text e}( U\cdot B)\Bigg]\tag*{(31)}\\\end{align*}
对于$ F^\text c$和$ F^{\text p}$进行Zha-Bilgen(Z-B)[36]分裂, 而将$ F^\text{MHD}$ 看作黏性项, 其空间离散的计算格式与$ G_o$相同$ F^\text{MHD}_o=0.5( F^\text{MHD}_i+ F^\text{MHD}_j)$, 时间上采用显式时间积分方法.
采用Z-B分裂的AUSM+-up格式来获取单元界面$o$上通量的过程为
\begin{equation*}\left.\begin{split}& F_o= F^\text c_o+ F^\text p_o+ F^\text {MHD}_o\\& F^\text p_o=[ 0,p_o I,p_o U_o],~ U_o=\dfrac{1}{2}( U_\text R+ U_\text L) & F^\text c_o= n\cdot F_\text c\\& F_\text c=\begin{cases}a_oM_o X_\text L,M_o>0\\a_oM_o X_\text R,M_o\leqslant0\end{cases}\end{split}\right\}\tag*{(32)}\end{equation*}
其中, L和R分别表示界面的左状态和右状态, 这里采用了0阶单元重构, 因此L和R 即表示界面的左侧单元和右侧单元, 可以选择$i$单元作为L单元而$j$单元表示R 单元, 反之亦可, 只需要保证单元界面$o$的法向由L指向R即可. $a_o=0.5(a_\text L+a_\text R)$ 表示界面声速, 界面声速具有很多不同计算方法, 这里采用最简单的代数平均值. $M_o$和$P_o$分别表示界面马赫数和压力, Liou[36]在文章中给出了非常详细的计算方法以及参数的选取, 这里不再赘述.
对于由式(27)所形成的大规模线性方程组, 采用MKL中的PardisoLU分解稀疏矩阵求解器直接求解.
2.2 背景磁场沿$x$方向
图2给出了不同时刻$x$方向磁感应强度的数值模拟结果.
显示原图|下载原图ZIP|生成PPT图2不同时刻x方向磁感应强度Bx数值模拟结果
-->Fig.2Numerical simulation of Bx at different time
-->
2.3 背景磁场沿$y$方向
图3给出与2.2节相同时间的$y$方向磁感应强度模拟结果.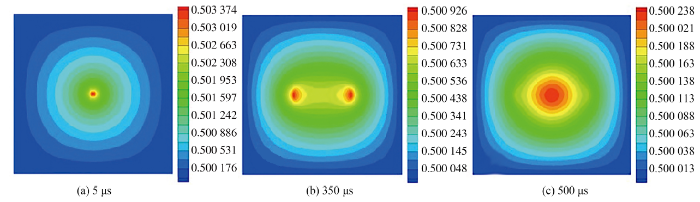
显示原图|下载原图ZIP|生成PPT图3不同时刻$y$方向磁感应强度$B_y$数值模拟结果
-->Fig.3Numerical simulation of $B_y$ at different time
-->
3 讨论分析
图4给出了爆炸前期相同时刻两种模拟得到的结果对比, 其中等值线为磁矢势在$z$方向的分量$A_z$, 表示磁力线. 从数值模拟结果来看, 当背景磁场方向不同时, 炸药爆轰产物运动和冲击波传播引起的磁场扰动有很大的不同, 也就是说当几何不对称的炸药在空间中放置的方向不同时, 将会产生不同的磁场扰动. 这种不同表现在量级上, 并且这种不同现象在炸药爆轰的初期较为明显, 而对于空间中磁场扰动的模式来说, 基本是相同的.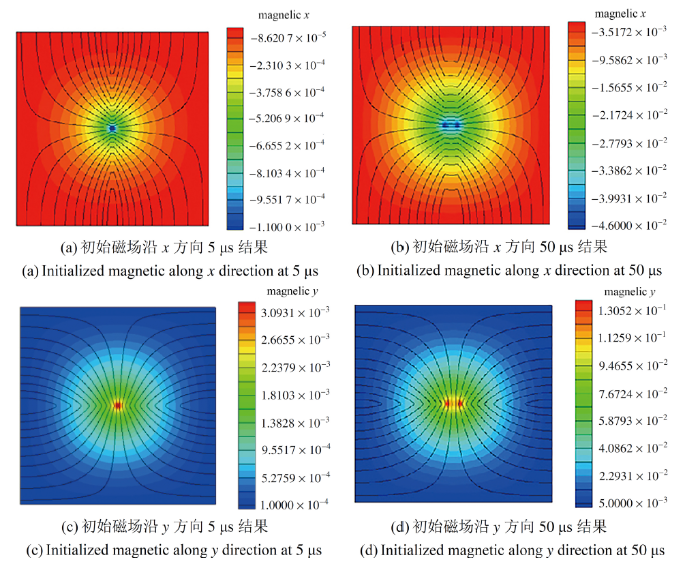
显示原图|下载原图ZIP|生成PPT图4不同磁场方向数值模拟结果对比
-->Fig.4Comparison between numerical simulations with different magnetic directions
-->
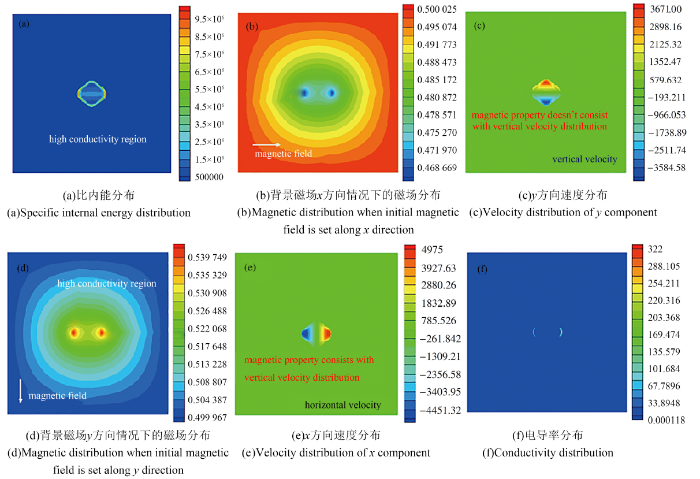
这主要是因为炸药的几何条件不对称引起了流场参数的空间不对称, 从图5给出的流场速度和比内能结果图可以看出. 由于背景磁场相对较弱, 对流场的干扰几乎可以忽略.
显示原图|下载原图ZIP|生成PPT图5150 μs 数值模拟结果
-->Fig.5Numerical results at 150 μs
-->
从图5的结果可以看到, 无论背景磁场是$x$方向还是$y$方向($x$和$y$的定义见第3节), 磁场扰动都会集中在$x$ 方向上. 如图5(b)为背景磁场指向$x$方向的模拟结果, 一般来说应该受到图5(c)所示的$y$方向速度影响较高, 然而实际上磁场扰动的特征分布与图5(e)所示的$x$方向速度分布特征相同, 这说明影响磁场扰动的主要因素并不是流场的速度场, 而是流场中的能量分布, 因为能量分布直接影响到电导率分布结果. 如图5(a)所示为比内能分布, 在$x$方向上存在比内能最高的区域, 刚好与磁场扰动的分布特征相同.
这主要是因为磁场的扩散受电导率直接影响, 而从图5(f)的结果来看, 电导率的空间分布差异很大, 在$x$方向有两个集中的地方, 导致这两个位置的磁场扩散较慢, 而其余地方的电导率极小, 产生的磁场扰动以极快的速度向周围扩散, 从而难以形成明显的磁场扰动积累. 可以说电导率决定了磁场扰动的模式和持续时间.
图6给出了爆轰产物膨胀后期相同时刻两种模拟得到的结果的对比, 等值线的意义与图4 相同, 表示磁力线, 当炸药爆轰产物膨胀一定时间之后, 后期的磁场演化模式以及磁场扰动的幅度基本相同. 这是因为当爆轰产物膨胀到一定程度之后, 就会逐渐变成球形膨胀, 因此即使初始几何形状不是球对称, 在爆炸过程的后期也会形成几何球对称的运动状态, 这时无论磁场方向如何, 爆轰产物的膨胀运动对磁场的扰动都是相同的. 并且在爆轰产物膨胀过程中, 爆轰产物的电导率会降低很多, 从而引起磁场扩散速度升高, 磁场最终在全场趋于平衡, 这一点从图4 和图6 可以明显看出来. 初期背景磁场为$y$方向情况下磁场扰动最高可以达到0.140 67 Gs(图4(d)), 背景磁场为$x$ 方向是相同时刻的磁场扰动在0.047 314 Gs(图4(b)), 之间几乎差了一个数量级. 而到了后期(图6(b)、图6(d)), 磁场为$y$方向的情况下最大磁场扰动在0.000 238 Gs, 磁场为$x$方向情况下最大磁场扰动在0.000 174 Gs, 两者几乎相当, 并且磁场的空间分布也几乎相同, 磁场整体上扰动量级比爆炸初期降低很多.
显示原图|下载原图ZIP|生成PPT图6不同磁场方向数值模拟结果对比
-->Fig.6Comparison between numerical simulations with different magnetic directions
-->
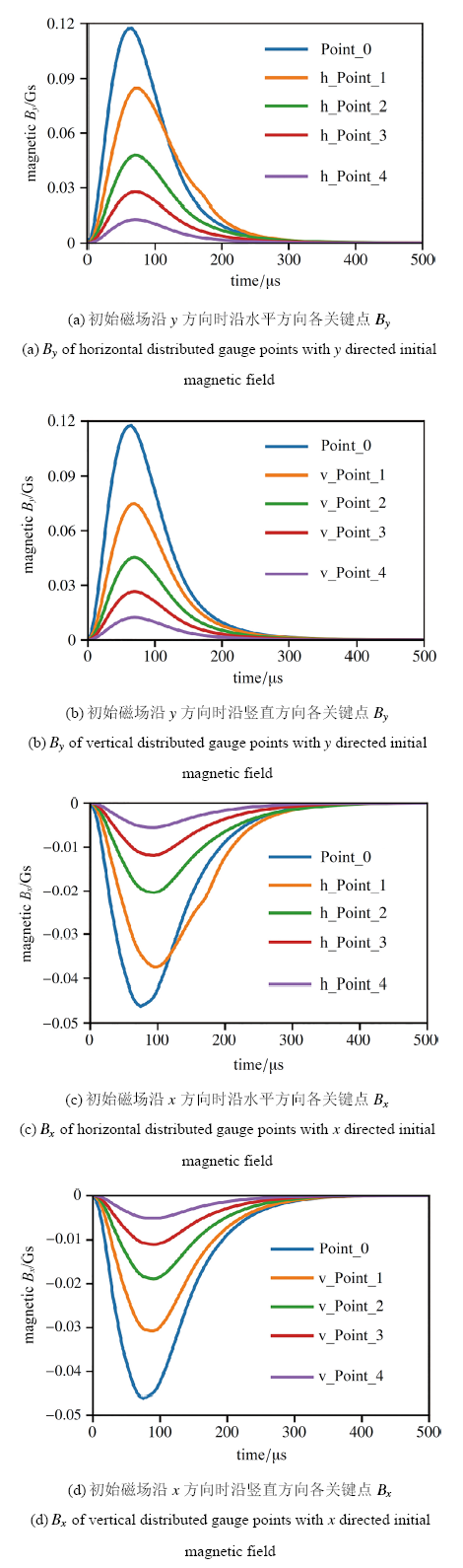
在对比的过程中我们发现, 磁场的等值线在边界处几乎与边界形状相同, 这是因为计算过程中选取了固定边界磁场强度的边界条件, 因此随着爆轰产物膨胀过程的发展, 扰动的峰值距离边界越来越近, 较高的磁场梯度导致磁场扩散很快, 磁场扰动的衰减越来越快. 这里需要说明边界条件对整体的规律讨论的影响, 图1的模型图表明, 模拟的空间尺度相对来说很大, 从图4可以看出, 这样可以保证模拟初期的结果受边界的影响不大(整体上扰动较大的磁场主要集中在中心附近的圆形区域); 在模拟的中后期, 我们看到随着爆轰产物的膨胀以及磁场的扩散, 边界条件对内部磁场产生了作用, 但是在这时候对于两种工况的模拟来说, 磁场的扰动从模式到数值基本上相当, 这一点从图6(a)中可以看出(扰动的分布以及峰值. 注意左边为背景磁场指向$x$方向结果, 右边为背景磁场指向$y$ 方向结果, 两者磁场扰动的幅度是相反的), 我们采用了相同的边界条件, 这样边界对于两种模拟结果的影响是相同的, 所以边界条件对于两种模拟结果异同的内部机理讨论并没有本质影响. 但这样的边界并不利于准确计算爆炸过程中远场的磁场扰动情况, 本文在远场的计算因为边界的原因导致结果将与实际情况有出入, 远场计算结果尚无法对实验进行直接指导.图7给出了图1标记的关键点处磁场扰动的时间历程曲线, 以$B_x$表示$x$方向磁场扰动值, 以$B_y$表示$y$方向磁场扰动值. h开头表示水平分布关键点, v开头表示竖直分布关键点.
显示原图|下载原图ZIP|生成PPT图7
-->Fig.7Magnetic field history curves on gauge points marked in
-->
从图7可以看出, 当初始磁场方向不同时, 各关键点得到的扰动模式几乎是一致的, 对应点的时程曲线较为相似, 不同之处体现在两个方面: 一个是扰动的幅值不同, 磁场方向与炸药较长的边的方向一致时扰动的幅值较高; 另一个不同之处在于峰值磁场扰动到达时间, 当初始磁场沿着炸药较长边方向时, 磁场扰动的峰值到达较早. 各关键点中0点在中心, 关键点1表征了近场的磁场扰动情况, 其余各点表征了远场磁场变化, 从图7(a) 和图7(b)各点时程曲线来看, 近场处在水平和竖直方向的磁场扰动差别较大, 而远场则几乎没有区别. 从磁场扰动到达峰值的时间来看, 关键点0 与其他关键点之间有明显区别, 而其他各点结果则基本相同, 约在$70\sim 90~\textrm{μ}\text s$ 之间, 这表明中心位置磁场扰动很大程度上是由导电流体运动压缩磁场引起, 其余各点的磁场扰动则是磁场扩散产生的. Kuhl[12] 针对1 kg的TNT 炸药爆炸产生的电磁信号进行了研究, 给出了10 m位置上信号的到达时间为$10~\textrm{μ}\text s$, 持续时间为$20~\textrm{μ}\text s$. 我们做了与之工况相同的算例, 给出了相同位置上磁感应强度随时间的变化曲线与文献[12]的结果对比, 对比结果在图8中给出.
显示原图|下载原图ZIP|生成PPT图8与文献中结果的对比
-->Fig.8Comparison with citation
-->
文献中给出的是因位移电流引起的电磁波扰动, 我们同样给出的也是电磁波结果, 这与我们计算磁场扩散时所采用的磁扩散项是一样的, 仅时间积分方法不同. 考虑炸药直径约为5 cm, 炸药从起爆到完全爆轰过程约为$10~\textrm{μ}\text s$, 由于我们采用瞬时起爆模型, 因此信号出现在0时刻, 以$-10~\textrm{μ}\text s$作为起时刻, 结果从信号出现时间到持续时间与文献结果都符合较好, 从时间尺度上来说我们的结果与文献[12] 的结果具有很好的一致性, 从而在一定程度上表明了本文结果的可靠性.
4 结 论
本文通过数值模拟方法研究了常规爆炸产生的磁场扰动现象, 基于热平衡电离模型和单流体MHD模型给出了流场和磁场演化的控制方程, 指出了磁场扩散与导电流体高速运动中引起的磁场运动是爆炸引起自然磁场扰动的机理, 通过计算爆炸力学领域常用的数值方法求解控制方程, 给出了炸药几何不对称特性对爆炸产生磁场扰动的影响, 对比了两种空间布置下的模拟结果, 可以得到如下结论:(1) 基于本文提出的机理, 可以获得爆炸过程中自然磁场扰动的结果;
(2) 几何不对称的炸药在摆放方向不同的时候, 爆炸产生的磁场扰动幅值将会有很大的不同, 这一点在目前已有的研究中完全被忽略了, 甚至没有人提出过这种可能性;
(3) 虽然两种工况模拟得到的磁场扰动幅值不同, 但整体的扰动模式是相同的, 主要表现在磁场扰动的空间分布上;
(4) 相同的空间电导率分布导致了不同工况下得到的磁场扰动模式相同.
本文目前的工作需要一些相关实验的验证, 同时在边界条件的处理上需要进一步考虑远场的计算, 以便可以精确计算远场磁场扰动的情况, 给出完全符合实际情况的模拟结果. 这些研究内容将在后续工作中逐步开展.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . |
| [3] | |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | // |
| [14] | . . |
| [15] | . . |
| [16] | . . |
| [17] | . . |
| [18] | . |
| [19] | . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . . |
| [26] | . . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . . |
