
RESEARCH ON THE CONVERSION METHOD OF AEROHEATING ENVIRONMENT OF HYPERSONIC VEHICLE
ZhaoJinshan
中图分类号:V211.7
文献标识码:A
通讯作者:
收稿日期:2018-03-14
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
展开
摘要
关键词:
Abstract
Keywords:
-->0
PDF (4142KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
准确预测飞行条件下的气动热环境是高超声速飞行器设计中所必须考虑的问题, 地面风洞实验是气动热预测的重要手段, 但由于风洞实验设备模拟能力的限制, 在进行气动热环境地面风洞实验的过程中, 难以完全模拟实际飞行情况, 导致气动热风洞实验的流场条件与实际飞行条件存在较大差别, 因此, 通过地面风洞实验在模型上获得的测热实验结果与实际飞行情况下的气动加热有很大差异, 通过风洞实验获得的气动热环境数据无法直接用于飞行情况下的热防护系统设计. 但由于风洞实验与飞行条件下引起的气动加热机理是相同的, 那么, 在风洞实验与飞行条件下, 模型与飞行器的几何尺度、马赫数、雷诺数、总温、总压、壁温比、攻角等参数对气动热的影响规律也是完全相同的, 通过研究这些参数对气动热的影响规律, 就可以建立气动热环境风洞实验模拟准则, 从而更好地将风洞实验数据应用到飞行条件下气动热环境预测中.在气动热风洞实验数据的关联换算方面, 国外从20世纪60年代起就开展了大量的风洞实验、飞行实验和理论研究, 特别是美国从1960年代开始在X-15、航天飞机等系列飞行器的研制过程中, 利用相关性与风洞数据外推方法, 成功解决了诸多局部气动热环境设计问题[1].
Quinn等[2-3], Robert等[4]通过拟合斯坦顿数与雷诺数之间的关系, 针对X-15飞行器建立了飞行条件和风洞实验条件下的气动热关联换算方法. Bertin等[5]采用与Quinn类似的方法, 拟合出正激波后雷诺数与斯坦顿数的关系, 并成功应用到航天飞机的气动热数据关联换算. John等[6]和Vernon[7]采用半经验的相关法和基于实验数据插值分析方法, 将航天飞机翼前缘、背风中心线及机身侧面的地面气动热实验数据有效地关联外推到飞行条件. Elam等[8]和Harthun等[9] 在航天飞机大量飞行实验数据基础之上, 针对早期建立的气动热风洞实验数据的关联外推方法开展了修正研究, 并采用该修正方法外推得到的航天飞机表面热流与飞行实验结果符合很好. Haney[10]总结了航天飞机发展过程中气动热地面实验数据外推预测飞行下热环境的主要方法. Miller等[11]通过在斯坦顿数上乘以黏性干扰系数和激波前后密度比作为新关联参数对双锥模型的气动热数据进行了相关性研究. Hozumi等[12] 采用黏性干扰系数除以无量纲焓差作为关联参数分别对HYFLEX 模型的身部及头锥部位在3 座不同风洞中的气动热数据开展了相关性研究, 取得了较好的关联结果. Scott等[13-15]针对X33, X38等复杂外形飞行器, 开展舵面干扰区域的热环境天地相关性研究, 获得了较好的结果. Ronald[16]针对高焓风洞实验设备, 对于简单的平板外形, 基于能量和雷诺数建立了复现飞行情况下热流密度和斯坦数的实验模拟方法.
在气动热天地相关性研究方面, 国内公开发表的关于高超声速气动热模拟理论和关联换算方法的研究论文很少. 中国科学院力学研究所姜宗林等[17] 对气动热关联方法研究进展进行了介绍, 并发展了一套基于多维空间相关理论的具有泛函优化特征的数据关联方法, 为开展高焓风洞气动热环境实验数据天地相关性研究提供了理论依据. 国防科技大学曾明等[18]对高温非平衡流下的流场模拟参数双尺度率开展了数值分析, 研究表明当离解非平衡起主导作用时, 模拟参数$\rho_{\infty}L$ 对于气动热特性是有效的. 中国航天空气动力技术研究院沙心国等[19], 纪锋等[20]针对平板? 锥组合体模型, 建立了斯坦顿数与考虑熵吞效应的黏性干扰系数之间的关系, 该方法可以将不同来流条件下不同缩比模型上下表面的斯坦顿数进行很好地关联. 中国空气动力研究与发展中心的徐翔等[21]通过推导边界层近似解热流公式, 建立了大面积无干扰区及凸起物局部干扰区域的气动热实验模拟理论和关联换算方法.
在以往的气动热实验数据关联换算方法研究中, 往往针对具体的飞行器开展研究, 并通过真实飞行实验后获得的气动热飞行实测数据, 对建立的关联方法进行人工修正, 导致建立的方法指向性较强, 很难推广应用于其他高超声速飞行器的热环境地面风洞实验数据外推应用. 例如, 在航天飞机气动热地面风洞实验数据外推应用时, 对于层流流态下迎风面典型高热流区的特征点, 认为在攻角相同的情况下, 以参考热流无因次化的无量纲热流值在风洞实验和飞行条件下是相同的, 即
\begin{equation*}\dfrac{(q/q_\text{ref})_\text{FLT}}{(q/q_\text{ref})_\text{WT}}=1\end{equation*}
式中, $q$代表典型特征点的绝对热流值, 下标ref代表参考值, 下标FLT代表飞行条件, 下标WT代表风洞实验条件.
针对航天飞机表面的典型特征点, 根据($q/q_\text{ref}$)$_\text{WT}$随攻角的变化关系和一英尺球头驻点热流计算公式就可以对飞行条件下的气动热进行预测. 但是实际上, 这种方法只有在气流相对飞行器物面撞击角较大的情况下才能适用, 而航天飞机再入时, 基本保持$40^{\circ}$攻角飞行, 恰好满足上面方法的应用条件. 但是对于气流相对飞行器物面撞击角较小的情况, 采用这种方法是不适用的, 因此这种方法无法推广到其他以小攻角飞行的扁平体外形飞行器.
因此, 本文拟从推导NS方程和边界层理论公式出发, 从物理含义上分析研究在开展层流流态下的气动热地面风洞实验时, 热流系数所需要模拟的主要流场参数, 并通过考虑边界层外缘流场参数的影响, 拟针对高超声速复杂外形飞行器表面不同位置, 建立实验数据关联换算方法. 为了验证建立的气动热关联换算方法的可靠性, 拟通过对美国开展过气动热飞行实验[22-23]的Reentry-F飞行器的激波风洞测热实验数据开展关联外推研究, 为今后进一步将气动热关联换算方法推广应用于高超声速复杂外形飞行器气动热地面风洞实验数据应用奠定基础.
1 气动热相似参数研究
通常情况下, 根据高超声速相似准则, 如果不考虑飞行条件下高温气体效应的影响, 假设实际飞行和风洞实验条件下的气体介质都是完全气体, 那么对于属于气体性质参数的比热比$\gamma$和普朗特数$Pr_{\infty}$就不需要考虑, 其中下标$\infty$表示自由来流参数, 因而目前国内外在开展气动力/热的地面风洞实验过程中主要模拟参数就是来流马赫数$M_{\infty}$、 雷诺数$Re_{\infty}$, 所以通常在分析地面风洞模拟能力时往往将$M_{\infty}$和$Re_{\infty}$的模拟能力作为依据, 比如航天飞机气动热风洞实验轨道模拟参数分析也是以此为依据. 但是, 仅通过模拟$M_{\infty}$和$Re_{\infty}$ 得到的气动热风洞实验数据无法直接用于飞行条件下的气动热环境预测. 下面, 本文将分别从NS方程的量纲分析和边界层近似解热流公式两个方面说明在进行气动热地面实验模拟时, 只模拟$M_{\infty}$和$Re_{\infty}$不足以完全模拟飞行条件下气动热环境的原因, 同时分析影响气动加热的关键物理参量, 研究给出在航天飞机气动热地面实验数据外推时采用的方法不具有通用性的原因.1.1 基于NS方程的气动热相似参数分析
地面风洞测热实验通常研究的是考虑黏性的可压缩定常流动问题, 这类问题可以用完全气体控制方程NS方程来描述, 为便于进行相似性分析, 通常将控制方程进行无量纲化处理. 本文选用的量纲为"1"的形式, 分析NS方程无量纲热流解的影响因素. 对于二维空间的坐标$x, y$, 时间$t$, 密度$\rho_{\infty}$, 两个方向的速度$u, v$, 温度$T$, 压力$p$, 动力学黏性系数$\mu$, 分别对应的无因次化量为: $L$, $L$, $L/U_{\infty}$, $\rho_{\infty}$, $U_{\infty}$, $U_{\infty}$, $T_{\infty}$, $p_{\infty}$, $\mu_{\infty}$, 其中, 下标"$\infty$"表示自由来流参数, $U_{\infty}$为来流速度, $L$为特征长度, 则在直角坐标系下, 完全气体无量纲化NS方程为[24-25]质量方程
\begin{equation*}\dfrac{\partial \partial t^*}(\rho^*)+\dfrac{\partial \partial x^*}(\rho^*u^*)+\dfrac{\partial}{\partial y^*}(\rho^*v^*)=0\end{equation*}
$x$方向动量方程
\begin{equation*}\begin{split}&\dfrac{\partial}{\partial t^*}(\rho^*u^*)+\dfrac{\partial}{\partial x^*}(\rho^*u^{*2})+\dfrac{\partial}{\partial y^*}(\rho^*u^*v^*)=\\&\quad\quad-\dfrac{1}{\gamma M^2_{\infty}}\dfrac{\partial}{\partial x^*}(p^*)+\dfrac{1}{Re}\Bigg(\dfrac{\partial}{\partial x^*}\tau^*_{xx}+\dfrac{\partial}{\partial y^*}\tau^*_{xy}\Bigg)\end{split}\end{equation*}
$y$方向动量方程
\begin{equation*}\begin{split}&\dfrac{\partial}{\partial t^*}(\rho^*v^*)+\dfrac{\partial}{\partial x^*}(\rho^*u^*v^*)+\dfrac{\partial}{\partial y^*}(\rho^*v^{*2})=\\&\quad\quad-\dfrac{1}{\gamma M^2_{\infty}}\dfrac{\partial}{\partial y^*}(p^*)+\dfrac{1}{Re}\Bigg(\dfrac{\partial}{\partial x^*}\tau^*_{xy}+\dfrac{\partial}{\partial y^*}\tau^*_{xy}\Bigg)\end{split}\end{equation*}
能量方程
\begin{equation*}\begin{split}&\dfrac{\partial}{\partial t^*}(\rho^*e^*)+\dfrac{\partial}{\partial x^*}\lbrack u^*(\rho^*e^*+p^*)\rbrack+\dfrac{\partial}{\partial y^*}\lbrack v^*(\rho^*e^*+p^*)\rbrack=\\&\quad\quad-\dfrac{1}{2}\Big(\gamma M^2_{\infty}-1\Big)\Bigg\lbrace \dfrac{\partial}{\partial t^*}\Big\lbrack \rho^*\Big(u^{*2}+v^{*2}\Big)\Big\rbrack+\\&\quad\quad\dfrac{\partial}{\partial x^*}\Big\lbrack u^*\rho^*\Big(u^{*2}+v^{*2}\Big)\Big\rbrack+\dfrac{\partial}{\partial y^*}\Big\lbrack v^*\rho^*\Big(u^{*2}+v^{*2}\Big)\Big\rbrack\Bigg\rbrace+\\&\quad\quad\dfrac{\gamma M^2_{\infty}\partial}{Re\partial x^*}(u^*\tau^*_{xx}+v^*\tau^*_{xy})+\dfrac{\gamma M^2_{\infty}\partial}{Re\partial y^*}(u^*\tau^*_{xy}+v^*\tau^*_{yy})+\\&\quad\quad\dfrac{\partial q^*_x}{\partial x^*}+\dfrac{\partial q^*_y}{\partial y^*}\end{split}\end{equation*}
两个方向的无量纲热流表达式
\begin{equation*}\begin{split}q^*_x=\dfrac{\gamma}{(\gamma-1)PrRe}\Bigg(\mu^*\dfrac{\partial T^*}{\partial x^*}\Bigg) q^*_y=\dfrac{\gamma}{(\gamma-1)PrRe}\Bigg(\mu^*\dfrac{\partial T^*}{\partial y^*}\Bigg)\end{split}\end{equation*}
式中"*"表示参数的无量纲量.
在求解过程中, 所有变量均采用量纲为1的值进行迭代求解. 在无量纲质量方程中, 不存在与来流条件相关的相似参数; 在无量纲动量方程和能量方程中, 与来流条件相关的相似参数为$\gamma$, $Pr_{\infty}$, $M_{\infty}$, $Re_{\infty}$.
因此, 目前的研究普遍认为: 对于量热完全气体, 如果两个流动的无量纲NS控制方程组相同, 即来流参数$\gamma$, $Pr_{\infty}$, $M_{\infty}$, $Re_{\infty}$ 相等, 再如果两个外形几何相似且用无量纲表示的壁面边界条件相同
\begin{equation*}T^*_\text w=\dfrac{T_\text w}{T_{\infty}}\tag*{(1)}\end{equation*}
则无量纲方程的解相等, 即对于整个流场的无量纲解$u/U_{\infty}$, $v/U_{\infty}$, $T/T_{\infty}$, $p/p_{\infty}$, 相对于无量纲坐标位置分布相等, 两个流动完全相似.
但事实上, 在无量纲热流表达式中, 除了与来流条件相关的相似参数$\gamma$, $Pr_{\infty}$, $Re_{\infty}$ 外, 黏性系数中还隐含来流温度$T_{\infty}$的影响, 以萨瑟兰公式为例, 无量纲黏性系数表达式为
\begin{equation*}\mu^*=\dfrac{\mu}{\mu_{\infty}}=(T^*)^{1.5}\dfrac{1+110/T_{\infty}}{T^*+110/T_{\infty}}\tag*{(2)}\end{equation*}
从式(2)中可以看到, 无量纲黏性系数受到与来流温度相关的参数$110/T_{\infty}$的影响, 也就是说, 即使保证来流参数$\gamma$, $Pr_{\infty}$, $M_{\infty}$, $Re_{\infty}$相等, 且无量纲壁面温度$T_\text w/T_{\infty}$相同, 只要$T_{\infty}$ 不同, 就会导致无量纲黏性系数不同, 进而造成通过求解无量纲NS 方程获得的无量纲流场参数不同, 温度边界层也不相似, 最终导致不同来流静温$T_{\infty}$下的无量纲热流系数存在一定的差别. 究其物理本质是因为, 由于来流温度不同, 造成流场黏性耗散不同, 且这种黏性耗散的影响并无法通过$\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$, $T_\text w/T_{\infty}$相等而完全覆盖.
因此, 综合整个无量纲形式的NS方程, 影响数值计算无量纲热流系数的主要参数应该为$\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$, $T_\text w/T_{\infty}$ 及$T_{\infty}$. 如果两个飞行器几何相似、上述参数相同且用无因次量表示的物面边界条件相同, 则无量纲方程的热流系数相等. 但是在实际风洞实验中, 通常根据高超声速相似准则, 将$\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$作为流动的相似参数进行模拟, 但是对于静温$T_{\infty}$, 除高焓爆轰激波风洞外[26-28], 大多数常规高超声速风洞和激波风洞均无法做到等效模拟, 造成地面风洞实验条件与飞行条件往往存在较大的差异, 因此需要开展气动热地面风洞实验数据的关联换算研究.
1.2 基于边界层理论的气动热相似参数分析
上面从NS方程角度分析了气动热环境风洞实验的主要模拟参数, 下面本文将从边界层方程近似解热流公式出发, 进一步对气动热实验模拟参数进行分析. 在进行理论分析的过程中, 假设两个前提条件: 一是攻角$\alpha$相同, 二是两个不同缩比模型的几何外形完全相似. 下面, 本文以参考焓平板热流公式[29]为例, 对大面积无干扰区的热流计算公式进行推导, 分析流场参数对无量纲热流的影响, 并由此得到气动热相似参数.对于平板热流公式[29]
$q_w(x)=0.332\rho_e \mu_ePr^{\frac{2}{3}}Re^{-0.5}_x\sqrt{\dfrac{\rho^*\mu^*}{\rho_\text e\mu_\text e}}(h_r-h_\text w)(3)$
代入(3)式并化简得
\begin{equation*}\begin{split}&q_\text w(x)=C_\text wp^{0.5}_\text eM^{0.5}_\text e(1+0.2M^2_\text e)^{0.25-n}T_\text s^{n-0.25+1}\cdot\\&\quad\quad\mu^{0.5}_\text e(T^*)T^{*,-n}\left(1-\dfrac{T_\text w}{T_\text s}\right)x^{-0.5}\end{split}\tag*{(4)}\end{equation*}
其中$T^*$为参考温度, $n$对于不同参考焓, 取不同的值
\begin{equation*}n=\begin{cases}0.125,h^*<209^3~\text{kJ/kg}\\0.14,\quad~~h^*\geqslant209^3~\text{kJ/kg}\end{cases}\end{equation*}
以Fay-Riddle驻点热流公式[30]进行无量纲化处理
\begin{equation*}q_\text{ws}=0.763Pr^{-2/3}(\rho_\text w\mu_\text w)^{0.1}(\rho_\text s\mu_\text s)^{0.4}(h_\text s-h_\text w)\sqrt{\Bigg\lgroup\dfrac{\text{d}u_\text e}{\text{d}x}\Bigg\rgroup_\text s}\tag*{(5)}\end{equation*}
令
\begin{equation*}\begin{split}&\sqrt{\Bigg\lgroup\dfrac{\text du_\text e}{\text dx}\Bigg\rgroup_\text s}=\dfrac{1}{R^{0.5}_n}\left\lbrack\dfrac{2(p_\text s-p_{\infty})}{\rho_\text s}\right\rbrack^{0.25}\\&\rho=\dfrac{P_\text s}{RT_\text s}\\&p_\text w=p_\text s\\&h=c_pT\end{split}\end{equation*}
代入式(5)并化简得
\begin{equation*}q_\text{ws}=C_\text s\cdot p_\text s^{0.5}\dfrac{1}{R_n^{0.5}}(\mu_\text w)^{0.1}(\mu_\text s)^{0.4}(T_\text s)^{0.85}(T_\text w)^{-0.1}\Bigg(1-\dfrac{T_\text w}{T_\text s}\Bigg)\tag*{(6)}\end{equation*}
式(4)除以式(6), 得到
\begin{equation*}\begin{split}&\dfrac{q_\text w(x)}{q_\text s}=C\left\lgroup\dfrac{p_\text e}{p_\text s}\right\rgroup^{0.5}\left\lgroup\dfrac{R_n}{x}\right\rgroup^{0.5}\left\lgroup\dfrac{T_\text s}{T^*}\right\rgroup^{n}\left\lgroup\dfrac{T_\text w}{T_\text s}\right\rgroup^{0.1}\cdot\\&\quad\quad\left\lgroup\dfrac{\mu_\text e}{\mu_\text s}\right\rgroup^{0.4}\left\lgroup\dfrac{\mu_\text e}{\mu_\text w}\right\rgroup^{0.1}\dfrac{M^{0.5}_\text e}{(1+0.2M^2_\text e)^{n-0.25}}\end{split}\tag*{(7)}\end{equation*}
上面分析过程中, $C_\text w$和$C_\text s$分别是平板热流公式和驻点热流公式推导过程中产生的常系数, $R_n$是驻点半径, $x$是特征长度, 下标e代表边界层外缘参数, 下标$\text s$代表驻点参数, 下标$\text w$代表壁面参数.
对于其他边界层近似解热流公式, 如Lees热流公式[31]等, 本文在相同假设条件下, 也进行了推导, 由于篇幅原因, 不再赘述. 虽然对于不同边界层近似解热流公式以Fay-Riddle驻点热流公式无因次化的无量纲表达式的幂指数存在一定的差别, 但是不同公式均可以简写成如下函数形式的无量纲热流系数关系式
\begin{align*}\dfrac{q_\text w(x)}{q_\text s}\sim f_{\text{qqs}}\left\lgroup M_\text e,\dfrac{p_\text e}{p_\text s},\dfrac{\mu_\text e}{\mu_\text s},\dfrac{\mu_\text e}{\mu_\text w},\dfrac{T_\text s}{T^*},\dfrac{T_\text w}{T_\text s},\sqrt{R_n/x}\right\rgroup\tag*{(8)}\end{align*}
其中, $\sqrt{R_n/x}$对于给定的飞行器外形为一常数, 不会随模型的缩比而变化, 并且根据高超声速牛顿理论[32], 边界层外缘马赫数$M_\text e$在外形相似, 攻角相同的前提下, 只与来流马赫数有关. 压力比有如下关系式
\begin{align*}\dfrac{p_\text e}{p_\text s}&=\Bigg(1-\dfrac{p_{\infty}}{p_\text s}\Bigg)\text{cos}^2\psi+\dfrac{p_{\infty}}{p_\text s}=\\&\quad~\text{cos}^2ψ+\dfrac{p_{\infty}}{p_\text s}(1-\text{cos}^2ψ)=\\&\quad~\text{cos}^2ψ+f(M_\infty)(1-\text{cos}^2ψ)\tag*{(9)}\end{align*}
式中, $ψ$为气流撞击角的余角. 从式(9)中可以看到, 压力比与来流马赫数及外形有关.
对于来流马赫数较大 (一般大于8) 的情况, $p_{\infty}/p_\text s\rightarrow0$; 对于气流撞击角较大的部位, 如大攻角情况下, 大钝头的航天飞机外形下表面, ($1-\text{cos}^2ψ$)趋近于一个小于1的有限值 (非小量) , 则有
\begin{align*}\dfrac{p_\text e}{p_\text s}\Rightarrow \text{cos}^2ψ\tag*{(10)}\end{align*}
即当地压力比与流场无关, 只与物面角有关. 结合式(8)可以得到, 对于相同外形在不同流场条件下以驻点热流无因次化的无量纲热流可以不考虑压力比$p_\text e/p_\text s$ 的影响.
而对于头部半径较小且身部物面角较小的外形, 如下表面较平的升力体外形(极限情况下即为平板外形), 当以$0^{\circ}$攻角飞行时, $ψ\rightarrow90^{\circ}$, 则有
\begin{align*}\dfrac{p_\text e}{p_\text s}\Rightarrow f(M_\infty)(1-\text{cos}^2ψ)\end{align*}
则当地压力比同时受到来流马赫数和气流撞击角共同影响, 即使对于相同外形, 在来流马赫数不同的流场条件下, 以驻点热流无因次化的无量纲热流也必须考虑压力比$p_\text e/p_\text s$ 的影响.
另外, 从上面边界层理论的角度分析来看, 对于以驻点热流无因次化的无量纲热流, 还受到$\mu_\text e/\mu_\text s$ 的影响, 而黏性系数比同时受到来流马赫数$M_{\infty}$和来流静温$T_{\infty}$的影响, 这与1.1 节基于NS方程的气动热相似参数分析的结论是一致的.
1.3 气动热相似参数分析确认
前面两节的理论分析表明, $\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$, $T_\text w/T_{\infty}$及$T_{\infty}$无论对于流场相似模拟还是气动热相似模拟均非常重要, 但目前在开展地面风洞实验时, 仅将$\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$参数作为衡量地面风洞实验模拟能力的关键参数, 对于来流温度$T_{\infty}$ 在气动热等效模拟中的重要意义尚未得到足够的重视, 因此本节将重点针对来流温度$T_{\infty}$不同造成气动热之间的差距开展验证确认. 本文选取Reentry-F外形飞行器[33]开展研究, 该飞行器为$5^{\circ}$半锥角的钝锥, 总长3962 mm, 头部半径2.54 mm, 20世纪60年代进行过自由飞行实验, 2011在中国空气动力研究与发展中心超高速所$\varPhi$2 m 激波风洞上开展过该外形1 : 4缩比模型的风洞实验[34], 因此, 具有较为充足的地面风洞实验和飞行实验数据来开展气动热关联换算理论研究. 6个流场状态见表1, 其中状态3 对应实际风洞实验状态, 状态6对应高度\mbox{24.38 km}的飞行实验状态, 其余4个状态在保证马赫数、雷诺数相同前提下, 通过改变来流静温、静压实现. 通过表1中的前5个状态, 可以研究在相同来流马赫数、雷诺数条件下, 来流温度对无量纲热流的影响; 通过表1中的最后两个状态, 可以分析在相同来流静温条件下, 来流马赫数对无量纲热流的影响; 通过第3 个状态和第6 个状态可以分析飞行实验和地面实验的无量纲热流存在差距的原因. 本文采用中国空气动力研究与发展中心超高速所发展的高超声速气动热数值并行计算软件AHENS对不同流场条件下的气动热环境开展数值计算, 该软件采用有限体积方法求解三维直角坐标系下的N-S 方程组. 本文计算采用的气体模型为量热完全气体, 壁面边界采用无滑移300 K 等温壁. 图1(a)是模型在风洞中的安装图, 图1(b)是模型下表面中心线热流计算结果与风洞实验结果的对比曲线, 由于风洞实验数据在0.45 m左右发生转捩, 本文仅针对层流区域的实验数据开展了对比分析, 从图中可以看到, 在状态3 的流场条件下, 对于$0\sim0.45~\text{m}$ 的层流区域, 数值计算结果和风洞实际测热结果符合的较好, 本文采用的数值计算程序具有较高的精度.Table 1
表1
表1相同马赫数相同雷诺数情况下不同流场条件
Table 1The typical flow field of the same Mach number and Reynolds number
| State | M∞ | Re∞ · L-1 /m-1 | T∞/K | /Pa | Tw/K |
|---|---|---|---|---|---|
| 1 | 8.64 | 1.08 x 107 | 40 | 278.34 | 300 |
| 2 | 8.64 | 1.08 x 107 | 77 | 827.37 | 300 |
| 3 | 8.64 | 1.08 x 107 | 90 | 1056.45 | 300 |
| 4 | 8.64 | 1.08 x 107 | 200 | 3367.09 | 300 |
| 5 | 8.64 | 1.08 x 107 | 221 | 3879.77 | 300 |
| 6 | 19.97 | 1.82 x 107 | 221 | 2803.19 | 300 |
新窗口打开
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图 1Reentry-F飞行器气动热结果
-->Fig.1Aeroheating results of Reentry-F
-->
图2是表1中6个不同状态下的计算结果, 其中图2(a), 图2(b)分别是在表1所列6不同状态下, 模型下表面中心线绝对热流和以驻点无因次化的无量纲热流对比曲线, 图2(c)是各状态分别以状态6的无量纲热流为基准作出的偏差曲线. 从图中可见: 对于前5个状态, 即使在自由来流的相似参数$\gamma$, $M_{\infty}$, $Re_{\infty}$, $Pr_{\infty}$ 相等, 壁温、几何外形完全相同的条件下, 由于自由来流温度$T_{\infty}$不同, 使得不同状态下的数值计算绝对热流差别很大, 采用驻点热流无因次化后的无量纲热流系数也存在一定差别. 在相同的来流马赫数、雷诺数条件下, 以驻点热流无因次化的无量纲热流随来流静温升高而升高, 来流静温最低的状态1 和静温最高的状态5之间的最大偏差达到15\%. 对于状态5 和状态6, 虽然自由来流温度$T_{\infty}$相同, 但是由于自由来流的$M_{\infty}$ 和$Re_{\infty}$ 不同, 导致无量纲热流系数也存在一定差别, 马赫数越高, 无量纲热流越低, 最大偏差达到17%. 对于风洞实验条件状态3和飞行条件状态6, 由于来流马赫数和静温均存在较大的差别, 导致无量纲热流不同, 前面分析已经指出, 无量热流随马赫数升高而降低, 随总温升高而升高, 飞行条件下的马赫数和总温均高于地面风洞实验条件, 因此在二者的作用下, 无量纲热流之间的偏差在12%左右.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图 2不同状态下表面中心线热流分布曲线比较
-->Fig.2The comparison of the heat flux on the centerline in different flow fields
-->
对于实际地面风洞实验, 很难同时模拟飞行环境下的总温和马赫数, 这就造成风洞实验中得到的模型表面的气动热数据, 仅能模拟热环境分布规律, 而无法将实验测得的热流值直接用于飞行条件下的热环境预测和热防护设计, 必须开展气动热实验数据的关联换算研究.
2 气动热关联换算方法研究
在气动热实验数据的分析过程中, 通常采用热流比拟系数的形式, 希望以此来消除或降低各种参数对气动热比拟系数的影响. 本文借助于热流比拟参数对风洞实验数据和飞行数据进行相关性研究, 以期能够使风洞实验和飞行条件下的气动热环境之间建立一定的联系, 并期望通过此类方法, 能够将风洞实验得到的气动热数据换算到飞行条件下.通常采用的比拟系数包括: 无量纲热流系数$q/q_\text s$、斯坦顿数$St$、换热系数$h_{\alpha}$. 不同的热流比拟系数对尺度、马赫数、雷诺数、总焓、壁焓以及壁温比等参数的依赖程度有所不同, 其对应的变化规律也有所不同. 大量理论分析研究发现, 利用无量纲热流系数$q/q_\text s$作为比拟系数更具有优势.
对于飞行器表面的不同部位, 流动特征不同, 黏性作用主导的边界层效应不同, 导致飞行器不同位置的气动热加热特征不同. 在采用边界层近似解热流公式计算高超声速飞行器大面积无干扰区域的流场结构和热流时, 对于非驻点流动(包括钝头体非驻点区域、平板和锥体等), 通常是将边界层看做一些具有局部外流和局部壁面条件的"局部解"连接而成, 即局部相似解. 本文在开展气动热关联换算方法研究时, 也正是以此为基础, 针对典型外形的边界层近似解热流公式开展换算方法研究. 因此, 本文在研究过程中, 通过考虑飞行器表面不同位置边界层外缘参数的影响, 建立了气动热关联换算方法.
假设在层流情况下, 对于实际全尺寸飞行器和风洞实验缩比模型, 全尺寸飞行器的几何尺度是风洞缩比模型的$L$倍, 则两个模型的几何尺度关系为
\begin{align*}&R_{n,\text{FLT}}=L\cdot R_{n,\text{WT}}\\&x_\text{FLT}=L\cdot x_\text{WT}\end{align*}
如果真实飞行器和缩比模型进行飞行实验和风洞实验的壁面条件完全相同, 且不考虑大小模型之间由于边界层厚度和边界层位移厚度的不同对边界层外缘参数的影响, 则根据边界层近似解热流公式的无量纲形式可以推导得到飞行条件和风洞实验条件下的气动热关联换算公式. 例如, 根据无量纲参考焓平板热流公式(7)可以推导得到基于以驻点热流无因次化的无量纲热流换算关系式
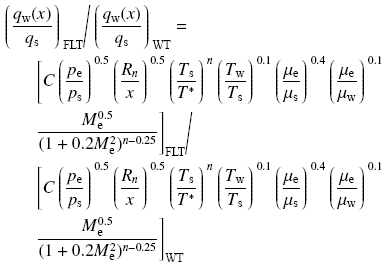
化简得
\begin{align*}&\left\lgroup\dfrac{q_\text w(x)}{q_\text s}\right\rgroup_{\text{FLT}}=\dfrac{\left\lgroup\dfrac{M^{0.5}_\text{e}}{(1+0.2M^2_\text e)^{n-0.25}}\right\rgroup_{\text{FLT}}}{\left\lgroup\dfrac{M^{0.5}_\text{e}}{(1+0.2M^2_\text e)^{n-0.25}}\right\rgroup_{\text{WT}}}\left\lgroup\dfrac{p_{\text e,\text{FLT}}}{p_{\text e,\text{WT}}}\right\rgroup^{0.5}\quad\quad\quad\quad\\&\quad\left\lgroup\dfrac{p_{\text s,\text{WT}}}{p_{\text s,\text{FLT}}}\right\rgroup^{0.5}\left\lgroup\dfrac{T_{\text s,\text{FLT}}}{T_{\text s,\text{WT}}}\right\rgroup^{n-0.1}\left\lgroup\dfrac{T^{*}_\text{WT}}{T^{*}_{\text{FLT}}}\right\rgroup^{n}\\&\quad\left\lgroup\dfrac{f_{T}(T_\text{s},M_\text{e})_{\text{FLT}}}{f_{T}(T_\text{s},M_\text{e})_{\text{WT}}}\right\rgroup^{0.5}\left\lgroup\dfrac{f_{T}(T_\text{s})_{\text{WT}}}{f_{T}(T_\text{s})_{\text{FLT}}}\right\rgroup^{0.4}\left\lgroup\dfrac{q_\text w(x)}{q_\text s}\right\rgroup_{\text{WT}}\tag*{(11)}\end{align*}
对于流动现象类似于平板外形或尖锥外形的流场, 均可采用式(11)进行关联换算, 其中$n$对于不同参考焓, 取不同的值
\begin{equation*}n=\begin{cases}0.125,h^*<209^3~\text{kJ/kg}\\0.14,\quad~~h^*\geqslant209^3~\text{kJ/kg}\end{cases}\end{equation*}
对于其他边界层近似解热流公式, 例如, 钝体热流公式, 也可采用相同的方法推导得到类似的气动热关联换算公式, 由于文章篇幅的原因, 本文无法给出根据每个边界层近似解公式得到的所有气动热关联换算公式的具体表达形式. 简单起见, 以函数形式的无量纲热流比拟系数关系式(8)为代表, 经过推导, 可以写出如下通用形式的以驻点热流无因次化的无量纲热流关联换算关系式
\begin{align*}&\left\lgroup\dfrac{q_\text w(x)}{q_\text s}\right\rgroup_{\text{FLT}}=\left\lgroup\dfrac{M_{\text e,\text{FLT}}}{M_{\text e,\text{WT}}}\right\rgroup^{a_{L}}\left\lbrack\dfrac{(1+0.2M^2_\text e)_\text{FLT}}{(1+0.2M^2_\text e)_\text{WT}}\right\rbrack^{b_{L}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\&\quad\quad\left\lgroup\dfrac{p_{\text e,\text{FLT}}}{p_{\text e,\text{WT}}}\right\rgroup^{c_{L}}\left\lgroup\dfrac{p_{\text s,\text{FLT}}}{p_{\text s,\text{WT}}}\right\rgroup^{d_{L}}\left\lgroup\dfrac{T_{\text s,\text{FLT}}}{T_{\text s,\text{WT}}}\right\rgroup^{e_{L}}\left\lgroup\dfrac{T^{*}_\text{FLT}}{T^{*}_{\text{WT}}}\right\rgroup^{f_{L}}\\&\quad\quad\left\lbrack\dfrac{f_{T}(T_\text{s},M_\text{e})_{\text{FLT}}}{f_{T}(T_\text{s},M_\text{e})_{\text{WT}}}\right\rbrack^{g_{L}}\left\lbrack\dfrac{f_{T}(T_\text{s})_{\text{FLT}}}{f_{T}(T_\text{s})_{\text{WT}}}\right\rbrack^{h_{L}}\left\lgroup\dfrac{q_\text w(x)}{q_\text s}\right\rgroup_{\text{WT}}\tag*{(12)}\end{align*}
式中, $q$代表物面冷壁热流, $p$代表压力, $T$代表温度, $M$代表马赫数, 下标FLT 和WT 分别对应飞行条件和地面实验条件, 下标$\text e$对应边界层外缘参数, 下标$\text s$ 对应波后总参数, $f_T$代表黏性系数公式. 综合所有边界层近似解热流公式的简化结果表明, $a_L$ 的取值范围为$0.225\sim0.5$, $b_L$ 的取值范围为$-0.5\sim0.125$, $c_L$ 的取值范围为$0.225\sim 0.5$, $d_L$的取值范围为$-0.5\sim-0.225$, $e_L$的取值范围为$0\sim-0.04$, $f_L$的取值范围为$-0.14\sim0$, $g_L$的取值范围为$0\sim0.5$, $h_L$的取值范围为$-0.4\sim0$.
如果已知飞行器驻点热流$q_{\text s,\text{FLT}}$, 则可以得到适用于飞行器表面大面积无干扰区域的绝对热流关联换算关系式
\begin{align*}&q_\text w(x)_{\text{FLT}}=\left\lgroup\dfrac{M_{\text e,\text{FLT}}}{M_{\text e,\text{WT}}}\right\rgroup^{a_{L}}\left\lbrack\dfrac{(1+0.2M^2_\text e)_\text{FLT}}{(1+0.2M^2_\text e)_\text{WT}}\right\rbrack^{b_{L}}\quad\quad\quad\quad\quad\quad\quad\\&\quad\left\lgroup\dfrac{p_{\text e,\text{FLT}}}{p_{\text e,\text{WT}}}\right\rgroup^{c_{L}}\left\lgroup\dfrac{p_{\text s,\text{FLT}}}{p_{\text s,\text{WT}}}\right\rgroup^{d_{L}}\left\lgroup\dfrac{T_{\text s,\text{FLT}}}{T_{\text s,\text{WT}}}\right\rgroup^{e_{L}}\left\lgroup\dfrac{T^{*}_\text{FLT}}{T^{*}_{\text{WT}}}\right\rgroup^{f_{L}}\\&\quad\left\lbrack\dfrac{f_{T}(T_\text{s},M_\text{e})_{\text{FLT}}}{f_{T}(T_\text{s},M_\text{e})_{\text{WT}}}\right\rbrack^{g_{L}}\left\lbrack\dfrac{f_{T}(T_\text{s})_{\text{FLT}}}{f_{T}(T_\text{s})_{\text{WT}}}\right\rbrack^{h_{L}}\left\lgroup\dfrac{q_\text w(x)}{q_\text s}\right\rgroup_{\text{WT}}q_{s,\text{FLT}}\tag*{(13)}\end{align*}
上式中各幂指数的取值范围同式(12).
当来流马赫数差别较大时, 对于物面附近气流流向角较小的部位, 如扁平体外形, 边界层外缘马赫数、静压与总压之比、静温与来流总温之比对无量纲热流比拟系数的影响均无法忽略, 需要采用式(13)对实际飞行条件和地面风洞实验条件下的无量纲热流开展关联换算; 当来流马赫数较高(大于9) 时, 对于物面附近气流流向角较大, 气流压缩性较强的部位, 所有幂指数均退化为0, 也就是说飞行条件下的无量纲热流与地面风洞实验条件下的无量纲热流基本相同, 地面实验测得的热流可以直接外推换算到飞行条件下, 这也是航天飞机下表面大面积无干扰区域在进行热防护设计时采用的主要准则[1]. 以上两点说明对于飞行器表面不同部位, 由于流动特征不同, 各流场参数对热流系数的影响程度也不同. 因此本文针对飞行器表面不同部位通过引入边界层近似解热流公式建立的气动热关联换算方法, 考虑了边界层外缘参数的影响, 具有一定的通用性.
3 气动热关联换算方法验证
为了对前文建立的关联换算方法进行验证, 本文采用Reentry-F飞行器开展了验证工作, 其中飞行实验数据来源于文献[22], 地面风洞实验数据在中国空气动力研究与发展中心超高速所$\varPhi2~\text m$激波风洞上通过2 mm薄膜热流传感器测得[34]. 本文选取的风洞实验状态为流场I: $Ma_{\infty}=8.69$, $P_0=9.1~\text{MPa}$, $T_0=1180~\text{K}$, $Re/L=6.65\times10^6~\text{m}^{-1}$;
流场II: $Ma_{\infty}=8.64$, $P_0=19.5~\text{MPa}$, $T_0=1348~\text{K}$, $Re/L=1.12\times10^7~\text{m}^{-1}$.
飞行状态为表1中所列状态6
$Ma_{\infty}=19.97$, $H=24.38~\text{km}$.
飞行实验结果显示, 在飞行器表面约$x/L=0.55$的位置发生了转捩, 而本文是针对层流流态下的换算方法研究, 因此这里只是针对Reentry-F飞行器层流区域的气动热环境开展换算, 以达到对层流关联换算方法进行验证的目的. 由于Reentry-F飞行器头部半径较小, 近似于尖前缘外形, 因此本文采用式(11)开展气动热外推换算. 对于边界层外缘参数的选取, 可以利用过激波总焓$h_0$保持不变的原理, 在流场中沿壁面法向方向, 取0.995倍的总焓处的流场参数作为边界层外缘参数. 值得指出的是, 对于边界层较薄、黏性干扰效应较弱的流场区域, 也可以采用欧拉方程计算得到的物面参数近似作为边界层外缘参数.
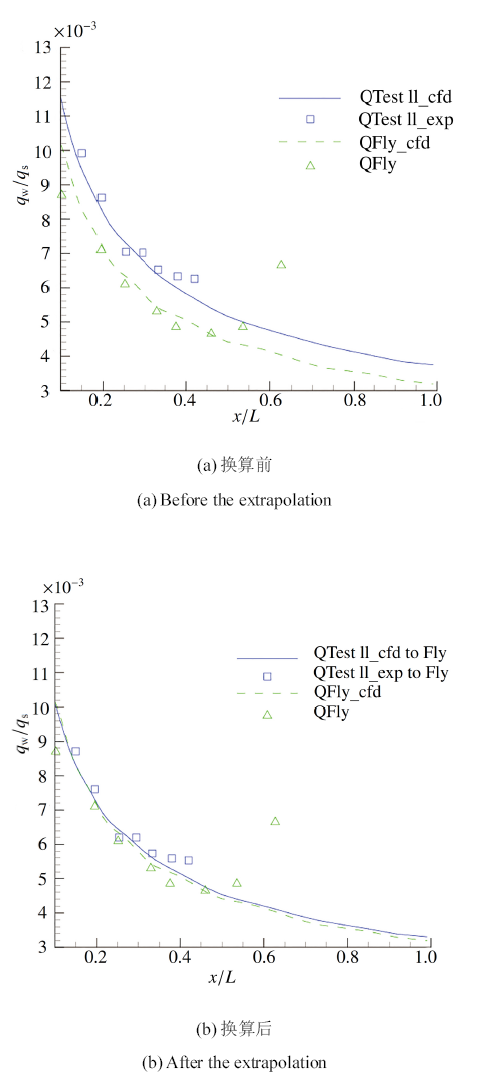
图3和图4是针对Reentry-F飞行器1 : 4缩比模型, 利用地面风洞实验流场I和II的测热结果和计算结果换算到飞行状态下的结果比较. 从图3(a)和图4(a)中均可以看出, 数值计算结果和实验测得的结果符合的较好, 这表明本文采用的数值方法是比较可靠的. 但是, 由于地面风洞实验流场的马赫数和总温均低于实际飞行条件, 导致两个不同的地面风洞实验流场的无量纲热流和飞行实验测得的无量纲热流之间均存在10\%左右的差距. 基于以驻点热流无因次化的无量纲热流, 采用本文建立的换算方法, 可以将流场I和II条件下的无量纲热流换算到飞行状态, 结果如图3(b)、图4(b)所示. 从图中可以看到, 尽管流场I和II的实验参数存在一定差别, 但换算后的无量纲热流均与飞行实测热流结果符合得较好. 本文建立的热环境关联换算方法可以把缩比模型在不同流场条件下的热流实验结果换算到飞行条件下, 这表明本文建立的关联换算方法是有效的.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图 3流场I换算至24.38 km结果
-->Fig.3Extrapolating to 24.38 km from wind tunnel experiment of flow field I
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图 4流场II换算至24.38 km结果
-->Fig.4Extrapolating to 24.38 km from wind tunnel experiment of flow field II
-->
热流之间差别较大, 且对于飞行器表面不同部位, 由于气体的压缩性和黏性效应均不同, 导致无量纲热流系数随流场参数的变化规律不同, 这就对实验数据的应用造成一定的困难. 本文建立的关联换算方法考虑了边界层外缘流场参数的影响, 可以将地面风洞实验数据有效地关联外推到飞行条件下, 表明本文建立的气动热关联换算方法对于提高地面气动热风洞试验数据应用水平, 降低飞行器的热防护设计冗余起到了一定的辅助作用.
4 结论
通过开展气动热环境影响参数及关联换算方法研究, 可以得到以下初步结论(1)本文针对层流流态下的气动热环境, 分别从无量纲NS方程和边界层理论角度分析研究了热流系数的主要影响参数, 结果表明: 对于不同缩比模型和不同流场条件下的测热实验, 如果攻角完全相同, 那么以驻点热流为参考的无量纲热流分布受到来流总温, 边界层外缘静温、马赫数、静压与总压之比的影响, 并且飞行器表面不同特征部位受到流场参数的影响不同, 导致对不同部位的气动热实验数据换算需要采用不同的参数.
(2) 通过Reentry-F外形的风洞实验数据对飞行条件的换算结果可以看出, 本项研究建立的气动热关联换算方法是可行的, 可以将地面风洞实验结果有效地换算到飞行条件下, 对热防护系统精确设计起到了一定的辅助作用.
(3) 气动热关联换算方法研究是非常复杂而困难的, 本文只是开展了初步的研究, 对于复杂外形的局部干扰区域、边界层转捩区及湍流区域的热环境关联换算方法, 需要进一步深入开展研究.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | |
| [16] | |
| [17] | . . |
| [18] | . . |
| [19] | . . |
| [20] | // // |
| [21] | . . |
| [22] | . |
| [23] | |
| [24] | |
| [25] | |
| [26] | . . |
| [27] | . . |
| [28] | . . |
| [29] | |
| [30] | . |
| [31] | . |
| [32] | |
| [33] | . . |
| [34] | // // |
