Muhammad Zaman ^1,
, Muhammad Nadeem ^1,
, Muhammad Sahid ^1,
, Kwangsoo Kim ^1,
, Guinyun Kim ^1,,
, Nguyen Thi Hien ^1,2,
,

Corresponding author: Guinyun Kim, gnkim@knu.ac.kr

1.Department of Physics and Center for High Energy Physics, Kyungpook National University, Daegu 41566, Republic of Korea
2.Institute of Physics, Vietnam Academy of Science and Technology, 10 Dao Tan, Hanoi, Vietnam
Received Date:2020-10-12
Available Online:2021-04-15
Abstract:The cross sections of the ⁵⁹Co(n, x) reaction in the average energy range of 15.2-37.2 MeV were measured using activation and an off-line γ-ray spectrometric technique. The neutrons were generated from the ⁹Be(p, n) reaction with proton beam energies of 25-45 MeV at the MC-50 Cyclotron facility of the Korean Institute of Radiological and Medical Sciences (KIRAMS). Theoretical calculations of neutron–induced reactions on ⁵⁹Co were performed using the nuclear model code TALYS-1.9. The results for the ⁵⁹Co(n, x) reactions were compared with the theoretical values obtained using TALYS-1.9 and the literature data provided in EXFOR and the TENDL 2019 nuclear data library. The theoretical values obtained using TALYS-1.9 with adjusted parameters are comparable to the experimental data. The measured reaction cross sections of a few radionuclides are new, and the others are comparable to the literature data, and thus, they can strengthen the database. The present study on cross sections leads to useful insight into the mechanisms of ⁵⁹Co(n, x) reactions.

HTML

--> --> -->

Neutron-induced reaction cross sections play a major role in the current nuclear science regarding human life. Such microscopic data are necessary for practical and theoretical applications. Evidently, with an increasing number of nuclear data applications, the requirements of nuclear data are also increasing [1]. Accurate knowledge of the cross section for neutron-induced reactions on ⁵⁹Co is of importance owing to its use as a structural material in fission and fusion reactors as well as its applicability to neutron dosimetry [2]. The natural cobalt element (⁵⁹Co) can be used as a target material for the production of medically and technologically important ⁵⁶Co, ⁵⁷Co, ⁵⁸Co, ⁵⁴Mn, and ⁵⁹Fe radionuclides. Among these, ^55,57,58Co offer potential applications in the synthesis of radio pharmaceuticals, research, and radiotherapy owing to their suitable decay characteristics. Moreover, ⁵⁴Mn is used for calibrating γ-ray detectors, labeling and tracing the transport of manganese containing materials, and treating hematologic diseases owing to the emission of low energy electrons. As a mono-energetic γ-ray emitter, it also reveals the shape parameters of a detector spectrum, such as the peak-to-total ratio. As natural cobalt is a mono-isotopic (⁵⁹Co) element, its neutron-induced reaction cross sections are suitable for the verification, testing, and improvement of theoretical models [3, 4]. Furthermore, the theoretical prediction of nuclear cross-section data is crucial in the absence of experimental data [5].
The nuclear reaction cross sections induced by different energy neutrons and photons remains a major problem in applications such as data evaluation [6], applied nuclear physics, nuclear models, and nuclear reaction codes [7]. Therefore, an experimental study on the input parameters for nuclear reaction codes is necessary [8]. For these purposes, it is important to obtain more experimental measurements with high accuracy.
Numerous measured ⁵⁹Co(n, x) reaction cross sections are available in the EXFOR data library [9]. According to EXFOR, the ⁵⁹Co(n, 2n)⁵⁸Co, ⁵⁹Co(n, p)⁵⁹Fe and ⁵⁹Co(n, α)⁵⁶Mn reaction cross sections are available in a wide range of neutron energies. However, the cross sections available for the ⁵⁹Co(n, 3n)⁵⁷Co, ⁵⁹Co(n, 4n)⁵⁶Co and ⁵⁹Co(n, α2n)⁵⁴Mn reactions are very much limited and scattered. Moreover, most of these data are based on the neutron energies of D+D and D+T reactions, whereas certain data are based on the neutron energy of the ⁷Li(p, n) reaction. Thus, in this work, the ⁵⁹Co(n, x) reaction cross sections within the average neutron energy range of 15.2-37.2 MeV were measured by using the activation method and an off-line γ-ray spectrometric technique. We used the ⁹Be(p, n) reaction for the production of the neutron flux. The new experimental cross section data can improve the quality of the neutron cross section database and are expected to aid in new evaluations [10]. Nuclear reaction cross sections of interest were also calculated using the computer code TALYS-1.9 [11]. The measured and calculated values from the present work were compared with the literature data provided in EXFOR and the TENDL-2019 library [12]. In this work, we focused on the analysis of the input level density, adjustable parameters for the stripping or pick-up process, and pre-equilibrium options of the TALYS-1.9 code to validate the experimental results.

The experiment was carried out at the MC-50 Cyclotron of the Korean Institute of Radiological and Medical Sciences (KIRAMS). A schematic view of the experimental setup is presented in Fig. 1. The fast neutrons were produced from the ⁹Be(p, n) reaction by injecting a proton beam on a 2-mm-thick ⁹Be metallic foil (purity ≤ 99%) with a size of 25 mm × 25 mm. Behind the Be-target, graphite plates were used to stop the lower energy proton beam. The thickness of the graphite plates was 12 mm each for the 35 and 45 MeV proton beams and 6 mm for the 25 MeV proton beam. ¹⁹⁷Au (~0.2 gm) and ⁵⁹Co (~0.1 gm) foils of approximately 100 μm thickness were placed at a distance of 3.5 cm behind the Be-graphite target, as discussed in our previous work [13, 14]. The γ-ray activities for the activated sample assembly were measured using an energy-calibrated HPGe detector connected to a PC-based 4K channel analyzer. The efficiency calibration of the detector system was conducted using a standard ¹⁵²Eu source.
Figure1. (color online) Schematic view of experimental setup for irradiation facility.

We calculated the neutron spectra using the MCNPX 2.6.0 code [15] based on the following considerations. Uwamino et al. [16] measured neutron spectra from the p + ⁷Li (carbon backing) reaction with proton energies of 20, 25, 30, 35 and 40 MeV, which were simulated by Simakov et al. [17] using the MCNPX 2.6.0 code. The quasi-mono energetic neutron sources produced from the p+Be reaction was experimentally measured by Uwamino et al. [18] and estimated by Rakopoulos et al. [19] using the MCNPX 2.6.0 code at the Svedberg Laboratory (TSL). Novak et al. [20] suggested that the MCNPX 2.6.0 simulation could be used to generate the neutron spectrum for the p+Li and p+Be reactions. We calculated the neutron spectrum using the MCNPX 2.6.0 code for the Be(p, xn) reaction at a proton energy of 40 MeV and compared it with the experimental spectrum of Uwamino et al. [18]. The results were found to be in good agreement, except for the low neutron energy tail part. The neutron energy spectra for the p+Be reaction at proton energies of 25, 35, and 45 MeV were generated using the MCNPX 2.6.0 code and are presented in Fig. 2. The high energy distributions arose from the ⁹Be(p, n) reaction, and the low energy tail part resulted from the break-up reaction [21]. In the present work, most of the (n, x) reactions of the ⁵⁹Co and ¹⁹⁷Au originated from the region of higher energy neutrons. The neutron peak energy and its width in the neutron spectra were estimated by Gaussian fitting. The FWHM of the Gaussian fitting was used to estimate the widths of the different energy peaks. The obtained peak energies and their widths were 37.20±2.20, 26.40±2.77, and 15.20±3.65 MeV for the proton beam energies of 45, 35, and 25 MeV, respectively.
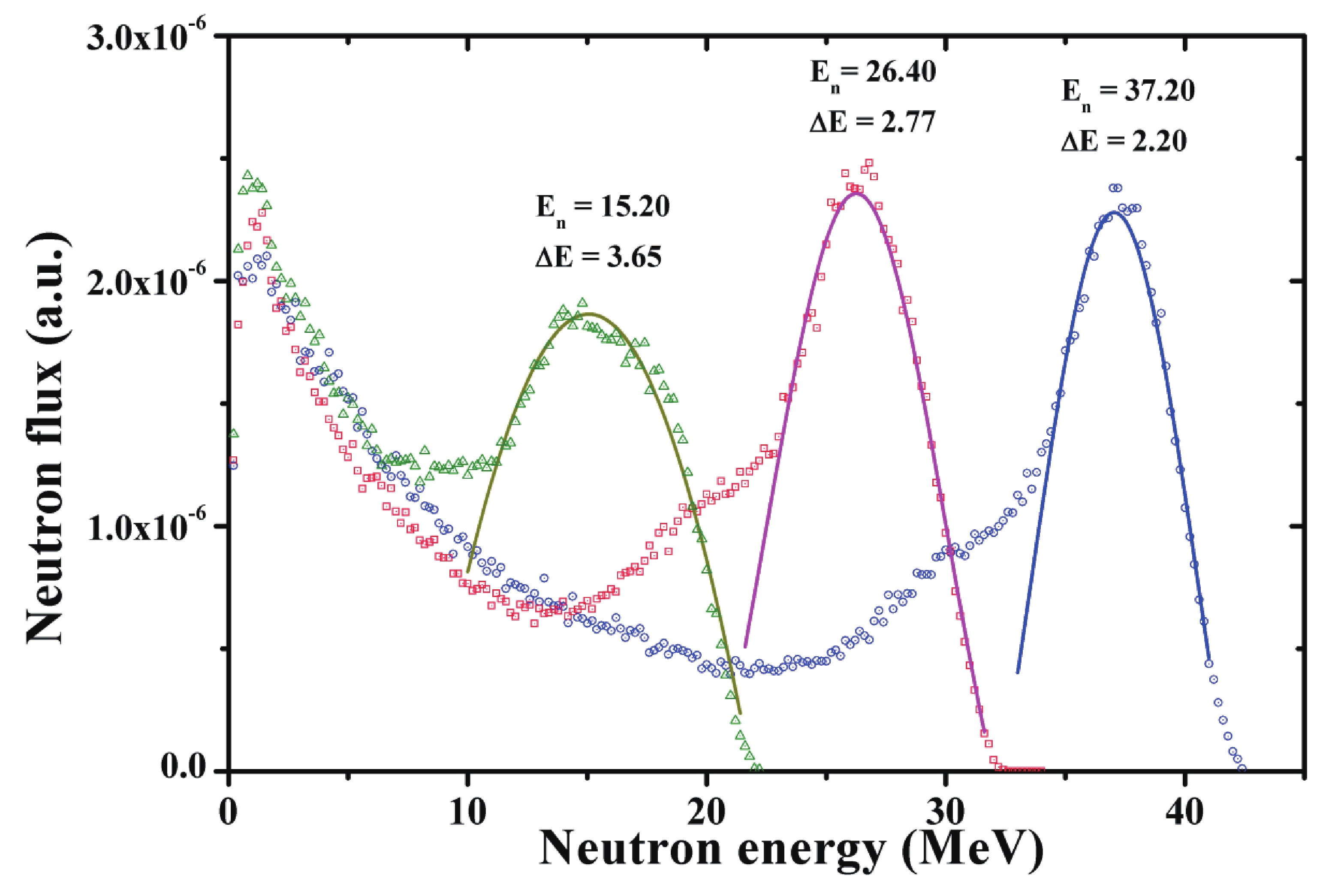Figure2. (color online) Neutron spectra calculated using MCNPX 2.6.0 code for proton beam energies of 25, 35 and 45 MeV.

2

-->

A.Neutron flux estimation

The neutron fluxes were estimated based on the photo-peak activities of the 355.68 keV γ-ray of ¹⁹⁶Au from the ¹⁹⁷Au(n, 2n) reaction at 25 MeV, 98.85 keV γ-ray of ¹⁹⁵Au from the ¹⁹⁷Au(n, 3n) reaction at 35 MeV, and 293.55 keV γ-ray of ¹⁹⁴Au from the ¹⁹⁷Au(n, 4n) reaction at 45 MeV proton beams, respectively. The neutron flux ${\phi _n}\left( {{E_n}} \right)$ was determined from the number of observed γ-rays (${N_{\rm obs}}$) under the photo-peak of an individual radionuclide of interest and the known cross sections ${\sigma _R}({E_n})$ of the ¹⁹⁷Au(n, xn; x=2-4) monitor reactions [22, 23]. The number of observed γ-rays (${N_{\rm obs}}$) was calculated by the following formula [14]:

${N_{\rm obs}} = C \cdot {\mkern 1mu} \int_{{E_{\rm th}}}^{{E_{\max }}} {{{\rm{\sigma }}_R}\left( {{E_n}} \right){\rm{\phi }}\left( {{E_n}} \right){\rm d}{E_n}} ,$

(1)

$C = \frac{{n{\mkern 1mu} {I_{\rm{\gamma }}}{{\rm{\varepsilon }}_{\rm{\gamma }}}\left( {1 - {{\rm e}^{ - {\rm{\lambda }}{\kern 1pt} {T_i}}}} \right){{\rm e}^{ - {\rm{\lambda }}{\kern 1pt} {T_c}}}\left( {1 - {{\rm e}^{ - {\rm{\lambda }}{T_{\rm clock}}}}} \right)}}{{{\rm{\lambda }}\left( {{T_{\rm clock}}/{T_{\rm count}}} \right)}},$

(2)

where n is the number of target atoms, I_γ is the branching intensity of the γ-rays of interest, ε_γ is the detection efficiency of the γ-ray, and λ is the decay constant (=ln2/T_1/2) for the produced isotope of the monitor reaction. Furthermore, T_i, T_c, T_clock, and T_count are the irradiation time, cooling time, clock time, and counting time, respectively. The nuclear spectroscopic data of the investigated radionuclides were obtained from the Lund University and Lawrence Berkeley National Laboratory database [24], which are presented in Table 1.

S. No	Nuclide	Jπ	T1/2	Decay mode	Eγ/keV	Iγ(100)	Contributing reaction	Eth-/MeV	${C_{br}}$ (Calculated)
									25 MeV	35 MeV	45 MeV
Reactions studied
1.	58Co	2+	70.86 d	EC	810.78	99.00	59Co(n, 2n)	10.63	0.87	0.36	0.20
2.	57Co	7/2?	271.79 d	EC	122.06 136.47	85.60 10.68	59Co(n, 3n)	19.35	?	0.79	0.39
3.	56Co	4+	77.27 d	EC	846.77 1238.28	100.0 67.6	59Co(n, 4n)	31.00	?	?	0.73
4.	59Fe	3/2?	44.50 d	β?	1099.25 1291.60	56.5 43.2	59Co(n, p)	0.800	0.56	0.28	0.14
5.	56Mn	3+	2.58 h	β?	846.77	98.9	59Co(n, α)	3.800	0.74	0.24	0.18
6.	54Mn	3+	312.3 d	EC	834.85	99.98	59Co(n, α2n)	12.14	?	0.61	0.59
Monitor reactions
7.	196Au	2?	6.18 d	EC(93); β?(7)	355.68	87.00	197Au(n, 2n)	8.11	087	?	?
8.	195Au	3/2+	186.09 d	EC	98.85	10.90	197Au(n, 3n)	14.79	?	0.67	?
9.	194Au	1?	38.02 h	EC	293.55	10.4	197Au(n, 4n)	23.21	?	?	0.58

Table1.Nuclear spectroscopic data of radio-nuclides from ⁵⁹Co(n, x) and ¹⁹⁷Au(n, xn) reactions and calculated factors (${C_{br}}$).

The neutron fluxes were determined in the neutron energy region from the reaction threshold of the ¹⁹⁷Au(n, xn; x=2-4) monitor reactions to the maximum neutron energies. The ${N_{\rm obs}}$ values under the characteristic photo-peak of the γ-rays of the reaction products ^194-196Au were related to the neutron flux ${\phi _n}\left( {{E_n}} \right)$ and cross sections ${\sigma _R}\left( {{E_n}} \right)$ of the ¹⁹⁷Au(n, xn; x=2-4) monitor reactions, which were obtained from the TENDL-2019 [14] library. However, the measured neutron flux for the peak neutron energy region ${\phi _n}\left( {{E_n}} \right)$ from ${E_P} - \Delta E$ to ${E_P} + \Delta E$ was estimated using the modified number of γ-rays ${M_{\rm obs}} = {C_{br}} \cdot {N_{\rm obs}}$. The correction factor ${C_{br}}$ can be calculated as the ratio of ${M_{\rm obs}}$ to ${N_{\rm obs}}$ [2, 25, 26]:

${C_{br}} = \frac{{{M_{\rm obs}}}}{{{N_{\rm obs}}}} = \frac{{\displaystyle\int_{{E_P} - \Delta E}^{{E_P} + \Delta E} {{\sigma _R}({E_n}){\phi _n}({E_n}){\rm d}{E_n}} }}{{\displaystyle\int_{{E_{th}}}^{{E_{\max }}} {{\sigma _R}({E_n}){\phi _n}({E_n}){\rm d}{E_n}} }},$

(3)

where ${\phi _n}({E_n})$ is the neutron flux calculated using the MCNPX 2.6.0 code, as shown in Fig. 2, ${E_{\rm th}}$ and ${E_{\max }}$ are the reaction thresholds of the monitor reactions and maximum neutron energy according to the proton energy, ${E_p}$ is the peak neutron energy, and $\Delta E$ is the standard deviation of the Gaussian fitted neutron spectra presented in Fig. 2. The calculated correction factors ${C_{br}}$ were obtained and are presented in Table 1. The cross section ${\bar \sigma _{RP}}$ could be assumed as constant over the peak width. Subsequently, the neutron fluence at the peak neutron energy ${\phi _{nP}}$ was obtained by means of Eq. (4):

${{\rm{\phi }}_{nP}} = \int_{{E_p} - \Delta E}^{{E_p} + \Delta E} {{{\rm{\phi }}_n}\left( {{E_n}} \right){\rm d}{E_n}} \approx \frac{{{C_{br}} \cdot {N_{\rm obs}}}}{{{{{\rm{\bar \sigma }}}_{RP}}}}.$

(4)

2 -->

B.Reaction cross section calculation

The ${C_{br}}$ parameters were also estimated for the ⁵⁹Co(n, x) reactions using the cross sections from the TENDL-2019 library and the calculated neutron spectra in Fig. 2. In this case, only the relative values of the cross sections were meaningful, as indicated in Eq. (4). The estimated ${C_{br}}$ parameters are listed in Table 1. Thereafter, the absolute production cross-sections $\left( {{{\bar \sigma }_{RP}}} \right)$ for the radio-nuclides ⁵⁶Mn, ⁵⁴Mn, ⁵⁹Fe, ⁵⁸Co, ⁵⁷Co, and ⁵⁶Co at the peak neutron energies were obtained according to the following formula:

${{\rm{\bar \sigma }}_{RP}} = \frac{{{C_{br}}}}{C} \cdot \frac{{{N_{\rm obs}}}}{{{{\rm{\phi }}_{nP}}}}.$

(5)

The measured cross sections for the ⁵⁹Co(n, x)^56-58Co, ⁵⁹Co(n, p)⁵⁹Fe, and ⁵⁹Co(n, αxn)^54,56Mn reactions based on Eq. (5) are presented in Table 2. The uncertainties of the measured cross sections were obtained, which were between 10.0% and 16.7%. The overall uncertainty was the quadratic sum of both the statistical and systematic errors. The statistical error resulted from counting statistics and was estimated to be 1.0%-4.0%. The systematic errors were owing to uncertainties in the irradiation time (~0.5%), the detection efficiency calibration (~4%), the uncertainty in the neutron flux (7.4%-14.8%), the half-life of the nuclides of interest, and the γ-ray abundance (~2%). The uncertainty in the neutron flux arose from the uncertainty in the cross section for the monitor reaction, the uncertainty owing to the subtraction of the low energy tail in the neutron spectrum, and the statistical uncertainty of the observed photo-peak count of the γ-ray from the reaction product of the monitor reaction. Honusek et al. [26] proposed an error of 5% in the neutron flux resulting from the subtraction of the low-energy tail in the neutron spectrum based on the MCNPX 2.6.0 simulation. The uncertainties in the cross sections of the monitor reactions were 7.568% for the ¹⁹⁷Au(n, 2n), 5.0% for the ¹⁹⁷Au(n, 3n), and 13.0% for the ¹⁹⁷Au(n, 4n) monitor reactions. The statistical uncertainty of the observed photo-peak count for the γ-ray from the reaction product of the monitor reaction was only 2.2%-1.9%. Thus, based on the quadratic sum of the values from the three sources, the uncertainty in the neutron flux was 7.4%-14.8%. The uncertainties in the nuclear reaction cross sections (σ_x) of the present work were also obtained based on the quadratic sum formula, which is given as

En/MeV	Reaction cross section/mb
	59Co(n, 2n)58Co	59Co(n, 3n)57Co	59Co(n, 4n)56Co	59Co(n, p)59Fe	59Co(n, α)56Mn	59Co(n, α2n)54Mn
15.20±3.65	712.42±74.81	?	?	43.31±4.95	27.02±2.82	?
26.40±2.77	464.60±47.19	275.65±28.48	?	23.69±3.47	6.25±0.69	3.18±0.43
37.20±2.20	232.11±38.06	185.48±31.75	10.815±1.89	14.81±2.43	10.04±1.71	58.74±9.67

Table2.Measured cross sections of the ⁵⁹Co(n, x) reactions.

${\left( {\frac{{\Delta {{\rm{\sigma }}_x}}}{{{{\rm{\sigma }}_x}}}} \right)^2} = \sum\limits_q {{{\left( {\frac{{\Delta {q_x}}}{{{q_x}}}} \right)}^2}}, $

(6)

where the parameters $ \left(q={N}_{\rm obs},{T}_{i},{I}_{\gamma },{\varepsilon }_{\gamma },{C}_{br},{\phi _{nP}}\right) $ that appear on the right-hand side of Eq. (6) are independent.
The results obtained in this work, together with the literature data, are shown in Figs. 3-8. The theoretical results were obtained from the TALYS-1.9 code with default and adjusted parameters for each investigated radionuclide. In the theoretical calculation using the TALYS-1.9 code with the back-shifted Fermi gas model, the three input parameters ldmodel, Cstrip a (0.7), alphald (0.102), and betald (0.11) played a vital role. Thus, these three parameters were adjusted within their recommended limits to obtain the excitation functions with relatively good descriptions of the experimental data. We compared the measured cross sections with the theoretical values obtained from the TALYS-1.9 code and data from the TENDL 2019 library.
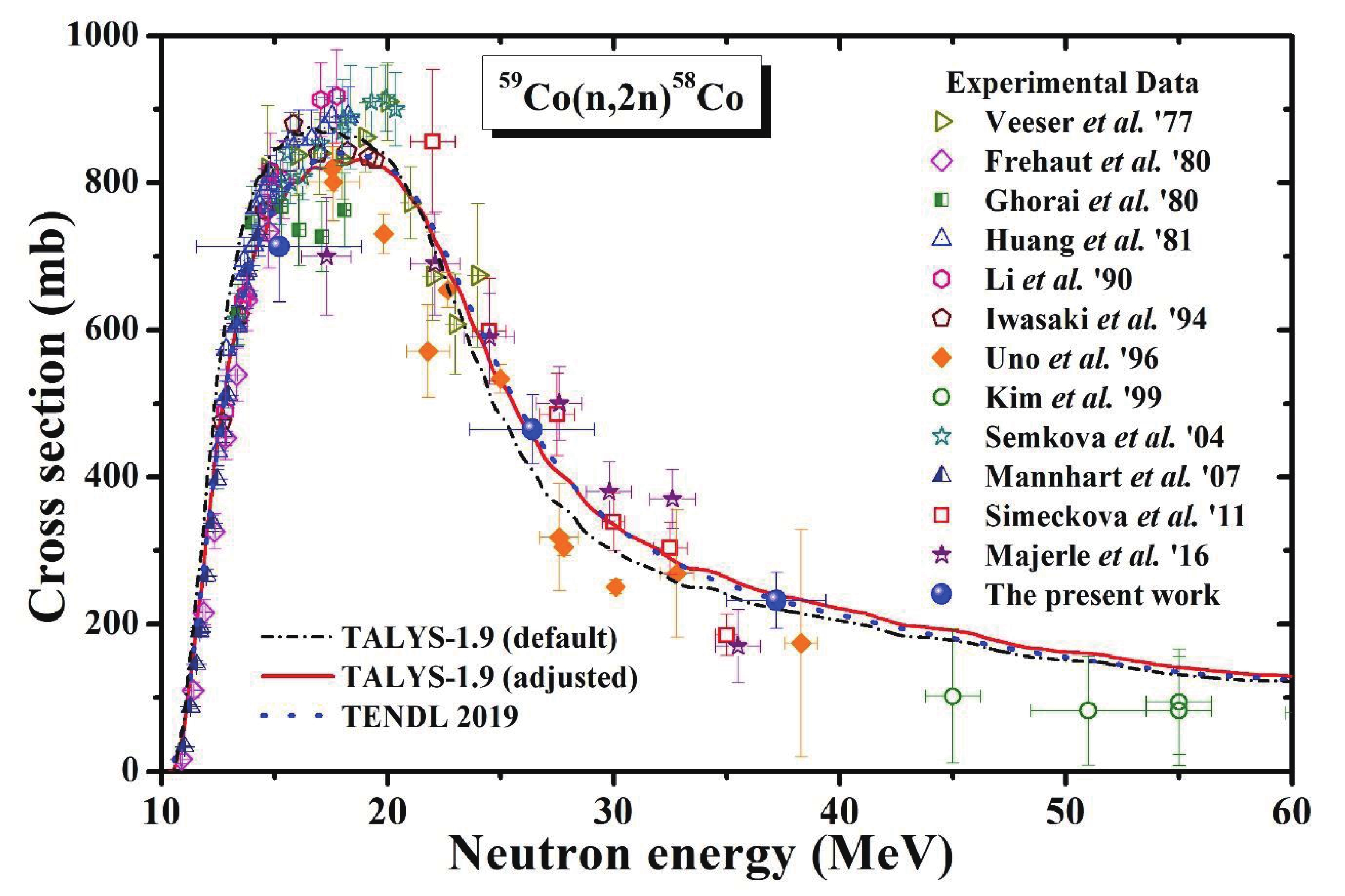Figure3. (color online) Comparison of ⁵⁹Co(n, 2n)⁵⁸Co reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.

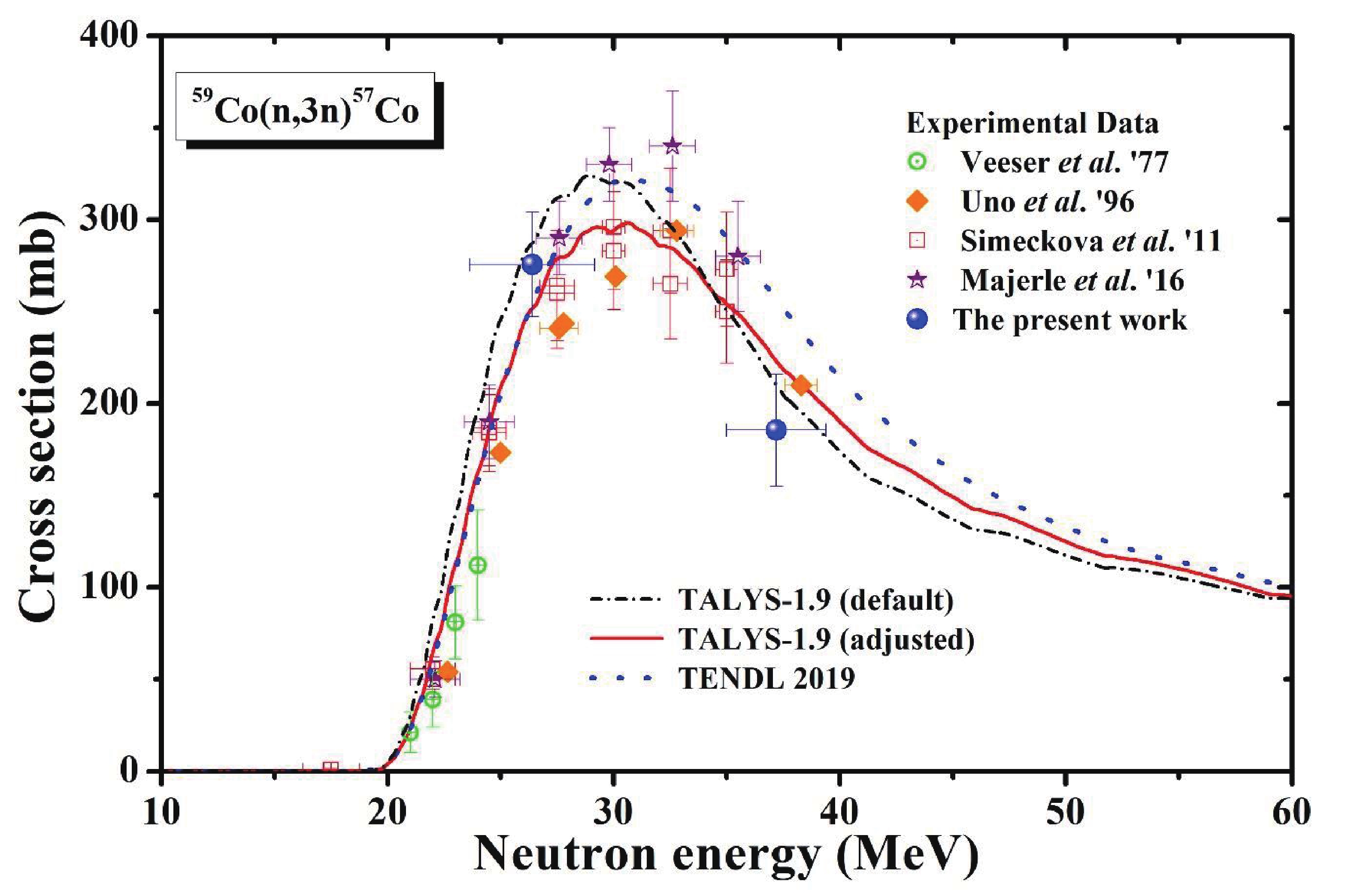Figure4. (color online) Comparison of ⁵⁹Co(n, 3n)⁵⁷Co reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.

Figure5. (color online) Comparison of ⁵⁹Co(n, 4n)⁵⁶Co reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.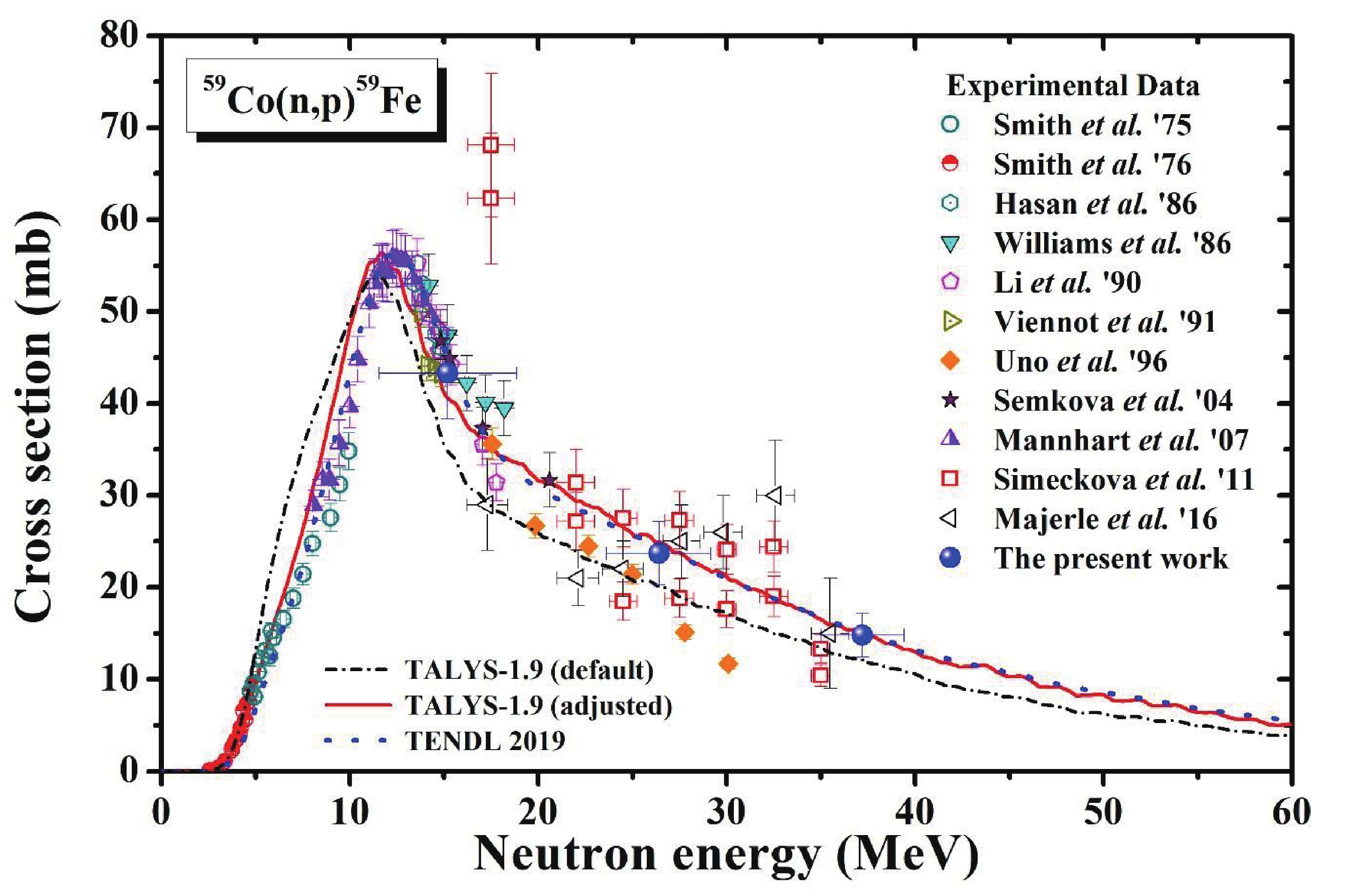

Figure6. (color online) Comparison of ⁵⁹Co(n, p)⁵⁹Fe reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.

Figure7. (color online) Comparison of ⁵⁹Co(n, α)⁵⁶Mn reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.

Figure8. (color online) Comparison of ⁵⁹Co(n, α2n)⁵⁴Mn reaction cross sections from present work with literature data and theoretical values. In this figure, TALYS-1.9 (default) and TALYS-1.9 (adjusted) indicate the theoretical data obtained using the TALYS-1.9 code with default and adjusted parameters, respectively.

2

-->

A.⁵⁹Co(n, 2n)⁵⁸Co reaction

The long-lived radionuclide ⁵⁸Co (T_1/2=70.86 d) was produced from the ⁵⁹Co(n, 2n)⁵⁸Co reaction with a threshold energy of 10.63 MeV, which decayed to ⁵⁸Fe with the EC (100%) process. The ⁵⁸Co was identified by the intense γ-line of 810.77 keV (I_γ = 99%). The cross sections of the ⁵⁹Co(n, 2n)⁵⁸Co reaction at neutron energies of 15.20±3.65, 26.40±2.77, and 37.20±2.20 MeV were obtained and are presented in Table 2. The measured cross sections of the present work, along with the literature data [2, 27-37], data from the TENDL 2019 library [12], and the theoretical values obtained using TALYS-1.9 with default parameters (TALYS-1.9 (default)) and TALYS-1.9 with adjusted parameters (TALYS-1.9 (adjusted)) are shown in Fig. 3. The theoretical values obtained from TALYS-1.9 (default) were in good agreement with the experimental values up-to 20 MeV but were underestimated at higher neutron energies. However, the theoretical values from TALYS-1.9 (adjusted) agreed well with the present data. A comparison of the present data with the literature data [20-31] and theoretical values demonstrated good agreement at neutron energies of 26.40±2.77 and 37.20±2.20 MeV, which confirmed the reliability of the present technique. However, the present results at a neutron energy of 15.20±3.65 MeV was slightly lower than the literature data and theoretical values. This may be owing to the broad neutron spectrum for the proton energy of 25 MeV.
2 -->

B.⁵⁹Co(n, 3n)⁵⁷Co reaction

The long-lived radionuclide ⁵⁷Co (T_1/2= 271.79 d) was produced from the ⁵⁹Co(n, 3n)⁵⁷Co reaction with a threshold energy of 19.35 MeV, which decayed to ⁵⁷Fe with the EC (100%) process. The cross section of the ⁵⁹Co(n,3n)⁵⁷Co reaction was measured by the intense γ-lines of 122.06 keV (I_γ = 85.6%) and 136.47 keV (I_γ = 10.68%). We counted two γ-lines with a long counting time to reduce the statistical uncertainties. We obtained the cross sections of the ⁵⁹Co(n, 3n)⁵⁷Co reaction at neutron energies of 26.40±2.77 and 37.20±2.20 MeV, and these values are listed in Table 2. The measured reaction cross sections of the present work, along with the literature data, TENDL-2019 data, and theoretical values obtained from TALYS-1.9 with default and adjusted parameters are presented in Fig. 4. It can be observed from Fig. 4 that the theoretical values from the TALYS-1.9 code with default parameters were overestimated compared to the experimental data below 35 MeV, whereas the data from the TENDL 2019 library were overestimated above 30 MeV. In the theoretical calculation, the two input parameters “Pshiftadjust” and “s2adjust” drastically changed the curve. The measured value at a neutron energy of 26.40±2.77 MeV was found to be in good agreement with the literature data [2, 27, 33, 37] and the theoretical values. However, the present value at the neutron energy of 37.20±2.20 MeV was slightly lower than the theoretical value.
2 -->

C.⁵⁹Co(n, 4n)⁵⁶Co reaction

The long-lived radionuclide ⁵⁶Co (T_1/2 = 77.27 d) was produced from the ⁵⁹Co(n, 4n)⁵⁶Co reaction with a threshold energy of 31.0 MeV, which decayed to ⁵⁶Fe with the EC (100%) process. The radionuclide ⁵⁶Co was identified via the 846.77 keV (I_γ = 100%) and 1238.28 keV (I_γ = 67.6%) γ-rays. In the present work, the ⁵⁹Co(n, 4n)⁵⁶Co reaction cross section was obtained at a neutron energy of 37.20±2.20 MeV and is displayed in Table 2. The measured reaction cross section, along with the literature data [2, 33, 34, 37, 38], TENDL 2019 data, and theoretical values from TALYS-1.9 with default and adjusted parameters are shown in Fig. 5. It can be observed from Fig. 5 that the theoretical data from the TALYS-1.9 (default) and TENDL 2019 data were overestimated compared to the experimental values. The theoretical value of the TALYS-1.9 (adjusted) was described better when estimate the cross section at low and higher neutron energies. The values reported by Kim et al. [34] were drastically underestimated in the other experimental values and the theoretical data. The theoretical data using the TALYS-1.9 code reproduced the present results very well.
2 -->

D.⁵⁹Co(n, p)⁵⁹Fe reaction

The radionuclide ⁵⁹Fe was produced from the ⁵⁹Co(n, p)⁵⁹Fe reaction at neutron energies of 15.20±3.65, 26.40±2.77, and 37.20±2.20 MeV. The threshold energy for the ⁵⁹Co(n, p)⁵⁹Fe reaction was 0.8 MeV. The reaction product ⁵⁹Fe (T_1/2 = 44.5 d) decayed to ⁵⁹Co through the β^- decay (100%). It was identified by the intense γ-lines of 1099.25 keV (I_γ = 56.5.0%) and 1291.6 keV (I_γ = 43.2%). We obtained data with different cooling times and finally determined their average values. The cross sections for the ⁵⁹Co(n, p)⁵⁹Fe reaction from the present work are presented in Table 2. The present results were compared with the literature data [2, 31, 33, 35-37, 39-43], TENDL 2019 data, and calculated values from the TALYS-1.9 code, as illustrated in Fig. 6. The theoretical values from TALYS-1.9 (default) were overestimated below 10 MeV and underestimated above 10 MeV compared to the experimental data. The theoretical values from TALYS-1.9 (adjusted) and the TENDL 2019 data were consistent with the present data. The pre-equilibrium process started after the sharp peak of the compound nucleus. In particular, the “Pshiftadjust” parameter was used to obtain a relatively good description of the experimental data at the pre-equilibrium process. The theoretical results obtained from TALYS-1.9 with adjusted parameters at lower and higher energies were described better than those with default parameters. The present data agreed very well with the theoretical values obtained from TALYS-1.9 with adjusted parameters over the investigated energy range.
2 -->

E.⁵⁹Co(n, α)⁵⁶Mn reaction

The radionuclide ⁵⁶Mn was produced from the ⁵⁹(n, α)⁵⁶Mn reaction with a threshold energy of 3.80 MeV. The radionuclide ⁵⁶Mn (T_1/2 = 2.58 h) underwent 100% β^- decays to produce ⁵⁶Fe. It was identified by an intense γ-line of 846.77 keV (I_γ = 98.9%). We measured the cross sections of the ⁵⁹(n, α)⁵⁶Mn reaction at neutron energies of 15.20±3.65, 26.40±2.77, and 37.20±2.20 MeV, as listed in Table 2. The present data were compared with the literature data [2, 29-31, 33, 36, 37, 44-48], data from the TENDL 2019 library, and theoretical values from TALYS-1.9 with default and adjusted parameters, as shown in Fig. 7. Fig. 7 indicates that the theoretical data from the TALYS-1.9 code with default parameters were overestimated compared to the experimental values. The theoretical calculations using the TALYS-1.9 code with adjusted parameters, such as the “Pshiftadjust” and “s2adjust” parameters, were used to obtain a relatively good description of the experimental data at the pre-equilibrium process. We obtained good agreement among the different experimental values. The calculated values using TALYS-1.9 with adjusted parameters at lower and higher neutron energies described the experimental data better than those with default parameters. Relatively good agreement was obtained between the present data and the theoretical data obtained from TALYS-1.9 with adjusted parameters in the investigated energy range.
2 -->

F.⁵⁹Co(n, α2n)⁵⁴Mn reaction

The relatively long-lived radionuclide ⁵⁴Mn was produced through the ⁵⁹Co(n, α2n) (E_th =12.14 MeV) reaction with neutron energies of 26.40±2.77 and 37.20±2.20 MeV. The reaction product ⁵⁴Mn (T_1/2 =312.3 d) decayed to ⁵⁴Cr through the EC (100%) process and it was identified by an intense γ-line of 834.85 keV (I_γ = 99.98%). The γ-ray spectrometry was performed with a long counting time to guarantee good counting statistics. We obtained data with different cooling times and finally determined their average values, as listed in Table 2. We compared the present data with the literature data [2, 33, 34, 37, 38, 49], as shown in Fig. 8. The theoretical data from the TALYS-1.9 code with default parameters and the data from the TENDL 2019 library were underestimated compared to the experimental values around the 40 MeV region, which was possibly owing to the underestimation of the compound nucleus processes. The experimental cross sections up to 30 MeV were in good agreement with the values from the TALYS-1.9 calculation using default and adjusted parameters. However, the calculated cross sections for the ⁵⁹Co(n, α2n)⁵⁴Mn reaction based on TALYS-1.9 with adjusted parameters were in good agreement with the experimental values. It can be observed from Fig. 8 that the theoretical data from the TALYS-1.9 code with adjusted parameters were consistent with the experimental data up to 45 MeV.

We measured new cross sections for the ⁵⁹Co(n, x) reactions in the neutron energy range between 15.2 and 37.2 MeV based on the ⁹Be(p, xn) reaction. The present data were compared with the literature data, TENDL 2019 data, and the theoretically calculated values using TALYS-1.9. Most of the present data were in good agreement with the existing literature data. The experimentally measured ⁵⁹Co(n, x) reaction cross sections from the present work and literature were comparable with the theoretical values from TALYS-1.9 with adjusted parameters. Thus, the experimental results of the present work will be useful as a benchmark to evaluate nuclear data. The results can also aid in determining the appropriate parameters for statistical models to obtain accurate neutron induced reaction cross sections of ⁵⁹Co.

The authors are thankful to the staff of the MC50 Cyclotron Laboratory at the Korea Institute of Radiological and Medical Sciences (KIRAMS) for the excellent operation and their support during the experiment.