Qu-Fei Song
, Su-Yang Xu
, Jun Su ^,
,

Corresponding author: Jun Su, sujun3@mail.sysu.edu.cn

Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China
Received Date:2020-10-22
Available Online:2021-04-15
Abstract:A nucleon-nucleus dynamics model was developed to investigate the proton-, neutron-, and deuteron-induced reactions at hundreds of MeV/nucleon. In this model, the trajectory of incident nucleon is described by classical mechanics, and the probability of reaction between the nucleon and nucleus is calculated by exponential damping. It is shown that the total reaction cross sections calculated by the model agree in general with the predictions by the CDCC and the experimental data. The model was applied to investigate the nucleon stripping in deuteron-induced reactions and its symmetry energy dependence.

HTML

--> --> -->

Breakup of weakly bound nuclei has drawn much attention in nuclear physics [1]. As a weakly bound nucleus, the deuteron can easily break up into a proton and neutron in deuteron-induced reactions [2, 3]. This process was speculated by Oppenheimer and Phillips in as early as 1935 [4]. Then, a lot of experiments were performed to measure the (d,p) and (d,n) reactions from Coulomb barrier to GeV energy region [5-9]. Generally, the reaction induced by a weakly bound nucleus is described by the quantum-mechanical approach of distorted-wave Born-approximation, in which the valence nucleon, core, and target are described by the approximated three-body wave functions [10]. Another successful model for describing breakup processes is the continuum-discretized coupled-channels (CDCC) method, in which the total wave function of the reaction system is expanded by the complete set of eigenfunctions of the two-body subsystem [3, 11]. The CDCC model and its extensions succeeded in reproducing experimental data on the scattering of both stable and unstable nuclei up to 200 MeV/nucleon [12-15]. Several semiclassical models or empirical parametrizations were also developed to study the deuteron breakup [16-18]. Recently, some investigations about the deuteron breakup were motivated by applications in the nuclear industry.
Nowadays, a large number of nuclear power plants are in operation owing to the greenhouse effect and energy shortages [19]. This brings the corresponding problem of radioactive waste disposal [20-22]. To solve this problem, researchers both in nuclear engineering and nuclear physics are focused on investigating the transmutation of the radioactive waste. In this regard, an experimental study showed that spallation reactions are a promising mechanism for the transmutation of long-lived fission products (LLFPs) [23]. In 2017, both proton- and deuteron-induced spallation reactions at 100-200 MeV/nucleon were measured. It was confirmed that both reactions are effective for the transmutation of $ ^{93} $Zr [24] and $ ^{107} $Pd [25]. In addition, it was pointed out in Ref. [24] that the effect of deuteron-induced spallation reactions may be better than that of proton-induced spallation reactions, given that the breakup of deuteron may give extra neutrons in the reaction, which will also contribute to the further transmutation of LLFPs.
Accurate cross section data of deuteron-induced spallation reactions are essential to design a viable and stable transmutation system using the deuteron. Owing to the difficulty of experimental measurements at this stage, data available in this scenario are still lacking [18], especially high-energy data. Nowadays, several deuteron experimental investigations have achieved great success, but the maximum experimental energy is still lower than 200 MeV/nucleon [26-28]. Therefore, a study on deuteron-induced reactions in the GeV/nucleon energy region is still necessary in this case.
On the other hand, data of the neutron-induced spallation are still required in the study of fast reactors and accelerator driven sub-critical systems (ADS) [29, 30]. In addition, these data are still very limited at present because of the difficulty to obtain neutrons in the GeV region and the impossibility of inverse dynamics [31-33]. In a previous study of ours, deuteron-induced spallation was proposed to measure indirectly the cross sections in neutron-induced reactions at hundreds of MeV [34]. However, a further study on the dynamics of neutron stripping in deuteron-induced spallation is needed. In this study, a simple model was developed to examine the mechanism of deuteron breakup and calculate the cross sections of neutron-stripping and proton-stripping reactions
The paper is organized as follows. In Sec. II, the method is described. In Sec. III, both the results and discussions are presented. Finally, a summary is given in Sec. IV.

In transport models for heavy ion collision, such as the quantum molecular dynamics model and the Boltzmann-Uehling-Uhlenbeck model, the interaction between the nucleon and nucleus is treated separately by the mean field interaction and nucleon-nucleon collisions [35, 36]. The former determines the classical trajectory of the nucleon, whereas the latter causes the transition of the nucleons in the momentum space and transfers a part of the incident energy to the target nucleus. This study only focused on properties of the incident nucleons that do not undergo nucleon-nucleon collision. Therefore, classical mechanics including only the mean field was applied to describe the trajectory of the incident nucleus. The total reaction cross section of nucleon-nucleon collision was used to calculate the probability of nucleon-nucleon collision.
2

-->

A.Trajectory of incident nucleon by classical mechanics

It is assumed that the mean field provided by the target nucleus stays static during the interaction. The time evolution of the incident nucleon in the mean field is governed by the Newtonian equation of motion

$ \vec{F} = \mu\frac{{\rm d}^{2} \vec{r}}{{\rm d}t^{2}}, $

(1)

where $ \mu $ is the reduced mass, and $ \vec{r} $ is the distance between the incident nucleon and target nucleus. The force includes Coulomb and nuclear forces. Assuming a hard-sphere distribution of charges in the target nucleus, the Coulomb force as a function of r can be expressed as

$\overrightarrow {{F_c}} (r) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{CZzr}}{{{R^3}}}\dfrac{{\vec r}}{r},\quad }&{r < R}\\{\dfrac{{CZz}}{{{r^2}}}\dfrac{{\vec r}}{r},\quad }&{r \geqslant R}\end{array}} \right. $

(2)

where C = $ \dfrac{e^2}{4\pi\epsilon_{0}} $ = 1.44 MeV$ \cdot $fm, Z is the charge number of target nucleus, z is the charge number of the incident nucleon (1 for proton and 0 for neutron), and R is the radius of the hard sphere, which is set as the experimental root-mean-square charge radius $ \sqrt{\langle{r}^2\rangle_{p}} $ taken from Ref. [37].
The nuclear force is written as

$ \begin{aligned}[b] \vec{F_{n}}(r) =& -\frac{\partial V_{n}}{\partial r}\frac{\vec{r}}{r}, \\ V_{n} =& \alpha\frac{\rho}{\rho_{0}}+\beta\frac{\rho^\gamma}{\rho_{0}^\gamma} +\frac{C_{sp}(\gamma_{i}+1)}{2}\frac{\rho^{\gamma_{i}}}{\rho_{0}^{\gamma_{i}}} \delta ^{2} +\frac{|\tau|}{\tau} \frac{C_{sp}}{2}\frac{\rho^{\gamma_{i}+1}}{\rho_{0}^{\gamma_{i}}}2\delta,\end{aligned} $

(3)

where $ V_{n} $ is the potential of the incident nucleon, $ \delta $ = ($ \rho_{n} - \rho_{p} $)/$ \rho $ is the isospin asymmetry, and $ \rho_{n} $, $ \rho_{p} $ and $ \rho $ are the neutron, proton, and nucleon densities of the target nucleus, respectively. $ \tau $ = 1/2 for neutrons and = ?1/2 for protons. The parameters used in this study were $ \rho_{0} $ = 0.16 fm$ ^{-3} $, $ \alpha $ = ?209.2 MeV, $ \beta $ = 156.4 MeV, $ \gamma $ = 1.35, $ C_{sp} $ = 38.06 MeV, $ \gamma_{i} $ = 0.75.
The following form of the nucleon density was used:

$ \rho_{i}(r) = \dfrac{\rho_{i0}}{1+{\rm exp}\left(\dfrac{r-R_{i}}{d_{i}}\right)}, $

(4)

where subscript i is p for proton or n for neutron. Parameters $ \rho_{i0} $, $ R_{i} $, and $ d_{i} $ are calculated by the following equations:

$ \begin{aligned}[b] \rho_{p_{0}}+\rho_{n_{0}} &= \rho_{0},\\ \frac{\rho_{p_{0}}}{\rho_{n_{0}}} &= \frac{Z}{N},\\ \int\rho_{p}(r){\rm d}\vec{r} &= Z,\\ \int\rho_{n}(r){\rm d}\vec{r} &= N,\\\int{r}^2\rho_{p}(r){\rm d}\vec{r} &= Z\langle{r}^2\rangle_{p},\\ \int{r}^2\rho_{n}(r){\rm d}\vec{r} &= N\langle{r}^2\rangle_{n}, \end{aligned} $

(5)

where Z and N are the proton and neutron numbers of the target nucleus, respectively, and $ \langle{r}^2\rangle_{i} $ is the mean-square radius of the nucleus, which can be taken from Refs. [37, 38].
Solving the equation of motion, i.e., Eq. (1), with initial conditions depending on impact parameter b and incident energy $ E_{\rm in} $, one can obtain distance $ \vec{r}(t) $ and velocity $ \vec{v}(t) $ = d$ \vec{r} $/dt as a function of time.
2 -->

B.Total reaction cross section of the reaction between nucleon and nucleus

Suppose that a nucleon beam with intensity I passes through a nuclear matter with density $ \rho $ and thickness $ {\rm d}x $; the probability of the nucleon-nucleon collision can then be expressed as

$ \frac{{\rm d}I}{I} = -\sigma\rho {\rm d}x, $

(6)

where $ \sigma $ is the cross section of the nucleon-nucleon collision. Applying the relationship $ {\rm d}x = v(t){\rm d}t $, one can calculate the probability for the incident nucleon passing through the target nucleus without nucleon-nucleon collision by the following time integral

$ P = \frac{I^{\rm out}}{I^{\rm in}} = {\rm exp}\left [-\int_{-\infty}^{+\infty} \sigma \rho v {\rm d}t\right]. $

(7)

The nucleon-nucleon collision is responsible for the transformation of the incident energy to the target nucleus. Thus, the reaction probability is $ 1-P $. Note that the initial conditions for Eq. (1) depend on impact parameter b. Thus, the total reaction cross section can be calculated by integrating over the impact parameter:

$ \sigma_{t} = \int_{0}^{+\infty}2\pi b[1-P(b)]{\rm d}b. $

(8)

We used three cross sections of the nucleon-nucleon collision to perform the calculation. The first one is the isospin independent, and constant cross section $ \sigma $ = 40 mb. Second, we applied the cross section of the nucleon-nucleon collision in free space taken from Ref. [39].

$\sigma _{pp}^{\rm free} = \sigma _{nn}^{\rm free} = \left\{ {\begin{array}{*{20}{l}}{34{{\left( {\dfrac{{{p_{{\rm{lab}}}}}}{{0.4}}} \right)}^{ - 2.104}},}&{{p_{{\rm{lab}}}}\leqslant 0.4}\\{23.5 + 1000{{\left( {{p_{{\rm{lab}}}} - 0.7} \right)}^4},}&{0.4 < {p_{{\rm{lab}}}}\leqslant 0.8}\\{23.5 + \dfrac{{24.6}}{{1 + \exp \left( { - \left( {{p_{{\rm{lab}}}} - 1.2} \right)/0.10} \right)}},}&{0.8 < {p_{{\rm{lab}}}}\leqslant 1.5}\\{41 + 60\left( {{p_{{\rm{lab}}}} - 0.9} \right)\exp \left( { - 1.2{p_{{\rm{lab}}}}} \right),}&{1.5 < {p_{{\rm{lab}}}}\leqslant 5.0}\end{array}} \right.$

(9)

$ \sigma _{np}^{\rm free} = \sigma _{pn}^{\rm free} = \left\{ {\begin{array}{*{20}{l}}{6.3555p_{\rm lab}^{ - 3.2481}\exp \left( { - 0.377{{\left( {\ln {p_{{\rm{lab}}}}} \right)}^2}} \right),}&{{p_{{\rm{lab}}}} \leqslant 0.4}\\{33 + 196{{\left| {{p_{{\rm{lab}}}} - 0.95} \right|}^{2.5}},}&{0.4 < {p_{{\rm{lab}}}} \leqslant 1.0}\\{24.2 + 8.9{p_{{\rm{lab}}}},}&{1.0 < {p_{{\rm{lab}}}} \leqslant 2.0}\\{42,}&{2.0 < {p_{{\rm{lab}}}} \leqslant 5.0}\end{array}} \right.$

(10)

$ \sigma \rho $ in Eq. (7) is expressed as

$\sigma \rho = \left\{ {\begin{array}{*{20}{l}}{\sigma _{pp}^{\rm free}{\rho _p} + \sigma _{pn}^{\rm free}{\rho _n},\quad {\rm for}\; p\; {\rm reaction}}\\{\sigma _{nn}^{\rm free}{\rho _n} + \sigma _{np}^{\rm free}{\rho _p},\quad {\rm for}\;n\; {\rm reaction}.}\end{array}} \right.$

(11)

The unit of the cross sections in Eqs. (9) and (10) is ${\rm mb}$, and $p_{\rm lab}$ (GeV/c) is the momentum in the laboratory frame.
Third, the in-medium factor proposed by Cai et al. [40] was considered. $ \sigma \rho $ in Eq. (7) is expressed as

$ \sigma \rho = \left\{{\begin{array}{*{20}{l}}{\sigma _{pp}^{\rm med}{\rho _p} + \sigma _{pn}^{\rm med}{\rho _n},\quad {\rm for}\; p\; {\rm reaction}}\\{\sigma _{nn}^{\rm med}{\rho _n} + \sigma _{np}^{\rm med}{\rho _p},\quad {\rm for}\; n\; {\rm reaction},}\end{array}} \right.$

(12)

$ \begin{aligned}[b]&\sigma_{p p}^{\rm med} = \sigma_{n n}^{\rm med } = \frac{1.0+0.1667 E_{\rm lab}^{1.05} \rho^{3}}{1.0+9.704 \rho^{1.2}} \sigma_{p p}^{\rm free}, \\ &\sigma_{n p}^{\rm med} = \sigma_{pn}^{\rm med} = \frac{1.0+0.0034 E_{\rm lab}^{1.51} \rho^{2}}{1.0+21.55 \rho^{1.34}} \sigma_{n p}^{\rm free}, \end{aligned} $

(13)

where $ E_{\rm lab} $ (MeV) is the kinetic energy in the laboratory frame.
2 -->

C.Deuteron-induced reaction

Let us assume that the positions of proton and neutron in the deuteron satisfy a Gaussian distribution. Let the center of the deuteron be at the origin of the coordinates; then, the probability density function that the neutron or proton is at point $ (x_{d}, y_{d}, z_{d}) $ is

$\begin{aligned}[b] f =& A\exp\left(-\frac{x_{d}^2+y_{d}^2+z_{d}^2}{L}\right)\\ =& A\exp\left(-\frac{r_{d}^2}{L}\right),\end{aligned} $

(14)

where $ r_{d} $ is the distance between the nucleon and the center of the deuteron. The root-mean-square radius of deuteron is $ \sqrt{\langle{r}^2\rangle} $ = 2.1421 fm. Based on the normalization conditions and the root-mean-square radius of deuteron, this function satisfies the following two equations:

$ \int f(r_{d}){\rm d}\vec{r_{d}} = 1, $

(15)

$ \int {r_{d}}^2 f(r_{d}){\rm d}\vec{r_{d}} = \langle{r}^2\rangle = (2.1421)^2{\rm fm}^{2}. $

(16)

Using these two equations, the parameters A and L of the Gaussian distribution can be found.
The deuteron-induced reaction is equivalent to one neutron and one proton reacting with the target nucleus. Let deuteron be incident with impact parameter b in the z-axis direction, and let us establish coordinates with deuteron center as origin. Then, according to the determined Gaussian distribution function, the probability of the neutron being located at point $ (x_{d}, y_{d}, z_{d}) $ can be found to be $ f{\rm d}x{\rm d}y{\rm d}z $. In this condition, the proton is at point $ (-x_{d}, -y_{d}, -z_{d}) $, and it can be seen from the geometric relationship that the impact parameter of the proton and neutron are functions of b, x, and y:

$ b_{p} = \sqrt{(b-x_{d})^2+y_{d}^2},\quad b_{n} = \sqrt{(b+x_{d})^2+y_{d}^2}. $

(17)

The probabilities of no collision $ P_{p} $ and $ P_{n} $ depend on $ b_{p} $ and $ b_{n} $, respectively. Similar to the calculation method of cross section in nucleon-induced reactions in subsection II B, the three components of the deuteron-nucleus total reaction cross section can be obtained by integrating over $ x_{d} $, $ y_{d} $, $ z_{d} $ and b. The cross section for the deuteron absorption is

$\begin{aligned}[b] \sigma_{d-ABS} =& \int 2\pi bdb\:\:[1-P_{n}(b_{n})][1\\&-P_{p}(b_{p})] \:\:f {\rm d}x_{d}{\rm d}y_{d}{\rm d}z_{d}, \end{aligned}$

(18)

the cross section for the nonelastic breakup where the proton is absorbed is

$ \sigma_{p-NEB} = \int 2\pi bdb\:\: P_{n}(b_{n})[1-P_{p}(b_{p})] \:\: f {\rm d}x_{d}{\rm d}y_{d}{\rm d}z_{d}, $

(19)

and the cross section for the neutron-stripping nonelastic breakup where the neutron is absorbed is

$ \sigma_{n-NEB} = \int 2\pi bdb\:\:[1-P_{n}(b_{n})]P_{p}(b_{p}) \:\: f {\rm d}x_{d}{\rm d}y_{d}{\rm d}z_{d}. $

(20)

It is evident that the three reaction cross sections depend only on the incident energy of deuteron and the nuclear density distribution of target nucleus. The total reaction cross section of deuteron-nucleus reactions is

$ \sigma_{t} = \sigma_{d-ABS}+\sigma_{p-NEB}+\sigma_{n-NEB}. $

(21)

Figure 1 shows the forces on the nucleons provided by $ ^{208} $Pb. Coulomb force on a proton increases linearly with increasing r for r $ < $ R and decreases for r $ > $ R. The nuclear force is a short-range force that has a significant effect only near the edge of the nucleus. In a rich neutron system such as $ ^{208} $Pb, owing to the symmetry energy in the nuclear potential, protons will be more attracted by nuclear force than neutrons. The $ F_{\rm total} $ on protons is mainly repulsive for r $ < $ R and mainly attractive for r $ > $ R. But for neutrons, there is no effect from the Coulomb force. They are simply attracted near the edge of the nucleus.
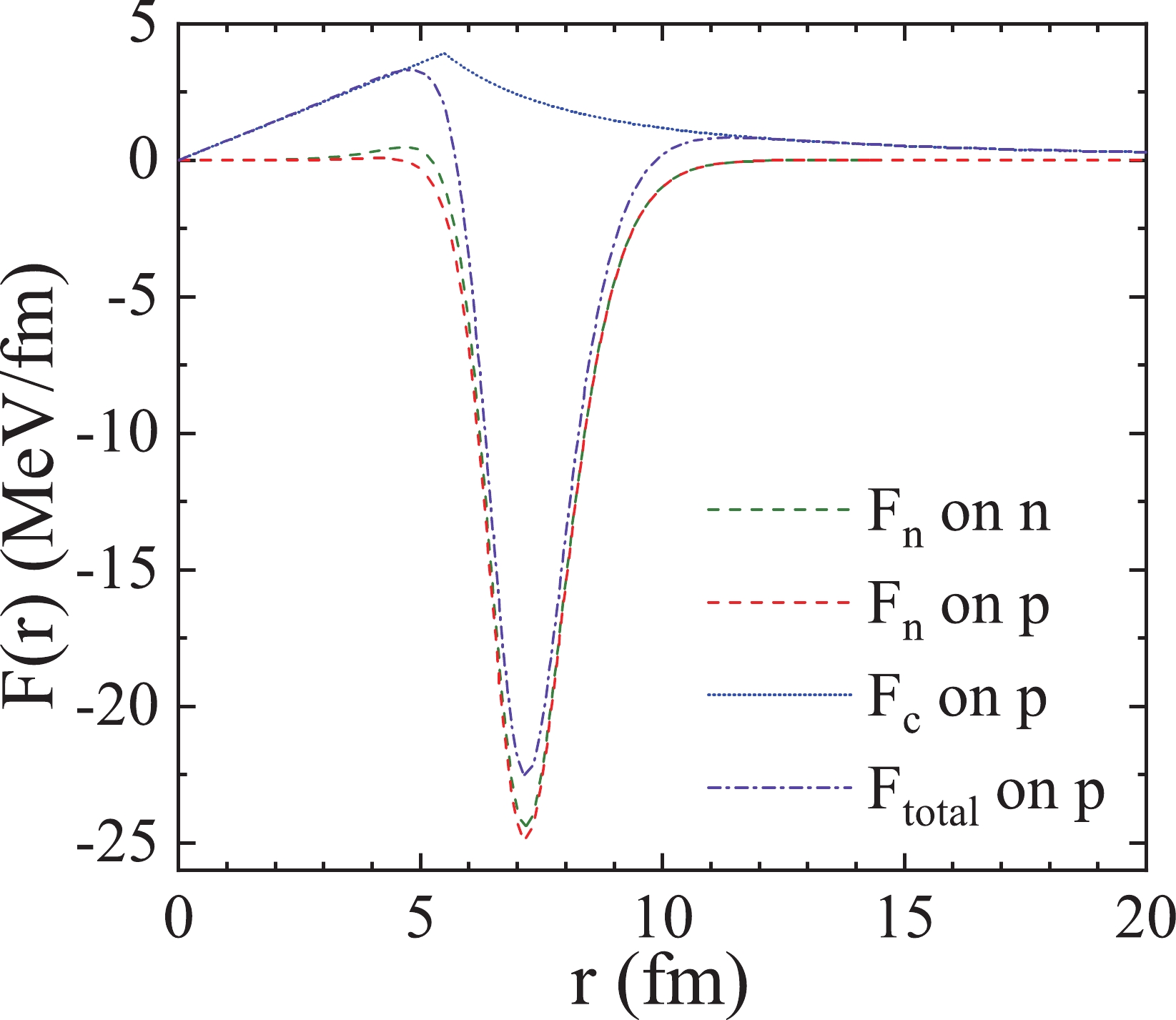Figure1. (color online) Forces on the nucleons in the reaction nucleon + $ ^{208} $Pb. The green and red dashed curves represent the nuclear force on neutron and proton, respectively. The blue dotted curve represents the Coulomb force on protons. The total force on protons is the sum of Coulomb and nuclear forces; it is depicted by the dash-dotted curve.

Figure 2 shows the trajectories of neutron and proton in reactions n + $ ^{208} $Pb and p + $ ^{208} $Pb at 200 MeV/nucleon and different impact parameters. The colors show the nuclear density distribution of $ ^{208} $Pb. For neutrons, when the impact parameter b is small, owing to the attraction of nuclear force, the trajectory has a significant deflection at the edge of the nucleus. However, after the neutron enters the interior of the nucleus, the nuclear force becomes small and the deflection is not evident. For b = 9 and 11 fm, the trajectories have no evident deflections, and the neutron does not enter the interior of the nucleus. Therefore, it will not cause the nucleon-nucleon collision. The proton trajectories are similar to the neutron trajectories when impact parameters are small. However, for b = 9 and 11 fm, it is repulsed by the Coulomb force and deflected out of the nucleus instead.
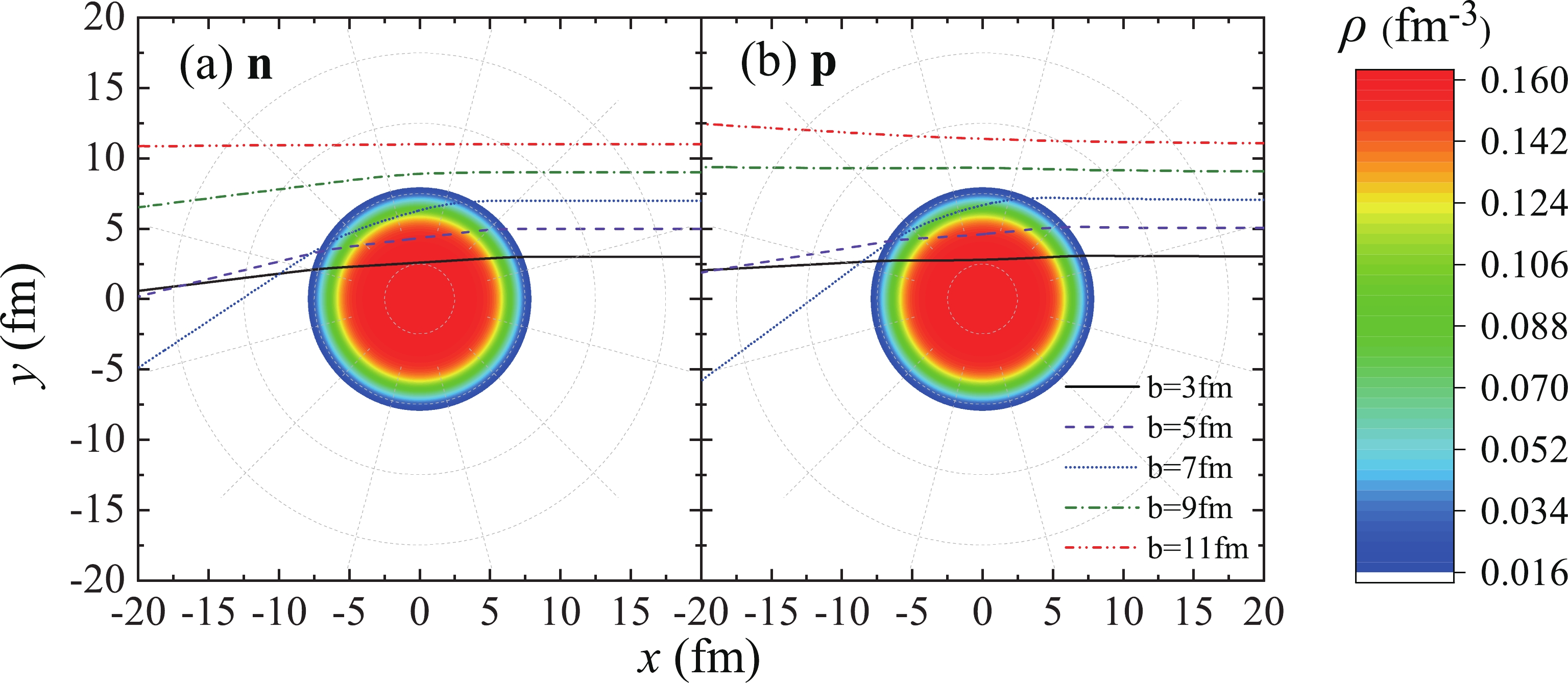Figure2. (color online) Trajectories of neutron and proton in reactions n + $ ^{208} $Pb and p + $ ^{208} $Pb at 200 MeV/nucleon and different impact parameters and nuclear density distribution of $ ^{208} $Pb. The center of mass of $ ^{208} $Pb is at (0,0). The different curves represent the trajectories of nucleons with different impact parameters.

Figure 3 is very similar to Fig. 2. It compares the trajectories of nucleons with different incident energies at the same impact parameters b = 7 fm in reactions n + $ ^{208} $Pb and p + $ ^{208} $Pb. Note that as the incident energy of the nucleon increases, the nucleon velocity becomes larger, and the deflection of the trajectories caused by the force provided by $ ^{208} $Pb becomes smaller. Therefore, in this case, higher-energy nucleons are less likely to enter the interior of the nucleus, and the probability of nucleon-nucleon collision will decrease.
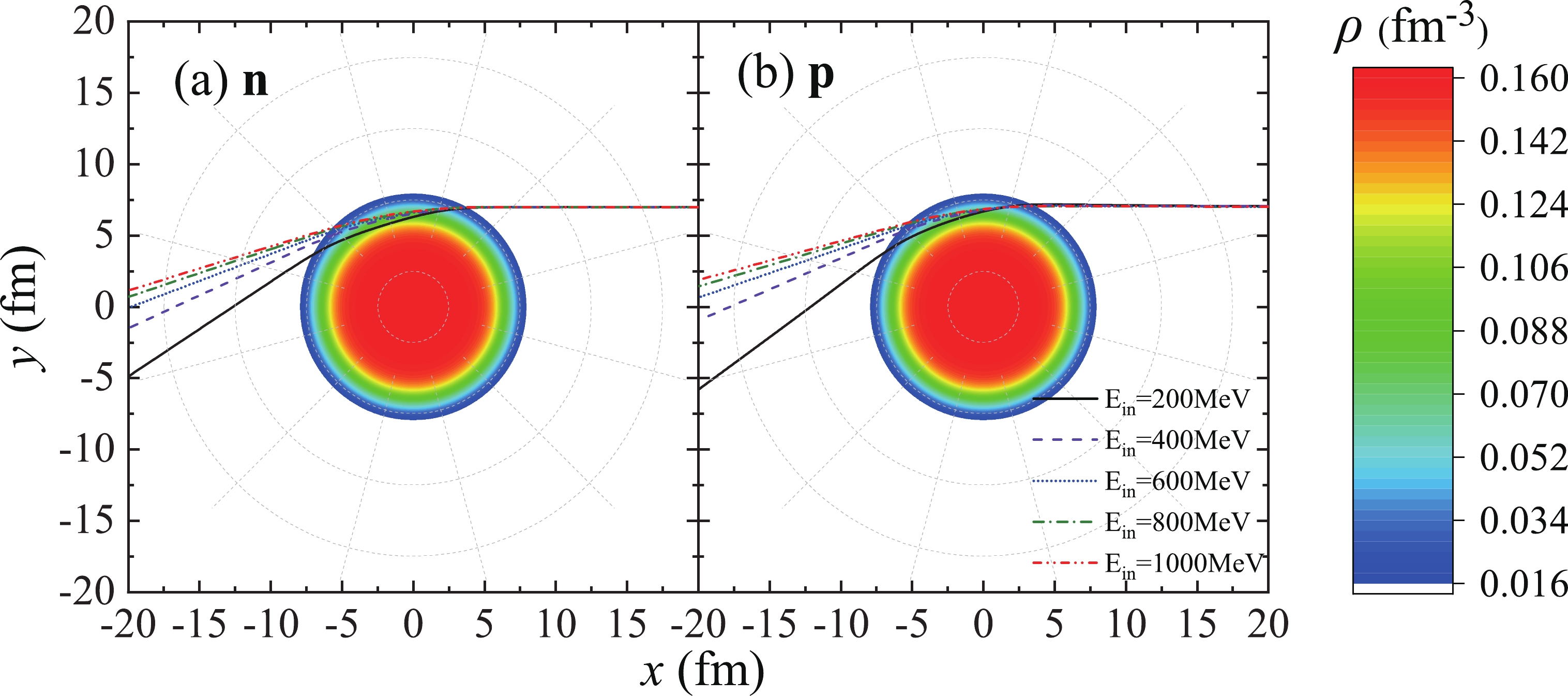Figure3. (color online) Same as Fig. 2 but for the trajectories of neutrons and protons at b = 7 fm. The different curves represent the trajectories of nucleons with different incident energies.

In the calculation using 40 mb, the probability of no collision is only related to the nucleon trajectory and density distribution of target nucleus. According to Eq. (7), it is evident that the probability of no collision $ P_{\rm no} $ will decrease if the nucleon trajectories pass through high-density regions. Otherwise, it will increase. Therefore, it can be concluded that $ P_{\rm no} $ is positively correlated with incident energies and impact parameters by combining Fig. 2 with Fig. 3. The corresponding results by using 40 mb are shown in Fig. 4.
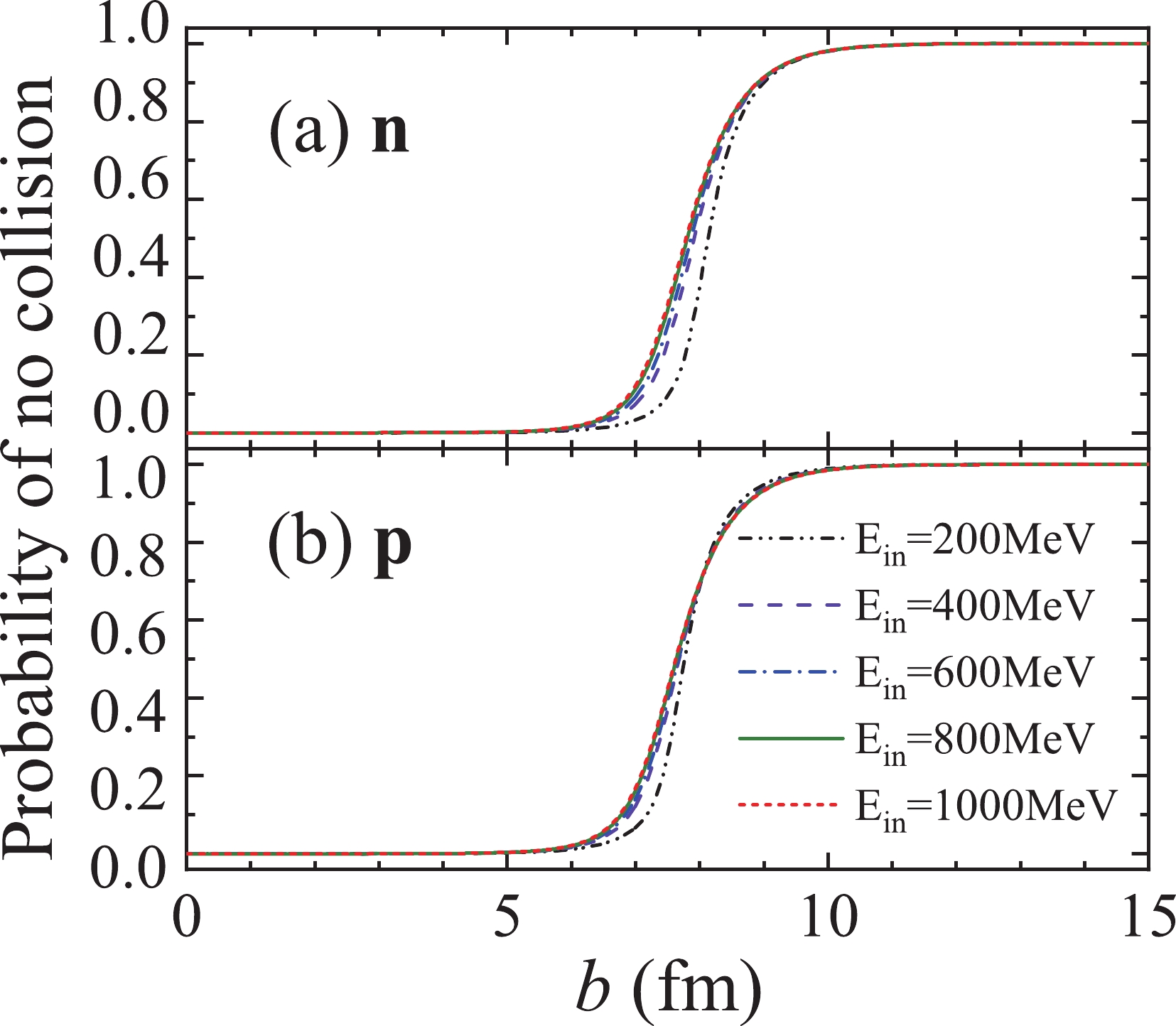Figure4. (color online) Comparison of the probability of no collision $ P_{\rm no} $ of neutrons with different incident energies calculated by using 40 mb; the same is depicted for protons. The different curves represent the probability of no collision of nucleons with different incident energies.

Fig. 5 presents a comparison between the $ P_{n} $ of proton and that of neutron calculated by using 40 mb at different incident energies. In Fig. 2 and Fig. 3, the difference between the trajectories of neutrons and protons is difficult to distinguish. However, in fact, owing to the repulsion of the Coulomb force, it is more difficult for protons than for neutrons to enter the high-density regions. This leads to the fact that in Fig. 5, $ P_{p} $ will be slightly larger than $ P_{n} $ under the same conditions, which means that in deuteron-induced reactions, the proton is more likely to be stripped than the neutron.
Figure5. (color online) Comparison between the $P_{\rm no}$ of protons and that of neutrons calculated by using 40 mb at different incident energies. The dashed and dash-dotted curves represent the probability of no collision of protons and neutrons, respectively.

To test the calculations using three type cross sections, the proton reaction cross sections were calculated and compared to the experimental data. Fig. 6 presents the cases for p + $ ^{208} $Pb reaction at 100-1000 MeV/nucleon. The nucleon collision cross section was regarded as a constant with value 40 mb. Therefore, the results decrease with increasing energy in the range of 100-1000 MeV/nucleon. Note that there is still a large gap between the results and the experimental data.
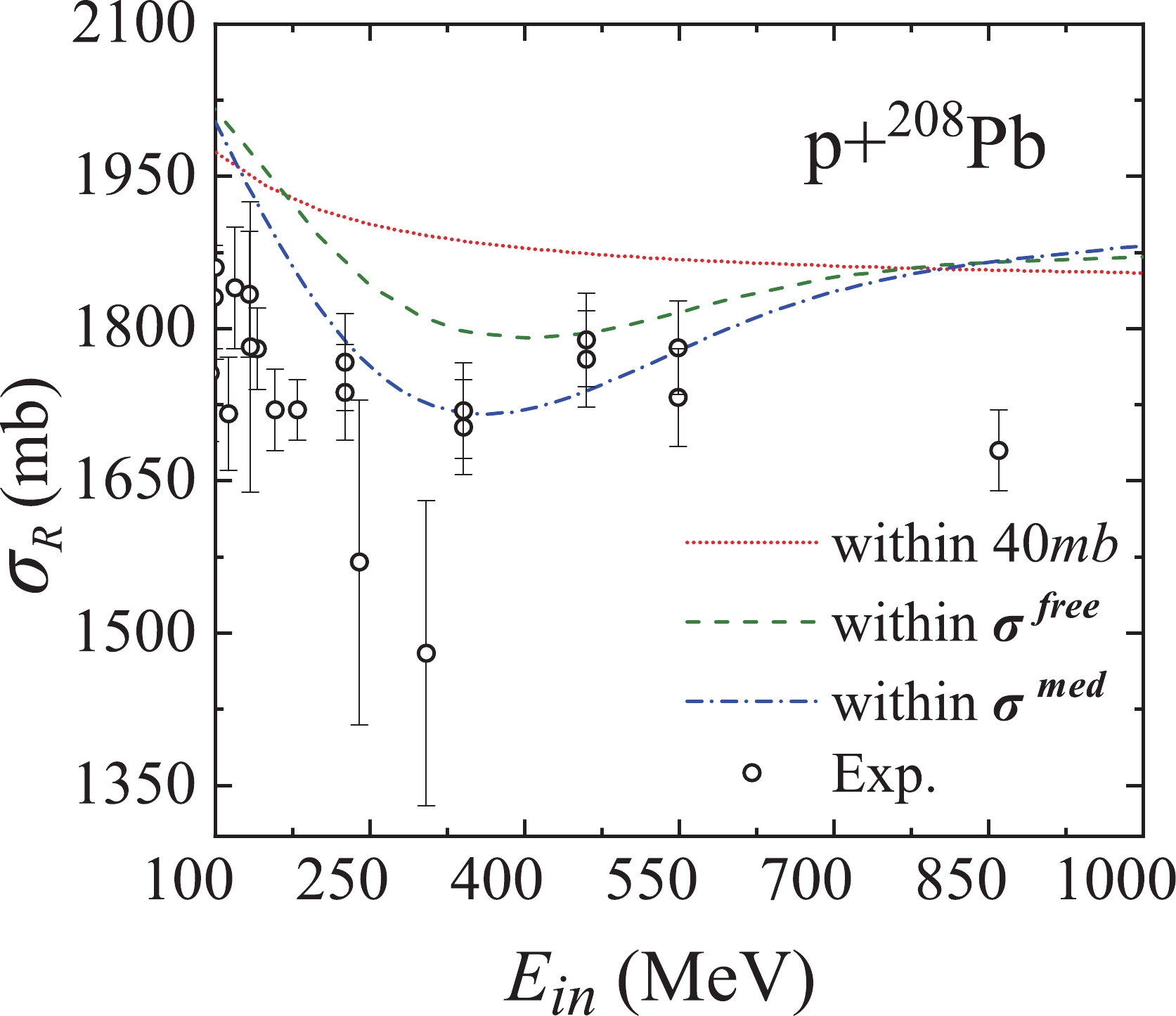Figure6. (color online) Calculated reaction cross sections by using three cross sections and experimental data for the p + $ ^{208}$Pb reaction as a function of incident proton energy. The dotted, dashed, and dash-dotted curves represent the calculations using 40 mb, cross section in free space, and in-medium cross section, respectively. The experimental data are taken from Ref. [41].

In the calculation using cross section in free space, a correction of the nucleon energy was added. The cross section of the nucleon-nucleon collision in free space is calculated by Eqs. (9) and (10). With the increase of energy, the cross section in free space shows a downward trend first and then slowly rises. This leads to a similar trend in the proton reaction cross section calculated by this method. Note that in Fig. 6, a significant effect was produced after using cross section in free space: the results became closer to the experimental data than previous results. However, they are still far from ideal.
In the calculation using in-medium cross section, a medium correction was added on the basis of energy correction. In this case, the nucleon-nucleon collision cross section depends on both energy and nuclear density. Fig. 6 shows that the results obtained by this calculation are closer to most experimental data than other calculations, thereby proving the validity of this calculation.
To test the calculation using in-medium cross section further, the model was used to study more nucleon-nucleus reactions for comparison with experimental data. Figure 7 shows the total reaction cross sections for $ ^{12} $C, $ ^{27} $Al, $ ^{65} $Cu, $ ^{120} $Sn, and $ ^{208} $Pb. For neutron-induced reactions, the calculation results reproduce the experimental data well in the region of 600-1000 MeV. However, in the region of 400-600 MeV, there are certain differences between the experimental data and the calculated results. For proton-induced reactions, calculated results are in good agreement with most of experimental data, except at 860 MeV. Experimental data in the high-energy region are still limited. Thus, this method needs further verification.
Figure7. (color online) Calculated nucleon-nucleus reaction cross sections by using in-medium cross section for $ ^{12} $C (dash-dot-dotted curve), $ ^{27} $Al (dash-dotted curve), $ ^{65} $Cu (dotted curve), $ ^{120} $Sn (dashed curve), and $ ^{208} $Pb (solid curve) as a function of incident deuteron energy. The a and b parts correspond to the neutron- and proton-induced reactions, respectively. Scattered points represent the corresponding experimental data, which are taken from Ref. [41] for proton-induced reactions, and from Refs. [42, 43] for neutron-induced reactions.

In Ref. [44], deuteron-nucleus total reaction cross sections up to 500 MeV/nucleon were calculated by the CDCC model. The data in 0-100 MeV/nucleon region is consistent with existing experimental data. To investigate the calculation using in-medium cross section further, the results were compared to the results of CDCC in Ref. [44]; the comparison is shown in Fig. 8. For d + $ ^{12} $C, d + $ ^{58} $Ni, and d + $ ^{120} $Sn reactions at 100-500 MeV/nucleon, the results of two calculations agree well with each other. For d + $ ^{208} $Pb reaction, in the 100-300 MeV/nucleon region, there is a small difference between the results of the two calculations. As the energy increases, the difference becomes negligible.
Figure8. (color online) Calculated deuteron-nucleus total reaction cross sections by using in-medium cross section for $ ^{12} $C (dashed curve), $ ^{58} $Ni (dash-dotted curve), $ ^{120} $Sn (dash-dot-dotted curve), and $ ^{208} $Pb (short-dashed curve) as a function of incident deuteron energy. The solid curves represent the results of CDCC, which are taken from Ref. [44].

Based on the consistency of this calculation with the experimental results and the calculations of the CDCC model, we continued to apply this method to study the nucleon stripping in deuteron-induced spallation reactions. Deuteron-nucleus total reaction cross sections calculated by using in-medium cross section are a sum of deuteron absorption cross sections and nucleon stripping cross sections. Figure 9 shows the calculated total reaction cross section and its components by using in-medium cross section for d + $ ^{208} $Pb reaction. In the 100-1000 MeV/nucleon region, the component of deuteron absorption is the largest component of $ \sigma _{\rm total} $. The components of the proton and neutron absorption also make large contributions. As mentioned above, protons are more easily stripped than neutrons. Thus, note that the cross section of proton absorption is smaller than the cross section of neutron absorption. These results demonstrate that the nucleon stripping processes play a significant role in deuteron-induced spallation reactions.
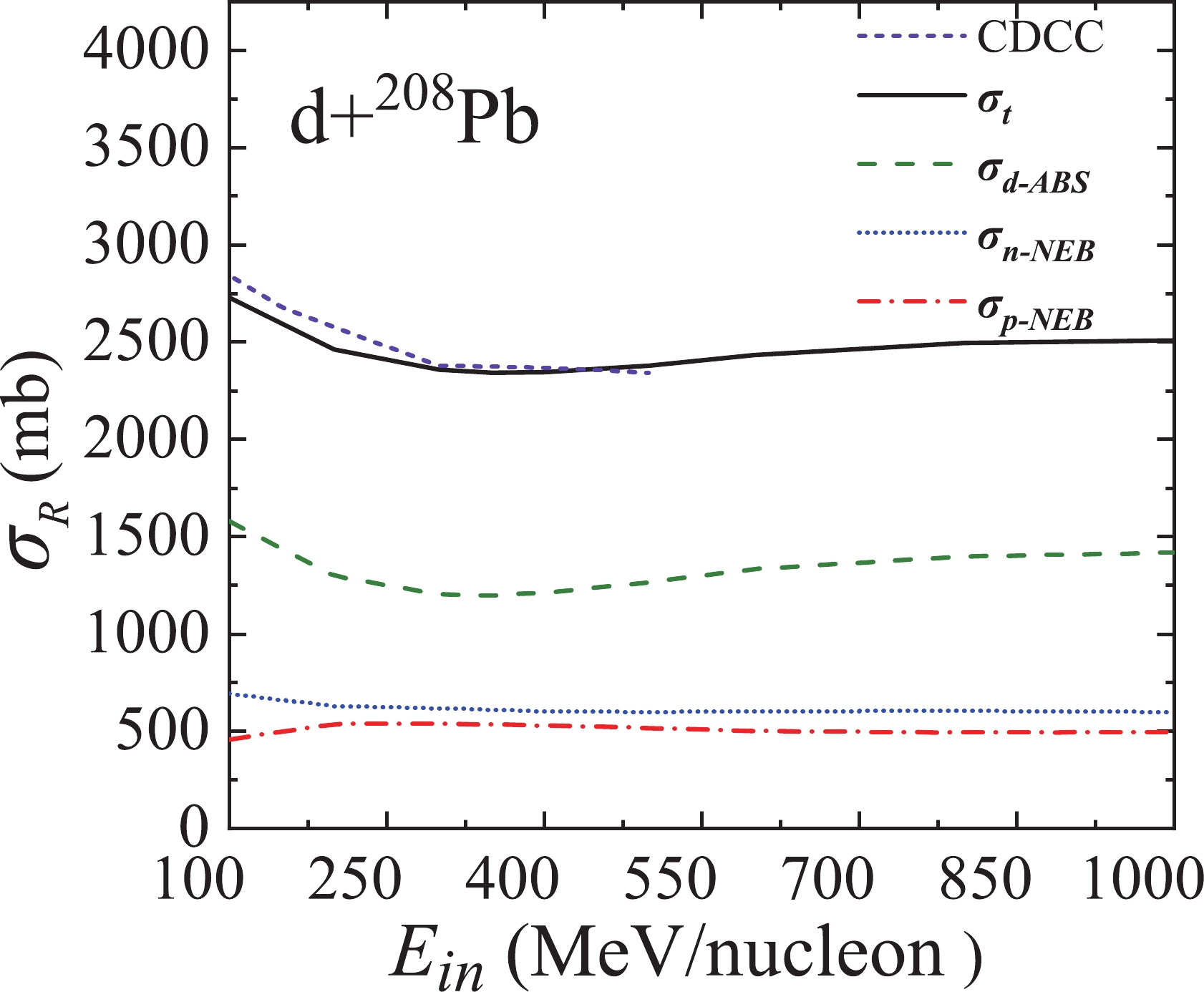Figure9. (color online) Calculated total reaction cross section and its components by using in-medium cross section for d + $ ^{208}$Pb reaction. The solid curve represents the total reaction cross section. The dashed, dotted, and dash-dotted curves represent the components from the absorption of deuteron, neutron, and proton, respectively. The short-dashed curve represents the total reaction cross section calculated by CDCC, which is taken from Ref. [44].

Figure 10 depicts the same as Fig. 9 but for the d + $ ^{137} $Cs reaction at 100-1000 MeV/nucleon. Compared with d + $ ^{208} $Pb reaction, the total reaction cross section of the d + $ ^{137} $Cs reaction is significantly reduced because $ ^{137} $Cs is smaller than $ ^{208} $Pb. However, it is worth noting that the contribution of the total reaction cross section reduction mainly comes from $ \sigma_{d-ABS} $, and $ \sigma_{n-NEB} $ and $ \sigma_{p-NEB} $ have not changed significantly. As the nucleus becomes lighter, the contribution of deuteron absorption decreases significantly, and the contributions of neutron and proton absorption will increase relatively.
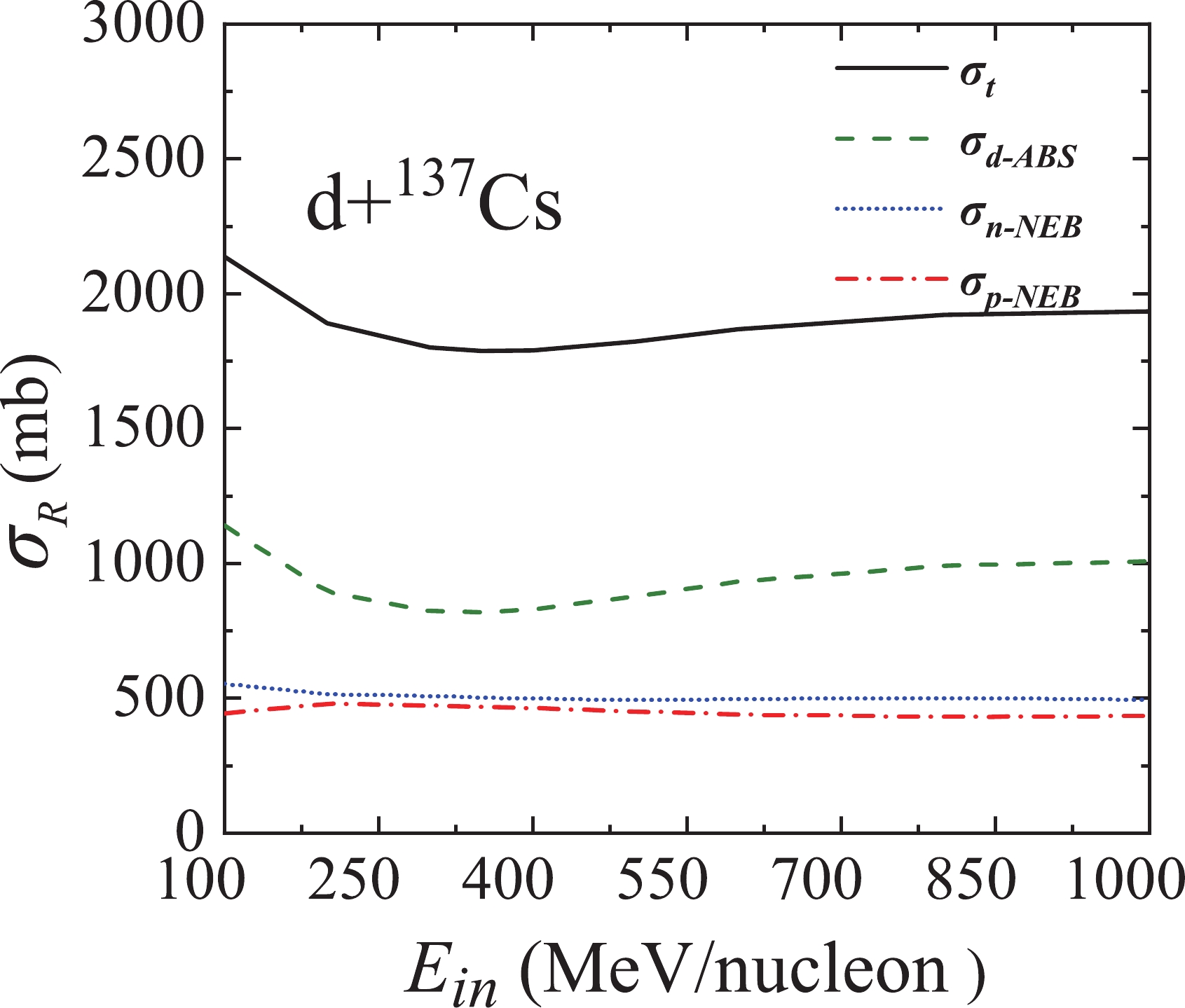Figure10. (color online) Same as Fig. 9 but for the d + $ ^{137}$Cs reaction at 100-1000 MeV/nucleon.

To verify this trend, the proportional contributions of $ \sigma_{d-ABS} $, $ \sigma_{n-NEB} $, and $ \sigma_{p-NEB} $ in different deuteron-induced reactions at 500 MeV/nucleon were calculated. The results are presented in Fig. 11. Note that the proportional contributions of $ \sigma_{n-NEB} $ and $ \sigma_{p-NEB} $ are positively correlated with the mass number of the target nucleus. Concerning $ \sigma_{d-ABS} $, the opposite is true. This means that for heavy nucleus reactions, deuteron absorption will dominate, while for light nucleus reactions, the components of nucleon absorption will make the most significant contribution.
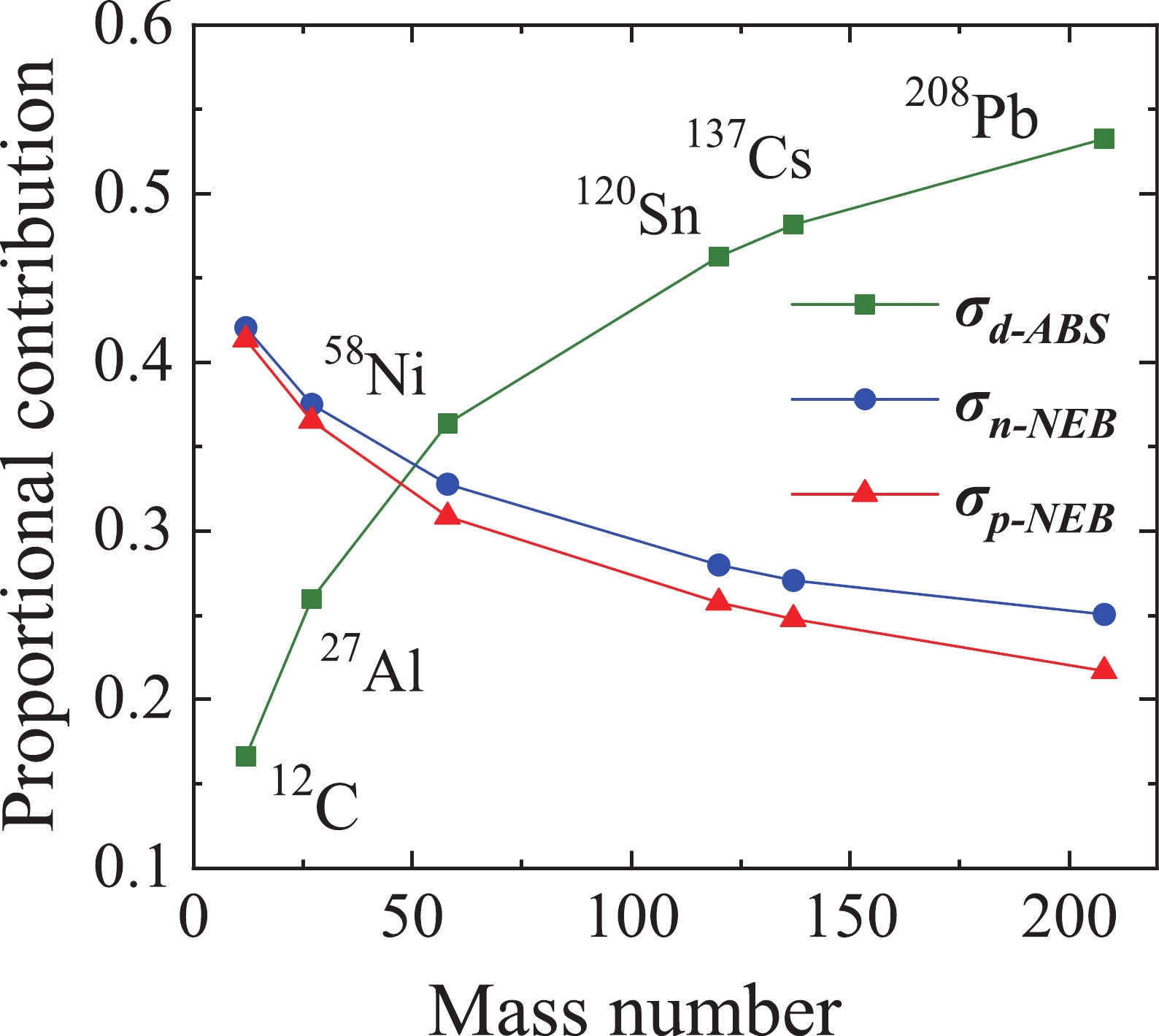Figure11. (color online) Proportional contributions of $ \sigma_{d-ABS} $, $ \sigma_{n-NEB} $, and $ \sigma_{p-NEB} $ in different deuteron-induced reactions at 500 MeV/nucleon. The horizontal axis represents the mass number of the target nucleus.

After obtaining the results of the proportional contribution of the three components, these data can be applied to the transmutation study of $ ^{137} $Cs. The proportion of the three components can help to understand the real reaction occurring in the deuteron reaction. Thus, it may help to predict the isotope production and discuss the transmutation efficiency. As mentioned in Ref. [24], stripped protons and neutrons may cause further transmutation. Knowing the data of stripped protons and neutrons can help to study the effects of further transmutation caused by them.
Figure 12 presents the relation between the proportion of $ \sigma_{n-NEB} $ to $ \sigma_{p-NEB} $ for d + $ ^{208} $Pb reactions and $ \gamma_{i} $ of symmetry energy in the nuclear potential. The last term of the nuclear potential in Eq. (3) is positive for neutrons and negative for protons. Thus, when $ \gamma_{i} $ is larger, the nuclear force provided to the neutron is greater, and the neutron is more likely to be attracted to the high-density regions and produce a reaction. By contrast, protons are more difficult to be attracted to high-density regions. Therefore, note that the proportion is positively correlated with $ \gamma_{i} $ in Fig. 12. In principle, the monotonicity of this proportion can be used in experimental studies to limit the value of $ \gamma_{i} $. However, this difference is not large enough, and the data error in actual experimental measurements may be even larger than this difference. Therefore, future studies could focus on searching for a more sensitive observation.
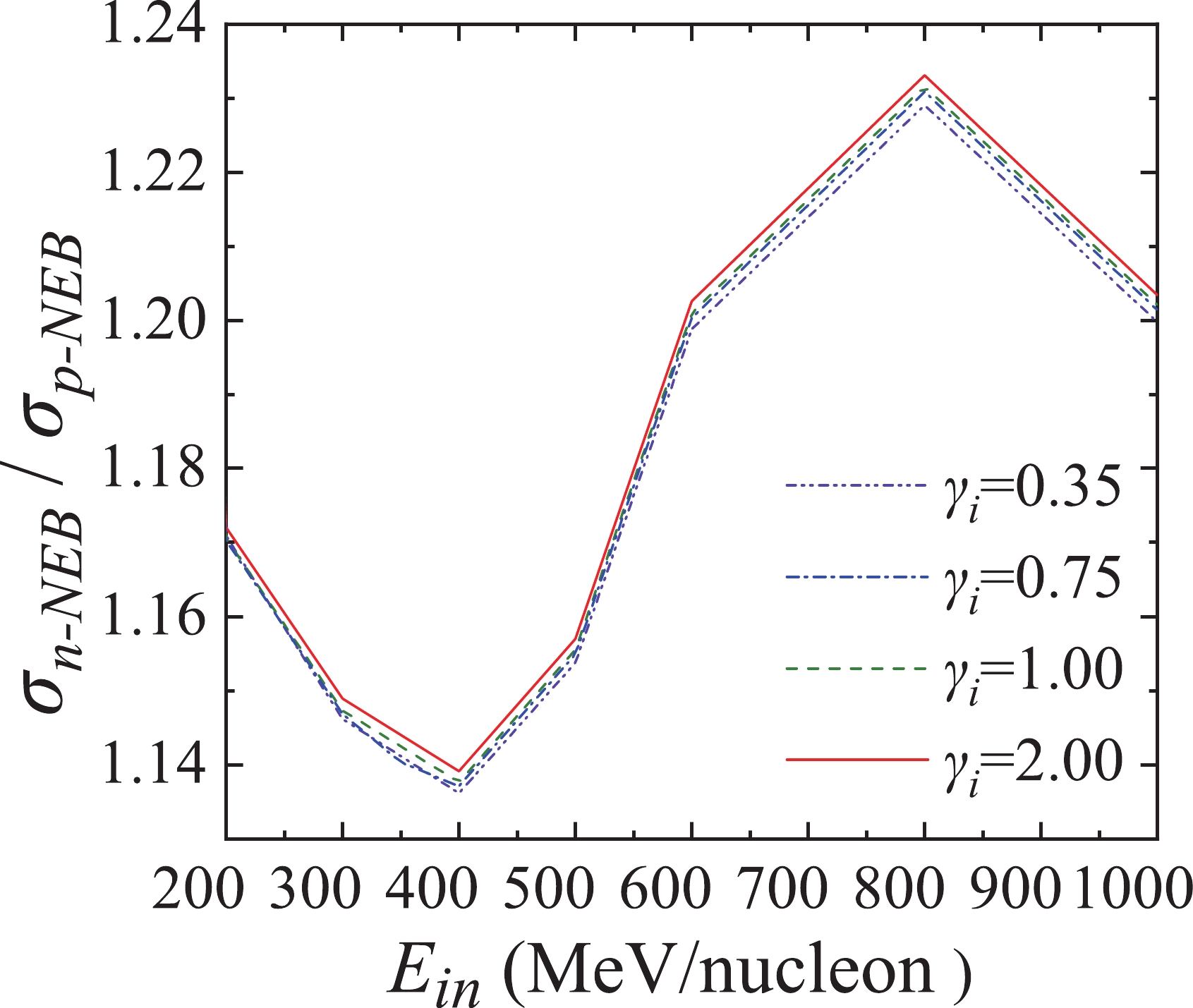Figure12. (color online) Proportion of $ \sigma_{n-NEB} $ to $ \sigma_{p-NEB} $ for d + $ ^{208} $Pb reactions with different incident deuteron energies. The solid, dashed, dash-dotted, and dash-dot-dotted curves represent the results when $ \gamma_{i} $ is equal to 0.35, 0.75, 1.00, and 2.00, respectively.

In summary, a nucleon-nucleus dynamics model was developed in which the trajectory of incident nucleons is described by classical mechanics, and the probability of reaction between nucleon and nucleus is calculated by the exponential damping. Through this nucleon-nucleus dynamics model, the total reaction cross sections of proton-, neutron-, and deuteron-induced reactions at the energy range from 100 to 1000 MeV were calculated. It is shown that the calculations of the total reaction cross sections of the proton- and neutron-induced reactions are generally in good agreement with the experimental data. The calculated total reaction cross sections of the deuteron-induced reactions by the proposed model and CDCC model agree with each other.
Then, the model was applied to investigate the nucleon stripping in deuteron-induced reactions. It was found that nucleon stripping processes play a significant role in deuteron-induced reactions at hundreds of MeV/nucleon, especially for light nucleus reactions. For the reactions at 500 MeV/nucleon, the contributions of the nucleon-stripping cross sections to the total reaction cross sections decreased from 83% for $ ^{12} $C target to 48% for $ ^{208} $Pb. When studying LLFPs transmutation, these data may help predict the isotope production and discuss the transmutation efficiency. Moreover, the ratio between the neutron-stripping and proton-stripping cross sections displays the symmetry energy dependence. Compared to the soft symmetry energy, the stiff symmetry energy provides a larger ratio. This effect may be applied to investigate the symmetry energy.