删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

中国人口省际流动重力模型的参数标定与误差估算

本站小编 Free考研考试/2021-12-29

赵梓渝¹^,, 魏冶²^,, 杨冉², 王士君², 朱宇³

1. 宁波大学公共管理系,宁波 315211

2. 东北师范大学地理科学学院,长春 130024

3. 福建师范大学地理研究所,福州 350007

Gravity model coefficient calibration and error estimation: Based on Chinese interprovincial population flow

ZHAOZiyu¹^,, WEIYe²^,, YANGRan², WANGShijun², ZHUYu³

1. Department of Public Administration, Ningbo University, Ningbo 315211, Zhejiang, China

2. School of Geographical Sciences, Northeast Normal University, Changchun 130024, China

3. Institute of Geography, Fujian Normal University, Fuzhou 350007, China

通讯作者:通讯作者:魏冶(1983-), 男, 吉林梨树人, 副教授, 博士, 主要从事城市与区域规划及GIS应用研究。E-mail: weiy742@nenu.edu.cn
收稿日期:2017-07-12
修回日期:2018-12-24
网络出版日期:2019-02-25
版权声明:2019《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家自然科学基金项目(41401172, 41630749)

作者简介:
-->作者简介：赵梓渝(1986-), 男, 吉林长春人, 博士, 主要从事城市网络及人口流动研究。E-mail: 171462539@qq.com

展开

摘要
空间交互模型被广泛应用于地理要素关系强度的模拟,然而目前大量研究或建立在模型参数标定理想化、模式化的假设条件下,或是在暗箱中完成,由此导致模拟结果与实际的偏差却被严重低估。基于2015年中国春运期间人口省际流动的城市间O-D数据,在逐日、分市的研究精度下,实证推算人口流动重力模型变量的回归系数,探究模型代理变量影响效应的空间异质性,并评估重力模型在人口流动模拟上的误差。结果显示：① 重力模型参数标定的复杂性体现在交互对象代理变量影响程度的非对称性,和变量回归系数的空间异质性随研究精度加深显著加剧两个方面,因此模型参数标定的模式化将导致估算结果空间差异的趋势收敛;② 2015年春运期间中国人口省际流动距离衰减系数为1.970,在地级行政单元视角下,人口流出地距离衰减系数值域为0.712（驻马店）~7.699（乌鲁木齐）,人口流入地系数值域为0.792（三亚）~8.223（乌鲁木齐）;③ 应用重力模型模拟人口流动结果与实测流（百度迁徙数据）存在显著误差。就加权绝对平均误差而言,拟合总误差为85.54%,其中空间相互作用效应造成了86.09%的实测流与模拟流的最大误差,相对流出力、相对吸引力分别造成57.73%、49.34%的模型误差。因此,空间交互效应仍然是当前最难以模式化的因素。

关键词：重力模型;回归系数;距离衰减系数;误差估算;人口流动;中国
Abstract
Simulations based on spatial interaction models have been widely applied to understand the strength of relationships between geographical elements, but many issues remain unclear and deviations between actual and simulated results have often been seriously underestimated. A high-precision Baidu migration process combined with mass relationships is applied in this study and enables the generation of regression coefficients of gravity model based on programmed large-scale regression simulations. A series of accuracy assessments are then developed for 2015 empirical projection daily regression coefficients that can be applied to Chinese spring interprovincial mobile gravity model variables as well as spatiotemporal research that utilizes regression coefficients within a heterogeneity research model. This approach also enables the error within the gravity model to be assessed in terms of floating population simulations. The results of this analysis lead to a number of clear conclusions, including the fact that parameter calibration complexity for the Chinese population mobility gravity model is reflected in the degree of influence asymmetry within spatial object interaction variables, and that the spatial heterogeneity of the variable regression coefficient increases in two distinct fashions. The first of these increases has to do with the overall influence of specific variables, including the fact that differences between proxies tend to be higher than inflow-outflow characteristics. In contrast, the second set of increases is related to economic levels, industrial scales, the proportion of the tertiary industry, and public service facilities. In this latter case, two-way population flow exerts a more profound influence on results and thus the scope of possible explanations for phenomena is more extensive. The regression coefficient for the existence of positive and negative proxy variables therefore relates to differences in spatial heterogeneity, including at the city level, and also assumes that floating population gravity model regression coefficients ignore spatiotemporal changes in the heterogeneity coefficient. This leads to spatial differences in estimated results and thus convergence trends, but further enables the identification of anisotropic interactions in extension space. The second main conclusion of this research is that the national scale population flow distance attenuation coefficient was 1.970 during the spring of 2015, while at the level of prefectural administrative units and given population outflow, the range encapsulated by this coefficient fell between 0.712 (Zhumadian) and 7.699 (Urumqi). Data also reveal a population inflow coefficient of 0.792 for this year that ranged as high as 8.223 in both Sanya and Urumqi. Population flow simulation results using the gravity model and including Baidu migration measured flow data were also subject to significant error. Third, the results of this analysis reveal a total fitting error of 85.54% in weighted absolute mean; the spatial interaction effect within this is responsible for a maximum error of 86.09% in actual and simulated flows, while relative outflow force and attractiveness encompass 57.73% and 49.34% of model error, respectively. These results show that the spatial interaction effect remains most difficult to model in terms of current factors.

Keywords：gravity model;regression coefficient;distance attenuation coefficient;error estimation;population flow;China

-->0
PDF (4607KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
赵梓渝, 魏冶, 杨冉, 王士君, 朱宇. 中国人口省际流动重力模型的参数标定与误差估算[J]. 地理学报, 2019, 74(2): 203-221 https://doi.org/10.11821/dlxb201902001
ZHAO Ziyu, WEI Ye, YANG Ran, WANG Shijun, ZHU Yu. Gravity model coefficient calibration and error estimation: Based on Chinese interprovincial population flow[J]. Acta Geographica Sinica, 2019, 74(2): 203-221 https://doi.org/10.11821/dlxb201902001

1 引言

空间相互作用是城市地理学的基础理论,在形式上表现为一种交换、联系和互动,具有随距离延伸而不断衰减的特征^[1]。重力模型和Wilson最大熵模型是20世纪70年代以来空间交互研究的两大基础模型^[2]。两个模型主要区别在于距离衰减函数这一模型内核的改进,Wilson模型使用的负指数函数随着距离的增加,衰减速度比重力模型的负幂律函数快得多,因此在空间上的作用域有限,长程交互模拟偏少^[3]。重力模型的幂函数具有无标度（scale-free）特征,暗示空间作用距离没有特征长度,从而使构造的空间过程模型与地理学第一定律没有矛盾^[4]。
重力模型的参数是特定地理系统总体特征的重要表征,也是模拟应用的前提和影响模型适宜性的关键因素。然而到目前为止,重力模型无论在理论研究还是实证应用中仍主要着眼于质量解释变量的种类扩展与类型细化,大量引入被认为影响空间交互关系的虚拟变量被视为增强模型解释力、提高拟合优度和研究有效性的重要手段,而不断被扩充变量的回归系数的标定却被严重忽视。不同的研究对象、时空背景、模型设定对应着不同的参数标定,但当前大部分研究或直接引用既有结论,或忽略代理变量回归系数的标定^[5,6,7],直接导致相关研究难以对模型代理变量的作用效应做出科学的预期与判断。
其次,距离衰减系数是对空间交互强度在地理距离上衰减速度的度量。不仅西方大量****忽视研究的时空背景差异使用相同的距离衰减系数^[8],国内****重力模型应用大都引用刘继生等在2000年基于城市系统分形性质提出的“2值”结论^[9],包括人口迁徙^[5]、金融体系^[6]、创新产出^[7]、城镇体系^[10,11]等各类型的研究对象。部分引力场模型应用将距离衰减系数赋值为1^[12,13,14],也有****认为该系数表征城市交互作用范围的尺度差异,其取值为1和2时可分别近似代表国家与地区尺度下城镇体系的辐射范围和影响距离^[15,16]。然而,距离衰减系数反映了交互过程中研究对象所要面对的多重空间约束^[17],其既受到模拟交互流类型的影响,如王成金实证推算指出中国城际公路、铁路、航空客流重力模型距离衰减系数分别为0.649、0.892和1.726^[18];也受到研究区域时空背景的影响。理论上信息化、交通革命背景下,空间交互将呈现出明显的时空压缩效应,因此距离衰减系数也将逐年下降^[19]。而在实证检验中,20世纪90年代以来中国铁路客流、物流的距离衰减系数却呈现出不断增长的趋势^[18]。这表明近年来在中国城镇发展的空间极化和高速交通网络所带来的时空压缩的双重效应影响下,一个“2值”远不足以解释地理要素交互过程中所面临的空间衰减效应;另一方面距离衰减系数也与地图类型^[20]、空间距离标定类型的选取有关。
再次,从城镇体系到城市网络,重力模型是长期以来中国区域空间交互模拟的重要手段^{[15, 21]},然而针对模拟结果的误差却被研究者避而不谈,最终导致至今仍无法定论空间效应是否能够通过模型量化^[22]。合理预期和控制估算模型的误差是保证科学严密性的基础。具体而言,通过重力模型进行空间交互强度模拟的误差到底有多大?误差产生的原因在于模型的自身缺陷,如尽管空间衰减现象已有理论假设曲线,但尚未有实证案例说明其适宜的数学模型^[23];还是由于模型构建过程中变量选取的片面性、回归系数的标定缺乏特定时空背景下的针对性,导致解释力不足;抑或由于空间效应未能准确模拟而造成。如果对于这一系列因素导致的后果无法进行预期和给出一个合理范围的推测,那么,增加或改变代理变量的常用手段无非是在主观臆测下徒增研究结论的复杂程度。
完善指标体系的构建、对模型参数的标定进行精确论证,是空间模拟过程严密性的前提及估算结果科学性的关键^[24]。自然要素和社会经济要素的分布存在非均衡性,客流和物流是具有空间衰减规律的实体流,是城市空间交互关系的重要表征^[17]。户籍制度改革通过破除居民特殊身份状态和降低落户门槛,打破了原有的城乡户籍壁垒和行政干预资源配置机制^[25],2013年中国流动人口达2.4亿,已经成为全球人口流动最为活跃的地区之一^[26]。转型期中国社会结构、文化背景和特殊的发展时期形成了春运这一带有显著时空规律性、高度行为集体性的社会现象^[27]。本文基于2015年中国春运期间301个地级及以上行政区划间人口省际流动数据,在春运期间全国、分市、逐日分市三个递进时空视角下实证估算人口流动重力模型代理变量的回归系数,探究回归系数的空间异质性,并评估重力模型在人口流动模拟上的误差,旨在指出重力模型参数标定的复杂性、以及模拟结果存在误差的现实情况。

2 数据来源与研究方法

2.1 数据来源

研究数据来源于百度地图迁徙。百度迁徙是基于定位服务（Location based service, LBS）技术,通过手机定位信息映射用户行为轨迹,塑造出人口流动过程中产生的起止城市、路径流强度,在数据精度上达到了个人层级,同时能够摒弃公路、铁路、航空等单一运输模式造成的数据片面性,为地理时空研究提供了实测流数据支撑^{[26,27,28,29]}。研究对象为中国大陆4个直辖市及297个地级行政区,共301个空间对象。2015年中国春运官方定义周期为2月4日-3月16日,由于数据获取原因,研究时间为2015年2月7日-3月18日（下文春运期间均指这一时段）,共计40 d。百度迁徙提供了一天内人口在各城市间省际流动的方向性与强度,为减少小概率事件对回归结果的影响,剔除研究期内总量低于10人次的人口流。处理后春运人口流动网络共包含19317条城市非对称流,承载人口流动强度7988.029万人次,占原始数据总量的97.7%。

2.2 重力模型回归系数的定量估算方法

重力模型公式^[2]为：

G_{ij} = k P_{i}^{α} P_{j}^{γ} d^{- β}

（1）
式中：G_ij是i、j两地的空间交互强度;k是残差;P_i和P_j分别是i地和j地的质量解释变量;α和γ是对应变量回归系数;d为空间距离,通常可以采用不同方式标定,如绝对地理距离、时间成本等;β为距离衰减系数。
将（1）式两边取自然对数构建多元线性回归方程：

\ln G_{ij} = \ln k + α \ln P_{i} + γ \ln P_{j} - β \ln d_{ij}

（2）
若

P_{in}^{α_{n}}

为城市i第n个质量解释变量,α_n为对应系数,则有：

P_{i}^{α} = P_{i 1}^{α_{1}} \times P_{i 2}^{α_{2}} \times P_{i 3}^{α_{3}} \times \dots \times P_{in}^{α_{n}}

（3）

P_{jn}^{γ_{n}}

同理,将复合质量代回公式（2）,则有中国人口省际流动重力模型估算公式：

\ln G_{ij} = \ln k + \overset{n}{\sum_{n = 1}} α_{n} \ln P_{in} + \overset{n}{\sum_{n = 1}} γ_{n} \ln P_{jn} - β \ln d_{ij}

（4）
在估算特定城市i重力模型时,其自身质量对回归结果没有贡献,原理等同于潜力模型,因此方程中α_nlnP_in是常数项,设：

c o_{n} = \overset{n}{\sum_{n = 1}} α_{n} \ln P_{in}

（5）
则估算城市i回归系数时：

\ln G_{ij} = \ln k + c o_{n} + \overset{n}{\sum_{n = 1}} γ_{n} \ln P_{jn} - β \ln d_{ij}

（6）
在3个研究时空尺度中,仅逐日、分市研究精度下回归模型数量已达24080个（40 d×301个人口流出地+40 d×301个人口流入地）,因此回归通过C#编程实现。

2.3 变量选择及其含义

国内****普遍认为,中国人口迁移流动的空间格局及其演变特征与区域之间、城乡之间社会经济发展水平（尤其是收入水平和就业机会）的差异、迁出地与迁入地间的距离和历史联系、迁入地的投资水平和环境、内陆与沿海地区不断变化的区位优势、迁出与迁入地的自然条件和文化特征等因素密切相关^[30,31,32]。本文通过4类10个代理变量考察研究对象对人口流动的影响机制（表1）。
Tab. 1
表1
表1人口省际流动回归解释变量描述与预期效应
Tab. 1Descriptions and expected effects of explanatory variables

变量名称	变量描述	变量预期效应
变量名称	变量描述	流出地i	流入地j
d	人口流关联城市直线距离(km)	-	-
dens_pop	人口密度(人/km²)	-	+
unemplo	城镇登记失业人员数(人)	+	-
wages	职工平均工资(元)	-	+
green	建成区绿化覆盖率(%)	-	+
SO₂	工业二氧化硫排放量(t)	-	-
books	每百人公共图书馆藏书(册.件)	+	+
GDP	地区生产总值(当年价格)(万元)	+	+
tertiary industry	第三产业占GDP比例(%)	+	+
hospital	医院卫生院数(个)	+	+

新窗口打开
第1类就业与收入水平指标：城镇登记失业人员数、职工平均工资用以解释流动个体就业机会与劳动报酬的满足程度。人口流入地的选择整体上是一个市场行为^[33],对于流动人口而言,谋取收入更高的非农就业机会是他们离乡背井的首要原因。因此,更多的就业机会和更高的收入水平是吸引外来人口集聚和防止本地区劳动力外流的重要因素。
第2类社会经济发展指标：地区生产总值、人口密度、工业二氧化硫排放量、第三产业占GDP比例用以衡量当前中国区域发展的显著不平衡及其对于人口流迁倾向所产生的影响。地区生产总值为流动主体提供了一种综合的预期效应,尽管不能直接体现,但却构成了隐性的非现金收入和成本价值^[34];人口密度考察了资源要素的空间集聚程度;标准化生产的成熟制造业从大城市中获得的集聚效益较小,却要支付高地租和高工资,于是倾向于成本较低的中小城市扩散,因此工业二氧化硫排放量考量了二产规模对于不同等级城市人口流动差异的影响;三产占比解释了流动人口对于就业类型需求的差异。
第3类公共服务、市政设施代理变量：建成区绿化覆盖率、每百人公共图书馆藏书、医院卫生院数是城市宜居性的重要表现。1980年以后新经济迁移理论强调家庭作为人口迁移决策主体的重要性,社会公共资源衡量了城市对于流动人口的接纳与安置能力,尤其是对于家庭迁居、代际流动的家庭策略影响尤为显著^[35]。
第4类变量为空间距离,即人口流关联城市的直线距离。数据来源于2015年《中国城市统计年鉴》。模型因变量为关联城市之间的有向非对称人口流强度。

2.4 误差估算方法

一个人口流动的交互系统中,实测与估算的区域人口流矩阵可以通过4项因素进行描述：整体效应、特定区域的相对流出力和相对吸引力、两个区域间的空间相互作用^[36]。因此,人口流动的实测矩阵与模拟矩阵可以被分解成以上4个因素,并用以评价其在交互模型中的不同运行作用,及考察模型模拟误差的产生是由于模型质量参数标定的不足还是由于空间交互的数学模型不足^[37],流动强度估算公式为：

G_{ij} = K P_{i} Q_{j} F_{ij}

（7）
式中：G_ij为城市i到城市j的人口流强度;K表示整体影响,等价于所有流动流强度的几何平均数;P_i为城市i的相对流出力,等价于城市i所有流出流的几何平均数与K的比值;Q_i为城市j的相对吸引力,等价于城市j所有流入流的几何平均数与K的比值;F_ij是关联城市的空间相互作用效应。

K = \sqrt[n]{\overset{n}{\prod_{i = 1, j = 1}} G_{ij}}

（8）

F_{ij} = K P_{i} Q_{j} / G_{ij}

（9）
观察流动流和模拟流动流可分别表示为：

G_{1 ij} = K_{1} P_{1 i} Q_{1 j} F_{1 ij}

（10）

G_{2 ij} = K_{2} P_{2 i} Q_{2 j} F_{2 ij}

（11）
由此,模拟流动G₂_ij计算公式为：

G_{2 ij} = \frac{K_{2}}{K_{1}} \frac{P_{2 i}}{P_{1 i}} \frac{Q_{2 j}}{Q_{1 j}} \frac{F_{2 ij}}{F_{1 ij}} G_{1 ij}

（12）
进一步,模拟区域流动模型的总误差可以被表示为：

G_{2 ij} - G_{1 ij} = (\frac{K_{2}}{K_{1}} \frac{P_{2 i}}{P_{1 i}} \frac{Q_{2 j}}{Q_{1 j}} \frac{F_{2 ij}}{F_{1 ij}} - 1) G_{1 ij}

（13）
由整体效应K、相对流出力P_i、相对吸引力Q_j和F_ij在两种流动流中的不同而造成的误差分别定义为E_kij、E_pij、E_qij、E_fij。在独立计算这4个误差时,将被计算误差之外的因素视为相等的处理方式,如计算E_kij时,假定前一个公式中的P₂_i=P₁_i、Q₂_j=Q₁_j、F₂_ij=F₁_ij,则：

E_{kij} = (\frac{K_{2}}{K_{1}} \frac{P_{2 i}}{P_{1 i}} \frac{Q_{2 j}}{Q_{1 j}} \frac{F_{2 ij}}{F_{1 ij}} - 1) G_{1 ij} = (\frac{K_{2}}{K_{1}} - 1) G_{1 ij}

（14）
同样的：

E_{pij} = (\frac{P_{2 i}}{P_{1 i}} - 1) G_{1 ij}

（15）

E_{qij} = (\frac{Q_{2 j}}{Q_{1 j}} - 1) G_{1 ij}

（16）

E_{fij} = (\frac{F_{2 ij}}{F_{1 ij}} - 1) G_{1 ij}

（17）
上述4个误差存在着彼此互相作用导致的复合误差,故将复合误差定义为E_oij：

E_{oij} = G_{2 ij} - G_{1 ij} - E_{kij} - E_{pij} - E_{qij} - E_{fij}

（18）
则总误差M_gij表示为：

M_{gij} = G_{2 ij} - G_{1 ij} = E_{kij} + E_{pij} + E_{qij} + E_{fij} + E_{oij}

（19）

3 全国人口省际流动重力模型回归结果

2015年春运期间中国人口省际流动重力模型回归方程全局调整R²和F值分别为0.422、743.704。从模型拟合优度、显著性（F检验）、变量回归系数预期与理论的相符性及其显著性（t检验）来看（表2）,本文选取的指标体系能够良好反应出研究期内人口双向流动的空间效应。
Tab. 2
表2
表22015年春运中国人口省际流动影响因素回归结果
Tab. 2Regression result of influencing factors of interprovincial population flow during the Spring Festival travel rush of China in 2015

迁出地变量	作为流出地变量(i)			作为流入地变量(j)
迁出地变量	非标准化系数	标准化系数	t	非标准化系数	标准化系数	t
dens_pop	0.017	0.005	0.748	-0.111^*	-0.038	-5.145
unemplo	0.132^*	0.049	5.222	-0.157^*	-0.061	-6.117
wages	-0.456^*	-0.042	-4.152	0.789^*	0.072	7.045
green	-0.41^*	-0.041	-6.845	-0.583^*	-0.054	-9.211
SO₂	-0.337^*	-0.164	-23.459	-0.236^*	-0.123	-17.033
books	0.061^*	0.026	2.543	0.337^*	0.142	14.120
GDP	0.546^*	0.225	15.754	1.087^*	0.452	31.439
tertiary industry	0.829^*	0.082	10.529	1.848^*	0.181	22.776
hospital	0.549^*	0.153	20.010	0.036	0.010	1.243
k	-17.345^*		-12.346
d	1.970^*	0.530	85.651

注：^*表示在1%的显著性水平上显著。

新窗口打开
地区生产总值（GDP）、第三产业占GDP比例（tertiary industry）、每百人公共图书馆藏书（books）与人口双向流动均呈正相关,符合预期效应。这意味着,无论观察对象作为人口流出地还是流入地,以上变量的增加均将同时增加其对应的人口流强度。由于对数变换后重力模型采用普通最小二乘法估计,因此各变量的系数可看作弹性系数,即在其他条件不变的情况下,解释变量每增加（或减小）1%,因变量发生相应大小的变化。平均地,若以上3个变量分别单一增加1%,则作为流出地,人口外迁强度将分别增加0.556%、0.817%和0.054%;作为流入地,人口集聚强度将分别增加0.984%、1.789%和0.345%。
工业二氧化硫排放量（SO₂）、建成区绿化覆盖率（green）与人口双向流动均呈负相关,即二产规模的扩大和绿化环境的改善将同时制约地区人口外迁和流入强度,其中绿化覆盖率作为流入地变量（j-green）时不符合预期效应。一方面二氧化硫排放量降低了城市人居环境,因此外来人口的集聚强度受到了这一变量的制约;另一方面人口背井离乡所支付的综合成本显然较人居环境的下降更高,因此二产规模的扩大满足了当地劳动力的工作需求,减少了本地区的人口流失。平均地,若以上两变量分别单一增加1%,则地区人口流出强度将分别减少0.336%、0.399%,而流入强度将分别减少0.244%、0.567%。
流出地工资水平（wage）的下降及失业人口规模（unemplo）的扩大将对本地区人口外迁形成推力效应,而流入地工资水平的提升和失业规模的下降将对人口集聚产生拉力效应,符合谋取更高的收入与就业机会是流动人口离乡背井的首要原因的预期效应^[33]。人口密度作为流出地变量（i-dens_pop）和医院数量作为流入地变量（j-hospital）时未通过至少10%的显著性水平检验,表明两个指标对于对应人口流动的影响不显著。
2015年中国春运期间人口省际流动距离衰减系数（β）为1.970,平均若两地之间距离增加1%,则人口流强度将下降1.941%。这一估算结果与蒲英霞等^[31]基于六普数据以省为研究精度的估算结果1.137、郑清菁等^[38]基于2010年中国城际铁路客运流的估算结果1.315有一定出入,与王成金^[18]的航空客流1.726的结果更为相近。若以本文数据、结论为标准,标定距离衰减系数为“2值”将在全国尺度上造成17.75%算数平均数的人口流模拟强度的下降。
新古典经济学认为人口迁徙是在迁出地和迁入地之间的工资水平、就业机会等方面区域差异的响应。结合标准化系数,首先,空间距离较其他代理变量的作用强度更为深刻,因此空间阻尼仍是当前中国人口省际流动过程中最显著的制约因素^[31]。其次,在城镇质量代理变量中,以地区生产总值（GDP）、工业二氧化硫排放量（SO₂）为代表的经济水平对人口省际双向流动产生了最为显著的影响作用。最后,代理变量在流出、流入地之间的作用强度存在不对称性,无论从整体作用还是特定变量,均呈现流入地影响强度高于流出地的特征（单一变量除了SO₂）。不对称性中的一个重要原因源于流动主体的主观选择性。较流出地,流入地的信息相对不完全状况增加了人口流迁的不确定性和风险。因此,只有在流入地具有充足的拉力时,才能驱动流动人口背井离乡以谋求更高的工作机会与收入水平。
2015年春运期间中国人口流动的逐日距离衰减系数值域为1.192（3月5日）~1.877（2月21日）。当年国家法定假日时间为2月18日-24日,初一、正月十五分别为2月19日和3月5日,而距离衰减系数的波动性与节假日时间完全吻合（图1）。从2月9日起返乡流高峰到来,系数大体呈增长趋势,在2月19日初一和2月21日初三出现两次陡增。2月25日迎来节后第一个工作日,当日距离衰减系数较24日显著下降。至此,春节返乡、返工流高峰结束,距离衰减系数也开始整体下降,至3月5日正月十五到达春运期间最低值。在元宵节后第二轮返工返校流高峰到来,距离衰减系数再次增加,随后呈平稳下降趋势。

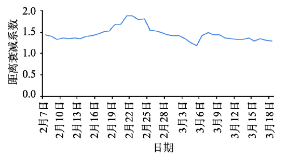显示原图|下载原图ZIP|生成PPT
图12015年春运期间中国人口省际流动距离衰减系数分日曲线
-->Fig. 1Diurnal curve of distance decay coefficient
-->

4 地级行政单元下回归拟合优度及变量回归系数的空间异质性

4.1 回归模型的拟合优度

首先对计算过程及结果做出说明：当测度城市作为人口流入地j时,其拉力效应恒定,因此自身变量可视为常量,而对应关联的流出地i的质量为变量,故回归结果本质上是探讨流出地i变量对于人口流动的推力效应。作为人口流出地,阿克苏、阿勒泰、和田等7个城市调整R²小于0.1,张家界、中山等30个城市介于0.1~0.4之间,锦州、汕头、延安等43个城市为0.5,成都、重庆、兰州等111个城市为0.6,深圳、拉萨、西安、郑州、长春、乌鲁木齐、广州等85个城市为0.7,北京、上海、天津等25个城市高达0.8。作为人口流入地,阿勒泰、和田、鹤岗等7个城市调整R²小于0.1,佳木斯、汕头等54个城市R²介于0.1~0.4之间,大连、乌鲁木齐、兰州等69个城市为0.5,拉萨、海口、银川等91个城市为0.6,西安、长春、沈阳、郑州、北京、天津、长沙等71个城市为0.7,上海、深圳、南京、武汉、广州等9个城市达到0.8。整体而言,绝大部分城市模型拟合优度、显著性检验结果优异。拟合优度较差城市普遍位于沿疆地区,此区域人口流动强度小,交互关系难以通过指标变量解释。同时,由于人口的流入或流出并不完全取决于流入地或流出地的属性,而是权衡各类因素之后的结果^[5],因此,研究对象的质量属性、关联人口流权重与其模型回归优度之间并不存在绝对的正相关。即便在拟合优度较高阈值内、一些等级高、人口流动强度大的城市之间,调整R²也存在明显的差异。

4.2 回归系数的空间异质性

剔除调整R²小于0.1的城市以提高研究的科学性。从图2来看,大量代理变量回归系数未通过10%显著性水平检验,单一变量回归系数通过数均不足城市总样本量的50%。当测度城市作为人口流出地i时,流入地代理变量回归系数显著性检验通过率最高的4项依次为工业二氧化硫排放量、医院数量、生产总值和三产占比;当测度城市作为人口流入地j时,流出地质量变量回归系数通过率最高的4项依次为三产占比、工业二氧化硫排放量、医院数量和工资水平。结合前文结论,经济发展类指标不仅对于中国人口省际双向流动产生了更为深刻的影响,同时其解释力的适用范围也更加广泛。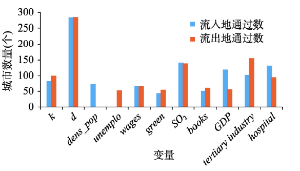

显示原图|下载原图ZIP|生成PPT
图2通过10%显著性检验城市数量统计
-->Fig. 2Test of the city number by 10% significance
-->

地统计学通常利用半变异函数解析地理要素的空间异质性特征^[39,40]。首先对流出地代理变量回归系数显著性检验通过率最高的工业二氧化硫排放量、医院数量和流入地变量三产占比、工业二氧化硫排放量进行K-S（kolmogorov-smirnov）正态分布检验,4项回归系数均服从正态分布要求（P_k-s > 0.05）。在此基础上对其进行半变异函数拟合,4项系数的块金值分别为0.795、0.294、0.571和0.801,块金值均大于0,即系数本身存在由于各种随机因素而引起正基底效应;基台值分别为0.932、0.986、0.900和1.225,综合表明中国春运期间人口省际流动重力模型变量的回归系数存在明显的空间异质性;从块金系数来看,流出地变量工业二氧化硫排放量为0.85,说明研究区域内空间异质性主要由随机因素控制,空间自相关较弱;流入地变量三产占比、工业二氧化硫排放量和流出地变量医院数量的块金系数分别为0.63、0.65、0.30,数值均介于0.25~0.75范围内,即空间异质性由随机部分和空间自相关性共同作用。
空间分层异质性是指层内方差小于层间方差的地理现象^[41,42],地理探测器是探测分层异质性,以及揭示其背后驱动力的统计学方法和有效工具。地理探测器中所包括的分异及因子探测,可以探测变量的空间分异性,用q值度量^[41]。对以上4项变量回归系数依次按照东北、东部、西部和中部的4大地理区划划分,作为分层标准,利用地理探测器探究在此分层方式下代理变量影响效应的空间分层异质性。结果显示,流出地变量工业二氧化硫排放量、医院数量的统计量q值分别为0.821、0.913,流入地变量三产占比、工业二氧化硫排放量的q值分别为0.761和0.700,表明4个代理变量的回归系数均存在显著的空间分层异质性,即就代理变量对于人口省际流动影响效应的差异性而言,地理区之间的差异要显著高于地理区内部差异。
以往研究认为,空间上邻近区域具有更高的属性和作用强度上的相似性^[43],但从图3来看,相似性现象尽管存在,但远不足以对整个空间的特征进行描述。随着研究精度的提高,模型变量选取、回归系数标定、效应预测的复杂性将显著加剧。以直辖市和省会城市为例,作为流出地时,工业二氧化硫排放量的回归系数均为负值,即中国直辖市和省会城市的人口流出强度受到流入地第二产业规模增加、环境恶化的负向影响。医院数量存在不同城市的差异,与福州（0.671^***）、上海（0.436^***）、天津（0.39^**）、昆明（0.36^**）、呼和浩特（0.971^*）、拉萨（1.117^*）的人口流出强度呈正相关,与南宁（-0.816^***）、长沙（-0.522^**）、重庆（-0.422^**）、成都（-0.366^*）呈负相关;作为流入地时,工业二氧化硫排放量的回归系数均为负值,医院数量、地区生产总值、三产占比均为正值,即中国直辖市和省会城市的人口流入强度一方面受到人口流出地的工业规模扩大的限制,另一方面也受到人口流出地经济社会发展水平的正向促进作用。

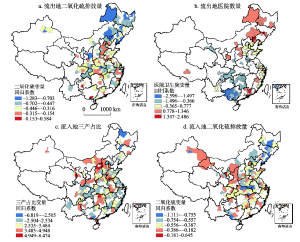显示原图|下载原图ZIP|生成PPT
图32015年春运期间中国人口流动重力模型质量变量回归系数的空间异质性
-->Fig. 3Spatial heterogeneity of quality parameters for population flow gravity model in 2015
-->

从区域角度来看,无论测度城市作为人口流入地还是流出地,工业二氧化硫排放量的回归系数在中国东北,尤以哈大走廊沿线城市为代表普遍呈负值水平,且显著低于全国其他地区,这在一定程度上与东北以工业为主要产业构成的发展现实相吻合。由于本地区工业规模及所提供的相关岗位可以满足当地劳动力谋求第二产业的工作需求,因此关联城市工业发展水平与东北地区人口的流出呈负相关,同时东北地区的人口流入强度也受到了流出地工业规模的制约,综合表明只有提供差异化工作机会才能够形成吸引东北人口的拉力及东北地区对于东北以外人口的拉力效应。流出地变量i-tertiary industry在普遍地区呈正值水平,即人口流出地的三产比例与中国大部分地区尤以中部地区人口流强度存在正相关关系。

5 地级行政单元下人口流动距离衰减系数的时空差异特征

5.1 距离衰减系数的空间异质性

2015年春运期间,作为流出地,中国人口省际流动距离衰减系数值域为0.712（驻马店）~7.699（乌鲁木齐）,在2.0~2.8区间共计152个城市呈现频次峰值（图4）;作为流入地,距离衰减系数值域为0.792（三亚）~8.223（乌鲁木齐）,在2.4~2.8区间共计134个城市呈频次峰值,与以往质量越大距离衰减作用越小^[44]的研究结论并不趋同。平均地,若人口流出、流入地与其关联城市的空间距离增加1%,则相对应的人口流动强度将分别下降0.706%~7.375%和0.785%~7.856%,存在明显的空间差异。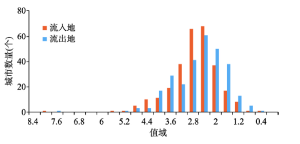

显示原图|下载原图ZIP|生成PPT
图42015年春运期间各市人口省际流动距离衰减系数分布值域
-->Fig. 4Distribution range of parameter β of interprovincial population flow during the Spring Festival travel rush in 2015
-->

对人口流入、流出地的距离衰减系数分别进行半变异函数拟合,其中二者块金系数分别为0.48和0.25,表明中国人口省际外迁时对于目的地的选择具有空间自相关性。在流动人口的迁移决策中,对流入地的选择是整个决策过程的重要组成部分。流动主体对不同地区进行成本、收益分析之后做出基于个体利益的综合考虑,这种整体性的抉择与偏好难以通过地区质量代理变量进行完整的考量,而空间衰减效应成为了观察人口流动空间偏好的重要视角。
基于距离衰减系数的高低差异,一方面存在以山东、河南、浙江为代表的人口流出、流入距离衰减系数双低省份（表3、图5）,和北京、上海、海口、郑州、济南等双低城市。首先,经济势能、信息交通可达性等外部条件是形成地区空间交互关系的重要动力。基于企业间和政治关系的人口流动行为显然受距离影响较小。因此,以北京、上海为代表的国家级政治和经济中心距离衰减系数低,符合距离衰减能够确定和推测中心节点吸引力辐射范围和外推趋势的观点^[18]。其次,地区中心、门户城市和功能上具有不可替代性的城市具有低距离衰减系数的特征,如作为省会和副省级城市的济南,旅游城市海口,交通枢纽郑州,在人口流动的城市空间交互过程中,能够在一定程度上克服地理空间制约的影响。
Tab. 3
表3
表3中国各省(自治区、直辖市)距离衰减系数值域表
Tab. 3Range of attenuation coefficient by province (autonomous region and municipality) in China

	作为人口省际流出地				作为人口省际流入地
省(省会)	省值域	省均值	省会	t值	省值域	省均值	省会	t值
安徽(合肥)	1.186~3.746	2.654	2.206	10.015	2.127~3.956	2.863	2.989	14.356
北京			2.213	16.062			1.959	15.501
福建(福州)	1.214~3.625	2.594	1.767	6.758	1.71~3.383	2.643	2.729	8.997
甘肃(兰州)	1.593~3.981	2.717	3.058	8.599	1.241~4.317	2.774	3.613	9.838
广东(广州)	1.614~4.241	3.165	3.73	16.698	2.6~5.462	3.857	3.927	21.168
广西(南宁)	3.689~5.432	4.268	4.166	14.809	1.668~4.225	3.200	3.536	14.967
贵州(贵阳)	0.994~3.379	2.043	3.379	10.427	2.306~4.24	3.251	4.24	15.387
海南(海口)			1.681	7.38	0.792~2.015	1.403	2.015	10.086
河北(石家庄)	1.931~2.913	2.356	2.534	13.355	2.518~3.153	2.820	2.671	15.252
河南(郑州)	0.712~2.359	1.767	1.936	8.839	1.398~2.978	2.312	2.317	11.658
黑龙江(哈尔滨)	1.846~4.245	3.113	3.037	12.486	2.497~3.387	3.006	3.275	13.643
湖北(武汉)	0.906~2.689	2.120	2.362	9.725	1.836~3.487	2.698	2.851	14.27
湖南(长沙)	2.123~4.302	3.285	3.084	12.384	1.697~4.768	3.375	3.595	16.775
吉林(长春)	2.496~3.65	3.036	2.627	9.902	2.23~3.753	2.874	3.069	12.541
江苏(南京)	1.62~3.048	2.415	2.89	16.333	2.375~3.061	2.761	2.981	18.623
江西(南昌)	1.636~4.939	3.075	2.537	9.727	0.99~4.45	2.508	3.028	14.7
辽宁(沈阳)	1.955~3.629	2.573	2.611	9.882	2.174~3.46	2.704	3.142	13.528
内蒙古(呼和浩特)	2.38~4.811	3.547	2.38	6.698	3.253~4.524	3.915	3.479	12.01
宁夏(银川)	2.302~4.197	3.136	4.197	10.011	2.027~4.733	3.129	4.733	15.044
青海(西宁)	2.126~3.516	2.821	3.516	10.615	2.476~4.409	3.443	4.409	12.26
山东(济南)	1.157~2.87	2.010	1.902	7.249	1.488~2.841	2.214	2.43	12.833
山西(太原)	1.881~2.96	2.542	2	7.809	2.089~3.119	2.708	2.669	10.58
陕西(西安)	1.931~4.141	2.960	4.077	16.265	2.752~4.563	3.452	4.061	16.509
上海			1.913	11.818			2.034	13.617
四川(成都)	1.583~3.717	2.522	3.631	11.278	2.026~4.409	2.992	3.433	12.843
天津			2.724	16.059			2.99	17.619
西藏(拉萨)			3.875	3.439			5.122	5.459
新疆(乌鲁木齐)	2.958~7.699	4.978	7.699	9.73	2.409~8.223	4.504	8.223	8.595
云南(昆明)	2.339~4.164	3.105	3.527	14.856	1.212~3.482	2.631	3.482	14.55
浙江(杭州)	1.554~2.563	1.955	1.995	9.69	1.893~3.379	2.604	2.639	11.624
重庆			3.51	14.261			3.914	18.671

注：省值域涉及城市均至少通过10%显著性水平检验,所有省会城市均通过1%显著性水平检验,海南省城市作为人口流出地时仅有海口一个城市通过10%显著性水平检验,西藏自治区城市作为人口流出和流入地时仅拉萨一个城市通过10%显著性水平检验。

新窗口打开

显示原图|下载原图ZIP|生成PPT
图52015年春运期间中国分市人口流动距离衰减系数空间差异
-->Fig. 5The population flow distance parameter β during the Spring Festival travel rush in 2015
-->

另一方面,也存在以新疆、内蒙古、广东为代表的人口省际流出、流入距离衰减系数双高省份,和乌鲁木齐、拉萨、银川、西宁、贵阳、西安、南宁等双高城市。首先,受到地理可达性、经济发展水平与社会生活习俗等多重因素影响,国家版图边疆地区人口向全国城市流动的平均路径更长,长距离流动的主观意愿较低,对距离更为敏感。其次,珠三角城市群经济发达,劳动密集型产业集聚极大刺激了劳动力需求,继而满足了近域经济相对落后省份劳动力务工的外迁行为,加之华南地区相似社会结构的文化认同感,形成了人口流动空间选择的共性,因此珠三角城群及其外围的广西、湖南、江西多省距离衰减系数普遍呈高值特征。从表3来看,作为人口流入、流出地时,广东省人口流动距离衰减系数均值分列全国第五和第四,而广州市距离衰减系数分列全国第六、七位,与版图边疆的西宁、拉萨相当。

5.2 距离衰减系数在时序上的差异特征

中国春运期间人口省际流动空间衰减效应存在明显的时空差异特征。图6为40 d中至少有20 d距离衰减系数通过10%显著性水平检验的183个城市的逐日距离衰减系数矩阵。可见,距离衰减系数对于中国人口春节前后在东部发达地区与中西部欠发达地区间循环流动的空间过程具有良好的体现,并能够进一步识别各市人口流出和流入的属性特征。整体而言,系数省内相似性、省际差异性显著。中国流动人口主要迁出地：河北省衡水、邢台;山西省忻州、大同、晋中;安徽省亳州、宣城、六安、宿州、蚌埠、安庆、芜湖、滁州;福建省宁德、龙岩、三明、南平;江苏省宿迁、淮安、盐城;江西省萍乡、抚州、吉安、宜春、上饶;山东省枣庄、泰安、济宁、菏泽、潍坊;浙江台州;广西省河池、梧州、贵港、玉林;河南省濮阳、安阳、新乡、商丘;湖北省十堰、咸宁、荆州、黄冈;湖南省益阳、常德、怀化、邵阳、岳阳、永州、衡阳、郴州、株洲;陕西省汉中、榆林、咸阳、渭南、宝鸡;四川省绵阳、广元、达州、宜宾、南充、泸州等城市,在春节前作为流入地,及春节后作为流出地时,距离衰减系数具有较高的显著性检验通过率。反之,则有大量未通过检验。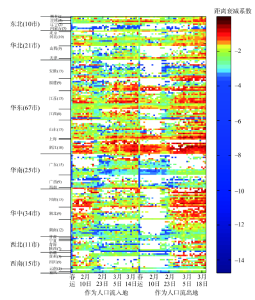

显示原图|下载原图ZIP|生成PPT
图6逐日分市人口流动距离衰减系数矩阵图
-->Fig. 6Matrix of the daily population flow distance parameter β
-->

作为中国流动人口主要迁入地的广东省,例如肇庆、江门、中山、珠海、惠州、佛山,在春节前作为人口流出地和春节后作为流入地时距离衰减系数通过率更高,反之存在大量未通过现象。春运期间广东省人口流动以近域发生为主,随距离的增加强度显著降低。如广东流动人口前三位来源省广西、湖南、江西累积贡献了广东67.6%的迁入规模^[27],三省均紧邻广东。因此,湛江、佛山、东莞、深圳、广州在春节前（尤以2月7日-2月23日）作为人口流出地,和春节后（尤以2月25日-3月4日）作为人口流入地时,所关联的人口流动具有明显的高距离衰减效应特征。

6 重力模型模拟的误差估算

利用重力模型对人口流动强度进行模拟,得到的模拟流与实测流之间的差值部分被视为由于数学模拟而造成的模型误差。基于前文误差估算方法,假设变量回归系数准确标定,模拟误差来源为变量的参数标定,从而探讨流出、流入地属性及空间效应能否得到良好的模型化。在全国尺度的19317条人口流中（表4）,人口省际流G_ij的实测流强度最大值（849495）仅为模拟流强度最大值（2228483）的三分之一,相对流出力P_i、相对吸引力Q_j、空间相互作用效应F_ij的实测与模拟最大值之比分别为1.15、1.44和1.71。
Tab. 4
表4
表4春运时期实际矩阵与模拟矩阵流动因素对比
Tab. 4Comparison of observation matrix and estimation matrix during Spring Festival

	因素	数量	最小值	最大值	中位数
实际矩阵	人口省际流(G_ij)	19317	10	849495	140
	整体影响(K)	1	231.84	231.84	231.84
	相对流出力(P_i)	301	0.08	5.4	0.89
	相对吸引力(Q_j)	301	0.06	26.94	0.47
	空间效应(F_ij)	19317	0	2014.03	0.8
模拟矩阵	人口省际流(G_ij)	19317	1	2228483	210
	整体影响(K)	1	231.78	231.78	231.78
	相对流出力(P_i)	301	0.02	4.7	0.98
	相对吸引力(Q_j)	301	0.01	18.67	0.6
	空间效应(F_ij)	19317	0.03	1175.37	0.9

新窗口打开
在分市计算结果对比中（图7）,就相对流出力P_i而言,有137个城市实测值高于模拟结果（图7a）,如北京（实测5.396,模拟1.959,后同）、重庆（3.756,1.237）、宜春（3.061,0.997）、阜阳（2.382,0.638）;有164个城市实测值低于模拟结果,如陇南（0.871,4.698）、马鞍山（0.576,4.054）、芜湖（0.975,4.051）、合肥（1.141,3.461）。二者分别占城市总量的45.51%和54.49%。就相对吸引力Q_j而言,有151个城市实测值高于模拟结果（图7b）,如东莞（10.436,1.647）、北京（26.932,18.656）、宁波（5.568,1.847）、中山（4.169,0.622）;有150个城市实测值低于模拟结果,如济南（0.747,4.168）、长沙（1.534,4.306）、马鞍山（0.548,2.944）。Shen在2005-2010年中国省级区划人口流动研究中指出,省级区划的实测与模拟的相对流出力、相对吸引力结果较为吻合。针对相对流出力,实测与模拟结果中省级区划按照力的大小排序无变化（河南相对流出力最大,西藏相对流出力最小）。针对相对吸引力,实测与模拟结果中省级区划按照力的大小排序也无变化（广东相对吸引力最大,西藏相对吸引力最小）^[37]。本文研究结果中,在统计量P_i、Q_j方面,模拟P_i、Q_j偏离真实P_i、Q_j的情况无论是比率和幅度都有所增加。按照相对流出力与相对吸引力大小对城市进行排序,实测与模拟排序情况差别较大。模拟P_i、Q_j排名前十位城市结果来看（表5）,估算流出力均显著高于实测流出力,估算吸引力呈现高位序城市低于实测吸引力、低位序城市高于实测吸引力的特征。

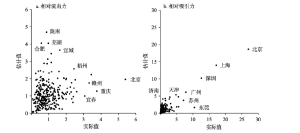显示原图|下载原图ZIP|生成PPT
图7实际与模拟城市相对流出力和吸引力散点图
-->Fig. 7Comparison of actual and estimated urban relative displacement
-->

Tab. 5
表5
表5估计P_i和Q_j排名前十位城市
Tab. 5Actual and estimated P_i and Q_j ranked in the top 10 cities

估计位序	城市	估计流出力	实际流出力	城市	估计吸引力	实际吸引力
1	陇南	4.698	0.871	北京	18.656	26.932
2	马鞍山	4.054	0.576	上海	14.002	17.106
3	芜湖	4.051	0.975	深圳	10.193	12.574
4	宣城	3.658	1.631	广州	6.100	7.824
5	合肥	3.461	1.141	天津	5.351	4.787
6	黄山	3.131	0.941	杭州	4.797	5.529
7	忻州	2.936	1.145	武汉	4.694	2.931
8	宿迁	2.886	0.726	长沙	4.306	1.534
9	齐齐哈尔	2.868	0.904	南京	4.170	2.749
10	梧州	2.579	2.447	济南	4.168	0.747

新窗口打开
表6展示了实测流与模拟流之间的相对误差,包括算数平均误差、绝对平均误差和加权绝对平均误差3种误差统计量。① 算数平均误差中,每一条流都被视为相同,未考虑人口流本身的质量大小,且误差值的正负存在抵消的情况^[22];② 绝对平均误差能够消除误差本身的正负抵消对于均值的影响,但同样不能考虑流动流强度;而加权绝对误差是能够合理考虑流动流本身强度,同时误差的正负不会对平均误差造成影响,故在综合考虑模型均值误差时,选用加权绝对平均误差更为合理。就加权绝对平均误差而言,模型拟合的总误差为85.54%。空间作用效应F_ij造成了实测流与模拟流最大的误差,达到86.09%;相对流出力P_i和相对吸引力Q_j分别造成57.73%、49.34%的模型误差;常数K造成0.03%的模型误差。总体而言,空间相互作用效应是流动模型中最难被模型化的。需要指出的是,相对流出力P_i和相对吸引力Q_j在模型中分别被7个自变量所解释,而空间相互作用效应仅被距离变量解释。
Tab. 6
表6
表6实际流与模拟流的相对误差百分比
Tab. 6Percentage of relative error between actual and estimated flow

因素	最小值	最大值	中位数	算数平均误差	绝对平均误差	加权绝对平均误差
常数(K)	0.03	0.03	0.03	0.03	0.03	0.03
相对流出力(P_i)	-90.87	924.18	-0.02	29.09	67.38	57.73
相对吸引力(Q_j)	-91.12	922.1	-1.2	36.09	76.47	49.34
空间作用效应(F_ij)	-99.75	32 625.3	2.52	196.81	256.84	86.09
其他复合因素(O_i_j)	-26 296.96	30 833.54	-9.39	-3.82	238.7	74.25
G_ij	-99.89	40 911.8	18.04	258.18	319.94	85.54

新窗口打开

7 结论与讨论

7.1 结论

本文基于百度迁徙提供的高精度、海量关系流数据,利用编程进行大规模的回归模拟,将中国人口流动重力模型代理变量的回归系数推算至地级行政单元精度。在理论上,指出空间交互模型应用中普遍被严重忽视的两个基本问题：模型变量的回归系数存在空间异质性和模拟结果较实测流存在显著误差。在此基础上,本文认为：利用空间交互模型进行关系模拟的科学性仍值得进一步论证和推敲;在实证上,论文展示了中国各省人口流动距离衰减系数的均值和值域,及31个直辖市和省会城市的系数,为今后区域尺度下人口流动重力模型应用提供了基础参考数据。
（1）中国人口流动重力模型参数标定的复杂性体现在两个方面：空间交互对象代理变量影响程度的非对称性,变量回归系数的空间异质性随着研究精度的加深显著加剧。① 无论从整体作用还是特定变量,代理变量的影响差异大致呈现流入地高于流出地的特征;② 经济发展类指标不仅对于人口双向流动产生了更为深刻的影响,同时其解释力的适用范围更加广泛;③ 地级行政单元下代理变量回归系数存在显著的空间异质性和分层异质性,地理区之间的差异要显著高于地理区内部差异,这与当前中国社会经济发展的区域显著不均衡性相符合。综上,假定人口流动重力模型代理变量回归系数的空间均质性、忽略各项因素作用效应随时空变化的异质性,将导致估算结果空间差异趋势的收敛,并进一步无法识别出交互作用在空间上延伸的各向异性。
（2）人口流动空间交互模型的距离衰减系数在相关研究中具有横向参考意义。基于实证推算,在全国尺度下人口流动距离衰减系数为1.970;在地级行政单元下,人口流出地距离衰减系数值域为0.712（驻马店）~7.699（乌鲁木齐）,人口流入地值域为0.792（三亚）~8.223（乌鲁木齐）,并可归类为空间衰减效应高、低两类省份及城市,其原因归结为可达性、城市职能、区域经济发展特征等差异所导致。距离衰减系数的时空波动性对各市春运期间人口流动的时空特征、流出和流入的属性差异具有识别作用,基本反映出中国春节前后流动人口在东部发达地区与中西部欠发达地区间循环流动的空间过程。
（3）重力模型对于中国地级市研究精度下人口流动强度的模拟存在明显的误差。就加权绝对平均误差而言,模型拟合的总误差为85.54%,空间相互作用效应造成了实测流与模拟流最大的误差,达到86.09%。因此,空间交互效应仍然是当前最难以模式化的因素。相对流出力、相对吸引力、残差分别造成57.73%、49.34%、0.03%的模型误差。这一结果有助于更好的解析人口流动空间交互的关系过程,为以往研究中不符合预期、变量解释力失效等现象或问题提供了一个理解视角,同时为空间交互关系模拟模型的改进提出了方向。

7.2 讨论

Shen运用中国2005-2010年间的区域迁徙数据和泊松迁徙模型,评估中国人口省级迁徙空间模拟的模型误差^[37],对比本文以地级行政区划为研究对象计算结果,一方面表明随着研究精度的加深,模型估算结果与实测值的误差将显著增加,另一方面利用空间交互模型对中国人口省际流迁的空间强度进行模拟,结果对于当前中国城市发展的极化效应存在明显的低估。
由于人类不同个体和群体之间在心理素质、思维习惯和行为准则等方面的差异性,人地关系系统的运行远比封闭的物理系统复杂。社会行为的嵌入决定了空间相互作用系统是一种适应性系统,因此,基于人口省际流动重力模型的参数标定也只适用于一定时空尺度下的特定对象间交互作用的模拟。
本文不足之处在于未考虑人口流出地和流入地的空间自相关。人口流动的空间自相关反映了交互系统中各个流出地、目的地或迁移流之间的相互依赖、相互制约的空间效应。然而在本文参数标定具有复杂性这一论点中,复杂性本身即是一个难以用指标量化的特征属性,而考虑空间自相关性后,将进一步加剧研究结论的复杂程度,但这也是下一步研究的方向。
The authors have declared that no competing interests exist.

中国人口省际流动重力模型的参数标定与误差估算

本站小编 Free考研考试/2021-12-29

Gravity model coefficient calibration and error estimation: Based on Chinese interprovincial population flow

1 引言