, 杨琳, 曾灿英Selection of environmental variables and their scales in multiple soil properties mapping: A case study in Heilongjiang Heshan Farm
SHIJingjing, YANGLin, ZENGCanying通讯作者:
收稿日期:2017-09-26
修回日期:2017-12-19
网络出版日期:2018-03-15
版权声明:2018《地理研究》编辑部《地理研究》编辑部
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1132KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
1 引言
土壤的形成与发展离不开环境因子的多尺度综合作用。对土壤重要环境因子的探索是了解土壤发生发展的重要研究内容,同时环境因子的选择也是土壤制图和采样中的重要环节[1,2,3,4,5],决定了土壤制图的精度和采样的效率。目前,针对不同的土壤属性进行制图或采样设计时,多根据专家知识结合研究区特点选择一组相同的环境因子[6,7,8,9],少有探查不同的环境因子对不同的土壤属性推测影响的研究[10]。然而,不同土壤属性的影响因子可能不同[11,12]。采用一组相同的环境因子对不同土壤属性的空间分布进行推测或进行采样设计时,无法充分体现不同属性成土因素的不同带来的空间分布上的差异,因而可能会降低土壤属性的推测精度或采样的效率。
环境因子对土壤属性空间分布的影响是具有尺度效应的,不同土壤属性的环境因子其作用的尺度可能不同[13]。不少研究者们探索了多尺度的地形因子与单尺度地形因子对土壤属性制图的影响[14,15,16,17]。研究表明,多尺度环境因子的加入,较单尺度地形因子表现出了更强大的推测能力。然而,目前的研究大多针对单种土壤属性,少有针对多种土壤属性,探索不同环境因子的尺度对土壤属性的影响[10]。研究不同土壤属性的相关环境因子及其作用尺度对于理解不同土壤属性的发生发展,及土壤推测制图具有重要意义。
本文有两个研究目标：第一,多种土壤属性其起作用的重要环境因子及其尺度是否不同,有何不同;第二,采用不同的环境因子集进行土壤属性空间分布推测的制图结果和精度的差异。本文以东北黑龙江鹤山研究区的5种土壤属性为例,选择12种地形因子并生成多尺度地形因子,计算每种土壤属性的环境因子重要性排序,并根据环境因子的重要性选择每种土壤属性的单尺度和多尺度环境因子集用于制图,并与基于专家知识选择的基准环境因子进行对比,以探查不同环境因子及其尺度对多种土壤属性推测的影响。
2 研究方法与数据来源
2.1 研究区概况
研究区位于黑龙江省黑河市嫩江县鹤山农场老莱河左岸,位置为48°53′24″N~48°59′24″N、125°8′24″E~125°16′12″E,面积为60.2 km2,海拔为276.1~363.4 m（图1）,地形起伏较缓。研究区处于寒温带季风草甸草原区,年降水量400~550 mm。该区的地貌主要是不同程度切割的山前洪积台地以及冲积湖积平原,当地称之为漫岗地。整个研究区的母质基本一致,多为黄土状亚粘土。原生植被为疏林草甸、灌丛草甸和杂类草草甸,但近五十年多被开垦为农田,主要农作物为小麦和大豆等,人类活动剧烈。2.2 采样数据
该研究区共采集98个样点[19,20],样点分布如图1所示。样点由三种采样方案所得：代表性采样,规则采样和横切线采样。其中代表性采样方案旨在采集土壤空间分布的典型点,共37个[20];规则样点布设在1100 m740 m的网格上,共41个;横切线样点布设在覆盖由山脊到山谷和微地貌的两条横切线上,共20个。可认为这些样点无论是在地理空间上还是属性空间上都对研究区有一个较好的覆盖。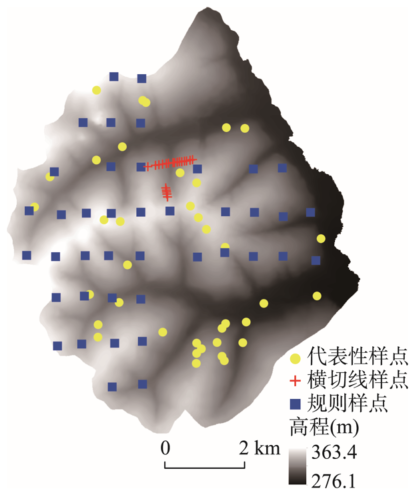
显示原图|下载原图ZIP|生成PPT图1研究区及样点分布图
-->Fig.1Study area and sampling points
-->
以表层（0~20 cm）土壤砂粒、粉粒、黏粒含量、表层有机质含量和土壤厚度为目标土壤属性。将所收集的98个样点的表层土壤样品进行自然风干、研磨,过10目筛的土壤样品采用激光粒度仪（英国马尔文公司Mastersizer 2000G型激光衍射粒度分析仪）测定土壤砂粒、粉粒、黏粒含量,过60目筛的土壤样品采用重铬酸钾法测定有机质含量[21]。样点的属性统计描述如表1所示。
Tab.1
表1
表1样点属性值统计描述
Tab.1The statistical description of samples
| 砂粒（g/kg） | 粉粒（g/kg） | 黏粒（g/kg） | 有机质（g/kg） | 厚度（cm） | |
|---|---|---|---|---|---|
| 最小值 | 33.95 | 277.23 | 0.00 | 22.45 | 15.00 |
| 25%分位数 | 134.82 | 630.16 | 0.84 | 35.98 | 65.75 |
| 中位数 | 198.94 | 747.90 | 54.63 | 41.83 | 92.50 |
| 均值 | 233.61 | 714.34 | 52.05 | 43.38 | 92.82 |
| 75%分位数 | 288.26 | 822.27 | 94.67 | 47.72 | 125.00 |
| 最大值 | 663.18 | 965.55 | 194.43 | 91.80 | 170.00 |
新窗口打开
2.3 环境因子数据的生成
该区母质和气候比较均一,地形是土壤形成和发展的主导因子[19]。因此,针对多种土壤属性,生成了12种地形因子（表2）。其中,DEM数据由11万的地形图生成,分辨率为10 m,其余地形因子由DEM数据基于SimDTA[22]、SoLIM[23]和Python软件计算得到（表2）。高程、坡度、坡向（取坡向角的余弦值）、平面曲率、剖面曲率、地形起伏度、地形粗糙指数和地形部位指数是基本地形属性。地形部位指数值接近0意味着局部平区或坡中部,大于0意味着靠近山脊,小于0意味着靠近山谷。地形湿度指数、距最近排水的高差、地形特征指数和坡位是派生地形属性,是由基本地形属性计算所得。距最近排水的高差通过每个栅格与最近排水栅格的高度差计算得来。地形特征指数则通过汇流面积及表面曲率指数[24]计算得来。坡位值域为1~5,分别代表山脊、坡肩、背坡、坡脚和河谷五个典型坡位。Tab.2
表2
表2环境因子数据
Tab.2The description of environmental variables
| 环境因子 | 英文代称 | 软件 | 分析尺度 |
|---|---|---|---|
| 高程 | Elevation | - | 10 m |
| 地形湿度指数 | TWI | SoLIM | n/a |
| 地形特征指数[24] | TCI | SimDTA | n/a |
| 坡位[25] | Slopepos | SimDTA | n/a |
| 距最近排水的高差[26] | Hand | Python | n/a |
| 坡度 | Slope | SoLIM | 30~490 m |
| 坡向（cosine） | Cosasp | SoLIM | 30~490 m |
| 平面曲率 | Planc | SoLIM | 30~490 m |
| 剖面曲率 | Profic | SoLIM | 30~490 m |
| 地形粗糙指数[27] | TRI | SimDTA | 30~490 m |
| 地形部位指数[28,29] | TPI | SimDTA | 30~490 m |
| 地形起伏度[30] | Relief | SimDTA | 30~490 m |
新窗口打开
多尺度地形因子一般可通过调节DEM的分辨率或（和）计算地形因子时的邻域大小而计算生成[14,15,16,17,18]。本文选择地形因子计算时的邻域大小来表达地形因子的不同尺度,这是因为分辨率的减小和邻域的增大,对地形因子有着相似的影响,但是邻域的增大,会避免不必要的细节丢失[16]。
本文中多尺度地形因子邻域大小设置分别为33、55、77,…,4949,对应计算的窗口大小为30 m、50 m、70 m,…,490 m。高程、地形湿度指数、地形特征指数、坡位,距最近排水的高差和计算邻域大小为33时的坡度、坡向、平面曲率、剖面曲率、地形粗糙指数、地形部位指数,地形起伏度为单尺度地形因子。研究区共生成173个地形因子。
环境因子的命名原则如下：高程、地形湿度指数、地形特征指数、坡位、距最近排水的高差仅用表2中的英文代称表示,其他地形因子为英文代称加邻域窗口大小,例如Slope5为邻域大小为55的坡度。
2.4 环境因子重要性排序
采用随机森林的变量重要性指标进行不同土壤属性的环境因子重要性排序[31,32,33,34]。随机森林方法由Breiman[31]创建,该方法是一种机器学习方法。随机森林是一系列决策树的集合,对于每棵决策树,由2/3的样本作为训练样本,其余的1/3作为Out-of-Bag（OOB）验证样本。采用预测精度的平均下降量作为计算环境因子重要性的指标。预测精度平均下降量为依次将每个变量替换为随机噪音后,所有决策树的OOB验证样本的预测精度的平均下降量。预测精度平均下降量越大的变量,重要性排序越靠前,其对土壤属性的推测能力越强,相应地,重要性排序越靠后的变量对土壤属性的推测能力越弱。本文根据重要性排序评价各因子对土壤属性的推测能力。本文中环境因子重要性排序采用R软件中的Random Forest包（随机森林包）。
2.5 不同土壤属性的环境因子集构建
为了探索环境因子及其尺度的不同对多种土壤属性制图的影响,构建了三个环境因子集。环境因子集1是从单尺度地形因子（共12个因子）中选取,环境因子集2是从共173个的全部环境因子中选取,环境因子集3是基准环境因子集,用于对比环境因子集1和2的制图结果与精度。基准环境因子集由前期研究中[20,35,36]所选四个基本地形因子（坡度、平面曲率、剖面曲率、地形湿度指数）组成。为了对比的公平性,环境因子集1和2的数量均为4个。环境因子集1和2中的环境因子根据环境因子重要性排序并去除因子的共线性来选择,具体方法如下：基于研究区的98个采样点,将相应的12个地形因子或173个地形因子输入随机森林中,得到环境因子的重要性排序;为去除环境因子共线性,设置环境因子相关性阈值,将环境因子相关性大于等于0.7的变量去除,保留重要性排序靠前的环境因子,即选择环境因子相关性小于0.7的重要性排序最靠前的4个环境因子。
2.6 土壤制图及评价
采用随机森林方法制图。随机森林被广泛应用于土壤制图[33],该方法较统计制图方法有许多突出的优点[32],也被证明是精度较高的一种制图方法。为了避免从全部98个样点中随机选择训练样点可能带来的偶然性,共设置了1000组独立的实验。即基于98个样点随机生成1000套独立的训练样点与验证样点,每组实验的训练样点与验证样点数量之比为21,训练样点和验证样点的数量分别为65个和33个。针对多种土壤属性,每组实验基于训练样点,根据上述选择的环境因子集1、环境因子集2和基准环境因子集3进行制图。验证样点采用均方根误差（RMSE）这一指标对制图的精度进行评价。对于每个环境因子集,可得到1000个RMSE结果。此外,随机选择利用三个环境因子集的基于一组样点的土壤图,对比制图结果的空间分布。
本文中随机森林模型的建立采用R软件中的Random Forest包（随机森林包）。
Tab.3
表3
表3每种土壤属性所选择的环境因子集1、环境因子集2和基准环境因子集3
Tab.3Subsets 1 and 2 of each soil property and the reference subset 3
| 砂粒 | 粉粒 | 黏粒 | 有机质 | 厚度 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 环境因子集1 | 环境因子集2 | 环境因子集1 | 环境因子集2 | 环境因子集1 | 环境因子集2 | 环境因子集1 | 环境因子集2 | 环境因子集1 | 环境因子集2 | 基准环境因子集 | ||||
| Slopepos | Slope31 | TPI3 | Planc39 | Elevation | Elevation | Elevation | Profic31 | TRI3 | Slope11 | Planc3 | ||||
| Ref3 | Planc39 | Slopepos | Slope45 | Slope3 | Planc45 | Hand | Elevation | Elevation | Cosasp43 | Profic3 | ||||
| TPI3 | Cosasp41 | Elevation | Profic11 | Planc3 | Profic25 | TRI3 | Planc11 | Hand | Elevation | Slope3 | ||||
| Hand | TWI | Hand | Cosasp43 | Hand | Slope15 | Slopepos | TPI17 | Cosasp3 | Planc19 | TWI | ||||
新窗口打开
3 结果分析
3.1 不同土壤属性的环境因子重要性分析
研究区5种土壤属性的单尺度因子（12个）的重要性排序结果如图2所示。可以看出,5种土壤属性的环境因子的重要性排序呈现很大的差异。对于机械组成中的砂粒和粉粒,地貌部位起了非常重要的作用,而黏粒的重要环境因子则非常不同,基本地形属性（高程、坡度、地形粗糙指数和平面曲率）起到重要作用。有机质和厚度的重要地形因子较为相似,主要包括高程、坡度和地形粗糙指数等,但各因子排序不同。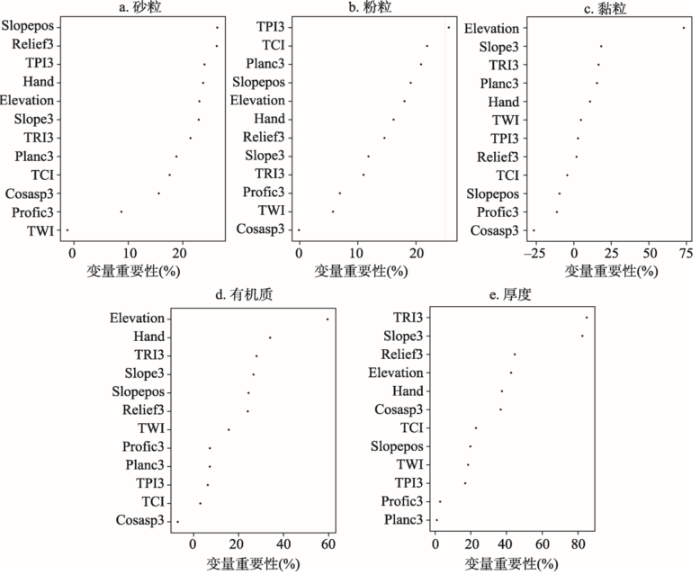
显示原图|下载原图ZIP|生成PPT图212个环境因子的变量重要性图
-->Fig. 2The sequencing graph of variable importance of 12 environmental variables
-->
此外,基准环境因子中的四个因子在五种土壤属性的重要性排序中均没有占据第一位,而且重要性排在前4位的因子与基准环境因子重叠较少。砂粒的前4个重要因子中无基准因子,粉粒前4个因子中仅出现平面曲率,黏粒前4个因子中出现坡度和平面曲率,有机质和厚度的前4个因子仅出现了坡度。一方面,这说明据专家知识选择的基准因子并不一定是对土壤属性影响最重要的因子;另一方面,现在有较多的地形因子为推测土壤属性提供了更多的选择。
环境因子集2所选出的多尺度环境因子及其尺度的重要性变化如图3所示。可以看出,首先,各土壤属性所选出的多尺度环境因子不同,但大多含有基准地形因子,地形部位指数仅在有机质中被选中。其次,多尺度环境因子随尺度变化对每种土壤属性的重要性明显不同,同一种环境因子对多种土壤属性起作用的最佳尺度大多不同。有机质和土体厚度,重要性值最高的地形因子其重要性随尺度的变化呈现明显单峰,其他多尺度地形因子重要性随着尺度虽有波动,但重要性低。其中,剖面曲率对有机质的最佳作用尺度为310 m,而对土体厚度而言,坡度的最佳作用尺度为110 m。
对于砂粒、黏粒和粉粒而言,选中的环境因子的重要性折线图大多呈现多峰,且最佳作用尺度的多个环境因子重要性相当。对砂粒而言,坡度的作用尺度为170~210 m和270~490 m,平面曲率的作用尺度为350~490 m,坡向作用尺度为410 m,环境因子最佳作用尺度大多为350~450 m。对粉粒而言,平面曲率的作用尺度为330~490 m,坡度的作用尺度为310 m和390~490 m,坡向的作用尺度为430 m,剖面曲率的作用尺度为90~110 m,除剖面曲率外,其他环境因子最佳作用尺度为350~450 m。对黏粒而言,坡度的作用尺度为90~210 m,剖面曲率的作用尺度为210~310 m,平面曲率的作用尺度为110~170 m和350~490 m, 各多尺度环境因子对黏粒的作用尺度不同。
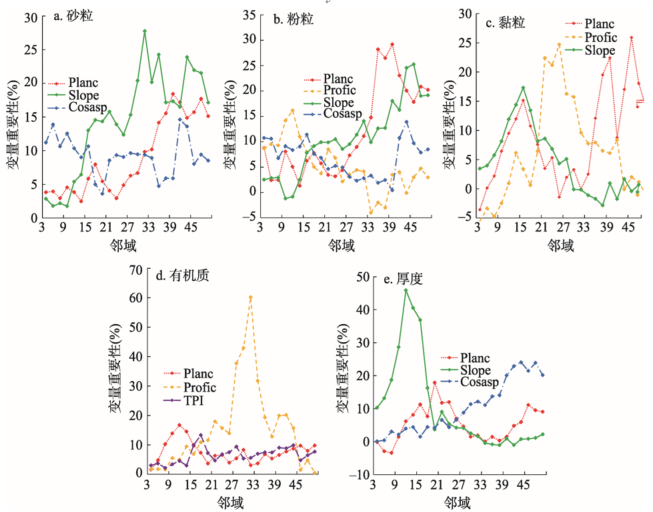显示原图|下载原图ZIP|生成PPT图3环境因子集2中多尺度环境因子随尺度变化时的变量重要性图
-->Fig. 3Variable importance of environmental variables in subset 2 with neighborhood size changing for the five soil properties
-->
3.2 不同土壤属性的环境因子集结果
每种土壤属性所选择的环境因子集1、环境因子集2和基准环境因子集3如表3所示。从环境因子集1看,距最近排水的高差（Hand）为每种土壤属性的重要环境因子,高程（Elevation）、坡位（Slopepos）为大多数土壤属性的重要环境因子。从环境因子集2看,砂粒的环境因子作用尺度大小为310~410 m,粉粒的重要环境因子中平面曲率（Planc）,坡度（Slope）和坡向（Cosasp）作用尺度为390~450 m,剖面曲率（Profic）的作用尺度为110 m,黏粒、有机质和土壤厚度的三个多尺度因子其作用的尺度不同,这与3.1所得结论基本一致。各土壤属性的环境因子集1与环境因子集2差异很大。除黏粒外,其他属性的环境因子集1与基准环境因子集均不相同。而环境因子集2除了尺度不同,与基准环境因子集中的环境因子重叠度较高。3.3 土壤制图与精度结果
利用三个环境因子集基于同一组样点得到土壤属性图如图4所示。从图4中看出3个环境因子集所得土壤属性的空间分布规律具有一定的相似性,但土壤属性空间分布的细节差异较大。Tab.4
表4
表4环境因子集1和2较基准因子集3和环境因子集2较环境因子集1的RMSE均值提高百分比（%）
Tab.4The improvements of the mean RMSEs of subset1 compared with subset 3, subset 2 compared with subset 3 and subset 2 compared with subset1 respectively (%)
| RMSE | 砂粒 | 粉粒 | 黏粒 | 有机质 | 厚度 |
|---|---|---|---|---|---|
| subset1_3 | -2.3* | 1.8* | 5.8* | 6.5* | 13.1* |
| subset2_3 | 7.8* | 11.1* | 21.3* | 17.7* | 20.6* |
| subset2_1 | 9.9* | 9.4* | 16.5* | 12.1* | 8.7* |
新窗口打开
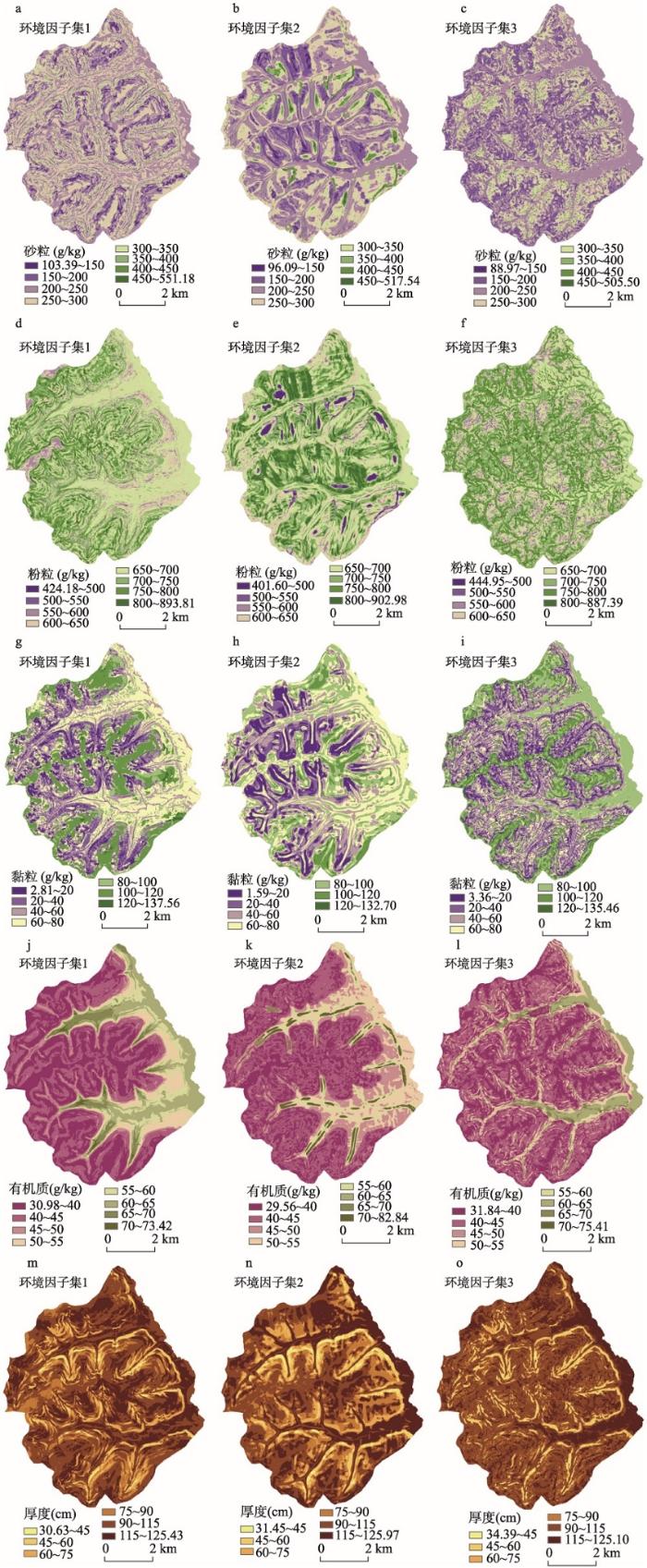显示原图|下载原图ZIP|生成PPT图4土壤属性制图结果
-->Fig. 4Map showing soil properties
-->
表4为1000套实验的三个环境因子集的RMSE均值提高百分比,其中subset1_3、subset2_3、subset2_1分别指环境因子集1和环境因子集2较基准环境因子集3,环境因子集2较环境因子集1的制图RMSE均值提高百分比。由表可以看出,环境因子集2较基准环境因子集3制图RMSE均值显著提高,提高百分比为7.8%~21.3%。环境因子集1较基准环境因子集而言,砂粒的制图精度并没有提高,反而降低,这可能是由于环境因子数量的原因。其他4种土壤属性的RMSE均值显著提高,提高百分比为1.8%~13.1%。环境因子集2较环境因子集1制图RMSE均值都显著提高,提高百分比为8.7%~16.5%。由此可见,选择适宜的尺度,可大大提高环境因子的推测能力。
各土壤属性基于三个环境因子集的RMSE分布箱线图如图5。图5得出的结论与表4类似。针对各土壤属性,在1000套实验中环境因子集2的大部分实验的制图RMSE值较环境因子集1和3的低。
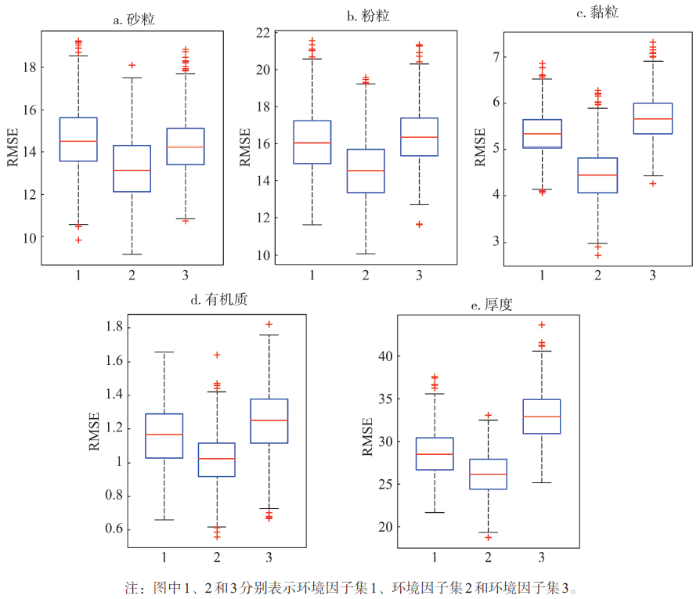显示原图|下载原图ZIP|生成PPT图5三个环境因子集的RMSE分布箱线图
-->Fig. 5The boxplot of three subsets' RMSE
-->
4 结论
本文以黑龙江鹤山小流域为例,探索不同土壤属性的重要相关环境因子及其作用尺度,并探讨了采用不同的环境因子集对土壤属性制图结果及其精度的影响。研究结果 表明：（1）仅考虑单尺度环境因子时,五种土壤属性的环境因子重要性排序差异很大,且按照专家知识选出的四个基准环境因子排名大多靠后,可见,据专家知识选择的基准环境因子并不一定是对土壤属性影响最重要的因子。
（2）当多尺度环境因子（多个计算邻域）参与时,各土壤属性排名靠前的因子多数是基准环境因子,尽管对各土壤属性的作用尺度不同,剖面曲率对有机质的最佳作用尺度为310 m,坡度对土壤厚度的最佳作用尺度为110 m,几个环境因子对砂粒和粉粒的最佳作用尺度为350~450 m,而几个环境因子对黏粒的最佳作用尺度有多个。此外,本文所采用的随机森林重要性指标可用于识别环境因子的最佳作用尺度,对于理解环境因子的成土作用具有指示意义。
（3）环境因子集1较基准环境因子集3而言,除砂粒外,对其他土壤属性预测的RMSE均值显著提高,提高百分比为1.8%~13.1%。环境因子集2较基准环境因子集3的制图RMSE均值都显著提高,提高百分比为7.8%~21.3%。环境因子集2较环境因子集1的制图RMSE均值都显著提高,提高百分比为8.7%~16.5%。由此可见,一方面,对于每种土壤属性而言,不同环境因子存在不同的最佳作用尺度。另一方面,选择地形因子的适宜尺度十分重要,选择适宜的尺度可大大提高预测精度,相比选择更多可用的地形因子而言,选择适宜的尺度更重要。
本文揭示了不同环境因子对不同属性作用的差异性,及进行土壤属性制图时环境因子尺度的重要性,因而在进行土壤属性制图乃至采样设计时,不应仅选择一套环境因子,而应根据每种土壤属性选择相应的环境因子及适宜的尺度。
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . Quantitative techniques for spatial prediction in soil survey are developing apace. They generally derive from geostatistics and modern statistics. The recent developments in geostatistics are reviewed particularly with respect to non-linear methods and the use of all types of ancillary information. Additionally analysis based on non-stationarity of a variable and the use of ancillary information are demonstrated as encompassing modern regression techniques, including generalised linear models (GLM), generalised additive models (GAM), classification and regression trees (RT) and neural networks (NN). Three resolutions of interest are discussed. Case studies are used to illustrate different pedometric techniques, and a variety of ancillary data. The case studies focus on predicting different soil properties and classifying soil in an area into soil classes defined a priori. Different techniques produced different error of interpolation. Hybrid methods such as CLORPT with geostatistics offer powerful spatial prediction methods, especially up to the catchment and regional extent. It is shown that the use of each pedometric technique depends on the purpose of the survey and the accuracy required of the final product. |
| [2] | . |
| [3] | . The conversion of point observations to a geographic field is a necessary step in soil mapping. For pursuing goals of mapping soil carbon at the landscape scale, the relationships between sampling scale, representation of spatial variation, and accuracy of estimated error need to be considered. This study examines the spatial patterns and accuracy of predictions made by different spatial modelling methods on sample sets taken at two different scales. These spatial models are then tested on independent validation sets taken at three different scales. Each spatial modelling method produced similar, but unique, maps of soil organic carbon content (SOC%). Kriging approaches excelled at internal spatial prediction with more densely spaced sample points. Because kriging depends on spatial autocorrelation, kriging performance was naturally poor in areas of spatial extrapolation. In contrast, the spatial regression approaches tested could continue to perform well in spatial extrapolation areas. However, the problem of induction allowed the potential for problems in some areas, which was less predictable. This problem also existed for the kriging approaches. Spatial phenomena occurring between sampling points could also be missed by kriging models. Use of covariates with kriging can help, but the requirement of capturing the full feature space in the map remains. Methods that utilize spatial association, such as spatial regression, can map soil properties for landscape scales at a high resolution, but are highly dependent on the inclusion of the full attribute space in the calibration of the model and the availability of transferable covariates. |
| [4] | . 土壤厚度信息对土壤碳储量估算、水文-生态过程模拟等有着重要影 响,但我国北方石质山区缺乏现势性好、分辨率高的土壤厚度分布数据及其快速获取方法.基于北方石质山区土壤厚度的分布特点,先将地貌信息和植被类型叠加生 成制图单元,再根据每类单元的特征,针对性地选取地形参数和地表覆被参数作为指示土壤厚度空间分布的环境变量,结合少量土壤样点,依据模糊推理模型,构建 了基于分层制图策略的土壤厚度空间推测方法.以河北省滦平县虎什哈流域为例,利用从ASTER GDEMs提取的地形变量和从我国环境减灾卫星影像(HJ-A)提取的地表覆被信息对土壤厚度进行了推测.结果表明,该方法精度较高,是利用免费地形和遥 感数据进行低成本快速土壤制图的实用途径. . 土壤厚度信息对土壤碳储量估算、水文-生态过程模拟等有着重要影 响,但我国北方石质山区缺乏现势性好、分辨率高的土壤厚度分布数据及其快速获取方法.基于北方石质山区土壤厚度的分布特点,先将地貌信息和植被类型叠加生 成制图单元,再根据每类单元的特征,针对性地选取地形参数和地表覆被参数作为指示土壤厚度空间分布的环境变量,结合少量土壤样点,依据模糊推理模型,构建 了基于分层制图策略的土壤厚度空间推测方法.以河北省滦平县虎什哈流域为例,利用从ASTER GDEMs提取的地形变量和从我国环境减灾卫星影像(HJ-A)提取的地表覆被信息对土壤厚度进行了推测.结果表明,该方法精度较高,是利用免费地形和遥 感数据进行低成本快速土壤制图的实用途径. |
| [5] | . . |
| [6] | . ABSTRACT Digital elevation models (DEMs) provide a good way of deriving landform attributes that may be used for soil prediction. The geostatistical techniques of kriging and cokriging are increasingly being applied to predicting soil properties. Whereas ordinary kriging (and universal kriging) utilise spatial correlation to determine the coefficients of the linear predictor, cokriging involves both inter-variable correlation and spatial covariation among variables. Multi-linear regression modelling also offers an alternative to predicting a soil variable by means of covariation. The performance of predicting four soil variables by these methods and two regression-kriging models are compared. The precision and bias of prediction of the six methods were dependent on the soil variable predicted. The mean error of prediction indicates reasonably small bias of prediction for all the soil variables by almost all of the methods. With the exception of topsoil gravel, for which multi-linear regression performed best, the root mean square error showed the two regression-kriging procedures to be best. Further analysis based on the mean ranks of performance by the methods confirmed this. All the kriging methods involving covariables (landform attributes) have a more smoothing effect on the predicted values, thus minimising the influence of outliers on prediction performance. Both the methods of regression-kriging show promise for predicting sparsely located soil properties from dense observations of landform attributes derived from the DEM. Histograms of subsoil clay residuals show outliers in the data set. These outliers are more evident in multi-linear regression, ordinary kriging and universal kriging than regression-kriging. There was a clear advantage in using the regression-kriging methods on those variables which had a small correlation with the landform attributes: root mean square errors for all the soil variables are much smaller than those resulting from any of the multi-linear regression, ordinary kriging, universal kriging or cokriging methods. |
| [7] | . Detailed information on the spatial variation of soils is desirable for many agricultural and environmental applications. This research explores three approaches that use soil fuzzy membership values to predict detailed spatial variation of soil properties. The first two are weighted average models with which the soil property value at a location is the average of the typical soil property values of the soil types weighted by fuzzy membership values. We compared two options to determine the typical property values: one that uses the representative values from existing soil survey and the other that uses the property value of a field observation typical of a soil type. The third approach is a multiple linear regression in which the soil property value at a location is predicted using a regression between the soil property and fuzzy membership values. We compared this to multiple linear regression with environmental variables. In a case study in the Driftless Area of Wisconsin, the models were also compared with a predictive model based on existing soil survey. The results showed that regression with environmental variables works well for areas where the soil-搕errain relationship is relatively simple but regression with fuzzy membership values is an improvement for areas where soil-搕errain relationships are more complicated. From the perspectives of data requirement and model simplicity as well as accuracy of prediction the weighted average with maximum fuzzy membership option has obvious advantages. |
| [8] | . 鉴于经典采样和空间采样存在的局限性，提出了一种旨在寻找典型点的目的性采样设计方法。该方法通过分析与目标地理要素空间分布具有协同变化关系的环境因子，提取地理要素空间变化的典型模式，进而在典型模式上布设样点，即可获得典型点，从而减少所需样本量。以位于黑龙江鹤山农场的2个研究区为例，分别选择土壤厚度和表层有机质2个土壤属性，通过对土壤属性空间变化的4个协同环境因子进行模糊c均值聚类，获得对应土壤属性空间变化模式的环境因子组合；根据其模糊隶属度结果设计典型点并进行采样，最后结合典型点的属性值与环境因子组合模糊隶属度结果，采用加权平均模型得到土壤属性空间分布图，反映了土壤属性随地形变化的连续性分布。基于独立野外验证点，选择了4个评价指标对所得属性图进行定量评价。结果表明：2个研究区验证点集的预测值和观测值一致性指数均较高，可见本研究提出的方法是一种有效的样点布设方法。研究还对在每一环境组合类设计不同数量典型点所得土壤属性制图结果的差异进行了讨论，认为典型点增多并不一定能提高土壤属性空间推测的精度。 . 鉴于经典采样和空间采样存在的局限性，提出了一种旨在寻找典型点的目的性采样设计方法。该方法通过分析与目标地理要素空间分布具有协同变化关系的环境因子，提取地理要素空间变化的典型模式，进而在典型模式上布设样点，即可获得典型点，从而减少所需样本量。以位于黑龙江鹤山农场的2个研究区为例，分别选择土壤厚度和表层有机质2个土壤属性，通过对土壤属性空间变化的4个协同环境因子进行模糊c均值聚类，获得对应土壤属性空间变化模式的环境因子组合；根据其模糊隶属度结果设计典型点并进行采样，最后结合典型点的属性值与环境因子组合模糊隶属度结果，采用加权平均模型得到土壤属性空间分布图，反映了土壤属性随地形变化的连续性分布。基于独立野外验证点，选择了4个评价指标对所得属性图进行定量评价。结果表明：2个研究区验证点集的预测值和观测值一致性指数均较高，可见本研究提出的方法是一种有效的样点布设方法。研究还对在每一环境组合类设计不同数量典型点所得土壤属性制图结果的差异进行了讨论，认为典型点增多并不一定能提高土壤属性空间推测的精度。 |
| [9] | . Abstract High-precision mapping of important soil services, such as soil organic C stocks, is basic for monitoring the effects of different soil management regimes and the effectiveness of agricultural policies. Proximal soil sensing methods have been often used in the last decades to limit costs, field work, and time and to obtain reliable and accurate maps. We tested the combined use of two proximal sensors, visible-near-infrared (Vis-NIR) and passive γ-ray spectrometers, to obtain highly detailed maps of C stocks of the topsoil (CS30' 0-30 cm) of nine pairs of fields in western Sicily using a limited number of sampling sites per field for traditional laboratory analysis (about one sample per hectare). Laboratory Vis-NIR diffuse reflectance spectroscopy allowed the number of data points per field to be increased, at the same time reducing the costs for laboratory analysis. The predictive model had a coefficient of determination (R05) of 0.77 and an error (RMSE) of 0.67 kg m6305. Data points predicted by Vis-NIR on the fine earth (<2 mm) and corrected for gravel content (CS30pred) were interpolated within each field using geographically weighted multiple regression and two sets of covariates: (i) digital elevation model derivatives, such as elevation, slope, plan and profile curvature, and topographic wetness index; and (ii) elevation and γ-ray total counts maps. Validation of 36 independent data points showed that the second method provided greater accuracy than the first. In particular, residual prediction deviation (RPD) showed a mean value of 2.19; however, three pairs of fields showed high error and low RPD. This methodology provides a cost-effective tool to interpolate C stocks within arable fields, limiting laboratory analysis. The accuracy of the CS30pred maps allows monitoring of the effects of agricultural management and/or soil erosion on the soil C pool. 08 Soil Science Society of America, 5585 Guilford Rd., Madison WI 53711 USA. All Rights reserved. |
| [10] | . 61Potentially useful predictors for digital soil mapping are often overlooked.61Different analysis scales should be treated as unique predictor variables.61The use of multi-scale predictor variables can greatly increase model performance.61Experimentation with subsets of predictor pools for data mining tools can be productive. |
| [11] | . Conventional survey methods have efficiencies in medium to low intensity survey because they use relationships between soil properties and more readily observable environmental features as a basis for mapping. However, the implicit predictive models are qualitative, complex and rarely communicated in a clear manner. The possibility of developing an explicit analogue of conventional survey practice suited to medium to low intensity surveys is considered. A key feature is the use of quantitative environmental variables from digital terrain analysis and airborne gamma radiometric remote sensing to predict the spatial distribution of soil properties. The use of these technologies for quantitative soil survey is illustrated using an example from the Bago and Maragle State Forests in southeastern Australia. A design-based, stratified, two-stage sampling scheme was adopted for the 50,000 ha area using digital geology, landform and climate as stratifying variables. The landform and climate variables were generated using a high resolution digital elevation model with a grid size of 25 m. Site and soil data were obtained from 165 sites. Regression trees and generalised linear models were then used to generate spatial predictions of soil properties using digital terrain and gamma radiometric survey data as explanatory variables. The resulting environmental correlation models generate spatial predictions with a fine grain unmatched by comparable conventional survey methods. Example models and spatial predictions are presented for soil profile depth, total phosphorus and total carbon. The models account for 42%, 78% and 54% of the variance present in the sample respectively. The role of spatial dependence, issues of scale and landscape complexity are discussed along with the capture of expert knowledge. It is suggested that environmental correlation models may form a useful trend model for various forms of kriging if spatial dependence is evident in the residuals of the model. |
| [12] | . Optimal selection of observation locations is an essential task in designing an effective ecohydrological process monitoring network, which provides information on ecohydrological variables by capturing their spatial variation and distribution. This article presents a geostatistical method for multivariate sampling design optimization, using a universal cokriging (UCK) model. The approach is illustrated by the design of a wireless sensor network (WSN) for monitoring three ecohydrological variables (land surface temperature, precipitation and soil moisture) in the Babao River basin of China. After removal of spatial trends in the target variables by multiple linear regression, variograms and cross-variograms of regression residuals are fit with the linear model of coregionalization. Using weighted mean UCK variance as the objective function, the optimal sampling design is obtained using a spatially simulated annealing algorithm. The results demonstrate that the UCK model-based sampling method can consider the relationship of target variables and environmental covariates, and spatial auto- and cross-correlation of regression residuals, to obtain the optimal design in geographic space and attribute space simultaneously. Compared with a sampling design without consideration of the multivariate (cross-)correlation and spatial trend, the proposed sampling method reduces prediction error variance. The optimized WSN design is efficient in capturing spatial variation of the target variables and for monitoring ecohydrological processes in the Babao River basin. |
| [13] | . Landscape characteristics show local, regional and supra-regional components. As a result pedogenesis and the spatial distribution of soil properties are both influenced by features emerging at multiple scales. To account for this effect in a predictive model, descriptors of the geomorphic signature are required at multiple scales. In this study, we present a new hyper-scale terrain analysis approach, referred to as Contextual Statistical Mapping (ConStat), which is based on statistical neighborhood measures derived for growing sparse circular neighborhoods. The statistical measures tested comprise basic descriptors such as the minimum, maximum, mean, standard deviation, and skewness, as well as statistical terrain attributes and directional components. We propose a data mining framework to determine the relevant statistical measures at the relevant scales to analyze and interpret the influence of these statistical measures and to map the geomorphic structures influencing soil formation and the regions where a statistical measure shows influence. We introduce ConStat on two landscape-scale DSM examples with different soil genesis regimes where the ConStat terrain features serve as proxies for multi-scale variations of climate and parent material conditions. The results show that ConStat provides high predictive power. The cross-validated R2 values range from 0.63 for predicting topsoil clay content in the Piracicaba area (Brazil) to 0.68 for topsoil silt content in the Rhine-Hesse area (Germany). The results obtained from data mining analysis allow for interpretations beyond conventional concepts and approaches to explain soil formation. As such it overcomes the trade-off between accuracy and interpretability of soil property predictions. |
| [14] | . Terrain characteristics, such as slope gradient, slope aspect, profile curvature, contour curvature computed from digital elevation model (DEM), are among the key inputs to digital soil surveys based on geographic information systems (GIS). These terrain attributes are computed over a neighborhood (spatial extent). The objective of this research was to investigate the combined effect of DEM resolution and neighborhood size on digital soil surveys using the Soil– Landscape Inference Model (SoLIM) approach. The effect of neighborhood size and DEM resolution on digital soil survey was examined through computing the required terrain attributes using different neighborhood sizes (from 3 to 5402m) for 3, 6, 9, 12, 18, and 2702m resolution DEM. These attributes were then compiled and used to digitally map soils using the SoLIM approach. Field work completed on a hillslope in Dane County, WI in the summer of 2003 was used to validate each of the SoLIM derived soil surveys for accuracy. The results of the soil survey validations suggest that there is a range of neighborhood sizes that produces the most accurate results for a given resolution DEM. This range of neighborhood sizes, however, varies from landscape to landscape. When the soils on a gently rolling landscape were mapped, the neighborhood sizes that produced the most accurate results ranged from about 33–4802m. When soils on short, steep backslope positions were mapped, the neighborhood size values that produced the most accurate results range from about 24–3602m. This paper also shows that it is not always the highest resolution DEM that produces the highest accuracy. Knowing which DEM resolution and neighborhood size combinations produce the most accurate digital soil surveys for a particular landscape will be extremely useful to users of GIS-based soil-mapping applications. |
| [15] | . Terrain attributes are the most widely used predictors in digital soil mapping. Nevertheless, discussion of techniques for addressing scale issues and feature selection has been limited. Therefore, we provide a framework for incorporating multi-scale concepts into digital soil mapping and for evaluating these scale effects. Furthermore, soil formation and soil-forming factors vary and respond at different scales. The spatial data mining approach presented here helps to identify both the scale which is important for mapping soil classes and the predictive power of different terrain attributes at different scales. The multi-scale digital terrain analysis approach is based on multiple local average filters with filter sizes ranging from 3 脳 3 up to 31 脳 31 pixels. We used a 20-m DEM and a 1:50 000 soil map for this study. The feature space is extended to include the terrain conditions measured at different scales, which results in highly correlated features (terrain attributes). Techniques to condense the feature space are therefore used in order to extract the relevant soil forming features and scales. The prediction results, which are based on a robust classification tree (CRUISE) show that the spatial pattern of particular soil classes varies at characteristic scales in response to particular terrain attributes. It is shown that some soil classes are more prevalent at one scale than at other scales and more related to some terrain attributes than to others. Furthermore, the most computationally efficient ANOVA-based feature selection approach is competitive in terms of prediction accuracy and the interpretation of the condensed datasets. Finally, we conclude that multi-scale as well as feature selection approaches deserve more research so that digital soil mapping techniques are applied in a proper spatial context and better prediction accuracy can be achieved. |
| [16] | . In: Boettinger J L, Howell D W, Moore A C, et al. The digital representation of the Earth-檚 surface by terrain attributes is largely dependent on the scale at which they are computed. Typically the effects of scale on terrain attributes have only been investigated as a function of digital elevation model (DEM) grid size, rather than the neighborhood size over which they are computed. With high-resolution DEM now becoming more readily available, a multi-scale terrain analysis approach may be a more viable option to filter out the large amount short-range variation present within them, as opposed to coarsening the resolution of a DEM, and thereby more accurately represent soil-landscape processes. To evaluate this hypothesis, two examples are provided. The first study was designed to evaluate the systematic effects of varying both grid and neighborhood size on terrain attributes computed from LiDAR. In a second study, the objective was to examine how the correlations between soil and terrain attributes vary with neighborhood size, so as to provide an empirical measure of what neighborhood size may be most appropriate. Results suggest that the overall representation of the land surface by terrain attributes is specific to the land surface, but also that the terrain attributes vary independently in response to spatial extent over which they are computed. Results also indicate that finer grid sizes are more sensitive to the scale of terrain attribute calculation than larger grid sizes. For the soil properties examined in this study, slope curvatures produced the highest coefficients of correlation when calculated at neighborhood sizes between 117 and 189 m. |
| [17] | . 61Neighborhood extent is the main factor controlling soil-topography correlations.61Grid resolution affects the accuracy of terrain attributes at sampling locations.61Fine scale (1–5m) DEMs did not provide stronger predictors of soil properties.61LiDAR's high cost and computational requirements limit utility for soil modeling. |
| [18] | . . |
| [19] | . Fuzzy membership function is an effective tool to represent relationship between soil and environment for predictive soil mapping. Usually construction of a fuzzy membership function requires knowledge on soil-landscape relationships obtained from local soil experts or from extensive field samples. For areas with no soil survey experts and no extensive soil field observations, a purposive sampling approach could provide the descriptive knowledge on the relationships. However, quantifying this descriptive knowledge in the form of fuzzy membership functions for predictive soil mapping is a challenge. This paper presents a method to construct fuzzy membership functions using descriptive knowledge. Construction of fuzzy membership functions is accomplished based on two types of knowledge: 1) knowledge on typical environmental conditions of each soil type and 2) knowledge on how each soil type corresponds to changes in environmental conditions. These two types of knowledge can be extracted from catenary sequences of soil types and the associated environment information collected at a few field samples through purposive sampling. The proposed method was tested in a watershed located in Heshan farm of Nenjiang County in Heilongjiang Province of China. A set of membership functions were constructed to represent the descriptive knowledge on soil-landscape relationships, which were derived from 22 field samples collected through a purposive sampling approach. A soil subgroup map and an A-horizon soil organic matter content map for the area were generated using these membership functions. Forty five field validation points were collected independently to evaluate the two soil maps. The soil subgroup map achieved 76% of accuracy. The A-horizon soil organic matter content map based on the derived fuzzy membership functions was compared with that derived from a multiple linear regression model. The comparison showed that the soil organic content map based on fuzzy membership functions performed better than the soil map based on the linear regression model. The proposed method could also be used to construction membership functions from descriptive knowledge obtained from other sources. |
| [20] | . Sampling design plays an important role in spatial modeling. Existing methods often require a large amount of samples to achieve desired mapping accuracy, but imply considerable cost. When there are not enough resources for collecting a large set of samples at once, stepwise sampling approach is often the only option for collecting the needed large sample set, especially in the case of field surveying over large areas. This article proposes an integrative hierarchical stepwise sampling strategy which makes the samples collected at different stages an integrative one. The strategy is based on samples' representativeness of the geographic feature at different scales. The basic idea is to sample at locations that are representative of large-scale spatial patterns first and then add samples that represent more local patterns in a stepwise fashion. Based on the relationships between a geographic feature and its environmental covariates, the proposed sampling method approximates a hierarchy of spatial variations of the geographic feature under concern by delineating natural aggregates (clusters) of its relevant environmental covariates at different scales. The natural occurrence of such aggregates is modeled using a fuzzy c-means clustering method. We iterate through different numbers of clusters from only a few to many more to be able to reveal clusters at different spatial scales. At a particular iteration, locations that bear high similarity to the cluster prototypes are identified. If a location is consistently identified at multiple iterations, it is then considered to be more representative of the general or large-scale spatial patterns. Locations that are identified less during the iterations are representative of local patterns. The integrative stepwise sampling design then gives higher sampling priority to the locations that are more representative of the large-scale patterns than local ones. We applied this sampling design in a digital soil mapping case study. Different representative samples were obtained and used for soil inference. We started with samples that are the most representative of the large-scale patterns and then gradually included the samples representative of local patterns. Field evaluation indicated that the additions of more samples with lower representativeness lead to improvements of accuracy with a decreasing marginal gain. When cost-effectiveness is considered, the representative grade could provide essential information on the number and order of samples to be sampled for an effective sampling design. |
| [21] | |
| [22] | . 为了在精细尺度下定量刻画地形特征,给地理建模提供更准确的定量地形参数,克服当今应用领域中常用商业软件的局限性,本研究讨论了面向栅格DEM的"简化数字地形分析软件"(SimDTA 1.0版本)。SimDTA实现了诸多计算局域和区域地形属性、定量描述地形部位信息的现有算法,以及新建算法。例如,针对一个实际的应用问题——坡位模糊分类,采用以坡位典型位置作为原型的新思路,在SimDTA中,实现了一个新的坡位模糊分类方法,能够克服现有其他方法忽略空间位置信息等问题。这一坡位模糊分类方法和SimDTA中实现的其他功能相结合,形成了一套完整的坡位模糊分类流程。本文通过在东北嫩江流域一个小区的实际应用和讨论来体现SimDTA的有效性和实用性。 . 为了在精细尺度下定量刻画地形特征,给地理建模提供更准确的定量地形参数,克服当今应用领域中常用商业软件的局限性,本研究讨论了面向栅格DEM的"简化数字地形分析软件"(SimDTA 1.0版本)。SimDTA实现了诸多计算局域和区域地形属性、定量描述地形部位信息的现有算法,以及新建算法。例如,针对一个实际的应用问题——坡位模糊分类,采用以坡位典型位置作为原型的新思路,在SimDTA中,实现了一个新的坡位模糊分类方法,能够克服现有其他方法忽略空间位置信息等问题。这一坡位模糊分类方法和SimDTA中实现的其他功能相结合,形成了一套完整的坡位模糊分类流程。本文通过在东北嫩江流域一个小区的实际应用和讨论来体现SimDTA的有效性和实用性。 |
| [23] | . SoLIM (Soil Land Inference Model) is a fuzzy inference scheme for estimating and representing the spatial distribution of soil types in a landscape. This study developed the inference method a step further to derive continuous soil property maps through two case studies. The first case illustrates the derivation of soil A horizon depth in a mountainous area in western Montana. It was found that the inferred depths are a closer fit to observed depths than those derived from the conventional soil map at both spatial and attribute levels. The second case shows the derivation of soil transmissivity values across a small catchment with a gentle environmental variation in Tumut, NSW, Australia. This case shows that the derived soil transmissivity map is comparable to the results from systematic field survey over a small area. SoLIM works well in an area where there is a good understanding of the relationships between soils and their formative environment and where the soil formative environment can be characterised using current geographical information system techniques. However, we experienced difficulty with the methodology when it was applied in an area where the environmental gradient is gentle and the soil formative environment cannot be very well described using the primitive environmental indices currently employed in SoLIM. |
| [24] | . Soil hydrological properties are highly variable in space. Field measurements of these properties are costly and error prone. As spatially distributed approaches become increasingly important in current hydrological and ecological modeling, an appropriate field sampling scheme to effectively capture spatial variability of hydrological processes becomes essential. A terrain-based slope classification system was applied to delineate the hillslope into representative hydrological domains. This model assumes that there are hydrological landscape units (LUs) along the hillslope in which distinct sets of hydrological and pedological processes occur. Possible water and material flows over the hillslope were first interpreted using a continuity equation of mass flow over the surface, and subsequently included in a terrain analysis. The developed terrain index is able to characterize the hydrological processes, accommodating both continuous and discrete concepts. The model was tested against the intensive soil moisture data at the Tarrawarra catchment, Australia [Water Resour. Res. 34 (1998) 2765]. The delineated soil-揕Us explain up to 73% of the average soil moisture variation when it is combined with other terrain parameters (surface curvature, upslope contributing area and slope aspect). Soil moisture at each LU shows significantly different variance characteristics when compared with other units, and the delineation procedure reduces the spatial variation of soil moisture within each LU. Random permutation and bootstrapping techniques indicate that stratified random sampling based on the delineated hillslope units significantly reduces the number of samples needed to estimate the average soil moisture and the overall error of estimation. |
| [25] | . Transition between slope positions (e.g., ridge, shoulder slope, back slope, foot slope, and valley) is often gradual. Quantification of spatial transitions or spatial gradations between slope positions can increase the accuracy of terrain parameterization for geographical or ecological modeling, especially for digital soil mapping at a fine scale. Current models for characterizing the spatial gradation of slope positions based on a gridded DEM either focus solely on the parameter space or depend on too many rules defined by topographic attributes, which makes such approaches impractical. The typical locations of a slope position contain the characteristics of the slope position in both parameter space and spatial context. Thus, the spatial gradation of slope positions can be quantified by comparing terrain characteristics (spatial and parametrical) of given locations to those at typical locations. Based on this idea, this paper proposes an approach to quantifying the spatial gradation of slope positions by using typical locations as prototypes. This approach includes two parts: the first is to extract the typical locations of each slope position and treat them as the prototypes of this position; and the second is to compute the similarity between a given location and the prototypes based on both local topographic attributes and spatial context. The new approach characterizes slope position gradation in both the attribute domain (i.e., parameter space) and the spatial domain (i.e., geographic space) in an easy and practicable way. Applications show that the new approach can quantitatively describe spatial gradations among a set of slope positions. Comparison of spatial gradation of A-horizon sand percentages with the quantified spatial gradation of slope positions indicates that the latter reflects slope processes, confirming the effectiveness of the approach. The comparison of a soil subgroup map of the study area with the maximum similarity map derived from the approach also suggests that the quantified spatial gradation of slope position can be used to aid geographical modeling such as digital soil mapping. |
| [26] | . This paper presents a detailed performance and sensitivity analysis of a recently developed hydrological landscape classification method based on dominant runoff mechanisms. Three landscape classes are distinguished: wetland, hillslope and plateau, corresponding to three dominant hydrological regimes: saturation excess overland flow, storage excess sub-surface flow, and deep percolation. Topography, geology and land use hold the key to identifying these landscapes. The height above the nearest drainage (HAND) and the surface slope, which can be easily obtained from a digital elevation model, appear to be the dominant topographical controls for hydrological classification. In this paper several indicators for classification are tested as well as their sensitivity to scale and resolution of observed points (sample size). The best results are obtained by the simple use of HAND and slope. The results obtained compared well with the topographical wetness index. The HAND based landscape classification appears to be an efficient method to ''read the landscape'' on the basis of which conceptual models can be developed. |
| [27] | . |
| [28] | . |
| [29] | |
| [30] | . Terrain position (e.g., ridge, mid-slope, valley) is a potentially useful variable with which to model environmental parameters and processes using geographical information systems. Digital elevation data spaced on a regular 30 m grid were generated over an area of flat to moderate topography in south-east Australia. Streams and ridges were mapped from the digital elevation model using a new algorithm that utilizes basic geographical principles. Ridge and stream lines closely followed the original contour map and improved upon the results from three alternative algorithms. Mid-slope positions were successfully interpolated from the stream and ridge lines by a modified measure of Euclidean distance. |
| [31] | |
| [32] | . |
| [33] | . Spatial estimates of tropical soil organic carbon (SOC) concentrations and stocks are crucial to understanding the role of tropical SOC in the global carbon cycle. They also allow for spatial variation of SOC in environmental process models. SOC is spatially highly variable. In traditional approaches, SOC concentrations and stocks have been derived from estimates for single or very few profiles and spatially linked to existing units of soil or vegetation maps. However, many existing soil profile data are incomplete and untested as to whether they are representative or unbiased. Also single means for soil or vegetation map units cannot characterize SOC spatial variability within these units. We here use the digital soil mapping approach to predict the spatial distribution of SOC. This relies on a soil inference model based on spatially referenced environmental layers of topographic attributes, soil units, parent material, and forest history. We sampled soils at 165 sites, stratified according to topography and lithology, on Barro Colorado Island (BCI), Panama, at depths of 0–10cm, 10–20cm, 20–30cm, and 30–50cm, and analyzed them for SOC by dry combustion. We applied Random Forest (RF) analysis as a modeling tool to the SOC data for each depth interval in order to compare vertical and lateral distribution patterns. RF has several advantages compared to other modeling approaches, for instance, the fact that it is neither sensitive to overfitting nor to noise features. The RF-based digital SOC mapping approach provided SOC estimates of high spatial resolution and estimates of error and predictor importance. The environmental variables that explained most of the variation in the topsoil (0–10cm) were topographic attributes. In the subsoil (10–50cm), SOC distribution was best explained by soil texture classes as derived from soil mapping units. The estimates for SOC stocks in the upper 30cm ranged between 38 and 116Mg ha 61021 , with lowest stocks on midslope and highest on toeslope positions. This digital soil mapping approach can be applied to similar landscapes to refine the spatial resolution of SOC estimates. |
| [34] | . This paper proposes, focusing on random forests, the increasingly used statistical method for classification and regression problems introduced by Leo Breiman in 2001, to investigate two classical issues of variable selection. The first one is to find important variables for interpretation and the second one is more restrictive and try to design a good parsimonious prediction model. The main contribution is twofold: to provide some experimental insights about the behavior of the variable importance index based on random forests and to propose a strategy involving a ranking of explanatory variables using the random forests score of importance and a stepwise ascending variable introduction strategy. |
| [35] | . 在没有土壤普查专家及土壤图的地区，获取土壤环境间关系的知识是基于知识进行预测性土壤制图中的关键问题。本文建立了一套应用模糊c均值聚类（Fuzzyc-means，FCM）获取土壤环境间关系知识的方法：得到对土壤形成发展具有重要作用的环境因子，建立环境因子数据库；对环境因子进行模糊聚类，得到环境因子组合隶属度分布图；根据隶属度值确定野外采样点；将环境因子组合与土壤类型对应，进而提取土壤-环境关系知识。为检验该方法的有效性，应用所得知识进行土壤制图，通过独立采样点对土壤图进行精度评价。本文在黑龙江鹤山农场一个研究区的应用结果表明，该方法仅需要少量的野外采样即可获得有效的土壤-环境关系知识，为预测性土壤制图提供必需的依据，同时也显著提高了野外采样的效率。 . 在没有土壤普查专家及土壤图的地区，获取土壤环境间关系的知识是基于知识进行预测性土壤制图中的关键问题。本文建立了一套应用模糊c均值聚类（Fuzzyc-means，FCM）获取土壤环境间关系知识的方法：得到对土壤形成发展具有重要作用的环境因子，建立环境因子数据库；对环境因子进行模糊聚类，得到环境因子组合隶属度分布图；根据隶属度值确定野外采样点；将环境因子组合与土壤类型对应，进而提取土壤-环境关系知识。为检验该方法的有效性，应用所得知识进行土壤制图，通过独立采样点对土壤图进行精度评价。本文在黑龙江鹤山农场一个研究区的应用结果表明，该方法仅需要少量的野外采样即可获得有效的土壤-环境关系知识，为预测性土壤制图提供必需的依据，同时也显著提高了野外采样的效率。 |
| [36] | . . |
