李明强, 郭田德, 韩丛英
中国科学院大学数学科学学院, 北京 100049
摘要: 近些年来，众多****提出基于新步长选择策略的加速梯度投影算法求解大规模优化问题。本文针对线性约束二次规划问题提出两种基于新步长的梯度投影算法。一种是基于采用自适应线搜索和Barzilai-Borwein步长的非单调投影算法。另一种是基于Yuan步长的单调投影算法。在较弱的假设条件下，给出这两种算法的全局收敛性。数值实验表明新算法比传统的梯度投影算法求解效率更高。
关键词: Barzilai-Borwein步长线性等式投影梯度
In this paper, we consider the quadratic programming problem

$\mathop {\min }\limits_{x \in \Omega } f\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{x}},$

(1)

where Q∈R^n×n is symmetric and positive definite, x, c∈Rⁿ, and the feasible region Ω is defined by

$\Omega = \left\{ {\mathit{\boldsymbol{x}} \in {{\bf{R}}^n},\mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}}} \right\},$

(2)

where A∈R^m×n, rank (A)=m, and m < n.
First of all, we give a brief review for the development of the efficient step length selections in gradient methods for minimizing a large scale strictly convex quadratic function f(x). Assume that g(x)=?f(x) can be obtained at every x and g_k=g(x_k) is the gradient at x_k. The classical examples of step size selections are the line searches used in the steepest descent (SD) and the minimal gradient (MG) methods, which minimize f(x_k-αg_k) and ‖g(x_k-αg_k)‖₂, respectively,

$\begin{array}{l}\alpha _k^{SD} = \mathop {\arg \min }\limits_\alpha f\left( {{\mathit{\boldsymbol{x}}_k} - \alpha {\mathit{\boldsymbol{g}}_k}} \right)\\\;\;\;\;\;\; = \frac{{\mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{g}}_k}}}{{\mathit{\boldsymbol{g}}_k^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{g}}_k}}},\end{array}$

(3)

$\begin{array}{l}\alpha _k^{MG} = \mathop {\arg \min }\limits_\alpha {\left\| {\mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{x}}_k} - \alpha {\mathit{\boldsymbol{g}}_k}} \right)} \right\|_2}\\\;\;\;\;\;\; = \frac{{\mathit{\boldsymbol{g}}_k^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{g}}_k}}}{{\mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{Q}}^2}{\mathit{\boldsymbol{g}}_k}}}.\end{array}$

(4)

Though the SD gradient method converges linearly, the convergence rate may be very slow, especially when Q is ill-conditioned in the sense that the condition number cond (Q) is very large. The cond (Q) is defined as follows:

${\rm{cond}}\left( \mathit{\boldsymbol{Q}} \right) = \frac{{{\lambda _n}\left( \mathit{\boldsymbol{Q}} \right)}}{{{\lambda _1}\left( \mathit{\boldsymbol{Q}} \right)}},$

where λ_n(Q) and λ₁(Q) represent the largest and smallest eigenvalues of Q, respectively.
In 1988, a significant step size selection is proposed by Barzilai and Borwein (see Ref.[1]),

$\alpha _k^{BB1} = \frac{{\mathit{\boldsymbol{s}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{s}}_{k - 1}}}}{{\mathit{\boldsymbol{s}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{y}}_{k - 1}}}},$

(5)

$\alpha _k^{BB2} = \frac{{\mathit{\boldsymbol{s}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{y}}_{k - 1}}}}{{\mathit{\boldsymbol{y}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{y}}_{k - 1}}}},$

(6)

where s_k-1=x_k-x_k-1 and y_k-1=g_k-g_k-1. We refer to the step size (5) or (6) as BB (Barzilai and Borwein) step size. From (3) and (4), we can easily obtained the fact that in the unconstrained case, α_k^BB1=α_k-1^SD and α_k^BB2=α_k-1^MG (see Ref.[2]). In other words, the step lengths (5) and (6) use the SD and MG step lengths with one delay, respectively. A feature of BB step size is that the sequences {f(x_k)} and {‖g_k‖₂} are non-monotone, in contrast to the SD and MG methods. Global convergence of the BB method was established by Raydan^[3] in the strictly convex quadratic case with either (5) or (6). Dai and Liao^[4] have shown that the BB method is R-linearly convergent in the n-dimensional case. Moreover, numerical results indicate that the BB method outperforms the method with (3) or (4) for convex quadratic functions (see also Ref.[2]). Starting from (5) and (6), BB-like methods with longer delays have been studied^[5-7]. In Ref.[5], Dai and Fletcher proposed a formula

$\alpha _k^M = \frac{{\sum\nolimits_{i = 1}^M {\mathit{\boldsymbol{s}}_{k - i}^{\rm{T}}{\mathit{\boldsymbol{s}}_{k - i}}} }}{{\sum\nolimits_{i = 1}^M {\mathit{\boldsymbol{s}}_{k - i}^{\rm{T}}{\mathit{\boldsymbol{y}}_{k - i}}} }},$

(7)

where M is a positive integer, and they suggest that M=2 is a better choice for box-constrained quadratic programming.
Recently, some monotone methods which are competitive to the BB-like method are proposed. One of these methods with step length

$\alpha _k^Y = \frac{2}{{\varphi _k^Y + 1\alpha _{k - 1}^{SD} + 1\alpha _k^{SD}}},$

(8)

where

$\varphi _k^Y = \sqrt {{{\left( {1\alpha _{k - 1}^{SD} - 1\alpha _k^{SD}} \right)}^2} + 4\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|_2^2\left\| {{\mathit{\boldsymbol{s}}_{k - 1}}} \right\|_2^2} ,$

was proposed by Yuan in Ref.[8]. A property of (8) is that if α_k^Y has been taken after α_k^SD, only one more step α_k^SD is needed to get the solution to the minimizer of the two-dimensional strictly convex quadratics. If x_k is obtained by (3), then s_k-1=-α_k-1^SDg_k-1. Thus a variant of (8) was proposed in Ref.[9] as follows:

$\alpha _k^{YY} = \frac{2}{{\varphi _k^{VY} + 1\alpha _{k - 1}^{SD} + 1\alpha _k^{SD}}},$

(9)

where

$\varphi _k^{VY} = \sqrt {{{\left( {1\alpha _{k - 1}^{SD} - 1\alpha _k^{SD}} \right)}^2} + \frac{{4\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|_2^2}}{{{{\left( {\alpha _{k - 1}^{SD}{{\left\| {{\mathit{\boldsymbol{g}}_{k - 1}}} \right\|}_2}} \right)}^2}}}} .$

Based on (9), Dai and Yuan^[9] proposed a gradient method whose step length is given by

${\alpha _k} = \left\{ \begin{array}{l}\alpha _k^{SD}\;\;\;\;{\rm{if}}\;{\rm{mod}}\left( {k,4} \right) = 1\;{\rm{or}}\;{\rm{2,}}\\\alpha _k^{VY}\;\;\;\;{\rm{otherwise}}.\end{array} \right.$

(10)

It is not difficult to verify the monotonicity of the method because α_k^VY≤2α_k^SD.
The efficiency of the project gradient methods with the above step length selections has been verified by a large amount of numerical experiments on box-constrained quadratic programming^[10-13] and Support Vector Machines(SVMs)^{[5, 14-16]}. Inspired by the success of these new step selection rules, we improve project gradient methods for (1).
1 PBB method analysisIn this section, we focus our attention on designing efficient project gradient type methods for solving (1). Here we let P denote the projection operator on Ω:

$\mathit{\boldsymbol{P}}\left( \mathit{\boldsymbol{x}} \right) = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{y}} \in \Omega } {\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right\|_2}$

(11)

$ = \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{T}}\left( {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{b}}} \right),$

(12)

where T=A^T(AA^T)^-1. Let d(x) be defined in terms of the gradient g(x) as follows:

$\begin{array}{l}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right) - \mathit{\boldsymbol{x}}\\\;\;\;\;\;\;\;\;\mathit{\boldsymbol{ = }} - \mathit{\boldsymbol{Hg}}\left( \mathit{\boldsymbol{x}} \right),\end{array}$

(13)

where H=I-A^T(AA^T)^-1A.
Given an iterate point x_k, the project gradient method for (1) computes the next point in the following form:

${\mathit{\boldsymbol{x}}_{k + 1}} = {\mathit{\boldsymbol{x}}_k} + {\alpha _k}{\mathit{\boldsymbol{d}}_k},$

(14)

where d_k=d(x_k) and α_k>0 is a step length. It is easy to know that s_k-i=α_k-id_k-i and y_k-i=α_k-iQd_k-i, so we obtain another form of (7)

$\alpha _k^M = \frac{{\sum\nolimits_{i = 1}^M {\alpha _{k - i}^2\mathit{\boldsymbol{d}}_{k - i}^{\rm{T}}{\mathit{\boldsymbol{d}}_{k - i}}} }}{{\sum\nolimits_{i = 1}^M {\alpha _{k - i}^2\mathit{\boldsymbol{d}}_{k - i}^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_{k - i}}} }}.$

(15)

We refer to the project gradient method with BB-like step length (15) as the projected BB method or PBB method. Obviously, the formula (5) is as a special case of (15) with M=1.
Compared with original project gradient method(PSD), the PBB method is much more effective. In PSD, there is α_k=α_k^SD′, where

$\begin{array}{l}\alpha _k^{SD'} = \mathop {\min }\limits_\alpha f\left( {{\mathit{\boldsymbol{x}}_k} + \alpha {\mathit{\boldsymbol{d}}_k}} \right)\\\;\;\;\;\;\;\; = - \frac{{\mathit{\boldsymbol{g}}_k^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_k}}}{{\mathit{\boldsymbol{d}}_k^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_k}}}.\end{array}$

(16)

In order to illustrate the performance of the PBB method for (1), we have generated 10 random test problems with n=1 000, m=200 and M=2. A, c and the initial point x₀ is generated randomly, b=Ax₀. Also Q is randomly generated with a range of condition numbers from 10² to 10⁴. The terminal condition is ‖d_k‖_∞ < 10^-4. The numerical results of the PBB method are presented in Table 1.
Table 1

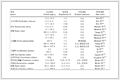Table 1 Numerical results of PSD and PBB methods Problem PBB PSD cond(Q) iter sec iter sec 10e+3 126 0.86 1145 5.57 10e+2 47 0.39 213 1.30 10e+3 94 0.69 977 4.64 10e+4 334 1.97 5 333 23.37 10e+3 115 0.81 1 019 4.61 10e+3 154 0.94 1 151 5.23 10e+4 351 1.66 4 673 20.40 10e+2 49 0.52 207 1.02 10e+2 56 0.47 219 1.06 10e+4 302 1.55 4 411 19.05 average 162.8 0.98 1 934.8 8.67

Table 1 Numerical results of PSD and PBB methods

In Table 1, cond(Q) is the condition number of Q, iter and sec denote the iteration numbers and the time required respectively.
From Table 1, we can see that the PBB method is much more effective in solving the 10 test problems compared with the PSD method. PBB method with an average of 162.8 iterations and 0.98 s have an obvious advantage than PSD with an average of 1 934.8 and 8.67 s.
2 Two efficient project gradient methodsThough the PBB method performs very well in solving (1), there is no theory to guarantee its global convergence in constrained case^[10]. To ensure global convergence of this method, we modify this method by incorporating some sort of line search. It is important that the line search does not degrade the performance of the unmodified PBB method.
Firstly, the sequence {f(x_k)} generated by the PBB method is non-monotone, so a non-monotone line search is necessary. Secondly, we take α_k^M as the step length at each iteration as much as possible. Based on these two considerations, the GLL (Grippo-Lampariello-Lucidi)^[17] non-monotone line search is a good choice. We refer to the modified PBB method with the GLL non-monotone line search as MPBB method (see Algorithm 1).
Table

Algorithm 1 MPBB method Step 1: Let x0 be a feasible point of (1), f0r=∞, f0s=f(x0), k=0, l=0, L, M∈N+, H=I-AT (AAT)-1A, α0M=1, k0s=k0r=0, i=h=0. Step 2: dk=-Hgk and terminate if ‖dk‖∞=0. Step 3: If f(xk+αkMdk)≥fhr ????????xk+1=xk+αkSD′dk ????else ????????xk+1=xk+αkMdk ????end. Step 4: If f(xk+1) < f(xkis) ????????ki+1s=k+1, kh+1r=k+1, i=i+1, l=0 ????else ????????l=l+1 if l=L ????h=h+1, $f_h^r = \mathop {\max }\limits_{0 \le j \le L} \left\{ {f\left( {{\mathit{\boldsymbol{x}}_{k_h^r + j}}} \right)} \right\}$ , kh+1r=khr+L, l=0 ????????end end. Step 5: k=k+1, goto Step2.

f(x_ki^s) is the smallest objective function value over the past k_i^s iterations, that is,

$f\left( {{\mathit{\boldsymbol{x}}_{k_i^s}}} \right) = \mathop {\min }\limits_{0 \le j \le k_i^s} f\left( {{\mathit{\boldsymbol{x}}_j}} \right).$

Obviously {f(x_ki^s)} is a strictly monotone decreasing sequence. If no smaller function value is found in L+1 iterations, the reference function value f_h^r will be updated by the maximum function value in most recent L+1 iterations.
Next, we will introduce a kind of monotone project gradient method with a new step length similar to (10). Now we give a general form of the monotone project gradient method for (1) (see Algorithm 2).
Table

Algorithm 2 Monotone algorithm Step 1: Let x0 be a feasible point of (1), k=0, H=I-AT (AAT)-1A. Step 2: dk=-Hgk and terminate if ‖dk‖∞=0. Step 3: xk+1= xk+αkdk, where αk=ρkαkSD′, ρk∈[0, 2]. Step 4: k=k+1; goto Step2. Step 5: k=k+1, goto Step2.

The following step length similar to α_k^VY

$\alpha _k^{VY'} = \frac{2}{{\varphi _k^{VY'} + 1\alpha _{k - 1}^{SD'} + 1\alpha _k^{SD'}}}$

(17)

where

$\varphi _k^{VY'} = \sqrt {{{\left( {1\alpha _{k - 1}^{SD'} - 1\alpha _k^{SD'}} \right)}^2} + \frac{{4\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|_2^2}}{{{{\left( {\alpha _{k - 1}^{SD'}{{\left\| {{\mathit{\boldsymbol{g}}_{k - 1}}} \right\|}_2}} \right)}^2}}}} $

is given by replacing α_k^SD with α_k^SD′ in (9). Following the formula (10), the step length

$\alpha _k^{SY} = \left\{ \begin{array}{l}\alpha _k^{SD'}\;\;\;\;{\rm{if}}\;{\rm{mod}}\left( {k,4} \right) = 1\;{\rm{or}}\;{\rm{2}}\\\alpha _k^{VY'}\;\;\;\;{\rm{otherwise}}\end{array} \right.$

(18)

is given. We refer to the project gradient method with (18) as the PSY method. Obviously, the methods PSD and PSY are special cases of the Algorithm 2.
Here we need to point out that α_k^VY′ may not have the similar property of (8) and (9) in two-dimensions for (1), but the numerical results will show that the PSY method is comparable to the PBB method.
3 Global convergence analysisIn this section, we analyze the global convergence of Algorithm 1 and Algorithm 2. In what follows, we denote the set of solutions to (1) by

${{\bf{X}}^ * } = \left\{ {{\mathit{\boldsymbol{x}}^ * } \in \Omega \left| {f\left( x \right) \ge f\left( {{x^ * }} \right),} \right.{\rm{for}}\;{\rm{all}}\;x \in \Omega } \right\},$

and the optimal value of (1) by f^*.
Theorem 3.1????If Algorithm 1 does not terminate in a finite number of iterations, there must exist a strictly monotone decreasing infinite subsequence in {f(x_k)}.
Proof????Let p be the length of the {f(x_ki^s)}. If p=+∞, {f(x_ki^s)} is the subsequence satisfying the requirement.
If p < +∞ is finite, there exists a const h₀ which satisfies k^r_h0=k_p^s. Without loss of generality, let h₀=0. Since no smaller function value is found after iteration k_p^s, the reference function f_h^r will be updated every L+1 iterations and the length of {f_h^r} is infinite. It is easy to see that

$f_{{h_0} + q}^r = f_q^r = \mathop {\max }\limits_{0 \le j \le L} \left\{ {f\left( {{\mathit{\boldsymbol{x}}_{k_q^r + j}}} \right)} \right\},q = 1,2, \cdots $

(19)

On the other hand,

$f_q^r > f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 1}^r + j}}} \right),j = 1,2, \cdots ,L.$

(20)

It follows from k_q+1^r=k_q^r+L, (19) and (20) that

$f_q^r \ge \mathop {\max }\limits_{0 \le j \le L} \left\{ {f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 1}^r + j}}} \right)} \right\}$

(21)

$ = f_{q + 1}^r.$

(22)

Let q=q+1 in (20), then f_q+1^r>f(x_k^rq+2+j), j=1, 2, …, L. Combining (22), we conclude that

$f_q^r > f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 2}^r + j}}} \right),j = 1,2, \cdots ,L.$

(23)

Let j=L in (20), then

$\begin{array}{l}f_q^r > f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 1}^r + L}}} \right)\\\;\;\;\;\; = f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 2}^r}}} \right)\end{array}$

(24)

It follows from (23) and (24) that

$f_q^r > \mathop {\max }\limits_{0 \le j \le L} \left\{ {f\left( {{\mathit{\boldsymbol{x}}_{k_{q + 2}^r + j}}} \right)} \right\} = f_{q + 2}^r$

which implies that either even or odd subsequence of {f_q^r} is strictly monotone decreasing. In conclusion, the theorem is true.
We give some properties of P(x) and d(x) which will be used in the following theorems, where P(x) and d(x) are defined as (11) and (13) respectively.
Proposition 3.1????(Properties of P(x) and d(x))
P1.?y∈Rⁿ and x∈Ω, (P(y)-y)^T(x-P(y))≥0.
P2.?x∈Ω, g(x)^Td(x)≤-d(x)^Td(x).
P3.?x^**∈Ω, d(x^**)=0 if and only if g(x^**)^T(x-x^**)≥0 for all x∈Ω.
P4.?x∈Rⁿ and x^**∈X^**={y∈Ω|d(y)=0}, we have

${\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right\|_2} \le \frac{{1 + {\lambda _n}}}{{{\lambda _1}}}{\left\| {\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right\|_2}.$

Proof????Firstly, P1 is the optimal condition of (11)(see Ref.[11]).
From P1, we can easily obtain P2 by replacing y with x-g(x) in P1.
P3 is proved as follows.
From the definition of d(x), we know that if d(x^**)=0, x^**=P(x^**-g(x^**)). If y is replaced by x^**-g(x^**) in P1, P1 yields

$\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right) \ge 0\forall \mathit{\boldsymbol{x}} \in \Omega .$

(25)

Conversely, due to P(x^**-g(x^**))∈Ω, we have

$\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right) \ge 0.$

From above inequality and P2, we obtain

$0 \le - \mathit{\boldsymbol{d}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right) \le 0$

which means d(x^**)=0.
Finally, we consider P4. In P1, y is replaced with x-g(x) and x is replaced with x^**, then we have inequality as follows,

$\begin{array}{l}{\left( {\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right) - \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)^{\rm{T}}}\\\left( {{\mathit{\boldsymbol{x}}^{ * * }}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)} \right) \ge 0.\end{array}$

(26)

In fact, by the definition of d(x) as (13), we know that (26) is equivalent to

$\begin{array}{*{20}{c}}{{{\left( {\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right) + }\\{\mathit{\boldsymbol{g}}{{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right) \ge \mathit{\boldsymbol{g}}{{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right).}\end{array}$

(27)

Rearranging (27), we have

$\begin{array}{l}\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right) - \mathit{\boldsymbol{g}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)\\\;\; \ge \mathit{\boldsymbol{d}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right) + {\left\| {\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right\|_2} + \\\;\;{\left( {\mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right) - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)\\\;\; \ge \mathit{\boldsymbol{d}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right) + {\left\| {\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right\|_2} + \\\;\;{\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)\\\;\; \ge \mathit{\boldsymbol{d}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right) + {\lambda _1}\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right\|_2^2.\end{array}$

(28)

On the other hand,

$\begin{array}{l}\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right) - \mathit{\boldsymbol{g}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)\\\;\;\; = \mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right) + {\left( {\mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right) - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right) - \\\;\;\;\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)\\\;\;\; = \mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right) + {\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Qd}}\left( \mathit{\boldsymbol{x}} \right)\\\;\;\; = \mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)} \right)} \right) + \\\;\;\;\;\;\;{\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Qd}}\left( \mathit{\boldsymbol{x}} \right).\end{array}$

(29)

Since P(x-g(x))∈Ω and from P3, then we have

$\begin{array}{l}\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^{ * * }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right) - \mathit{\boldsymbol{g}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)\\\;\;\; \le {\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Qd}}\left( \mathit{\boldsymbol{x}} \right).\end{array}$

(30)

Combining (28) and (30), we obtain that

$\begin{array}{l}\mathit{\boldsymbol{d}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right) + {\lambda _1}\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right\|_2^2\\\;\; \le {\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Qd}}\left( \mathit{\boldsymbol{x}} \right).\end{array}$

(31)

Rearranging (31), we have

$\begin{array}{l}{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right\|_2} \le \frac{{{{\left( {{\mathit{\boldsymbol{x}}^{ * * }} - \mathit{\boldsymbol{x}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{Q}}} \right)\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)}}{{{\lambda _1}{{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^{ * * }}} \right\|}_2}}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le \frac{{1 + {\lambda _n}}}{{{\lambda _1}}}{\left\| {\mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{x}} \right)} \right\|_2}.\end{array}$

(32)

This completes the proof.
Now, we give the following theorem about the equivalent optimal conditions of (1).
Theorem 3.2????Suppose x^* is a feasible point of (1), the following results are equivalent:
E1.x^*∈X^*.
E2.d(x^*)^Tg(x^*)=0.
E3.d(x^*)^TQd(x^*)=0.
E4.d(x^*)=0.
Proof E1?E4:
From P3, d(x^*)=0 is equivalent to

$\mathit{\boldsymbol{g}}{\left( {{\mathit{\boldsymbol{x}}^ * }} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^ * }} \right) \ge 0,\forall \mathit{\boldsymbol{x}} \in \Omega .$

The above inequality implies that x^* is the solution of the following linear programming

$\begin{array}{*{20}{c}}{\min \mathit{\boldsymbol{g}}{{\left( {{\mathit{\boldsymbol{x}}^ * }} \right)}^{\rm{T}}}\mathit{\boldsymbol{x}}}\\{{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{x}} \in \Omega .}\end{array}$

(33)

Obviously, (1) and (37) have the same KKT system, so x^*∈X^*.
Since E1?E4, d(x^*)=0. Then proposition E1?E2 and E1?E3 can be easily obtained. From E2 and P2, we have that d(x^*)=0, which means E1 is established.
E3?E1:
Assume E1 is not established, that is, x^*?X^*. From P2 and E2, we have d(x^*)^Tg(x^*) < 0. As f(x) is quadratic and d(x^*)^TQd(x^*)=0, we have f(x^*+αd(x^*))=f(x^*)+αg(x^*)^Td(x^*). Let α→+∞, then f(x^*+αd(x^*))→-∞ which contradicts that (1) is bounded below. Thus, x^* belongs to X^*.
According to Theorem 3.2 and P4, we can see that X^*=X^**. Then, for all feasible points x?X^*,

$\mathit{\boldsymbol{d}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}\mathit{\boldsymbol{Qd}}\left( \mathit{\boldsymbol{x}} \right) > 0.$

Thus, the formula (15) and (18) are well defined unless x_k is a optimal point of (1).
Finally, we present the global convergence of Algorithm 2.
Theorem 3.3????If Algorithm 2 does not terminate in a finite number of iterations and the sequence {ρ_k} has an accumulation point $\tilde \rho \in \left({0, 2} \right)$ , then the sequence {f(x_k)} generated by Algorithm 2 converges to f^*.
Proof????Observe that for all k,

${\phi _k}\left( \rho \right) = f\left( {{\mathit{\boldsymbol{x}}_k} + \rho \alpha _k^{SD'}{\mathit{\boldsymbol{d}}_k}} \right)$

is a quadratic convex function of the variable ρ. From the definition of α_k^SD′, we get that ?_k(ρ) attains global minimum when ρ=1. Hence by symmetry of the quadratic convex function ?_k(ρ), ?_k(0)=?_k(2) and for any ρ∈[0, 2], ?_k(ρ)≤?_k(0). Therefore

${\phi _k}\left( {{\rho _k}} \right) = f\left( {{\mathit{\boldsymbol{x}}_{k + 1}}} \right) \le f\left( {{\mathit{\boldsymbol{x}}_k}} \right),$

for all k. The above inequality implies that {f(x_k)} is a monotonically decreasing sequence. Furthermore, f(x_k) is bounded below, so {f(x_k)} a convergent sequence,

$\mathop {\lim }\limits_{k \to + \infty } \left( {f\left( {{\mathit{\boldsymbol{x}}_k}} \right) - f\left( {{\mathit{\boldsymbol{x}}_{k + 1}}} \right)} \right) = 0.$

(34)

Because ${\tilde \rho }$ is an accumulation point of {ρ_k} and $\tilde \rho \in \left({0, 2} \right)$ , there exists a const β∈(0, 1) and subsequence ρ_kj∈[β, 2-β]. Using the properties of ?_k we have

$\begin{array}{l}f\left( {{\mathit{\boldsymbol{x}}_{{k_j}}}} \right) - f\left( {{\mathit{\boldsymbol{x}}_{{k_{j + 1}}}}} \right) = {\phi _{{k_j}}}\left( 0 \right) - {\phi _{{k_j}}}\left( {{\rho _{{k_j}}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ge {\phi _{{k_j}}}\left( 0 \right) - {\phi _{{k_j}}}\left( \beta \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \beta {{\phi '}_{{k_j}}}\left( 0 \right) - \frac{{{\beta ^2}}}{2}{{\phi ''}_{{k_j}}}\left( 0 \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \beta \alpha _{{k_j}}^{SD'}\mathit{\boldsymbol{g}}_{{k_j}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{{k_j}}} - \frac{{{\beta ^2}}}{2}\alpha _{{k_j}}^{SD'2}\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_{{k_j}}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{\beta \left( {2 - \beta } \right)}}{2}\frac{{{{\left( {\mathit{\boldsymbol{g}}_{{k_j}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{{k_j}}}} \right)}^2}}}{{\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_{{k_j}}}}}\end{array}$

Since g^T_kjd_kj≤-d^T_kj≤0, then |g^T_kjd_kj|≥|d^T_kjd_kj|. Thus, we have that

$\begin{array}{l}f\left( {{\mathit{\boldsymbol{x}}_{{k_j}}}} \right) - f\left( {{\mathit{\boldsymbol{x}}_{{k_j} + 1}}} \right) \ge \frac{{\beta \left( {2 - \beta } \right)}}{2}\frac{{{{\left( {\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{{k_j}}}} \right)}^2}}}{{\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{d}}_{{k_j}}}}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ge \frac{{\beta \left( {2 - \beta } \right)\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{{k_j}}}}}{{2{\lambda _{\max }}\left( \mathit{\boldsymbol{Q}} \right)}}.\end{array}$

(35)

Let j→+∞ in the (35), then

$\begin{array}{*{20}{c}}{0 = \mathop {\lim }\limits_{j \to + \infty } \left( {f\left( {{\mathit{\boldsymbol{x}}_{{k_j}}}} \right) - f\left( {{\mathit{\boldsymbol{x}}_{{k_{j + 1}}}}} \right)} \right)}\\{ \ge \mathop {\lim }\limits_{j \to + \infty } \frac{{\beta \left( {2 - \beta } \right)\mathit{\boldsymbol{d}}_{{k_j}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{{k_j}}}}}{{2{\lambda _{\max }}\left( \mathit{\boldsymbol{Q}} \right)}} \ge 0.}\end{array}$

From the above inequality, we conclude that d_kj→0, j→+∞.
It follows from P4 that x_kj converges to some optimal point x^*∈X^*. Since f(x) is continuous, we have

$f\left( {{\mathit{\boldsymbol{x}}_{{k_j}}}} \right) \to {f^ * }.$

As {f(x_k)} is decreasing and bounded from below, the whole sequence {f(x_k)} converges to f^*.
4 Numerical experimentsIn this section, we report the numerical results of the project gradient methods proposed in this paper. The test problems are designed based on nine parameters n, m, ncond, l_x, u_x, l_A, u_A, l_c, u_c. In particular, we denote Q=PΛP^T, where

$\mathit{\boldsymbol{P}} = \mathop {\mathit{\Pi }}\limits_{i = 1}^3 \left( {\mathit{\boldsymbol{I}} - 2{\mathit{\boldsymbol{\omega }}_i}\mathit{\boldsymbol{\omega }}_i^{\rm{T}}} \right)$

and ω₁, ω₂, ω₃ are random unit vectors, and Λ is diagonal matrix whose i-th component is defined by

$\log {\lambda _i} = \frac{{i - 1}}{{n - 1}}n{\rm{cond}},i = 1, \cdots ,n.$

The initial point x₀, matrix A and the linear term c are generated by Matlab function rand with entries in [l_x, u_x], [l_A, u_A], [l_c, u_c] respectively. b is built as b=Ax₀. In our tests, we have fixed (l_x, u_x, l_A, u_A, l_c, u_c)=(-5, 5, -10, 10, -10, 10). m, n, and ncond are positive integers chosen randomly in the interval [50, 800], [1 000, 2 000] and [2, 6] by the function randint respectively. As the stopping criterion we use

${\left\| {{\mathit{\boldsymbol{d}}_k}} \right\|_\infty } \le {10^{ - 4}}{\left\| {{\mathit{\boldsymbol{d}}_0}} \right\|_\infty }.$

All tests are conducted on a Windows XP professional computer (Pentium R, 2.79 GHZ) with Matlab 7.10.
Firstly, we generate 100 random test problems to test the PBB method and the MPBB method with M=1, 2, …, 15. The numerical results are reported in Table 2, where Aiter and Asec denote the average number of iterations and time required with regard to these 100 test problems respectively.
Table 2

Table 2 Testing the PBB and MPBB methods as M increases M PBB MPBB Aiter Asec Aiter Asec 1 309.96 3.85 176.37 2.58 2 282.61 3.61 138.73 2.14 3 277.23 3.57 145.46 2.25 4 268.54 3.49 154.15 2.30 5 277.43 3.57 149.62 2.27 6 268.04 3.47 154.87 2.29 7 277.60 3.56 155.44 2.23 8 282.33 3.61 156.89 2.33 9 278.53 3.57 156.09 2.33 10 282.42 3.58 157.24 2.32 11 285.95 3.64 166.88 2.44 12 291.98 3.72 170.28 2.49 13 297.73 3.76 172.13 2.45 14 303.85 3.80 176.87 2.56 15 295.85 3.73 177.33 2.52

Table 2 Testing the PBB and MPBB methods as M increases

From Table 2, we see that the PBB method performs worse as M(M>6) increases with rare exception, so does the MPBB method (M>2). On the whole, the iterations and time of these two methods have a tendency to ascend with the growth of M. At the same time, we suggest M=6 for the PBB method and M=2 for the MPBB method. Also we conclude that the MPBB method performs much better than PBB method.
Table 3 lists the numbers of iterations and time required by the PSD, PBB (M=6), MPBB (M=2) and PSY methods for 15 random problems. From this table, we can clearly see that the PSD method is significantly slower than the other three methods. Although, the PSY is slightly worse than the MPBB method, the PSY method performs better than PBB method. What's more, the MPBB method proposed by us is not only to guarantee the convergence of PBB method but also to perform much better than the latter one.
Table 3

Table 3 Comparison of numerical results for random test problems among the methods Problem PSD PBB MPBB PSY ncond m n Iter Sec Iter Sec Iter Sec Iter Sec 2 661 1 906 145 3.73 47 2.04 33 2.15 43 2.58 5 793 1 833 5 553 84.23 402 7.84 201 5.41 232 7.73 2 258 1 805 251 4.11 59 1.31 52 1.28 54 1.88 3 242 1 288 1 195 8.88 118 1.09 121 1.22 119 1.58 2 383 1 015 129 0.94 41 0.48 40 0.59 42 0.70 4 676 1 334 1 035 9.25 137 2.08 93 1.78 126 2.70 2 716 1 686 117 3.03 41 2.01 32 2.05 46 2.30 2 226 1 802 241 3.63 61 1.48 52 1.30 62 1.92 4 418 1 388 3 107 25.16 207 2.29 153 1.84 179 2.75 6 322 1 107 22 329 123.30 810 4.77 262 1.64 418 3.75 3 470 1 914 1 005 15.17 111 2.52 118 2.92 147 4.42 5 78 1 910 25 911 469 548 9.81 192 2.95 208 4.72 6 489 1 906 26 883 486.67 1 090 21.93 253 5.97 227 7.25 2 638 1 128 69 1.39 40 1.18 26 1.14 25 1.16 5 689 1 777 6 569 102.78 357 7.60 194 5.28 255 8.06 5 399 1 511 14 087 161.25 519 5.93 237 3.37 300 5.92 4 766 1 060 225 2.38 74 1.58 49 1.43 50 1.54 average 6 403 88.53 274.23 4.47 124 2.49 149 3.59

Table 3 Comparison of numerical results for random test problems among the methods

5 ConclusionsIn this paper, we proposed two methods, MPBB and PSY, for quadratic programming with linear equality constraints (QPLE) based on the efficient step length selections and have established their convergence under mild assumptions. Our numerical results demonstrate that the new project gradient methods with these step selection rules have superiority over the methods with classical step length.
References

[1]	Barzilai J, Borwein J M. Two-point step size gradient methods[J].IMA Journal of Numerical Analysis, 1988, 8(1):141–148.DOI:10.1093/imanum/8.1.141
[2]	Zhou B, Gao L, Dai Y H. Gradient methods with adaptive step-sizes[J].Computational Optimization and Applications, 2006, 35(1):69–86.DOI:10.1007/s10589-006-6446-0
[3]	Raydan M. On the Barzilai and Borwein choice of steplength for the gradient method[J].IMA Journal of Numerical Analysis, 1993, 13(3):321–326.DOI:10.1093/imanum/13.3.321
[4]	Dai Y H, Liao L Z. R-linear convergence of the Barzilai and Borwein gradient method[J].IMA Journal of Numerical Analysis, 2002, 22(1):1–10.
[5]	Dai Y H, Fletcher R. New algorithms for singly linearly constrained quadratic programs subject to lower and upper bounds[J].Mathematical Programming, 2006, 106(3):403–421.DOI:10.1007/s10107-005-0595-2
[6]	Raydan M. The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem[J].SIAM Journal on Optimization, 1997, 7(1):26–33.DOI:10.1137/S1052623494266365
[7]	Yuan Y. Gradient methods for large scale convex quadratic functions[M].Berlin: Springer Heidelberg, 2010: 141-155.
[8]	Yuan Y. A new stepsize for the steepest descent method[J].Journal of Computational Mathematics, 2006:149–156.
[9]	Dai Y, Yuan Y X. Analysis of monotone gradient methods[J].Journal of Industrial and Management Optimization, 2005, 1(2):181.DOI:10.3934/jimo
[10]	Dai Y H, Fletcher R. Projected Barzilai-Borwein methods for large-scale box-constrained quadratic programming[J].Numerische Mathematik, 2005, 100(1):21–47.DOI:10.1007/s00211-004-0569-y
[11]	Hager W W, Zhang H. A new active set algorithm for box constrained optimization[J].SIAM Journal on Optimization, 2006, 17(2):526–557.DOI:10.1137/050635225
[12]	Zhou B, Gao L, Dai Y. Monotone projected gradient methods for largescale box-constrained quadratic programming[J].Science in China Series A, 2006, 49(5):688–702.DOI:10.1007/s11425-006-0688-2
[13]	De Asmundis R, di Serafino D, Riccio F, et al. On spectral properties of steepest descent methods[J].IMA Journal of Numerical Analysis, 2013:drs056.
[14]	Zanni L, Serafini T, Zanghirati G. Parallel software for training large scale support vector machines on multiprocessor systems[J].Journal of Machine Learning Research, 2006, 7(7):1467–1492.
[15]	Serafini T, Zanghirati G, Zanni L. Parallel decomposition approaches for training support vector machines[J].Advances in Parallel Computing, 2004, 13:259–266.DOI:10.1016/S0927-5452(04)80035-2
[16]	Zanghirati G, Zanni L. A parallel solver for large quadratic programs in training support vector machines[J].Parallel computing, 2003, 29(4):535–551.DOI:10.1016/S0167-8191(03)00021-8
[17]	Grippo L, Lampariello F, Lucidi S. A nonmonotone line search technique for Newton's method[J].SIAM Journal on Numerical Analysis, 1986, 23(4):707–716.DOI:10.1137/0723046