薛珊, 赵武奇, 高贵田, 吴忠. 苦瓜片气体射流冲击干燥特性及干燥模型[J]. , 2017, 50(4): 743-754 https://doi.org/10.3864/j.issn.0578-1752.2017.04.014
XUE Shan, ZHAO WuQi, GAO GuiTian, WU Zhong. Drying Characteristics and Model of Bitter Melon Slice in Air-Impingement Jet Dryer[J]. Scientia Acricultura Sinica, 2017, 50(4): 743-754 https://doi.org/10.3864/j.issn.0578-1752.2017.04.014

0 引言

【研究意义】苦瓜,又称之为凉瓜、锦荔枝、赖葡萄,系葫芦科苦瓜属植物,是一种日常生活中十分常见的蔬菜,属一年生草质藤木植物,原产于亚热带,现在热带、亚热带和温带都能够种植^[1]。苦瓜营养丰富,含蛋白质、糖类、多种氨基酸、粗纤维、维生素、矿物质等营养成分,其中Vc含量高达（56—120）mg/100 g,居于瓜类蔬菜之首^[2-3]。现代医药学研究表明,苦瓜具有降低血糖、抗肿瘤以及提高人体免疫力等功能,是一种药食兼用的保健食品^[4-7]。新鲜的苦瓜水分含量较高,且不耐冷藏,货架期短^[8],而苦瓜干制是苦瓜贮藏的重要手段之一。将苦瓜干制不仅能平衡淡旺季需求、缩减存储空间、丰富产品结构,而且可以使人们充分利用苦瓜的保健价值^[3]。气体射流冲击技术是近几年才引入中国的一种干燥技术,在干燥过程中,由于喷出的气体具有极高的速度,使得气流与物料表面产生非常薄的边界层,从而提高了传热效率和热质交换速率,缩短了干燥时间。已有研究表明,气体射流冲击干燥的换热系数比传统热风干燥的换热系数要高出几倍甚至一个数量级^[9-10]。因此,气体射流冲击干燥技术对于提高干制品品质、节约能耗、缩短干燥时间等均具有重要意义。【前人研究进展】现有的苦瓜干制方法主要有热风干燥、真空干燥、真空冷冻干燥、喷雾干燥、微波干燥以及联合干燥等^[3,11-12]。但已有的研究大多数都探讨的是不同干燥条件对苦瓜中各种营养成分的影响,这些营养成分主要包括苦瓜多糖、多肽、皂苷、Vc、叶绿素、黄酮等,而关于苦瓜干燥过程中干燥特性和干燥模型的研究较少。气体射流冲击干燥技术是一种新型干燥技术,目前已经成功应用于紫薯^[10]、无核紫葡萄^[13]、哈密瓜^[14]、杏子^[15]、胡萝卜^[16]、种子^[17]、板栗^[18]、党参^[19]的研究中,并且取得了显著的效果。其中,李文峰等^[10]通过对紫薯干燥模型的建立,很好的描述了干燥过程中紫薯的水分散失规律;杨文侠等^[13]通过对无核紫葡萄干燥模型的建立,为在线监测无核紫葡萄的含水率提供了理论依据;张茜等^[14]通过对哈密瓜干燥模型的建立,为哈密瓜片的工业化生产提供了理论依据等。现有文献未见到将气体射流冲击技术应用于苦瓜干制的报道。【本研究切入点】目前,苦瓜片的制备方法主要是传统的晒干法和烘干法,但其存在干燥周期长、品质难以控制或能耗高等不足,且对于苦瓜片干燥过程中的传质特性还不清楚;而气体射流冲击干燥技术不仅具有传热速度快,能耗低,产品品质佳的优势,还可以为苦瓜片的新型干燥技术提供理论基础。【拟解决的关键问题】本研究采用气体射流冲击干燥技术对苦瓜片进行干燥,并探究风温、切片厚度和风速对苦瓜片干燥特性的影响,确定最适的干燥模型,为进一步研究苦瓜片干燥过程中质的传递提供理论依据。

1 材料与方法

试验于2016年3月在陕西师范大学食品工程与营养科学学院食品工程实验室进行。

1.1 试验原料

苦瓜购买于寿光市农圣庄园农业发展有限公司,挑选无腐烂、成熟度适中、直径为5 cm左右的鲜苦瓜（品种为赛碧绿F1）,在3℃条件下贮藏。鲜苦瓜样品的平均干基湿含量为95.3%（烘干法测定,105℃烘干至恒重^[20]）。

1.2 主要仪器及试验装置

电子天平：BS224S型,北京赛多利斯系统有限公司;风速计：AVM-03,泰仪电子工业股份有限公司;电冰箱：海尔BCD-210G/C,青岛海尔股份有限公司;烘箱：常州远宇干燥设备有限公司;刀具和尺子。
本研究所用的气体射流冲击干燥试验设备为陕西师范大学食品工程实验室设计,其结构原理见文献[10]。

1.3 干燥试验

从冰箱中取出保存的鲜苦瓜,先用自来水冲洗干净,然后用纸巾将其表面的水吸干,待其恢复到室温;用刀切去苦瓜两端,并从中间纵向切成两半,去瓤,并按照试验要求切片。为节省称重时间,将处理好的苦瓜片均匀平铺于自制金属网筛中。干燥试验风温设置在40—80℃范围内以每10℃为间隔（温度太低,干燥时间太长;温度太高,干燥产品色泽差）;风速由变频器控制并在9—13 m·s^-1范围内可调;切片厚度为2—6 mm（苦瓜片太薄干燥后易破碎,太厚干燥耗时太长）,以1 mm为间隔。具体试验安排如表1所示。
Table 1
表1
表1试验设计和试验参数
Table 1Experiment design and parameters

试验序号 No.	风温（T） Temperature (℃)	风速（V） Air velocity (m·s-1)	切片厚度（D） Slice thickness (mm)
1	40	11	4
2	50	11	4
3	60	11	4
4	70	11	4
5	80	11	4
6	60	9	4
7	60	10	4
8	60	12	4
9	60	13	4
10	60	11	2
11	60	11	3
12	60	11	5
13	60	11	6

新窗口打开
本试验固定喷嘴到物料托盘的距离为15 cm,在开始试验前先预热设备约30 min,当设备运行稳定后将装有苦瓜片的金属网筛（15 cm×15 cm×10 cm）放入干燥室内,在不同时间间隔取出金属网筛,并测定样品质量,从而得出样品的质量变化。具体称重时间为：干燥过程前15 min内每3 min测定一次,15—30 min时每5 min测定一次,30—60 min时每10 min测定一次,之后每30 min测定一次,直至相隔两次的质量变化不大于0.005 g为止^[21],每次称重时间不超过20 s,且称重时间不计入干燥时长。所有试验均重复3次,取平均值。

1.4 水分比、干燥速率

干燥试验中的水分比（MR）表示一定干燥条件下物料的剩余水分率。水分比按式（1）计算^[22]：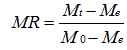
（1）
式中：M₀为物料初始干基含水量（g·g^-1）;M_t为任意t时刻的干基含水量（g·g^-1）;M_e为干燥达到平衡时的干基含水量（g·g^-1）。
干燥速率（drying rate）按式（2）计算：
（2）
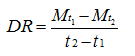
式中： Mt1为t₁时刻物料的干基含水量（g·g^-1）; Mt2为t₂时刻物料的干基含水量（g·g^-1）。
干基含水率（M_t）按式（3）计算：
（3）
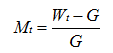
式中：W_t为任意t时刻物料的总质量（g）;G为干物质质量（g）。

1.5 有效水分扩散系数

有效水分扩散系数（D_eff）描述的是物料在干燥过程中内部水分转移的重要参数,反应了水分在物料内部扩散迁移的难易程度。其值越大,表明水分在物料内部扩散迁移越容易;反之,则表示扩散迁移越困难。其值可通过菲克第二扩散方程^[23]来计算,如下式：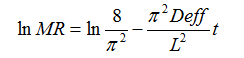
（4）
式中：D_eff为物料干燥过程中的水分有效扩散系数（m²·s^-1）;L为苦瓜的切片厚度（mm）;t为干燥时间（s）。
有效水分扩散系数还可以利用斜率法计算,通过LnMR对时间t 绘图确定斜率后再由式 （5）计算^[9]。
（5）

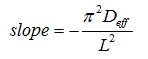
1.6 干燥活化能

干燥活化能（E_a ）表示的是物料在干燥过程中,脱除1 mol的水分所需要的能量,活化能越大表示物料越难被干燥。物料的水分有效扩散系数和温度的依赖关系可以用阿伦尼乌斯公式（Arrhenius equation）来描述,通过阿伦尼乌斯公式可以估算出水分扩散活化能,如公式（6）^[16,20]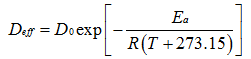
（6）
式中：D₀为物料中的扩散基数,是定值（m²·s^-1）;E_a为物料的干燥活化能（kJ·mol^-1）;R为气体摩尔常数,其值为8.314 J·mol^-1·K^-1;T为物料的干燥温度（℃）。

1.7 干燥模型的拟合

所选的5种干燥模型如表2所示,将试验获得的苦瓜干燥曲线数据与表2中的数学模型进行拟合筛选。确定系数（R²）是筛选样品干燥曲线最佳干燥模型的首要因素,除确定系数外,卡方（χ²）和均方根误差（RMSE）也可用于确定拟合程度。通常认为最适模型应具有较高的R²,较低的χ²和RMSE^[14]。这些统计参量根据式（7）—（9）进行计算：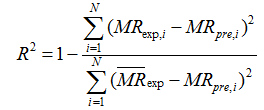
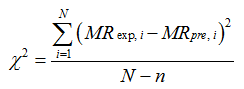
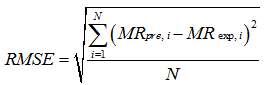
（7）
（8）
（9）
（7）—（9）式中：MR_exp,i表示第i个试验测得的水分比;MR_pre,i表示第i个预测的水分比;N为试验测得数据的组数;n为模型常数的个数。
Table 2
表2
表2干燥曲线拟合的数学模型
Table 2Drying mathematical models

序号 No.	模型名称 Model names	模型方程 Model equation
1 2 3 4 5	Page[24] Modified page[25] Logarithmic[26] Henderson and Pabis[27] Two term exponential[22]	MR=exp(-ktn) MR=exp[-(kt)n] MR=aexp(-kt)+c MR=aexp(-kt) MR=aexp(-kt)+(1-a)exp(-kat)

新窗口打开

1.8 模型的验证

将苦瓜片分别在风速为11 m·s^-1、切片厚度为4 mm、风温55℃条件下（Ⅰ条件下）和风温为60℃、风速为11 m·s^-1、切片厚度为3.5 mm条件下（Ⅱ条件下）按1.3进行试验,将试验所得到的数据分别与1.7中所确定的最适模型的预测值进行比较分析,以检验模型的拟合效果。

1.9 统计与分析

利用Excel和Origin8.0软件进行数据处理、绘图及模型拟合分析,显著性水平取0.05。

2 结果

2.1 苦瓜片气体射流冲击干燥特性

2.1.1 风温对苦瓜片射流冲击干燥特性的影响 将风速固定为11 m·s^-1,切片厚度固定为4 mm,在不同风温条件下进行气体射流冲击干燥试验,并将所得的试验数据绘制成干燥曲线和干燥速率曲线,如图1、图2所示。由图1可以看出,在干燥初期,物料的水分比变化比较大,随着干燥时间的增加,苦瓜片的水分比呈现降低的趋势,且风温越高,干燥所需时间越短,水分比下降越快。在风温分别为40、50、60、70和80℃条件下,苦瓜片干燥时间分别为210、180、150、90和60 min,与40℃时的干燥时间相比,80℃时所需的干燥时间缩短了71.4%,说明风温对苦瓜片的干燥时间有明显的影响,适当的提高风温可缩短苦瓜片的干燥时间,但在实际生产中应综合考虑干燥效率、产品品质及能耗等,从而确定合理的干燥风温。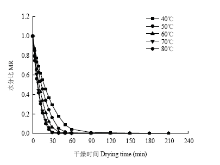
显示原图|下载原图ZIP|生成PPT
图1温度对干燥曲线的影响
-->Fig. 1Effects of temperature on drying curves
-->

由图2可以看出,风温越高,苦瓜片的干燥速率越大。这是因为随着风温的增加,使得物料中的水分子运动加剧,从而加快了物料的水分散失。苦瓜片的干燥过程主要为降速阶段,未见明显的恒速干燥阶段,且随着干燥时间的延长,干燥速率逐渐下降。这可能是因为苦瓜片在干燥过程中,随着干燥时间的延长,水分蒸发的界面不断向内部迁移,使得水分迁移的距离不断增加,从而导致干燥速率的不断降低^[28]。
显示原图|下载原图ZIP|生成PPT
图2温度对干燥速率曲线的影响
-->Fig. 2Effects of temperature on drying rate curves
-->

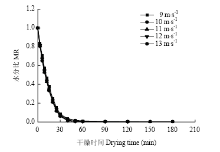
2.1.2 风速对苦瓜片射流冲击干燥特性的影响 将风温固定为60℃,切片厚度固定为4 mm,在不同风速条件下进行气体射流冲击干燥试验,并将所得的试验数据绘制成干燥曲线和干燥速率曲线,如图3、图4所示。由图3可以看出,随着干燥时间的增加,苦瓜片的水分比呈现降低的趋势,且风速越高,干燥所需时间越短,水分比下降越快。在风速分别为9、10、11、12和13 m·s^-1条件下,苦瓜片干燥时间分别为180、180、150、120和120 min,风速在13 m·s^-1比9 m·s^-1时的干燥时间缩短了33.3%。由此可知,在试验的风速条件范围内,风速对苦瓜片的干燥时间有一定影响,但不如风温影响明显。
显示原图|下载原图ZIP|生成PPT
图3风速对干燥曲线的影响
-->Fig. 3Effects of air velocities on drying curves
-->

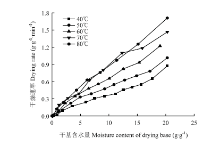
由图4可以看出,随着风速的增加,苦瓜片的干燥速率增大,但风速的变化对苦瓜片干燥速率的影响不明显,且呈现一定的波动。与风温的变化一样,整个干燥过程为降速干燥,没有明显的恒速干燥阶段。
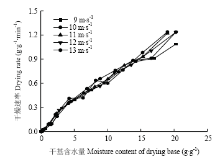显示原图|下载原图ZIP|生成PPT
图4风速对干燥速率曲线的影响
-->Fig. 4Effects of air velocities on drying rate curves
-->

2.1.3 切片厚度对苦瓜片射流冲击干燥特性的影响 将风温固定为60℃,风速固定为11 m·s^-1,在不同切片厚度条件下进行气体射流冲击干燥试验,并将所得的试验数据绘制成干燥曲线和干燥速率曲线,如图5、图6所示。由图5可以看出,随着干燥时间的增加,苦瓜片的水分比呈现降低的趋势,且切片厚度越薄,干燥所需时间越短,水分比下降越快。在切片厚度分别为2、3、4、5和6 mm条件下,苦瓜片干燥时间分别为120、120、150、180和210 min,干燥风温在2 mm比6 mm时的干燥时间缩短了42.9%,说明切片厚度对苦瓜片的干燥时间有一定的影响。
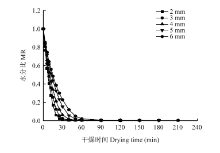显示原图|下载原图ZIP|生成PPT
图5切片厚度对干燥曲线的影响
-->Fig. 5Effects of slice thickness on drying curves
-->

由图6可以看出,切片厚度越薄,苦瓜片的干燥速率越大,这可能是由于切片厚度变薄时,使得物料中水分的传递距离减少,样品的比表面积增加所导致的^[21]。与风温和风速对干燥速率曲线的影响一致,切片厚度的干燥速率曲线也为降速干燥,没有明显的恒速干燥阶段。
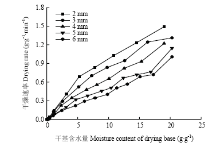显示原图|下载原图ZIP|生成PPT
图6切片厚度对干燥速率曲线的影响
-->Fig. 6Effects of slice thickness on drying rate curves
-->

2.2 有效扩散系数

表3为不同试验条件下苦瓜片气体射流冲击干燥水分有效扩散系数的计算值。由表3可以看出,当风温分别为40、50、60、70和80℃时,水分有效扩散系数分别为8.4300×10^-10、9.8475×10^-10、1.1681×10^-9、2.1075×10^-9和2.9667×10^-9 m²·s^-1。风温越高,水分有效扩散系数越大,风温为80℃比40℃时的水分有效扩散系数增大了约2.52倍。当风速分别为9、10、11、12和13 m·s^-1时,水分有效扩散系数分别为9.4580×10^-10、9.4334×10^-10、1.1681×10^-9、1.5395×10^-9和1.5533×10^-9 m²·s^-1。风速越大,水分有效扩散系数越大,风速为13 m·s^-1 比9 m·s^-1 时的水分有效扩散系数增大了约0.64倍。当切片厚度分别为2、3、4、5和6 mm时,水分有效扩散系数分别为3.5060×10^-10、8.3840×10^-10、1.1681×10^-9、1.5318×10^-9和1.8193×10^-9 m²·s^-1。切片厚度越厚,水分有效扩散系数越大,切片厚度为6 mm比2 mm时的水分有效扩散系数增大了4.19倍。因此,切片厚度对水分有效扩散系数的影响最为明显。在所有试验组中,在风温为80℃、风速11 m·s^-1、切片厚度为4 mm时的水分有效扩散系数达到最高值,为2.9667×10^-9 m²·s^-1。
Table 3
表3
表3不同干燥条件苦瓜片的水分有效扩散系数
Table 3Moisture effective diffusion coefficients of bitter gourd slice under different drying conditions

序号 No.	风温（T） Temperature (℃)	风速（V） Air velocity (m·s-1)	切片厚度（D） Slice thicknes (mm)	线性回归公式 Linear regression formula	R2	有效水分扩散系数 Deff (m2·s-1)
1	40	11	4	lnMR=-5.2001×10-4t-0.3722	0.9486	8.4300×10-10
2	50	11	4	lnMR=-6.0744×10-4t-0.6895	0.9589	9.8475×10-10
3	60	11	4	lnMR=-7.2052×10-4t-0.8922	0.9774	1.1681×10-9
4	70	11	4	lnMR=-1.3000×10-3t-0.5472	0.9832	2.1075×10-9
5	80	11	4	lnMR=-1.8300×10-3t-0.0988	0.9487	2.9667×10-9
6	60	9	4	lnMR=-5.8342×10-4t-0.8673	0.9825	9.4580×10-10
7	60	10	4	lnMR=-5.8190×10-4t-0.9734	0.9503	9.4334×10-10
8	60	12	4	lnMR=-9.4967×10-4t-0.5360	0.9639	1.5395×10-9
9	60	13	4	lnMR=-9.5814×10-4t-0.6252	0.9804	1.5533×10-9
10	60	11	2	lnMR=-8.6507×10-4t-1.2390	0.9714	3.5060×10-10
11	60	11	3	lnMR=-9.1941×10-4t-0.9270	0.9617	8.3840×10-10
12	60	11	5	lnMR=-6.0472×10-4t-0.6845	0.9841	1.5318×10-9
13	60	11	6	lnMR=-4.9878×10-4t-0.6224	0.9601	1.8193×10-9

新窗口打开

2.3 干燥活化能

图7表示水分有效扩散系数的自然对数InDeff与1/(T+273.15)的关系,由图中的直线回归方程可以求出苦瓜片的干燥活化能E_a为29.89 kJ·mol^-1,说明在气体射流冲击干燥过程中,从苦瓜片中去除1 kg的水分所需要的最低能量约为1 660.56 kJ。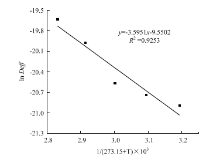
显示原图|下载原图ZIP|生成PPT
图7水分有效扩散系数与干燥温度的关系曲线
-->Fig. 7The relation curves of moisture effective diffusion coefficients and drying temperatures
-->

2.4 干燥模型的拟合效果

通常选择具有较高R²,较低χ²和RMSE的模型为最适模型,更适合于描述在干燥过程中物料的水分散失规律。本研究用苦瓜片气体射流冲击干燥试验的数据对5个干燥模型方程进行拟合,得到的数据分析结果如表4。
Table 4
表4
表4苦瓜片干燥模型参数值及R²、RMSE和χ²
Table 4Gourd bitter slice drying model parameters, R², RMSE and χ²

试验序号 No.	模型名称 Model No.	模型方程 Model equation	模型参数 Model parametric			R2	RMSE		χ2
	Page	MR=exp(-ktn)	k	n
1			0.03535	1.05226		0.99834		0.01449	0.000210
2			0.03800	1.13289		0.99809		0.01551	0.000241
3			0.05426	1.12318		0.99874		0.01228	0.000151
4			0.06295	1.16350		0.99922		0.00979	0.000096
5			0.07799	1.11340		0.99859		0.01315	0.000173
6			0.04262	1.16816		0.99929		0.00930	0.000086
7			0.04801	1.15729		0.99913		0.01015	0.000103
8			0.05116	1.13055		0.99871		0.01267	0.000160
9			0.05559	1.11576		0.99788		0.01609	0.000259
10			0.06189	1.23605		0.99887		0.01151	0.000133
11			0.05116	1.22366		0.99899		0.01117	0.000125
12			0.04577	1.08353		0.99829		0.01442	0.000208
13			0.04401	1.04030		0.99868		0.01268	0.000161
	Modified page	MR=exp[-(kt)n]	k	n
1			0.04173	1.05351		0.99834		0.01449	0.000210
2			0.05576	1.13470		0.99810		0.01551	0.000240
3			0.07468	1.12433		0.99874		0.01227	0.000151
4			0.09285	1.16386		0.99922		0.00979	0.000096
5			0.10111	1.11452		0.99859		0.01315	0.000173
6			0.06713	1.16886		0.99929		0.00929	0.000086
7			0.07253	1.15817		0.99913		0.01015	0.000103
8			0.07211	1.13173		0.99871		0.01267	0.000160
9			0.07502	1.11738		0.99788		0.01609	0.000259
10			0.10527	1.23719		0.99887		0.01151	0.000133
11			0.08807	1.22472		0.99899		0.01117	0.000125
12			0.05805	1.08499		0.99829		0.01442	0.000208
13			0.04967	1.04143		0.99868		0.01268	0.000161
	Logarithmic	MR=aexp(-kt)+c	a	k	c
1			1.00997	0.04098	-0.00815	0.99800		0.01648	0.000272
2			1.03306	0.05527	-0.01454	0.99621		0.02269	0.000515
3			1.0286	0.07454	-0.01192	0.99714		0.01922	0.000370
4			1.04021	0.09270	-0.01708	0.99679		0.02086	0.000435
5			1.03020	0.09901	-0.01944	0.99769		0.01775	0.000315
6			1.03799	0.06815	-0.00894	0.99641		0.02168	0.000470
7			1.03263	0.07360	-0.00768	0.99651		0.02105	0.000430
8			1.03476	0.07118	-0.01737	0.99710		0.01981	0.000392
9			1.03032	0.07374	-0.01739	0.99670		0.02098	0.000400
10			1.04412	0.10784	-0.0127	0.99378		0.02815	0.000792
续表4 Continued table 4
试验序号 No.	模型名称 Model No.	模型方程 Model equation	模型参数 Model parametric			R2	RMSE		χ2
11			1.04961	0.08920	-0.01639	0.99442		0.02736	0.000749
12			1.01884	0.05729	-0.01084	0.99750		0.01811	0.000328
13			1.00715	0.04908	-0.00583	0.99847		0.01412	0.000199
	Henderson and Pabis	MR=aexp(-kt)	a	k
1			1.00385	0.04177		0.99783		0.01659	0.000275
2			1.02204	0.05714		0.99560		0.02356	0.000555
3			1.01979	0.07671		0.99667		0.01995	0.000398
4			1.02751	0.09666		0.99591		0.02244	0.000504
5			1.01589	0.10399		0.99667		0.02023	0.000409
6			1.03130	0.06959		0.99614		0.02167	0.000470
7			1.02692	0.07495		0.99629		0.02091	0.000437
8			1.02193	0.07420		0.99628		0.02147	0.000461
9			1.01749	0.07690		0.99585		0.02254	0.000508
10			1.03427	0.11119		0.99312		0.02835	0.000804
11			1.03710	0.09271		0.99352		0.02825	0.000798
12			1.01088	0.05879		0.99714		0.01865	0.000348
13			1.00287	0.04977		0.99837		0.01409	0.000199
	Two term exponential	MR=aexp(-kt)+(1-a)exp(-kat)	a	k
1			1.49365	0.04988		0.99864		0.01314	0.000173
2			1.63639	0.07269		0.99831		0.01460	0.000213
3			1.61944	0.09637		0.99891		0.01139	0.000130
4			1.68419	0.12480		0.99922		0.00979	0.000096
5			1.59678	0.12870		0.99874		0.01244	0.000155
6			1.69433	0.09074		0.99937		0.00876	0.000077
7			1.67891	0.09712		0.99927		0.00925	0.000086
8			1.63161	0.09375		0.99887		0.01186	0.000141
9			1.60441	0.09590		0.99811		0.01522	0.000232
10			1.76932	0.14920		0.99864		0.01260	0.000159
11			1.75718	0.12383		0.99880		0.01215	0.000148
12			1.55247	0.07186		0.99859		0.01311	0.000172
13			1.45333	0.05797		0.99889		0.01164	0.000135

新窗口打开
从表4中可以看出,所选模型的R²都在0.9900以上,均在可接受的范围^[29]。从模型1到模型5,R²的范围分别是0.99788—0.99929、0.99788—0.99929、0.99378—0.99847、0.99312—0.99837和0.99811—0.99937;RMSE的范围分别是0.00930—0.01609、0.00929—0.01609、0.01412—0.02815、0.01409—0.02835和0.00876—0.01522;χ²的范围分别是0.000086—0.000259、0.000086—0.000259、0.000199—0.000792、0.000199—0.000804和0.000077—0.000232。其中5号模型,即Two term exponential模型的具有最高的R²（0.99937）,最低的RMSE（0.00876）和最低的χ²（0.000077）,从而此模型具有最高的拟合度。因此,在风温40—80℃、风速9—13 m·s^-1、切片厚度为2—6 mm内,所选的5个模型中Two term exponential模型是最适合描述苦瓜片在气体射流冲击干燥过程中的水分变化规律,并对此模型进行拟合分析。

2.5 模型中参数的回归结果

由2.4结果可知Two term exponential模型中的干燥常数a和k与干燥条件（风温、风速和切片厚度）呈现一定的线性变化,可表示为:
a=x₁+ x₂T+ x₃V+ x₄D （10）
k=y₁+ y₂T+ y₃V+ y₄D （11）
式中,T为干燥风温（℃）;V为干燥风速（m·s^-1）;D为切片厚度（mm）;x₁、x₂、x₃、x₄为常数;y₁、y₂、y₃、y₄为常数。
根据各次试验的风温、风速和切片厚度及Two term exponential模型中的a和k值,并用Origin 8.0数据处理软件对相关数据进行线性回归,分别求出Two term exponential模型中的x₁、x₂、x₃、x₄和y₁、y₂、y₃、y₄的值,并代入式（10）、（11）得：
a=2.06071+0.00254T–0.02271V–0.08367D （12）
k=0.05665+0.0021T–6.95×10^-4V–0.02344D （13）
把（12）和（13）代入Two term exponential模型方程中,得到苦瓜片气体射流冲击干燥模型为：
MR=Aexp(-Bt)+(1-A)exp(-BAt) （14）
其中,A=2.06071+0.00254T-0.02271V-0.08367D
B=0.05665+0.0021T-6.95×10^-4V-0.02344D

2.6 模型的验证效果

利用在Ⅰ条件和Ⅱ条件下的试验数据对模型的准确度进行检验,其中图8和图9分别是Ⅰ条件和Ⅱ条件下实测值和模型预测值的相关性结果。从图中可以看出,R²均大于0.99,说明实测值与预测值具有较好的吻合度。因此,在试验条件下,Two term exponential模型能较好的预测苦瓜片在气体射流冲击干燥过程中水分的散失规律。
显示原图|下载原图ZIP|生成PPT
图8Ⅰ（A）、Ⅱ（B）条件下预测值与实测值的相关性
-->Fig. 8Correlation between the actual and predicted values underⅠ (A) and Ⅱ (B) conditions
-->

3 讨论

3.1 不同干燥条件对苦瓜片气体射流冲击干燥特性的影响

现有文献少见将气体射流冲击干燥技术应用于苦瓜片干燥的报道,对苦瓜片的干燥特性、干燥动力学研究甚少。从图1—图6可知,改变风温、风速和切片厚度都会引起干燥曲线和干燥速率曲线的变化,但风温的影响最为明显,说明物料在干燥过程中水分的散失主要是通过热扩散。在不同干燥条件下,苦瓜片在1—4 h内基本完成干燥,所需干燥时间均较短,故将气体射流冲击技术应用于苦瓜片干燥,不仅具有较高的干燥效率,还可有效降低干燥能耗。从苦瓜片的干燥曲线可以看出,在0—30 min内物料的水分比急剧下降,随着干燥时间的推移,水分比变化趋于缓慢,这与紫薯^[10]、哈密瓜^[14]、杏子^[15]、板桥党参片^[19]等的气体射流冲击干燥曲线具有相似规律,但比它们具有更高的干燥速率和更短的干燥时间。这一方面可能是因为物料之间具有一定的差异性,另一方面则可能是由于新鲜苦瓜本身含水量较高。从苦瓜片的干燥速率曲线可以看出,苦瓜片的气体射流冲击干燥过程属于降速干燥,见明显的恒速干燥阶段,这与大多数食品物料干燥速率曲线相似^{[15,21,23,30]},可能是因为：（1）物料在干燥初期,含水量较大,有较大的干燥速率,随着干燥时间的不断进行,物料自身的含水量变少,干燥速率也随之减少。（2）物料在干燥过程中,干燥前期的水分散失导致物料体积收缩,内部显微结构遭到破坏。随着干燥时间的不断进行,水分散失越多,物料体积收缩的程度也会越大：内部显微结构破坏越严重,内层水分向外迁移受到的阻力也会越大,因此干燥速率也会下降。（3）物料在干燥过程中,首先被干燥的是外部及浅表层水分,这些水分扩散迁移到空气中的距离小,所需时间短,当干燥到物料内部水分时,由于内部水分扩散迁移到空气中的距离相对增加从而使得干燥速率变小。本研究未对不同干燥条件下的干制品品质及能耗进行探索,有待进一步完善。

3.2 有效扩散系数

苦瓜片气体射流冲击干燥的水分有效扩散系数随着风温、风速和切片厚度的增加而增加,该结果与紫薯^[10]的气体射流冲击干燥具有相似的结果。从表3可以看出,风温、切片厚度对水分有效扩散系数的影响较风速明显。在用气体射流冲击干燥技术的相关研究中,李文峰等^[10]研究的紫薯的有效扩散系数范围在0.7086×10^-9—3.5431×10^-9m²·s^-1,张茜等^[14]研究的哈密瓜片的有效扩散系数为2.38×10^-9—4.55×10^-9 m²·s^-1,而本研究中苦瓜片的有效扩散系数的范围3.5060×10^-10—2.9667×10^-9 m²·s^-1,其有效扩散系数变化范围较大,占了2个数量级。一部分原因可能与苦瓜物料本身的性质有关;一部分原因可能是苦瓜本身的含水量较高,用来散失的水分高于其他果蔬类;也可能是因为苦瓜的自由水分含量较大,导致其散失的水分不稳定,变化范围较大。

3.3 干燥模型的拟合

许多研究发现,很多物料在进行气体射流冲击干燥时,在相应的试验条件下,Modified page模型和Page模型为最适合的干燥模型,如哈密瓜^[14]、党参^[19]等的气体射流冲击干燥。但由于物料的差异性和所选模型种类的不同,本研究所得到的最适模型为Two term exponential模型。

4 结论

4.1 苦瓜片的气体射流冲击干燥主要为降速干燥。

4.2 风温、风速和切片厚度对苦瓜片的气体射流冲击干燥特性都有影响,且风温>切片厚度>风速。其中,风温和切片厚度的影响较风速明显。但在实际情况下,由于风温太高,会导致苦瓜片外观变黄,营养成分大量损失,因此,在实际生产过程中干燥温度不宜超过60℃。

4.3 苦瓜片气体射流冲击干燥的水分有效扩散系数随着风温、风速、切片厚度的增加而增加。最高的水分有效扩散系数为2.9668×10^-9 m²·s^-1,活化能为29.89 kJ·mol^-1。

4.4 在风温为40—80℃、风速为9—13 m·s^-1、切片厚度为2—6 mm条件下,对所选的5个模型与所测的数据进行拟合,发现所选模型都能较好地描述苦瓜片在气体射流冲击干燥过程中水分的变化规律,但Two term exponential模型的拟合度最好,是苦瓜片气体射流冲击干燥的最适模型。

The authors have declared that no competing interests exist.

---

参考文献文献选项 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子