客观质量评估算法根据参考原始图像的程度,评估算法可以分为3类:全参考(Full Reference, FR)、半参考(Reduce Reference,RR)和无参考(No Reference,NR)。其中,全参考图像质量评估算法使用了原始图像作为失真图像的参照图像;半参考图像质量评估算法中仅使用了部分参照图像的信息;无参考图像质量评估算法没有使用任何的参照图像中的信息作为先验数据。然而,在许多实际应用中,特别是在大数据应用领域,获取全部或部分的参考图像信息是非常昂贵的,甚至是不可能的。而无参考图像质量评估不依靠任何参考图像的信息,比全参考图像质量评估和半参考图像质量评估具有更大的实际应用前景。
在过去的几十年中,图像质量评估领域得到很大的发展,已经有针对视觉内容设计的各种图像质量评估算法。大多数传统的评估指标都是全参考算法,诸如峰值信噪比算法(Peak Signal-to-Noise Ratio, PSNR)和均方误差(Mean Square Error, MSE),它们通过简单地计算参考和失真图像之间的像素差异来预测图像的视觉质量。由于其简单有效,这些方法在工业界和学术界得到广泛的应用。其没有考虑人类视觉系统的属性,因此,无法获得与人类感知较一致的质量预测结果。为了解决这个问题,许多研究人员根据人类视觉系统的特点,提出了各种不同的评估算法,如结构相似性(Structural Similarity, SSIM)算法[1]、梯度幅度相似性偏差(Gradient Magnitude Similarity Deviation, GMSD)算法[2]、自然图像质量评估(Natural Image Quality Evaluator, NIQE)算法[3]、以及盲/无参考图像空间质量评估(Blind/Referenceless Image Spatial Quality Evaluator, BRISQUE)算法[4]。
但是,上述的评估算法是专为自然图像设计的,对屏幕内容图像效果不好。通常,屏幕内容图像由计算机生成,由文本、图形和图像组成,具有特殊的布局,导致这2种图像在统计特征上存在明显差异。对于屏幕内容图像的研究,Yang等[5]进行了主观实验并构建了一个SIQAD数据库,基于该数据库,提出了各种针对屏幕内容图像的评估算法, 且提出了SPQA(SCI Perceptual Quality Assessment)算法,该算法通过分析图像区域和文本区域的质量感知特征来考虑图像整体质量。Wang等通过考虑视野自适应和局部信息内容加权,提出了SQI(SCI Quality Index)算法[6],且基于主要视觉信息和不可预测的不确定性提取图像的统计特征,然后提出了半参考模型[7]。Shao等[8]通过利用稀疏表示框架提出了BLIQUP-SCI(Blind Quality Predictor for SCI)算法。Fang等[9]通过对图像亮度和纹理特征的局部和全局表示,提出了NRLT(No Reference quality assessment method by incorporating statistical Luminance and Texture features)算法。
现有的针对屏幕内容图像质量评估的无参考算法[8-9]不能与主观感知产生较高的一致性,因此,针对屏幕内容图像设计有效的无参考质量评估算法仍然存在挑战。本文结合文本、图形、图像和布局对屏幕内容图像质量的影响,提出了针对屏幕内容图像的基于边缘和结构的无参考质量评估(Blind quality assessment for screen content images based on Edge and Structure, BES)算法。
与自然图像不同,屏幕内容图像由具有大量边缘的文本、图形和图像组成,并且人类视觉系统对边缘高度敏感。因此,BES算法首先对失真图像的亮度分量进行双三次插值处理,然后使用Gabor滤波器的虚部对插值后的亮度分量提取边缘,并计算每个失真图像的边缘特征。
屏幕内容图像以独特的布局显示文本、图形和图像,因此,BES算法提取结构特征来表示屏幕内容图像的布局,首先使用双三次插值对失真图像进行插值,然后使用Scharr滤波器在插值后的失真图上计算得到局部二值模式(Local Binary Pattern, LBP)图,接着通过LBP图计算得到结构特征。与其他算法中直接使用频率直方图描述全局信息不同[9],BES算法通过累加图像中具有相同LBP模式的像素的梯度值来表示失真图像的结构特征。
利用相应的方法提取边缘特征和结构特征,将随机森林回归(Random Forest Regression,RFR)算法作为映射函数,将边缘和结构特征映射为主观质量分数。
1 BES算法 Guo等[10]研究表明,通过双三次插值处理,可以减少屏幕内容图像和自然图像之间的统计特征差异,使得输入的屏幕内容图像在统计特征上更加类似于自然图像,以便更好地表示图像。Ni等[11]通过实验证明了Gabor滤波器的虚部可以有效地提取边缘信息。文献[1]中表明,图像结构携带重要的视觉信息,人类视觉系统可以通过获取图像结构信息来感知和理解图像。因此,通过双三次插值处理之后,结合屏幕内容图像的边缘和结构特征来表示图像。最后,利用随机森林回归算法将从多尺度中提取的边缘和结构特征映射为主观质量分数。
1.1 提取边缘特征 根据生理学实验发现,二维Gabor滤波器可以有效地模拟哺乳动物视觉皮层中的简单细胞感受野剖面[12-13],说明了Gabor滤波器可以有效地表征人类视觉系统感知。因此,利用Gabor滤波器提取屏幕内容图像的边缘特征。
BES算法首先将失真的屏幕内容图像从RGB颜色空间转换为LMN颜色空间[14],以便提取亮度分量。这里选择LMN颜色空间的原因是颜色空间转换过程中的权重针对人类视觉系统进行了优化[15]。接着使用双三次插值来对每个输入的失真屏幕内容图像的亮度分量进行插值,将其进行放大,平滑图像中的边缘。双三次插值的表达式为
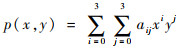 | (1) |
式中:aij为一个邻近像素的权重系数,这个权重系数是根据像素分布导数计算得来的。
在空间域中,二维Gabor滤波器可以描述为由正弦平面波调制的高斯核函数,其虚部是奇对称的并且是用于检测边缘的有效工具。文献[18-19]表明,水平或垂直方向的视觉灵敏度高于其他方向。因此,选择水平和垂直方向,即θ=0和θ=π/2(θ为Gabor滤波器中的方向参数),以获得水平和垂直方向上的Gabor滤波器,分别表示为gh和gv。将通过双三次插值处理过的输入图像的亮度分量与每个Gabor滤波器进行卷积,以获得水平和垂直方向的边缘图,卷积计算公式为
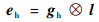 | (2) |
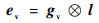 | (3) |
式中:“?”表示卷积计算;l为通过双三次插值处理过的输入图像的亮度分量;eh和ev分别为水平和垂直方向的梯度图,接着将这2个结果相加得到最终的梯度图,表示为e,即
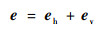 | (4) |
这里将e的绝对值直方图作为输入图像的边缘特征,直方图分组设置为10,因此用一个10维向量{f1, f2, …, fk}来表示边缘特征,向量中第n(1≤n≤k=10)个元素的计算式为
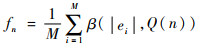 | (5) |
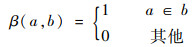 | (6) |
式中:Q(n)为第n个分组的取值范围;M为图像中的像素个数;ei为图像中第i个像素。
1.2 提取结构特征 文献[1]中表明,图像结构信息的有效提取和描述对图像感知质量评估有很大帮助。本文提出的算法中,先利用双三次插值对失真图像进行插值, 接着分别使用水平和垂直方向的Scharr滤波器与插值后的图像进行卷积计算,得到梯度图,计算公式为
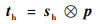 | (7) |
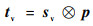 | (8) |
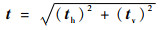 | (9) |
式中:p为插值后的失真屏幕内容图像;sh和sv分别为水平和垂直方向的Scharr滤波器;th和tv分别为插值后的图像和对应方向的Scharr滤波器经过卷积计算后得到的水平和垂直方向的插值后图像的梯度图;t为最终的插值后图像的梯度图。
接着,基于上述得到的梯度图利用LBP算子来提取插值后图像的结构信息。LBP算子是用来描述中心像素和其周围像素的关系[16],常规的LBP算子表达式为
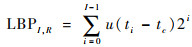 | (10) |
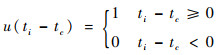 | (11) |
式中:I和R分别为周围像素数量和邻域的半径;tc为局部区域中心位置像素的梯度值;ti为邻接位置的梯度值。为了获得旋转不变性,局部旋转不变均匀LBP算子[16]定义为
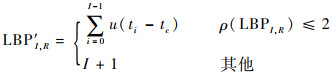 | (12) |
 | (13) |
式中:ρ为按位旋转的像素数量。局部旋转不变均匀LBP具有I+2种模式,可以表示局部显著的梯度结构。受文献[17]的启发,该算法在梯度图中累加具有相同LBP模式的像素的梯度值,并将其作为结构特征,计算公式为
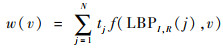 | (14) |
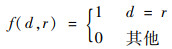 | (15) |
式中:N为图像的像素个数;v∈[0, V]为可能的LBP模式;tj为LBP模式的权重。在本文中,设置I=8,邻域半径设置为R=1,这样一张失真图的结构特征将由一个10维向量来表示。在图 1中给出了SIQAD数据库中典型的失真图,及其对应的边缘图、LBP图和表示特征的直方图。
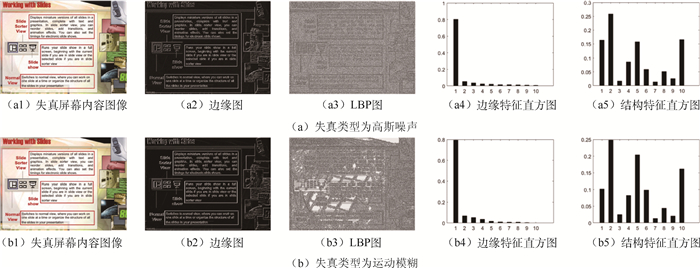 |
| 图 1 失真屏幕内容图像以及对应的特征图和特征直方图示例 Fig. 1 Examples of distorted screen content images, their feature maps, and feature histograms |
| 图选项 |
1.3 回归模型 给定一张失真屏幕内容图像,根据上述算法,在每个尺度上可以获得20维特征,包括10维边缘特征和10维结构特征。文献[18]表明,人类视觉系统可以从粗略到细致地获得图像信息。因此,为了使提取的图像特征更符合人类视觉系统的特点,本文对图像进行4次下采样,并在这4个尺度上以及原尺度上提取特征。因此,对于每张失真图像,总共提取100维特征。在实验中,将双三次插值因子设置为2,并将随机森林回归算法作为映射函数,把质量感知特征映射为主观质量分数。将随机从数据库中选择的80%图像用来训练模型,然后将剩余图像作为测试集并计算出其视觉质量分数。该实验进行1 000次,然后将其中位数作为最终的结果。
2 实验结果 为了测试所提算法的性能,本文在2个数据库SIQAD[5]和SCID[19]上,将所提算法与其他评估算法进行对比实验,实验结果如表 1和表 2所示。SIQAD数据库包含20张原始图像和980张失真图像,980张失真图像有7种失真类型,每种失真类型有7种失真等级。这7种失真类型包括高斯噪声(GN)、高斯模糊(GB)、运动模糊(MB)、对比度变化(CC)、JPEG压缩(JPEG)、JPEG2000压缩(J2K),基于层划分的压缩(LSC)。SCID数据库具有40张原始图像和1 800张失真图像,失真图像中有9种失真类型,每种失真类型有5种失真等级。这9种失真类型包括GN、GB、MB、CC、JPEG、J2K,颜色饱和度变化(CSC)、具有抖动的颜色量化(CQD),高效视频编码标准(HEVC-SCC)。这2个数据库都提供了平均主观得分差(DMOS)作为主观评分。
表 1 SIQAD数据库上的实验结果 Table 1 Experimental results on SIQAD database
| 指标 | 失真 类型 | 全参考 | 无参考 | ||||||||||||
| PSNR | SSIM | MAD | GMSD | SPQA | SQI | ESIM | GFM | NIOE | BRISQUE | GWH-GLBP | NRLT | BES | |||
| PLCC | GN | 0.905 3 | 0.880 6 | 0.885 2 | 0.895 6 | 0.892 1 | 0.882 9 | 0.889 1 | 0.899 0 | 0.863 4 | 0.904 5 | 0.849 3 | 0.898 3 | 0.909 0 | |
| GB | 0.850 3 | 0.910 4 | 0.912 0 | 0.909 4 | 0.905 8 | 0.920 2 | 0.923 4 | 0.914 3 | 0.756 0 | 0.890 9 | 0.909 8 | 0.882 6 | 0.922 4 | ||
| MB | 0.704 4 | 0.806 0 | 0.836 1 | 0.843 6 | 0.831 5 | 0.878 9 | 0.888 6 | 0.866 2 | 0.548 7 | 0.857 1 | 0.832 0 | 0.861 1 | 0.869 4 | ||
| CC | 0.740 1 | 0.743 5 | 0.393 3 | 0.782 7 | 0.799 2 | 0.772 4 | 0.764 1 | 0.810 7 | 0.355 5 | 0.541 7 | 0.410 8 | 0.787 8 | 0.822 4 | ||
| JPEG | 0.754 5 | 0.748 7 | 0.766 2 | 0.774 6 | 0.769 6 | 0.821 8 | 0.799 9 | 0.839 8 | 0.598 0 | 0.288 7 | 0.572 9 | 0.781 2 | 0.757 6 | ||
| J2K | 0.789 3 | 0.774 9 | 0.834 4 | 0.850 9 | 0.825 2 | 0.827 1 | 0.788 8 | 0.848 6 | 0.516 5 | 0.350 9 | 0.716 3 | 0.748 9 | 0.818 2 | ||
| LSC | 0.780 5 | 0.730 7 | 0.818 4 | 0.855 9 | 0.795 8 | 0.831 0 | 0.791 5 | 0.828 8 | 0.586 9 | 0.286 5 | 0.551 2 | 0.730 9 | 0.757 5 | ||
| ALL | 0.585 8 | 0.756 1 | 0.546 7 | 0.729 1 | 0.858 4 | 0.864 4 | 0.878 8 | 0.882 8 | 0.426 1 | 0.359 1 | 0.787 4 | 0.848 2 | 0.870 5 | ||
| SRCC | GN | 0.879 0 | 0.869 4 | 0.872 1 | 0.885 6 | 0.882 3 | 0.860 2 | 0.875 7 | 0.879 5 | 0.842 9 | 0.887 5 | 0.828 7 | 0.874 7 | 0.885 1 | |
| GB | 0.857 3 | 0.892 1 | 0.908 7 | 0.911 9 | 0.901 7 | 0.924 4 | 0.923 9 | 0.913 2 | 0.649 4 | 0.871 5 | 0.894 1 | 0.865 6 | 0.904 5 | ||
| MB | 0.713 | 0.804 1 | 0.835 7 | 0.844 1 | 0.825 5 | 0.88 1 | 0.893 8 | 0.869 9 | 0.427 2 | 0.865 3 | 0.822 9 | 0.843 2 | 0.857 1 | ||
| CC | 0.682 8 | 0.640 5 | 0.390 7 | 0.637 8 | 0.615 4 | 0.667 7 | 0.610 8 | 0.703 8 | 0.132 4 | 0.313 5 | 0.246 0 | 0.599 6 | 0.658 2 | ||
| JPEG | 0.756 8 | 0.757 6 | 0.767 4 | 0.771 2 | 0.767 3 | 0.818 9 | 0.798 9 | 0.843 4 | 0.510 9 | 0.220 8 | 0.480 3 | 0.738 6 | 0.707 2 | ||
| J2K | 0.774 6 | 0.760 3 | 0.838 2 | 0.843 6 | 0.815 2 | 0.816 9 | 0.782 7 | 0.844 4 | 0.323 8 | 0.301 8 | 0.701 7 | 0.731 5 | 0.793 9 | ||
| LSC | 0.793 | 0.737 1 | 0.815 4 | 0.859 2 | 0.800 3 | 0.843 2 | 0.795 8 | 0.844 5 | 0.394 4 | 0.184 4 | 0.504 9 | 0.667 5 | 0.729 1 | ||
| ALL | 0.557 0 | 0.756 6 | 0.583 1 | 0.730 5 | 0.841 6 | 0.854 8 | 0.863 2 | 0.873 5 | 0.382 7 | 0.662 | 0.719 4 | 0.824 5 | 0.848 8 | ||
| RMSE | GN | 6.337 2 | 7.704 4 | 6.939 1 | 6.635 4 | 6.739 4 | 6.827 2 | 6.683 5 | 7.408 3 | 6.013 7 | 7.682 9 | 6.310 0 | 6.106 2 | ||
| GB | 7.737 6 | 6.361 9 | 6.226 9 | 6.981 6 | 6.430 1 | 5.827 0 | 6.145 9 | 9.802 6 | 6.479 2 | 6.146 6 | 6.689 2 | 5.597 4 | |||
| MB | 9.228 7 | 7.060 0 | 7.132 29 | 6.981 6 | 7.222 3 | 5.963 9 | 6.518 4 | 10.613 6 | 6.198 2 | 6.934 7 | 6.428 4 | 6.432 3 | |||
| CC | 8.459 1 | 6.818 4 | 11.565 | 7.829 7 | 7.618 4 | 8.114 1 | 7.363 8 | 11.467 8 | 9.966 | 11.198 | 7.560 1 | 6.713 5 | |||
| JPEG | 6.116 5 | 5.640 6 | 6.038 | 5.942 7 | 6.000 0 | 5.640 1 | 5.100 9 | 7.286 9 | 8.603 7 | 7.323 8 | 5.712 1 | 5.988 0 | |||
| J2K | 6.381 9 | 6.180 4 | 5.727 6 | 5.459 1 | 5.870 6 | 6.387 7 | 5.498 5 | 8.331 8 | 9.094 | 6.775 0 | 6.505 8 | 5.704 8 | |||
| LSC | 5.333 6 | 4.937 9 | 4.902 5 | 4.412 1 | 5.166 4 | 5.215 0 | 4.773 6 | 6.815 9 | 7.871 2 | 7.028 9 | 5.783 6 | 5.390 8 | |||
| ALL | 11.601 | 10.855 | 11.986 | 9.797 2 | 7.342 1 | 7.198 2 | 6.831 0 | 6.723 4 | 12.794 1 | 11.717 | 8.672 6 | 7.444 7 | 6.914 7 | ||
表选项
表 2 SCID数据库上的实验结果 Table 2 Experimental results on SCID database
| 指标 | 失真 类型 | 全参考 | 无参考 | |||||||||
| PSNR | SSIM | MAD | IFC | GSIM | NIQE | BRISQUE | GWH-GLBP | NRLT | BES | |||
| PLCC | GN | 0.953 0 | 0.935 4 | 0.931 5 | 0.889 7 | 0.917 0 | 0.832 4 | 0.964 5 | 0.861 9 | 0.968 1 | 0.939 8 | |
| GB | 0.777 2 | 0.871 1 | 0.855 9 | 0.840 6 | 0.844 9 | 0.591 2 | 0.584 7 | 0.714 4 | 0.667 2 | 0.855 3 | ||
| MB | 0.761 5 | 0.879 4 | 0.836 2 | 0.337 2 | 0.838 3 | 0.539 0 | 0.643 4 | 0.673 6 | 0.590 6 | 0.931 4 | ||
| CC | 0.743 5 | 0.690 3 | 0.498 7 | 0.119 8 | 0.867 5 | 0.284 0 | 0.473 4 | 0.252 0 | 0.499 3 | 0.812 2 | ||
| JPEG | 0.839 3 | 0.858 1 | 0.925 1 | 0.876 2 | 0.937 3 | 0.682 4 | 0.587 9 | 0.769 4 | 0.851 2 | 0.820 5 | ||
| J2K | 0.917 6 | 0.858 6 | 0.938 1 | 0.857 0 | 0.944 1 | 0.709 9 | 0.551 5 | 0.664 5 | 0.832 6 | 0.795 4 | ||
| CSC | 0.062 2 | 0.089 0 | 0.129 6 | 0.076 4 | 0.056 0 | 0.219 6 | 0.187 9 | 0.213 4 | 0.196 3 | 0.311 0 | ||
| HEVC-SCC | 0.799 1 | 0.863 5 | 0.895 3 | 0.791 8 | 0.883 5 | 0.428 9 | 0.441 8 | 0.614 2 | 0.533 4 | 0.587 5 | ||
| CQD | 0.921 0 | 0.866 8 | 0.901 4 | 0.765 5 | 0.897 4 | 0.578 7 | 0.714 6 | 0.603 4 | 0.725 0 | 0.830 3 | ||
| ALL | 0.762 2 | 0.757 9 | 0.771 9 | 0.628 5 | 0.704 2 | 0.339 2 | 0.630 3 | 0.664 7 | 0.706 0 | 0.785 2 | ||
| SRCC | GN | 0.942 4 | 0.917 1 | 0.926 2 | 0.887 7 | 0.911 2 | 0.850 5 | 0.987 1 | 0.866 9 | 0.961 2 | 0.933 3 | |
| GB | 0.702 | 0.869 8 | 0.860 3 | 0.835 1 | 0.842 0 | 0.346 2 | 0.516 2 | 0.701 9 | 0.625 0 | 0.847 9 | ||
| MB | 0.737 5 | 0.858 8 | 0.829 6 | 0.447 7 | 0.819 4 | 0.369 1 | 0.626 5 | 0.641 9 | 0.512 3 | 0.788 3 | ||
| CC | 0.726 5 | 0.656 4 | 0.478 4 | 0.119 8 | 0.830 4 | 0.100 4 | 0.309 6 | 0.231 4 | 0.303 1 | 0.477 3 | ||
| JPEG | 0.823 1 | 0.849 0 | 0.924 2 | 0.877 0 | 0.936 6 | 0.629 1 | 0.546 9 | 0.743 0 | 0.838 2 | 0.795 7 | ||
| J2K | 0.907 4 | 0.843 9 | 0.933 0 | 0.845 7 | 0.934 9 | 0.654 0 | 0.499 7 | 0.639 8 | 0.791 6 | 0.763 4 | ||
| CSC | 0.090 8 | 0.096 3 | 0.144 0 | 0.052 1 | 0.121 4 | 0.040 1 | 0.014 3 | 0.098 6 | 0.100 9 | 0.109 8 | ||
| HEVC-SCC | 0.807 4 | 0.826 3 | 0.877 1 | 0.786 9 | 0.873 0 | 0.392 1 | 0.244 4 | 0.485 1 | 0.452 4 | 0.465 4 | ||
| CQD | 0.908 0 | 0.776 6 | 0.902 4 | 0.736 8 | 0.863 4 | 0.439 7 | 0.558 0 | 0.504 6 | 0.592 3 | 0.754 8 | ||
| ALL | 0.751 2 | 0.714 6 | 0.757 6 | 0.579 9 | 0.699 3 | 0.272 7 | 0.606 6 | 0.621 1 | 0.686 6 | 0.761 3 | ||
| RMSE | GN | 3.809 3 | 4.445 8 | 4.571 4 | 5.738 0 | 5.012 7 | 6.960 2 | 3.236 9 | 6.362 3 | 3.167 9 | 4.516 2 | |
| GB | 6.663 3 | 5.199 8 | 5.447 5 | 5.735 4 | 5.664 8 | 8.442 2 | 8.476 7 | 7.311 0 | 7.756 7 | 5.436 5 | ||
| MB | 7.084 3 | 5.204 4 | 5.994 7 | 10.290 5 | 5.960 7 | 8.984 9 | 8.243 7 | 7.931 1 | 8.697 9 | 6.425 3 | ||
| CC | 5.986 7 | 6.476 7 | 7.759 0 | 8.887 6 | 4.452 4 | 8.482 1 | 7.717 8 | 8.569 8 | 7.689 1 | 5.183 6 | ||
| JPEG | 8.171 8 | 7.717 9 | 5.707 6 | 7.243 1 | 5.236 9 | 10.900 1 | 12.138 6 | 9.494 8 | 7.889 7 | 8.634 2 | ||
| J2K | 6.322 2 | 8.156 2 | 5.510 3 | 8.198 6 | 5.246 2 | 11.167 3 | 13.125 7 | 11.586 3 | 8.714 8 | 9.254 0 | ||
| CSC | 9.820 3 | 9.800 3 | 9.756 4 | 9.810 6 | 9.823 9 | 9.348 9 | 9.496 6 | 9.523 4 | 9.535 6 | 9.265 4 | ||
| HEVC-SCC | 8.400 9 | 8.503 7 | 6.198 8 | 8.496 9 | 6.517 6 | 12.369 5 | 12.354 5 | 10.827 0 | 11.556 2 | 11.138 2 | ||
| CQD | 4.981 4 | 7.985 5 | 5.535 4 | 8.226 9 | 5.640 6 | 10.376 3 | 8.708 3 | 10.002 5 | 8.850 8 | 7.101 5 | ||
| ALL | 9.168 2 | 9.613 3 | 8.973 9 | 11.015 7 | 10.055 2 | 13.327 1 | 10.996 7 | 10.520 5 | 9.981 1 | 8.831 9 | ||
表选项
本文使用3个常用指标来评估主观和客观评分之间的一致性:皮尔森线性相关系数(Pearson Linear Correlation Coefficient,PLCC),斯皮尔曼等级相关系数(Spearman Rank-order Correlation Coefficient,SRCC)和根均方根误差(Root Mean Squared Error,RMSE)。PLCC可用于评估预测的准确性,SRCC可用于评估预测的单调性,RMSE是评估预测一致性的一种方法。PLCC和SRCC值越高,算法的性能越好。相反,较小的RMSE表示更好的精度。
不同的图像质量评估算法可能会产生不同范围的分数,为了将各种评估算法进行比较,就需要把评估分数映射到共同的分数空间,这里使用逻辑斯蒂函数对评估分数进行映射:
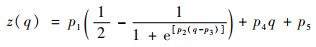 | (16) |
式中:p1、p2、p3、p4和p5是5个拟合参数;q为拟合前数据集;z(q)为拟合后数据集。
为了证明本文提出的算法的优越性,本文将其与以下经典的质量评估算法进行比较:PSNR、SSIM[1]、GMSD[2]、MAD(Most Apparent Distortion)[20]、SPQA[5]、SQI[6]、ESIM(Edge Similarity)[19]、GFM(Gabor Feature Model)[11]、NIQE[3]、IFC(Information Fidelity Criterion)[21]、BRISQUE[4]、GWH-GLBP(Gradient-Weighted Histogram of Local Binary Pattern calculated on the Gradient map)[17]、GSIM(Gradient Similarity)[22]以及NRLT[11]。在这些评估算法中,SPQA、SQI、ESIM、GFM和NRLT是针对屏幕内容图像设计的算法,其余的算法是为自然图像设计的。
表 1和表 2分别列出了上述图像质量评估算法在SIQAD数据库和SCID数据库上每种失真类型以及整体性能的测试结果。在2个表列出来的全参考算法中,每个测量指标(即PLCC、SRCC和RMSE)的最佳值用黑色粗体显示,而无参考算法中的每个测量指标的最佳值用黑色粗体加下划线显示。这些用来比较的算法的程序源代码都是从原始地址下载的。在表 1中,对于SQI算法,失真类型上的RMSE值没有提供。
从表 1中可以看出,针对屏幕内容图像设计的全参考算法,即SPQA、SQI、ESIM和GFM,实现了比针对自然图像设计的全参考算法更好的性能,即PSNR、SSIM、MAD和GMSD。在数据库SIQAD中,本文BES算法在所有无参考算法中取得最佳的性能,其中除了NRLT算法,其余算法都是针对自然图像提出的,只考虑了图像部分的特征,忽略了文字部分的特点,使得性能不佳;NRLT算法结合亮度和结构特征来表示图像,但是图像中存在大量文字,文字对亮度的敏感度低于图像部分,而本文BES算法利用图像中存在大量边缘这一特性,结合图像的特殊布局来表示图像,PLCC指标相比NRLT算法提高了2.63%。
本文BES算法的整体性能甚至高于专门为屏幕内容图像设计的全参考算法SPQA和SQI。其中,SPQA算法主要是考虑图像的亮度以及锐度特征,SQI算法结合图像局部结构相似性以及局部信息内容加权来计算图像分数,但是这2个算法都没有考虑图像中文字存在大量边缘这一特点,导致性能较低。在单个失真类型上,BES算法的性能除了在JPEG失真类型上略低于NRLT算法外,在其他失真类型上的性能都是无参考算法中最好的。
从表 2中可以看出,在SCID数据库中,BES算法的整体性能在3个指标上不仅高于对比的无参考算法,而且高于经典的全参考算法,即PSNR、SSIM、MAD、IFC和GSIM。其中,NRLT是对比方法中是先进的无参考算法,所提算法PLCC指标相比其提高了11.22%。在单个失真类型上,除了在GN、JPEG、J2K以及HEVC-SCC这4种失真类型上性能比其他无参考算法低以外,对于其余5种失真类型,BES算法的性能在无参考算法中都是最高的。
3 结论 本文根据人类视觉系统特点提出了一种新的针对屏幕内容图像的基于边缘和结构的无参考质量评估(EBS)算法,此算法是基于边缘信息和结构信息。提出的BES算法经实验验证,得到:
1) 本文算法考虑到屏幕内容图像具有特殊布局以及丰富边缘这2个特征,利用Gabor滤波器和LBP算子分别提取边缘和结构特征,并从5个尺度上提取特征,实现了与主观感知较高的一致性。
2) 本文算法可以实现对多种失真类型的屏幕内容图像较好的质量评估效果,在数据库SIQAD和SCID上的性能都优于经典的评估算法,甚至优于一些全参考算法。
通过实验验证,本文算法的屏幕内容图像质量评估效果取得一定的提升,提高了与主观感知的一致性。在未来,可以分别从图像区域和文字区域考虑,进一步提高该图像的质量评估效果。
参考文献
| [1] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. |
| [2] | XUE W, ZHANG L, MOU X, et al. Gradient magnitude similarity deviation:A highly efficient perceptual image quality index[J]. IEEE Transactions on Image Processing, 2014, 23(2): 684-695. |
| [3] | MITTAL A, SOUNDARARAJAN R, BOVIK A C. Making a 'completely blind' image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209-212. DOI:10.1109/LSP.2012.2227726 |
| [4] | MITTAL A, MOORTHY A K, BOVIK A C. No-reference image quality assessment in the spatial domain[J]. IEEE Transactions on Image Processing, 2012, 21(12): 4695-4708. DOI:10.1109/TIP.2012.2214050 |
| [5] | YANG H, FANG Y, LIN W. Perceptual quality assessment of screen content images[J]. IEEE Transactions on Image Processing, 2015, 24(11): 4408-4421. DOI:10.1109/TIP.2015.2465145 |
| [6] | WANG S, GU K, ZENG K, et al. Objective quality assessment and perceptual compression of screen content images[J]. IEEE Computer Graphics and Applications, 2016, 38(1): 47-58. |
| [7] | WANG S, GU K, ZHANG X, et al. Reduced-reference quality assessment of screen content images[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 28(1): 1-14. |
| [8] | SHAO F, GAO Y, LI F, et al. Toward a blind quality predictor for screen content images[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 48(9): 1-10. |
| [9] | FANG Y, YAN J, LI L, et al. No reference quality assessment for screen content images with both local and global feature representation[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1600-1610. |
| [10] | GUO X, HUANG L, GU K, et al. Naturalization of screen content images for enhanced quality evaluation[J]. IEICE Transactions on Information and Systems, 2017, 100(3): 574-577. |
| [11] | NI Z, ZENG H, MA L, et al. A Gabor feature-based quality assessment model for the screen content Images[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4516-4528. DOI:10.1109/TIP.2018.2839890 |
| [12] | DAUGMAN J G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters[J]. Journal of the Optical Society of America A, 1985, 2(7): 1160-1169. DOI:10.1364/JOSAA.2.001160 |
| [13] | JONES J P, PALMER L A. An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex[J]. Journal of Neurophysiology, 1987, 58(6): 1233-1258. DOI:10.1152/jn.1987.58.6.1233 |
| [14] | GEUSEBROEK J M, VAN DEBOOMGAARD R, SMEULDERS A W M, et al. Color invariance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(12): 1338-1350. DOI:10.1109/34.977559 |
| [15] | GEUSEBROEK J M, VAN DEBOOMGAARD R, SMEULDERS A W M, et al.Color and scale: The spatial structure of color images[C]//Proceedings of the European Conference on Computer Vision.Berlin: Springer, 2000: 331-341. |
| [16] | OJALA T, PIETIKAINEN M, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. Classification with Local Binary Patterns, 2002, 24(7): 971-987. |
| [17] | LI Q, LIN W, FANG Y. No-reference quality assessment for multiply-distorted images in gradient domain[J]. IEEE Signal Processing Letters, 2016, 23(4): 541-545. DOI:10.1109/LSP.2016.2537321 |
| [18] | HUGHES H C, NOZAWA G, KITTERLE F. Global precedence, spatial frequency channels, and the statistics of natural images[J]. Journal of Cognitive Neuroscience, 1996, 8(3): 197-230. DOI:10.1162/jocn.1996.8.3.197 |
| [19] | NI Z, MA L, ZENG H, et al. ESIM:Edge similarity for screen content image quality assessment[J]. IEEE Transactions on Image Processing, 2017, 26(10): 4818-4831. DOI:10.1109/TIP.2017.2718185 |
| [20] | ERIC C L, DAMON M C. Most apparent distortion:Full-reference image quality assessment and the role of strategy[J]. Journal of Electronic Imaging, 2010, 19(1): 011006. DOI:10.1117/1.3267105 |
| [21] | SHEIKH H R, BOVIK A C, DE VECIANA G, et al. An information fidelity criterion for image quality assessment using natural scene statistics[J]. IEEE Transactions on Image Processing, 2005, 14(12): 2117-2128. DOI:10.1109/TIP.2005.859389 |
| [22] | LIU A, LIN W, NARWARIA M. Image quality assessment based on gradient similarity[J]. IEEE Transactions on Image Processing, 2012, 21(4): 1500-1512. DOI:10.1109/TIP.2011.2175935 |
