目前机电系统的故障诊断方法一般分为两大类:基于模型的故障诊断方法和基于数据的故障诊断方法。基于模型的故障诊断方法依赖于获得较为精确的系统动态模型[4]。EMA的物理模型可以用一阶微分方程逼近,若利用EMA的物理模型确定各种故障模式对应的故障特征向量,结合基于数据的故障诊断方法将会获得更为准确的诊断结果[5]。递推最小二乘(Recursive Least Square,RLS)方法常被用来辨识模型中的故障特征参数,比如利用自回归滑动平均模型(Auto Regressive Moving Average model,ARMA)可以通过RLS方法来辨识EMA中的故障特征参数的实时取值[6]。RLS方法的不足之处在于,渐变性故障的初始阶段故障参数变化不明显,预测精度较差[7]。基于数据的故障诊断方法,无需精确的数学模型,但需要一个完备的数据库来训练和验证诊断算法。相对而言,基于数据的故障诊断方法具有自学习、自组织和自推理能力,使用起来更加灵活[8]。比如,基于特定的故障模式和属性,小波神经网络(Wavelet Neural Network,WNN)、多项式神经网络、概率神经网络、径向基神经网络、神经模糊结构等多种类型的模糊逻辑和神经网络工具已经被广泛应用于各种机电系统的故障诊断[9-12]。使用神经网络方法可以利用神经网络融合故障信号测量数据,建立故障特征与故障类别之间的相互关系,对渐变性故障进行预测[7]。但是,单纯使用神经网络方法难以满足EMA渐变性故障的预诊断的精度需求。
为此,本文提出一种基于动态小波神经网络(Dynamic Wavelet Neural Network,DWNN)的EMA渐变性故障诊断方法。利用小波多级分解算法来对传感器接收信号的频率分量进行取舍,利用动态神经网络的反馈机制来预测故障特征参数的演变趋势。与ARMA方法相比,DWNN方法利用小波分解算法去除了传感器测量信号中高频分量的影响,便于准确估计故障特征参数变化趋势,对EMA渐变性故障进行预诊断。
1 问题描述 1.1 EMA故障诊断特征向量 EMA是一种机电伺服系统,通过控制电机转速来带动减速传动机构,输出力矩驱动舵面负载。EMA的物理模型可以简化为一阶微分方程[13]:
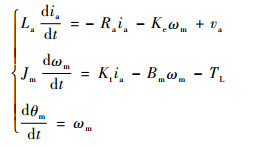 | (1) |
式中:Jm为EMA机电伺服系统的惯性;Bm为EMA机电伺服系统的阻尼;La为电机的电枢电感;Ra为电机的电枢电阻;va和ia分别为电机的电枢电压和电枢电流;ωm和θm分别为转速和电枢角度;Ke为电磁系数;Kt为转矩系数;TL为转子的负载转矩。
下面分析EMA中部件存在的典型渐变性故障。首先,电枢绕组匝间短路故障是电机常见性缺陷,轻微的匝间短路,EMA仍可继续运行;当匝间短路严重时,电枢电流显著增大,绕组温度升高,使电机振动加剧,甚至被迫停机。在EMA模型式(1)中,电枢绕组匝间短路表现为电机的电枢电感La和电枢电阻Ra发生变化。其次,EMA工作时其中机电传动装置的磨损是不可避免的,传动装置丝杆和滚珠磨损须经过长时间的演化,最终演变为故障或失效,当滚珠丝杆副磨损严重时,在EMA模型式(1)中机电伺服系统的阻尼Bm会发生变化。另外,EMA中控制面损失,将会导致EMA机电伺服系统的惯性Jm发生变化。综上,EMA潜在故障可以通过实际的物理参数来反映[13],即其故障特征向量可以选取为
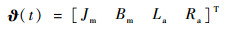 |
若能测得故障特征向量中各个参数的变化过程,将有助于判断EMA发生的电枢绕组匝间短路和传动机构过度磨损等典型部件的渐变性故障。但是这些故障参数不能由传感器直接测量。已有的研究表明使用RLS方法可以辨识出EMA的一阶差分方程,进而求出这些参数,使用RLS方法存在的困难是由于在渐变性故障的初始阶段故障参数变化不明显,预测精度较差,且不能同时辨识上述参数[14-15]。为了更准确地诊断EMA中发生的渐变性故障,并且能够处理同时发生的多个渐变性故障,本文使用DWNN模型具有的并行处理和自学习能力来辨识这些参数,对EMA的渐变性故障进行诊断。
1.2 DWNN模型 小波函数具有多分辨率特征,可以处理EMA故障中所需要的不同带宽数据,也可以处理某一传感器采集到信号中的多个频率分量。利用WNN模型可以将故障特征指示到相应的故障模式[16]。典型的WNN神经元函数f:Rn→R可以描述为
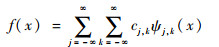 | (2) |
式中:系数cj, k为函数f在小波函数ψj, k(x)的投影,j和k分别为伸缩因子和平移因子。ψj, k(x)具有时间和频率变换内核,可描述为
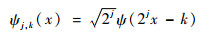 | (3) |
式中:小波函数ψj, k(x)由其母函数ψ(x)伸缩和平移得到。小波的多分辨率特性主要体现在j和k的取值。
利用小波的多分辨率特性,可以对采集到的信号在时域和频域权衡取舍。WNN是一种静态模型,只能反映输入与输出之间建立的一种静态关系[17]。为了对EMA系统故障的时间演变进行建模,需要在WNN的基础上引入反馈,形成DWNN模型。
一般反馈环节的记忆能力可以描述为
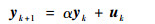 | (4) |
式中:uk为k时刻的控制输入;yk+1为k+1时刻的输出值;α为自反馈系数,0≤α≤1。对式(4)进行迭代计算可得
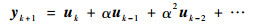 | (5) |
可见,反馈单元的输出是其输入过去值的滑动平均和,因反馈的存在,提供了对输入信号的一个无限的记忆。对EMA中的故障特征参数而言,随采样点之间距离的加大,它们之间的互相影响应该越来越小,因此,对输入信号进行了截断处理,只保留了N个。另外,为了弥补由于截断输入信号所造成的相关信息损失,利用反馈网络的自身的记忆能力对输出信号时间序列进行了相空间重构,得到重构维数为M的预测信息。
将以上的反馈环节引入WNN,形成DWNN,其基本结构如图 1所示。
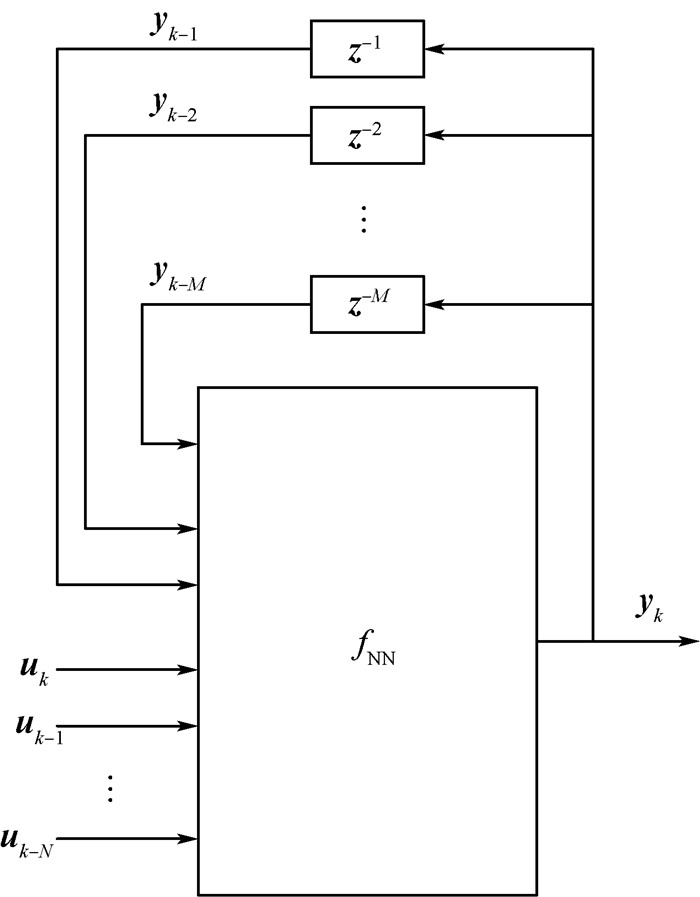 |
| 图 1 DWNN基本结构 Fig. 1 Basic structure of DWNN |
| 图选项 |
图 1所示的DWNN结构可以用公式描述为
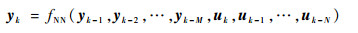 | (6) |
式中:fNN为神经网络函数;N为控制输入uk保留的过去输入值的数目;M为输出yk保留的过去输出值的数目。例如,本文uk为电机在k时刻的测量电流,yk为电机在k时刻的转速或故障特征参数。式(6)可以抽象理解为差分方程,这与EMA的数学模型非常契合。
DWNN模型遵循递归方式,能够将历史的和现在的数据映射到未来的数据,非常适合复杂系统故障的分类和预测[18]。EMA是一个由电机、减速装置、电控单元等部件组合而成的复杂系统,其故障模式包括机械振动、卡死、阻塞等事件,也包括电气和电子故障事件,比如短路、传感器漂移、器件失效等。本文设计的DWNN模型能够从传感器数据中获得重要的故障特征,从而判断故障的位置、程度和演变趋势。
1.3 EMA故障诊断问题 神经网络训练本质上是状态方程和测量方程的状态估计问题。在DWNN网络训练时,将权重w作为状态变量,并将输入和传感器的测量值{ui, zi}i=1NS作为样本进行训练,其中NS为训练样本总数。其状态方程和测量方程描述为
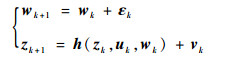 | (7) |
式中:h(·)为神经网络输入输出关系函数;ε为零均值的过程噪声向量,其协方差矩阵为cov(ε)=E(εεT)=Q;v为零均值的测量噪声向量,其协方差矩阵为cov(v)=E(vvT)=R。
设计DWNN模型需要确定神经网络的结构和参数,具体包括输入、输出的数目,以及小波节点数目和拓扑。根据式(2),神经元函数中包含无穷多个小波,工程上必须要对小波函数的数据进行截断。本文采用了k均值聚类来确定神经网络的节点数,每个聚类代表着一个节点。另外,记忆数据(即式(6)中M和N的取值)的选取会影响到故障的预测结果。若M和N的取值过大,可能会产生过拟合的预测结果;若M和N的取值偏小,会影响预测结果的准确性。本文根据EMA的物理方程来确定M和N的取值。
2 故障诊断算法 2.1 算法描述 给定训练样本{ui, zi}i=1NS,来训练DWNN的权重参数,是本文故障诊断算法的主要目的。本文使用了解耦无迹卡尔曼滤波器(Decoupling Unscented Kalman Filter, DUKF)来完成这一工作。采用DUKF的训练框架如图 2所示。
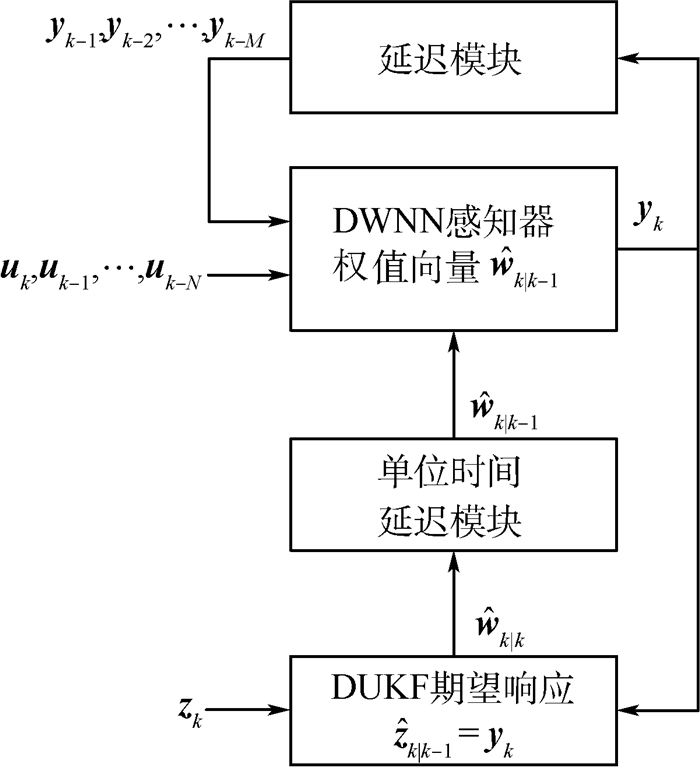 |
| 图 2 DUKF训练框架 Fig. 2 Training framework of DUKF |
| 图选项 |
图 2描述了DWNN的监督学习过程。当DWNN的输出向量yk与传感器实际测得的值zk之间存在差异,就可以通过DUKF获得权重wk的变化,进而预测EMA渐变性故障发生的可能性。
2.2 DUKF算法 在所设计DWNN中,采用了DUKF来跟踪模型中不同频率分量的信号状态。与UKF算法相比,DUKF算法忽略了神经网络取值之间的耦合,将多个0值引入到协方差矩阵Pk|k中,降低了滤波器算法的计算复杂度。
采用DUKF算法对DWNN感知器输出信号进行处理。DUKF通过在频率分量信号均值附近产生一组Sigma点,然后通过加权产生方差预测估计。其中,权重和状态的时域更新过程同式(7)。在滤波处理过程中,本文采用比例修正Sigma点的方法,将方差为Pk|k+1的n维随机向量
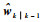
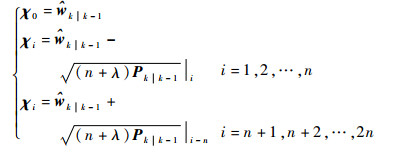 | (8) |
式中: χi(i=0, 1, …, 2n)表示由随机向量
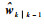
1) DUKF测量值更新
产生测量方程的对应Sigma点,并计算预测估计值:
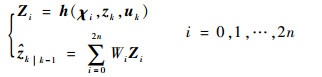 | (9) |
计算卡尔曼增益Kk:
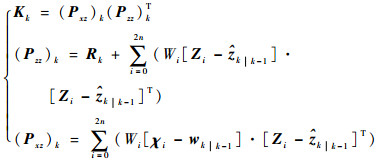 | (10) |
式中:Zi为Sigma点对应的观测向量; Wi为Sigma点χi的加权因子,计算式为
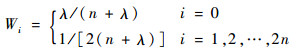 | (11) |
2) DUKF估计值更新
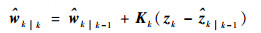 | (12) |
误差协方差更新:
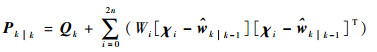 | (13) |
利用DUKF算法对输入输出数据进行处理,对神经网络进行离线训练,然后在线预测新的测量值。
对于DUKF算法,WNN的输入信号分量的输出数据为归一化数据。因为对这些分量的预测都是基于小波理论来实现的,满足正交特性。将各个分量的预测方差估计进行叠加后为原始信号的预测方差。
3 仿真算例与分析 以某型EMA的物理模型为对象, 对本文所提出的基于DWNN的故障诊断方法进行了验证。选取EMA的工作电流ia和电机转速ωm组成传感器测量向量z;选取EMA的供电电压va和负载转矩TL组成输入向量u;选取电枢绕组电感La和电阻Ra、机电伺服系统的惯性Jm和阻尼Bm组成故障特征向量?。然后通过询问相关领域的专家或查找相关研究文献将选取的故障特征参数与相应的故障模式关联起来,建立如表 1所示的故障特征表。
表 1 故障特征 Table 1 Fault features
| 故障模式 | 故障特征参数变化 | |||
| Bm | Jm | Ra | La | |
| 传动机构过度磨损 | +10% | |||
| 控制面损失 | -10% | |||
| 电枢绕组匝间短路 | -10% | -10% | ||
| 注:“+”表示特征参数增大;“-”表示特征参数减小。 | ||||
表选项
针对EMA电枢绕组匝间短路故障和传动机构过度磨损等典型部件的渐变性故障,进行了故障诊断实例的仿真。分别通过ARMA和DWNN两种方法来检测故障特征向量?中相应特征参数的变化,从而判断正在发生的故障。
3.1 绕组匝间短路故障诊断 假设EMA电枢绕组匝间短路开始发生在第100 s,电枢绕组匝间短路发生后会以指数函数的方式演变,在短期内造成电枢绕组更多的匝数短路。为了模拟电枢绕组匝间短路故障,这里通过在模型参数中加入与时间相关的指数权值来植入故障,加速了故障的演变过程。需要说明的是,EMA中的渐变性故障的发生通常是一个缓慢时变过程。
同时假设电枢绕组的电感值和电阻值与绕组的匝数是正相关的。即绕组匝数减少,电感值和电阻值会相应的减小。
分别应用ARMA和DWNN方法进行故障检测,诊断结果如图 3所示。图 3中的点划线为EMA的电枢绕组电感La和电阻Ra参数在正常情况下的不确定性边界,假设这些参数的摄动范围为±5%。图 3中的粗实线反映了使用DWNN方法对参数La和Ra的估计结果;图中的细实线反映了使用ARMA方法对参数La和Ra的估计结果。
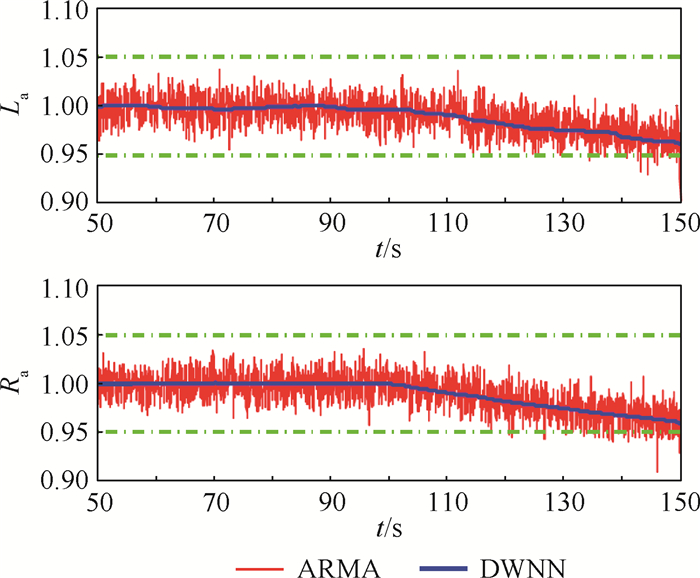 |
| 图 3 绕组匝间短路故障特征参数变化曲线 Fig. 3 Fault characteristic parameter variation curves of interturn short circuit of winding |
| 图选项 |
从图 3中可知,使用DWNN方法对参数La和Ra估计,获得的估计结果更平滑,这是因为采用小波分解算法(本文采用了3级小波分解算法),将被辨识信号分解成多个高频分量和低频分量,低频分量称为“近似”分量,反映信号总体趋势,高频信号则反映信号的逐次逼近过程,通过神经网络的学习,在参数估计时强调了低频分量的作用,而减弱了高频分量对估计结果的影响。考虑到本文主要针对EMA中的渐变性故障进行诊断,可以忽略高频分量的影响,以能够准确地获得信号的变化趋势。相对而言,使用ARMA方法对参数La和Ra估计,若要去除信号中高频分量的影响,必须人为增加滤波算法;若滤波算法的使用不当,反而会影响辨识的准确性。本文使用ARMA方法时,对测量信号进行了高频滤波。
3.2 传动机构磨损故障诊断 EMA传动机构磨损是一个缓慢时变的过程,本文通过改变故障特征参数的指数权值,加速了该故障的演变过程。假设EMA传动机构磨损在第100 s显现出来,即仿真过程中在第100 s对传动机构磨损故障特征参数Bm做了处理,改变了该故障特征参数的指数权值。
分别应用ARMA和DWNN方法进行故障检测,诊断结果如图 4所示。图 4中的点划线为EMA的传动系统阻尼Bm参数在正常情况下的不确定性边界,假设这些参数的摄动范围为±5%。图 4中的粗实线反映了使用DWNN方法对参数Bm的估计结果;图中的细实线反映了使用ARMA方法对参数Bm的估计结果。
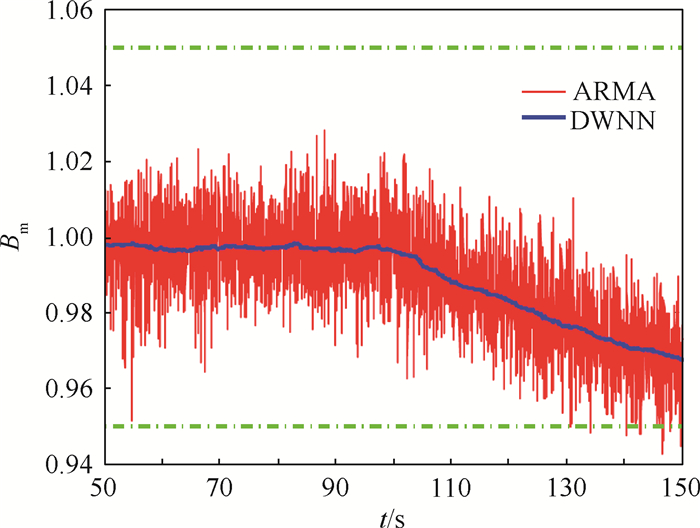 |
| 图 4 传动机构磨损故障特征参数变化曲线 Fig. 4 Fault characteristic parameter variation curves of wear of transmission device |
| 图选项 |
从图 4中可知,使用DWNN方法对参数Bm估计,获得的结果更稳定。相对而言,使用ARMA方法对参数Bm估计具有一定的不确定性。
根据表 1给定的设定值,EMA故障特征参数的变化大于10%时,可以认定EMA中相关部件发生了故障。若能提前发现EMA故障特征参数的变化大于5%,就可以根据故障特征参数的变化趋势来预测可能发生的故障,在EMA故障发生之前对故障进行预诊断。结合图 3和图 4可以发现,使用DWNN方法对故障特征参数进行跟踪可以准确地判断故障特征参数的变化趋势,实现对EMA渐变性故障的诊断。
另外,由于使用了DUKF来完成训练故障特征参数,诊断匝间绕组短路故障,只需要EMA的电枢电压va和电枢电流ia来训练故障特征参数电枢电感La和电枢电阻Ra;诊断传动机构磨损故障,只需要EMA的转速ωm和负载转矩TL来训练故障特征参数阻尼Bm。因此,本文方法可以有效诊断同时存在的多渐变性故障。
4 结论 1) 针对EMA中的渐变性故障,使用DWNN方法可以利用小波分解算法去除信号中高频分量的影响,获得更为平滑的故障特征参数估计值。
2) 使用DWNN方法可以准确地判断故障特征参数的变化趋势,从而实现对EMA中匝间绕组短路和传动机构磨损等渐变性故障的预诊断。
本文提出的DWNN方法能处理类似于EMA的机电设备中各种类型的渐变性故障,但是对于EMA的突变性故障,仍需要优化故障特征参数的估计过程,来减小故障特征参数突变后的检测时间。
参考文献
| [1] | BALABAN E, SAXENA A, NARASIMHAN S, et al.Experimental validation of a prognostic health management system for electro-mechanical actuators: AIAA-2011-1518[R].Reston: AIAA, 2011. |
| [2] | QIAN Y, YAN R. Remaining useful life prediction of rolling bearings using an enhanced particle filter[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(10): 2696-2707. |
| [3] | BALABAN E, SAXENA A, NARASIMHAN S, et al. Prognostic health-management system development for electromechanical actuators[J]. Journal of Aerospace Information Systems, 2015, 12(3): 329-344. DOI:10.2514/1.I010171 |
| [4] | BYINGTON C, WATSON M, EDWARDS D, et al.A model-based approach to prognostics and health management for flight control actuators[C]//IEEE Aerospace Conference.Piscataway, NJ: IEEE Press, 2004: 3551-3562. |
| [5] | NARASIMHAN S, ROYCHOUDHURY I, BALABAN E, et al.Combining model-based and feature-driven diagnosis approaches-a case study on electromechanical actuators[C]//Proceedings of 21st International Workshop on Principles of Diagnosis.Washington, D.C.: NASA, 2010: 1-8. |
| [6] | DIXON R, PIKE A W. Application of condition monitoring to an electromechanical actuator:A parameter estimation based approach[J]. Computing and Control Engineering Journal, 2002, 13(2): 71-81. DOI:10.1049/cce:20020203 |
| [7] | DAUBECHIES I. The wavelet transform, time-frequency localization and signal analysis[J]. IEEE Transactions on Information Theory, 2015, 36(5): 961-1005. |
| [8] | BADIHI H, RAD J S, ZHANG Y M, et al.Data-driven model-based fault diagnosis in a wind turbine with actuator faults[C]//International Mechanical Engineering Congress and Exposition.New York: ASME, 2014: 1-6. |
| [9] | NAPOLITANO M R, AN Y, SEANOR B A. A fault tolerant flight control system for sensor and actuator failures using neural networks[J]. Aircraft Design, 2000, 3(2): 103-128. DOI:10.1016/S1369-8869(00)00009-4 |
| [10] | YANG K, SHAN G, ZHAO L.Application of wavelet packet analysis and probabilistic neural networks in fault diagnosis[C]//Proceedings of 20066th World Congress on Intelligent Control and Automation.Piscataway, NJ: IEEE Press, 2006: 4378-4381. |
| [11] | JING J, LIU H, LU C. Fault diagnosis of electro-mechanical actuator based on WPD-STFT time-frequency entropy and PNN complexity[J]. Vibro Engineering PROCEDIA, 2017, 14(2): 130-135. |
| [12] | GUO P, SUN L, LI H, et al. Vibration fault diagnosis of hydropower unit based on multi-fractal spectrum and improved BP neural network[J]. Journal of Hydroelectric Engineering, 2014, 33(3): 299-305. |
| [13] | WANG J, LI T, XIE R, et al.Fault feature extraction for multiple electrical faults of aviation electro-mechanical actuator based on symbolic dynamics entropy[C]//Proceedings of IEEE International Conference on Signal Processing Communications and Computing.Piscataway, NJ: IEEE Press, 2015: 421-426. |
| [14] | DELGADO M, GARCIA A, URRESTY J C, et al.Evaluation of machine learning techniques for electro-mechanical system diagnosis[C]//Proceedings of European Conference on Power Electronics and Applications.Piscataway, NJ: IEEE Press, 2011: 1-10. |
| [15] | MARZAT J, PIET-LAHANIER H, DAMONGEOT F, et al. Model based fault diagnosis for aerospace systems:A survey[J]. Journal of Aerospace Engineering, 2012, 226(10): 1329-1360. |
| [16] | ZHANG Q, BENVENISTE A. Wavelet networks[J]. IEEE Transactions on Neural Networks, 1992, 3(6): 889-898. DOI:10.1109/72.165591 |
| [17] | BILLINGS S, WEI H L. A new class of wavelet networks for nonlinear system identification[J]. IEEE Transactions on Neural Networks, 2005, 16(4): 862-874. DOI:10.1109/TNN.2005.849842 |
| [18] | BECERIKLI Y. On Three intelligent systems:Dynamic neural, fuzzy, and wavelet networks for training trajectory[J]. Neural Computation and Applications, 2004, 13(4): 339-351. |
| [19] | MOON C, KWON Y. Sensorless speed control of permanent magnet synchronous motor by unscented kalman filter using various scaling parameters[J]. Journal of Electrical Engineering & Technology, 2016, 11(2): 347-352. |
