液体受到周期性垂直激励形成的振动频率为超声激励频率1/2的液体表面波统称为Faraday波[6]。Benjamin和Ursell[7]推导了圆柱形容器中自由表面波运动的振幅方程,并用稳定性理论得出不同条件下表面波振动频率可为超声激励频率的1/2、1或者3/2倍。Eisenmenger[8]基于线性流变振荡理论对Faraday波的形成进行理论分析和实验验证,测量了不同超声激励频率下毛细波波长及形成毛细波的初始激励振幅,给出激励振幅与毛细波振幅的关系。Peskin和Raco[9]对薄液膜进行线性稳定性分析,导出了超声雾化的雾粒直径与超声激励频率、换能器振幅和薄液膜厚度之间的关系。Sindayihebura等[10-11]分析了超声激励频率、振幅、平均膜厚、液体黏度等对驻波的影响。菅永军等[12-14]忽略表面张力的影响, 用两变量时间展开法得到具有立方项以及底部驱动项影响的非线性振幅方程。当受迫振动频率较低时,表面张力可忽略,但在高频条件下表面张力不可忽略。Higginbotham等[15]通过实验观察到低频振荡器产生与亚谐波Faraday波相关的液滴,高频振荡器产生与谐波响应一致的液滴;中频振荡器可根据驱动振幅激发任何一种响应的液滴。在高频振荡器中, 可以通过增大驱动振幅改变雾化液滴的尺寸。Li和Umemura[16]基于不可压缩欧拉方程对Faraday波不稳定性进行了两相流仿真,从物理上探讨了液体韧带是如何从振动的液体层脱离。刘财兴等[17]从实验与理论两方面研究了垂直激励低黏度硅油在低频范围内Faraday波的特性,发现随着超声激励频率增大,驻波图案的波峰数增加,模态复杂化,对应的驱动振幅减小。Sheldrake等[18]系统地探索了振幅、频率、体积(或深度)、温度和大气压力对垂直壁圆形容器中Faraday波形的影响。赵文定等[19]由Faraday波振幅方程导出了稳定条件下的色散关系,利用参量共振方程得到了在亚简谐条件下本征波矢的取值范围。Tadrist等[20]导出了由垂直振动液体表面产生的Faraday表面波模型。
综上所述,Faraday波多在较低的激励频率下研究,对超声激励下Faraday波的理论和实验研究较少。Faraday波的波长与激励频率有关,通过增大激励频率可得到微纳尺度波长的表面波,进而有利于获得微纳颗粒。本文针对超声激励频率为35kHz条件下液膜表面形成Faraday波进行有限元仿真和实验,对Faraday波的形成机理进行探究。
1 CFD有限元仿真分析 对薄液膜施加垂直其表面的超声振动,在液膜表面激发排列整齐的正方形表面波阵列,即Faraday波。通过CFD有限元仿真对Faraday波的形成机理进行探究,并对Faraday波的形成过程及相关条件进行讨论。
1.1 计算模型 表面波的几何形状与液体体积有关,而较少的液体体积不影响仿真结果。三维计算模型虽然直观,但考虑到计算时长和硬件限制,二维计算模型时间成本较低,且不影响仿真结果,故选择二维计算模型。
该计算模型采用超声激励频率为35kHz,所用液体为蒸馏水(室温为20℃)。蒸馏水的表面张力为0.072N/m,动力黏度为0.001N·s,密度为1000kg/m3[21]。
表面波波长由开尔文公式[22]计算:
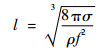 | (1) |
式中:l为表面波波长;σ为液体表面张力;ρ为液体密度;f为超声激励频率。
将相关数据代入式(1)可知,35kHz超声激励水薄膜形成表面波的波长约为113.87μm,因此模型长度设置为1mm, 约为理论波长的8.7倍,液膜厚度为0.05mm。为研究薄液膜表面波的运动情况,设置液体域上方的空气域高度为液膜厚度的2倍,即为0.1mm。因此,CFD有限元仿真二维计算模型由2个矩形组成,分别为上方空气域矩形及下方流体域矩形。空气域矩形长度为1mm,宽度为0.1mm,流体域矩形长度为1mm, 宽度为0.05mm[23]。
在该二维计算模型中,以非结构网格对计算域进行网格划分,考虑到表面波波长和液膜底部侧壁及空气域上边界对表面波影响较小,液膜底部和侧壁一个网格的长度设置为10μm,空气域上边界一个网格长度设置为10μm,空气域两侧边界和流体域上边界对表面波的形成影响较大,因此对这两部分网格进行加密处理,设置一个网格长度为5μm,使每个表面波波长方向上划分有20个网格,以保证计算的有效性[24]。计算模型如图 1所示。
 |
| 图 1 计算模型 Fig. 1 Calculation model |
| 图选项 |
采用多相流模型(VOF)对气液交界面的运动情况进行追踪显示。在计算模型中,除空气域的上边界条件为压力出口(pressure-out)之外,其余的边界条件均为壁(wall), 液体域中的侧壁无剪切滑移作用[25],具体如图 1所示。通过动网格及用户自定义函数(UDF)功能,在流体域下边界施加超声振动[26]。设施加超声振动位移为
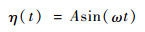 | (2) |
式中:ω为超声激励角频率,;A为超声激励振幅;t为时间。
流体域底部作简谐运动,其轴向速度为
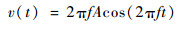 | (3) |
通过相图和流线图,对超声激励下液体表面波的形成过程进行分析。
1.2 仿真结果与分析 利用动网格和UDF功能对流体域施加35kHz超声振动。图 2所示为超声激励频率35kHz、超声激励振幅8μm条件下不同时刻薄液膜的气液相图。
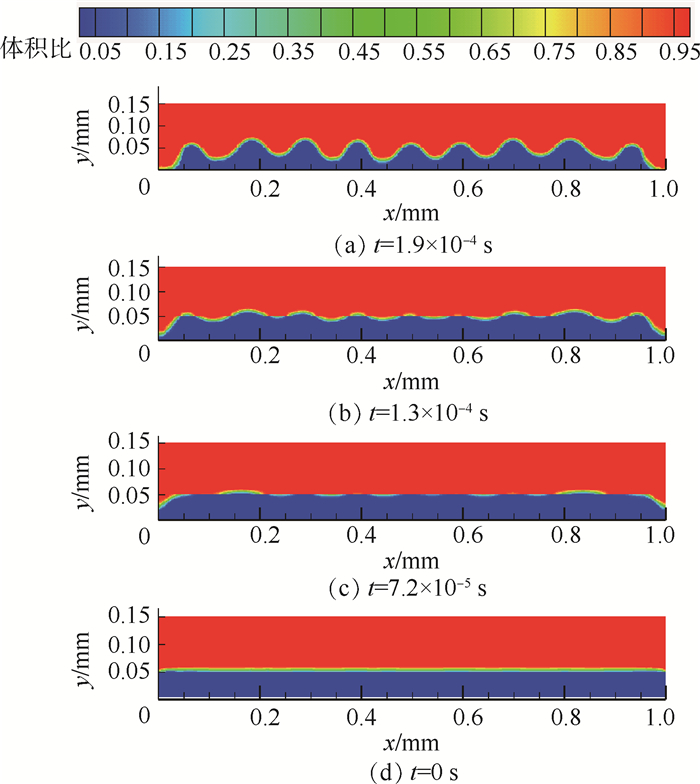 |
| 图 2 超声激励频率35kHz、超声激励振幅8μm条件下不同时刻的Faraday波相图 Fig. 2 Phase diagram of Faraday wave at different moments under ultrasonic excitation frequency 35kHz and ultrasonic excitation amplitude 8μm |
| 图选项 |
从图 2中可知,当施加超声激励后,薄液膜表面从静止状态开始振动,经历一段时间(7.2×10-5 s),在液膜表面中心位置存在振幅较小的表面波动;随着时间推移(1.3×10-4s),液膜表面波动较明显,振幅不断增大;当经历多个周期超声激励(1.9×10-4s)后,液膜表面波动现象逐渐趋于稳定,振幅不再增加,波峰波谷随着时间作交替变换,波节位置基本保持不变。
图 3为超声激励频率35kHz时,不同超声激励振幅的气液相图。如图 3所示,当施加超声激励振幅为2、4μm时,表面波动不明显;当施加超声激励振幅增加为6、8、10μm时,薄液膜表面出现较明显的均匀表面波,且中间位置表面波一致性好;当施加超声激励振幅为12μm时,表面波振幅较大,形成脖子,表面波波峰脖子以上液体有脱离液膜主体的趋势,即超声雾化即将发生。
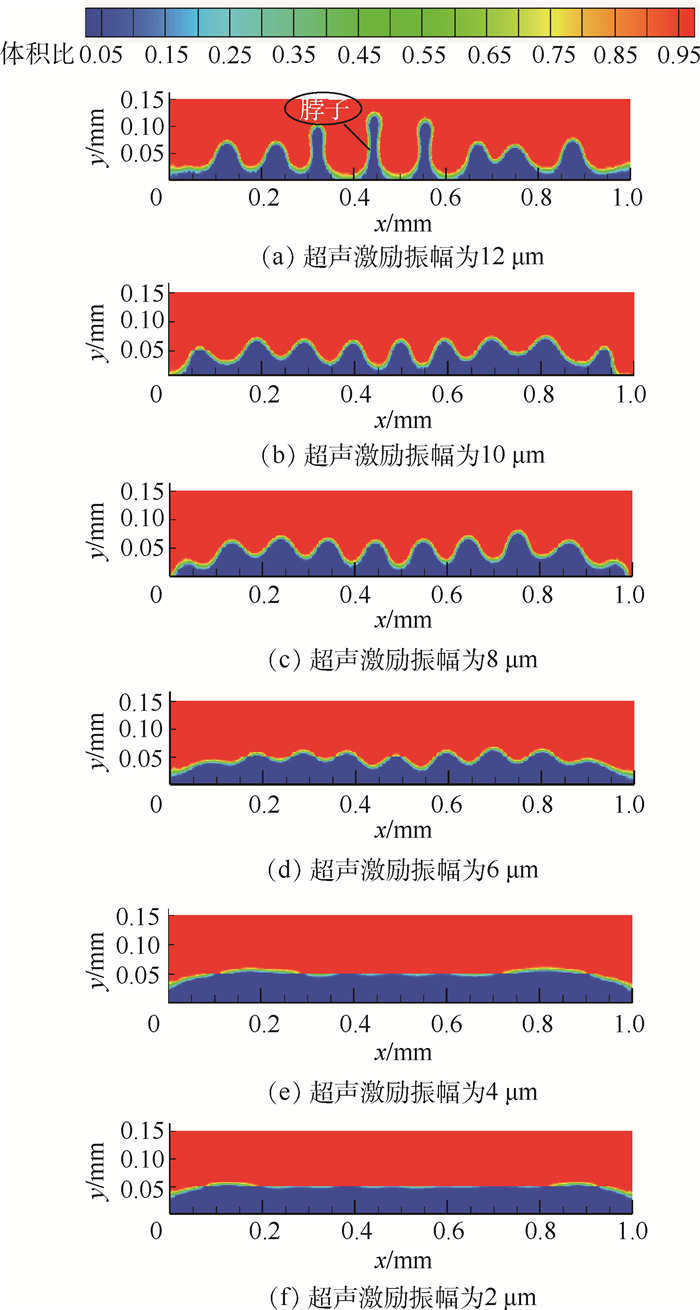 |
| 图 3 超声激励频率35kHz条件下不同超声激励振幅的Faraday波相图 Fig. 3 Phase diagram of Faraday wave under different ultrasonic excitation amplitudes at ultrasonic excitation frequency 35kHz |
| 图选项 |
由图 3可知,当超声激励振幅超过某一临界值α时,在液膜表面产生表面波;超声振幅增加,表面波振幅随之增加;当超声激励振幅超过临界值β时,薄液膜表面的表面波波峰处形成脖子,脖子以上液体不再恢复到薄液膜主体,即发生超声雾化现象。在不同超声激励振幅下,表面波波长基本无变化,即某一种液体在同一超声激励频率下,改变超声激励振幅仅改变表面波振幅,对表面波波长无影响。
图 4所示为施加超声激励频率35kHz,超声激励振幅8μm条件下,1.9×10-4s时刻的气液相图,表 1为图 4中各个波峰位置处的坐标值及形成的表面波波长。表面波波长为后一波峰坐标位置与前一波峰位置坐标的差值,最终得出该时刻表面波平均波长。
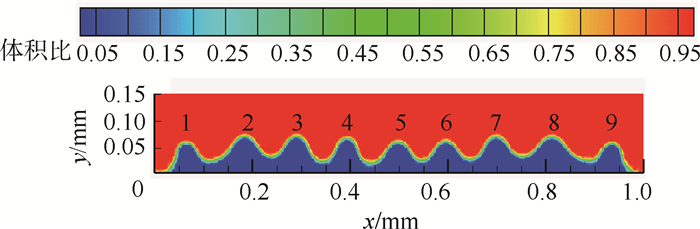 |
| 图 4 超声激励频率35kHz、超声激励振幅8μm条件下1.9×10-4s时刻的Faraday波相图 Fig. 4 Phase diagram of Faraday wave at 1.9×10-4s under ultrasonic excitation frequency 35kHz and ultrasonic excitation amplitude 8μm |
| 图选项 |
表 1 图 4中各个波峰位置处的坐标及波长 Table 1 Coordinates and wavelength at each peak position in Fig. 4
| 序号 | 横向坐标/μm | 波长/μm |
| 1 | 58.26 | 122.9 |
| 2 | 181.2 | 105.7 |
| 3 | 286.9 | 103.7 |
| 4 | 390.6 | 103.7 |
| 5 | 494.3 | 99.9 |
| 6 | 594.2 | 101.9 |
| 7 | 696.1 | 115.2 |
| 8 | 811.3 | 124.9 |
| 9 | 936.2 |
表选项
从图 4可知,薄液膜表面形成了结构一致的表面波。在薄液膜表面有9个波峰,第1个波峰和第9波峰的方向不是竖直向上,这可能是由于表面张力的存在使处于边缘处的液膜有一定坡度,造成波峰方向有偏差,其余波峰方向竖直向上,且相邻波峰之间长度基本一致。通过取点测量,各个波峰横向坐标如表 1所示,9个波峰之间的平均距离为109.74μm,即表面波平均波长为109.74μm,与式(1)计算的理论值113.87μm的误差为3.6%。
图 5为一个超声激励周期表面波的流线图。其中,T为一个超声激励周期, ti为仿真经历时间。超声激励频率为35kHz,超声激励振幅为8μm。从流线图可知:
 |
| 图 5 一个超声激励周期Faraday波的流线图 Fig. 5 Streamline diagram of Faraday wave in an ultrasonic excitation period |
| 图选项 |
1) 远离薄液膜的空气域速度方向始终和超声激励(液膜底面)的速度方向保持一致,薄液膜附近空气域的速度方向有偏差,此部分空气域速度变化较快,液体域速度存在滞后现象。
2) 超声激励竖直向下的速度逐渐减小转向为竖直向上并增大到最大值的过程中(图 5(a)、(b)和(f)),波峰左侧空气域和流体域的速度矢量组成一个顺时针闭环,波峰右侧空气域和流体域的速度矢量组成一个逆时针闭环。表面波波峰和波谷先短暂增加然后衰减至液膜表面基本为平面,空气抑制表面波增长。
3) 超声激励竖直向上的速度由最大值逐渐减小转向并增加到竖直向下最大值的过程中(图 5(c)~(e)),波峰左侧空气域和流体域的速度矢量组成一个逆时针闭环,波峰右侧空气域和流体域的速度矢量组成一个顺时针闭环,空气促进波峰波谷增长。
4) 图 5中x=0.5mm处表面波在(a)中为波峰,在(f)中为波谷,即一个超声激励周期约为液膜表面波运动周期的1/2,超声激励与表面波运动存在不断变化的相位差,一个相位差变化周期约为2个超声激励周期。图 6所示为图 5中x=0.5mm处表面波与超声激励的相位变化,图中η为位移量。
 |
| 图 6 Faraday波和超声激励相位差 Fig. 6 Phase difference between Faraday wave and ultrasonic excitation wave |
| 图选项 |
表面波是外加周期性垂直激励后流体域和空气域相互作用形成的。超声激励竖直向下的速度逐渐减小转向为竖直向上且不断增加到最大值的过程中,由于液体域惯性较大,液体域波峰处液体保持原来的运动趋势,波峰处空气域速度方向随超声激励的变化而变化,因此在波峰左侧形成顺时针速度矢量闭环,在波峰右侧形成逆时针速度矢量闭环,此过程中空气域抑制波峰和波谷的增长;同理,当超声激励竖直向上的速度由最大值逐渐减小转向并增加到最大值的过程中,在波峰左侧形成逆时针矢量闭环,在波峰右侧形成顺时针矢量闭环,空气域促进波峰波谷的增长。
2 实验分析 为测试超声激励表面波的形成状态,实验采用35kHz超声波发生器和圆锥形变幅杆组成超声振动系统,通过超景深显微镜(VHX-2000)观察变幅杆发射端薄液膜表面的运动情况,实验装置如图 7所示。
 |
| 图 7 实验装置平台 Fig. 7 Experimental device platform |
| 图选项 |
将工作液(蒸馏水)均匀涂覆在变幅杆发射端。通过超声振动系统对液膜施加纵向振动,激励液膜表面形成Faraday波。在超声振动系统上方搭建超景深显微镜,观测液膜表面状态。图 8为通过超景深显微镜观察到的薄液膜表面超声激励产生的Faraday波阵列。
 |
| 图 8 表面驻波阵列 Fig. 8 Surface standing wave array |
| 图选项 |
在图 8中,液膜表面存在均匀分布点阵,其中亮点为表面波波峰或波谷,彼此相间,表面波波节位置基本不变,2个亮点之间的距离为表面波波长的1/2,3个亮点之间的距离为一个表面波波长。通过测量,3个亮点之间距离的平均值约为117.6μm。因此,实验获得表面波的振动频率约为超声激励频率的1/2,理论误差为3.3%。实验测得的表面波波长大于理论值,这可能是由开尔文公式未考虑重力波的影响和测量误差的存在造成。
3 结论 通过实验和CFD有限元仿真分析,对薄液膜在超声激励下形成的表面波进行了研究。
1) 通过CFD有限元仿真分析,同一超声激励频率下,当超声激励振幅超过临界值α时,经历数个超声激励周期后,薄液膜表面激发形成Faraday波。随超声激励振幅增加,Faraday波振幅增大,当超声激励振幅超过临界值β时,会产生超声雾化现象。此外,表面波波长不随超声激励振幅的改变而改变。
2) 通过对一个超声激励周期表面波流线图分析,在超声激励竖直向下的速度逐渐减小转向为竖直向上且不断增加到最大值的过程中,波峰处存在速度矢量闭环,空气抑制表面波的增长;当超声激励竖直向上的速度由最大值逐渐减小并转向增大到竖直向下最大值的过程中,波峰处存在速度矢量闭环,空气促进表面波的生长。液膜表面的表面波是在外部周期性激励下由空气与液体相互作用形成的。表面波波峰或波谷与超声激励存在不断变化的相位差,一个相位差变化周期约为2个超声激励周期。
3) 超声振动激励薄液膜表面形成Faraday波,实验测量的Faraday波波长与理论计算值相比较,得出35kHz超声激励形成Faraday波的振动频率约为超声激励频率的1/2,与CFD有限元仿真分析结果一致。
参考文献
| [1] | 雷成龙.利用液-固界面效应制备球形金属粉末及其性能研究[D].南京: 南京大学, 2016: 14-25. LEI C L.Preparation of spherical metal powder by liquid-solid interface effect and its properties[D]. Nanjing: Nanjing University, 2016: 14-25(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10284-1016123733.htm |
| [2] | 乐国敏, 李强, 董鲜峰. 适用于金属增材制造的球形粉体制备技术[J]. 稀有金属材料与工程, 2017, 46(4): 1162-1168. LE G M, LI Q, DONG X F. Preparation of spherical powders for metal additive manufacturing[J]. Rare Metal Materials and Engineering, 2017, 46(4): 1162-1168. (in Chinese) |
| [3] | 高正江, 周香林, 李景昊, 等. 高性能球形金属粉末制备技术进展[J]. 热喷涂技术, 2018, 10(3): 1-9. GAO Z J, ZHOU X L, LI J H, et al. Advances in preparation technology of high performance spherical metal powders[J]. Thermal Spraying Technology, 2018, 10(3): 1-9. DOI:10.3969/j.issn.1674-7127.2018.03.001 (in Chinese) |
| [4] | 张海庆. 均匀颗粒成型法(UDS)原理及应用[J]. 天津冶金, 2001(1): 39-40. ZHANG H Q. Principle and application of uniform particle forming method (UDS)[J]. Tianjin Metallurgy, 2001(1): 39-40. DOI:10.3969/j.issn.1006-110X.2001.01.011 (in Chinese) |
| [5] | SONG W, SHUMLAK U. Ultrasonically aided electrospray source for charged particles approaching monodisperse distributions[J]. Journal of Propulsion & Power, 2012, 26(2): 353-363. |
| [6] | FARADAY M. On the forms and states of fluids on vibrating elastic surfaces[J]. Proceedings of the Royal Society of London, 1831, 121: 299-340. |
| [7] | BENJAMIN T B, URSELL F. The stability of the plane free surface of a liquid in vertical periodic motion[J]. Proceedings of the Royal Society of London, 1954, 225(1163): 505-515. DOI:10.1098/rspa.1954.0218 |
| [8] | EISENMENGER W. Dynamic properties of surface tension of water and aqueous solutions of surface active agents with standing capillary waves in the frequency range from 10kHz to 1.5 MHz[J]. Acoustica, 1959, 9: 327-340. |
| [9] | PESKIN R L, RACO R J. Ultrasonic atomization of liquids[J]. The Journal Acoustical Society of America, 1963, 34(1): 6-15. |
| [10] | SINDAYIHEBURA D, BOLLE L. Theoretical and experimental study of the behavior of liquid film free surfaces driven by transverse ultrasonic vibrations[J]. WIT Transactions on Modelling and Simulation:Computational Modelling of Free and Moving Boundary Problems, 1995, 13: 67-74. |
| [11] | SINDAYIHEBURA D, BOLLE L, CORNET A, et al. Theoretical and experimental study of transducers aimed at low-frequency ultrasonic atomization of liquids[J]. The Journal of the Acoustical Society of America, 1998, 103(3): 1442-1448. DOI:10.1121/1.421300 |
| [12] | 菅永军, 鄂学全, 柏威. 参数激励圆柱形容器中的非线性Faraday波[J]. 应用数学和力学, 2003, 24(10): 1057-1068. JIAN Y J, E X Q, BAI W. Nonlinear Faraday waves in parameter-excited cylindrical vessels[J]. Applied Mathematics and Mechanics, 2003, 24(10): 1057-1068. DOI:10.3321/j.issn:1000-0887.2003.10.009 (in Chinese) |
| [13] | JIAN Y J, E X Q. Instability analysis of nonlinear surface waves in a circular cylindrical container subjected to a vertical excitation[J]. European Journal of Mechanics B-Fluids, 2005, 24(6): 683-702. DOI:10.1016/j.euromechflu.2005.03.002 |
| [14] | 长龙, 菅永军, 刘全生. 圆柱形容器中垂直激励的弱黏性流体界面波[J]. 内蒙古大学学报(自然版), 2014, 45(4): 353-359. CHANG L, JIAN Y J, LIU Q S. The interface of weakly viscous fluids with vertical excitation in cylindrical vessels[J]. Journal of Inner Mongolia University (Natural Science Edition), 2014, 45(4): 353-359. (in Chinese) |
| [15] | HIGGINBOTHAM A P, GUILLEN A, JONES N, et al. Evidence of the harmonic Faraday instability in ultrasonic atomization experiments with a deep, inviscid fluid[J]. The Journal of the Acoustical Society of America, 2011, 130(5): 2694. DOI:10.1121/1.3643816 |
| [16] | LI Y, UMEMURA A. Two-dimensional numerical investigation on the dynamics of ligament formation by Faraday instability[J]. International Journal of Multiphase Flow, 2014, 60: 64-75. DOI:10.1016/j.ijmultiphaseflow.2013.12.002 |
| [17] | 刘财兴, 杜会静, 王怀翔. 垂直激励低黏度硅油的法拉第波研究[J]. 大学物理, 2016, 35(4): 52-59. LIU C X, DU H J, WANG H X. Faraday wave study of vertically excited low viscosity silicone oil[J]. University Physics, 2016, 35(4): 52-59. (in Chinese) |
| [18] | SHELDRAKE M, SHELDRAKE R. Determinants of Faraday wave-patterns in water samples oscillated vertically at a range of frequencies from 50-200 Hz[J]. Water, 2017, 9: 1-27. |
| [19] | 赵文定, 王思慧, 范周游, 等. 理想流体的法拉第波模态[J]. 物理实验, 2017, 37(1): 13-18. ZHAO W D, WANG S H, FAN Z Y, et al. Faraday wave modes of ideal fluids[J]. Physics Experiment, 2017, 37(1): 13-18. DOI:10.3969/j.issn.1005-4642.2017.01.003 (in Chinese) |
| [20] | TADRIST L, SHIM J B, GILET T, et al. Faraday instability and subthreshold Faraday waves:Surface waves emitted by walkers[J]. Journal of Fluid Mechanics, 2018, 848: 906-945. DOI:10.1017/jfm.2018.358 |
| [21] | DUMOUCHEL C, SINDAYIHEBURA D, BOLLE L. Application of the maximum entropy formalism on sprays produced by ultrasonic atomizers[J]. Particle & Particle Systems Characterization, 2003, 20(2): 150-161. |
| [22] | RAYLEIGH J W S B, LINDSAY R B. The theory of sound[M]. New York: Dover Publications, 1945: 344. |
| [23] | EHRHORN J, SEMKE W. Numerical modeling of vibration induced atomization of liquids[J]. Folia Parasitologica, 2013, 45(3): 196-198. |
| [24] | YULE A J, AL-SULEIMANI Y.A CFD prediction of wave development and droplet production on surface under ultrasonic excitation[C]//Preceding of Institute for Liquid Atomization and Spray Systems-Europe, 2002. |
| [25] | HONG Y, JIE H, GU X Z, et al. Study on ultrasonic spray technology for the coating of vascular stent[J]. Science China Technological Sciences, 2011, 54(12): 3358-3370. DOI:10.1007/s11431-011-4580-0 |
| [26] | 蔡耀中.超声微泡发生方法及装置设计研究[D].杭州: 杭州电子科技大学, 2014: 46. CAI Y Z.The design and study of ultrasonic micro bubbles generator and technique[D]. Hangzhou: Hangzhou Dianzi University, 2014: 46(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10336-1014229101.htm |
