关联波门是指以目标的一步预测为中心,用来确定目标的观测值可能出现范围的一块区域[4]。波门的大小主要依赖于预测误差、正确接收回波的概率、雷达测量误差等其他因素,应最大可能地使得真实量测落入其中,同时尽量避免引入杂波[5-7]。当群目标发生上述机动时,由于跟踪算法的参数设置难以与目标实际运动模式完全匹配,波门内可能没有真实量测,因此出现误跟甚至失跟的现象。
以交互式多模型(Interacting Multiple Model, IMM)算法[8-9]为代表的动态多模型算法考虑了各模型间的切换,采用混合估计跟踪目标运动状态。IMM算法较高的效费比,使其迅速成为该领域研究的主要方向,相应的改进算法也被大量提出[10]。
针对上述问题,本文首先将IMM算法与CGT算法结合,利用最新量测信息将转移概率改进为自适应;其次,设计了一种自适应关联波门的CGT算法,针对群整体机动及分离机动,能够自适应对关联波门进行调整。本文创新点在于将自适应转移概率的多模型算法与CGT算法相结合以跟踪群的机动行为,将分离和整体机动时的跟踪波门改进为自适应以提高跟踪精度。仿真实验证明本文算法提高了杂波背景下对机动群目标跟踪的精度,具有实用价值。
1 转移概率自适应IMM-CGT算法 1.1 IMM-CGT算法 CGT算法通过计算当前时刻椭圆波门内确认量测的中心坐标,将航迹预测中心和确认量测中心进行关联。利用群的速度预测下一时刻群波门,外推点作为波门中心,落入波门内的量测用于群的更新。将IMM算法与CGT算法结合,利用多个模型间的交互作用,可以实现机动情形下对群中心的跟踪估计,具体流程如下:
假设有一批由T个目标组成的飞机编队,系统的状态方程为
 | (1) |
式中:F(k)为状态转移矩阵;G(k)为输入控制矩阵;u(k)为输入信号; V(k)为零均值高斯白噪声;X(k+1)为群中心的全局状态向量,在二维坐标系中,
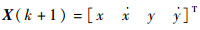
系统的量测方程为
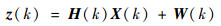 | (2) |
式中:H(k)为量测矩阵;z(k)为时刻群中心的量测值;W(k)为均值为零的高斯白噪声。设Z(k)为k时刻的量测集合:
 | (3) |
其中:mk为k时刻的量测个数。
1) 状态估计的交互作用
设从模型i转移到模型j的转移概率为Pij,其中i, j=1, 2, …, N,令

 | (4) |
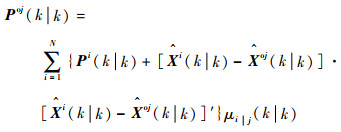 | (5) |
式中:
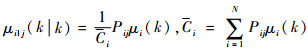
2) 针对群中心一步预测建立关联波门
将交互后的群中心状态向量
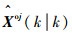
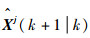
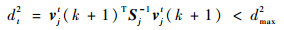 | (6) |
式中:vjt(k+1)为量测zjt(k+1)相对群中心量测预测值
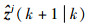
3) 建立新群
选择候选回波中归一化距离最小的量测作为该群的种子量测。设定有关种子量测的临近标准,判断所有量测是否在以该种子量测为中心的群内。计算新群中心
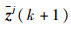
4) 模型条件滤波
利用Kalman滤波计算模型j估计群中心的滤波新息vj(k+1)、增益Kj(k+1)、协方差更新Pj(k+1|k+1)以及状态更新
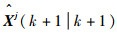
5) 模型概率更新
假定服从高斯分布,则模型j的可能性为
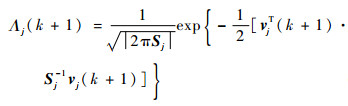 | (7) |
则模型j的概率更新为
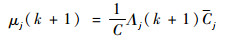 | (8) |
式中:
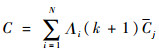
6) 输出融合
利用模型概率对各个子滤波器的输出进行融合,得到群中心的状态和协方差估计为
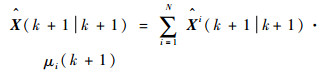 | (9) |
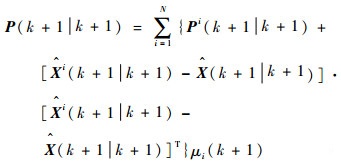 | (10) |
1.2 转移概率自适应 传统IMM算法中Markov转移概率是根据先验信息或人为主观确定的[11],并且在估计过程中保持不变,由于目标的机动性和先验信息的失真,固定的转移概率不能反映目标运动模式的转换,造成了一定的估计误差,因此需要通过后验信息对转移概率进行实时地修正[12]。文献[13]指出模型集应尽可能选择在目标真实运动模式附近,跟踪精度才越高。
文献[14]指出,模型转移概率是采样时间的函数,即
 | (11) |
式中:Mj(k)为模型的时间, j=1, 2, …, N,从Mi(k-1)到Mj(k)服从马氏链。一步预测概率为
 | (12) |
利用贝叶斯定理,式(12)可以表示为
 | (13) |
式中:
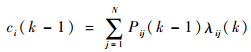
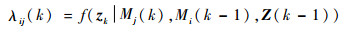 | (14) |
其中:f(·)为概率密度函数;Z(k-1)用模型i的滤波估计值近似,所以式(14)可以表示为
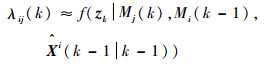 | (15) |
对于量测序列Z(k),假设转移概率在时间间隔k到k+1不变,即
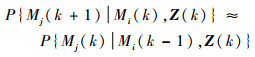 | (16) |
所以,Pij(k)≈Pij(k-1|k)。
对所有的i, j=1, 2, …, N, i≠j,初值设为
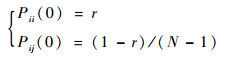 | (17) |
式中:r为常数,且0≤r≤1。除了在循环开始的时候要设置初值,在实际应用中,当Pij(k)=0或1时,需在算法的进程中进行重初始化。
2 关联波门自适应的CGT算法 关联波门指的是在给定概率PG条件下,包含目标量测的最小体积空间,它是以被跟踪目标的一步预测为中心,确定该目标下一时刻可能出现的一块区域[15]。群在运动过程中可能出现加(减)速、转弯等整体机动以及分离、合并等特殊机动,造成关联波门内有效量测数目减少,使得估计误差增大。因此,在机动时刻需要调整波门,确保真实量测落入。以群的整体转弯和群分离为例,失跟示意图如图 1所示。
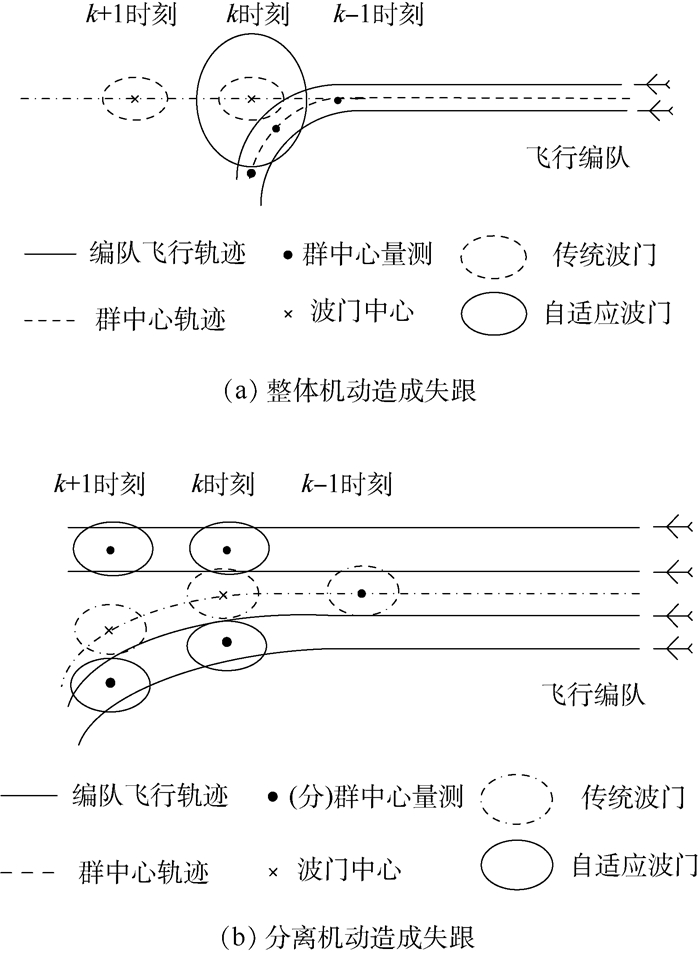 |
| 图 1 群目标失跟示意图 Fig. 1 Schematic diagram of losing group target |
| 图选项 |
2.1 整体机动的自适应关联波门 设
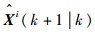
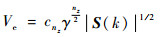 | (18) |
式中:nz为目标量测向量的维数;cnz为与量测向量维数相关的常量;γ为关联波门门限值。可见通过修正新息协方差可以对关联波门进行调整。根据真实的新息协方差S(k)计算公式,采用最大机动模型对应的协方差对S(k)进行自适应调整,即
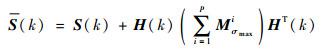 | (19) |
式中:p为波门放大次数;Miσmax为第i次的扩展步长,此处设为最大机动水平所对应模型的协方差矩阵。假设k时刻模型j的机动水平最大,即
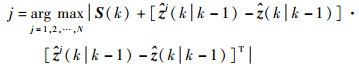 | (20) |
p值的选取对跟踪效果也有一定的影响。若p值过小,当目标发生较大的机动时,将出现量测丢失;若p值过大,波门内的候选回波中就会出现杂波,并且当波门过大时,滤波器需要处理的数据增多,因此影响了跟踪的实时性。上述2种情况都会影响群内量测的分布情况,从而影响群中心的估计精度。
下面计算增大新息协方差带来的跟踪误差。在单次递推计算中,由于新息协方差的调整,最终的滤波输出发生了相应变化。
滤波增益:
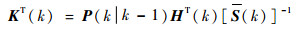 | (21) |
滤波输出:
 | (22) |
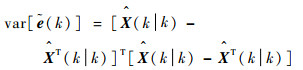 | (23) |
式中:
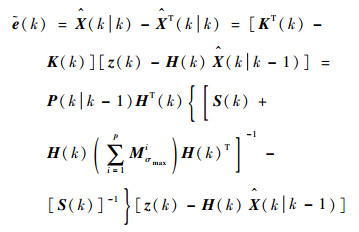 | (24) |
2.2 分离机动的自适应关联波门 1) 群分离检测
假设群目标在某一时刻分离为2个小群。在原有的IMM-CGT算法结构中,将距离一步预测值最近的回波作为种子量测,而后建立新群;在群分离场景中,分离后的各分群间距将随时间递增,因此,大群中心的一步预测值可能更靠近某一分群,致使在建立新群时,另一分群的量测可能无法进入波门,所以关联波门内量测数量骤减。因此实际滤波值并不是两分群的中心,而是偏向了某一分群,即“群中心拖引”。三分群等更多分群的原理类似。因此,可以将群内目标数量估计的变化率作为检测群分离的依据。若某一时刻该值超过阈值η,则判定为群分离。
2) 群划分
检测到群分离后,本文基于k均值(k-means)聚类,将分离后的大群划为若干个分群进行跟踪。具体步骤如下:
步骤1 ??预设聚类小群的数量n。
步骤2 ??选择聚类中心。选择彼此距离尽量远的点作为聚类中心,即“最远”原则,这样能够选出极有可能不在同一簇的点[17],主要分为以下几步:①随机选择接收回波中的某一量测点作为第1个聚类中心。②计算剩余点到第1个聚类中心的距离,从中选择最大距离对应的点作为第2个聚类中心。③分别计算剩余点到前2个聚类中心的距离,2个距离中的较小值作为该点到前2个聚类中心的“得分”,选择“得分”最高对应的点作为第3个聚类中心。④以此类推,完成聚类中心的初始化。
步骤3 ??根据群内各点与聚类中心的几何距离,形成n个分群。而后采用1.1节中的方法计算各分群的种子量测、建立新群及滤波更新,对于分离后的群目标,若发生加(减)速、转弯等整体机动,同样采用2.1节方法自适应调整波门。
综上,自适应关联波门的IMM-CGT算法流程图如图 2所示。
 |
| 图 2 自适应关联波门IMM-CGT算法流程图 Fig. 2 Flowchart of IMM-CGT algorithm with adaptive correlation gate |
| 图选项 |
3 仿真实验 利用MATLAB仿真软件进行Monte Carlo实验,验证改进算法的有效性实验结果的评价指标采用跟踪估计的均方根误差(RMSE)、失跟率和平均有效量测数量,将RMSE定义为
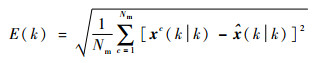 | (25) |
式中:Nm为Monte Carlo仿真次数;xc(k|k)和
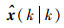
定义失跟率为目标失跟次数与仿真次数的比率。若连续k1个采样周期位置估计误差Δp都超过失跟检测阈值Δp0,则判定为失跟。对于两坐标雷达,有
 | (26) |
式中:Δx、Δy分别为x和y方向上的位置估计误差。k1取4,Δp取量测标准差的5倍。
平均有效量测数量表示在未失跟的仿真中,有效量测数量之和在仿真次数和采样次数上的平均,可通过下式计算得到:
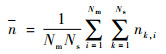 | (27) |
式中:Ns为单次Monte Carlo实验中的仿真步数;nk, i为在第i次Monte Carlo实验中,第k个采样时刻关联波门内有效量测的数量。
3.1 仿真条件 跟踪由8个目标组成的群目标,群中各目标的初始位置在(500, 1 000) m处随机产生,各目标的间距在150~300 m之间,模拟飞机编队,目标在x-y平面内运动。检测概率Pd=0.98,门概率PG=0.999 7,关联波门的门限值γ=16,量测误差为100 m。采样间隔为1 s,仿真运动时间为90 s,Monte Carlo仿真次数为50次。在滤波过程中产生随机的杂波,初始杂波密度λ=10-6个/m2,杂波空间位置服从高斯分布,个数服从泊松分布。IMM算法的模型集选取匀速(Constant Velocity, CV)模型和协同转弯(Coordinate Turn, CT)模型,初速度为(300, 100)m/s,转弯速率为5 rad/s,运动场景设置如表 1所示。
表 1 运动场景 Table 1 Motion scenes
| 机动类型 | 机动时刻及行为 |
| 整体机动 | t=0~30 s,匀速 |
| t=31~60 s,右转 | |
| t=61~90 s,匀速 | |
| 分离机动 | t=0~34 s,匀速 |
| t=35 s,群分离 | |
| 分群1:t=36~45 s,匀速;t=46~60 s,左转 | |
| 分群2:t=36~60 s,右转 |
表选项
3.2 算法性能对比 1) IMM-CGT算法性能分析
图 3为杂波密度λ=10-6个/m2时IMM-CGT算法对群整体机动和分离机动场景下的运动轨迹及群中心估计。
 |
| 图 3 IMM-CGT算法跟踪性能 Fig. 3 Tracking performance of IMM-CGT algorithm |
| 图选项 |
从图 3(b)和(c)可以看出,传统IMM-CGT算法跟踪分离后的群目标时,大群中心的预测值偏向于其中某一分群,而不是跟踪各分群的中心。
2) 群分离检测及跟踪
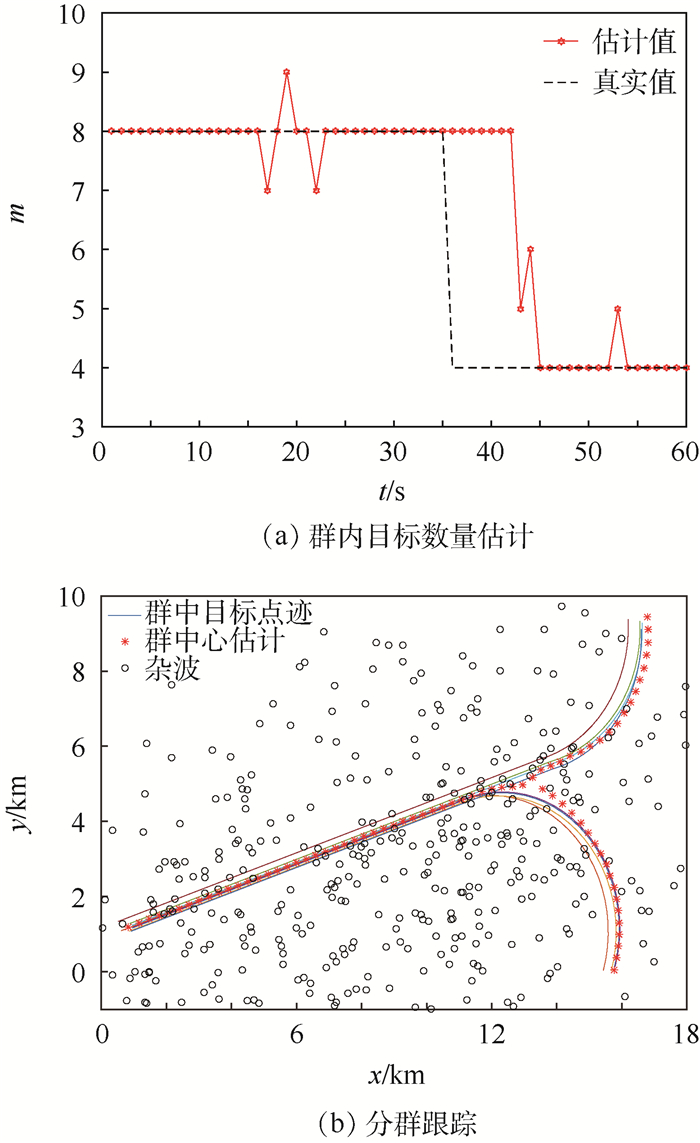
图 4为本文算法对群分离场景的检测及跟踪。
 |
| 图 4 群分离检测与跟踪 Fig. 4 Separation detection and tracking of group |
| 图选项 |
由图 4(a)可以看出,由于传统CGT算法在群分离后发生了“群中心拖引”,当群在t=42 s时完全分离时,群内的目标数量估计骤减,故基于此进行群分离检测。由图 4(b)可以看出,本文提出的IMM-CGT算法能够对分群进行准确的跟踪。
3) 自适应转移概率的跟踪性能分析
图 5为杂波密度λ=10-6个/m2时固定模型转移概率与本文自适应算法的性能对比。
 |
| 图 5 自适应转移概率与固定转移概率性能比较 Fig. 5 Performance comparison of adaptive and fixed transition probability |
| 图选项 |
由图 5(a)和(b)可以看出,相比于传统固定转移概率,本文算法能够根据目标机动自适应调整,增强了优势模型的主导作用。传统算法中优势模型概率的平均值为0.58,而在本文算法中,提高至0.7,有效地减少了模型间的不利竞争,由图 5(c)可以看出估计误差减小。由于IMM算法本身存在着模型切换时间滞后的问题,自适应转移概率的算法也没有明显改善这一缺点,表现为机动时刻的误差相对较大。
4) 自适应关联波门的跟踪性能分析
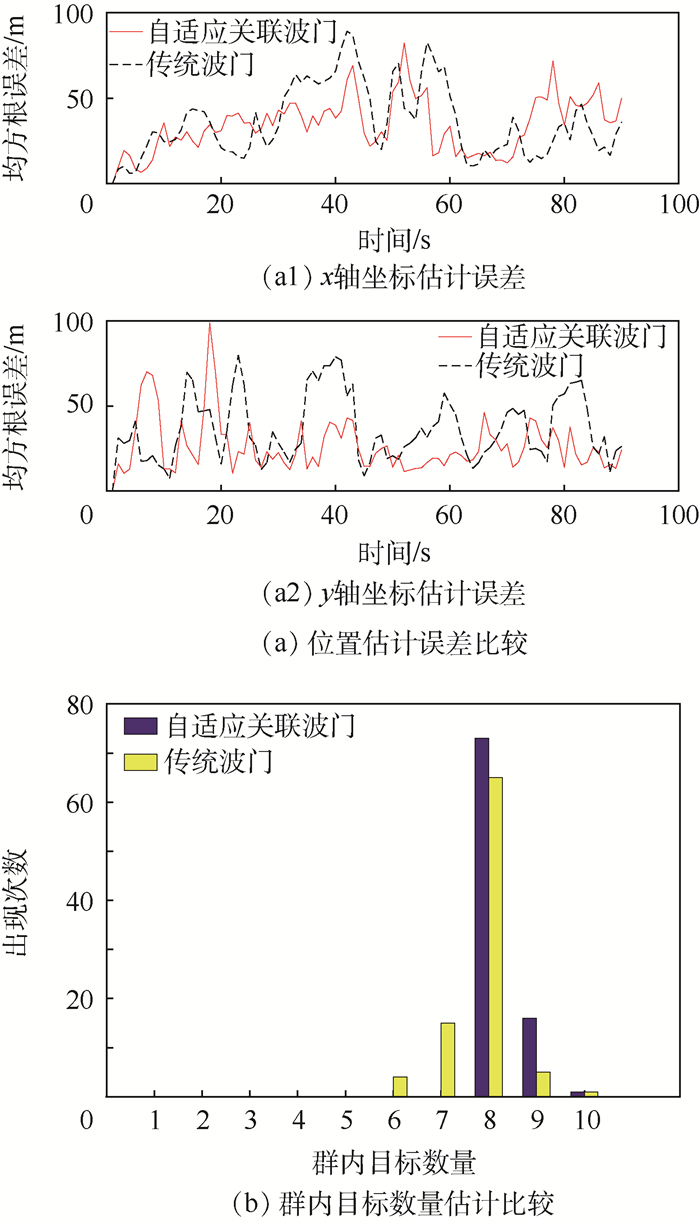
图 6为传统波门与自适应关联波门在位置估计误差及目标数量估计方面的性能对比。表 2和表 3分别为不同杂波密度下,传统波门与自适应关联波门在失跟率及平均有效量测数量的对比。
 |
| 图 6 自适应关联波门与传统波门性能比较 Fig. 6 Performance comparison of adaptive correlation gate and traditional gate |
| 图选项 |
表 2 不同杂波密度下的失跟率 Table 2 Tracking loss rate under different clutter density
| λ/(10-6个·m-2) | 自适应关联波门/% | 传统波门/% |
| 1 | 1.50 | 2.40 |
| 2 | 2.47 | 4.40 |
| 3 | 3.73 | 4.51 |
| 4 | 3.84 | 5.13 |
| 5 | 4.40 | 6.47 |
表选项
表 3 不同杂波密度下的平均有效量测数量 Table 3 Average effective measurement number under different clutter density
| λ/(10-6个·m-2) | 自适应关联波门/% | 传统波门/% |
| 1 | 8.088 9 | 7.977 8 |
| 2 | 8.333 3 | 7.655 6 |
| 3 | 8.177 8 | 8.411 1 |
| 4 | 8.411 1 | 8.366 7 |
| 5 | 8.622 2 | 8.311 1 |
表选项
由图 6(a)可以看出,通过自适应地实时调整波门大小,减少了机动时刻的真实量测丢失,所以在机动时刻,相对传统固定波门,估计误差有了明显的降低;从图 6(b)可以看出,自适应关联波门的IMM-CGT算法对群内目标数量的估计更接近于真实值,波门内量测数量的估计分布也相对集中。通过表 2和表 3数据可以看出,2种算法的失跟率和平均有效量测数量都随着杂波密度的增加而增加,在各种量测条件下,具有自适应关联波门的算法均能有效降低失跟率。
5) 不同波门放大次数对跟踪误差的影响
不同波门放大次数时位置估计的RSME结果如图 7所示。由图 7可知,适当放大波门可以减少因目标机动而造成的量测丢失,减小跟踪误差;但当波门放大次数超过某一范围时,波门内混入较多杂波,此时,杂波对估计群中心的影响将大于丢失的真实量测,因此跟踪误差增大。该环境下最佳波门放大次数p=2。
 |
| 图 7 不同波门放大次数的估计误差 Fig. 7 Estimation error for different gate enlarging times |
| 图选项 |
4 结论 1) CGT算法与IMM算法相结合,增强了对群目标机动模式的适应性,通过将最新量测值引入转移概率的计算,通过后验信息对转移概率进行实时地修正,增强了优势模型的主导性,减小了模型间的“不利竞争”,降低了跟踪误差。
2) 针对机动时刻关联波门内真实量测丢失而导致的误跟甚至失跟的问题,结合群整体机动与分离机动特性,提出了一种群分离检测的方法并设计了群的自适应关联波门。利用新息协方差对机动时刻的关联波门进行自适应调整,提高了跟踪精度。
3) 仿真结果表明,本文算法减小了杂波背景下机动群目标跟踪的RSME,降低了失跟率,提高了对群内目标数量估计的准确性。
参考文献
| [1] | KOCH W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059. DOI:10.1109/TAES.2008.4655362 |
| [2] | 耿文东, 王元钦, 董正宏. 群目标跟踪[M]. 北京: 国防工业出版社, 2014: 15-27. GENG W D, WANG Y Q, DONG Z H. Group-targets tracking[M]. Beijing: National Defense Industry Press, 2014: 15-27. (in Chinese) |
| [3] | 李昌玺, 周焰, 郭戈, 等. 弹道导弹群目标跟踪技术综述[J]. 战术导弹技术, 2015(3): 66-73. LI C X, ZHOU Y, GUO G, et al. Summary of group tracking technology based on ballistic missile[J]. Tactical Missile Technology, 2015(3): 66-73. (in Chinese) |
| [4] | JI W Y, ROBERTS S J. Robust measurement validation in target tracking using geometric structure[J]. IEEE Signal Processing Letters, 2010, 17(5): 493-496. DOI:10.1109/LSP.2010.2041695 |
| [5] | LOPEZ R, DANèS P. Low-complexity IMM smoothing for jump markov nonlinear systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1261-1272. DOI:10.1109/TAES.2017.2669698 |
| [6] | CHENG T, LI X R, HE Z.Comparison of gating techniques for maneuvering target tracking in clutter[C]//International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2014: 1-8. |
| [7] | WANG M H, WAN Q, YOU Z S. A gate size estimation algorithm for data association filters[J]. Science in China Series F, 2008, 51(4): 425-432. |
| [8] | LI X R, JILKOV V P. Survey of maneuvering target tracking.Part I.Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 39(4): 1333-1364. |
| [9] | LI X R, JILKOV V P. Survey of maneuvering target tracking.Part V.Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255-1321. DOI:10.1109/TAES.2005.1561886 |
| [10] | 周卫东, 孙天, 储敏, 等. 交互式多模型粒子滤波优化重采样算法[J]. 北京航空航天大学学报, 2017, 43(5): 865-871. ZHOU W D, SUN T, CHUN M, et al. Interacting multiple model particle filter optimization resampling algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(5): 865-871. (in Chinese) |
| [11] | ZHENG D, WANG S.A new interacting multiple model algorithm for maneuvering target tracking based on adaptive transition probability updating[C]//IET International Radar Conference.London: IET, 2015: 5-6. |
| [12] | 郭志, 董春云, 蔡远利, 等. 时变转移概率IMM-SRCKF机动目标跟踪算法[J]. 系统工程与电子技术, 2015(1): 24-30. GUO Z, DONG C Y, CAI Y L, et al. Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking[J]. System Engineering and Electronics, 2015(1): 24-30. (in Chinese) |
| [13] | GRANSTROM K, WILLETT P, BAR-SHALOM Y. Systematic approach to IMM mixing for unequal dimension states[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 2975-2986. DOI:10.1109/TAES.2015.150015 |
| [14] | 宗群, 王丹丹, 邵士凯, 等. 多无人机协同编队飞行控制研究现状及发展[J]. 哈尔滨工业大学学报, 2017, 49(3): 1-14. ZONG Q, WANG D D, SHAO S K, et al. Research status and development of multi UAV coordinated formation flight control[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 1-14. (in Chinese) |
| [15] | GUO Y, THARMARASA R, RAJAN S, et al. Passive tracking in heavy clutter with sensor location uncertainty[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1536-1554. DOI:10.1109/TAES.2016.140820 |
| [16] | 靳标, 纠博, 苏涛, 等. 一种用于杂波中机动目标跟踪的自适应关联波门设计方法[J]. 西安交通大学学报, 2014, 48(10): 35-41. JIN B, JIU B, SU T, et al. A Method to design adaptive correlating gate for maneuvering target tracking in clutter[J]. Journal of Xi'an Jiaotong University, 2014, 48(10): 35-41. DOI:10.7652/xjtuxb201410006 (in Chinese) |
| [17] | 杜明洋, 毕大平, 王树亮, 等. 一种混合的机动群目标分离检测跟踪算法[J]. 西安交通大学学报, 2018, 52(10): 116-123. DU M Y, BI D P, WANG S L, et al. A hybrid algorithm to detect and track maneuvering group target splitting[J]. Journal of Xi'an Jiaotong University, 2018, 52(10): 116-123. (in Chinese) |
