锂电池不仅便于携带, 而且续航时间长于镍镉电池, 工作中的安全等级大于氢电池, 已成为现今电池的支柱。锂电池不仅促进了新能源和新型环保技术的更新换代, 而且推动了当今信息时代的快速发展^[1]。
锂电池寿命预测技术主要有2种方法, 分别为直接测量和间接测量。无论是脉冲快速充电, 还是以恒定电流或恒定电压进行分段式充放电实验, 锂电池的容量随着电池使用时间和充放电循环次数的增加而不断减少, 当其下降到某个阈值时, 必须终止放电, 停止使用, 否则会对使用设备造成较大的永久性损害, 增加危险因素和不稳定程度。电池的容量是反映电池健康程度的重要指标之一^[2]。
通过对国内外研究现状进行分析, 常见的寿命预测可分为3类:基于统计分布、数据驱动和模型驱动的预测方法^[3]。其中, 数据驱动是锂电池寿命预测的主要方法, 其在统计学和数据挖掘等理论指导下, 借助神经网络和支持向量机(Support Vector Machine, SVM)等机器学习算法, 总结输出变量间的关系, 建立输入与输出变量间的关系模型^[4]。神经网络有着收敛速率慢、训练时间长的缺点, SVM的核函数必须满足Mercer条件^[5]。相关向量机(Relevance Vector Machine, RVM)是一种基于贝叶斯框架下的模型, 其泛化能力强, 具有不确定表达能力, 与SVM相比, 核函数不需要满足Mercer条件。因此本文采用RVM进行锂电池寿命预测并对结果进行分析, 一般RVM模型使用单一的核函数, 其泛化能力较弱。针对这一问题, 本文提出了基于组合核函数的RVM锂电池寿命预测模型, 该模型泛化能力更强, 进而提高了锂电池剩余寿命的预测精度。
1 相关向量机 在数学研究领域中, RVM^[6]是一种在已有数据上进行建模的技术, 是Tipping^[7]在SVM的基础上改进提出的。虽然RVM和SVM拥有相同的函数形式的模型, 但是两者的理论基础完全不同, SVM是利用最小化原则构造风险最小的模型结构, 而RVM是利用贝叶斯框架来训练和构建学习机, 在原理上建立高斯过程模型^[8]使得协方差最小。
RVM考虑从一组输入样本{x_i}_i=1^N与对应的目标{t_i}_i=1^N进行建模, 当遇到新样本x_*利用得到的模型, 预测目标t_*, 由于退化数据往往带有噪声, 通常在模型中加入不确定项来反映噪声影响。一般建立的非线性模型形式为^[9]

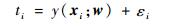(1)

式中:w为权值向量; y(x_i; w)为一个未知的非线性函数; ε_i表示服从均值为0且方差为σ²的独立同分布高斯噪声。未知函数y(x_i; w)可以表述为一组基函数的线性组合:

(2)

式中:w_n为权值; φ(x_i)=[φ₀(x_i), φ₁(x_i), …, φ_N(x_i)]^T为非线性基函数, 式(1)向量形式为

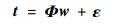(3)

式中:t为假定的目标值; Φ为φ(x_i)的向量形式, φ(x_i)=[1, K(x_i, x₁), K(x_i, x₂), …, K(x_i, x_N)]^T, K(x_i, x_j)表示核函数; Φ为对每个训练样本定义的基函数。
由贝叶斯推理得

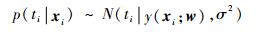(4)

式中:N(t_i|y(x_i; w), σ²)表示均值为y(x_i; w), 方差为σ²。一般可以直接使用最大似然估计来求解未知参数w和σ², 但这样会导致过拟合问题, RVM模型中, 为了确保模型具有较好的泛化能力, 首先为每个权重赋予一个高斯先验分布p(w|α), α为超参数, p(w|α)= , 其中每个超参数α_i对应权重w_i, 负责调整权重大小。则使用历史数据估计目标t_*可表示为

(5)

由贝叶斯公式可以得

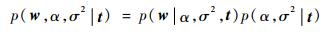(6)

(7)

(8)

式(7)是由2个高斯分布卷积得到, 所以式(7)仍服从高斯分布, 因此式(8)也为高斯分布, 具体形式为

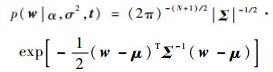(9)

该后验概率的协方差Σ和均值μ分别为

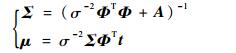(10)

式中:A=diag(α₀, α₁, …, α_N)。

(11)

现认为求p(α, σ²|t)最大后验概率估计等价于求p(t|α, σ²)的最大后验概率估计, 由式(7)可知, p(t|α, σ²)服从高斯分布, p(t|α, σ²)的均值为0, 协方差为Σ=σ²I+ΦA^-1Φ^T。
使用迭代法确定参数α, σ²迭代公式为

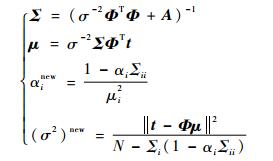(12)

预测过程:对于新的输入x_*, 相应的预测输出t_*的概率分布为

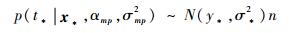(13)

(14)

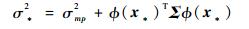(15)

式中:y_*为t_*的预测值; α_mp和σ_mp²为式(12)取得的收敛值; 当参数α_i不趋于0时, 对应的基函数矢量φ(x_i)则称为相关向量^[10]。
2 核函数的选择 已知被广泛使用的高斯核函数为

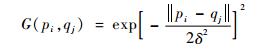(16)

式中:p为空间中任一点; q为核函数中心; δ为带宽。
高斯核函数是基于距离方程的核函数, 可以满足在测试点附近有较快的衰减, 但是在无限远处却不能保证有一定的衰减速率, 所以需要构建一个核函数来满足无限远处的衰减。
高斯核函数具有一定的缺陷, 因此通过改进高斯核函数来进一步提高核函数性能, 将距离方程放到指数的分母上, 这样函数的特性曲线能使其在远离测试点的时候仍有一定的衰减速率^[11]。因此初步构建的核函数为

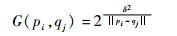(17)

从函数的特性曲线来看, 函数满足在测试点附近有较快的衰减速率, 在无限远处仍能保持适当的衰减, 为了获得更好的预测性能, 在此加入了位移参数γ, 函数微调变量λ和幅度调节参数G, 则最终修正的高斯核函数为

(18)

式中:δ²为带宽变量; γ为位移参数; λ为函数微调变量。最关键的核参数依旧是带宽δ和位移参数γ。
由于高斯核函数是典型的局部性核函数, 其只能保证在测试点附近极小的范围内对数据点有影响, 多项式核函数是应用最广泛的全局核函数, 其表达式为

(19)

为了兼顾局部核函数与全局核函数的优势, 本文选取了多项式核函数和改进的高斯核函数相结合的核函数使之具有有更好的特性^[11]。其表达式为

(20)

式中:m为调节多项式核函数和高斯核函数的参数, 其取值范围为0≤m≤1。当m=0时, 核函数退化为改进高斯核函数; 当m=1时, 核函数退化为多项式核函数。
本文计算RVM预测结果的偏差度、标准差、拟合程度以及运行时间, 用来评价预测结果的精准度^[12], 其中运行时间由MATLAB系统函数给出。
预测结果偏差度:

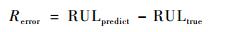(21)

式中:RUL_predict为预测结果值; RUL_true为电池实际电容值。
预测结果标准差:

(22)

预测结果拟合程度:

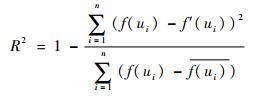(23)

式中:R²越接近1表示拟合程度越好; f(u_i)为锂电池的真实电容值; f′(u_i)为预测的剩余电容值; 为所有预测剩余电容值的平均值; n为样本数量。
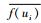
3 锂电池寿命预测 3.1 锂电池剩余寿命预测框架 健康状态的可直接对在线运行的锂电池而言, 电池充放电可能并不完全, 使用安时法得到的容量并不准确, 并且一般的传感器也无法监测电池内部的状态。要进行锂电池在线剩余寿命预测需要提取能反映电池健康状态的可直接在线测量的间接健康因子; 构建出在线可测量的间接健康因子后, 结合已有的历史电池容量退化数据, 建立在线可测量的间接健康因子与电池容量的关系模型; 将在线采集到的间接健康因子数据作为输入, 通过得到的关系模型计算出对应使用周期下的电池容量的估计值。经分析发现当给定一定电压范围时, 等电压放电时间间隔会随着循环使用周期增加而逐渐减小, 与电池容量有着相似的退化趋势。
本文首先将等电压放电时间间隔作为锂电池的间接健康因子, 然后使用RVM模型建立间接健康因子与电池容量的关系模型, 最后通过得到的关系模型预测出锂电池的容量和剩余寿命。锂电池的剩余寿命预测流程图如图 1所示。

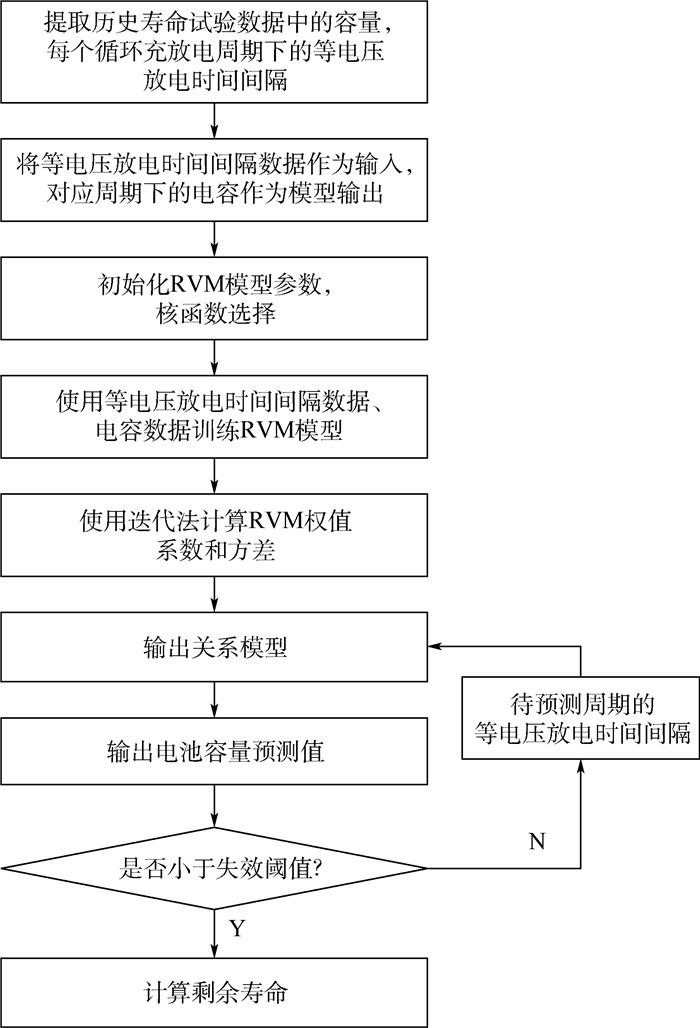图 1 RVM预测方法流程 Fig. 1 RVM predictive method process

图选项

3.2 锂电池数据分析 本实验所用的原始数据来源于NASA公布的Battery Data Set中的B0005、B0006、B0007和B0018这4组电池的充放电循环数据。
通过对这4组电池的电池容量进行对比分析, 可得出4组电池的大概退化趋势近似(见图 2)^[13], 但是电池的电池容量上下限和实验充放电循环次数有所不同, 因此实验中对不同型号的电池失效阈值和实验预测起点的选择不同, 对于B0005、B0006和B0018这3个电池选取1.38 A·h作为电池的失效阈值, 对于B0007则选取1.2 A·h作为失效阈值。

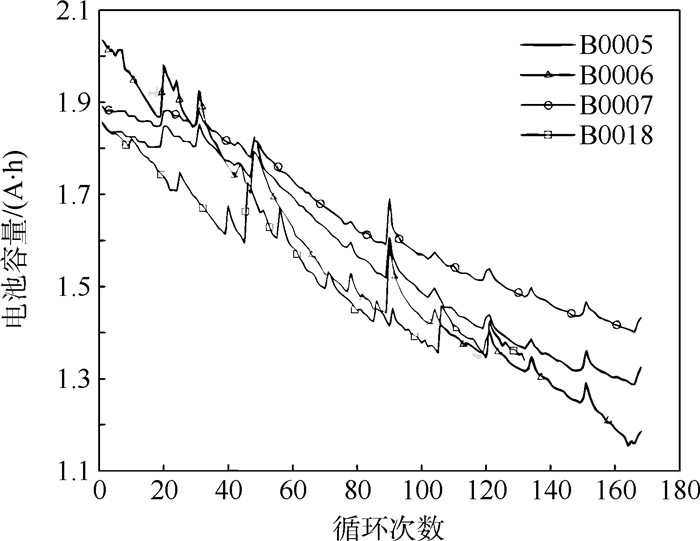图 2 4组电池容量退化趋势 Fig. 2 Four groups of battery capacity degradation trends

图选项

3.3 预测结果 利用组合核函数对B0005、B0006、B0007和B0018这4组锂电池样本数据进行预测, 并与使用单一的高斯核函数的RVM预测模型进行对比。在此过程中经过多次实验, 发现在组合核函数的参数G=1, m=0.55, γ=0.8, λ=2时, 实验结果最好。其预测结果的偏差度、标准差、拟合程度和运行时间见表 1~表 4。
表 1 B0005电池预测结果 Table 1 B0005 battery prediction results

预测方法	预测起点	偏差度	标准差	拟合程度	运行时间/s
组合核函数	70	0.003 365 5	0.013 604	0.979 43	3.221
高斯核函数	70	0.010 356	0.013 678	0.979 42	2.938

表选项






表 2 B0006电池预测结果 Table 2 B0006 battery prediction results

预测方法	预测起点	偏差度	标准差	拟合程度	运行时间/s
组合核函数	80	0.006 954 2	0.016 442	0.972 59	3.634
高斯核函数	80	0.008 217	0.017 83	0.967 837	3.718

表选项






表 3 B0007电池预测结果 Table 3 B0007 battery prediction results

预测方法	预测起点	偏差度	标准差	拟合程度	运行时间/s
组合核函数	80	0.000 959 2	0.010 576	0.974 3	3.71
高斯核函数	80	0.002 875 8	0.011 009	0.972 19	3.593

表选项






表 4 B0018电池预测结果 Table 4 B0018 battery prediction results

预测方法	预测起点	偏差度	标准差	拟合程度	运行时间/s
组合核函数	60	-0.000 522	0.008 783	0.975 64	2.188
高斯核函数	60	-0.026 622	0.029 332	0.777 98	1.954

表选项






3.4 结果分析 本文采用组合核函数, 使用等电压放电时间间隔及其对应的电容值作为样本集, 使用迭代循环优化预测模型的超参数^[14], 对B0005、B0006、B0007和B0018这4组电池继续预测剩余电容值, 根据总的循环次数选取适当的预测起点得到以下结果:
本文对传统的高斯核函数进行了改进, 增强了其性能, 并将学习能力强、泛化能力弱的改进高斯核函数和泛化能力强、学习能力弱的多项式核函数组合起来形成组合核函数, 改进了RVM的性能^[15]。
在实验预测中可以很清楚地发现组合核函数相比传统的高斯核函数有着更好的性能, 偏差度大幅度减小, B0005、B0006、B0007和B0018电池预测结果的偏差度分别减小了67.5%、15.4%、66.6%和98.0%。
由于传统的高斯核函数是局部核函数^[16], 对部分电池的预测结果有较好的拟合程度, 但是其泛化能力很弱, 并不适用于所有电池。从实验结果可以看出, 组合核函数在保证了预测精度的条件下, 泛化能力也明显优于高斯核函数。B0005电池预测结果的拟合程度并没有很大的改观, B0006、B0007和B0018电池预测结果的拟合程度分别提高了0.5%、0.2%和25.4%。此次改进实验对B0018号电池的预测精度提高最为明显。
4 结论 本文对传统的高斯核函数进行了改进, 应用改进的RVM对锂电池寿命进行预测实验, 得到了以下结论:
1) 使用组合核函数的RVM模型预测结果的偏差度大幅度减小, 预测精度得到了提高, 其中B0006、B0007和B0018电池的预测精度分别提高了0.5%、0.2%和25.4%。
2) 4种电池的预测结果表明使用组合核函数的RVM模型泛化能力好于使用单一高斯核函数的RVM模型。

参考文献

[1]	张卓识.锂离子电池建模与故障预测方法研究[D].大连: 大连海事大学, 2016. ZHANG Z S.Study of lithium-ion battery modeling and prognostics method[D].Dalian: Maritime Affairs University of Dalian, 2016(in Chinese).
[2]	朱亮标.基于数据驱动的锂离子电池剩余寿命预测模型及软件实现[D].广州: 华南理工大学, 2014. ZHU L B.Remaining life prediction model and Software implementation for lithium-ion battery based on data-driven[D].Guangzhou: Institutes of Technology of South China, 2014(in Chinese).
[3]	艾力, 房红征, 于功敬, 等. 基于数据驱动的卫星锂离子电池寿命预测方法[J].计算机测量与控制, 2015, 23(4): 1262–1265. AI L, FANG H Z, YU G J, et al. Research on data-driven life prediction methods of satellite lithium-ion battery[J].Computer Measurement & Control, 2015, 23(4): 1262–1265.DOI:10.3969/j.issn.1671-4598.2015.04.059(in Chinese)
[4]	郑方丹.基于数据驱动的多时间尺度锂离子电池状态评估技术研究[D].北京: 北京交通大学, 2017. ZHENG F D.Multi-time scale state estimation of lithium-ion batteries using data driven method[D].Beijing: Beijing Jiaotong University, 2017(in Chinese).
[5]	赵春辉, 张燚. 相关向量机分类方法的研究进展与分析[J].智能系统学报, 2012, 7(4): 294–301. ZHAO C H, ZHANG Y. Research progress and analysis on methods for classification of RVM[J].CAAI Transactions on Intelligent Systems, 2012, 7(4): 294–301.DOI:10.3969/j.issn.1673-4785.201112019(in Chinese)
[6]	杨树仁, 沈洪远. 基于相关向量机的机器学习算法研究与应用[J].计算机技术与自动化, 2010, 29(1): 43–47. YANG S R, SHEN H Y. Research on data-driven life prediction methods of satellite lithium-ion battery[J].Computer Measurement & Control, 2010, 29(1): 43–47.(in Chinese)
[7]	TIPPING M.The relevance vector machine, 2000[C]//Advances in Neural Information Processing Systems.Cambridge: MIT Press, 2000: 652-658.
[8]	黄海.锂离子动力电池老化特性研究与循环寿命预测[D].济南: 山东大学, 2016. HUANG H.Research on aging performances and cycle-life predictions of Li-ion battery[D].Jinan: Shandong University, 2016(in Chinese).
[9]	王立昆, 杨新峰. 一种基于RVM回归的分类方法[J].电子科技, 2011, 24(5): 14–16. WANG L K, YANG X F. A classification method based on RVM regression[J].Electronic Science and Technology, 2011, 24(5): 14–16.(in Chinese)
[10]	周建宝.基于RVM的锂离子电池剩余寿命预测方法研究[D].哈尔滨: 哈尔滨工业大学, 2013: 20-23. ZHOU J B.Research on lithium-ion battery remaining useful life estimation with relevance vector machine[D].Harbin: Harbin Institute of Technology, 2013: 20-23(in Chinese).
[11]	杨柳, 张磊, 张少勋, 等. 单核和多核相关向量机的比较研究[J].计算机工程, 2010, 36(12): 195–197. YANG L, ZHANG L, ZHANG S X, et al. Comparison research of single kernel and multi-kernel relevance vector machine[J].Computer Engineering, 2010, 36(12): 195–197.(in Chinese)
[12]	豆金昌.锂离子电池健康评估及剩余使用寿命预测方法研究[D].南京: 南京航空航天大学, 2013. DOU J C.Health assessment and remaining useful life prediction of Li-ion battery[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese).
[13]	李晗, 萧德云. 基于数据驱动的故障诊断方法综述[J].控制与决策, 2011, 26(1): 1–9. LI H, XIAO D Y. Survey on data fault diagnosis methods[J].Control and Decision, 2011, 26(1): 1–9.(in Chinese)
[14]	张金, 魏影, 韩裕生, 等. 一种改进的锂离子电池剩余寿命预测算法[J].电子技术应用, 2015, 41(8): 110–112. ZHANG J, WEI Y, HAN Y S, et al. An improved particle filter algorithm for lithium-ion battery remaining useful life prediction[J].Application of Electronic Technique, 2015, 41(8): 110–112.(in Chinese)
[15]	李柱.锂离子电池寿命预测方法研究[D].淮南: 安徽理工大学, 2017. LI Z.Study on remaining useful life prediction method for lithium-ion batteries[D].Huainan: Anhui University of Science and Technology, 2017(in Chinese).
[16]	杨丽.基于模型驱动的锂离子电池剩余寿命预测方法研究[D].哈尔滨: 哈尔滨工业大学, 2016. YANG L.Research on lithium-ion battery rul model driven prognosis method[D].Harbin: Harbin Institute of Technology, 2016(in Chinese).