为了抑制NLOS误差的影响,国内外已提出多种解决方案,Wylie和Holtzman[8]提出了一种重构法,对NLOS误差进行校正,减小NLOS误差的影响,该方法需要利用视距(LOS)情况下的先验信息,在较差的环境中难以实现。Chen[9]提出了一种残差加权法,通过对定位结果进行加权平均以减小NLOS误差影响,该方法需要较多的基站参与定位。文献[10]通过引入校正因子代入最小二乘算法,逐步迭代降低NLOS的影响,主要应用于室外环境,在室内环境中健壮性差、精度低。
本文通过对UWB信道模型IEEE 802.15.4a[11]的仿真,分析了非视距误差对UWB室内定位的影响,利用NLOS环境下信号的传播时延特性,由概率论知识估计附加时延的均值与方差[12],修正测量值,根据修正后的数据,利用Chan算法与粒子群算法相结合的协同定位算法进行定位,该算法在抑制NLOS误差的同时,提高了室内定位精度,满足定位的要求,而且Chan算法与粒子群算法在无线传感器网络定位中都有着广泛的应用,因此协同定位算法适用于实际应用中。
1 定位算法 TDOA定位算法是通过测量2个基站到达目标位置的传播时间差来确定目标位置,由时间差可以得到1条以2个基站为焦点的双曲线,因此只需2组时间差值,得到2条双曲线,其交点就是待测目标位置[13]。
1.1 Chan算法 Chan算法[14]是一种具有解析表达式的典型TDOA算法,在测量误差较小的情况下可达到克拉美罗下界(CRLB)。设定位目标位置坐标为(x,y),第i个基站坐标为(xi,yi),基站到目标位置的距离为di,第1个基站与第i个基站到目标位置的距离差为di, 1,由此可以得到
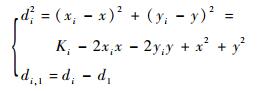 | (1) |
式中:Ki=xi2+yi2。由于
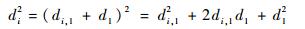 | (2) |
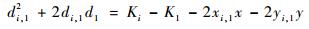 | (3) |
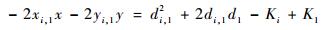 | (4) |
式中:xi, 1=xi-x1; yi, 1=yi-y1。非线性方程组就变成了线性方程组,求出方程组中的x、y值就求得目标位置坐标。令za=[zpT, R1],zp=[x, y]T,假设za的元素间相互独立,则za的最大似然估计为
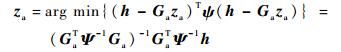 | (5) |
式中:Ψ=E(ψψT)=c2BQB, B=diag{d10, d20, …, dM0},di0为di (i=1, 2, …,M)无噪声时的表达式,Q为TDOA的协方差矩阵,c为电磁波在空气中的传播速度。当目标位置距离较远时,di0与d0很接近,故B≈d0I,式(5) 近似为
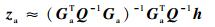 | (6) |
式中:
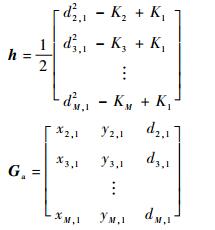 |
当目标位置距离较近时,可以利用式(6) 得到一个初始值来计算矩阵B,代入式(5) 即可获得第1次加权最小二乘估计值。
利用上面得到的第1次的估计值,再重新构造误差方程组进行第2次估计得
 | (7) |
式中:
 |
式中:za, 1和za, 2分别为目标位置x坐标和y坐标;za, 3为第1个基站到目标位置的距离。通过2次最小二乘法得到目标位置的最终坐标为
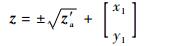 | (8) |
可以看出,以上2次最小二乘估计都是基于系统测量误差服从均值为0的前提下,系统测量误差包含在该算法的加权矩阵内,因此在一定程度上消除了系统误差的影响。
1.2 粒子群算法 粒子群算法[15]模仿鸟类的觅食行为,通过迭代寻优计算,能快速地找到近似解。该算法具有实现简单、精度高、收敛快等优点,在处理非线性优化问题和组合优化问题时有很好的效果[16],因此适用于求解TDOA非线性方程组,将双曲线方程组作为粒子群算法待优化函数,求得的最优解即为目标位置坐标。算法流程如下:
1) 初始化种群和设置参数。设定参数的运动范围,学习因子c1、c2,当前的进化代数k。其中第i个粒子(i=1, 2, …, S)的位置表示为Xi、速度表示为Vi,取粒子群当前最优解为B。
2) 个体适应度评价。
3) 由式(9) 和式(10) 更新粒子的速度和位置。
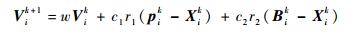 | (9) |
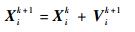 | (10) |
式中:w为惯性权重; r1和r2为0到1的随机数; k=1, 2, …,G;i=1, 2, …, S。
4) 计算更新后的粒子的适应度值,比较当前适应值f(Xi)与自身历史最优值pi,如果f(Xi)较好,则置pi为当前值f(Xi),并更新粒子位置。
5) 比较粒子当前适应值f(Xi)与种群最优值B,如果f(Xi)优于B,则更新B的值。
6) 检查终止条件,若满足预设条件,则结束寻优;否则k=k+1,转至3)。
粒子群算法流程图如图 1所示。
 |
| 图 1 粒子群算法流程图 Fig. 1 Flowchart of particle swarm algorithm |
| 图选项 |
2 超宽带传播信道模型 UWB通信是一种使用非常宽的频带来收发数据的技术,因此其信道特征与传统的窄带通信系统有所不同[17]。IEEE 802.15.4 a[11]工作小组基于诸多信道模型的建议和基于实测数据的归纳,提出了能普遍接受的信道模型,其中包括2~10 GHz的UWB信道模型,共分为4种环境:居住环境、室内办公环境、户外环境和工业环境,每种环境均分为LOS情况和NLOS情况[18]。本文主要研究室内居住环境LOS与NLOS情况下UWB信号的传输。图 2(a)和图 2(b)分别为室内LOS(CM1) 和NLOS情况下(CM2) 信道的冲激响应。
 |
| 图 2 CM1信道和CM2信道冲激响应 Fig. 2 Impulse response of CM1 channel and CM2 channel |
| 图选项 |
从图 2可以看出LOS情况下,首径的幅度最大,传递的能量最高,而NLOS情况下,多径幅度衰减较慢,时间弥散性强,幅度最大的径也不是第一个到达,这是由于信号在传播过程遇到障碍物发生反射和折射现象引起的。在CM1和CM2信道下,采用基于脉冲序列最大能量的到达时间测距算法,发送信号为二阶微分高斯脉冲,直接序列编码调制,发射机与接收机的实际距离为14.142 m,基于脉冲序列最大能量的到达时间测距算法能量块仿真结果如图 3所示,通过MATLAB软件仿真,测得LOS和NLOS情况下,脉冲序列最大能量值对应的时延为t1=47.35 ns,t2=50.15 ns,测距误差为e1=0.062 9 m,e2=0.902 9 m,可见,NLOS误差对于UWB信号室内传播产生了很大的影响。
 |
| 图 3 CM1信道和CM2信道基于脉冲序列最大能量到达时间测距算法的能量块图 Fig. 3 Energy block diagram of maximum energy arrival time ranging algorithm based on pulse sequence of CM1 channel and CM2 channel |
| 图选项 |
3 非视距误差补偿 NLOS误差在不同信道下服从指数分布、均匀分布与Delta分布[19]。本文认为其近似服从指数分布进行分析,概率密度函数为
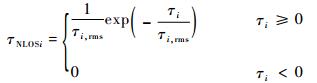 | (11) |
式中:τi, rms为信道决定的均方根时延扩展,表示为τi, rms=T1diεξ,T1为τi, rms在di=1 km时的中值,由IEEE 802.15.4 a[11]信道模型仿真可得,室内NLOS环境下均方根时延扩展T1≈19 ns,ε为0.5~1之间的一个常数, ξ表示服从均值为0、方差σξ=4~6 dB的对数正态分布的随机变量。可知,ln τi, rms~N(ln(T1diε), σξ2),可以得到τNLOSi的概率密度函数为
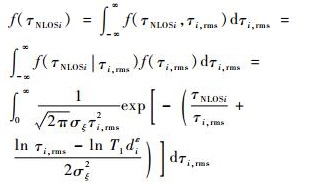 | (12) |
由此可计算NLOS误差的均值和方差[20]:
 | (13) |
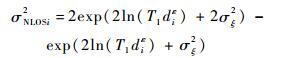 | (14) |
在TDOA算法中,Ri, 1表示第1个和第i个基站到目标位置的距离差,则有
 | (15) |
式中:
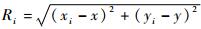
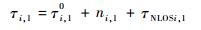 | (16) |
式中:τi, 10为LOS环境下的TDOA值;ni, 1为系统的测量误差,服从N(0, σni, 12)的高斯分布;τNLOSi, 1为NLOS引起的附加时延误差,均值为μNLOSi, 1,方差为σNLOSi, 12。
由式(13) 和式(14) 可得
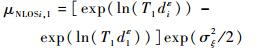 | (17) |
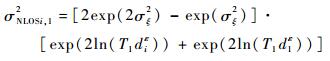 | (18) |
可以看出τNLOSi, 1服从正均值的高斯分布,使得整体误差均值不为0,这使得定位精度受到很大影响,因此,需要对TDOA测量值进行修正:
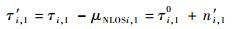 | (19) |
其中n′i, 1服从N(0, σni, 12+σNLOSi, 12)正态分布,这样就符合Chan算法极大似然估计条件,然后将优化后的TDOA测量值代入Chan算法和粒子群算法中进行定位估计。
4 协同定位算法 在LOS环境下,Chan算法的加权矩阵只考虑了均值为0的测量误差,2次最小二乘估计在一定程度上抵消了系统测量误差带来的影响,而NLOS误差的存在会使总体误差为正均值,也就是说位置的估计是有偏的,会使得Chan算法的定位精度有所下降。而粒子群算法求解非线性方程经过多次迭代受到NLOS误差的影响较小,计算快速准确且鲁棒性好。因此,本文提出一种在NLOS环境下改进的定位算法,即利用Chan算法与粒子群算法相结合的协同定位算法进行定位。
由于在NLOS环境下,粒子群算法优于Chan算法,因此,首先利用粒子群算法获得一个初始位置,用此初始位置修正TDOA测量值τ′i, 1和系统测量的协方差Q′,Chan算法利用修正后的数据进行计算得到N组解,然后将这N组解作为粒子群算法的种群初始位置更新迭代,粒子群在更新速度和位置时,采用线性递减的时变权重[22],这样粒子群算法在开始时具有良好的全局搜索能力,能快速定位到近似全局最优解的区域,随着权重递减,后期具有良好的局部搜索能力,能快速找到最优解,会得到更好的算法性能。算法具体步骤如下:
1) 假设在NLOS环境下,共测得M组TDOA数据,根据基站坐标,利用粒子群算法获得一个初始估计位置。
2) 由以上初始位置计算目标位置与各基站之间的距离di,根据式(17) 计算μNLOSi, 1,由式(19) 计算TDOA修正值τ′i, 1。
3) 根据式(18) 计算σNLOSi, 12,重构系统测量误差的协方差Q′。
4) 根据重构后的τ′i, 1和Q′,用Chan算法计算N组目标位置坐标(N≥100)。
5) 根据修正后的τ′i, 1作为TDOA测量值,用粒子群算法估计目标位置,将Chan算法得到的N组数据作为粒子群算法的初始种群位置。
6) 更新粒子的位置和速度,惯性权重采用从0.90线性递减到0.10的时变权重,计算更新后的粒子适应度值,寻找最优解。
7) 检查终止条件,若满足,则停止迭代,否则重复第6) 步。
协同定位算法有两大优势:① Chan算法结果作为粒子群算法的初值,缩小了粒子群的搜索范围,加快了收敛速度;② 粒子群在更新速度和位置时,采用线性递减的时变权重,具有较好的全局搜索能力和局部搜索能力,能更快地找到最优解。因此,相比于单一算法,协同定位算法收敛速度快,定位精度高,具有更好的定位能力。
5 仿真实验与分析 5.1 仿真条件设置 本文用MATLAB仿真工具进行算法验证,仿真采用IEEE802.15.4 a[11]信道模型CM1和CM2,设定在一个20 m×20 m的二维空间中,存在4个基站(BS1~BS4) 和1个目标位置,目标位置真实坐标取(14.142,14.142),其位置信息如图 4所示。
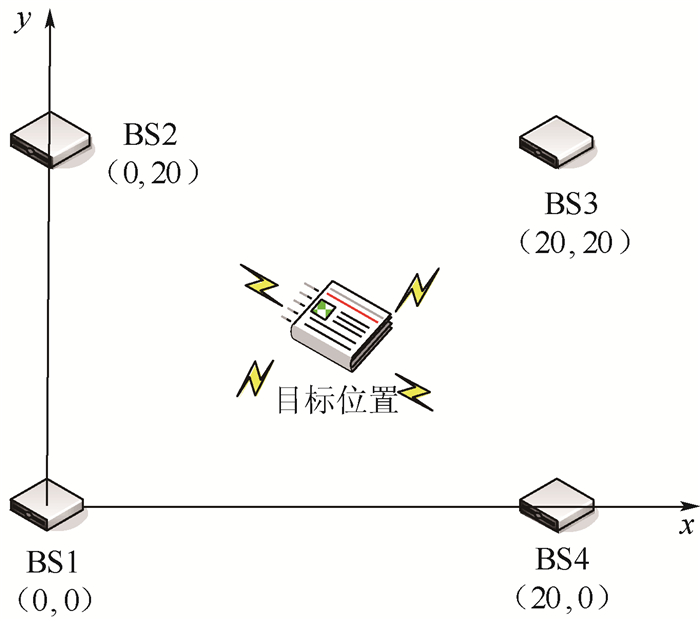 |
| 图 4 基站位置信息 Fig. 4 Location information of base station |
| 图选项 |
误差累积分布函数(CDF)表示随机变量小于等于某个数值的概率,在此用均方根误差(RMSE)来计算误差累积分布函数,来对定位的结果进行衡量。仿真结果由100次独立估计过程得到, 均方根误差定义如下:
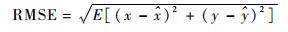 | (20) |
5.2 仿真结果与分析
5.2.1 定位精度 1) LOS环境下:图 5(a)和图 5(b)分别表示Chan算法和粒子群算法在LOS情况下的定位性能对比。TDOA测量值系统测量误差服从均值为0的高斯分布,在此标准差分别取0.15、0.25和0.35 m进行定位估计。从图 5中可以看出,Chan算法和粒子群算法定位精度均受到系统测量误差的影响,而且随着测量误差的增大定位误差也增大。通过图 5(a)和图 5(b)对比,可以得出,在LOS环境下,Chan算法和粒子群算法的定位结果曲线趋势大致相同,定位性能并没有很大差距。
 |
| 图 5 Chan算法和粒子群算法在系统测量误差不同时的定位性能对比 Fig. 5 Comparison of positioning performance between Chan algorithm and particle swarm algorithm with different system measurement errors |
| 图选项 |
2) NLOS环境下:图 6(a)和图 6(b)分别表示Chan算法和粒子群算法在相同的系统测量误差标准差(0.35 m)下,LOS环境与NLOS环境定位性能的对比,可以看出,NLOS误差均造成2种算法定位性能下降,且对Chan算法的影响大于粒子群算法,因此,在NLOS环境下,粒子群算法表现出更高的定位优势。
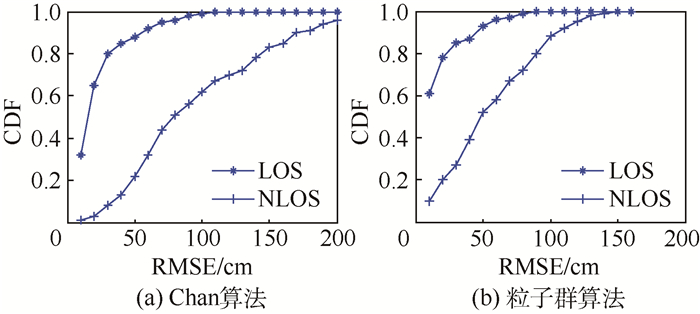 |
| 图 6 Chan算法和粒子群算法在LOS环境与NLOS环境定位性能的对比 Fig. 6 Comparison of positioning performance in LOS and NLOS environment between Chan algorithm and particle swarm algorithm |
| 图选项 |
3) NLOS误差补偿后:NLOS误差的存在使得系统误差为正均值,位置的估计有偏,Chan算法的定位精度有所下降,因此协同定位算法适用于NLOS环境下。图 7表示Chan算法和粒子群算法NLOS误差补偿后和协同定位算法之间的定位性能对比。可以看出,NLOS误差补偿后Chan算法定位性能有了很大提高,这是因为TDOA的修正值是无偏的,消除了NLOS附加时延带来的误差,而粒子群算法的定位精度没有得到明显的改善。协同定位算法的定位性能明显优于2种算法补偿后的定位性能,通过计算均方根误差平均值,定位精度提高30%左右,满足室内定位的要求。
 |
| 图 7 Chan算法和粒子群算法NLOS误差补偿后和协同定位算法之间的定位性能对比 Fig. 7 Comparison of positioning performance among Chan algorithm after NLOS error compensation, particle swarm algorithm after NLOS error compensation, and collaborative localization algorithm |
| 图选项 |
5.2.2 收敛速度 图 8表示在NLOS环境下,单一粒子群算法和协同定位算法的收敛曲线对比,可见,协同定位算法的收敛速度相比于单一粒子群算法较快,这是因为协同定位算法将NLOS误差补偿后的Chan算法结果作为粒子群算法的迭代初值,从而缩小了粒子群的搜索范围,加快了收敛速度,而且协同定位算法在更新速度和位置时,采用线性递减的时变权重,具有较好的全局搜索能力和局部搜索能力,能更快地找到最优解。
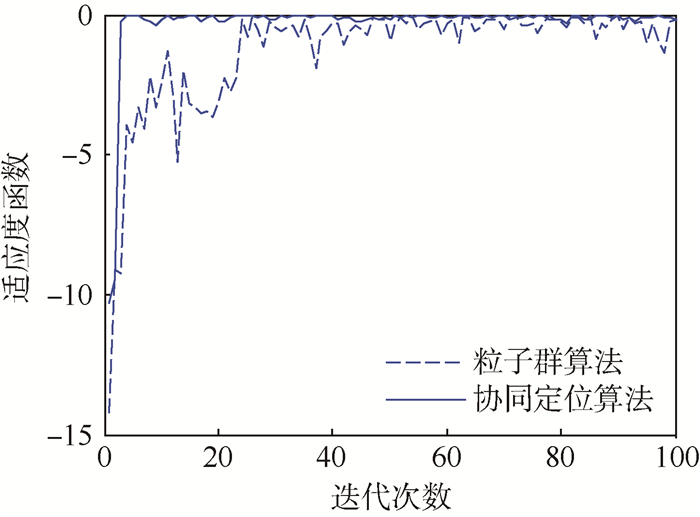 |
| 图 8 粒子群算法和协同定位算法的收敛曲线对比 Fig. 8 Comparison of convergence curves between particle swarm algorithm and collaborative localization algorithm |
| 图选项 |
6 结论 1) 根据NLOS环境下附加时延和由信道决定的均方根时延扩展的联合统计特性,估计NLOS误差的均值和方差,并对TDOA测量值进行修正。在此基础上,提出了一种在室内NLOS环境下,采用时变权重的粒子群算法与Chan算法相结合的协同定位算法进行UWB室内定位。
2) 在理论分析和仿真的基础上进行了实验验证。实验结果表明:在NLOS环境下,TDOA测量值修正后,协同定位算法相比于单一算法有更好的定位性能,定位精度提高30%左右,满足室内定位要求。
参考文献
| [1] | TARZIA S P, DINDA P A, DICK R P, et al.Indoor localization without infrastructure using the acoustic background spectrum[C]//Proceedings of the 9th International Conference on Mobile Systems, Applications, and Services.New York:ACM, 2011:155-168. |
| [2] | CIURANA M, BARCELO A F, MARTIN E I. Comparative performance evaluation of IEEE 802.11v for positioning with time of arriva[J].Computer Standards & Interfaces, 2011, 33(3): 344–349. |
| [3] | IMMOREEV I Y. Ultrawideband radars:Features and capabilities[J].Journal of Communications Technology and Electrnics, 2009, 54(1): 1–26.DOI:10.1134/S106422690901001X |
| [4] | LI C, ZHUANG W H. Hybrid TDOA/AOA mobile user location for wideband CDMA cellular systems[J].IEEE Transactions on Wireless Communications, 2002, 1(3): 439–447.DOI:10.1109/TWC.2002.800542 |
| [5] | SILVENTOINEN M I, RANTALAINEN T.Mobile station emergency locating in GSM[C]//Proceedings of the 1996 IEEE International Conference on Personal Wireless Communications.Piscataway, NJ:IEEE Press, 1996:232-238. |
| [6] | DAMIEN B, DAVIDE D. Position error bound for UWB location in dense cluttered environments[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 44(2): 613–615. |
| [7] | 张宴龙, 陈卫东, 陈畅. 基于非视距鉴别的室内移动节点跟踪算法[J].中国科学技术大学学报, 2014, 44(10): 828–834. ZHANG Y L, CHEN W D, CHEN C. Mobile location tracking based on NLOS identification in indoor environments[J].Journal of University of Science and Technology of China, 2014, 44(10): 828–834.DOI:10.3969/j.issn.0253-2778.2014.10.005(in Chinese) |
| [8] | WYLIE M P, HOLTZMAN J.Non-line of sight problem in mobile location estimation[C]//1996 5th IEEE International Conference on Universal Personal Communications.Piscataway, NJ:IEEE Press, 1996, 2:827-831. |
| [9] | CHEN P C.A non-line-of-sight error mitigation algorithm in location estimation[C]//1999 IEEE Wireless Communications and Networking Conference.Piscataway, NJ:IEEE Press, 1999, 1:316-320. |
| [10] | 王洪雁, 兰云飞, 裴炳南, 等. 非视距环境下基于到达时间差的一种定位算法[J].计算机仿真, 2007, 24(9): 116–119. WANG H Y, LAN Y F, PEI B N, et al. A location algorithm based on time difference of arrival in the non-line-of-sight environment[J].Journal of Computer Simulation, 2007, 24(9): 116–119.(in Chinese) |
| [11] | MOLISCH A F, BALAKRISHNAN K, CHONG C C, et al. IEEE 802.15.4a channel model-final report[J].IEEE P802, 2004, 15(4): 0662. |
| [12] | 段凯宇, 张力军. 一种在NLOS环境下提高精度的TDOA定位方法[J].南京邮电学院学报, 2005, 25(5): 15–19. DUAN K Y, ZHANG L J. An accuracy improved location method based on TDOA in NLOS environment[J].Journal of Nanjing College of Posts and Telecommunications, 2005, 25(5): 15–19.(in Chinese) |
| [13] | LIN L X, SO H C, CHAN F K W, et al. A new constrained weighted least squares algorithm for TDOA-based localization[J].Signal Processing, 2013, 93(11): 2872–2878.DOI:10.1016/j.sigpro.2013.04.004 |
| [14] | CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing, 1994, 42(8): 1905–1915.DOI:10.1109/78.301830 |
| [15] | POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J].Swarm Intelligence, 2007, 1(1): 33–57.DOI:10.1007/s11721-007-0002-0 |
| [16] | KULKARNI R V, VENAYAGAMOORTHY G K. Particle swarm optimization in wireless-sensor networks:A brief survey[J].IEEE Transactions on Systems, Man, and Cybernetics, Part C:Applications and Reviews, 2011, 41(2): 262–267.DOI:10.1109/TSMCC.2010.2054080 |
| [17] | BATRA A, BALAKRISHNAN J, AIELLO G R, et al. Design of a multiband OFDM system for realistic UWB channel environments[J].IEEE Transactions on Microwave Theory and Techniques, 2004, 52(9): 2123–2138.DOI:10.1109/TMTT.2004.834184 |
| [18] | MOLISCH A F, FOERSTER J R, PENDERGRASS M. Channel models for ultrawideband personal area networks[J].IEEE Wireless Communications, 2003, 10(6): 14–21.DOI:10.1109/MWC.2003.1265848 |
| [19] | GREENSTEIN L J, ERCEG V, YEH Y S, et al. A new path-gain/delay-spread propagation model for digital cellular channels[J].IEEE Transactions on Vehicular Technology, 1997, 46(2): 477–485.DOI:10.1109/25.580786 |
| [20] | 杨北亚, 熊辉, 丁宏, 等. 应用NLOS鉴别补偿的无线传感器网络TDOA定位算法[J].重庆理工大学学报, 2015, 29(10): 120–126. YANG B Y, XIONG H, DING H, et al. TDOA location algorithm based on NLOS error identification and compensation in wireless sensor network[J].Journal of Chongqing University of Technology, 2015, 29(10): 120–126.DOI:10.3969/j.issn.1674-8425(z).2015.10.022(in Chinese) |
| [21] | ALAVI B, PAHLAVAN K. Modeling of the TOA-based distance measurement error using UWB indoor radio measurements[J].IEEE Communications Letters, 2006, 10(4): 275–277.DOI:10.1109/LCOMM.2006.1613745 |
| [22] | 刘金琨, 沈晓蓉, 赵龙. 系统辨识理论及MATLAB仿真[M].北京: 电子工业出版社, 2014: 215-227. LIU J K, SHEN X R, ZHAO L. System identification theory and MATLAB simulation[M].Beijing: Publishing House of Electronics Industry, 2014: 215-227.(in Chinese) |
