目前,国内外****对人和人工智能机器如何进行合作,更好地完成任务进行了深入的研究,并发表了大量的研究成果[6-12]。陈军等[11]研究了人对无人机的干预方式,采用分层干预策略,满足不同层次的决策需求。Cummings[12]和史美萍[13]等对人机协同路径规划也展开了研究,人在规划中所充当的角色是通过直观判断增加或删除航路点实现对路径的修正。任鹏和高晓光[14-15]利用人的智慧和综合判断能力,选出最优航迹,在遇到突发威胁时,由人设置重规划的起始点和终止点。谭雁英[16]提出通过人机交互界面在理想位置设定子目标点,引导无人机重规划航迹从而规避突发威胁。Sun和Cai [17]提出由人对突发威胁的危险性进行评估,采用云模型解算得到引导点,从而启发A*算法寻优得到规避路径。这些研究的侧重点主要集中于人机交互的机制或控制权限的决策分配上,或者在航迹规划中,通过人手动地在操作界面上删除或增加航路点以改变航迹。但对于人如何真正地参与到航迹规划之中,实现人在回路动态调整航迹,既充分发挥人的决策和判断能力,又充分利用计算机的高效快速计算性能,还处于探索阶段,需要进一步的研究。
1 问题描述 如图 1所示,当无人机按预先规划的静态航迹飞行到某处时,探测到突发威胁,如果按照无人机自主航迹规划方法,将根据设定的目标函数机械地规划得到最优航迹,如航迹2所示。虽然从规划的结果来看,航迹2可以成功规避突发威胁,航程最短,并且不会进入其他威胁的区域,但是航迹2经过的区域属于威胁密集区域,危险系数增大,如果在飞行途中再次遭遇其他突发威胁,无人机若想重规划一条经过无威胁区域的航迹将非常困难。由于人可以从全局了解掌握威胁环境,设想由人对当前威胁态势做出判断,向无人机发送指令“向左转弯”,无人机将根据人的指令,重新规划航迹,在任务完成时间和燃油消耗允许的范围之内,规划得到航迹1。
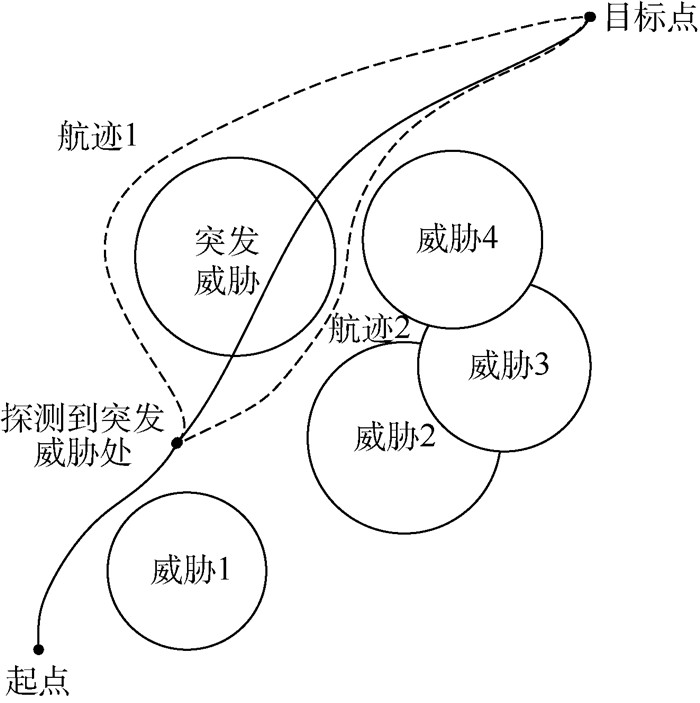 |
| 图 1 自主航迹规划与人机合作航迹规划方向选择示意图 Fig. 1 Schematic diagram of direction selection between autonomous path planning and human-machine cooperative path planning |
| 图选项 |
本文所采用的思路是由人和无人机合作进行航迹规划,将人的经验知识和智能决策融入到航迹规划中,利用人的认知能力,对威胁态势做出判断,给出规避突发威胁的方向,并对当前任务的紧急程度进行判断,无人机将根据人推理决策得到的信息,采用模糊控制的方法自主解算得到引导点,引导航迹进行修正,实现对突发威胁的规避。人只需提供决策信息,具体实施仍由计算机来做,避免了人直接添加删除航路点或直接设置实时规划的起始点和终止点时的随意性,受人工作状态和主观判断影响较大,在人疲劳状态,容易引起误操作。
2 航迹规划建模 2.1 规划空间 本文主要围绕在飞行过程中,无人机探测到突发威胁,针对如何实时规划航迹,实现对突发威胁的规避展开研究。假定飞机在遇到突发威胁之前已到达预定高度,处于巡航阶段,航迹规划暂且只考虑二维水平面规划。威胁模型采用等效圆来表示:
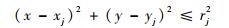 | (1) |
式中:(x, y) 为无人机当前位置;(xj, yj) 为第j个威胁的中心坐标;rj为威胁作用半径。
2.2 无人机自身约束条件 无人机自身约束条件主要考虑最大转弯角、最小步长、最大航程和最小转弯半径等因素。
2.3 代价函数 代价函数定义为
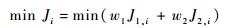 | (2) |
式中:w1、w2为权重系数;J1, i为第i个航迹节点到目标点 (xg, yg) 的距离代价,定义如下:
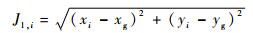 | (3) |
J2, i为第i个航迹节点的威胁代价,定义如下:
 | (4) |
其中:λi为调节系数;M为威胁的总个数。
假设整条航迹共由N段航迹组成,则共有N+1航迹节点。严格意义上说,整条航迹的威胁代价应为N段航迹威胁强度的积分累加和,为简化方便,当步长取较小值时,用N+1个航迹点的威胁代价累加求平均值作为整条航迹的威胁代价:
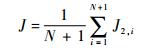 | (5) |
2.4 航迹节点扩展 航迹节点的扩展方式采用如下方法:
 | (6) |
 | (7) |
 | (8) |
式中:(xi+1, yi+1) 表示下一航迹节点;l为扩展步长;V0为巡航速度;Δt为无人机探测信息更新的时间间隔。通过每次找到最佳航向角ψi+1best,从而确定下一个航迹节点。而最佳航向角ψi+1best的确定采用下述方法:以当前位置P (xi, yi) 为圆心,步长l为半径做圆,根据最大转弯角φmax的限制,得到如图 2所示的扇形区域,当前速度方向如Vi所示,然后在圆弧上等距取N个点,分别计算这N个点的代价,代价最小的点的方位角即为最佳航向角ψi+1best。
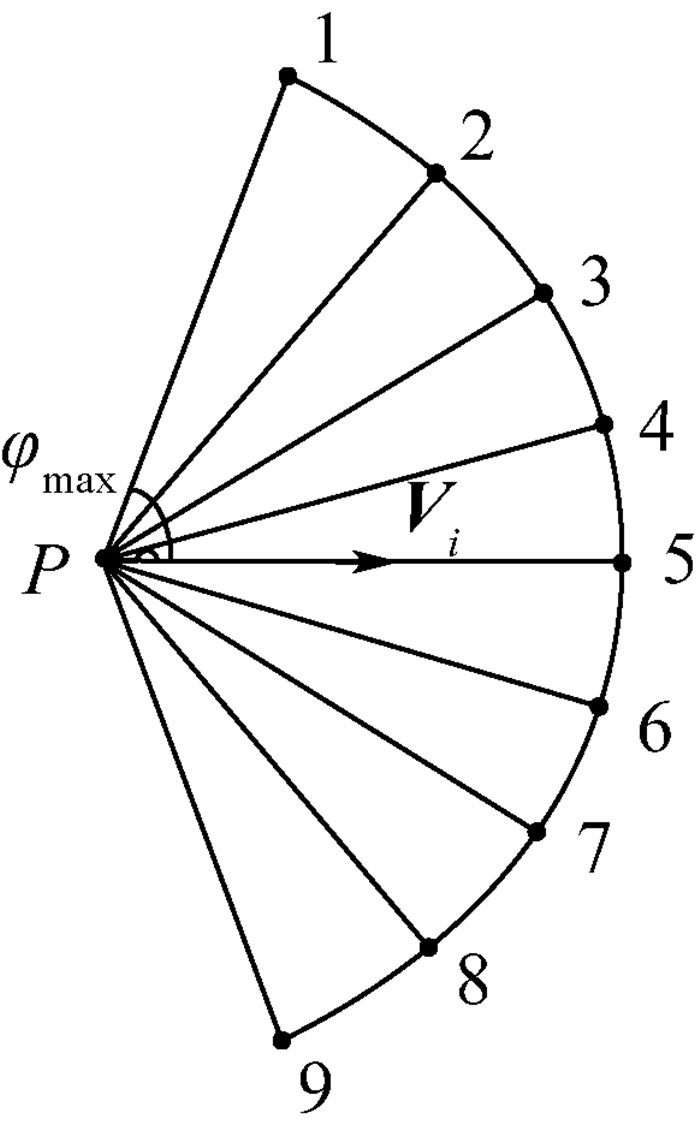 |
| 图 2 航迹节点扩展示意图 Fig. 2 Schematic diagram of path nodes extension |
| 图选项 |
2.5 引导点设置 如图 3所示,当无人机在A点探测到突发威胁O,操作员根据当前遇到的威胁状况和整个战场环境对威胁态势做出判断,然后向无人机发送规避方向的指令,向左或向右转弯。通过设置引导点,牵引无人机改变航向,规避突发威胁。引导点位置的确定,对于无人机规避突发威胁非常重要。无人机在执行任务时,如果任务紧急,通常要求无人机能尽快到达目标点。若引导点距离威胁源较近时,虽然航程减小,完成任务时间缩短,但受威胁的概率增加;若引导点距离威胁源较远时,虽然受威胁的概率减小,但航程增大,完成任务时间延长。所以,需要在安全性和航程之间做出平衡,合理确定引导点与威胁之间的距离,使无人机既能安全地规避突发威胁又能使航程代价较小。
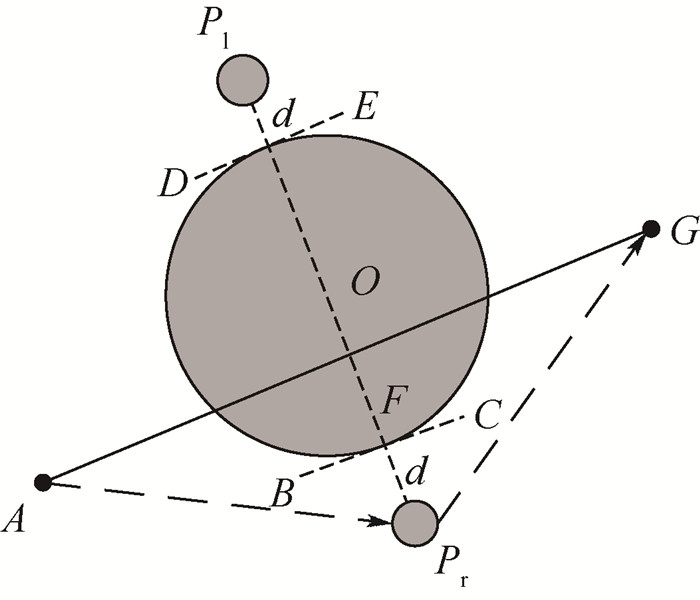 |
| 图 3 引导点与突发威胁之间的几何关系 Fig. 3 Geometric relationship between guide point and unexpected threat |
| 图选项 |
引导点需要与突发威胁保持一定的距离,保证无人机沿规划航迹飞行的安全。如图 3所示,连接遭遇突发威胁点A和目标点G,由威胁源中心点向AG引垂线,BC、DE与威胁区域相切,确定引导点即在垂线上与BC或DE相距为d的位置,如图 3中左引导点Pl或右引导点Pr所示,下面将主要对距离d的确定进行阐述。
3 模糊推理 在之前的一些研究人机合作航迹规划的文献中,对于无人机遭遇突发威胁的规避,提出的方法是人在人机交互的界面上通过鼠标点击,鼠标点击的位置即为引导点的位置。这种方法具有很大的随意性,受人的工作状态影响较大,容易导致误操作。基于此,本文采用了一种模糊推理的方法,将人的经验知识和认知判断能力融入到推理模型中,把无法用精准数学模型描述的人的经验知识用模糊集合表达,通过计算机解算得到引导点相距威胁边界距离d。既能充分利用人的高度智能,又可以有效地克服人的误操作和随意性。
由于机器无法识别任务的重要性,不能对任务的紧急程度进行判断,因而借助人,给出任务紧急程度的描述。而人们在描述任务时,通常会采用非常紧急、紧急、不紧急等模糊性语言描述,无法用精确的数值进行量化,而模糊推理正是将这类不精确的、模糊的语言描述,通过一定的规则,与精确的数值表达建立联系。通过借助模糊数学,为每一个描述性元素建立其对应的模糊集合。这个模糊集合采用隶属函数刻画。
3.1 隶属函数 每个元素对应的模糊集合是通过隶属函数来表征的。无人机被雷达探测的概率将影响无人机的安全性。当无人机在执行任务时,任务越紧急,则要求无人机越快到达指定目标点。此时,在无人机速度一定的情况下,规划航迹的总航程应越短,所以操作员对任务的紧急程度的判断将影响航程。另外还需要考虑无人机自身约束,所以,确定模糊推理的输入量为无人机被雷达探测的概率、任务的紧急程度、与威胁边界的夹角,输出量为引导点与威胁之间距离d。确定它们的隶属函数如下:
1) 无人机被雷达探测概率p:对于每种类型的雷达,其工作效率和对目标的探测概率是不一样的,因而对无人机具有不同的杀伤效果。通过传感器网络,可以对敌方不同的雷达参数信息进行搜集统计,从地面控制站获取相关信息。所以,对于雷达探测概率,可以根据经验知识,采用Gauss函数和Sigmoid函数相结合,建立其隶属函数如图 4(a)所示。将无人机被雷达探测的概率p设为[0, 1]之间,定义模糊子集为很大 (VB)、一般 (MB)、较小 (S)。
 |
| 图 4 输入输出隶属函数 Fig. 4 Membership function of input and output |
| 图选项 |
2) 任务紧急程度η:由于无人机在执行任务时,通常都有时间硬性要求,要在规定的时间内到达指定目的地,所以在此,将任务的紧急程度η分为[0, 10]个等级,定义模糊子集为非常紧急 (VI)、紧急 (MI)、不紧急 (I),建立隶属函数如图 4(b)所示。
3) 无人机与突发威胁之间的角度θ:无人机遭遇突发威胁时,其与威胁边界之间角度关系如图 5所示。
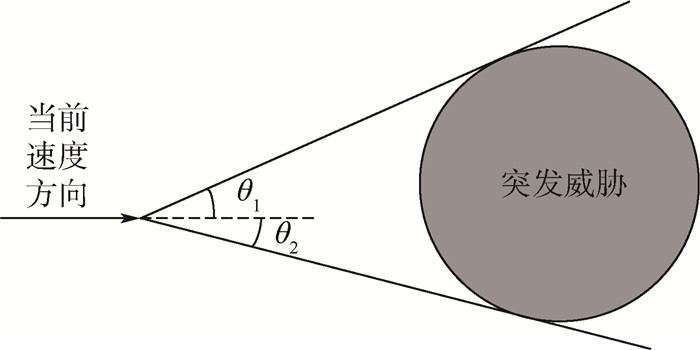 |
| 图 5 无人机与威胁边界之间角度关系 Fig. 5 Angle relationship between UAV and unexpected threat's border |
| 图选项 |
如果与威胁边界之间的角度较大,应设置引导点距离威胁较近,以此减小航迹转弯角,避免超过无人机最大转弯角的限制;如果与威胁边界之间的角度较小,应设置引导点距离威胁较远,以此在保证满足最大转弯角限制条件下,降低危险性。由图 5可知无人机与威胁边界的角度最大为90°,所以将无人机与威胁之间的角度θ设定为[0, 1.6]rad之间,定义模糊子集为很大 (VH)、一般 (MH)、较小 (L),建立隶属函数如图 4(c)所示。
4) 引导点与威胁之间距离 (输出量)d:模糊推理的输出为引导点与威胁边界的距离d,设定d为[0, 5] km之间,定义模糊子集为远 (F)、中 (M)、近 (C),建立隶属函数如图 4(d)所示。
3.2 模糊规则 模糊规则采用如下语句进行描述:
If p is Ai and η is Bi and θ is Ci, then d is Di
其中:Ai、Bi、Ci和Di分别为p、η、θ和d所对应的在相应论域上的模糊子集。根据不同的输入状态,可以得到27条规则,每条规则对应一种输出状态,其具体对应规则如表 1所示,以第1条规则为例,有
If p is S and η is I and θ is L, then d is M
表 1 模糊规则 Table 1 Fuzzy rules
| 规则序号 | 输入 | 输出 | |||
| p | η | θ | d | ||
| 1 | S | I | L | C | |
| 2 | S | I | MH | C | |
| 3 | S | I | VH | C | |
| | | | | | |
| 25 | VB | VI | L | M | |
| 26 | VB | VI | MH | C | |
| 27 | VB | VI | VH | C | |
表选项
模糊推理系统包含2种类型:一种输出量是关于输入量的函数,称之为Sugeno型;另一种是输出量是某一模糊集合,称之为Mamdnai型。因为输出量d的模糊集合已知,所以采用Mamdnai型,模糊关系的运算采用最大-最小合成[18],则有
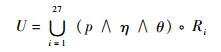 | (9) |
 | (10) |
式中:U为模糊输出的集合; “∧”为取小运算符; “°”为合成运算符; Ri为与第i条规则相对应的模糊蕴涵关系。
结合表 1信息,可以得到输出量d的模糊集合。在实际应用中,需要用d的精确值,所以,需对d进行清晰化处理。
3.3 清晰化 采用加权平均法对模糊输出量进行清晰化处理。假设在模糊输出集合U上某处元素为di,i=1, 2, 3,与其相对应的隶属度为μU (di),则
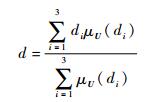 | (11) |
得到最终输出量精确值d。
3.4 规划流程 航迹规划的流程如图 6所示。
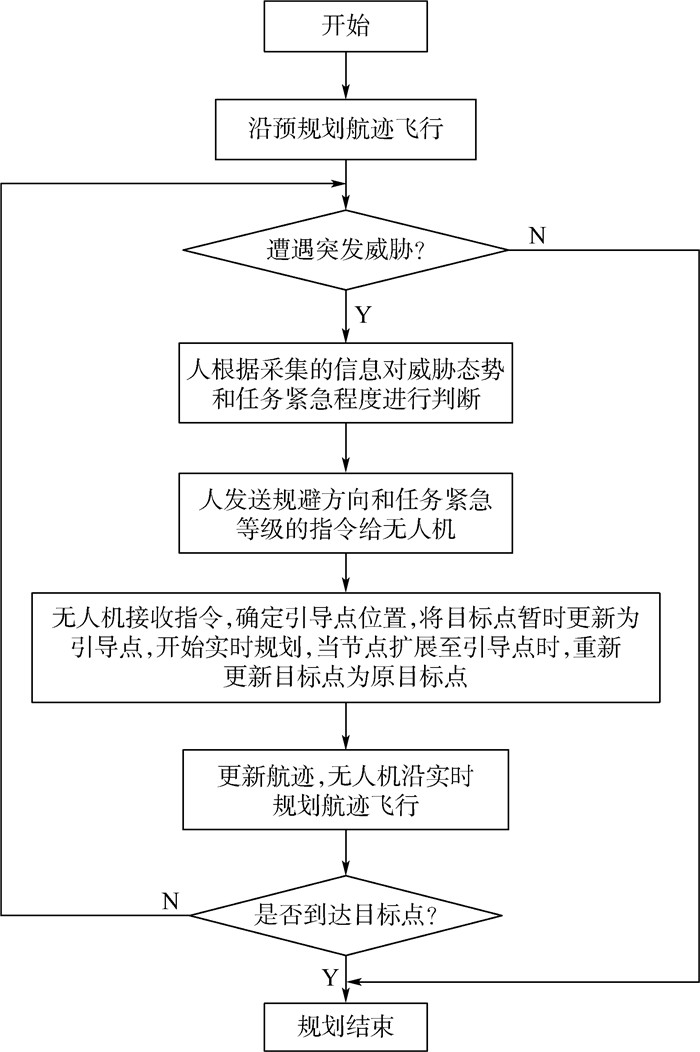 |
| 图 6 无人机航迹规划流程 Fig. 6 UAV path planning procedure |
| 图选项 |
4 仿真实验 仿真实验在处理器为Intel (R) Core (TM)2 E7400,内存为2 GB的PC机上进行,操作系统为Windows XP,采用MATLAB编程进行仿真。规划区域为70 km×70 km的矩形区域,无人机初始位置位于 (5, 5) km处,目标点位于 (60, 60) km处。w1=1×10-3,w2=5,l=0.4 km。无人机的雷达探测半径为6 km,最大转弯角φmax为60°,从初始位置出发,为无人机规划一条到目标点的最优路径。目前已探明的威胁信息如表 2所示。
表 2 威胁具体信息 Table 2 Specific information of threats
| 威胁序号 | 中心坐标/km | 作用半径/km |
| 1 | (10,25) | 6 |
| 2 | (16,32) | 7 |
| 3 | (36,22) | 9 |
| 4 | (40,42) | 6 |
| 5 | (47,40) | 6 |
| 6 | (47,46) | 7 |
| 7 | (50,10) | 7 |
表选项
4.1 突发威胁规避仿真 根据已掌握的环境信息,采用自主航迹规划得到静态参考航迹如图 7所示。由图 7可知,针对已掌握的航迹信息,在未出现突发威胁的情况下,可以得到一条较优静态规划参考航迹,该航迹可以有效避开已知威胁,并且航程较短。
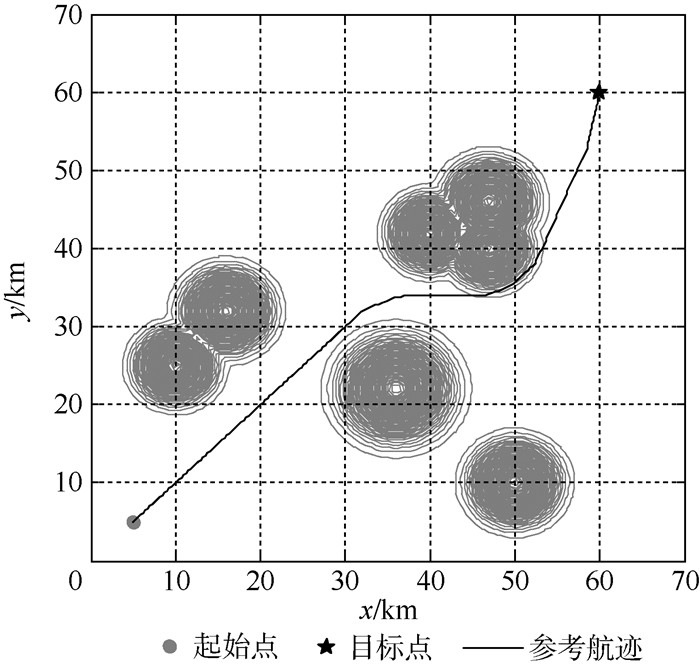 |
| 图 7 无人机自主航迹规划参考航迹 Fig. 7 UAV autonomous path planning reference path |
| 图选项 |
当无人机沿预先规划的静态参考航迹飞行时,在某时刻,探测到一处突发威胁 (敌方雷达),经分析判断该威胁对无人机的探测概率为0.8,突发威胁的中心位于 (20, 20) km,作用半径为5 km,此时无人机位置坐标为 (13.7, 13.7) km,经计算得到此时无人机与突发威胁右边界的角度约为0.6 rad。按照文献[19]的方法和本文的方法,分别进行自主实时航迹规划和人机合作实时航迹规划。人机合作规划时,首先由人对威胁态势进行分析。若选择从左侧进行规避,将进入威胁密集区域,同时受到威胁1、威胁2和突发威胁影响,所以,此时,人对威胁环境进行判断后,选择向右进行规避,将向无人机发送向右规避的指令。通过仿真,2种方法规划航迹如图 8所示。
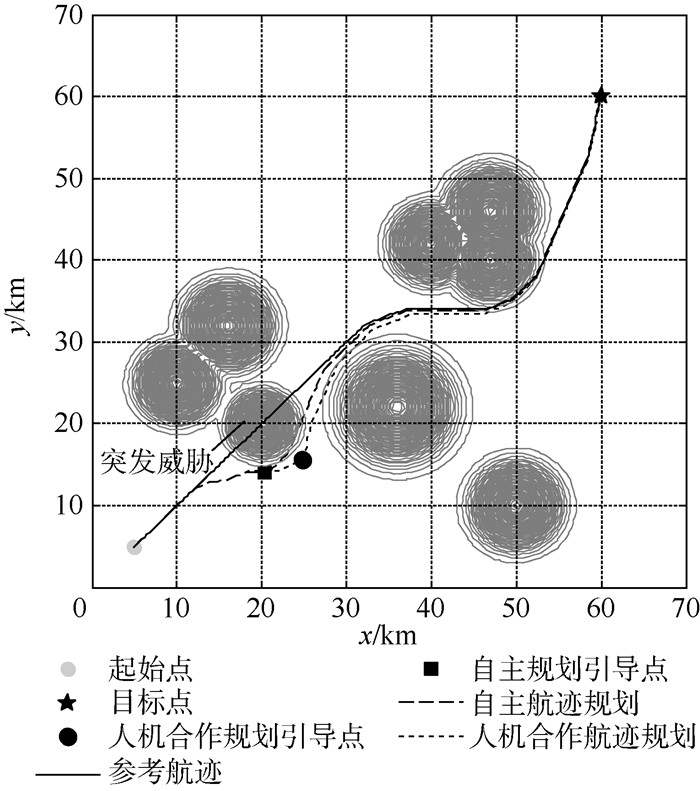 |
| 图 8 自主航迹规划与人机合作航迹规划 Fig. 8 UAV autonomous path planning and human-machine cooperative path planning |
| 图选项 |
对航迹规划结果的评价指标进行统计,为排除随机误差的影响,试验100次,取平均值作为最终的统计结果,得到不同规划方式时航迹结果如表 3所示。
表 3 自主航迹规划与人机合作航迹规划引导点位置 Table 3 Position of guide point with autonomous path planning and human-machine cooperative path planning
| 规划方式 | d/km | 节点数 | 时间/s | 总航程/km | 威胁代价 | 引导点位置/km |
| 自主航迹规划 | 1.000 | 208 | 0.953 | 85.996 | 0.443 | (20.300, 14.000) |
| 人机合作航迹规划 | 1.403 | 208 | 1.137 | 86.724 | 0.364 | (24.742, 15.697) |
表选项
从图 8和表 3可知,无人机自主实时规划得到的航迹将更加靠近突发威胁,威胁概率增加,飞行的安全性降低。人机合作航迹规划时,可以根据任务需要设置紧急程度调整引导点的位置,提高了安全性,却是以牺牲时间为代价的。而自主航迹规划时只能根据固定的规则进行规划,无法实现对子目标点的动态调整,但是,无人机自主航迹规划时间更短,时效性更好。由于此处对时间的统计没有统计人的操作反应时间和发送指令时间,如果考虑这两者的时间因素,无人机自主航迹规划将比人机合作航迹规划在时间上的优势将更大。
综合看来,这2种方法各有利弊,面对简单规划环境,时间要求特别紧迫,敌方雷达等威胁较小时,适宜采用无人机自主航迹规划的方法,而在面对复杂规划环境,敌方雷达等威胁较大时,适宜采用人机合作航迹规划的方法。
4.2 不同规避方向航迹仿真 为说明人对规避方向选择的重要性,对采取不同规避方向下,无人机航迹规划进行了仿真,仿真结果如图 9所示。
 |
| 图 9 选择不同规避方向时的实时航迹规划 Fig. 9 Real-time path planning when different evasion directions are chosen |
| 图选项 |
从仿真结果来看,对于突发威胁,选择右侧引导进行规避明显优于从左侧进行规避。从左侧进行规避将进入多威胁交叉作用区域,危险性明显增加。当面对突发威胁,采用无人机自主航迹规划时,由于从左、右两侧进行规避时,航向偏角相等,并且从左侧规避时,航程更短,由于无人机无法对后续将飞越区域的威胁态势进行判断,当无人机默认优先考虑航程因素进行规划时,将选择从左侧进行规避。而在加入了人这一环节时,人可以对整体环境的威胁态势进行判断,意识到从左侧规避威胁时,将进入威胁交叉区域,危险性显著提高,果断发送“向右”规避指令,无人机自主解算得到引导点,成功实现对突发威胁的规避。
为进一步说明,不同规避方向的选择对航迹规划结果的影响,选取评价航迹优劣的部分指标,进行了对比研究。对于时间的统计,只统计了计算机接到规划指令后开始到规划结束的时间,暂未考虑人的反应时间和发送指令时间。共试验100次,对结果进行统计,取平均值作为最终统计结果如表 4所示。
表 4 不同规避方向航迹规划结果对比 Table 4 Comparison of path planning results with different evasion directions
| 规避方向 | d/km | 节点数 | 时间/s | 总航程/km | 威胁代价 | 引导点位置/km |
| 左侧引导 | 1.403 | 185 | 1.121 | 82.404 | 0.595 | (15.258, 24.304) |
| 右侧引导 | 1.403 | 208 | 1.137 | 86.724 | 0.364 | (24.742, 15.697) |
表选项
从数据统计的结果可以看出,从左侧引导进行规避,虽然总航程较短,节点数更少,但规划时间相差小,并且威胁概率显著增加,从安全角度出发,是不利于无人机飞行的。在航程和规划时间优势并不明显的情况下,应该优先确保无人机飞行的安全,可见从右侧进行规避优于从左侧进行规避。说明,规避方向的选择将直接影响航迹规划的效果,人在这一环节扮演了重要的角色,可见,实现人机合作航迹规划,利用人的高度智能和决策判断能力,有利于得到更符合实际战场环境的航迹,有利于提高无人机飞行的安全性。
4.3 不同任务紧急程度航迹仿真 为研究人对任务紧急程度的判断对航迹规划的影响,分别取不同的任务紧急程度η=2,5,8进行航迹规划仿真,结果如图 10(a)所示,将引导点位置局部放大如图 10(b)所示。
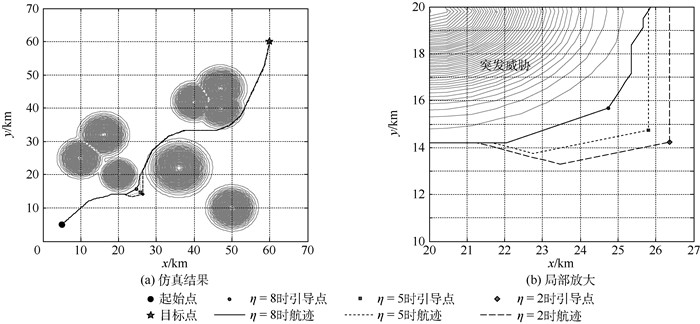 |
| 图 10 不同任务紧急程度时引导点的位置 Fig. 10 Guide point position with different task emergency levels |
| 图选项 |
对航迹规划结果的评价指标进行统计,试验100次,取平均值作为最终的统计结果,结果如表 5所示。
表 5 不同任务紧急程度航迹规划结果对比 Table 5 Comparison of path planning results with different task emergency levels
| 任务紧急程度 | d/km | 节点数 | 时间/s | 总航程/km | 威胁代价 | 引导点位置/km |
| η=2 | 3.595 | 215 | 1.144 | 89.447 | 0.307 | (26.365, 14.224) |
| η=5 | 2.833 | 212 | 1.141 | 88.390 | 0.328 | (25.800, 14.736) |
| η=8 | 1.403 | 208 | 1.137 | 86.724 | 0.364 | (24.742,15.697) |
表选项
从图 10和表 5中可知,人对任务紧急程度的判断将直接影响引导点与突发威胁边界距离d。当任务紧急程度越高时,引导点距离威胁越近,无人机将选择从靠近威胁边界处绕过突发威胁,总航程减短,保证无人机尽快到达指定目标点。当任务紧急程度较低时,引导点距离威胁较远,无人机将选择从远离威胁边界处绕过突发威胁,以此降低危险性,充分保证安全。通过由人根据作战需求,对任务紧急程度作出判断,给出不同的任务等级,可以动态调整航迹。可以根据作战任务的实际情况,确定在规划时是航程优先还是安全性优先。
参考文献
| [1] | 朱大奇, 孙兵, 李利. 基于生物启发模型的AUV三维自主路径规划与安全避障算法[J].控制与决策, 2015, 30(5): 798–806. ZHU D Q, SUN B, LI L. Algorithm for AUV's 3-D path planning and safe obstacle avoidance based on biological inspired model[J].Control and Decision, 2015, 30(5): 798–806.(in Chinese) |
| [2] | WEN N F, SU X H, MA P J. Online UAV path planning in uncertain and hostile environments[J].Journal of Machine Learn & Cybernation, 2015, 8(2): 1–19. |
| [3] | 何平川, 戴树岭. 一种改进UAV三维航迹实时规划算法[J].北京航空航天大学学报, 2010, 36(10): 1248–1251. HE P C, DAI S L. Improved 3-D real-time trajectory algorithm for UAV[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(10): 1248–1251.(in Chinese) |
| [4] | 姚远, 周兴社, 张凯龙, 等. 基于稀疏A*搜索和改进人工势场的无人机动态航迹规划[J].控制理论与应用, 2010, 27(7): 953–959. YAO Y, ZHOU X S, ZHANG K L, et al. Dynamic trajectory planning for unmanned aerial vehicle based on sparse A* search and improved artificial potential field[J].Control Theory & Applications, 2010, 27(7): 953–959.(in Chinese) |
| [5] | ZHENG C W, LI L, XU F J, et al. Evolutionary route planner for unmanned air vehicles[J].IEEE Transaction on Robotics, 2005, 21(4): 609–620.DOI:10.1109/TRO.2005.844684 |
| [6] | HOWITT S L, RICHARDS D.The human machine interface for airborne control of UAVs[C]//2nd AIAA"Unmanned Unlimited"Conference and Workshop and Exhibit 2003.Reston:AIAA, 2003. |
| [7] | JOSE M, CANINO R, JESUS G H, et al. Human computer interactions in next-generation of aircraft smart navigation management systems:Task analysis and architecture under an agent-oriented methodological approach[J].Sensors, 2015, 15(3): 5228–5250.DOI:10.3390/s150305228 |
| [8] | CUMMINGS M L, ANDREW C, CHRISTIN H. The role of human-automation consensus in multiple unmanned vehicle scheduling[J].Human Factors and Ergonomics Society, 2010, 52(1): 17–27.DOI:10.1177/0018720810368674 |
| [9] | JEAN M H. Towards a cognitive approach to human-machine cooperation in dynamic situations[J].Human-Computer Studies, 2001, 54(4): 509–540.DOI:10.1006/ijhc.2000.0454 |
| [10] | ANDREW S C, JASON C R, KIMBERLY F, et al.Innovative systems for human supervisory control of unmanned vehicles[C]//Proceedings of the Human Factors and Ergonomics Society 56th Annual Meeting, HFES 2012.Santa Monica, CA:Human Factors an Ergonomics Society Inc., 2012:531-535. |
| [11] | 陈军, 张新伟, 徐嘉. 有人/无人机混合编队有限干预式协同决策[J].航空学报, 2015, 36(11): 3652–3665. CHEN J, ZHANG X W, XU J. Human/unmanned-aerial-vehicle team collaborative decision-making with limited intervention[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(11): 3652–3665.(in Chinese) |
| [12] | CUMMINGS M L, MARQUEZ J J, ROY N. Human-automated path planning optimization and decision support[J].Human-Computer Studies, 2012, 70(2): 116–128.DOI:10.1016/j.ijhcs.2011.10.001 |
| [13] | 史美萍. 基于人机协同的月球车路径规划技术研究[D]. 长沙: 国防科学技术大学, 2006: 20-43. SHI M P.Research on path planning technology for lunar rover based on the human-machine cooperation[D].Changsha:School of National University of Defense Technology, 2006:20-43(in Chinese). |
| [14] | 任鹏, 高晓光. 人机协同智能航迹规划算法[J].系统仿真学报, 2015, 27(2): 313–319. REN P, GAO X G. Man-machine coordinated intelligent flight path planning algorithm[J].Journal of System Simulation, 2015, 27(2): 313–319.(in Chinese) |
| [15] | 任鹏, 高晓光. 有限干预下的UAV低空突防航迹规划[J].系统工程与电子技术, 2014, 36(4): 679–684. REN P, GAO X G. Human intervention flight path planning for UAV low-altitude penetration[J].Systems Engineering and Electronics, 2014, 36(4): 679–684.(in Chinese) |
| [16] | 谭雁英. 基于人机合作策略下的SAS算法的多无人机路径再规划[J].西北工业大学学报, 2014, 32(5): 688–692. TAN Y Y. Path replanning approach for multiple UAVs based on SAS algorithm under human automation collaboration[J].Journal of Northwestern Polytechnical University, 2014, 32(5): 688–692.(in Chinese) |
| [17] | SUN X X, CAI C. Human-machine cooperation in unmanned aerial vehicle path planning based on cloud model[J].Automatic Target Recognition and Image Analysis, 2011, 8003(1): 554–561. |
| [18] | 李国勇, 杨丽娟. 神经·模糊·预测控制及其MATLAB实现[M].北京: 电子工业出版社, 2013: 100-112. LI G Y, YANG L J. Neural·fuzzy·predictive control and realization through MATLAB[M].Beijing: Electrics Industry Press, 2013: 100-112.(in Chinese) |
| [19] | 张帅, 李学仁, 张建业, 等. 基于动态步长的无人机三维实时航迹规划[J].北京航空航天学报, 2016, 42(12): 2745–2754. ZHANG S, LI X R, ZHANG J Y, et al. UAV 3D real-time path planning based on dynamic step[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(12): 2745–2754.(in Chinese) |
