在各类常见的飞机结构件中,筋特征(简称筋)广泛存在于内外形轮廓、槽腔之中,或单独作为凸台筋存在,其主要作用在于减轻结构件的重量,加强关键部位的强度等。筋的数控编程烦琐且易出错。据国内有关文献的统计,筋特征的加工约占飞机结构件总加工特征数的35%,其数控编程工作量约占零件编程总工作量的50%^[1]。而这类结构件的数控加工时间与数控编程时间的比值约为1∶10^[2],因此提高数控编程效率是提高这类飞机结构件加工效率的关键。解决这个问题首先需要完成CAD系统向CAM、CAPP系统的信息传递,建立零件的实体模型与加工特征、加工工艺之间的映射关系,从而为飞机结构件的快速自动编程提供数据信息。而特征识别技术是实现CAD/CAM/CAPP三者有机集成的理想接口^[3]。即对不同特征的准确、快速识别是实现数控编程、特征加工的首要前提。
特征识别技术至今已发展近40年,取得了丰硕的成果,如最小条件子图法^[4]、基于知识推理的方法^[5]、基于体剖分的方法^[6]、基于属性邻接图^[7]等。然而由于该技术本身的复杂性,仍有许多未突破的难点^[8],如相交特征的识别、复杂曲面零件的识别等。近年来,飞机结构件上复杂特征的识别问题也得到了一些关注。谭丰^[1]、施建飞等^[9]将工艺知识归纳为一系列解释和识别规则,并融入基于图的识别中,对飞机结构件的筋特征进行识别。这种基于特征种子面(水平筋顶面)属性边点图的筋特征识别方法对相交特征的识别具有很好的效果,但对于直接生长在腹板上的斜顶筋,则算法失效,因而具有一定的局限性。闫海兵^[10]提出一种抑制过渡特征(过渡转角和过渡底圆)的识别方法,实现了在不改变零件实体模型的情况下抑制过渡特征。但其对复杂特征的识别结果无法保证完全正确,需要交互识别修正,因此这种方法不能完全实现特征的自动识别。
综上,针对飞机结构件的筋特征,仍缺乏一种准确且高效的识别方法。本文提出基于约束Delaunay三角剖分的飞机结构件筋特征识别算法。首先,引入广义腹板概念,给出筋的表示模型;其次,识别广义腹板,基于约束Delaunay三角剖分识别并构建筋特征;最后,结合实例对算法进行分析和验证。
1 筋的表示模型1.1 广义腹板狭义上,飞机结构件底面中除凸台顶面、平筋顶之外的水平拓扑面称为腹板面。而腹板面、凸台顶面和平筋顶的共同特点是其所依赖的面属于零件的正向(即z轴正向)可加工水平面。因此给出广义腹板面的定义:飞机结构件中的腹板面、凸台顶面和平筋顶统称为广义腹板面,即广义腹板。
广义腹板一般属于上层槽腔的底面、下层槽腔或凸台的顶面(本文所述槽均为广义槽^{[11, 12]})。图 1表示了零件中广义腹板与槽的关系。图中:数字编号①～⑤为该零件中的水平面,其中的①、②、③层为平顶筋,④、⑤层为腹板。

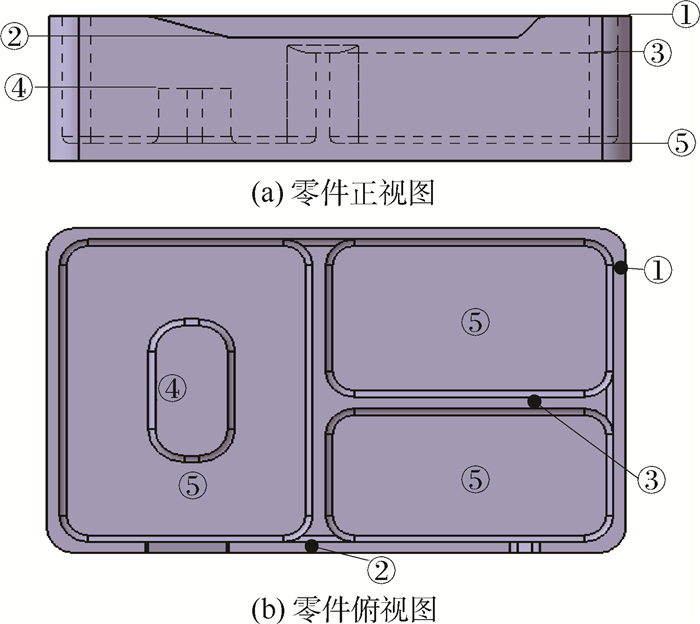图 1 广义腹板与槽的关系Fig. 1 Relationships between generalized bottom plane and pocket

图选项

从图 1中可以看出,广义腹板一定属于某个槽的底面。本文在识别筋特征的过程中,在给定的加工坐标系下,将零件上每一个正向可加工的水平面构建为一个广义腹板节点,表示为GFB。当广义腹板所依赖的水平面为腹板面时,构建对应的腹板节点Fuban;为平顶筋面时,构建对应的筋节点Rib,再根据其分支构建多个平顶筋节点。构成GFB的水平表面表示为f_h,则广义腹板的巴科斯-诺尔范式(Backus-Naur Form,BNF)为
〈GFB〉::=(〈Layernum〉,〈F_h〉,〈Type〉)
〈Type〉::=(〈Fuban〉〈Rib〉)
式中:Layernum为该广义腹板节点的层数;F_h为f_h的集合;Type为该节点实际对应的类型。
1.2 筋的几何属性结合飞机结构件中筋特征的几何形状和加工工艺特点,对筋特征的几何属性(F_G)定义如下。
定义1 飞机结构件中筋特征的待加工面称为主加工面,简称主面,表示为f_m;主面在沿刀轨运动方向的约束面称为限制面,表示为f_l;用于表示筋特征高度的面称为顶面和底面,表示为f_t和f_b;主面与限制面或底面间的连接面称为底圆面,表示为f_r;主面与顶面间的连接面称为过渡面,表示为f_a;与主面关联的,除去限制面、底圆面和过渡面等其他的面称为侧面,表示为f_s。
根据主面几何类型及拓扑结构,典型筋的几何属性如图 2所示。

图 2 筋几何属性示意图Fig. 2 Schematic diagram of geometrical attribute of rib

图选项

1.3 筋的参数属性除几何属性外,筋特征的其他一些参数也是筋特征识别必不可少的,简称参数属性P_A。P_A主要包括筋条宽度Width、筋高Height、筋位置Location、刀轴参考方向ToolAxis和导动元DriveCell等,结构化表示为
〈P_A〉::=(〈Width〉,〈Height〉,〈Location〉,〈ToolAxis〉,〈DriveCell〉)
1.4 范式表达及层次模型设RF表示一个筋特征,结合筋的类型SubType、几何属性F_G和参数属性P_A等相关信息,RF的BNF表达式为
〈RF〉::=(〈SubType〉,〈ID〉,〈F_G〉,〈P_A〉,
[〈RF_f〉],{〈RF_c〉})
〈SubType〉::=(〈R_f〉〈R_d〉〈R_b〉)
〈F_G〉::=(〈F_m〉,[F_l],〈f_t〉,〈f_b〉,[F_r],
[F_a],〈F_s〉)
〈P_A〉::=(〈Width〉,〈Height〉,〈Location〉,
〈ToolAxis〉,〈DriveCell〉)
式中:ID 为当前节点的编号;RF_f为RF的父节点;RF_c为RF的子节点;R_f、R_d和R_b分别为平顶筋、斜顶筋和曲顶筋;F_m、F_l、F_r、F_a和F_s分别为f_m、f_l、f_r、f_a和f_s的集合。
为识别平顶筋和斜顶筋,将不同高度的广义腹板面构建平顶筋/腹板间的层间父子关系,平顶筋与关联的斜顶筋和曲顶筋间则构建层内的父子关系。平顶筋间的层间父子关系与平顶筋和斜顶筋间的层内父子关系是构成广义腹板特征树状结构的基础。图 3所示为某零件中广义腹板的层次模型,该图表达了广义腹板间的层次关系以及平顶筋与斜顶筋间的父子关系。

图 3 广义腹板树状模型Fig. 3 Tree-model of generalized bottom plane

图选项

图 3中,零件上的每一个正向可加工的水平面对应一个GFB,广义腹板从低到高排列构成广义腹板间的层间关系。对于筋类的GFB,根据其面的分支数可能被拆分为多个平顶筋,每个平顶筋最多关联2个斜顶筋;而腹板类GFB,则可能关联多个斜顶筋。
1.5 面的凹凸性为识别斜顶筋,对面的凹凸性进行定义与识别。由于筋特征中只有底圆面和过渡面需要判断其凹凸性,且这2种面一般为(近)圆柱面,本文仅讨论圆柱面的凹凸性。
对于圆柱面f,取其U、V向的中间参数线的交点作为面f的中心点p_c,p_c对应的原点为p_O,提取面f在p_c处的体外法向v_n。图 4所示为圆柱面的凹凸性。计算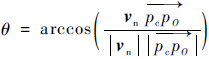，若0≤θ<90°,则f为凹圆柱面;否则,f为凸圆柱面。

图 4 圆柱面的凹凸性Fig. 4 Cylinder surface being convex or concave

图选项

2 筋的识别与构建2.1 广义腹板面的识别在给定加工坐标系下,水平面的正确识别是识别平顶筋的基础,平顶筋或腹板的底圆面是识别斜顶筋的基础。然而,由于模型重构、格式转换等常导致某些面丢失底层几何信息,因此,为保证能将所有水平面和圆柱面识别出来,本文采用面向精度要求的近二次规则面识别方法来识别近平面和近圆柱面。图 5为近二次规则面识别方法示意图。首先识别NURBS曲面类型中的近平面和圆柱面,然后根据平面法向与z轴的夹角提取出所有的水平面以及筋特征关联的底圆面和过渡面。具体如下:

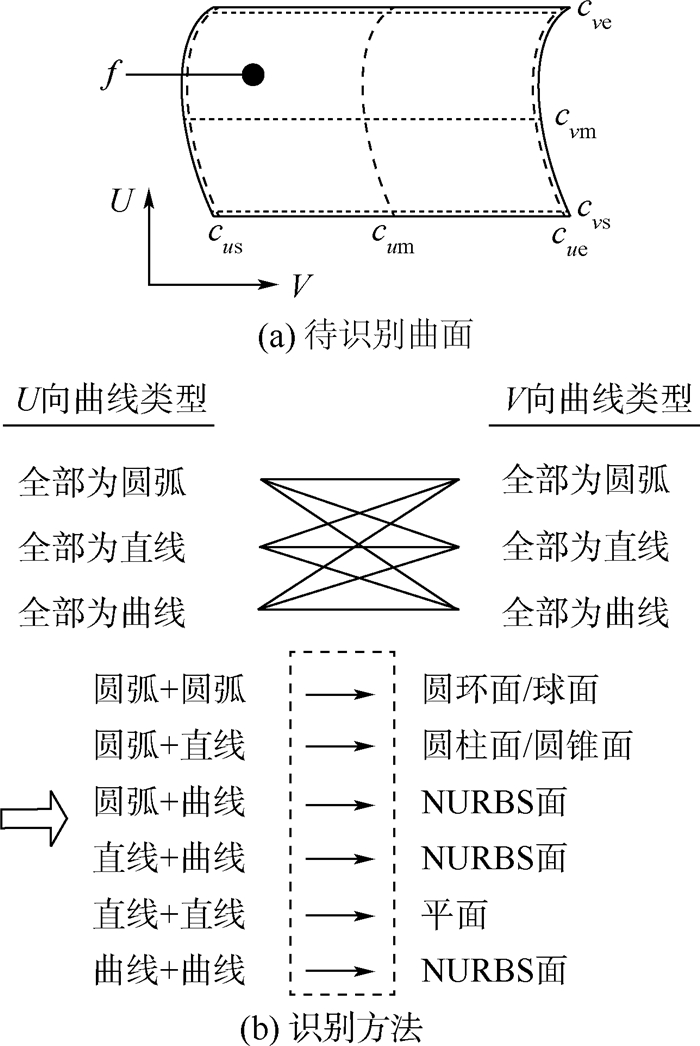图 5 近二次规则面识别方法示意图Fig. 5 Schematic diagram of recognition of approximate square regular surface

图选项

已知加工精度ε_m,面f为NURBS类型,其U向参数范围为[p_us,p_ue],V向参数范围为[p_vs,p_ve],分别在p_us、(p_us+p_ue)/2和p_ue处取U向参数线c_us、c_um和c_ue;类似地,分别在p_vs、(p_vs+p_ve)/2和p_ve处取V向参数线c_vs、c_vm和c_ve。建立以下近平面识别规则。
规则1 近平面识别。若c_us、c_um、c_ue、c_vs、c_vm和c_ve中至少5条参数线为直线,则f为近平面。
完成平面类型的识别后,进一步提取每个平面的体外法向N,设其与加工侧坐标系z轴的夹角为θ。若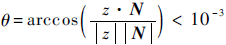,则该平面为正向水平面。
规则2 近圆柱面识别。如果f满足以下条件之一:
1) c_us、c_um和c_ue均为半径相同的圆弧,圆心两两互不重合,并且c_vs、c_vm和c_ve均为相互平行的直线。
2) c_vs、c_vm和c_ve均为半径相同的圆弧,圆心两两互不重合,并且c_us、c_um和c_ue均为相互平行的直线。
则f为近圆柱面。
完成圆柱面类型的识别后,进一步提取每个圆柱面的轴线,设其与加工侧坐标系z轴的夹角为θ。当θ=π/2时,利用圆柱面凹凸性判断方法,若圆柱面为凹,则为底圆面;若圆柱面为凸,则为过渡面。
2.2 广义腹板面的三角网格划分由于难以从面的几何/拓扑角度准确判断广义腹板面的类型,本文采用约束Delaunay三角剖分^[13]的方法从微观的角度对广义腹板面进行识别。首先,对多边形区域的边界进行离散,按照逐点插入算法进行约束Delaunay三角剖分;其次,根据剖分结果对平顶筋面和腹板面进行区分;最后,提取并修改平顶筋面的中轴线以便拆分平顶筋及构建后续的加工操作。
2.2.1 边界离散与区域三角剖分多边形区域边界的离散精度与剖分结果及剖分效率有着直接的关系。离散点越密,则剖分结果越接近多边形,但效率也越低;离散点过于稀疏,效率较高,但可能存在不理想的剖分结果。因此,平衡这两者间的关系对最终的平顶筋面和腹板面的识别至关重要。
对于某正向水平面f_h,设其边界点为{P_i},在当前坐标系下的坐标为(x_i,y_i),当长度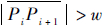(w为平顶筋的平均宽度,可根据经验预设定),则加密点{P_k},有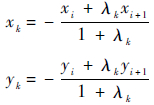

式中: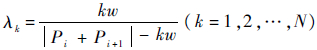，N为需要加密的点的个数。
进一步判断加密后的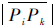和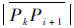,直到相邻加密点间的距离小于w。图 6所示为平顶筋面和腹板面边界的离散点加密后的状态。

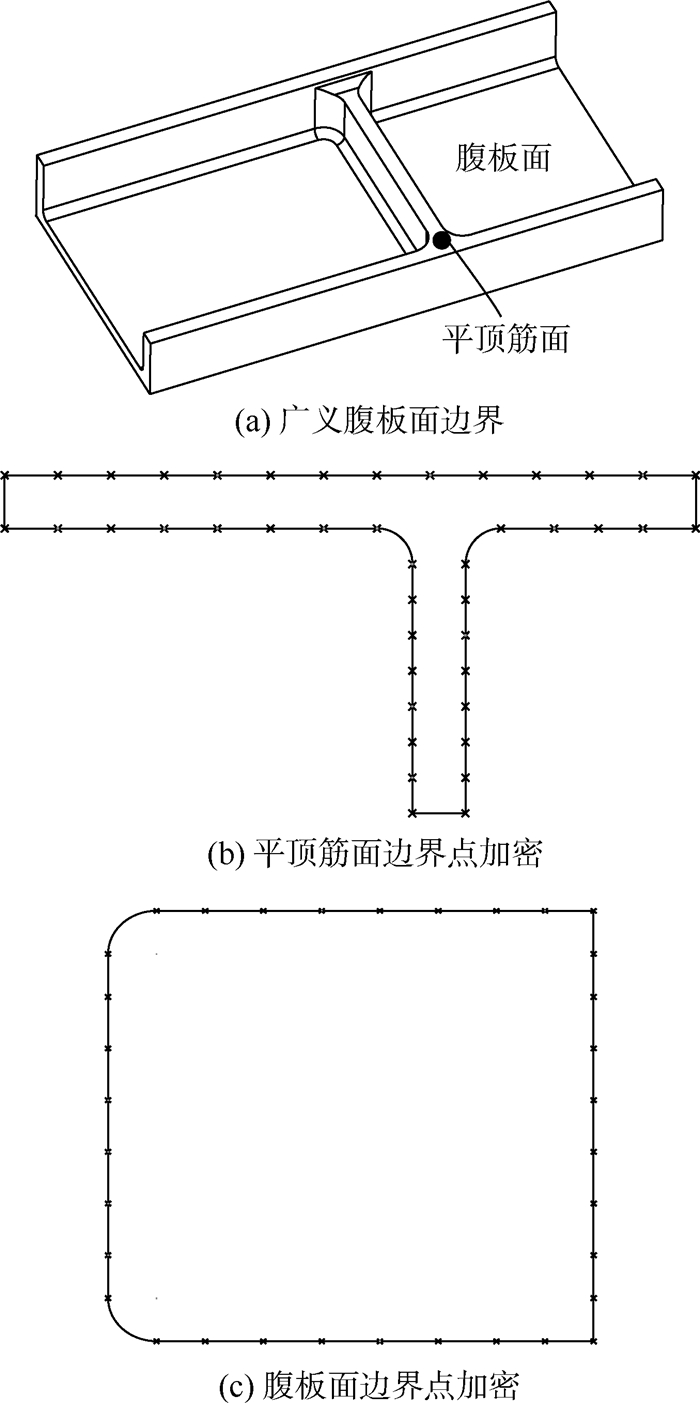图 6 广义腹板面边界点的离散点加密Fig. 6 Making dense discrete points of generalized bottom planes boundary points

图选项

得到加密点后,利用插入算法^[14]将待剖分区域进行Delaunay三角剖分。提取每个三角形的重心:P((x1+x2+x3)/3,(y1+y2+y3)/3),判断P是否在多边形内,将重心不在多边形内的三角形剔除。最终得到边界约束的Delaunay三角剖分结果,剖分后的三角形单元简称三角元。
2.2.2 平顶筋面和腹板面的区分当待剖分的水平面为平顶筋面时,每个三角元大小相似且边长不超过2w;而当待剖分的水平面为腹板面时,存在一些狭长的三角元,至少有一条边的长度远大于w。据此,可区分平顶筋面和腹板面。
定义2 设加工坐标系下的一个正向水平面为f_h,Delaunay(f_h)表示对f_h执行约束Delaunay三角剖分,{Δ_i}(i=1,2,…,n)为剖分后得到的三角形集,若Δ_i的每条边的长度均小于1.5w,则Δ_i称为规范三角形;若Δ_i中至少2条边的长度大于1.5w,则Δ_i称为异常三角形。
根据定义2可区分平顶筋面和腹板面。
规则3 平顶筋面和腹板面的区分。设{Δ_i}(i=1,2,…,n)为水平面f_h执行Delaunay(f_h)后得到的三角形集,{Δ_j}(j=0,1,…,k,k≤n)为{Δ_i}中的异常三角形集合。若k＞[n/3]+1,则f_h为腹板面;否则,f_h为平顶筋面。
图 7所示为广义腹板面的约束Delaunay三角剖分。图 7(a)中有三角元34个,其中规范三角形0个,异常三角形28个,则该面为腹板面;图 7(b)中有三角元41个,其中规范三角形38个,异常三角形3个,则该面为平顶筋面。

图 7 广义腹板面的约束Delaunay三角剖分Fig. 7 Constrained Delaunay triangulation of generalized bottom plane

图选项

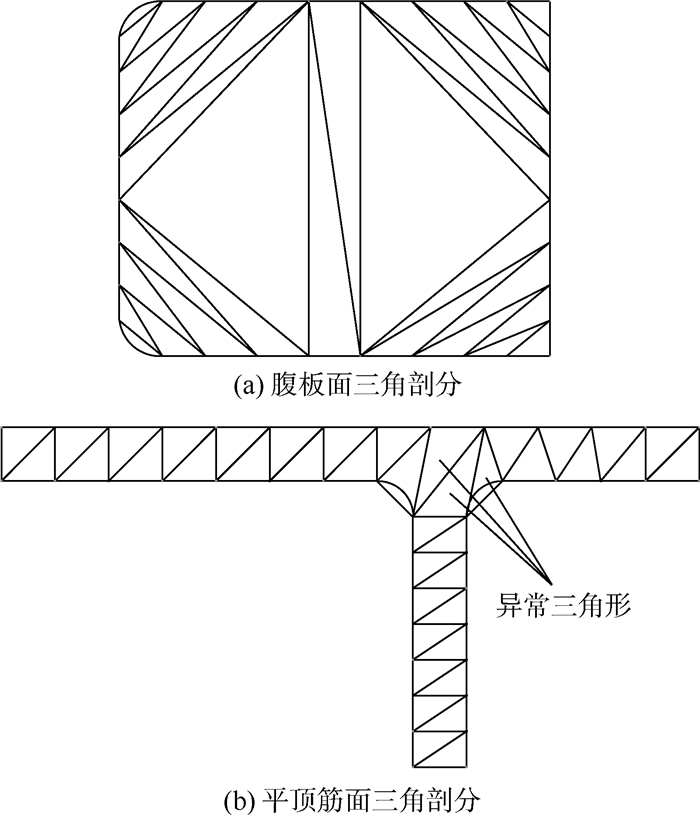
2.2.3 平顶筋面中轴线提取当识别的水平面为平顶筋面时,为拆分平顶筋面以进一步识别斜顶筋及构建后续的加工操作,需提取其中轴线作为导动元。中轴线的提取可利用Delaunay三角剖分的结果来进行。根据每个三角元与其所邻接三角元的关系进行分类^[15]:只有一边有邻接三角形的为边界三角形,表示为Δ_e,两边有邻接三角形的为中间三角形,表示为Δ_m,三边有邻接三角形的为内部三角形,表示为Δ_i。
图 8所示为三角元的分类及其中轴线。由图 8(a)可知,Δ_e存在于平顶筋面分支的出入口处;Δ_i存在于分支交叉口处;而Δ_m则在分支出入口与交叉口的中间过渡部位,且其数量最多。平顶筋面中轴线的提取可通过连接3种三角形中轴线的方式获得。本文将三角形上属于多边形边界的边称为界边,两邻接三角形的公共边称为邻边。因此,Δ_e由2条界边和1条邻边组成,其中轴线为邻边中点与两界边交点的连线;Δ_m由1条界边和2条邻边组成,其中轴线为两邻边中点的连线;Δ_i由3条邻边组成,其中轴线为其重心与3条邻边中点的连线。图 8(b)所示为3类三角形中轴线的分类及连接方式。

图 8 三角元的分类及其中轴线Fig. 8 Classification of triangular elements and their medial axis

图选项

2.2.4 中轴线的合并与修改将所有三角形的中轴线连接可得到平顶筋面的中轴线网络。每条中轴线的搜索开始于Δ_e,依次由Δ_m的中轴线连接,结束于Δ_i或Δ_e。平顶筋面中轴线的条数可由Δ_e和Δ_i的个数得出。设某一平顶筋面f进行约束Delaunay三角剖分后,得到n个Δ_e,m个Δ_i,则f中的中轴线有(3m+n)/2条。图 9所示为中轴线的处理。从图 9中可看出,平顶筋面分支的出入口和交叉口处的中轴线不够光顺,其作为加工操作的导动元将使得刀具频繁摆动。因此,本文在中轴线合并后拟采用样条线方式对中轴线经过的点进行拟合。

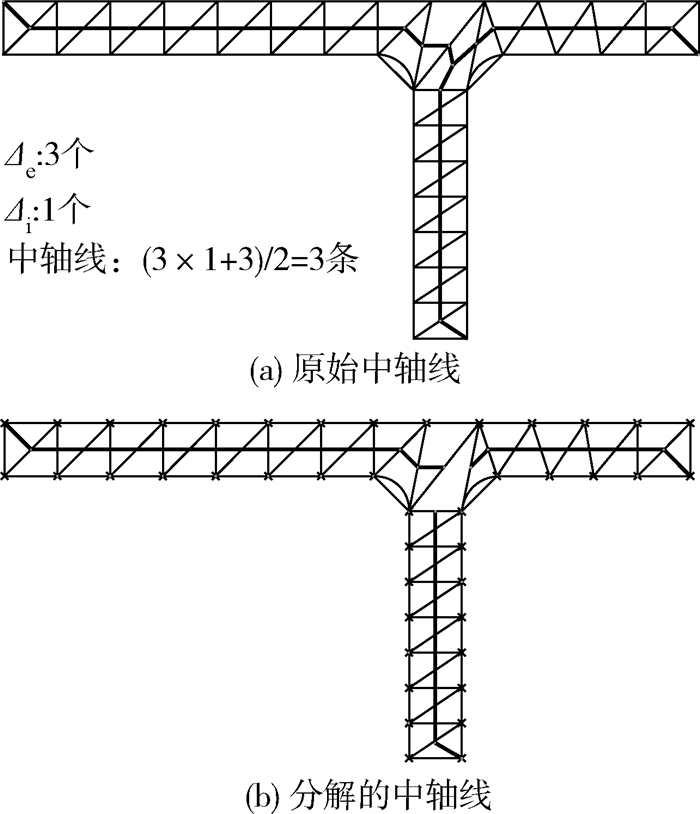图 9 中轴线的处理Fig. 9 Processing of medial axis

图选项

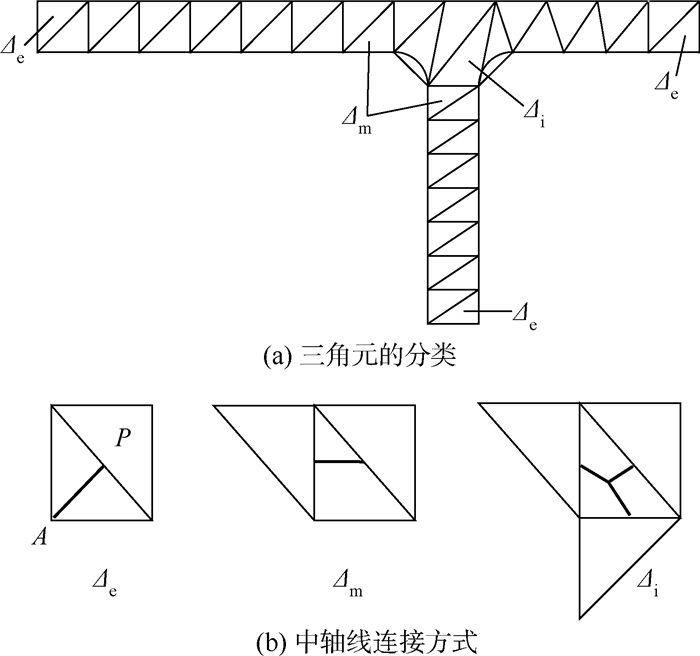
将所有中轴线在Δ_i的重心处断开使其成为独立的线段,如图 9(b)所示。根据该内部三角形所邻接的三角形类型,其组合的类型可能为Δ_i & Δ_i、Δ_i & Δ_m和Δ_i & Δ_e。不同的组合类型,需采取不同的合并规则。
图 10所示为内部三角形与邻接三角形的组合类型。Δ_i & Δ_i型组合的中轴线仅为1个点,一般存在于十字交叉口处,如图 10(a)所示,该中轴线可直接删除;Δ_i & Δ_e型组合的中轴线为1条短线段,一般存在于边界的突起处,如图 10(b)所示,也可直接删除;Δ_i & Δ_m型组合的中轴线(见图 10(c))最为常见,本文主要对这种组合类型的中轴线进行合并与修改。

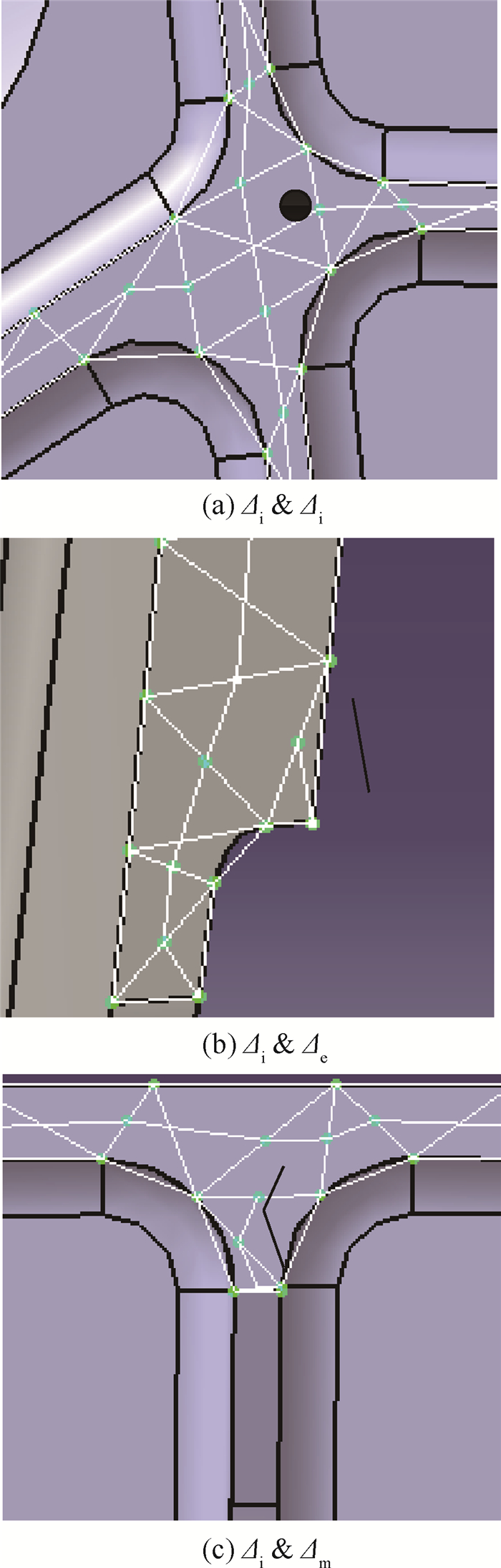图 10 内部三角形与邻接三角形的组合类型Fig. 10 Composite type of inner triangles and their adjacent triangles

图选项

在对中轴线进行合并前,需先对其进行有效性判断。如图 10(c)所示,Δ_i & Δ_m型组合的中轴线只关联2个三角形,其长度小于刀具的直径,加工时无需单独在此处补一刀,该中轴线也可以直接删除。因此,可根据中轴线所关联的三角形的个数及其长度来判断该中轴线是否需要合并。
规则4 中轴线的合并。设某一平顶筋面f进行约束Delaunay三角剖分后,∃{Δ_ii}n i=1,(n≥1),对Δ_ii,其所关联的中轴线为{S_ij}m j=1,(m=3),若S_ij在Δ_ii处的邻接三角形为Δ_i或Δ_e,则删除S_ij;否则,保留S_ij,并取沿其曲线内部走向的切矢V_ij,对于Δ_ii关联的任意2条中轴线S_ij、S_ik(1≤j,k≤3),其关联的切矢V_ij与V_ik间的最大夹角θ_ijk=Max(〈V_ij,V_ik〉),若θ_ijk≥θ_m(θ_m为夹角合并阈值,最大取θ_m=π),则中轴线S_ij和S_ik可合并。
图 11所示为中轴线的合并。图 11中的T形平顶筋面经约束Delaunay三角网格剖分后,其中轴线(图 11中点划线所示)在Δ_i的重心处断开,利用规则4可知,S_i1、S_i2间的夹角最大,因此S_i1、S_i2可合并。提取满足合并条件的中轴线上的点,将这些点拟合成光顺的曲线段,则该曲线段可用于构建后续加工操作的导动元。

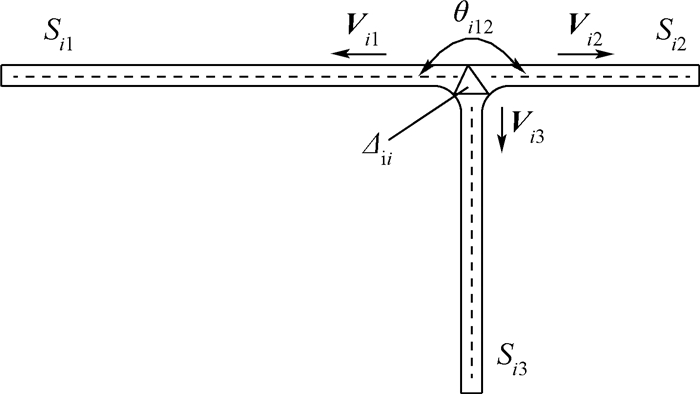图 11 中轴线的合并Fig. 11 Combination of medial axes

图选项

2.3 广义腹板面子特征识别与构建从筋的表示模型可知,每张水平面可构建一广义腹板特征,而斜顶筋一般作为广义腹板的子特征。为了构建每层广义腹板的层次模型,需对广义腹板关联的子特征进行识别与构建。由于腹板面子特征的构建原理与平顶筋面子特征的构建原理相同,在此仅以平顶筋面子特征的识别与构建为例阐述本文方法。
2.3.1 平顶筋面拆分子特征的构建一张平顶筋面经三角剖分及中轴线合并后,可能存在多条有效的中轴线。每条中轴线将对应一个加工操作步。因此,对每条中轴线构建一子特征以方便后续加工操作的自动生成。平顶筋拆分子特征的流程如图 12所示。

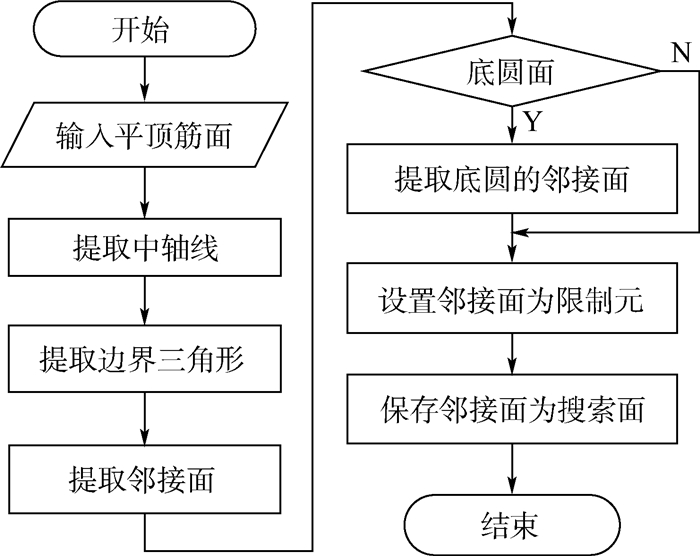图 12 平顶筋拆分子特征流程Fig. 12 Flowchart of flat rib division into sub-features

图选项

Step 1 提取当前平顶筋面的中轴线,构造拆分特征节点,设置其节点类型为平顶筋。
Step 2 提取每条中轴线首末端的Δ_e。
Step 3 提取每个Δ_e的界边。
Step 4 判断界边的邻接面是否为底圆面类型,若是则设置为当前子特征的底圆面,否则转入Step 6。
Step 5 提取与该子特征底圆面相切的邻接面。
Step 6 设置邻接面为当前子特征的限制元并保存邻接面,以作为子特征关联斜顶筋的搜索面。
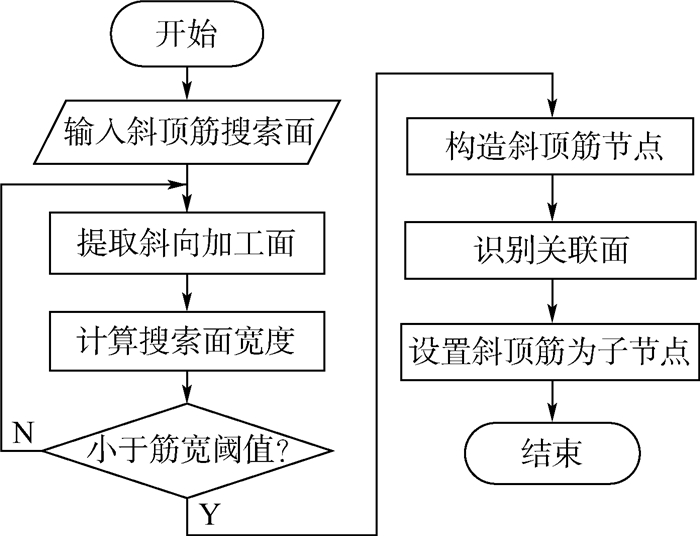
2.3.2 平顶筋关联斜顶筋的识别与构建从构成斜顶筋的拓扑面及其邻接的拓扑面来看,斜顶筋一般生长于广义腹板上且通过底圆面或过渡面与广义腹板相连。因此,可通过广义腹板面的关联面提取斜顶筋面,进而识别并构建相应的斜顶筋特征。图 13是平顶筋关联斜顶筋的识别与构建流程。

图 13 平顶筋关联斜顶筋的识别与构建流程Fig. 13 Flowchart of recognition and construction for declining rib connected with flat rib

图选项

Step 1 获取平顶筋面的斜顶筋搜索面。
Step 2 判断每个搜索面的加工面类型,提取其中的斜向加工面。
Step 3 计算搜索面的主面宽度,若符合设定的筋宽阈值,则继续提取其可能关联的圆柱面作为斜顶筋的过渡面或底圆面,否则返回Step 2。
Step 4 构造斜顶筋节点,并根据主面的几何类型设置当前斜顶筋的类型(斜顶筋或曲顶筋)。
Step 5 根据主面或底圆面,提取其关联的侧壁面作为限制面。
Step 6 设置当前斜顶筋节点为相应平顶筋面拆分特征的子节点,算法结束。
3 实 例该算法已在CATIA V5平台上实现,并集成在“飞机复杂结构件快速数控编程系统”中,应用于实际生产。本文给出2个典型零件对算法的有效性和时效性进行分析和验证。
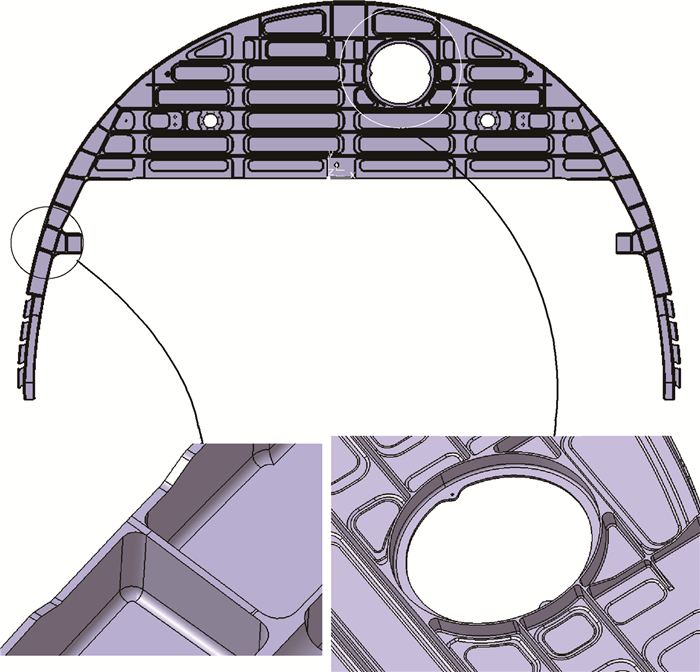
3.1 有效性分析图 14所示框类零件尺寸为3 505 mm×2 130 mm×65 mm,其筋特征数量多,具有典型性和代表性。经统计,该零件共有广义腹板197个,其中腹板面118个,平顶筋面79个。平顶筋面共有146个平顶筋,所有平顶筋关联107个斜顶筋,识别结果如表 1所示。

图 14 零件模型Fig. 14 Part model

图选项

表 1 广义腹板识别结果统计Table 1 Results of generalized bottom plane recognition

特征类型	广义腹板	腹板面	平顶筋面	平顶筋	斜顶筋
正确	197	118	79	146	107
错误	0	0	2	0	16
正确率/%	100	100	97.5	100	87

表选项


由表 1可知,该测试实例有多个斜顶筋未识别出来。进一步分析,该类斜顶筋未直接生长于任何广义腹板上,因此无法被广义腹板关联到。由于此类斜顶筋一般通过竖直侧壁与广义腹板过渡,而本文算法建立在广义腹板面识别的基础上,因此该算法适用于直接与广义腹板相连的斜顶筋的识别。在此,仅简单给出斜顶筋识别算法的改进方法:设加工方向(一般为加工坐标系z轴正向)为r,面s为搜索面,s内某点处的体外法向为n,r与n的夹角为θ,a为垂直于r的平面,a与s的交线长度为d,斜顶筋特征的宽度范围为[d_min,d_max],斜顶筋满足如下条件:
1) 0° < θ<90°。
2) d∈[d_min,d_max]。
此外,从表 1中可看出平顶筋面存在2个识别错误,这是由模型存在细碎曲面片产生的,可通过碎面处理(碎面提取和拼合)的方法修正。碎面产生的原因及处理的具体算法本文不在此讨论。
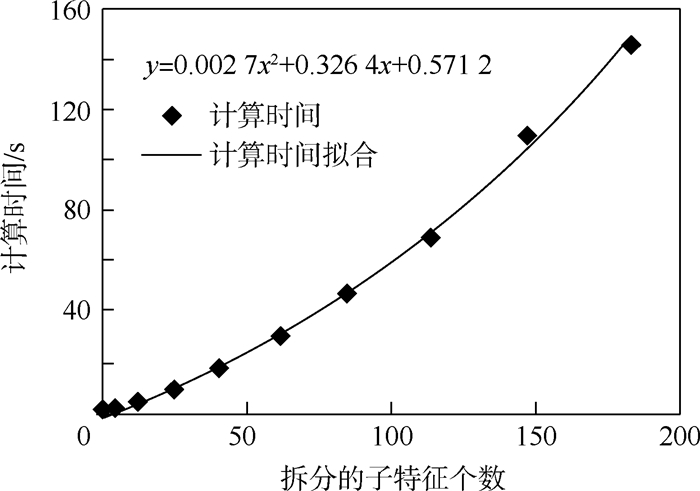
3.2 时效性分析为计算本文所提出筋特征识别与构建算法的时效性,构建了n×n(n≤10)个槽结构的零件模型,图 15所示为时间复杂度测试零件。图 15中只有一个水平面为平顶筋面,拆分成若干个子特征,筋的宽度为3 mm。算法中给定的筋宽阈值为5,程序对该平顶筋面进行约束Delaunay三角剖分所花时间与该零件槽个数、中轴线条数等相关数据的关系如表 2所示。表中:L为布局;N_s为面总数;N_p为槽总数;N_r为平顶筋拆分总数;N_m为合并后中轴线条数;T为计算时间。算法时间复杂度函数为
y=0.002 7x²+0.326 4x+0.571 2
式中:y为计算时间;x为拆分的子特征个数。二次多项式拟合曲线如图 16所示。

图 15 时间复杂度测试零件Fig. 15 Part model for time complexity test

图选项

表 2 平顶筋识别结果与程序运行时间统计Table 2 Results of flat rib recognition and runtime of program

L	Ns	Np	Nr	Nm	T/s
1×1	23	2	1	1	1.577
2×2	74	5	5	3	2.798
3×3	159	10	13	5	5.187
4×4	278	17	25	7	9.988
5×5	431	26	41	9	17.463
6×6	618	37	61	11	30.965
7×7	839	50	85	13	47.206
8×8	1 094	65	113	15	69.861
9×9	1 383	82	145	17	110.214
10×10	1 706	101	181	19	146.195

表选项

图 16 时间复杂度Fig. 16 Time complexity

图选项

由此可知,在给定的剖分系数下,本文的识别算法在几十秒内便可识别出所有的平顶筋子特征,并将中轴线合并。因此,本文的算法正确且效率较高。
4 结 论为识别飞机结构件中广泛存在的筋特征以实现筋加工的自动数控编程,本文提出基于约束Delaunay三角剖分的筋特征识别与构建算法,其实现的主要步骤如下:
1) 提出了广义腹板模型并给出筋的表示模型,依据相关规则对广义腹板进行识别。
2) 利用约束Delaunay三角剖分对广义腹板进行三角剖分,以进一步识别平顶筋面并提取平顶筋面的中轴线。
3) 根据中轴线条数对平顶筋面进行拆分并识别关联的斜顶筋,构建平顶筋拆分子特征和斜顶筋特征,实现零件中筋特征的层次模型表达。
经大量实例测试表明,该算法能正确且快速地识别出飞机结构件中的筋特征,并能直接映射到后续的加工操作中,实现筋特征的自动数控编程。
参考文献

[1]	谭丰.飞机结构件筋特征快速数控编程技术研究与实现[D].南京:南京航空航天大学,2010:1,9-25. TAN F.Research and implementation on rapid NC programing technology of aircraft structural parts rib feature[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:1,9-25(in Chinese).
	Cited By in Cnki (2)
[2]	LI Y G,DING Y F,MOU W P,et al.Feature recognition technology for aircraft structural parts based on a holistic attribute adjacency graph[J].Proceedings of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture,2010,224(2):271-278.
	Click to display the text
[3]	高曙明.自动特征识别技术综述[J].计算机学报,1998,21(3):281-288. GAO S M.A survey of automatic feature recognition[J].Chinese Journal of Computers,1998,21(3):281-288(in Chinese).
	Cited By in Cnki (253)
[4]	GAO S,SHAH J J.Automatic recognition of interacting machining features based on minimal condition sub-graph[J].Computer-Aided Design,1998,30(9):727-739.
	Click to display the text
[5]	MARCHETTA M G,FORRADELLAS R Q.An artificial intelligence planning approach to manufacturing feature recognition[J].Computer-Aided Design,2010,42(3):248-256.
	Click to display the text
[6]	WOO Y,SAKURAI H.Recognition of maximal features by volume decomposition[J].Computer-Aided Design,2002,34(3):195-207.
	Click to display the text
[7]	SUNIL V B,AGARWAL R,PANDE S S.An approach to recognize interacting features from B-Rep CAD models of prismatic machined parts using a hybrid (graph and rule based) technique[J].Computers in Industry,2010,61(7):686-701.
	Click to display the text
[8]	BABIC B,NESIC N,MILJKOVIC Z.A review of automated feature recognition with rule-based pattern recognition[J].Computers in Industry,2008,59(4):321-337.
	Click to display the text
[9]	施建飞,李迎光,刘旭,等.基于属性边点图的飞机结构件筋特征识别方法[J].计算机集成制造系统,2014,20(3):521-529. SHI J F,LI Y G,LIU X,et al.Rib feature recognition method for aircraft structural parts based on vertex attributed adjacency graph[J].Computer Integrated Manufacturing Systems,2014,20(3):521-529(in Chinese).
	Cited By in Cnki
[10]	闫海兵.飞机结构件复杂加工特征识别技术的研究与实现[D].南京:南京航空航天大学,2010:10-18. YAN H B.Research and implementation of complicated machining features recognition technology for the aircraft structural parts[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:10-18(in Chinese).
	Cited By in Cnki (15) | Click to display the text
[11]	YU F F,DU B R,REN W J,et al.Slicing recognition of aircraft integral panel generalized pocket[J].Chinese Journal of Aeronautics,2008,21(6):585-592.
	Click to display the text
[12]	于芳芳.飞机整体壁板快速数控加工编程系统关键技术研究与开发[D].北京:北京航空航天大学,2008:35-38. YU F F.Research and development of rapid NC machining programming system for aircraft integral panel[D].Beijing:Beihang University,2008:35-38(in Chinese).
	Cited By in Cnki (6)
[13]	刘少华,程朋根,史文中.约束 Delaunay 三角网生成算法研究[J].测绘通报,2004(3):4-7. LIU S H,CHENG P G,SHI W Z.Algorithm study of the constrained Delaunay triangulation generation[J].Bulletin of Surveying and Mapping,2004(3):4-7(in Chinese).
	Cited By in Cnki (65)
[14]	蒲浩,宋占峰,詹振炎.基于约束Delaunay三角剖分的道路三维建模方法[J].华中科技大学学报(自然科学版),2005,33(6):111-113. PU H,SONG Z F,ZHAN Z Y.3D-modelling for roads based on constrained Delaunay triangulation[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2005,33(6):111-113(in Chinese).
	Cited By in Cnki (30)
[15]	艾廷华,郭仁忠.基于约束Delaunay结构的街道中轴线提取及网络模型建立[J].测绘学报,2000,29(4):348-354. AI T H,GUO R Z.Extracting center-lines and building street network based on constrained Delaunay triangulation[J].Acta Geodaetica et Cartographica Sinica,2000,29(4):348-354(in Chinese).
	Cited By in Cnki (61)