四旋翼飞行器是一种欠驱动系统,具有4个控制输入和6个自由度,它是一种静不稳定系统,需要实时对系统控制才能保证飞行器的稳定^[1].四旋翼飞行器具有4个独立的电机分别驱动,可以在差动力矩的作用下,实现俯仰和滚转运动,偏航运动由两组旋翼产生的反扭力矩之差实现,总升力为4个旋翼产生的升力之和.文献^{[2, 3, 4, 5, 6]}分别基于PID、H_∞、模糊控制、LQ控制、回路成型理论设计四旋翼飞行器的控制器,文献^{[7, 8]}针对四旋翼飞行器的非线性模型研究了基于反馈线性化的控制问题,而反馈线性化是建立在系统精确建模的基础之上的,系统建模误差对控制效果影响较大.文献^{[9, 10]}研究反步法控制问题,反步法同样需要建立精确的系统模型,并且抗干扰能力较弱.文献^[11]研究了基于动态面的四旋翼控制方法,该方法可有效降低反步控制中的导数爆炸问题,但仍然无法从根本上解决反步控制对精确系统模型的依赖问题.文献^{[12, 13]}研究了欠驱动滑模控制问题,滑模控制具有较好的鲁棒性,但是由于这类算法并未对系统干扰进行实时估计,当干扰较大时,其控制效果并不理想.可见上述控制方法对控制对象的参数变化及外界干扰较为敏感且都未实现其各个控制通道的解耦.文献^{[14, 15]}利用自抗扰控制实现了四旋翼飞行器的姿态解耦控制,但是并未深入研究飞行器的轨迹跟踪问题,并且对自抗扰控制的参数优化并未做深入的研究和分析.本文针对欠驱动四旋翼飞行器的控制特性,设计一种基于自抗扰控制的四旋翼飞行器姿态解耦控制算法.可以实现对四旋翼飞行器姿态控制系统的动态解耦线性化,本文利用ESO实现系统对总扰的实时估计,最后实现对系统耦合项及干扰的实时补偿,仿真结果表明系统解耦效果优良,并在姿态解耦的基础之上研究飞行器的鲁棒轨迹跟踪问题.由于自抗扰解耦控制算法中参数较多,本文利用粒子群优化算法对参数进行整定.1 Quadrotor UAV模型选用机体坐标系描述飞行器的运动,坐标原点和机体重心重合,系统示意图如图 1所示.

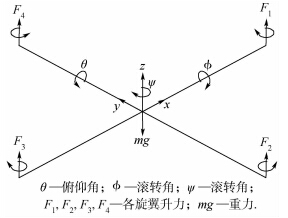
图 1 欠驱动四旋翼UAV飞行原理Fig. 1 Flying principle of underactuated quadrotor UAV

图选项

假设飞行器重心为载体系原点,电机升力面和重心位于同一个平面上,得到系统的数学模型^[16]为

式中:ξ,v∈R分别代表地面坐标系下载体的位置和速度;e₃=^{[0, 0, 1]T};R为机体坐标系到地面坐标系的转换矩阵;F为除重力以外作用于飞行器机体上的合外力向量;η=[φθψ]^T为飞行器载体的欧拉角;ω为载体坐标下的角速度;W(η)为绕机体轴的三轴角速度到欧拉角速率的转换矩阵;J为飞行器的惯性矩阵;τ为飞行器的控制力矩,定义系统输入如下:
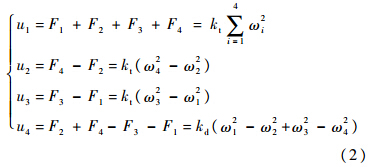
式中:k_t为升力系数;k_d为拖拉系数;ω_i(i=1,2,3,4)为各旋翼转速;u₁为高度控制输入;u₂为滚转控制输入;u₃为俯仰控制输入;u₄为偏航控制输入.将式(1)展开得到的四旋翼飞行器的数学模型^[17]:
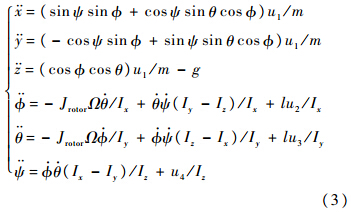
式中:Ω=ω₂+ω₄－ω₁－ωsub>3;J_rotor为电机的转动惯量;I_x、I_y和I_z为轴向惯性主矩;l为旋翼中心到机体重心的距离.定义四旋翼飞行器的系统状态变量如下:
式中:状态量x和y属于间接驱动状态;状态量θ、φ、ψ和z属于直接驱动状态,轨迹控制结构如图 2所示.

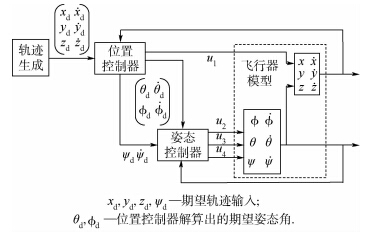图 2 四旋翼轨迹控制系统结构图Fig. 2 Structure diagram of quadrotor aircraft

图选项

2 自抗扰控制系统结构自抗扰控制(Active Disturbance Rejection Control,ADRC)首先由中国科学院系统科学研究所韩京清研究员提出^[18],该方法利用扩张观测器实现系统扩张状态的估计,它不依赖系统模型并具有很强的鲁棒性,二阶自抗扰控制的基本结构如图 3所示^[19].

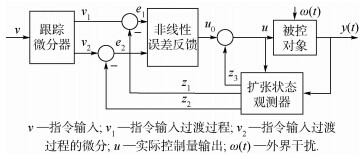图 3 自抗扰控制结构图Fig. 3 Structure diagram of active disturbance

图选项

3 姿态控制系统自抗扰解耦控制从式(3)可看出,四旋翼飞行器是一个具有6自由度和4个控制输入的欠驱动系统,姿态控制是整个飞行控制的关键和基础,由于四旋翼飞行器的位置控制是以由姿态控制为基础的,因此精确地控制飞行器姿态,就可以实现对飞行器位置和速度的高精度控制.本文设计一种基于ADRC控制的四旋翼解耦控制系统.四旋翼姿态子系统方程如下^[20]:
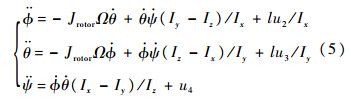
将式(5)进行整理得
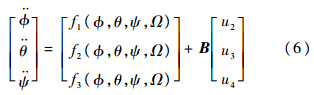
式中：
可见式(5)是一个MIMO(Multiple-Input Multiple-Output)非线性耦合系统,定义b₁=l/I_x;b₂=l/I_y;b₃=1.f_i(i=1,2,3)为系统的动态耦合部分,本文采用自抗扰控制中的扩张状态观测器(Extended State Observer,ESO)对动态耦合部分进行快速跟踪和估计,并在控制律中对动态耦合部分进行实时补偿,然后对控制律进行相应修正,则可将MIMO非线性系统转换成相互独立的SISO(Single-Input Single-Output)线性子系统,也可称为动态补偿线性化.四旋翼解耦结构图如图 4所示.

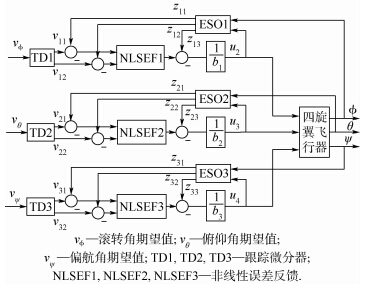图 4 四旋翼飞行器姿态解耦控制结构图Fig. 4 Structure diagram of quadrotor aircraft attitude decoupling control

图选项

下面以滚转角φ为例,来详细说明欠驱动四旋翼解耦抗干扰控制.自抗扰解耦控制包括3个主要部分.3.1 安排过渡过程传统的微分器会产生噪声放大效应,以至于无法利用,ADRC采用两个惯性环节输出之差来实现微分功能,可有效解决噪声放大效应,二阶积分器串联型系统的最速反馈闭环系统为
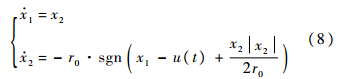
式中:r₀为速度因子；变量x₁(t)将在加速度r₀的限制下最快地跟踪输入信号u(t)；x₂(t)是x₁的微分,由于函数sgn()会导致系统进入稳态时会发生颤振.为避免系统颤振现象的发生,采用非线性函数fhan()替代,则离散最速反馈系统为式(9).滚转角跟踪微分器输出为
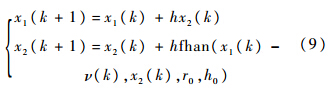
式中：
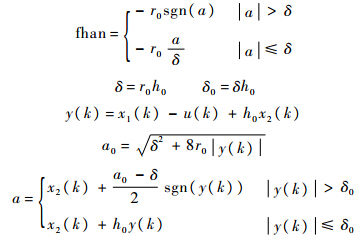
其中：h为积分步长;h₀为滤波因子^[21].3.2 基于ESO的动态补偿线性化将四旋翼飞行器的滚转角φ方程写成如下形式:
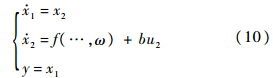
式中：x₁=φ;x₂=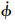;b=l/I_x;ω为外界干扰;f(…,ω)为各种扰动作用(包括建模、未建模动态和外扰)的总和.总扰动a=f(…,ω),当作未知的被扩张状态变量,即x₃=a,那么式(10)变成如下线性系统: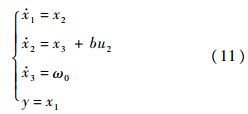
然后对上述系统建立非线性扩张状态观测器:
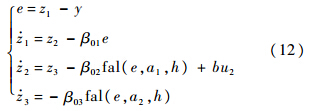
式中：
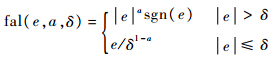
选择适当的参数β₀₁、β₀₂、β₀₃和a_i(i=1,2)，则非线性扩张状态观测器状态变量z_i能很好地跟踪原系统各状态变量x_i.其中z₃→x₃=f(…,ω),尽管f(·)和ω都未知,但扩张状态z₃仍可以很好地估计出系统总扰动a^[22].四旋翼飞行器俯仰角θ和偏航角ψ采用相同的算法处理,实现各个通道的动态补偿线性化.3.3 四旋翼飞行器的非线性误差反馈大量研究表明采用适当的非线性误差组合控制效果优于线性组合.本文中采用如下形式的非线性反馈形式:
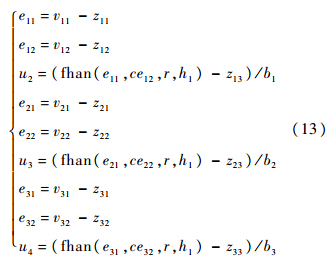
式中：r为控制量增益;c为阻尼系数;h₁为精度因子.4 自抗扰解耦控制参数的PSO优化从上述分析可以看出,四旋翼ADRC解耦控制算法中需要设定的参数较多,其参数的选取对控制性能影响较大,安排过渡过程中的参数包括速度因子r₀和滤波因子h₀.扩张状态观测器共有a₁、a₂、δ、β₀₁、β₀₂和β₀₃6个参数.NLSEF中参数包括控制量增益r、阻尼系数c、精度因子h₁.在上述参数中,r₀是根据过渡过程快慢的需要来决定的,r₀和h₀应根据实际情况协调选择.a₁一般取0.5,a₂=0.25,以便于系统实现.δ为fal函数的线性区间宽度,实际系统一般取为0.01左右.β₀₁、β₀₂和β₀₃并不因控制对象的而改变^[23].本文利用粒子群优化(Particle Swarm Optimization,PSO)算法对r、c和h₁ 3个参数进行优化组合,以实现最优控制.4.1 适应度函数的构造适应度函数构造合理与否直接关系到PSO算法搜索的全局最优值是否能到达控制系统的最优,根据四旋翼飞行器控制系统的特性和性能要求来确定适应度函数.本文构造的适宜度函数如下:
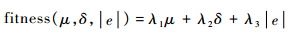
式中：μ为上升时间;δ为超调量;|e|为指令和反馈误差绝对值的和;λ_i(i=1,2,3)为权值,根据各个指标的大小及重要性进行调整.4.2 PSO优化算法计算过程下面利用PSO算法实现四旋翼自抗扰解耦控制的参数优化,参数自寻优算法如下.第1步 随机产生三维粒子.第2步 将产生的三维粒子作为系统参数代入到四旋翼自抗扰解耦控制算法中,计算适应度函数值.第3步 将上一步计算得到的适应度值和粒子个体最优值P_i的适应度函数值比较,如果优于P_i则更新个体最优值P_i.第4步 将上一步得到的个体最优适应度值P_i和粒子全局最优值P_g进行比较,优于P_g则更新P_g.第5步 更新粒子的位置和速度.第6步 是否超过迭代次数,没有则返回第2步,超过则停止迭代.5 算法仿真及实验为验证解耦及抗干扰效果,设定四旋翼飞行器姿态初始值为(φ,θ,ψ)=(0°,0°,0°).当t=1 s时,φ_d=10°;当t=3 s时,θ_d=9.5°;当t=5 s时,ψ_d=sin(t)(单位：(°));当5 s＜t＜7 s时施加5sin(t)的系统总扰.四旋翼自抗扰解耦PSO参数优化:PSO粒子数为50,迭代次数为100,粒子维度为3,对于自抗扰解耦控制的3个参数范围为:r∈(10,1 000),c∈(0.5,50),h₁∈(0.000 01,0.01).上升时间μ权重λ₁=1,超调量δ权重λ₂=700,指令和反馈误差绝对值的和|e|权重λ₃=100.最后,在本文姿态解耦算法的基础上对飞行器的轨迹跟踪进行仿真研究,姿态控制系统是四旋翼飞行器轨迹控制的核心,外环轨迹控制算法采用PD实现,期望轨迹分别为矩形和圆形.矩形轨迹为边长为10 m的正方形,圆形轨迹半径为10 m,高度均为20 m.图 5为四旋翼飞行器姿态解耦控制仿真曲线,从图中可以看出,在当t=1 s时,滚转角指令φ_d=10°,俯仰角几乎保持为零,同样当t=3 s时,俯仰角指令θ_d=9.5°,滚转角并未受到其耦合作用的影响,仍然保持为10°.

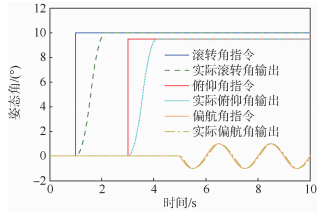图 5 四旋翼UAV自抗扰解耦控制姿态跟踪Fig. 5 Attitude tracking of quadrotor UAV active disturbance decoupling control based on ADRC

图选项

图 6为图 5的局部放大图,从图中可以看出,在t=3 s时刻,由于俯仰角的变化,滚转角有轻微震荡,在5 s＜t＜7 s时段,由于系统总扰的作用,俯仰角也有很小量的变化.可以看出本文算法将通道间耦合及外部干扰进行了有效抑制,其影响几乎可以忽略.

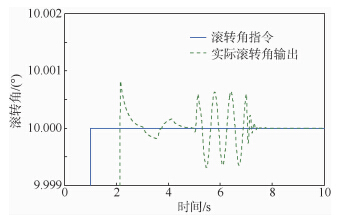图 6 滚转角跟踪局部放大曲线Fig. 6 Local amplification curve of roll angle tracking

图选项

图 7为滚转角通道中总扰动的ESO估计,在t=3 s，由于θ_d=9.5°,通道间出现较大耦合项.在5 s＜t＜7 s时间段为系统总扰估计.

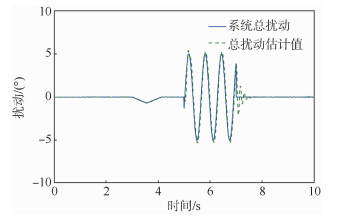图 7 系统总扰动的ESO估计曲线Fig. 7 Estimation curve of total system disturbance by ESO

图选项

图 8为文献^[9]的四旋翼飞行器姿态反步控制算法,在t=5 s时刻,俯仰角明显受到滚转角耦合作用的影响,产生振荡.在t=15 s时,滚转角也受到俯仰角的耦合作用影响,产生明显的波动.在25 s＜t＜35 s时间段,由于外部干扰的存在,滚转角和俯仰角都发生了明显的振荡.

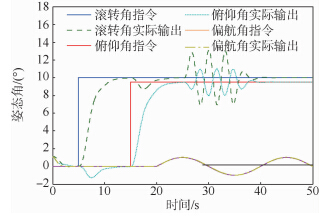图 8 四旋翼飞行器反步姿态控制Fig. 8 Backstepping attitude control of quadrotor aircraft

图选项

图 9为基于PID的四旋翼飞行器姿态控制曲线,由于外部干扰的存在,姿态角波动明显,其对干扰的抑制能力趋近于反步法.

图 9 四旋翼飞行器PID姿态控制Fig. 9 PID attitude control of quadrotor aircraft

图选项

图 10为矩形轨迹跟踪,可以看出在相同干扰情况下,本文算法跟踪能力优于其余两种算法,图 11为圆形轨迹跟踪曲线,本文算法同样具有一定优势.

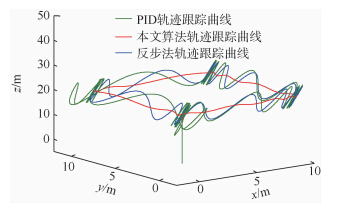图 10 四旋翼矩形轨迹跟踪Fig. 10 Rectangular trajectory tracking of quadrotor

图选项

图 11 四旋翼圆形轨迹跟踪Fig. 11 Circular trajectory tracking of quadrotor

图选项

图 12为自抗扰参数的寻优曲线,当迭代次数为12时,PSO算法基本达到系统全局最优,利用PSO寻优得到的控制量增益r=23.557 8,阻尼系数c=38.238 6,精度因子h₁=0.004 5.遗传算法(Genetic Algorithm,GA)所采用的初始种群大小为20,采用保存最优个体的随机选择方式,交叉操作采用均匀交叉算子实现,交叉概率为0.9,用高斯变异算子实现变异操作,变异概率根据进化代数自适应调节.从图 12可看出GA算法的寻优能力略低于PSO算法,因此本文采用PSO优化得到的参数.

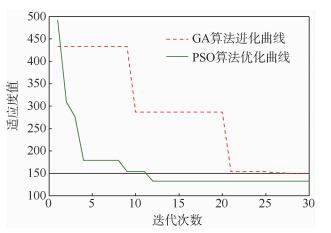图 12 自抗扰参数寻优Fig. 12 Parameter optimization of ADRC

图选项

图 13为本文进行的四旋翼飞行器定点悬停实验,飞行器可实现指定经纬度和指定高度的悬停,其空间位置精度基本满足要求.图 14为飞行实验的高度曲线,高度可以稳定保持在13 m.图 15为飞行实验的俯仰角曲线,时间跨度为500 s,波动在±2°之间,图 16为飞行实验的滚转角曲线,波动在±3°之间.

图 13 四旋翼飞行器定点悬停实验Fig. 13 Hovering experiment of quadrotor aircraft

图选项

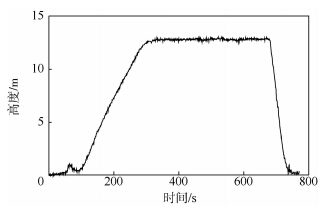图 14 四旋翼飞行器实际飞行高度曲线Fig. 14 Height curve of actual flight of quadrotor aircraft

图选项

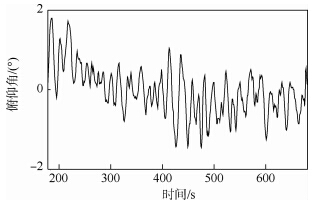图 15 四旋翼飞行器实际飞行俯仰角曲线Fig. 15 Pitch angle curve of actual flight of quadrotor aircraft

图选项

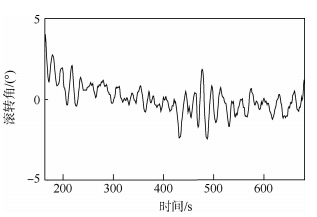图 16 四旋翼飞行器实际飞行滚转角曲线Fig. 16 Roll angle curve of actual flight of quadrotor aircraft

图选项

6 结 论1) 利用自抗扰(ADRC)姿态解耦算法实现对四旋翼飞行器姿态的高品质控制,并对状态间耦合项和系统复合干扰实现了精确的估计.2) 验证了本文姿态控制算法能够提高系统轨迹跟踪的鲁棒性,通过仿真验证其较其他算法有一定优势.3) 设计了实际飞行控制系统,可实现一些简单的飞行任务,如按照指定航迹和指定位置高度的飞行,将会进一步研究,将本文算法及其他先进控制方法应用到实际飞行器中.本文所设计的姿态解耦控制及轨迹跟踪系统实现难度小,由于该算法只需测量状态输出就可实现对状态间耦合项及系统复合干扰的估计,对硬件系统要求较低,因此具有实际应用的价值.
参考文献

[1]	Madani T, Benallegue A.Backstepping control for a quadrotor helicopter[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ:IEEE Press, 2006:3255-3260.
	Click to display the text
[2]	Salih A L, Moghavvemi M, Mohamed H A F, et al.Flight PID controller design for a UAV quadrotor[J].Scientific Research and Essays, 2010, 5(23):3660-3667.
	Click to display the text
[3]	Mokhtari A, Benallegue A, Daachi B.Robust feedback linearization and GH∞ controller for a quadrotor unmanned aerial vehicle[J].Journal of Electrical Engineering, 2006, 57(1):20-27.
	Click to display the text
[4]	Santos M, López V, Morata F.Intelligent fuzzy controller of a quadrotor[C]//Proceedings of 2010 IEEE International Conference on Intelligent Systems and Knowledge Engineering(ISKE), 2010:141-146.
	Click to display the text
[5]	Bouabdallah S, Noth A, Siegwart R.PID vs LQ control techniques applied to an indoor micro quadrotor[C]//2004 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS).Piscataway, NJ:IEEE Press, 2004, 3:2451-2456.
	Click to display the text
[6]	王树刚.四旋翼直升机控制问题研究[M].哈尔滨:哈尔滨工业大学, 2006:53-59. Wang S G.Research of quadrotor control[M].Harbin:Harbin Institute of Technology, 2006:53-59(in Chinese).
[7]	Altug E, Ostrowski J P, Mahony R.Control of a quadrotor helicopter using visual feedback[C]//2002 IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2002, 1:72-77.
	Click to display the text
[8]	Lee D, Kim H J, Sastry S.Feedback linearization vs.adaptive sliding mode control for a quadrotor helicopter[J].International Journal of Control, Automation and Systems, 2009, 7(3):419-428.
	Click to display the text
[9]	Bouabdallah S, Siegwart R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]//2005 IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2005:2247-2252.
	Click to display the text
[10]	Mian A A, Daobo W.Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter[J].Chinese Journal of Aeronautics, 2008, 21(3):261-268.
	Click to display the text
[11]	Wang Y Q, Wu Q H, Wang Y.Distributed cooperative control for multiple quadrotor systems via dynamic surface control[J].Nonlinear Dynamics, 2014, 75(3):513-527.
	Click to display the text
[12]	王璐, 李光春, 王兆龙, 等.欠驱动四旋翼无人飞行器的滑模控制[J].哈尔滨工程大学学报, 2012, 33(10):1248-1253. Wang L, Li G C, Wang Z L, et al.Sliding mode control of an underactuated Quadrotor UAV[J].Journal of Harbin Engineering University, 2012.33(10):1248-1253(in Chinese).
	Cited By in Cnki (18)
[13]	Bouadi H, Bouchoucha M, Tadjine M.Sliding mode control based on backstepping approach for an UAV type quadrotor[J].International Journal of Applied Mathematics and Computer Sciences, 2008, 4(1):12-17.
[14]	王俊生, 马宏绪, 蔡文澜, 等.基于ADRC的小型四旋翼无人直升机控制方法研究[J].弹箭与制导学报, 2008, 28(3):31-34. Wang J S, Ma H X, Cai W L, et al.Research on micro quadrotor control based on ADRC[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(3):31-34(in Chinese).
	Cited By in Cnki (38)
[15]	李杰, 齐晓慧, 韩帅涛.基于自抗扰技术的四旋翼姿态解耦控制方法[J].电光与控制, 2013, 20(3):44-48. Li J, Qi X H, Han S T.Attitude decoupling control for quadrotor aircraft based on active disturbance rejection control technique[J].Electronics Optics & Control, 2013, 20(3):44-48(in Chinese).
	Cited By in Cnki (7)
[16]	Raffo G V, Ortega M G, Rubio F R.An integral predictive/nonlinear control structure for a quadrotor helicopter[J].Automatica, 2010, 46(1):29-39.
	Click to display the text
[17]	Salazar-Cruz S, Escareno J, Lara D, et al.Embedded control system for a four-rotor UAV[J].International Journal of Adaptive Control and Signal Processing, 2007, 21:189-204.
	Click to display the text
[18]	Zhao C Z, Huang Y.ADRC based input disturbance rejection for minimum-phase plants with unknown orders and/or uncertain relative degrees[J].Journal of Systems Science and Complexity, 2012, 25(4):625-640.
	Click to display the text
[19]	韩京清.自抗扰控制器及其应用[J].控制与决策, 1998, 13(1):19-23. Han J Q.Auto-disturbances-rejection controller and it's application[J].Control and Decision, 1998, 13(1):19-23(in Chinese).
	Cited By in Cnki (725)
[20]	Nikolakopoulos G, Alexis K.http://html.rhhz.net/BJHKHTDXXBZRB/Switching%20networked%20attitude%20control%20of%20an%20unmanned%20quadrotor[J].International Journal of Control, Automation and Systems, 2013, 11(2):389-397.
	Click to display the text
[21]	崇阳, 张科, 王靖宇.一种基于模糊ADRC的舵机控制算法设计与实现[J].西北工业大学学报, 2011, 29(2):217-221. Chong Y, Zhang K, Wang J Y.Design and application of a servo control system based on fuzzy active disturbance rejection controller[J].Journal of Northwestern Polytechnical University, 2011, 29(2):217-221(in Chinese).
	Cited By in Cnki (14)
[22]	周黎妮, 唐国金, 李海阳.航天器姿态机动的自抗扰控制器设计[J].系统工程与电子技术, 2007, 29(12):2122-2126. Zhou L N, Tang G J, Li H Y.Active disturbance rejection controller design for spacecraft attitude maneuver[J].Systems Engineering and Electronics, 2007, 29(12):2122-2126(in Chinese).
	Cited By in Cnki (25)
[23]	韩京清.自抗扰控制技术[M].北京:国防工业出版社, 2008:280-287. Han J Q.Active disturbance rejection control technique[M].Beijing:National Defense Industry Press, 2008:280-287(in Chinese).