卫星导航系统是国家重要基础设施.接收机是系统与用户的惟一接口,卫星导航信号的捕获是接收机信号处理部分的核心技术,用于搜索卫星信号并将其牵引至跟踪范围内^{[1, 2]}.捕获是对扩频码相位和载波频率的二维搜索过程,捕获系统将可能的码相位和载波频率搜索范围分成若干分格,一个码相位分格与一个载波频率分格构成一个搜索单元.搜索控制逻辑采用某种策略遍历各搜索单元,检测信号是否存在,并给出码相位和载波频率的粗略估计^{[2, 3, 4, 5, 6, 7]}.搜索策略可以是串行的也可以是并行的.在检测某个搜索单元时,一般采用门限判决法进行检测^{[8, 9]},检测量可使用输入信号与本地复现信号相关结果的功率值,若检测量高于门限,则认为信号存在,该搜索单元对应的值就是码相位与载波频率的估计值.这种单次检测的虚警概率和检测概率往往不能满足要求^{[9, 10]},可以通过增加预检测积分时间或是增加非相干累加次数的方式来改善检测性能,但会使计算量和检测时间都大幅增加.另一种提高检测性能的方法是采用多次滞留的检测算法,如M/N检测算法、(1+M/N)检测算法以及Tong检测算法等^{[2, 8, 10]}.M/N算法适用于信号较强的情况,且检测时间较长,(1+M/N)算法是单次检测与M/N检测的结合体,也只适用于强信号情况^[8].Tong算法是一种可变滞留次数检测算法,其结构简单灵活,可以通过调整参数适应各种环境下的信号检测.国内外****对Tong算法已进行了比较多的研究^{[5, 6, 9, 10, 11, 12, 13, 14, 15]},这些研究讨论了Tong算法的虚警概率、检测概率和噪声单元平均滞留次数等性质,但对检测信号单元的平均滞留次数却少有研究.实际上,在并行搜索过程中,信号单元滞留次数对总捕获时间将有比较重要的影响,同时也会影响到最大滞留次数等算法参数的选择,对它的研究将有助于合理设置算法参数,提高检测性能.本文将对信号单元滞留次数的均值和方差进行详细推导,给出最大滞留次数限定方法,分析算法参数对检测性能的影响,并给出参数设置方法.本文以GPS(Global Positioning System)C/A(Coarse/Acquisition)码信号为例进行讨论,所得结论也可适用于北斗二号系统公开服务信号.1 Tong检测算法结构Tong算法结构如图 1所示^[2].该算法设定一个向上/向下计数器k,最大值为A,初始值为B.若检测量超过判决门限V_t,则k加1,否则减1,当K=A时捕获成功,k=0时该搜索单元被否决,进入下一搜索单元进行检测.为防止k在A与0之间徘徊,可规定一个最大滞留次数N_max,如在某一单元的滞留次数超过N_max,则放弃此单元.

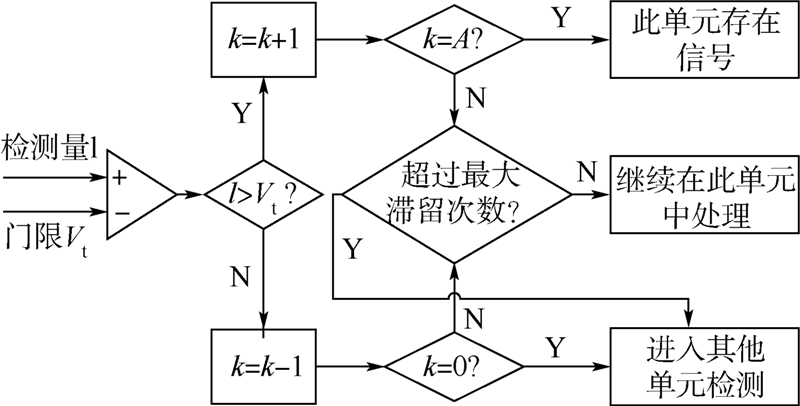
图 1 Tong检测算法结构Fig. 1 Structure of Tong detection algorithm

图选项

图 1中的检测量l为功率检测量,表达式为
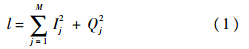
式中,I_j,Q_j为相关器I路与Q路输出的预检测积分结果;M为非相干累加次数.用H₁表示信号存在,H₀表示信号不存在.对功率检测量做归一化处理:z=l/σ_n².其中,σ_n²是I路或Q路预检测积分结果中噪声的功率.可以证明^[2],z满足如式(2)和式(3)所示的卡方分布：
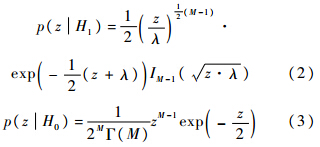
式中,λ=2M·(s/n)=2M·(c/n)·T_I,s/n为预检测信噪比,c/n为预检测载噪比,T_I为预检测积分时间；Γ(M)=(M－1)!为伽玛函数.设归一化判决门限为NV_t,则单次检测概率P_d和虚警概率P_f分别为

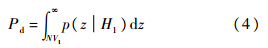
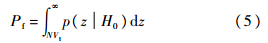
总检测概率P_D与总虚警概率P_F与单次检测概率和单次虚警概率有如下关系^{[5, 12]}:
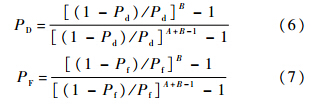
2 滞留次数的统计特性2.1 平均滞留次数2.1.1 噪声搜索单元平均滞留次数检测噪声单元的平均滞留次数N_n已有明确结论,如式(8)所示^[12].其中,r=(1－P_f)/P_f.
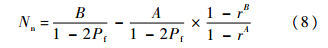
2.1.2 信号搜索单元平均滞留次数以下来推导检测信号单元时滞留次数的平均值.假定检测正在信号单元中进行,第n次判决时,计数器值k=i,或记为k(n)=i,下一次判决时计数器的值只能加1或减1,加1的概率为P(k(n+1)=i+1|k(n)=i)=P_d;减1的概率为P(k(n+1)=i－1k(n)=i)=1－P_d.假定计数器从到达i后到结束对此单元的检测的滞留次数为X(i),其均值为N_s(i)=E[X(i)k=i]=E[X(i)k(n)=i].暂时忽略最大滞留次数的制约(事实上,通过合理设置N_max可以使滞留次数超过N_max的概率极小,而且考虑N_max制约时,难以得到闭式解).这时,结束检测主要分为两种情况:一是计数器到达A,信号捕获成功;二是计数器到达0,发生漏检.在第1种情况下,X(i)的最小可能取值为A－i,即每次判决后计数器的值均加1,一直到达A.则N_s(i)可表示为
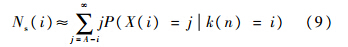
则由全概率公式可得

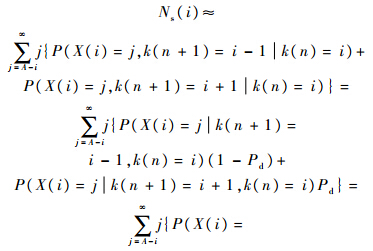
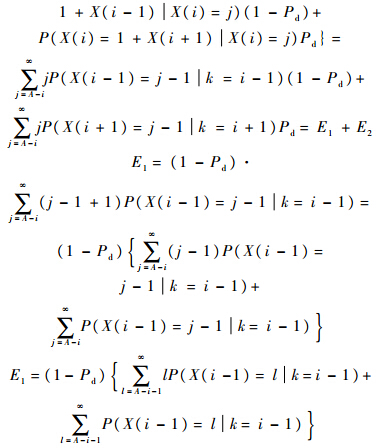
由于X(i－1)的最小值为A－i+1,因此有P(X(i－1)=A－i|k=i－1)=P(X(i－1)=A－i－1|k=i－1)=0
故而,E₁可表示为
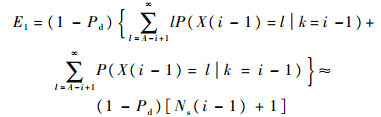
用相同方法处理E₂得:E₂≈P_d[N_s(i+1)+1].由以上推导可得
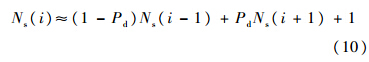
在第2种情况下,即发生漏检时，X(i)的最小值为i,即每次判决计数器的值均减1,一直到达0.用与上面类似的推导办法,可得出这时N_s(i)的递推形式与式(10)一致.当计数器到达A时,宣布信号存在,因此没有滞留,故而N_s(A)=0;当计数器到达0时,此单元被放弃,发生漏检,也没有滞留,因此N_s(0)=0.如此便得到递推关系的两个边界条件.综上所述,可得平均滞留次数的递推模型为
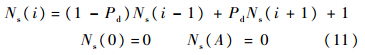
令a=(1－P_d)/P_d,b=1/P_d,解差分方程得
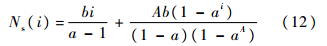
令i等于计数器初始值B,并将a与b表达式代入式(12),可得检测信号单元的平均滞留次数为
2.2 信号搜索单元滞留次数方差令D_s(i)为计数器值为i时滞留次数X(i)的方差,由方差的定义容易得到
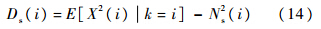
令R_s(i)=E[X²(i)k=i].对R_s(i)的讨论也分为成功捕获和发生漏检两种情况.使用与推导均值时类似的方法处理R_s(i),可以得到两种情况下相同的递推表达式.计数器到达0和A的时候,X(i)为确定性事件,且等于0,因此R_s(0)=R_s(A)=0.递推模型为
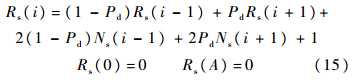
此差分方程较复杂,这里不做通解推导.在实际应用中可通过数值方法求解.令Δ(i)=R_s(i)－R_s(i+1),对式(15)变形可得
式中
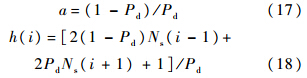
可以解得
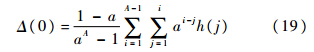
通过数值计算可得Δ(0)的值,进而得到R_s(1)=R_s(0)－Δ(0)=－Δ(0),再通过式(15),求得各个R_s(i).令i=B,由式(14)可得检测信号单元的滞留次数方差为
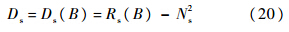
2.3 最大滞留次数的选择方法在下面的分析中将会看到,信号单元的平均滞留次数往往远大于噪声单元的平均滞留次数,因此最大滞留次数的选择以信号单元的情况为准.可依据3西格玛原则,取最大滞留次数为
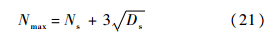
3 Tong检测算法性能分析检测一般采用涅曼-皮尔逊准则,即恒虚警准则.限定总虚警概率P_F后,由式(7)求得单次虚警概率P_f,由式(5)求得门限后,可由式(4)求得单次检测概率P_d,然后由式(6)求得总检测概率P_D,由式(8)、式(13)分别求得噪声单元平均滞留次数N_n和信号单元平均滞留次数N_s.分析使用GPS C/A码信号,预检测积分时间T_I=1 ms,非相干累加次数M=1.限定总虚警概率P_F=10^－6.3.1 检测概率分析图 2是Tong算法的总检测概率曲线.可以看出,增加A和B均能使总检测概率提高,增加B的效果比增加A的效果更明显.

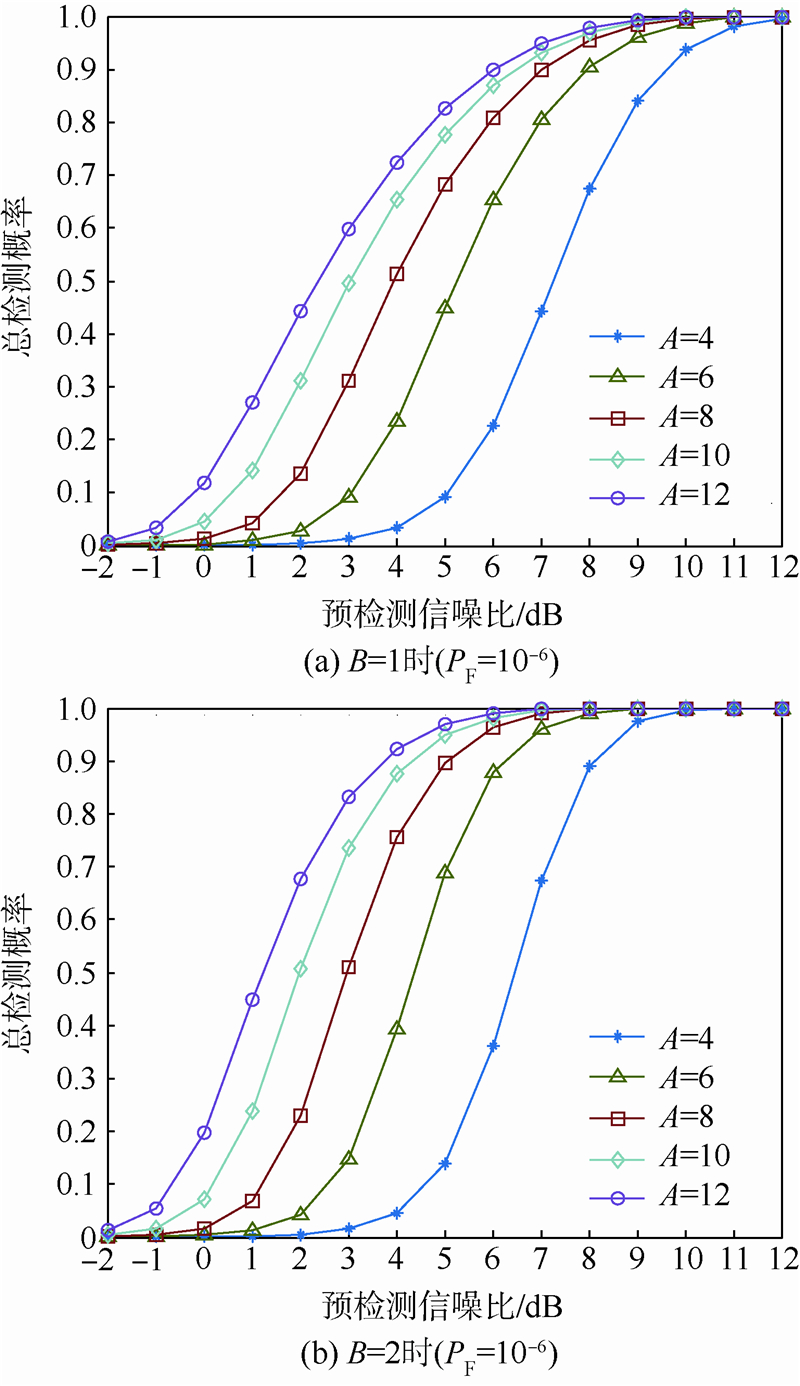图 2 Tong算法总检测概率Fig. 2 Total detection probabilities of Tong algorithm

图选项

3.2 平均滞留次数分析3.2.1 噪声搜索单元中的平均滞留次数表 1为不同A与B下,噪声单元平均滞留次数.可以看出,增加A与B的值均会使噪声单元的平均滞留次数增加,增加B的效果更为明显.表 1 不同A与B下噪声搜索单元平均滞留次数Table 1 Average dwell times of noise search unit for different A and B

A	B
	4	6	8	10	12
1	1.02	1.14	1.33	1.57	1.83
2	2.04	2.27	2.65	3.11	3.61

表选项


3.2.2 信号搜索单元中的平均滞留次数表 2与表 3为不同A与B下,信号单元的平均滞留次数.其中,表 2中的数据在预检测信噪比s/n=6 dB情况下得到,表 3中的数据在预检测信噪比s/n=9 dB情况下得到.表 2 不同A与B下信号搜索单元平均滞留次数(s/n=6 dB)Table 2 Average dwell times of signal search unit for different A and B (s/n=6 dB)

B	A
	4	6	8	10	12
1	2.93	6.04	8.05	10.00	11.98
2	4.00	6.81	8.44	10.22	12.13

表选项


表 3 不同A与B下信号搜索单元平均滞留次数(s/n=9 dB)Table 3 Average dwell times of signal search unit for different A and B (s/n=9 dB)

B	A
	4	6	8	10	12
1	3.26	5.15	7.10	9.08	11.07
2	2.62	4.32	6.21	8.17	10.15

表选项


从表 2和表 3可以看出,信号单元的平均滞留次数远大于噪声单元的平均滞留次数,增大A会使信号单元的平均滞留次数增加.在A一定时,若s/n较低,则B较小时,平均滞留次数也较小,B较大时,平均滞留次数也较大.这是由于当s/n较低时,尤其当A也较小时,检测概率也较低,例如s/n=6 dB,A=4,B=1时,P_d=48.36%,P_D=22.60%;A=4,B=2时,P_d=48.32%,P_D=36.02%,这种情况下很容易发生漏检,计数器值减小并到达0的概率较大,此时不同B值下的单次检测概率较为接近,则B越小,计数器越容易到达0,平均滞留次数也越小.随着A的增大,检测概率也在增大,计数器值增加并到达A的可能性变大,但单次检测概率仍不是很高,中间过程有可能出现反复,例如s/n=6 dB,A=8,B=1时,P_d=83.99%,P_D=80.94%;A=8,B=2时,P_d=83.78%,P_D=96.25%,B较小时单次检测概率稍大,因此平均滞留次数稍小.在A一定时,若s/n较高,则B较小时,平均滞留次数较大,B较大时,平均滞留次数较小.这是由于,若s/n较高,则检测概率也较高,例如s/n=9 dB时,A=4,B=1时,P_d=86.31%,P_D=84.19%;A=4,B=2时,P_d=86.28%,P_D=97.48%;A=12,B=1时,P_d=99.30%,P_D=99.29%;A=12,B=2时,P_d=99.27%,P_D=99.99%.这时,计数器值增加并到达A的概率较大,且不同B值下的单次检测概率较为接近,则初始位置越接近A,平均滞留次数越小.随着A的增加,不同B值下的平均滞留次数之差趋于定值,即计数器初始位置之差,例如,B=1和B=2两种情况下的平均滞留次数之差随着A的增加趋于1.表 4是不同A与B值及预检测信噪比s/n情况下信号单元的平均滞留次数.表 4 不同A,B和s/n下信号搜索单元平均滞留次数Table 4 Average dwell times of signal search unit for different A,B and s/n

A	B	(s/n)/dB
		6	7	8	9	10
4	1	2.93	3.34	3.40	3.26	3.12
4	2	4.00	3.80	3.21	2.62	2.25
6	1	6.04	5.69	5.36	5.15	5.05
6	2	6.81	5.62	4.79	4.32	4.10
8	1	8.05	7.59	7.28	7.10	7.03
8	2	8.44	7.28	6.58	6.21	6.06
10	1	10.00	9.53	9.23	9.08	9.02
10	2	10.22	9.13	8.49	8.17	8.04
12	1	11.98	11.50	11.21	11.07	11.02
12	2	12.13	11.06	10.44	10.15	10.04

表选项


由表 4可以看出,除了A=4,B=1情况外,其他各种A,B组合情况下的信号单元平均滞留次数随着s/n的提高而减小.这是由于随着s/n的提高,检测概率将增加,计数器到达A的可能性增大,中间的反复过程减少,平均滞留次数随之下降.另外,由图 2可以看出,随着s/n的提高,在一定的A,B组合下,总检测概率增加的趋势越来越缓慢,单次检测概率增加的趋势也将变缓,这造成平均滞留次数下降趋势的减缓,逐渐接近成功捕获所需的最低滞留次数.对于A=4,B=1的情况,上面已经提到,当s/n较低时,漏检概率较大,例如s/n=6 dB时,P_d=48.36%,P_D=22.60%,又由于B值较小,因此计数器很容易到达0,造成平均滞留次数较小;当s/n有所提高时,检测概率也会增加,但仍然不很高,例如s/n=7 dB时,P_d=61.53%,P_D=44.24%,这会造成中间过程的反复,致使平均滞留次数增加;若s/n继续增加,则检测概率迅速增加,例如s/n=10 dB时,P_d=94.20%,P_D=93.84%,这时,中间反复过程减少,平均滞留次数降低.4 算法参数设置Tong算法的主要可调参数是A与B.通过以上分析可知,当信号较强(即s/n较大)时,A和B的值不需要取很大就能满足检测概率的需求.对于串行搜索,检测多数情况下在噪声单元中进行,适当增大A、减小B可以在保证检测概率的前提下,减小噪声单元中的平均滞留次数,例如可选A=8,B=1;对于并行搜索,信号单元滞留次数影响较大,可以适当减小A、增大B,这样可以在保证检测概率的前提下,减小信号单元中的平均滞留次数,缩短捕获时间,例如可选A=6,B=2.在信号较为微弱(即s/n较小)的情况下,对串行搜索,可以通过增加A的方法来提高检测概率,例如,可选A=12,B=1,这样既能保证检测性能,又能使噪声单元的平均滞留次数不至于过大;对并行搜索,可以通过增加A或B的方法,尤其是增加B的方法来提高检测概率,可选A=10,B=2或者A=8,B=2,这样既能保证高检测概率,又可以使信号单元的平均滞留次数不至于过大.总之,参数的选择应依据信号强弱和搜索方式,并且要折衷考虑对检测概率与平均滞留次数的影响.5 结 论1) 在涅曼-皮尔逊准则下,增加计数器上限A和初值B能使Tong检测算法的总检测概率提高,增加B的效果尤为明显.2) 增加A与B的值会使检测噪声单元的平均滞留次数增加,增加B的效果更为明显.3) 信号单元的平均滞留次数远大于噪声单元的平均滞留次数,增大A会使信号单元的平均滞留次数增加.若预检测信噪比s/n较低,则B较小时,平均滞留次数也较小,B较大时,平均滞留次数也较大;若s/n较高,则B较小时,平均滞留次数较大,B较大时,平均滞留次数较小.4) A与B一定时,一般情况下信号单元平均滞留次数随着s/n的提高而减小.若A与B均较小,则信号单元平均滞留次数随着s/n的提高先增大而后减小.5) A与B的选择需依据信号强弱和搜索方式,并且要折衷考虑对检测概率与平均滞留次数的影响.6) 最大滞留次数可依据信号单元滞留次数的均值和方差,采用3西格玛原则确定.
参考文献

[1]	谢刚. GPS原理与接收机设计[M].北京:电子工业出版社,2009:349-389. Xie G.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2009:349-389(in Chinese).
[2]	寇艳红. GNSS软件接收机与信号模拟器系统研究[D].北京:北京航空航天大学,2006. Kou Y H.The study on GNSS software receiver and signal simulation system[D].Beijing:Beijing University of Aeronautics and Astronautics,2006(in Chinese).
[3]	张丽娜. Galileo系统BOC信号处理实验平台研究与实现[D].北京:北京航空航天大学,2007. Zhang L N.BOC signals processing platform in Galileo system design and research[D].Beijing:Beijing University of Aeronautics and Astronautics,2007(in Chinese).
[4]	邓炜. 导航卫星信号处理算法测试平台研究与实现[D].北京:北京航空航天大学,2006. Deng W.Navigation satellite signal process algorithm testing platform design and research[D].Beijing:Beijing University of Aeronautics and Astronautics,2006(in Chinese).
[5]	Kaplan E D, Hegarty C J.Understanding GPS:principles and applications[M].2nd ed.Boston:Artech House Inc,2006:223-227.
[6]	Enge P K. The global positioning system:signals,measurements,and performance[J].International Journal of Wireless Information Networks,1994,1(2):83-105.
	Click to display the text
[7]	Tusi J B Y. Fundamentals of global positioning system receivers:a software approach[M].New York:John Wiley & Sons Inc,2000:133-164.
[8]	孙礼. GPS接收机系统的研究[D].北京:北京航空航天大学,1998. Sun L.The study on GPS receiver system[D].Beijing:Beijing University of Aeronautics and Astronautics,1998(in Chinese).
[9]	姚铮, 崔晓伟,陆明泉,等.应用于GPS接收机的序贯检测器性能分析[J].清华大学学报:自然科学版,2007,47(7):1166-1169. Yao Z,Cui X W,Lu M Q,et al.Performance analysis of sequential detector for GPS receivers[J].Journal of Tsinghua University:Science and Technology,2007,47(7):1166-1169(in Chinese).
	Cited By in Cnki (13)
[10]	马琳,崔嵬, 吴嗣亮.极低信噪比环境下含近邻约束的改进唐检测判决算法[J].系统工程与电子技术,2011,33(8):1745-1749. Ma L,Cui W,Wu S L.Improved Tong multiple trial algorithm with near neighbor constraint in extremely low SNR condition[J].Systems Engineering and Electronics,2011,33(8):1745-1749 (in Chinese).
	Cited By in Cnki (3)
[11]	Tong P S. A suboptimum synchronization procedure for pseudo noise communication systems[C]//IEEE 1973 National Telecommunications Conference Vol.II.Piscataway,NJ:IEEE Press,1973:26D1-26D5.
[12]	李思超, 叶甜春,徐建华.唐检测器的驻留时间及检测性能分析[J].电子测量技术,2009,34(3):53-55. Li S C,Ye T C,Xu J H.Analysis on resident time and detection performance of Tong detector[J].Electronic Measurement Technology,2009,34(3):53-55(in Chinese).
	Cited By in Cnki (5)
[13]	Daffara F, Vinson P.Improved search algorithm for fast acquisition in a DSP-based GPS receiver[C]//Proceeding of ISSSE 98.Piscataway,NJ:IEEE Press,1998:310-314.
	Click to display the text
[14]	孙晓峰, 刘云飞,王西夺.高动态条件下Tong检测技术应用研究[J].无线电工程,2012,42(4):34-36. Sun X F,Liu Y F,Wang X D.Application research of Tong detection based on high dynamic environment[J].Radio Engineering,2012,42(4):34-36(in Chinese).
	Cited By in Cnki (1)
[15]	马琳,崔嵬, 田静,等.基于马尔科夫链的含有检测次数约束条件的唐检测器[J].宇航学报,2011,32(8):1799-1804. Ma L,Cui W,Tian J,et al.Study on Tong detector with number of detection times constraint based on Markov chain[J].Journal of Astronautics,2011,32(8):1799-1804(in Chinese).
	Cited By in Cnki