系统科学的核心科学问题是挖掘各领域复杂系统集体行为的涌现机制。传统上，统计物理学基于系统的哈密尔顿量（能量）和统计分布，研究大量个体组成系统的集体行为。相变与临界现象作为系统最显著的集体行为，其理论研究以序参量作为出发点。当前，人们迫切需要研究涉及气候、生命、生态、社会、金融等的自然和社会复杂系统，这些系统的集体行为及相变临界现象与人类密切相关。例如，地球作为一个典型的自适应复杂系统，Lenton等人于2008年在美国科学院院刊发文，指出地球复杂系统可能存在15个潜在临界要素。2019年，他们进一步在Nature发文，指出其中的亚马孙雨林、北极海冰、大西洋环流、北方森林、澳大利亚珊瑚礁、格林兰冰原、永久冻土、西南极冰原、东南极冰原九个临界要素已经接近或者处于临界点，可能引起地球系统的巨变，需要人类给予特别关注。对于微观的细胞生命系统，当细胞内特定分子聚集在一起、发生相分离，会引起细胞性质和功能发生改变。相分离已成为当前生命科学研究中的一个热点。对于上述复杂系统，分析系统的临界因素是否接近或处于临界点，以及不同临界因素之间是否存在关联，是当前复杂系统研究中的重大科学问题。对于广泛的复杂系统，人们缺乏它们的哈密尔顿量、统计分布、序参量。但是，随着科技的发展，人们可越来越多获取复杂系统的实验及观测数据，如何由这些数据出发研究复杂系统的集体行为及相变与临界现象，成为当前一项非常紧迫的研究任务。


针对上述问题，北京师范大学陈晓松教授与合作者最近提出了一个解决方案。他们从吉布斯提出的统计系综出发，基于复杂系统个体的观测或模拟数据，构建复杂系统的微观态和统计系综。以描述系统微观态的高维矢量作为列，系统个体的演化序列作为行，可以得到归一的统计系综矩阵。利用奇异值分解方法，统计系综矩阵可分解为

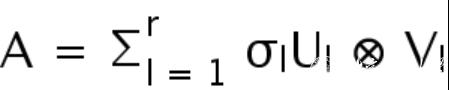
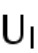
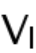
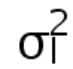
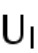
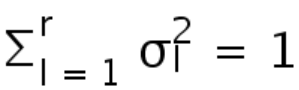
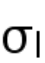
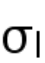
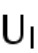
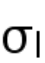
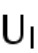
这里是本征微观态，描述该本征微观态的时间演化，表示克罗内克积。表示在系综中的概率，满足归一化条件。系统集体行为由具有较大的本征微观态描述，若某个本征值的热力学极限由零变为有限，类似于有限比例玻色气体处于最低能级时，系统发生玻色-爱因斯坦凝聚，这里统计系综发生本征微观态的凝聚，预示复杂系统发生了相变，相变的序参量由表示，涌现的新相由描述。


该团队将本征微观态方法成功地应用于三维伊辛模型（图1）、地球表面温度（图2、3、4、5）、中国股票（图6）价格三类不同的复杂系统，揭示了这些系统的集体行为及相变与临界现象，证实该理论框架可用于一般平衡和非平衡系统。本征微观态方法开辟了研究复杂系统集体行为的一个新途径，提供了一个可以研究复杂系统相变与临界现象的理论框架，统一地处理平衡态和非平衡态相变。





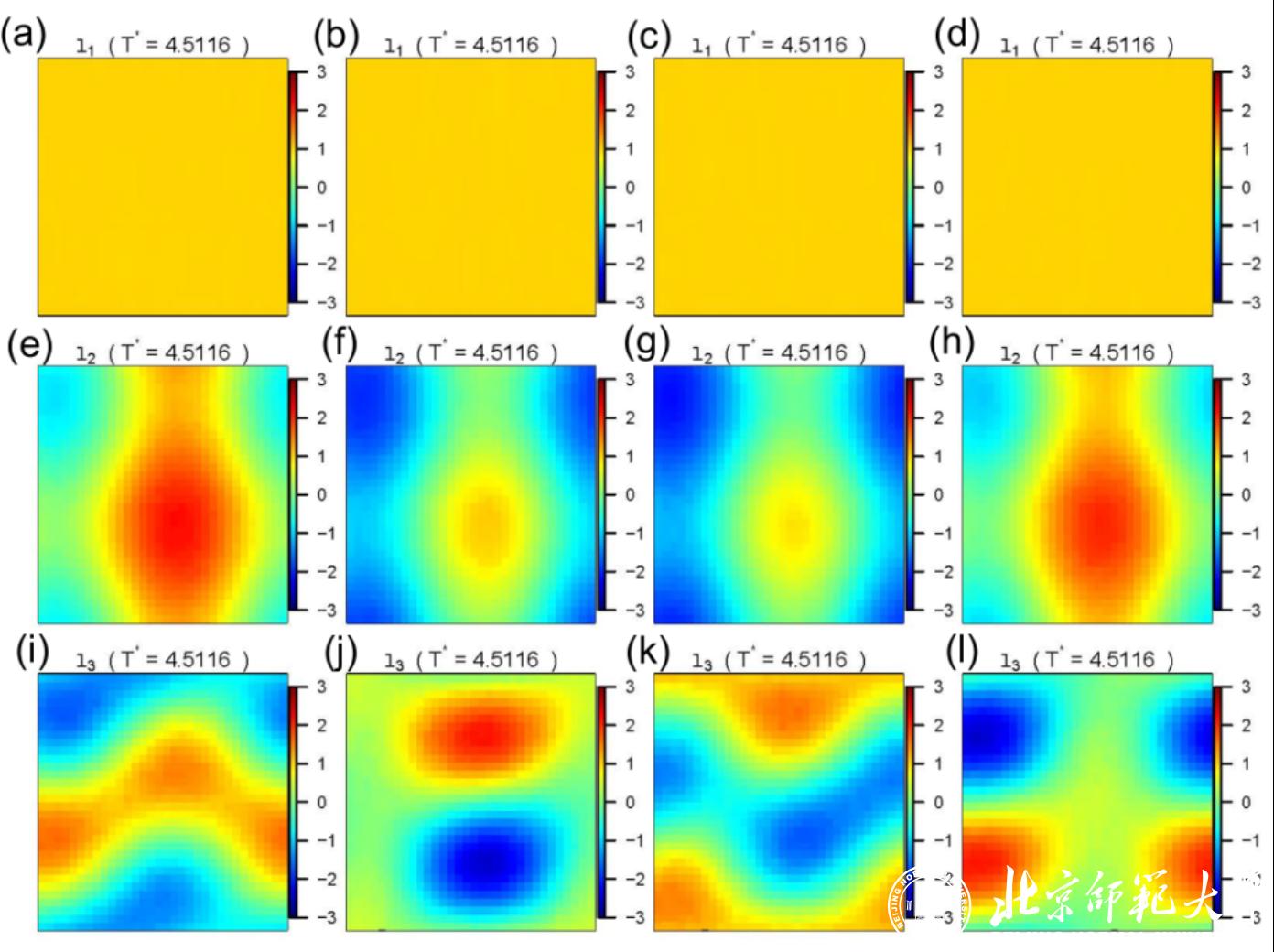
图1 三维伊辛模型临界点本征微观态的空间分布，各行依次对应第一、二、三大本征微观态，各列代表三维正方体不同高度的截面






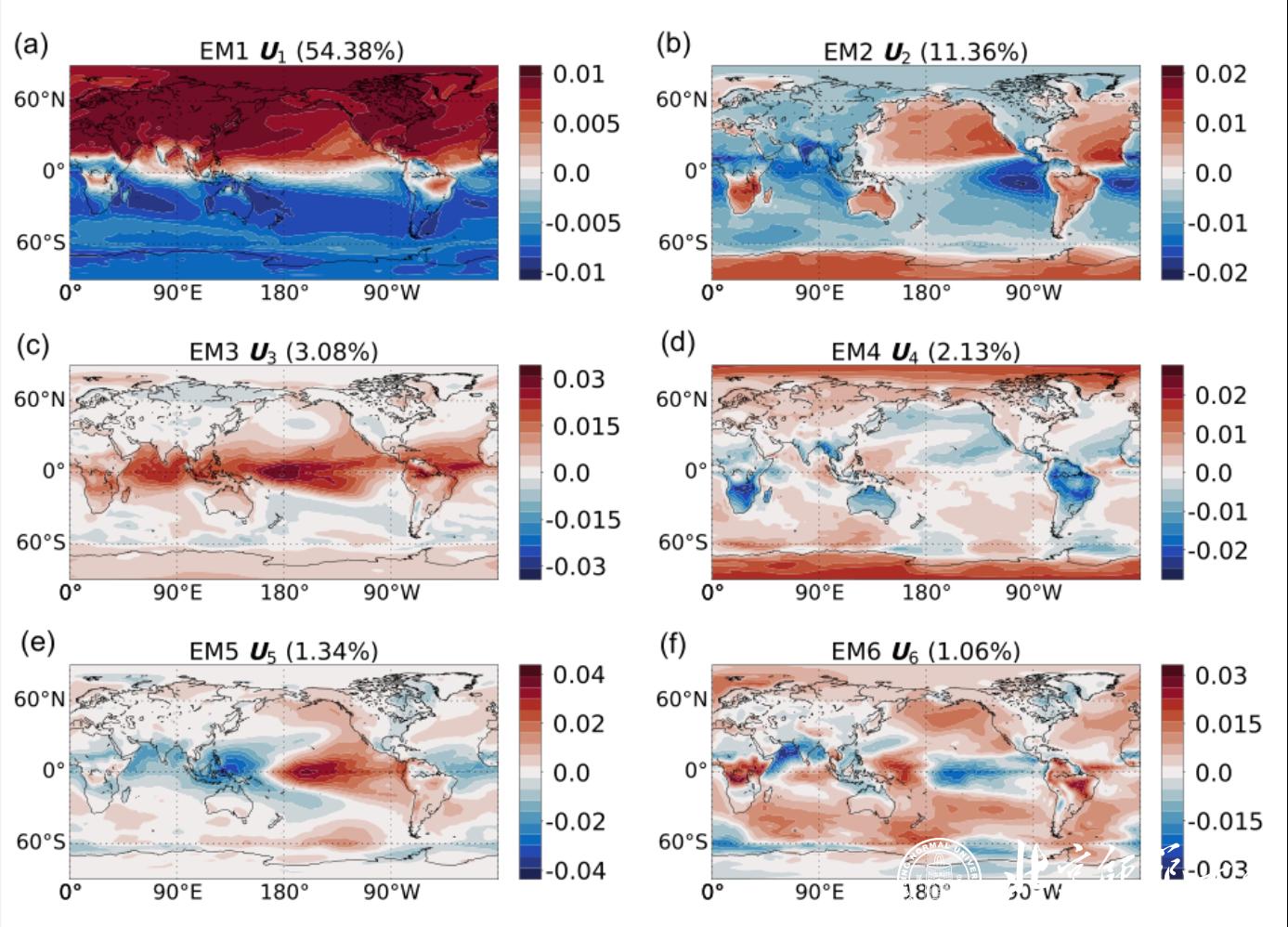
图2 地球系统表面温度的前六大本征微观态，它们分别对应年循环、海陆差异、赤道区域、非线性半年震荡（SAO）、厄尔尼诺等气候现象，具有显著的气候意义。





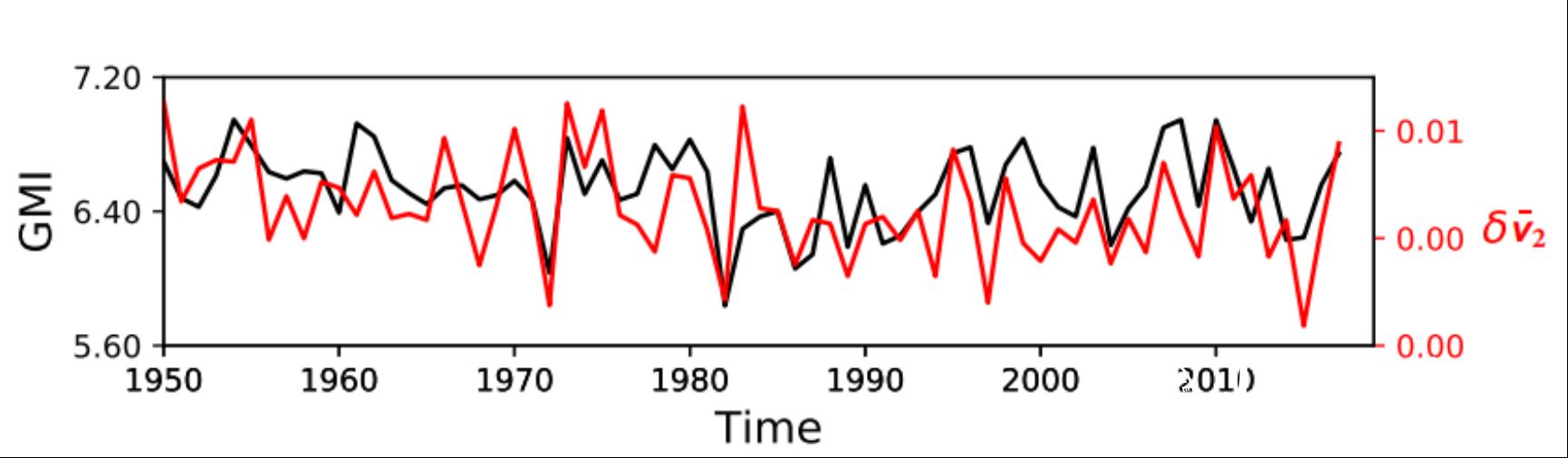
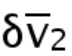
图3 地球系统表面温度的第二大本征微观态动力学演化在夏冬两季差值与全球季风指数（GMI）的对比。图中，黑线表示全球季风指数 (GMI)， 红线表示第二大本征微观态动力学演化在夏冬两季差值。



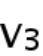
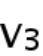
图4 地球系统表面温度的第三大本征微观态动力学演化。在 70 年代中期发生演化趋势的转变，这与发生在 1976-1977 年的气候转变相一致。








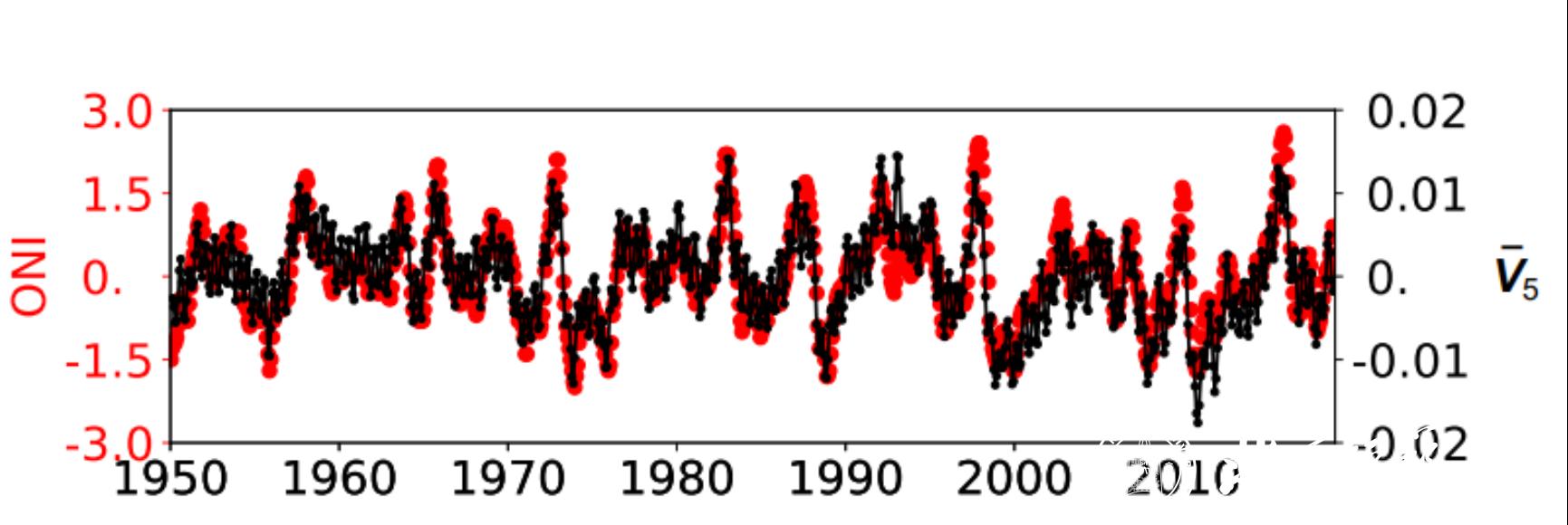
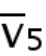
图5 地球系统表面温度的第五大本征微观态动力学演化的滑动平均与海洋尼诺指数(ONI)的对比。图中黑点表示第五大本征微观态动力学演化的滑动平均, 滑动步长为一个月，平均窗口的长度为90天，红点表示海洋尼诺指数。



图6 中国股价前三大本征微观态的时间演化，分别与上证100指数（SSE100 Index）、上证能源指数（SSE Energy Sector Index），上证材料指数（SSE Materials Index）相对应，表明本征微观态方法可同时捕获整体与各行业门类的演化趋势。


文章已作为Editor’s Suggestion 发表在Commun. Theor. Phys. 73 (2021) 065603。
原文链接：https://doi.org/10.1088/1572-9494/abf127