摘要/Abstract

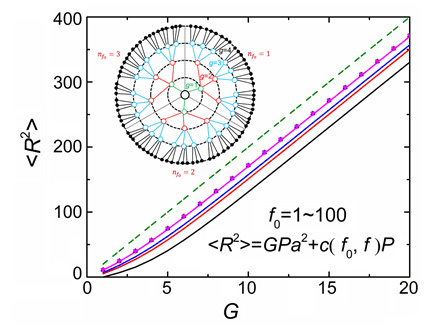
树枝形大分子因其高度支化的特殊结构，在传感、载药、催化等众多领域有着广泛的应用潜力.运用高斯链模型推导了溶液体系中树枝形均聚物的自洽场方程组.并在不考虑体积排除作用的条件下，计算了θ溶液中分子的中心链节官能度f₀、支化点官能度f、间隔链段的聚合度P、以及总代数G对链节浓度分布及均方回转半径的影响.计算结果显示，链节浓度分布总是符合"dense-core"的模型，即在所有计算参数组合下，链节浓度总是沿径向单调下降，并随f₀、f和G的增加而单调增加.自洽场计算得到的树枝形均聚物的均方回转半径R与Rouse动力学模型的计算结果基本一致，在f₀、f和G的数值较大时，都能够得到<R²>≈GPa²的标度律关系.
关键词: 树枝形均聚物, 自洽场理论, 链节浓度分布, 标度律
The dendrimers are a unique class of branched macromolecules with defined architectures synthesized by iterative reaction steps. Because of their highly branched structures, the dendrimers have a wide potential application in many fields, including sensing, drug delivery, catalysis, etc. In order to understand the thermal equilibrium behavior of the dendritic homopolymers in solution, we derived the self-consistent field theory (SCFT) for the dilute dendrimer solutions. The center segment is anchored on the origin of the space, and the shape of the dendrimer is assumed to be spherically symmetric. The pre-averaged interaction parameter u is employed to represent the volume exclusion interaction between the segments. We only focus on the dendrimer immersed in the θ solvent, where the volume exclusion interaction between the segments is negligible (u=0). The number density of the segments, φ(r), is calculated via systematically changing the topological parameters of the molecule, including the functionality f₀ of the central segment, the functionality f of the branching points, the degree of polymerization of the spacers P, and the total generation number G. With all parameter combinations, φ(r) was found always maximized at the center and monotonically decreasing along the radial direction. Thus, the dendrimers in θ solvent obeys the "dense-core" model instead of the "dense-shell" model. Increasing f₀, f and G results in the increase of φ(r) with any radius r. However, increasing P causes the decrease of φ(r) near the center region and the increase of φ(r) with larger r. The size of the dendrimer, analyzed by calculating the radius of gyration R, increases with f₀, f, G and P. R calculated by our SCFT agrees well with the results obtained by the Rouse dynamics. With large f₀, f and G, both SCFT and the Rouse dynamics predict the scaling law <R²>≈GPa².
Key words: dendrimer, self-consistent field theory, segment density profile, scaling law


PDF全文下载地址:

点我下载PDF