
 , 马聪玉1, 沈岩柏1, 宋振国2,3
, 马聪玉1, 沈岩柏1, 宋振国2,3 1. 东北大学 资源与土木工程学院,辽宁 沈阳 110819;
2. 矿物加工科学与技术国家重点实验室,北京 100160;
3. 北京矿冶科技集团有限公司,北京 100160
收稿日期:2020-11-11
基金项目:国家自然科学基金资助项目(51874075, 51974066);矿物加工科学与技术国家重点实验室开放基金资助项目(BGRIMM-KJSKL-2019-10)。
作者简介:崔宝玉(1982-),男, 山东烟台人, 东北大学副教授;
沈岩柏(1978-),男, 黑龙江密山人, 东北大学教授, 博士生导师。
摘要:水力旋流器入料口的最优尺寸尚无明确评价标准.基于数值试验方法,考察了入料口直径对流场特性和分离性能的影响,提出了一种基于内部稳定流场的入料口直径设计方法.结果表明,入料口直径的下限可根据能量消耗确定,当入料口直径低于下限时,流体碰撞加剧促使部分压力能转化为内能,外侧自由涡区域呈现出类似强制涡的特性.入料口直径的上限可根据流场稳定性确定,当入料口直径超过上限时,进入的液流将直接撞击在溢流管壁上,导致流场稳定性变差,粗颗粒在沉砂中的分配率减少,分离精度降低.最终确定了入料口直径的最优取值范围为0.18D≤Di≤0.26D.
关键词:水力旋流器入料口直径优化设计稳定流场计算流体力学
Design of Inlet Diameter of Hydrocyclone Based on Stable Flow Field
CUI Bao-yu1

 , MA Cong-yu1, SHEN Yan-bai1, SONG Zhen-guo2,3
, MA Cong-yu1, SHEN Yan-bai1, SONG Zhen-guo2,3 1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. State Key Laboratory of Mineral Processing, Beijing 100160, China;
3. BGRIMM Technology Group, Beijing 100160, China
Corresponding author: CUI Bao-yu, E-mail: cuibaoyu@mail.neu.edu.cn.
Abstract: There are no definite evaluation criteria for the optimum size of inlet diameter of hydrocyclone yet. Effects of inlet diameter on flow field characteristics and separation performance are investigated numerically. A theoretical design method of the inlet diameter based on the inner stable flow field was proposed. The results show that the lower limit of the inlet diameter can be determined based on energy consumption. When the inlet diameter is less than the lower limit, the collision between fluids is more severe, and part of the pressure energy is converted into the internal energy. Consequently, the outer free vortex region presents a characteristic similar to the forced vortex. The upper limit of the inlet diameter can be achieved according to the stable flow field. When the inlet diameter exceeds the upper limit, the feed stream will directly impinge on the vortex finder, causing poor flow field stability. As a result, the recovery of coarse particles in the underflow will decrease sharply and the separation sharpness will also decrease. Finally, the optimal range of the inlet diameter is determined as 0.18D≤Di≤0.26D.
Key words: hydrocycloneinlet diameteroptimum designstable flow fieldcomputational fluid dynamics(CFD)
目前,水力旋流器已广泛应用于选矿厂的澄清、浓密和固-固分级等作业[1-2].入料口直径直接控制入料速度,影响分离粒度、分离效率和分离精度等分离性能指标,是水力旋流器最重要的几何参数之一[3].优化入料口直径,可最大程度减少湍流混合对旋流分离的不利影响[4].Rietema的优化研究表明[5],最优入料口直径为0.28D;而Kelsall的试验研究发现[6],最优入料口直径为0.08D,其中D为水力旋流器直径.Bradley研究认为,适宜的入料口直径取值范围为0.14D~0.17D.由于不同****在优化研究过程中所选用的设计准则不尽相同,所使用的水力旋流器参数配置及物料性质各异,入料口直径的最优取值范围尚没有统一的标准[3],亟需建立一种基于水力旋流器分离理论的入料口直径设计方法.
水力旋流器旋流分离实质是不同性质颗粒在旋流复合力场中运移行为差异所致.水力旋流器内部流场是颗粒运移的载体,直接决定颗粒的运移行为.稳定的内部流场是固体颗粒实现有效旋流分离的前提[7].因此,可以根据内部流场特性确定最优的入料口直径设计,这不仅可从理论上揭示最优入料口直径制定的根本原因,也可为水力旋流器的设计提供一种适用性更广的方法.水力旋流器内部流场为一种复杂的三维多相强湍流流场[8],计算流体力学(computational fluid dynamics, CFD) 以其省时、省力、高效等特点被广泛应用于复杂多相流的研究,可对水力旋流器内部流体的流动过程进行数字化描述[9-10].
本文采用数值试验方法,系统分析了入料口直径对流场特性的影响,根据流场稳定原理制定了最优的入料口直径设计.考察了入料口直径对分离性能的影响,分析了内部流场特性变化对颗粒空间分布的影响机制.本研究可为水力旋流器的优化研究提供更好的理论指导.
1 数值模型的建立1.1 模拟策略水力旋流器内复杂多相流的模拟策略如图 1所示.
图 1(Fig. 1)
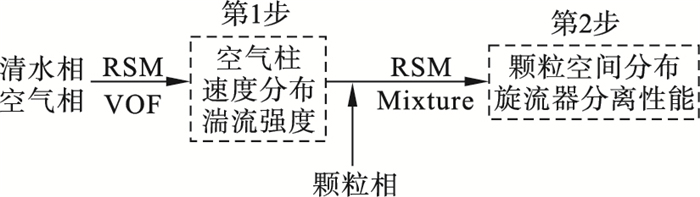 | 图 1 模拟策略Fig.1 Simulation strategy |
第1步,分析不同入料口直径时水力旋流器的内部流场特性.采用雷诺应力模型RSM(Reynolds stress model) 描述湍流运动,该模型已被证实可以精准预测旋流器内液流的速度分布[11-12].采用流体体积(volume of fluid, VOF)模型来捕捉气液界面,通过计算可以获得不同入料口直径对应的气-液两相流场特性.
第2步,在气-液两相流场结果基础上,引入颗粒相,分析不同流场特性对应的旋流分离结果.在这一阶段,湍流的描述仍采用RSM模型,颗粒相和气相的运动采用混合模型(Mixture).Mixture与VOF模型相比,不仅可以用于相间无滑移的计算,也可用于各相之间有速度差的计算[13],其控制方程如下.
混合相的连续性方程:
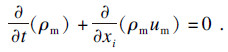 | (1) |
混合相的动量方程为
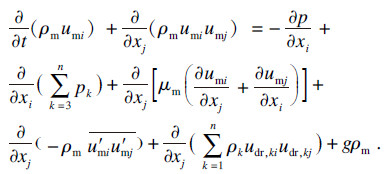 | (2) |
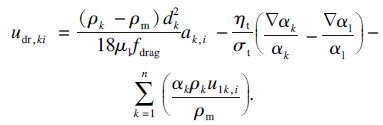 | (3) |
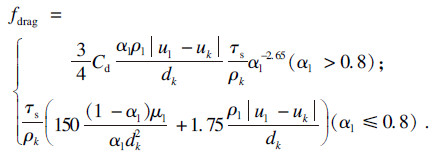 | (4) |
清水相和气相间的曳力由Schiller和Naumann曳力模型决定:
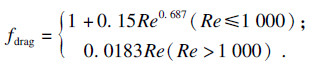 | (5) |
1.2 模拟条件为了考察入料口直径对水力旋流器内部流程特性及分离性能的影响,只设置入料口直径为变量,其他几何参数保持不变.水力旋流器的几何参数配置如图 2a所示.入料口直径(Di) 变化范围为0.10D~0.34D.入料口横截面为矩形,矩形的长宽比保持固定不变(a/b=1.5),入料口直径等于对应的等面积圆的直径[14].综合考虑计算精度和计算时间,整个计算域被离散为4.0×105个六面体网格,如图 2b所示.
图 2(Fig. 2)
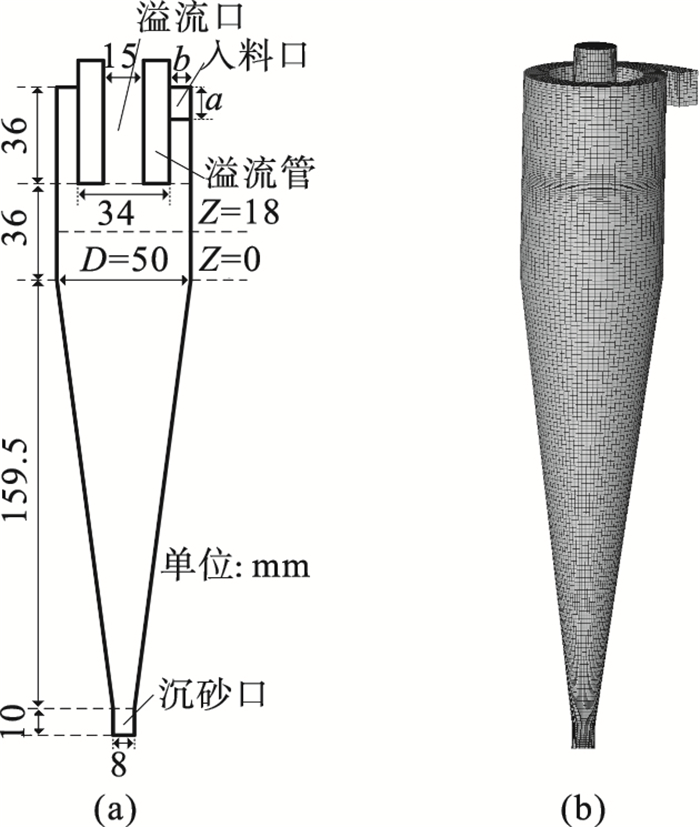 | 图 2 水力旋流器示意图Fig.2 Schematic diagram of hydrocyclone (a)—几何参数; (b)—网格结构. |
入口边界设置为质量流入口边界,入口流量固定为35 L/min,溢流口和沉砂口边界设置为压力出口边界,均直接与大气相通,压强设置为101 325 Pa,空气在两个出口处的回流系数均设置为1.水力旋流器器壁设置为无滑移边界条件,并利用标准壁面函数将近壁处物理量与湍流核心区的相应物理量联系起来.以石英纯矿物样品为研究对象,石英样品密度为2673kg/m3,给料固体体积分数为5%,采用激光粒度分析仪测定样品的粒度组成,将石英给料分成12个粒级,每个粒级用平均粒度来表征,具体如表 1所示.
表 1(Table 1)
| 表 1 给料的粒度分布及各粒级体积分数分布 Table 1 Size distribution and respective volume fraction of particles in the feed |
1.3 模型验证在系统开展数值试验之前,需要验证数值模型的可靠性.通过将激光多普勒测速仪(laser Doppler anemometry, LDA) 测试得到的速度分布与数值模拟试验得到的速度分布对比,验证了湍流模型的可靠性,试验结果如图 3所示.结果表明,数值试验结果和LDA测试结果的速度分布吻合很好,靠近空气柱区域的速度分布计算值和测试值之间略有差别,主要原因在于实际流场测试时空气柱的存在会对激光产生一定的反射作用,从而造成测试误差.
图 3(Fig. 3)
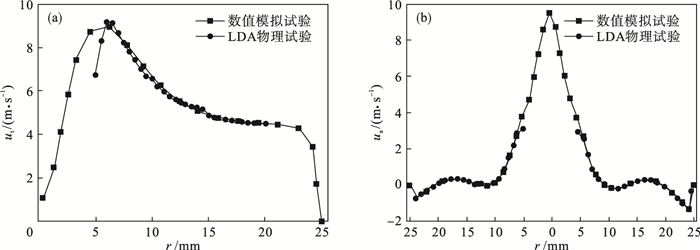 | 图 3 速度分布测试结果与数值模拟比较Fig.3 Comparison between experimental and simulated results of velocity distribution (a)—切向速度;(b)—轴向速度. |
利用Delgadillo的物理试验数据对Mixture多相流模型进行了验证,不同粒度颗粒在沉砂中的分配率(εu)如图 4所示.Mixture多相流数值模拟结果与Delgadillo物理试验结果的趋势吻合,微细颗粒分离结果计算值与试验值间略有差别,但微细颗粒分离效率数值计算结果与Delgadillo物理测试的分流比结果接近[15],这与微细颗粒与液流的跟随性较好,其在沉砂中的分配率与分流比有关的理论一致,故本文开展的数值试验是可靠的.
图 4(Fig. 4)
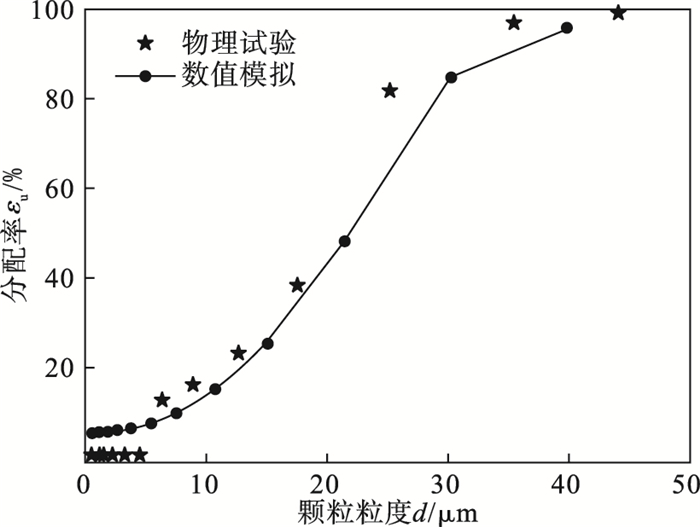 | 图 4 分配曲线计算结果与测试结果比较Fig.4 Comparison of the simulated and measured partition curves |
2 结果与讨论2.1 流场特性分析2.1.1 切向速度切向速度(ut) 直接决定颗粒所受离心力大小,入料口直径对切向速度的影响如图 5所示.
图 5(Fig. 5)
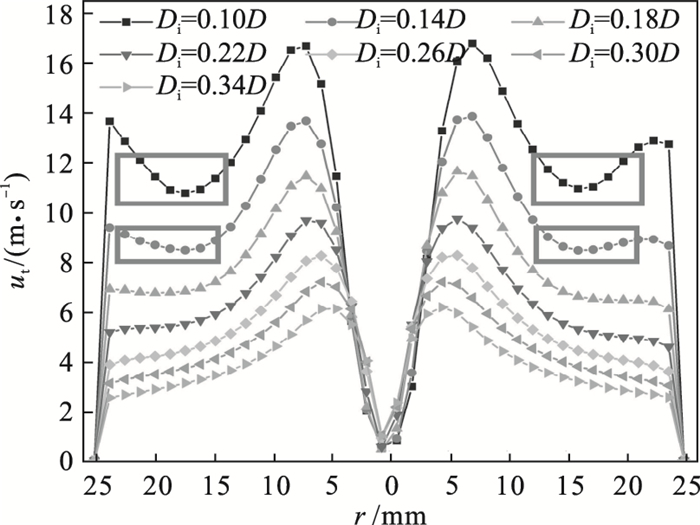 | 图 5 入料口直径对切向速度分布的影响Fig.5 Effects of inlet diameter on the distribution of tangential velocity |
当给料流量固定时,随着入料口直径增大,入料速度逐渐降低,切向速度亦随之降低,对应固体颗粒所受离心力逐渐减小.切向速度分布遵循组合涡分布规律,内部为强制涡,外部为自由涡.自由涡区域流体运动遵循utrn=C,其中指数n为小于1的正数.当入料口直径太小时(Di < 0.18D),自由涡区域的切向速度随着回转半径(r) 的减小而降低(如图 5框中所示),亦即此时指数n值为负,切向速度呈现出类似强制涡的特性.这主要是由于入料口直径太小时,入料速度非常大,液流与液流之间及液流与器壁之间的碰撞非常剧烈,一部分压力能被转化为内能,导致能量损失增加.
2.1.2 轴向速度入料口直径对轴向速度(ua) 分布的影响如图 6所示.
图 6(Fig. 6)
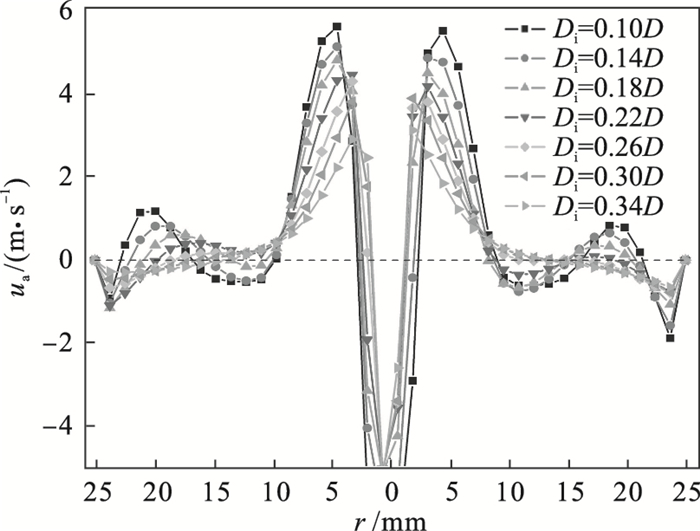 | 图 6 入料口直径对轴向速度分布的影响Fig.6 Effects of inlet diameter on the distribution of axial velocity |
从图中可以看出,外旋流区域轴向速度方向向下,内旋流区域轴向速度方向向上,随着入料口直径增大,轴向速度逐渐降低.这主要是由于入料口直径增大,入料速度降低,对应三个分速度(切向速度、轴向速度和径向速度) 均降低.此外,随着入料口直径增大,轴向速度缓变区(axial velocity wave zone, AVWZ) 逐渐缩小,AVWZ即为轴向速度变化缓慢且方向交替变化的区域[16].有研究表明,AVWZ的存在可以提高水力旋流器的分离精度[13].连接轴向速度为0的各点,即可绘制轴向零速包络面(locus of zero vertical velocity, LZVV),LZVV的形状和位置对旋流分离结果有显著影响.因水力旋流器内部为轴对称流场,且旋流分离主要发生在锥段,故研究了入料口直径对锥段LZVV的影响,如图 7所示.
图 7(Fig. 7)
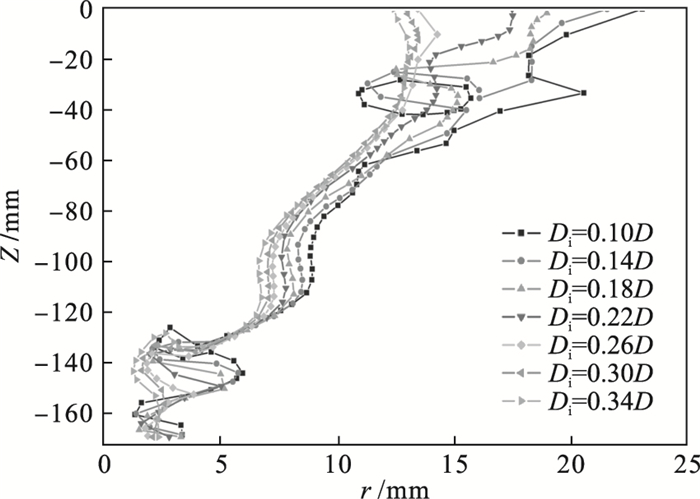 | 图 7 入料口直径对LZVV的影响Fig.7 Effects of inlet diameter on the LZVV |
从图中可以看出,随着入料口直径增大,LZVV逐渐向轴心方向移动,因而外旋流区域扩大,分流比增加.
2.1.3 空气柱稳定性水力旋流器内部流场稳定性可用空气柱的稳定性来表征,空气柱的稳定性可用空气柱直径不随时间变化来表示[17],不同入料口直径时空气柱直径(da) 随时间的变化情况如图 8所示,为了简化分析只列出了两种典型的入料口直径.
图 8(Fig. 8)
 | 图 8 入料口直径对空气柱稳定性的影响Fig.8 Effects of inlet diameter on the air core stability (a)—Di=0.10D;(b)—Di=0.34D. |
当入料口直径取值位于0.10D~0.30D之间时,空气柱直径不随时间变化而变化,亦即空气柱稳定性很好.随着入料口直径进一步增加(Di=0.34D),空气柱直径随时间变化而变化,空气柱稳定性被破坏,空气柱的不稳定将会造成内部流场的不稳定[18].
2.1.4 湍流强度不同入料口直径时湍流强度分布云图如图 9所示,湍流强度的定义为流体脉动速度的均方根值与流体平均速度的比值,因此湍流强度为无量纲量.随着入料口直径增大,水力旋流器内部流场的湍流强度逐渐增强.当入料口直径接近或超过溢流管直径时(Di > 0.26D),因给料液流直接冲击溢流管,造成内部流场稳定性降低,湍流强度急剧增加,局部高强度湍流将会破坏固体颗粒沿径向的规则分布[19].
图 9(Fig. 9)
 | 图 9 入料口直径对湍流强度的影响Fig.9 Effects of inlet diameter on the turbulence intensity (a)—Di=0.10D; (b)—Di=0.14D; (c)—Di=0.18D; (d)—Di=0.22D; (e)—Di=0.26D; (f)—Di=0.30D; (g)—Di=0.34D. |
2.2 分离性能分析2.2.1 分配曲线不同入料口直径时对应的沉砂分配曲线如图 10所示.随着入料口直径增大,粗颗粒及中等粒度颗粒在沉砂中的分配率降低,这是因为这部分颗粒主要受离心力作用,随入料口直径增大,切向速度减小,故而颗粒所受离心力降低.微细颗粒在沉砂中的分配率随入料口直径增大而增加,这是因为微细颗粒主要受湍流耗散作用,其在沉砂中的分配率与分流比有关.此外,随着入料口直径增大,分配曲线主线段的斜率减小,分离精度降低,这与AVWZ的消失及颗粒所受离心力的减小有关.此外,当入料口直径非常小时(Di < 0.18D),粗颗粒在沉砂中的分配率略有降低,如表 2所示.这是由于此时颗粒与颗粒之间及颗粒与器壁之间的碰撞非常剧烈,部分压力能转化为了内能,实际转化为的旋转动能降低[20].
图 10(Fig. 10)
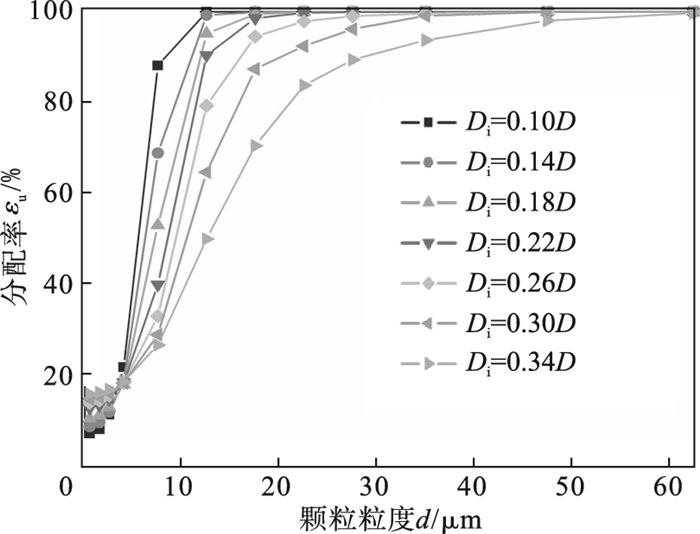 | 图 10 入料口直径对沉砂分配率的影响Fig.10 Effects of inlet diameter on solids distribution ratio in the underflow |
表 2(Table 2)
| 表 2 入料口直径对固体颗粒沉砂分配率的影响 Table 2 Effects of inlet diameter on solids distribution ratio in the underflow? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2.2 固体颗粒空间分布固体颗粒的空间分布可以用不同粒度颗粒的平衡回转半径分布来表征.颗粒平衡回转半径是指颗粒最大体积分数所在的半径[21].入料口直径对颗粒平衡回转半径的影响如图 11所示.随着入料口直径增大,各粒度颗粒的平衡回转半径均沿径向向轴心移动.以7.5 μm粒度颗粒为例,随着入料口直径增大,该粒级颗粒平衡回转半径位置与LZVV的相对位置发生了显著改变,导致该粒级颗粒在沉砂中的分配率急剧降低.
图 11(Fig. 11)
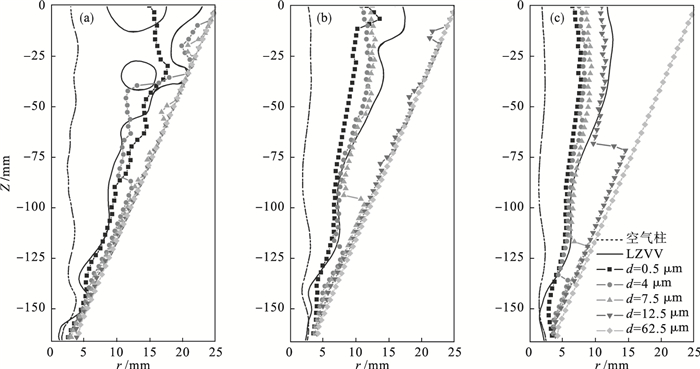 | 图 11 入料口直径对颗粒平衡回转半径分布的影响Fig.11 Effects of inlet diameter on the particle rotational equilibrium radius distribution (a)—Di=0.10D; (b) —Di=0.22D; (c)—Di=0.34D. |
3 结论1) 稳定的内部流场是固体颗粒实现有效旋流分离的前提, 以内部流场稳定性为指标,确定了入料口直径的最优取值范围(0.18D≤Di≤0.26D).
2) 在最优范围内,随着入料口直径增大,切向速度降低,AVWZ缩小,LZVV沿径向逐渐向轴心移动.各粒度颗粒的平衡回转半径均向轴心移动,对应粗颗粒及中等粒度颗粒在沉砂中的分配率降低,而微细颗粒在沉砂中的分配率增加,分离精度降低.
3) 入料口直径取值低于最优范围下限时,流体之间的碰撞增强,能量损失严重,外部自由涡区域的切向速度呈现出类似强制涡的特性,造成粗颗粒在沉砂中的回收率略有降低.
4) 入料口直径取值高于最优范围上限时,亦即入料口直径接近或超过溢流管直径时,给料液流将直接冲击溢流管壁,造成空气柱稳定性降低,湍流强度增加,分离精度下降.此外,此时水力旋流器内涡流强度非常低,导致粗颗粒在沉砂中的分配率急剧减小.
参考文献
| [1] | Mustafa A K Q. Hydrocyclone flow characteristics and measurements[J]. Flow Measurement and Instrumentation, 2020, 73: 101741. DOI:10.1016/j.flowmeasinst.2020.101741 |
| [2] | 崔宝玉. 水力旋流器流场及分离过程的数值试验研究[D]. 沈阳: 东北大学, 2014. (Cui Bao-yu. Numerical study on flow field and separating process of hydrocyclone[D]. Shenyang: Northeastern University, 2014. ) |
| [3] | Ni L, Tian J, Song T, et al. Optimizing geometric parameters in hydrocyclones for enhanced separations: a review and perspective[J]. Separation and Purification Reviews, 2019, 48(1): 30-51. DOI:10.1080/15422119.2017.1421558 |
| [4] | Ji L, Kuang S B, Yu A B. Numerical investigation of hydrocyclone feed inlet configurations for mitigating particle misplacement[J]. Industrial and Engineering Chemistry Research, 2019, 58(36): 16823-16833. DOI:10.1021/acs.iecr.9b01203 |
| [5] | Rietema K. Performance and design of hydrocyclones: parts Ⅰ to Ⅳ[J]. Chemical Engineering Science, 1961, 15(3): 298-325. |
| [6] | Kelsall D F. A further study of the hydraulic cyclone[J]. Chemical Engineering Science, 1953, 2(6): 254-272. DOI:10.1016/0009-2509(53)80044-8 |
| [7] | Zhang C E, Cui B Y, Wei D Z, et al. Predicting the optimum range of feed flow rate in a hydrocyclone using the method combined flow pattern and equation model[J]. Powder Technology, 2017, 319: 279-288. DOI:10.1016/j.powtec.2017.06.064 |
| [8] | Ji L, Chen J, Kuang S B, et al. Prediction of separation performance of hydrocyclones by a PC-based model[J]. Separation and Purification Technology, 2019, 211: 141-150. DOI:10.1016/j.seppur.2018.09.073 |
| [9] | 王学涛, 崔宝玉, 魏德洲, 等. 深锥型浓密机内部流场特性模拟[J]. 东北大学学报(自然科学版), 2020, 41(3): 418-423. (Wang Xue-tao, Cui Bao-yu, Wei De-zhou, et al. Simulation on the internal flow field characteristics of deep-cone thickener[J]. Journal of Northeastern University(Natural Science), 2020, 41(3): 418-423.) |
| [10] | 张彩娥, 魏德洲, 崔宝玉, 等. 渐变截面型入料口夹角对旋流器流场及压降的影响[J]. 东北大学学报(自然科学版), 2017, 38(6): 859-863. (Zhang Cai-e, Wei De-zhou, Cui Bao-yu, et al. Effects of inlet angle on the flow pattern and pressure drop of a hydrocyclone with gradual change section type inlet[J]. Journal of Northeastern University(Natural Science), 2017, 38(6): 859-863.) |
| [11] | Vakamalla T R, Mangadoddy N. Numerical simulation of industrial hydrocyclones performance: role of turbulence modelling[J]. Separation and Purification Technology, 2017, 176: 23-39. DOI:10.1016/j.seppur.2016.11.049 |
| [12] | Zhang C E, Cui B Y, Wei D Z, et al. Effects of underflow orifice diameter on the hydrocyclone separation performance with different feed size distributions[J]. Powder Technology, 2019, 355: 481-494. DOI:10.1016/j.powtec.2019.07.071 |
| [13] | Zhao Q, Cui B Y, Wei D Z, et al. Numerical analysis of the flow field and separation performance in hydrocyclones with different vortex finder wall thickness[J]. Powder Technology, 2019, 345: 478-491. DOI:10.1016/j.powtec.2019.01.030 |
| [14] | Tang B, Xu Y X, Song X F, et al. Effect of inlet configuration on hydrocyclone performance[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(7): 1645-1655. DOI:10.1016/S1003-6326(17)60187-0 |
| [15] | Zhang C E, Wei D Z, Cui B Y, et al. Effects of curvature radius on separation behaviors of the hydrocyclone with a tangent-circle inlet[J]. Powder Technology, 2017, 305: 156-165. DOI:10.1016/j.powtec.2016.10.002 |
| [16] | Yang Q, Wang H L, Wang J G, et al. The coordinated relationship between vortex finder parameters and performance of hydrocyclones for separating light dispersed phase[J]. Separation and Purification Technology, 2011, 79(3): 310-320. DOI:10.1016/j.seppur.2011.03.012 |
| [17] | Xu Y X, Song X F, Sun Z, et al. Numerical investigation of the effect of the ratio of the vortex-finder diameter to the spigot diameter on the steady state of the air core in a hydrocyclone[J]. Industrial and Engineering Chemistry Research, 2013, 52(15): 5470-5478. DOI:10.1021/ie302081v |
| [18] | Zou J, Wang C X, Ji C. Experimental study on the air core in a hydrocyclone[J]. Drying Technology, 2016, 34(7): 854-860. DOI:10.1080/07373937.2015.1046554 |
| [19] | Vakamalla T R, Kumbhar K S, Gujjula R, et al. Computational and experimental study of the effect of inclination on hydrocyclone performance[J]. Separation and Purification Technology, 2014, 138: 104-117. DOI:10.1016/j.seppur.2014.10.013 |
| [20] | Ji L, Kuang S, Zheng Q, et al. Computational analysis and optimization of hydrocyclone size to mitigate adverse effect of particle density[J]. Separation and Purification Technology, 2017, 174: 251-263. DOI:10.1016/j.seppur.2016.10.034 |
| [21] | Vakamalla T R, Koruprolu V B R, Arugonda R, et al. Development of novel hydrocyclone designs for improved fines classification using multiphase CFD model[J]. Separation and Purification Technology, 2017, 175: 481-497. DOI:10.1016/j.seppur.2016.10.026 |
