
 , 金雄程, 林录样
, 金雄程, 林录样 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2020-08-21
基金项目:国家自然科学基金资助项目(51605083); 中央高校基本科研业务费专项资金资助项目(N180304022); 国家留学基金委资助项目(201906085037)。
作者简介:吕昊(1982-),男,辽宁铁岭人,东北大学讲师,博士。
摘要:通过Gamma随机过程描述机车轮缘与滚动圆直径的磨耗过程, 研究了运用Copula函数和四阶矩方法计算轮缘退化与滚动圆直径退化的相关可靠性方法, 通过动力学软件仿真得到列车不同阶段的动力学指标.研究了镟修周期为20万km的车轮退化过程的可靠性及车轮直径退化过程的灵敏度, 利用Monte Carlo仿真(MCS)验证了该方法的正确性.结果表明: 镟修周期为20万km时车轮达到预期寿命的可靠性高, 基于Copula函数相关失效退化模型计算的可靠性高于独立失效模型计算的可靠性, 轮径退化可靠性模型的灵敏度研究说明镟修过程中应该要选取对轮径削减较少的方案.
关键词:Gamma过程退化过程四阶矩镟修周期可靠性维修
Wheel Gamma Degradation Process Based on Copula Function
LYU Hao

 , JIN Xiong-cheng, LIN Lu-yang
, JIN Xiong-cheng, LIN Lu-yang School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LYU Hao, E-mail: lvhao@me.neu.edu.cn.
Abstract: The wear process of the wheel flange and the rolling circle diameter was described by the Gamma random process, and the method of calculating the reliability of the wheel flange degradation and the rolling circle diameter degradation was studied by using the Copula function and the fourth-order moment method, and the dynamic indexes of the train at different stages were obtained by dynamics software simulation. The reliability of the wheel degradation process with a rotation cycle of 200, 000 km and the sensitivity of the wheel diameter degradation process were studied. The correctness of the method was verified by Monte Carlo simulation (MCS).The results showed that the reliability of wheels reaching the expected life is high when the rotation cycle is 200, 000 km, and the reliability calculated based on the Copula function correlation failure degradation model is higher than that calculated by the independent failure model. The sensitivity study of the wheel diameter degradation reliability model indicates that the scheme with less reduction of wheel diameter should be selected during the rotation repair.
Key words: Gamma processdegradation processfourth-order momentrotation periodreliability maintenance
高速列车车轮磨耗是车轮失效的一个重要因素, 是预测车轮镟修时间的一个重要物理量.车轮磨耗会直接影响车辆的动力特性并最终影响列车的运行安全.踏面工作过程中出现磨损、擦伤及踏面剥离是一种磨损退化过程, 影响车辆安全运行、造成车体晃动、降低乘客舒适度、产生噪声, 从可靠性角度分析, 这种随时间的退化会造成车辆可靠度的降低.对踏面实施镟修可以改善上述磨损退化的影响, 但是如何确定镟修周期, 对车轮寿命可靠度进行精确预测是涉及重要经济效益的课题.车轮踏面即车轮径向截面上由轮缘和踏面形成的轮廓线,车轮轮缘和踏面外形的选择不仅影响车轮的磨耗和使用寿命, 而且直接关系到机车车辆的曲线通过性能和走行质量.由于轮对的特殊结构, 两个不同直径的轮缘与滚动圆同钢轨进行接触并产生摩擦磨损.本文研究的磨耗量主要分为在踏面滚动圆直径的磨耗和轮缘的磨耗, 进一步研究两者的磨耗过程及相关可靠性.
可靠性模型是一种基于零件失效模式建立的产品可靠性计算方法, 许多研究者针对目标机械产品提出了许多有效的可靠性模型[1-6].对退化可靠性模型的大量研究还是在近20多年, 运用的模型主要有退化轨道模型、Gamma过程模型、Poison过程模型、Wiener过程模型等.目前的研究主要集中在独立退化的模型建立、参数估计、寿命预测等, 也有涉及相关性退化过程的研究, 总体较之独立退化的研究要少. Lu等[7]运用两阶段法建立非线性退化轨道模型, 并利用蒙特卡洛模拟(MCS)计算失效时间分布及置信区间. Whitmore等[8]建立了具有时间尺度变换的Wiener过程的退化模型, 采用了Arrhenius外推法建立加速退化试验的退化模型和模型参数估计.Whitmore等[9]提出一种适用于两个组件均为线性均值的二元变量Wiener过程预测失效寿命, 并通过极大似然法估计参数. Sun等[10]提出了一种基于Gauss-Poison联合分布的累计损失退化失效模型, 并与Weibull模型进行比较, 证明了该模型的精确性. Pan等[11]通过Gamma过程分别建立两个性能的退化模型, 建立二元Birnbaum-Saunders分布逼近近似两个性能相关条件下的寿命分布,并以MCMC结合极大似然估计参数和置信区间. Jia等[12]提出了使用Copula函数建立串联、并联和k-out-of-n system系统的相关可靠性.与此同时, 轮轨关系的研究也有了进一步的发展.文献[13]提出了一种基于Kalker简易理论的非平稳蠕滑力快速计算方法.文献[14-21]基于试验、数值仿真和代数方法对高速列车车轮退化过程的磨耗机理、磨耗分布等进行了深入的研究.文献[22]根据跟踪实测数据运用最小二乘法建立车轮磨耗预测模型并通过数值仿真验证模型的正确性.
基于车轮轮缘和踏面滚动圆直径的退化数据, 以Gamma过程建立退化模型, 通过Copula函数建立相关退化关系, 并通过全参数法(IFM)估计参数, 运用四阶矩和Edgeworth级数计算车轮镟修的可靠性.
1 基于Copula函数的Gamma退化过程1.1 Gamma过程车轮退化过程是一个单调非减的过程, Gamma过程具有非负增量, 且Gamma过程是一个纯跳跃过程, 可以用来描述连续的微小磨损, 也可以用来描述较大的冲击性损伤.因此Gamma过程可以很好地描述车轮的退化过程.Gamma过程[7]具有以下特点:
1) 满足X(0)=0;
2) X(t)具有非负独立增量;
3) 对于任意的t≥0, 满足X(t+Δt)-X(t)~Ga(αΔt, β).
Ga(α, β)中α>0表示形状参数, β>0表示尺度参数.当α为常数时, Gamma过程为平稳过程; 当α=ktb时, Gamma过程为非平稳过程.Gamma过程的密度分布函数为
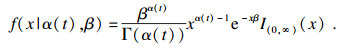 | (1) |
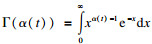
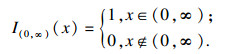 | (2) |
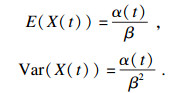 | (3) |
根据Sklar理论, 假设有两个边缘分布的CDFs R1(X1)和R2(X2), 且R(X)∈[0, 1], X1和X2是随机变量, H(u, v)为一个联合分布, 可得二元Copula函数为
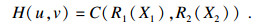 | (4) |
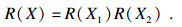 | (5) |
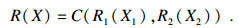 | (6) |
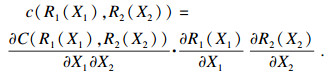 | (7) |
1) Gumbel Copula:
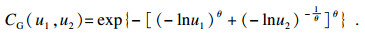 | (8) |
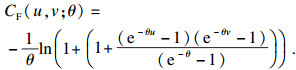 | (9) |
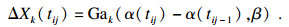 | (10) |
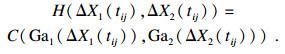 | (11) |
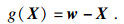 | (12) |
随机参数向量X和状态函数g(X)可表示为
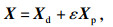 | (13) |
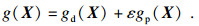 | (14) |
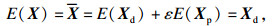 | (15) |
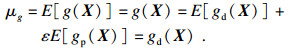 | (16) |
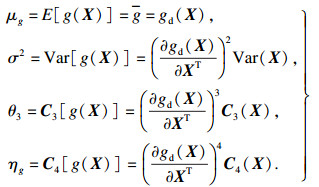 | (17) |
运用Edgeworth级数方法, 可以将标准化了的随机变量的任意分布的概率分布函数近似地展开成标准的正态分布函数[24]:
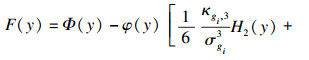 |
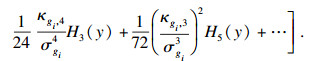 | (18) |
Hj(y), j=1, 2, …, 为j阶Hermite多项式, 递推关系为
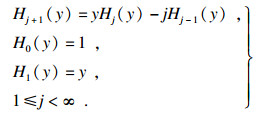 | (19) |
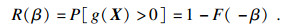 | (20) |
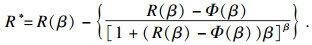 | (21) |
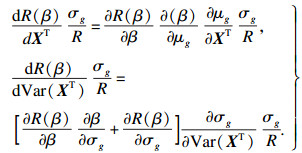 | (22) |
状态函数为
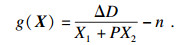 | (23) |
单个镟修周期内, 车轮的退化可靠性为
 | (24) |
车轮在单个镟修周期与整个轮径退化过程构成串联系统, 可得总的可靠性为
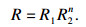 | (25) |
2.3 仿真验证利用SIMPACK多体动力学软件建立列车模型, 轨道根据高速铁路设计标准, 曲线半径为5 500 m, 缓和曲线为700 m, 超高为160 mm.分别将实测得到的5组踏面拟合后载入模型, 测量计算模型的Sperling指标、脱轨系数和轮重减载率[25].
Sperling平稳性指标用于评价车辆运行品质与乘坐舒适度, 评价指标W的表达式为
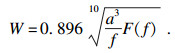 | (26) |
利用轮重减载率和脱轨系数评价车辆系统的脱轨安全性, 轮重减载率的第二限度为0.6, 脱轨系数的安全限度为0.8.
3 参数估计二元非平稳Gamma退化模型的未知参数向量为[k1, b1, β1, k2, b2, β2, θ], 其中ki, bi, βi, θ为Gamma函数中的形参和实参等变量参数, 如式(3)、式(8)、式(9)所示, 这些参数决定了Gamma函数的具体分布形式和基本特征.当测得样本为n个时, 可以得到n个样本的退化数据{Xij,i=1, 2, …, n; j=1, 2, …, m}, Xij表示第i个样品第j次的退化累积量.增量ΔXij=Xij-Xij-1~Ga(αΔt, β), 极大似然估计函数为[23]
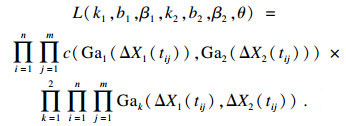 | (27) |
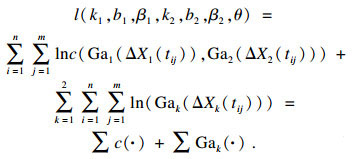 | (28) |
4 数值算例已知机车6246在第一次镟修后运行到第二次镟修里程时磨耗数据如图 1所示, 该数据表示轮缘从镟修后到再次镟修轮缘和踏面直径的退化量.
图 1(Fig. 1)
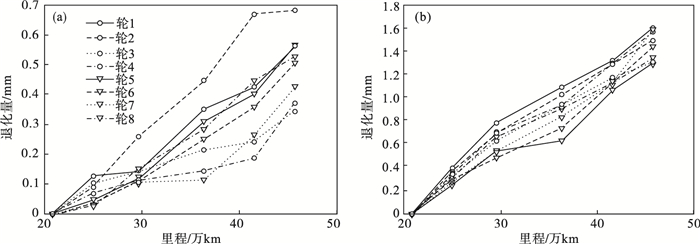 | 图 1 车轮退化过程Fig.1 Wheel degradation process (a)—踏面;(b)—轮缘. |
运用两阶段法估计一个镟修周期内的轮缘退化和踏面直径退化的联合分布的参数如表 1所示.
表 1(Table 1)
| 表 1 似然函数参数 Table 1 Likelihood function parameters |
Frank Copula的θ值为4.522 8, Gumbel Copula的θ值为1.809 9.根据AIC信息准则检验Copula模型的参数估计:
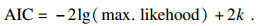 |
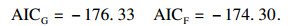 |
不同相关模式和不相关条件下的可靠性概率分布如图 2所示,具体数值如表 2所示.由图 2可知, 当镟修周期为20万km时, 退化独立时的可靠性较相关失效时的可靠性较低, 会造成不必要的浪费; Gumbel Copula相关模型和Frank Copula相关模型相比, Gumbel Copula模型在上尾部的可靠性较高.
图 2(Fig. 2)
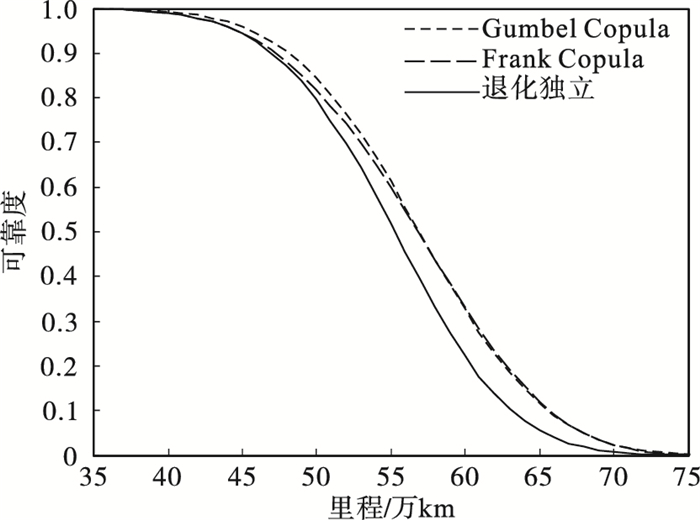 | 图 2 可靠性概率分布对比Fig.2 Comparison of reliability probability distributions |
表 2(Table 2)
| 表 2 Comparison of reliability probability distributions Table 2 Reliability at 200 000 km |
轮径从920 mm磨耗到840 mm, 以20万km为镟修周期, 考虑轮径的退化过程, 车轮达到预期寿命的可靠性Rd=0.999 51.车轮全寿命镟修过程的可靠性为
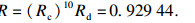 |
图 3(Fig. 3)
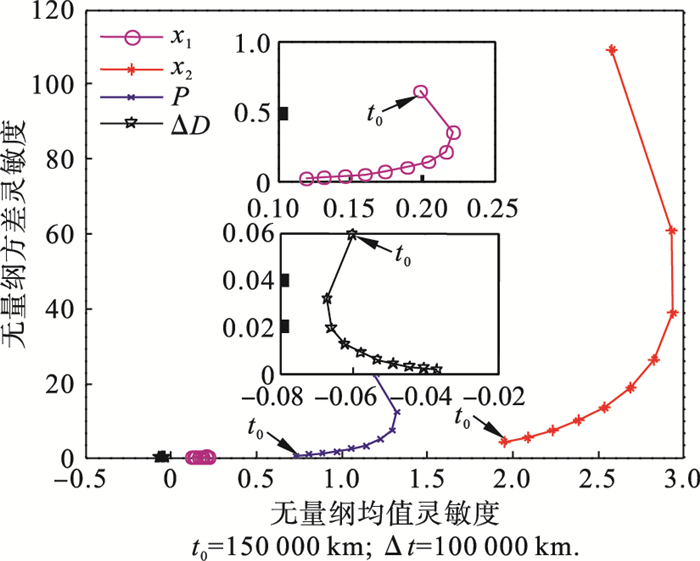 | 图 3 无量纲灵敏度Fig.3 Dimensionless sensitivity |
通过108次Monte Carlo数值仿真模拟轮缘、踏面和轮径镟修10次的退化过程, 得到如表 3所示结果.踏面和轮缘退化轨迹的模拟结果如图 4所示.
表 3(Table 3)
| 表 3 Monte Carlo失效率 Table 3 Failure rate of Monte Carlo |
图 4(Fig. 4)
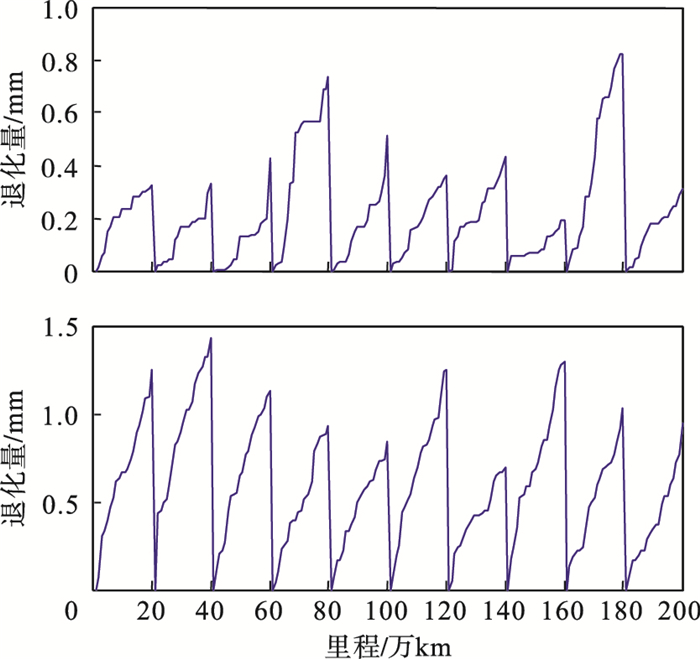 | 图 4 踏面和轮缘退化轨迹模拟Fig.4 Simulation of the tread and wheel flange degradation trajectory (a)—踏面;(b)—轮缘. |
由SIMPACK仿真得到的列车动力学指标如图 5所示, 随着踏面磨耗的加剧, 列车舒适度下降明显, 轮重减载率和脱轨系数略有上升, 但不明显.在列车镟修后运行15万km~45万km时, 列车的舒适度急剧下降, 因此有必要进行镟修.
图 5(Fig. 5)
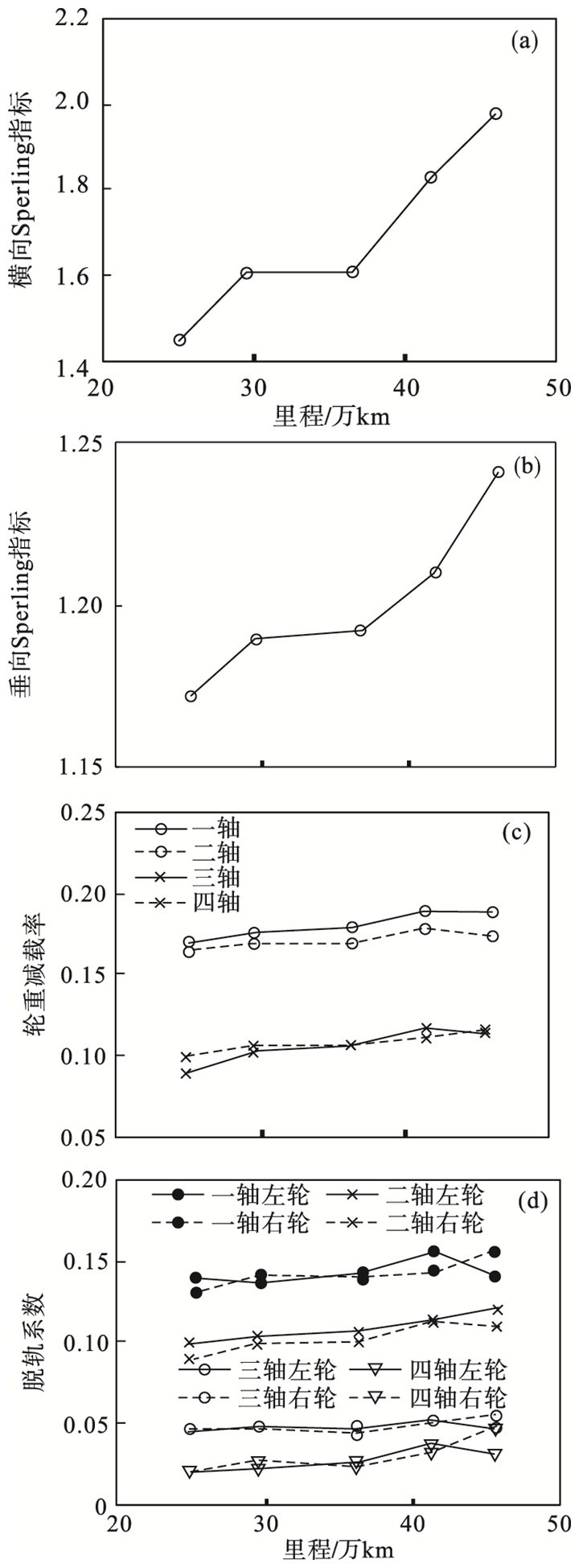 | 图 5 列车动力学随车轮磨耗加剧的变化Fig.5 Changes of train dynamics with increased wheel wear |
5 结论1) 退化量相互独立时的可靠性小于Gumbel Copula和Frank Copula相关失效可靠性.退化独立时的可靠性较相关失效时的可靠性较低, 会造成不必要的浪费; Gumbel Copula相关模型和Frank Copula相关模型相比, Gumbel Copula模型在上尾部的可靠性较高.
2) 在轮径退化可靠性模型中, 轮径退化对轮缘退化最灵敏, 其次是对镟修中每恢复1 mm需要消耗的轮径比较灵敏, 因此镟修过程中应该选取对轮径削减较少的方案.
3) 在一个镟修周期内, 列车动力学仿真中的动力学指标随着列车的踏面和轮缘的磨耗的增大而劣化.
参考文献
| [1] | 郝广波, 谢里阳, 李莉. 载荷共享并联系统疲劳累积损伤可靠性模型[J]. 东北大学学报(自然科学版), 2009, 30(2): 262-265, 278. (Hao Guang-bo, Xie Li-yang, Li Li. Reliability model of cumulative fatigue damage of load-sharing parallel system[J]. Journal of Northeastern University(Natural Science), 2009, 30(2): 262-265, 278.) |
| [2] | 王正, 谢里阳, 李兵. 机械零件动态可靠性模型及失效率研究[J]. 东北大学学报(自然科学版), 2007, 28(11): 1620-1623. (Wang Zheng, Xie Li-yang, Li Bing. Time-dependent reliability model and failure rate study of mechanical components[J]. Journal of Northeastern University(Natural Science), 2007, 28(11): 1620-1623.) |
| [3] | 王正, 谢里阳, 李兵. 考虑载荷作用次数的失效相关系统可靠性模型[J]. 东北大学学报(自然科学版), 2007, 28(5): 704-707. (Wang Zheng, Xie Li-yang, Li Bing. Reliability model of failure-dependent system with frequency of loading taken into account[J]. Journal of Northeastern University(Natural Science), 2007, 28(5): 704-707. DOI:10.3321/j.issn:1005-3026.2007.05.025) |
| [4] | 孙志礼, 张风和, 何雪宏. 两端截尾分布的应力-强度干涉模型[J]. 东北大学学报(自然科学版), 1998, 19(3): 3-5. (Sun Zhi-li, Zhang Feng-he, He Xue-hong. Stress-strength interference model of cutting off-tail distribution at two ends[J]. Journal of Northeastern University(Natural Science), 1998, 19(3): 3-5.) |
| [5] | 闫明, 张义民, 孙志礼. 机械零件相关失效可靠度及灵敏度计算的Monte Carlo方法[J]. 东北大学学报(自然科学版), 2011, 32(6): 834-837. (Yan Ming, Zhang Yi-min, Sun Zhi-li. Monte Carlo method for calculating the reliability and sensitivity of mechanical parts related failure[J]. Journal of Northeastern University(Natural Science), 2011, 32(6): 834-837. DOI:10.3969/j.issn.1005-3026.2011.06.019) |
| [6] | 涂宏茂, 孙志礼, 姬广振. 考虑失效模式相关性的机械系统可靠性分析[J]. 东北大学学报(自然科学版), 2017, 38(10): 1453-1458. (Tu Hong-mao, Sun Zhi-li, Ji Guang-zhen. Reliability analysis for mechanical system with correlated failure modes[J]. Journal of Northeastern University(Natural Science), 2017, 38(10): 1453-1458. DOI:10.12068/j.issn.1005-3026.2017.10.017) |
| [7] | Lu C J, Meeker W Q. Using degradation measures to estimate a time-to-failure distribution[J]. Technometrics, 1993, 35(2): 161-174. DOI:10.1080/00401706.1993.10485038 |
| [8] | Whitmore G A, Schenkelberg F. Modeling accelerated degradation data using Wiener diffusion with a time scale transformation[J]. Lifetime Data Analysis, 1997, 3(1): 27-45. DOI:10.1023/A:1009664101413 |
| [9] | Whitmore G A, Crowder M J, Lawless J F. Failure inference from a marker process based on a bivariate Wiener model[J]. Lifetime Data Analysis, 1998, 4(3): 229-251. DOI:10.1023/A:1009617814586 |
| [10] | Sun Q, Zhou J, Zhong Z, et al. Gauss-Poisson joint distribution model for degradation failure[J]. IEEE Transactions on Plasma Science, 2004, 32(5): 1864-1868. DOI:10.1109/TPS.2004.835964 |
| [11] | Pan Z, Sun Q, Feng J. Reliability modeling of systems with two dependent degrading components based on gamma processes[J]. Communications in Statistics-Theory and Methods, 2016, 45(7): 1923-1938. DOI:10.1080/03610926.2013.870201 |
| [12] | Jia X, Wang L, Wei C. Reliability research of dependent failure systems using copula[J]. Communications in Statistics-Simulation and Computation, 2014, 43(8): 1838-1851. DOI:10.1080/03610918.2013.800879 |
| [13] | Shen Z, Li Z. A fast non-steady state creep force model based on the simplified theory[J]. Wear, 1996, 191(1/2): 242-244. |
| [14] | Cui D, Li L, Jin X, et al. Optimal design of wheel profiles based on weighed wheel/rail gap[J]. Wear, 2011, 271(1): 218-226. |
| [15] | Jin X, Wu L, Fang J, et al. An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behaviour of a wheel/rail system[J]. Vehicle System Dynamics, 2012, 50(12): 1817-1834. DOI:10.1080/00423114.2012.695022 |
| [16] | Han P, Zhang W. A new binary wheel wear prediction model based on statistical method and the demonstration[J]. Wear, 2015, 324: 90-99. |
| [17] | Zhong W, Hu J J, Shen P, et al. Experimental investigation between rolling contact fatigue and wear of high-speed and heavy-haul railway and selection of rail material[J]. Wear, 2011, 271(9): 2485-2493. |
| [18] | Zhai W, Wang K, Cai C. Fundamentals of vehicle-track coupled dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1349-1376. DOI:10.1080/00423110802621561 |
| [19] | Zeng J, Wu P. Study on the wheel/rail interaction and derailment safety[J]. Wear, 2008, 265(9): 1452-1459. |
| [20] | Liu X, Zhai W. Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains[J]. Wear, 2014, 314(1): 282-290. |
| [21] | Jin X. Key problems faced in high-speed train operation[J]. Journal of Zhejiang University(Science A), 2014, 15(12): 936-945. |
| [22] | Li X, Jin X, Wen Z, et al. A new integrated model to predict wheel profile evolution due to wear[J]. Wear, 2011, 271(1): 227-237. |
| [23] | Wang X, Balakrishnan N, Guo B, et al. Residual life estimation based on bivariate non-stationary Gamma degradation process[J]. Journal of Statistical Computation and Simulation, 2015, 85(2): 405-421. DOI:10.1080/00949655.2013.824448 |
| [24] | 卢昊, 张义民, 赵长龙, 等. 多失效模式机械零件可靠性灵敏度估计[J]. 机械工程学报, 2012(2): 63-67. (Lu Hao, Zhang Yi-min, Zhao Chang-long, et al. Reliability sensitivity estimation of mechanical components with multiple failure modes[J]. Journal of Mechanical Engineering, 2012(2): 63-67.) |
| [25] | 崔大宾. 高速车轮踏面设计方法研究[D]. 成都: 西南交通大学, 2013. (Cui Da-bin. Study on wheel profile design method for high-speed train[D]. Chengdu: Southwest Jiaotong University, 2013. ) |
