唐俊林1,张栋1,王孟阳2,刘亮亮2
(1.西北工业大学 航天学院,西安 710072;2.空天飞行器设计陕西省重点实验室(西北工业大学),西安 710072)
摘要:
为化解敌方空袭的威胁,提高中等规模防空火力任务分配问题的求解效率,提出一种性能优越的链式多种群遗传算法(CMPGA)。首先建立改进的防空火力任务分配模型,综合考虑目标威胁程度、可拦截性判断等因素。目标威胁程度考虑目标的高度、速度、射程以及相对距离等威胁因素。可拦截性判断考虑时间约束、空间约束和性能约束,并将其融入杀伤概率的计算中,以简化模型的约束条件。其次提出CMPGA算法求解中等规模防空火力的最优任务分配方案。算法中综合运用了种群重复个体的数量限制策略、适应度相近个体的交叉变异策略、陷入局部极值时部分较优解的删除策略、链式环中种群当前最优解的传递策略。算法充分利用多种群并行搜索的优点,加快收敛速度,持续保持种群多样性,避免陷入局部极值。在标准测试函数的仿真以及防空火力任务分配问题的应用中,通过与几种典型优化算法的对比分析,结果表明CMPGA算法的性能优势较大,能以较高的概率快速地搜寻到最优解,从而验证了该算法的有效性和优越性。
关键词: 防空火力任务分配 遗传算法 链式多种群 多样性保持 分层选择
DOI：10.11918/202101056
分类号:E91,TJ761.13
文献标识码:A
基金项目:国家自然科学基金(61903301)
Air defense firepower task assignment based on improved chainlike multi-population genetic algorithm
TANG Junlin1,ZHANG Dong1,WANG Mengyang2,LIU Liangliang2
(1.School of Astronautics, Northwestern Polytechnical University, Xian 710072, China; 2. Shaanxi Key Laboratory of Aerospace Flight Vehicle Design (Northwestern Polytechnical University), Xian 710072, China)
Abstract:
In view of the threat of enemy air attack and the efficiency of solving the task assignment problem of medium-scale air defense firepower, a chainlike multi-population genetic algorithm (CMPGA) with superior performance was proposed. First, an improved air defense firepower task allocation model was established, which comprehensively investigates the threat degree of target and the interceptability judgment. The target threat degree was studied in terms of the threat factors such as the height, speed, range, and relative distance of the target. The time constraints, space constraints, and performance constraints were considered in the interceptability judgment, which was integrated into the kill probability to simplify the constraints of the model. Then, the CMPGA algorithm was proposed to solve the optimal allocation scheme of medium-scale air defense firepower. The algorithm utilized the strategy of limiting the number of repetitive individuals in the population, the cross mutation strategy of individuals with similar fitness, the deletion strategy of partial optimal solution when falling into local extremum, and the transfer strategy of the current optimal solution in the chain link. Combining the advantages of multi-population parallel search, the algorithm could speed up convergence speed, maintain the diversity of population, and avoid falling into local extremum. In the simulation of standard test function and the application to air defense firepower task allocation problem, the proposed algorithm was compared with several typical optimization algorithms. Results show that the CMPGA algorithm had advantageous performance and could quickly find the optimal solution with high probability, which indicates the effectiveness and superiority of the algorithm.
Key words: air defense firepower task assignment genetic algorithm chainlike multi-population diversity maintenance hierarchical selection
唐俊林, 张栋, 王孟阳, 刘亮亮. 改进链式多种群遗传算法的防空火力任务分配[J]. 哈尔滨工业大学学报, 2022, 54(6): 19-27. DOI: 10.11918/202101056.
TANG Junlin, ZHANG Dong, WANG Mengyang, LIU Liangliang. Air defense firepower task assignment based on improved chainlike multi-population genetic algorithm[J]. Journal of Harbin Institute of Technology, 2022, 54(6): 19-27. DOI: 10.11918/202101056.
基金项目 国家自然科学基金(61903301) 作者简介 唐俊林(1996—), 男, 硕士生 通信作者 张栋, zhangdong@nwpu.edu.cn 文章历史 收稿日期: 2021-01-15
Abstract Full text Figures/Tables PDF
改进链式多种群遗传算法的防空火力任务分配
唐俊林1, 张栋1
, 王孟阳2, 刘亮亮2 1. 西北工业大学 航天学院, 西安 710072;
2. 空天飞行器设计陕西省重点实验室(西北工业大学), 西安 710072
收稿日期: 2021-01-15
基金项目: 国家自然科学基金(61903301)
作者简介: 唐俊林(1996—), 男, 硕士生
通信作者: 张栋, zhangdong@nwpu.edu.cn
摘要: 为化解敌方空袭的威胁, 提高中等规模防空火力任务分配问题的求解效率, 提出一种性能优越的链式多种群遗传算法(CMPGA)。首先建立改进的防空火力任务分配模型, 综合考虑目标威胁程度、可拦截性判断等因素。目标威胁程度考虑目标的高度、速度、射程以及相对距离等威胁因素。可拦截性判断考虑时间约束、空间约束和性能约束, 并将其融入杀伤概率的计算中, 以简化模型的约束条件。其次提出CMPGA算法求解中等规模防空火力的最优任务分配方案。算法中综合运用了种群重复个体的数量限制策略、适应度相近个体的交叉变异策略、陷入局部极值时部分较优解的删除策略、链式环中种群当前最优解的传递策略。算法充分利用多种群并行搜索的优点, 加快收敛速度, 持续保持种群多样性, 避免陷入局部极值。在标准测试函数的仿真以及防空火力任务分配问题的应用中, 通过与几种典型优化算法的对比分析, 结果表明CMPGA算法的性能优势较大, 能以较高的概率快速地搜寻到最优解, 从而验证了该算法的有效性和优越性。
关键词: 防空火力任务分配 遗传算法 链式多种群 多样性保持 分层选择
Air defense firepower task assignment based on improved chainlike multi-population genetic algorithm
TANG Junlin1, ZHANG Dong1
, WANG Mengyang2, LIU Liangliang2 1. School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China;
2. Shaanxi Key Laboratory of Aerospace Flight Vehicle Design (Northwestern Polytechnical University), Xi'an 710072, China
Abstract: In view of the threat of enemy air attack and the efficiency of solving the task assignment problem of medium-scale air defense firepower, a chainlike multi-population genetic algorithm (CMPGA) with superior performance was proposed. First, an improved air defense firepower task allocation model was established, which comprehensively investigates the threat degree of target and the interceptability judgment. The target threat degree was studied in terms of the threat factors such as the height, speed, range, and relative distance of the target. The time constraints, space constraints, and performance constraints were considered in the interceptability judgment, which was integrated into the kill probability to simplify the constraints of the model. Then, the CMPGA algorithm was proposed to solve the optimal allocation scheme of medium-scale air defense firepower. The algorithm utilized the strategy of limiting the number of repetitive individuals in the population, the cross mutation strategy of individuals with similar fitness, the deletion strategy of partial optimal solution when falling into local extremum, and the transfer strategy of the current optimal solution in the chain link. Combining the advantages of multi-population parallel search, the algorithm could speed up convergence speed, maintain the diversity of population, and avoid falling into local extremum. In the simulation of standard test function and the application to air defense firepower task allocation problem, the proposed algorithm was compared with several typical optimization algorithms. Results show that the CMPGA algorithm had advantageous performance and could quickly find the optimal solution with high probability, which indicates the effectiveness and superiority of the algorithm.
Keywords: air defense firepower task assignment genetic algorithm chainlike multi-population diversity maintenance hierarchical selection
防空火力任务分配是防空指挥的重要环节，是决定作战效果的关键因素之一[1]。其目的是最大化武器装备作战效能，寻求敌方目标逃脱概率最小的方案[2]。
目前的研究中，防空火力任务分配模型考虑的重要因素包括目标的威胁程度和火力单元对目标的杀伤概率。文献[3]从分配控制条件、弹目相对距离和飞行时间3个方面，归纳了火力单元对目标的拦截可行性判断逻辑。文献[4]细化了防空火力任务分配通用模型，从多个方面评估目标威胁程度，构建杀伤区、发射区模型和单发导弹杀伤概率模型。因此，制定详细的威胁程度评估方法和可拦截性判断对防空火力任务分配的实际应用具有重要意义。
随着计算机技术的发展，智能优化算法已经成为解决防空火力任务分配等组合优化问题的重要方法。除了遗传算法、粒子群算法等经典算法之外，布谷鸟搜索算法[5]、合同网拍卖算法[6]和博弈论[7]等方法也可以用于求解任务分配问题。文献[8]通过控制初始种群中变量的取值范围和改进变异策略来提高搜索效率。文献[9]提出非支配排序算法(NSGA-Ⅲ)，引入具有良好收敛性和分布性的参考点来指导进化。面对极大的计算复杂性，文献[10]提出一种基于改进遗传算法的元启发式算法来改善随机任务分配问题的求解。文献[11]提出针对具体问题的种群初始化方法，重新定义了配对限制和选择操作。文献[12]提出一种基于遗传算法的anytime算法，引入元级控制，来确定算法的停机时刻。文献[13]提出多种群迁移遗传算法，利用种群间的迁移机制代替选择算子的筛选机制，并改进交叉和变异算子等操作。文献[14]提出一种基于ER网络的多种群遗传算法，研究子种群网络结构对优势基因在子种群间传播速度以及算法性能的影响。防空火力任务分配的实时性要求很高，响应过慢则可能贻误战机。传统智能优化算法及其改进算法，在种群规模和迭代次数受限时并不能稳定找到全局最优解。
针对目前防空火力任务分配模型以及智能优化算法所面临的问题，本文构建了一种改进的防空火力任务分配模型。模型细化目标威胁程度的评估方法，并将可拦截性约束条件简化。此外，进一步提出链式多种群遗传算法(Chainlike multi-population genetic algorithm, CMPGA)，运用链式多种群环、多样性保持、分层选择、去顶操作等策略，加快收敛速度并提高全局搜索能力。
1 防空火力任务分配模型 1.1 作战场景与决策变量为保护防御要地，在其周围部署m个位置不同的火力单元。假定空情显示有n个目标从各个方向袭来，我方需快速作出响应，将来袭目标分配给各火力单元，以化解敌方空袭威胁。防空火力任务分配的方案用矩阵D={dij}, i∈1, 2, …, m, j∈1, 2, …, n描述, 矩阵D的各个元素为
$d_{i j}= \begin{cases}1, & \text { fire } i \rightarrow \text { target } j \\ 0, & \text { fire } i \not\rightarrow \text { target } j\end{cases}$ (1)
1.2 目标函数最大化作战效能的目标函数建立如下:
$\min F=\sum\limits_{j}^{n} W_{j} \prod\limits_{i}^{m}\left(1-d_{i j} P_{i j}\right)$ (2)
式中：Pij为火力i对目标j的杀伤概率, Wj为目标j的威胁程度系数,
1.3 约束条件防空火力任务分配考虑的约束条件如下：
1) 每个火力单元最多分配μi个目标，μi为火力单元i的打击通道数，即
$\sum\limits_{j}^{n} d_{i j} \leqslant \mu_{i}, \forall i$ (3)
2) 每个目标最少分配1个火力单元，最多分配λj个火力单元，即
$1 \leqslant \sum\limits_{i}^{m} d_{i j} \leqslant \lambda_{j}, \forall j$ (4)
1.4 目标威胁程度模型威胁程度的评估如下：
1) 目标飞行高度威胁因子。当敌方来袭目标在低空出现时，攻击意图明显，己方的防御时间短促，威胁程度显著增强。目标飞行高度威胁因子为[15]
$\mu_{h}=\left\{\begin{array}{cc}1, & h \leqslant h_{\mathrm{c}} \\e^{-k_{1}\left(h-h_{\mathrm{c}}\right)^{2}}, & h>h_{\mathrm{c}}\end{array}\right.$ (5)
式中高度的临界值hc=1 500 m，衰减参数k1=10-11。
2) 目标飞行速度威胁因子。飞行速度越快的目标一定程度上拥有更强的机动能力和作战能力，己方拦截更加困难，威胁程度也更大。目标飞行速度威胁因子为[15]
$\mu_{v}=1-\mathrm{e}^{-\alpha v}$ (6)
式中α=0.001 5。
3) 目标射程威胁因子。在区域防空作战中，来袭目标可能是飞机或者导弹。导弹的射程直接反映导弹的杀伤威力。短程、中程导弹射程短，杀伤力有限。远程、洲际导弹搭载核弹头，破环性极强。当目标类型为导弹时，目标射程威胁因子为[4]
$\mu_{L}=\left\{\begin{array}{lr}0.4, & L \leqslant 1\ 000 \\0.4+0.3 \times \frac{L-1\ 000}{5\ 000-1\ 000}, & 1\ 000<L \leqslant 5\ 000 \\0.7+0.3 \times \frac{L-5\ 000}{8\ 000-5\ 000}, & 5\ 000<L \leqslant 8\ 000 \\1.0, & L>8\ 000\end{array}\right.$ (7)
式中L为导弹的射程，km。
4) 目标距离威胁因子。目标距离己方防御要地中心的距离r也反映目标的威胁程度。目标距离己方防御要地中心的距离r越小，威胁程度越大。目标距离威胁因子为
$\mu_{r}=1-\frac{r}{r_{\max }}$ (8)
式中rmax为己方相对于防御要地中心的最大可探测距离。
综上所述，目标威胁系数由各威胁因子及其权重加权求和得到：
$W_{j}=w_{h} \mu_{h}+w_{v} \mu_{v}+w_{L} \mu_{L}+w_{r} \mu_{r}$ (9)
式中wh、wv、wL、wr分别为目标飞行高度威胁因子、目标飞行速度威胁因子、目标射程威胁因子和目标距离威胁因子的权重，均由专家经验给出。
1.5 可拦截性判断模型具体判断过程如下：
1) 若火力单元i不满足对目标j的可拦截性条件，则令Pij=0。如此处理可将一些约束条件融入杀伤概率的计算中，有利于约束条件的简化。目标可拦截性判断如下[3]：如图 1所示，点A为目标的位置，点B为火力单元的位置，以点B为圆心的圆是火力单元的杀伤区。
Fig. 1
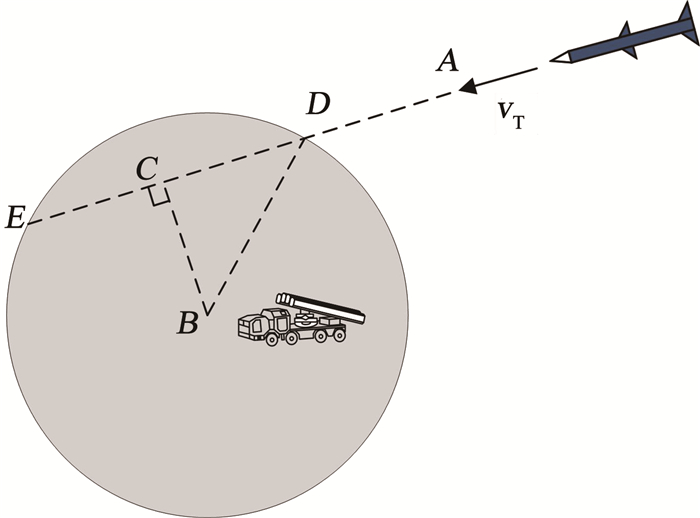图 1 火力单元与目标的相对位置 Fig. 1 Relative position of fire unit and target ① 航路捷径约束。航路捷径LBC为目标速度矢量与火力单元的最短距离，即
$L_{B C}=L_{A B} \sin \angle E A B$ (10)
火力单元无法拦截航路捷径大于其杀伤半径Ri的目标，即
$L_{B C}>R_{i} \rightarrow P_{i j}=0$ (11)
② 最大拦截速度约束。火力单元无法拦截速度超过其最大可拦截速度vmaxi的目标，即
$v_{j}>v_{\max i} \rightarrow P_{i j}=0$ (12)
③ 目标飞离时间约束。火力单元无法拦截即将飞离其杀伤区的目标。若目标j的预估飞离时间TAE小于火力单元i的准备时间Tri和其防空导弹的预估飞行时间Tfi之和，则目标j不满足火力单元i的拦截条件，即：
${Tr}_{i}+T f_{i}>T_{A E} \rightarrow P_{i j}=0$ (13)
$T f_{i}=\frac{1.1 R_{i}}{v_{i}}$ (14)
$T_{A E}=\frac{L_{A E}}{v_{j}}$ (15)
式中：vj为目标j的飞行速度，vi为火力单元i拦截导弹的飞行速度。
④ 拦截高度约束。火力单元的可拦截高度应介于其杀伤区高低界之间，即:
$h_{j}<h_{i \min } \rightarrow P_{i j}=0$ (16)
$h_{j}>h_{i \max } \rightarrow P_{i j}=0$ (17)
式中：hj为目标j的飞行高度，himin、himax分别为火力单元i的杀伤区低界与高界。
2) 若火力单元i满足对目标j的可拦截性条件，即航路捷径约束、最大拦截速度约束、目标飞离时间约束、拦截高度约束、杀伤概率取经验值Pij。
2 基于链式多种群遗传算法的防空火力任务分配针对上文所建防空火力任务分配模型，提出一种链式多种群遗传算法(CMPGA)。首先提出传统遗传算法的改进措施，包括多样性保持、分层选择、去顶操作。在此基础上提出链式多种群环结构，既让多种群共享当前最优解，又一定程度上保留单个种群进化的独立性。
2.1 改进型遗传算法 2.1.1 编码方式采用二进制编码，即表示防空火力任务分配方案的矩阵D={dij}, i∈1, 2, …, m, j∈1, 2, …, n。
2.1.2 适应度评价适应度表征个体的优劣程度。适应度越大，个体越优秀。适应度函数取目标函数的倒数:
$f(\boldsymbol{D})=\frac{1}{F(\boldsymbol{D})}$ (18)
2.1.3 分层选择按轮盘赌策略从父种群中选择与父种群规模相同的N个个体，等待完成交叉变异操作后生成子种群。轮盘赌策略根据个体的适应度确定被选择的概率，个体适应度越高，被选择的概率越大。种群中适应度为f(Dk)的第k个个体被选择的概率为
$P_{k}=\frac{f\left(\boldsymbol{D}_{k}\right)}{\sum\limits_{i=1}^{N} f\left(\boldsymbol{D}_{i}\right)}$ (19)
式中N为种群规模。
遗传算法中，适应度相近的个体经过交叉变异后更有可能产生比父代优秀的子代个体，所以采用分层选择策略能加快种群的进化速度。所分层数根据种群大小确定，以3层为例说明。除初代种群以外，父种群中的个体已按适应度从优到劣排列，可以直接采取如下操作：从父种群的0~N/2个体中选择N/3个个体进入子种群，从父种群的N/2+1~N个体中选择N/3个个体进入子种群，从整个父种群中选择N/3个个体进入子种群。对父种群的分层如图 2所示。
Fig. 2
图 2 种群分层 Fig. 2 Population stratification 2.1.4 单点交叉操作对父代两个任务分配矩阵的每一行执行单点交叉操作。对第i行，随机生成区间(0, 1)的数r1，若r1 < Pcro，则对第i行执行交叉操作；否则不进行交叉。其中，Pcro为交叉概率。随机生成区间(1, n)的整数r2，交换两个矩阵第i行第r2列之后的序列。交叉后两个任务分配矩阵可能会违反约束条件，需进行冲突消解。交叉过程如图 3所示。
Fig. 3
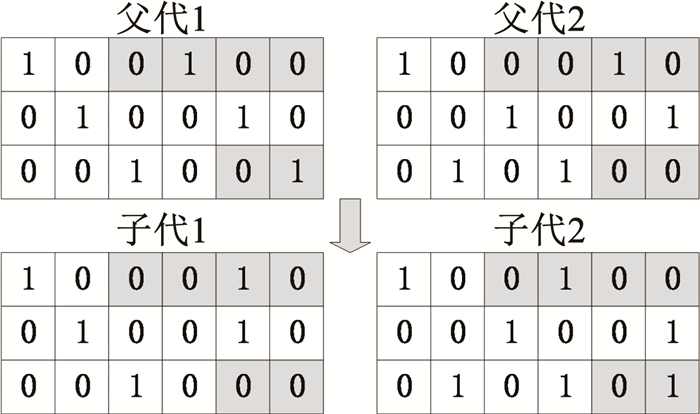图 3 交叉操作 Fig. 3 Cross operation 2.1.5 变异操作对任务分配矩阵的每个基因位，以Pmu的变异概率将0置为1，或将1置为0。为了增强遗传算法的局部寻优能力，每个基因位变异后都对任务分配矩阵进行冲突消解，并计算个体的适应度，若适应度大于该基因位变异前的适应度，则不对该个体后续的基因位执行变异操作。
2.1.6 多样性保持策略借鉴NSGA-Ⅱ的思想，将子种群与父种群合并，从中选择结构不同的个体组成新的父种群[16]。将经过交叉变异的子种群和父种群合并，对合并种群的2N个个体按适应度从优到劣进行排序，依次选择结构不同的N个个体组成新一代的父种群。
为避免迭代后期种群同质化严重，在合并种群中从优到劣依次选择个体进入新父种群时，同一结构的个体最多只能有Nsi个进入新父种群。这使得新父种群中同一适应度的个体不超过Nsi，从而能持续维持种群的多样性，降低算法陷入局部极值的概率。对合并种群的2N个个体进行排序后，结构相同的个体适应度也相同，往往集中在一起。每次从合并种群中将待选个体加入新父种群前，需计算新父种群中与当前个体适应度相同的个数，若小于Nsi时，将待选个体加入，若等于Nsi时，舍弃当前个体。当Nsi=2时，从合并种群中选择个体的过程如图 4所示。
Fig. 4
图 4 多样性保持的选择过程 Fig. 4 Selection process of diversity maintenance 2.1.7 去顶操作在合并种群中从优到劣依次选择个体进入新父种群前，需判断合并种群的最优个体相较于前代是否改变。若最优个体连续Ga代未发生改变，说明该种群可能陷入了局部最优。为跳出局部最优，采用后退的思维方式，将已经搜寻到的一部分最优秀的个体删除，即将局部最优解删除，剩余个体继续参与后续的遗传操作，重新搜寻最优解。若最优个体连续Ga代未改变，跳过前面的Nj个个体，从第Nj+1个个体开始依次选择个体加入新父种群；否则，从第1个个体开始选择。若去顶操作后种群多样性不足，生成随机个体补全新父种群。当Nj=10时，对合并种群的去顶操作如图 5所示。
Fig. 5
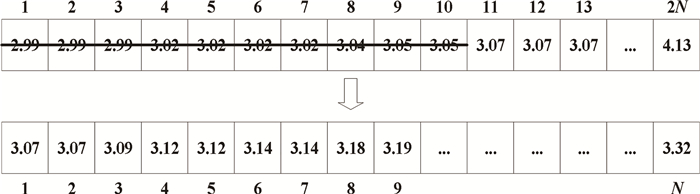图 5 去顶操作 Fig. 5 Topping operation 2.2 基于CMPGA的防空火力任务分配基于上述改进型遗传算法，利用多种群并行搜索的思想提出CMPGA算法。一般多种群进化算法每次迭代完成后都会将当前最优解在所有种群范围内共享[17]。这样多种群间的信息共享过于频繁，并不能充分发挥多种群的优势。本文所提算法每隔数代才会出现当前最优解的传递，并且每次只有一个种群将移民算子传递给其后一个种群。当间隔代数达到Gr时，将种群Pf的当前最差解替换为种群Pl的当前最优解。
$P_{\mathrm{f}}={\rm mod} \left(\left\lfloor\frac{G}{G_{\mathrm{r}}}\right\rfloor, N_{\mathrm{p}}\right)$ (20)
$P_{\mathrm{l}}={\rm mod} \left(\left\lfloor\frac{G}{G_{\mathrm{r}}}\right\rfloor-1, N_{\mathrm{p}}\right)$ (21)
式中：G为当前迭代数,
以首尾相连的Np个种群为例，假设当前种群为Pi, i∈0, 1, …, Np-1, 间隔代数达到Gr时，将种群Pi+1的最差解替换为种群Pi的当前最优解；当间隔代数再次达到Gr时，将种群Pi+2的最差解替换为种群Pi+1的当前最优解，如此循环往复。当前种群为PNp-1时，其最优解传递给种群P0。当种群Pi将最优解传递给种群Pi+1后，需要相隔Gr×(Np-1)代，才会接受到来自种群Pi-1的最优解。这样既保留各种群自身进化的独立性，也能适时共享其他种群的最优解。4个种群构成的链式环结构如图 6所示。
Fig. 6
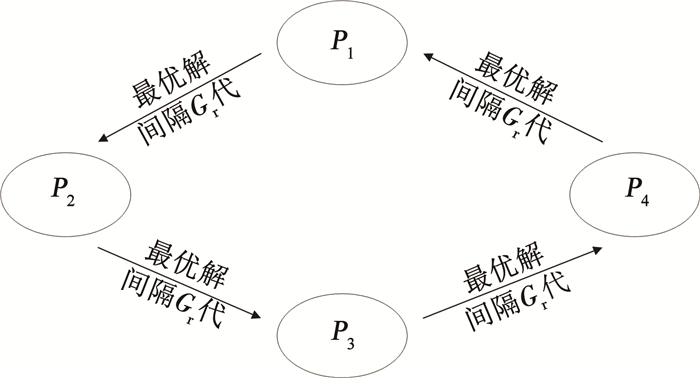图 6 链式多种群环结构图 Fig. 6 Structure of chainlike multi-population ring 在CMPGA算法中，种群数量的增加对性能的提升十分显著。算法流程图如图 7所示。
Fig. 7
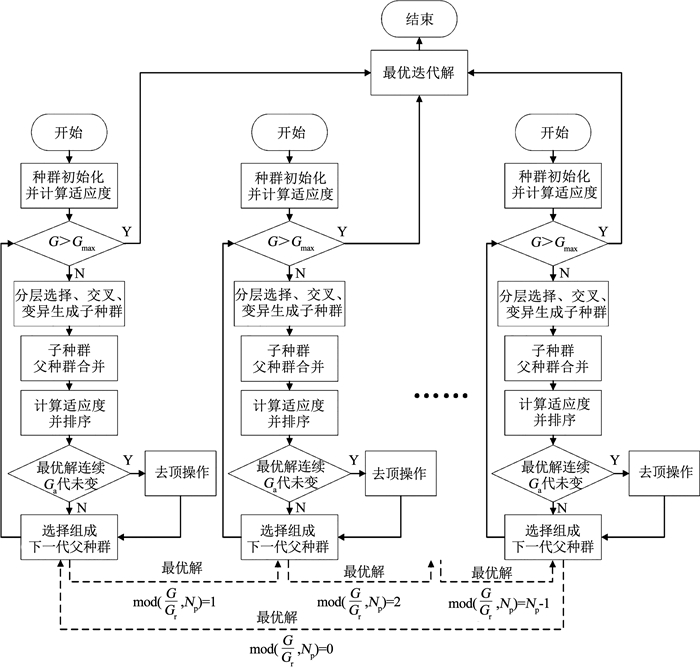图 7 链式多种群遗传算法流程图 Fig. 7 Flow chart of chainlike multi-population genetic algorithm 基于CMPGA算法的防空火力任务分配具体步骤如下。
算法 ? CMPGA算法求解任务分配问题
Step 1? 分别随机初始化各个种群P0, P1, …, PNp-1，并计算个体的适应度。
Step 2? 若达到最大进化代数，输出所有种群的全局最优解。否则，跳转至step3。
Step 3 ?采用轮盘赌策略和分层选择策略分别对各个种群执行选择操作，生成待交叉变异、与父种群规模相同的子种群。
Step 4 ? 分别对各个子种群执行交叉、变异操作。
Step 5? 分别将各个子种群和对应的父种群合并，并对合并种群的个体按适应度从优到劣排序。
Step 6? 分别从各个合并种群中选择结构不同的N个个体组成新父种群。当种群最优解连续Ga代未变时，从合并种群的第Nj+1个个体开始依次选择个体加入新父种群；否则，从合并种群的第1个个体开始依次选择。
Step 7? 当间隔代数达到Gr时，将种群Pf的当前最差解替换为种群Pl的当前最优解。当间隔代数未达到Gr时，不进行任何操作。跳转至step2。
2.3 冲突消解策略本文采用冲突消解策略以使算法获得满足约束条件的解，结构如图 8所示。
Fig. 8
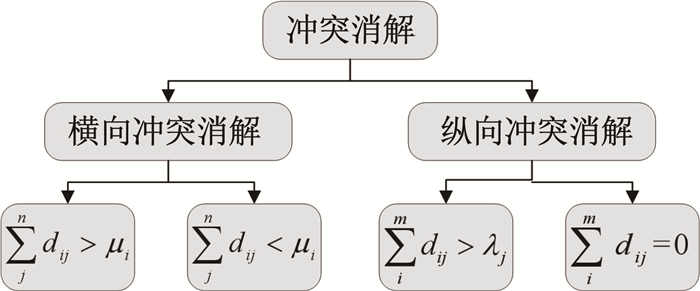图 8 冲突消解 Fig. 8 Conflict resolution 为尽量不破坏个体的结构，冲突消解策略可分为：
1) 横向冲突消解。对于任务分配矩阵的每一行，当为火力单元分配的目标数量大于该火力单元的通道数μi，即
2) 纵向冲突消解。对于防空火力任务分配矩阵的每一列，当为目标分配的火力单元过多，即
3) 漏网目标消解。属于纵向冲突消解的一部分。对于防空火力任务分配矩阵的每一列，当为目标分配的火力单元数量为0，即
3 仿真结果为了验证CMPGA算法的性能，本文选取3个标准测试函数，寻找它们的全局极小值。其后，在火力资源通道数大于来袭目标数时，对中等规模算例进行仿真，以验证防空火力任务分配模型的有效性。
3.1 算法性能测试采用3种标准单目标优化测试函数对CMPGA算法进行对比测试。
1) Schaffer函数。
$f(x, y)=0.5+\frac{\left(\sin \sqrt{x^{2}+y^{2}}\right)^{2}-0.5}{\left(1+0.01\left(x^{2}+y^{2}\right)\right)^{2}} $ (22)
$-10 \leqslant x, y \leqslant 10$ (23)
该函数有无数个极小值点，在(0, 0)处取得最小值0，具有强烈振荡的形态。
2) Shubert函数。
$\begin{aligned}f(x, y)=&\left\{\sum\limits_{i=1}^{5} i \cos [(i+1) x+i]\right\} \times \\&\left\{\sum\limits_{i=1}^{5} i \cos [(i+1) y+i]\right\}\end{aligned}$ (24)
$-10 \leqslant x, y \leqslant 10$ (25)
此函数存在760个局部极小值，极难找到全局最优解，在(-1.425 13, 0.800 32)处取得最小值-186.730 9。
3) Eggholder函数。
$\begin{aligned}f(x, y)=&-(y+47) \sin \left(\sqrt{\left|y+\frac{x}{2}+47\right|}\right)-\\& x \sin (\sqrt{|x-(y+47)|})\end{aligned}$ (26)
$-512 \leqslant x, y \leqslant 512$ (27)
此函数多峰值, 在(x, y)=(512, 404.231 9)处取得全局最小值-959.640 7。
针对以上3个标准测试函数，分别利用链式多种群遗传算法(CMPGA)、多种群遗传算法(Multi-population genetic algorithm, MPGA)[17]、遗传算法(Genetic algorithm, GA)和二进制离散粒子群算法(Binary discrete particle swarm optimization, BDPSO)求解全局极小值，均采用二进制编码和单点交叉策略，每种算法各运行100次，进行对比分析见表 1~3。
表 1
表 1 4种算法求解Schaffer函数100次运行结果对比 Tab. 1 Comparison of results of 100 runs of four algorithms for solving Schaffer function 算法名称 种群规模 进化代数 平均值 最优解 最优解次数 CMPGA 130*3 200 0 0 100
MPGA 500*3 300 0 0 100
BDPSO 600 400 0.003 21 0 67
GA 600 400 0 0 96
表 1 4种算法求解Schaffer函数100次运行结果对比 Tab. 1 Comparison of results of 100 runs of four algorithms for solving Schaffer function
表 2
表 2 4种算法求解Shubert函数100次运行结果对比 Tab. 2 Comparison of results of 100 runs of four algorithms for solving Shubert function 算法名称 种群规模 进化代数 平均值 最优解 最优解次数 CMPGA 100*6 200 -186.730 897 -186.730 9 91
MPGA 500*3 300 -186.730 872 -186.730 9 63
BDPSO 600 400 -186.730 128 -186.730 9 16
GA 600 400 -186.730 852 -186.730 9 48
表 2 4种算法求解Shubert函数100次运行结果对比 Tab. 2 Comparison of results of 100 runs of four algorithms for solving Shubert function
表 3
表 3 4种算法求解Eggholder函数100次运行结果对比 Tab. 3 Comparison of results of 100 runs of four algorithms for solving Eggholder function 算法名称 种群规模 进化代数 平均值 最优解 最优解次数 CMPGA 100*6 200 -959.585 02 -959.640 5 97
MPGA 500*3 300 -959.255 16 -959.640 5 86
BDPSO 600 400 -957.075 51 -959.640 5 43
GA 600 400 -958.804 44 -959.640 5 70
表 3 4种算法求解Eggholder函数100次运行结果对比 Tab. 3 Comparison of results of 100 runs of four algorithms for solving Eggholder function
由表 1可知，CMPGA、MPGA、GA算法均能较为稳定地求得Schaffer函数的全局极小值，BDPSO算法容易陷入局部极值。由表 2可知，CMPGA算法能较为稳定地求得Shubert函数的全局极小值，MPGA、BDPSO与GA算法均容易陷入局部极值。由表 3可知，CMPGA算法仍能较为稳定地求得Eggholder函数的全局极小值，MPGA和GA算法性能次之。BDPSO算法容易陷入局部极值。由以上3个测试函数的求解可知，从收敛的快速性和结果的稳定性来看，CMPGA算法均能以较小的种群规模和进化代数，较高的概率寻得全局最优解，其性能明显领先于MPGA、BDPSO和GA算法。
3.2 仿真算例假设某次防空作战中，己方部署8个位置不同的火力单元。火力单元对目标的经验杀伤概率由[0.5, 1.0]的随机数生成，计算目标威胁程度时，wh，wv，wL，wr均为0.25，己方防御中心位置为(0, 0), 其最大可探测距离rmax=90 000 m。各个火力单元及目标的参数见表 4、5。
表 4
表 4 火力单元参数 Tab. 4 Fire unit parameters 编号 位置/km 杀伤高低界/km 速度v/(m·s-1) 杀伤半径Ri/km 拦截速度vmaxi/(m·s-1) 准备时间Tri/s 通道数μi 1 (0, 20) (0.4, 15) 400 50 600 0.1 3
2 (27, 18) (0.4, 15) 450 50 650 0.1 3
3 (18, 27) (0.4, 15) 460 50 580 0.1 3
4 (9, 36) (0.4, 15) 470 50 580 0.1 3
5 (36, -9) (0.4, 15) 480 50 620 0.1 3
6 (27, -18) (0.4, 15) 450 50 610 0.1 3
7 (18, -27) (0.4, 15) 420 50 620 0.1 3
8 (0 -20) (0.4, 15) 490 50 620 0.1 3
表 4 火力单元参数 Tab. 4 Fire unit parameters
表 5
表 5 目标参数 Tab. 5 Target parameters 编号 x/km y/km 高度h/m 速度v/(m·s-1) 航向角φ/(°) 射程L/km 1 20 45 3 000 350 225 4 000
2 25 40 3 000 350 225 4 000
3 30 35 3 000 350 225 4 000
4 35 30 2 000 450 225 6 000
5 40 25 2 000 450 225 6 000
6 45 20 2 000 450 225 6 000
7 50 15 2 000 450 225 6 000
8 55 10 2 000 450 225 6 000
9 60 5 2 000 450 225 6 000
10 20 -45 5 000 250 135 800
11 25 -40 5 000 250 135 800
12 30 -35 5 000 250 135 800
13 35 -30 1 500 500 135 8 000
14 40 -25 1 500 500 135 8 000
15 45 -20 1 500 500 135 8 000
16 50 -15 1 500 500 135 8 000
17 55 -10 1 500 500 135 8 000
18 60 -5 1 500 500 135 8 000
表 5 目标参数 Tab. 5 Target parameters
3.3 仿真结果防空火力任务分配问题的搜索空间随目标和火力单元数量的增加而急剧增大。大多数文献的仿真算例规模较小，易于求解。本文通过与二进制离散粒子群算法(BDPSO)、遗传算法(GA)和多种群遗传算法(MPGA)的对比，来体现CMPGA算法能以更大的概率快速搜寻到最优解。
CMPGA算法各参数取值为：最大进化代数200，种群数Np=5，种群规模N=80，共分为3层，交叉概率Pcro=0.9，变异概率Pmu=0.01，最大重复次数Nsi=1，传递间隔代数Gr=30，去顶代数Ga=65，去顶个数Nj=10。
BDPSO算法各参数取值为：最大进化代数500，粒子群规模SN1=500，速度惯性因子w=1.0，学习因子c1=2，学习因子c2=2。
GA算法为：最大进化代数500，遗传种群规模SN2=500，交叉概率Pcro=0.6，变异概率Pmu=0.01。采用精英策略，将当代适应度排序前SN2/10个较优解直接复制到下一代，防止已搜寻到的最优解丢失。
MPGA算法为：最大进化代数500，种群数量3，各种群规模SN3=500，交叉概率Pcro=0.6，变异概率Pmu=0.01，采用上述精英策略。
4种算法各运行100次的结果见表 6和如图 9所示。
表 6
表 6 4种算法100次运行结果对比 Tab. 6 Comparison of results of 100 runs of four algorithms 算法名称 种群规模 进化代数 平均值 最差解 最优解 最优解次数 CMPGA 80*5 200 0.478 018 0.512 31 0.477 49 97
MPGA 300*5 300 0.485 540 0.540 69 0.477 49 55
BDPSO 500 500 0.484 998 0.520 25 0.477 49 48
GA 500 500 0.489 856 0.530 94 0.477 49 41
表 6 4种算法100次运行结果对比 Tab. 6 Comparison of results of 100 runs of four algorithms
Fig. 9
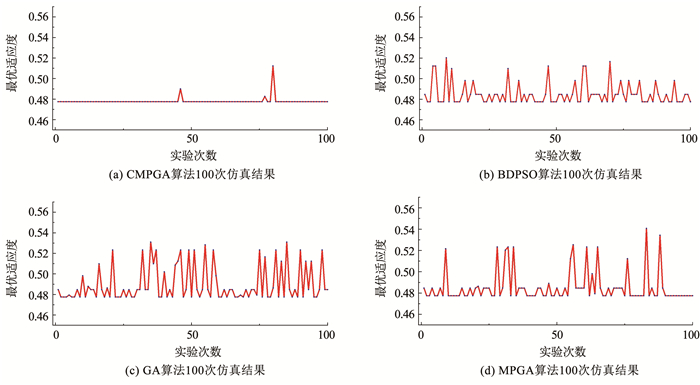图 9 4种算法100次仿真结果 Fig. 9 Simulation results of 100 runs of four algorithms 如表 6和图 9可知，火力单元数大于目标数时，局部最优解较多，3种对比算法获得最优解的概率均较低。本文所提CMPGA算法，以种群总规模400，200次的迭代仍有约97%的概率获得全局最优。4种算法均求得此算例的最优解见表 7。
表 7
表 7 最优分配方案 Tab. 7 Optimal allocation scheme 火力单元 分配目标 火力单元 分配目标 1 16, 17, 18 5 4, 13, 16
2 3, 6, 12 6 2, 9, 11
3 1, 17, 18 7 2, 8, 10
4 5, 14, 15 8 4, 7, 13
表 7 最优分配方案 Tab. 7 Optimal allocation scheme
为具体说明CMPGA算法快速收敛的性能，分别选取4种算法某次运行中目标函数的变化如图 10所示。
Fig. 10
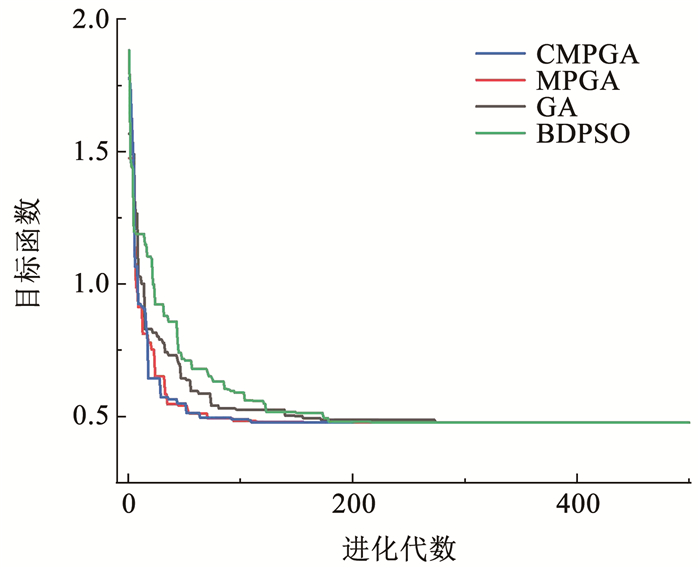图 10 单次运行结果对比 Fig. 10 Comparison of single run results 由图 10可知，CMPGA的收敛速度与MPGA相当。BDPSO和GA的收敛速度较慢。4种算法的单次运行时长见表 8。
表 8
表 8 单次运行时长对比 Tab. 8 Comparison of single run duration 算法名称 种群规模 进化代数 单次运行时长/s CMPGA 80*5 200 12.479
MPGA 500*3 300 59.056
BDPSO 500 500 21.647
GA 500 500 32.482
表 8 单次运行时长对比 Tab. 8 Comparison of single run duration
从单次运算时长来看，3种对比算法所需的种群规模和进化代数较大，运行时长较长。综合考虑运算时长和寻优性能，CMPGA算法为首选。
仿真表明，本文所提的CMPGA算法，通过多种策略的结合，同时具有收敛快速和全局寻优能力强的优点，能够以极高的概率搜寻到最优解。
4 结论1) 本文提出改进的防空火力任务分配模型，详细介绍目标威胁程度的计算，并将可拦截性判断融入杀伤概率中，以简化模型的约束条件。本文使用有效的冲突消解策略，尽可能少地破环个体结构，以保证算法易于寻优。
2) 综合运用链式多种群环、多样性保持、分层选择、去顶操作等策略，提出CMPGA算法，大幅提升遗传算法的寻优性能。为验证算法性能的优越性，仿真选取3个标准测试函数和中等规模的任务分配算例。仿真结果表明，算法快速收敛的同时能有效跳出局部极值。
参考文献
[1] 陈黎, 王中许, 武兆斌, 等. 一种基于先期毁伤准则的防空火力优化分配[J]. 航空学报, 2014, 35(9): 2574.
CHEN Li, WANG Zhongxu, WU Zhaobin, et al. A kind of antiaircraft weapon-target optimal assignment under earlier damage principle[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2574. DOI:10.7527/S1000-6893.2014.0048
[2] 张蛟, 王中许, 陈黎, 等. 具有多次拦截时机的防空火力分配建模及其优化方法研究[J]. 兵工学报, 2014, 35(10): 1644.
ZHANG Jiao, WANG Zhongxu, CHENG Li, et al. Modeling and optimization on antiaircraft weapon-target assignment at multiple interception opportunity[J]. Acta Armamentarii, 2014, 35(10): 1644. DOI:10.3969/j.issn.1000-4093.2014.10.019
[3] 杨荣军, 闫德恒, 杨荣, 等. 区域防空拦截可行性与火力分配算法研究[J]. 弹道学报, 2016, 28(4): 57.
YANG Rongjun, YAN Deheng, YANG Rong, et al. Study on region antiaircraft interception feasibility and weapon-target allocation algorithm[J]. Journal of Ballistics, 2016, 28(4): 57. DOI:10.3969/j.issn.1004-499X.2016.04.011
[4] 贾健. 多平台防空协同任务分配问题研究[D]. 北京: 北京理工大学, 2016
JIA Jian. Cooperative task allocation in multi-platform air defense[D]. Beijing: Beijing Institute of Technology, 2016
[5] 孙海文, 谢晓方, 孙涛, 等. 改进型布谷鸟搜索算法的防空火力优化分配模型求解[J]. 兵工学报, 2019, 40(1): 189.
SUN Haiwen, XIE Xiaofang, SUN Tao, et al. Improved cuckoo search algorithm for solving antiaircraft weapon-target optimal assignment model[J]. Acta Armamentarii, 2019, 40(1): 189. DOI:10.3969/j.issn.1000-1093.2019.01.022
[6] 王然然, 魏文领, 杨铭超, 等. 考虑协同航路规划的多无人机任务分配[J]. 航空学报, 2020, 41(S2): 724234.
WANG Ranran, WEI Wenling, YANG Mingchao, et al. Task allocation of multiple UAVs considering cooperativeroute planning[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724234. DOI:10.7527/S1000-6893.2020.24234
[7] 周兴旺, 丁颖峰. 空袭火力资源分配综述[J]. 电子信息对抗技术, 2016, 31(6): 44.
ZHOU Xingwang, DING Yingfeng. Overview on air-raid firepower resources allocation[J]. Electronic Information Warfare Technology, 2016, 31(6): 44. DOI:10.3969/j.issn.1674-2230.2016.06.009
[8] 王然辉, 王超. 面向对地打击武器-目标分配问题的遗传算法变量取值控制技术[J]. 兵工学报, 2016, 37(10): 1889.
WANG Ranhui, WANG Chao. Variable value control technology of genetic algorithm for WTA of ground target attacking[J]. Acta Armamentarii, 2016, 37(10): 1889. DOI:10.3969/j.issn.1000-1093.2016.10.016
[9] LI You, KOU Yingxin, LI Zhanwu, et al. An improved nondominated sorting genetic algorithm Ⅲ method for solving multi-objective weapon-target assignment part Ⅰ: The value of fighter combat[J]. International Journal of Aerospace Engineering, 2018, 2018(PT.2): 1. DOI:10.1155/2018/8302324
[10] JIA Zhenyue, YU Jianqiao, AI Xiaolin, et al. Cooperative multiple task assignment problem with stochastic velocities and time windows for heterogeneous unmanned aerial vehicles using a genetic algorithm[J]. Aerospace Science and Technology, 2018, 76: 112. DOI:10.1016/j.ast.2018.01.025
[11] LI Xiaoyang, ZHOU Deyun, PANQian, et al. Weapon-target assignment problem by multi-objective evolutionary algorithm based on decomposition[J]. Complexity, 2018, 1. DOI:10.1155/2018/8623051
[12] 冯超, 景小宁. 复合打击下具有多次拦截时机的火力分配问题[J]. 航空学报, 2016, 37(11): 3444.
FENG Chao, JING Xiaoning. Weapon target assignment at multiple interception opportunities in composite strikes[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3444. DOI:10.7527/S1000-6893.2016.0082
[13] HAO Kun, ZHAO Jiale, YU Kaicheng, et al. Path planning of mobile robots based on a multi-population migration genetic algorithm[J]. Sensors, 2020, 20(20): 5873. DOI:10.3390/s20205873
[14] SHI Xiaoqiu, LONG Wei, LI Yanyan, et al. Multi-population genetic algorithm with ER network for solving flexible job shop scheduling problems[J]. PLOS ONE, 2020, 15(5): 1. DOI:10.1371/journal.pone.0233759
[15] 谢永杰. 多平台防空导弹任务分配及协同制导方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019
XIE Yongjie. Research on task assignment and cooperative guidance of multi-platform air defense missile[D]. Harbin: Harbin Institute of Technology, 2019
[16] DEB K, PRATAP K, AGARWAL K, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182. DOI:10.1109/4235.996017
[17] 董浩, 李烨. 基于多种群遗传算法的虚拟机优化部署研究[J]. 控制工程, 2020, 27(2): 335.
DONG Hao, LI Ye. Research on optimization of virtual machine deployment based on multi-population genetic algorithm[J]. Control Engineering of China, 2020, 27(2): 335. DOI:10.14107/j.cnki.kzgc.170671
