程国柱1,2,程瑞1,徐亮3
(1.东北林业大学 交通学院, 哈尔滨 150040;2.重庆市交通运输工程重点试验室(重庆交通大学), 重庆 404100; 3.长春工程学院 土木工程学院, 长春 130012)
摘要:
为降低小半径曲线段路侧事故概率,选取道路线形指标(圆曲线半径、硬路肩宽度、纵坡坡度、超高横坡度、圆曲线加宽)、路面状况(路面附着系数)、交通特性(车速、车型)8个路侧事故风险因素进行PC-crash仿真试验,收集12 800组数据. 采用CHAID(Chi-squared automatic interaction detection)决策树技术识别了影响路侧事故发生的显著性风险因素,探讨各种风险因素之间交互作用对路侧事故的影响,并利用贝叶斯网络构建了路侧事故概率预测模型. 根据概率模型预测结果,提出了路侧事故多发路段判别方法,并进行案例验证. 研究结果表明:对路侧事故影响程度最大的显著性风险因素为车速,其次为圆曲线半径、车型、路面附着系数和硬路肩宽度；当80 km/h
关键词: 交通工程 概率预测 PC-crash CHAID决策树 贝叶斯网络 路侧事故
DOI：10.11918/201912094
分类号:U491.31
文献标识码:A
基金项目:中央高校基本科研业务费专项资金(2572019AB26); 国家自然科学基金面上项目(51778063); 教育部人文社会科学研究规划基金(18YJAZH009); 重庆市交通运输工程重点试验室开放基金(2018TE05)
Probabilistic prediction of roadside accidents in outer lane of small radius curve sections of highways
CHENG Guozhu1,2,CHENG Rui1,XU Liang3
(1. School of Traffic and Transportation, Northeast Forestry University, Harbin 150040, China; 2. Chongqing Key Laboratory of Traffic & Transportation (Chongqing Jiaotong University), Chongqing 404100, China; 3. School of Civil Engineering, Changchun Institute of Technology, Changchun 130012, China)
Abstract:
To reduce the probability of roadside accidents in small curve sections of highways, eight roadside accident risk factors including road geometric design indexes (horizontal curve radius, hard shoulder width, longitudinal slope, superelevation slope, and widen value of curve), pavement condition (adhesion coefficient), and traffic characteristics (running speed and vehicle type) were chosen to carry out PC-crash simulation test, and a total of 12 800 accident data sets were collected. Chi-squared automatic interaction detection (CHAID) decision tree technique was employed to identify significant risk factors, and the comprehensive influence of the interaction of various factors on roadside accidents was discussed. These factors were then chosen as predictors of probability of roadside accidents in Bayesian network analysis to establish the probabilistic prediction model of roadside accidents. Finally, according to probabilistic prediction results, the identification method for roadside accidents black spots was proposed and verified through tests. Results show that running speed had the greatest effect on the occurrence of roadside accidents, followed by horizontal curve radius, vehicle type, adhesion coefficient, and hard shoulder width. When 80 km/h
Key words: traffic engineering probabilistic prediction PC-crash CHAID decision tree Bayesian network roadside accidents
程国柱, 程瑞, 徐亮. 公路小半径曲线段外侧车道路侧事故概率预测[J]. 哈尔滨工业大学学报, 2021, 53(3): 178-185. DOI: 10.11918/201912094.
CHENG Guozhu, CHENG Rui, XU Liang. Probabilistic prediction of roadside accidents in outer lane of small radius curve sections of highways[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 178-185. DOI: 10.11918/201912094.
基金项目 中央高校基本科研业务费专项资金(2572019AB26); 国家自然科学基金面上项目(51778063); 教育部人文社会科学研究规划基金(18YJAZH009); 重庆市交通运输工程重点试验室开放基金(2018TE05) 作者简介 程国柱(1977—)，男，教授，博士生导师 通信作者 程瑞，ruicheng1992@yeah.net 文章历史 收稿日期: 2019-12-18
Abstract Full text Figures/Tables PDF
公路小半径曲线段外侧车道路侧事故概率预测
程国柱1,2, 程瑞1
, 徐亮3 1. 东北林业大学 交通学院, 哈尔滨 150040;
2. 重庆市交通运输工程重点试验室(重庆交通大学), 重庆 404100;
3. 长春工程学院 土木工程学院, 长春 130012
收稿日期: 2019-12-18
基金项目: 中央高校基本科研业务费专项资金(2572019AB26); 国家自然科学基金面上项目(51778063); 教育部人文社会科学研究规划基金(18YJAZH009); 重庆市交通运输工程重点试验室开放基金(2018TE05)
作者简介: 程国柱(1977—)，男，教授，博士生导师
通信作者: 程瑞，ruicheng1992@yeah.net
摘要: 为降低小半径曲线段路侧事故概率，选取道路线形指标(圆曲线半径、硬路肩宽度、纵坡坡度、超高横坡度、圆曲线加宽)、路面状况(路面附着系数)、交通特性(车速、车型)8个路侧事故风险因素进行PC-crash仿真试验，收集12 800组数据. 采用CHAID(Chi-squared automatic interaction detection)决策树技术识别了影响路侧事故发生的显著性风险因素，探讨各种风险因素之间交互作用对路侧事故的影响，并利用贝叶斯网络构建了路侧事故概率预测模型. 根据概率模型预测结果，提出了路侧事故多发路段判别方法，并进行案例验证. 研究结果表明：对路侧事故影响程度最大的显著性风险因素为车速，其次为圆曲线半径、车型、路面附着系数和硬路肩宽度；当80 km/h < v≤100 km/h，300 m < R≤600 m时，设置硬路肩宽度≥1.5 m能够明显减少路侧事故风险；与小型客车相比，载重货车更易发生路侧事故，且硬路肩宽度对载重货车路侧事故有更显著的影响，当100 km/h < v≤120 km/h，300 m < R≤600 m时，设置硬路肩宽度≥2.25 m能够明显减少载重货车路侧事故风险.
关键词: 交通工程 概率预测 PC-crash CHAID决策树 贝叶斯网络 路侧事故
Probabilistic prediction of roadside accidents in outer lane of small radius curve sections of highways
CHENG Guozhu1,2, CHENG Rui1
, XU Liang3 1. School of Traffic and Transportation, Northeast Forestry University, Harbin 150040, China;
2. Chongqing Key Laboratory of Traffic & Transportation (Chongqing Jiaotong University), Chongqing 404100, China;
3. School of Civil Engineering, Changchun Institute of Technology, Changchun 130012, China
Abstract: To reduce the probability of roadside accidents in small curve sections of highways, eight roadside accident risk factors including road geometric design indexes (horizontal curve radius, hard shoulder width, longitudinal slope, superelevation slope, and widen value of curve), pavement condition (adhesion coefficient), and traffic characteristics (running speed and vehicle type) were chosen to carry out PC-crash simulation test, and a total of 12 800 accident data sets were collected. Chi-squared automatic interaction detection (CHAID) decision tree technique was employed to identify significant risk factors, and the comprehensive influence of the interaction of various factors on roadside accidents was discussed. These factors were then chosen as predictors of probability of roadside accidents in Bayesian network analysis to establish the probabilistic prediction model of roadside accidents. Finally, according to probabilistic prediction results, the identification method for roadside accidents black spots was proposed and verified through tests. Results show that running speed had the greatest effect on the occurrence of roadside accidents, followed by horizontal curve radius, vehicle type, adhesion coefficient, and hard shoulder width. When 80 km/h < v≤100 km/h and 300 m < R≤600 m, with the hard shoulder width not less than 1.5 m, the risk of roadside accidents could be significantly reduced. Compared with cars, trucks were more prone to be involved in roadside accidents, and the hard shoulder width had a more significant impact on the roadside accidents of trucks. When 100 km/h < v≤120 km/h and 300 m < R≤600 m, with the hard shoulder width not less than 2.25 m, the risk of roadside accidents of trucks could be significantly reduced.
Keywords: traffic engineering probabilistic prediction PC-crash CHAID decision tree Bayesian network roadside accidents
路侧事故一般定义为车辆离开行车道、越过道路边缘或中心线，随后与路侧行道树、护栏、电线杆等固定物发生碰撞，甚至发生翻车、坠入深沟或河流的事故. 根据美国致命事故报告系统(FARS)统计，平均每年路侧事故数量占死亡事故的39%以上. 在中国，超过3人以上死亡的交通事故中，约有50%属于路侧事故. 欧洲的一项研究也表明，每年约20%的道路交通事故为路侧事故，而路侧事故死亡率却超过35%. 另据相关研究[1]显示，大约1/3的路侧事故发生在弯道路段，且小半径曲线路段往往被视为路侧事故多发区域[2-3]. 导致路侧事故的原因有很多，如道路线形设计不良、驾驶人采取不恰当的避让措施、注意力不集中或者高速经过弯道路段导致车辆转向不足等.
一些学者和专家在路侧事故致因方面已经开展了大量的研究，证实了道路几何特征对路侧事故起着重要的作用[4]. 例如，在道路设计方面，文献[5]认为增大路肩宽度可以减少平曲线路段侧翻事故. 文献[6]通过分析道路几何线形和路侧特征对路侧事故频率的影响，发现道路宽度少于12英尺的公路比标准宽度为12英尺的公路更容易发生路侧事故. 因此，如果车辆行驶在较窄的车道上，车辆驶入路侧的频率将会增加，而车道数量对路侧事故的影响很小[5]. 文献[7]研究得出设置宽度为4~5英尺的路侧净区可减少约90%的车辆与路侧固定物碰撞事故. 此外，文献[8]证实了路面边缘沉降和湿滑的道路表面容易导致车辆驶入路侧边沟. 文献[9]从车辆驶入路侧的可能性与路侧本体特征两个层次建立了路侧安全性评估模型. 在路侧设计方面，文献[10-11]主要通过分析路侧事故发生频率与边坡坡度、桥梁、护栏、沟渠、及路侧固定物密度和间距等之间的关系来识别风险因素.
早期一些研究学者使用对数正态回归模型来研究路侧事故频率. 然而，后来发现这种传统线性回归模型用于事故预测的准确率较低. 随着交通安全研究的不断发展，泊松和负二项回归模型(NB)在事故预测方面得到了广泛应用. 之后，为了解决事故预测中数据零值较多的问题，零堆积泊松(ZIP)和零堆积负二项式(ZINB)回归模型相继得以推广使用[12]. 虽然各种统计回归模型能够根据大量的事故数据预测路侧事故数量或频率，但并不适用于路侧事故概率值的计算. 此外，根据事故数或事故频率预测获得的研究成果往往受不同地域、交通特性等因素影响，不具备普适性. 考虑到事故发生概率更能够表征路段事故多发的程度，故开展事故发生概率预测优于开展事故数或事故频率预测. 综上，为了鉴别路侧事故多发路段，降低路侧事故发生率，本文首先利用PC-crash软件获取路侧事故数据，随后使用CHAID决策树技术识别了导致路侧事故发生的显著性风险因素，探讨了各种风险因素之间交互作用对路侧事故的影响，据此利用贝叶斯网络构建了基于显著性风险因素的路侧事故概率预测模型，实现了对路侧事故概率的定量分析. 最后根据概率模型预测结果，给出了对应不同车速和车型的圆曲线半径、路面附着系数和硬路肩宽度风险因素阈值，提出了路侧事故多发路段判别方法，并予以验证. 研究成果可为交通安全管理部门识别和排查路侧事故风险因素提供参考，为今后道路改扩建工程中线形优化设计和安全对策的实施提供指导.
1 仿真试验本文所采用的PC-crash仿真软件可进行车-车、车-人及单车事故的碰撞模拟再现. 相关文献[13]证明PC-crash软件在模拟单车侧翻事故方面表现良好. 本次试验选取圆曲线半径、硬路肩宽度、纵坡坡度、超高横坡度、圆曲线加宽、路面附着系数、车速和车型8个风险因素作为输入变量，车辆最终状态作为输出变量. 其中，车辆最终状态包括驶离行车道和正常行驶. 驶离行车道是指车辆发生侧翻或车轮驶入边坡，表示发生路侧事故，如图 1所示. 车辆正常行驶表示未发生路侧事故.
Fig. 1
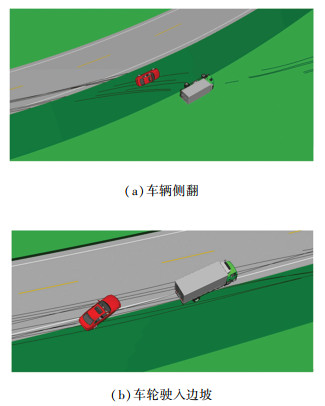图 1 发生路侧事故 Fig. 1 Occurrence of roadside accidents 在PC-crash仿真软件中，本文根据《公路路线设计规范》[14]相关规定，建立了行车道宽度为3.75 m，边坡坡度为1∶1，边坡高度为5 m的双向两车道道路模型，如图 1所示. 选择BMW-116d autom和ASCHERSLEBEN KAROSS作为小型客车和载重货车的代表车型，并将车辆初始位置设定在单向行车道的中心处. 车辆参数设置见表 1，其中小型客车配有ABS和ESP装置，载重货车配有ABS装置.
表 1
表 1 车辆参数 Tab. 1 Vehicle parameters 车型 长度/m 宽度/m 高度/m 轴距/m 质量/kg 重心高度/m 重心距前轴距离/m 轮胎规格 小型客车 4.325 1.765 1.420 2.690 1 385 0.450 1.210 215/50R 16 (621 mm)
载重货车 6.370 2.500 3.100 3.700 7 200 1.200 1.070 7.50R 16 (719 mm)
表 1 车辆参数 Tab. 1 Vehicle parameters
当车辆行驶至曲线路段，考虑到驾驶人对车辆的转向控制和速度选择，故在每次试验前对车速进行提前设置，并根据不同圆曲线半径对车辆转向进行提前设定. 例如，当圆曲线半径为200 m时，通过将车辆转弯半径设置为200 m，仿真软件会自动将左前轮、右前轮转向角调整为1.57°和1.54°，以匹配上述圆曲线半径. 另外，在圆曲线加宽设置方面，根据规范[14]规定，当圆曲线半径为200 m时，进行相应加宽值设置，其中，小型客车对应加宽值为0.4 m，载重货车对应加宽值为0.6 m. 其余各个变量的取值为：圆曲线半径分别取200、300、400、500、600 m；硬路肩宽度分别取0.75、1.5、2.25、3 m；纵坡坡度分别取0%、2%、4%、6%；超高横坡度分别取0%、2%、4%、6%；路面附着系数分别取0.2、0.4、0.6、0.8；车速分别取40、60、80、100、120 km/h.
根据上述每种风险因素的取值，建立了5×4×4×4×4=1 280种道路组合. 通过对车辆施加5种初始速度，并设置对应车型的圆曲线加宽值，分别开展载重货车和小型客车的仿真试验，共收集1 280×5×2=12 800组数据. 其中9 759组未发生路侧事故，占76.2%；3 041组发生路侧事故，占23.8%.
2 风险因素识别 2.1 CHAID决策树CHAID决策树作为一种数据挖掘方法，能够从大量数据中提取重要信息，该方法具有多项分叉的数据分割特点，数据原始节点会被划分为尽可能多的子组，然后新的子组又会被继续划分，这一过程一直持续到不能再划分为止. 为了确定最优分割，该方法使用χ2独立检验检查每次分组规则，即将Bonferroni方法调整的p值作为分割准则，p值越小说明分割的优度越大[15].
本文将仿真数据分为训练数据集(70%)和测试数据集(30%)，用于交叉验证，并使用穷举CHAID算法构建树模型，因为该算法可以检查数据所有可能的分组. 为了限制决策树的生长，将分组水平设置为4. 此外，为了减小数据内在的不平衡性，本文选择了100∶1的误分类成本比，以保证该算法对路侧事故进行更准确的分类和识别. 最终生成的树模型将会给每个子节点提供输出变量的百分比值，该值表示每个子节点所对应分类规则的置信度水平，代表了路侧事故发生的比例.
2.2 树模型结果分析通过CHAID决策树对训练集和测试集进行分类识别，模型结果显示，总体分类准确率均为94%. 另外，训练集和测试集中各个节点的p=0.001 < 0.05(显著性水平)，表明树模型分类相当准确，没有过度拟合. 树模型从12 800个数据中选取了3 888个数据作为测试集，所有测试数据通过不同的分支被划分为66个子节点，如图 2所示.
Fig. 2
图 2 识别风险因素的树结构 Fig. 2 Decision tree for identification of risk factors CHAID决策树最终将圆曲线半径、硬路肩宽度、路面附着系数、车速和车型纳入树结构中，表明这些变量是影响路侧事故发生的显著性风险因素. 而超高横坡度、纵坡坡度和圆曲线加宽被模型剔除，说明对路侧安全改善作用不大. 由于受到文章篇幅限制，本文只展示了分类规则置信度较高的树结构，如图 2所示，图中“No”表示没有发生路侧事故，“Yes”表示发生路侧事故.
由图 2可知，在第1分组水平下，树模型首先根据车速对数据进行分类，说明车速对路侧事故的影响较为显著，而其余风险因素被视为此分组水平下的非显著性风险因素，依次类推可得到第2、3、4分组水平下的数据分类情况. 通过决策树对3 888个测试数据进行分析，对生成的分类规则进行筛选和整理，见表 2. 其中v为车速，km/h；R为圆曲线半径，m；μ为路面附着系数；w为硬路肩宽度，m. 各分类规则中的“—”表示数据在对应分组水平下没有被继续分类.
表 2
表 2 分类规则 Tab. 2 Classification rules 规则编号 数据分类 路侧事故比例/% 第1分组水平 第2分组水平 第3分组水平 第4分组水平
1 v∈(0, 40] — — — 0
2 v∈(40, 60] R∈(0, 200] μ∈(0, 0.2] — 57.9
μ∈(0.2, 0.8] — 0
3 v∈(40, 60] R∈(200, +∞) — — 0
R∈(0, 300] — — 53.7
4 v∈(60, 80] R∈(300, 400] — — 6.4
R∈(400, +∞) — — 0
5 v∈(60, 80] R∈(0, 300] μ∈(0, 0.2] — 100
6 v∈(60, 80] R∈(0, 300] μ∈[0.6, 0.8] 载重货车
小型客车 64.9
6.1
7 v∈(60, 80] R∈(300, 400] w∈(0, 0.75] — 11.1
w∈[1.5, +∞) — 0
8 v∈(80, 100] R∈(300, 400] w∈(0, 0.75] — 66.7
w∈[1.5, +∞) — 5.4
9 v∈(80, 100] R∈(400, 600] w∈(0, 0.75] 载重货车
小型客车 36.4
0
w∈[1.5, +∞) — 0
10 v∈(100, 120] R∈(300, 400] 载重货车 w∈(0, 1.5] 77.3
w∈[2.25, +∞)38.5
11 v∈(100, 120] R∈(400, 600] 载重货车 w∈(0, 1.5] 56.8
w∈[2.25, +∞) 0
表 2 分类规则 Tab. 2 Classification rules
由表 2可知，每条分类规则对应不同的风险因素组合以及路侧事故比例. 通过分析各种风险因素之间交互作用对路侧事故的影响，得到如下结论：
1) 由分类规则1可得，当v≤40 km/h时，其余风险因素对路侧事故均不起作用，且路侧事故比例为0%，故40 km/h被认为是保证路侧事故不发生的相对安全车速.
2) 由分类规则2~11可得，当v>40 km/h时，圆曲线半径对路侧事故有显著影响，且随着圆曲线半径增大路侧事故逐渐减少.
3) 由分类规则6、9可得，在相同线形指标情况下，载重货车比小型客车更容易发生路侧事故，一种解释是由于载重货车的重心较高，比小型客车更容易翻车.
4) 由分类规则2、5、6可得，当40 km/h < v≤60 km/h，R≤200 m时，以及当60 km/h < v≤80 km/h，R≤300 m时，路面附着系数对路侧事故有显著影响，且随着路面附着系数增大路侧事故比例逐渐减少. 因此对于符合上述运行速度和圆曲线半径的路段，应加强路面铺装防滑措施.
5) 由分类规则7可得，当60 km/h < v≤80 km/h，300 m < R≤400 m时，硬路肩宽度对减少路侧事故发挥了一定作用，但改善不明显；由分类规则8和9可得，当80 km/h < v≤100 km/h，300 m < R≤600 m时，硬路肩宽度对路侧事故有显著影响，且设置硬路肩宽度≥1.5 m能够明显减少路侧事故风险. 因此对于运行速度为80 km/h < v≤100 km/h且圆曲线半径为300 m < R≤600 m的路段，应设置硬路肩宽度≥1.5 m.
6) 由分类规则9可得，当80 km/h < v≤100 km/h，400 m < R≤600 m时，如果硬路肩宽度为0.75 m，载重货车路侧事故比例为36.4%，小型客车路侧事故比例为0%；如果硬路肩宽度≥1.5 m，无论对于载重货车还是小型客车，路侧事故比例均为0%. 说明与小型客车相比，硬路肩宽度对载重货车路侧事故有更显著的影响.
7) 由分类规则10、11可得，当100 km/h < v≤120 km/h，300 m < R≤600 m时，设置硬路肩宽度≥2.25 m能够明显减少载重货车路侧事故风险. 因此对于符合上述运行速度和圆曲线半径的路段，应设置硬路肩宽度≥2.25 m，以保障载重货车行驶安全.
3 路侧事故概率计算 3.1 贝叶斯网络贝叶斯网络分析是一种通过图形的形式来展现一组选定变量的联合概率分布的技术[16]，其结构是一个有向无环图，其中节点集表示各种变量，有向边表示变量之间的依赖关系，变量之间的置信水平或相关强度可以使用条件概率表(CPT)来描述. 贝叶斯网络利用概率来表示各种形式的不确定性，应用概率规则来实现训练和推理过程，表达式为
$P\left(B_{i j} \mid B_{i j}\right)=\frac{P\left(A_{j} \mid B_{i j}\right) P\left(B_{i j}\right)}{\sum\limits_{j=1}^{m} P\left(A_{j} \mid B_{i j}\right) P\left(B_{i j}\right)},$ (1)
$P\left(A_{j} \mid \prod\limits_{i=1}^{n} B_{i j}\right)=\frac{\prod\limits_{i=1}^{n} P\left(B_{i j} \mid A_{j}\right) P\left(A_{j}\right)}{\sum\limits_{j=1}^{m} \prod\limits_{i=1}^{n} P\left(B_{i j} \mid A_{j}\right) P\left(A_{j}\right)} .$ (2)
式中：P(Aj|Bij) (i=1, 2, …, n; j=1, 2, …, m)为在风险因素Bij的作用下，仿真车辆最终状态Aj的先验概率；P(Bij|Aj)为在车辆最终状态Aj发生的条件下，风险因素Bij的条件概率；P(Aj|
3.2 路侧事故概率预测模型本文在决策树分析结果的基础上建立了贝叶斯网络结构，并借助Netica软件中的梯度下降(gradient descent)算法对贝叶斯网络进行自主学习和推理，可以得到每个风险因素的先验概率和条件概率分布，构建的路侧事故概率预测模型如图 3所示，其中在“车型”节点中，0表示载重货车，1表示小型客车；在“路侧事故”节点中，0表示没有路侧事故发生，1表示路侧事故发生. 证据敏感度分析中交互信息值(mutual info)见表 3，根据表 3可得各风险因素对路侧事故影响程度由大到小依次为：车速、圆曲线半径、车型、路面附着系数和硬路肩宽度.
Fig. 3
图 3 贝叶斯网络预测模型 Fig. 3 Bayesian network prediction model 表 3
表 3 以“路侧事故”为查询节点的证据敏感性分析 Tab. 3 Sensitivity analysis results of node "roadside accident" 节点 交互信息值 比例/% 信念方差 路侧事故 0.807 31 100 0.186 250 6
车速 0.183 13 22.7 0.042 740 6
圆曲线半径 0.119 11 14.8 0.031 102 7
车型 0.016 41 2.03 0.004 286 1
路面附着系数 0.013 45 1.67 0.003 647 8
硬路肩宽度 0.009 37 1.16 0.002 441 1
表 3 以“路侧事故”为查询节点的证据敏感性分析 Tab. 3 Sensitivity analysis results of node "roadside accident"
3.3 概率模型结果分析根据构建的贝叶斯网络预测模型，可以计算得到不同变量组合下的路侧事故概率. 例如已知某路段为干燥沥青路面，限速80 km/h，道路半径为335 m，硬路肩宽度为1.75 m，需要预测该路段载重货车发生路侧事故的概率. 首先将60 km/h < v≤80 km/h. 300 m < R≤400 m、0.6≤μ≤0.8、1.5 m≤w≤2.25 m及车型为0的状态设为100%，然后通过Netica软件对网络自动更新，可求得载重货车以60 km/h < v≤80 km/h的速度行驶，在该路段发生路侧事故的概率为1.45%，如图 4所示.
Fig. 4
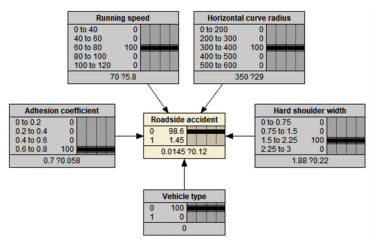图 4 路侧事故概率计算 Fig. 4 Probability calculation of roadside accidents 此外，所建立的概率模型还可以预测任意数量(1~5)变量影响下的路侧事故概率. 例如，已知某路段限速80 km/h，硬路肩宽度为0.75 m，但缺乏其他线形指标的情况下，同样可以计算出小型客车以60 km/h < v≤80 km/h的速度通过上述路段发生路侧事故的概率为17%，如图 5(a)所示. 又如，某路段为干燥沥青路面，道路半径和硬路肩宽度未知，如果路段限速80 km/h，那么小型客车路侧事故概率为5.04%，载重货车路侧事故概率为15.4%，概率均较低；如果路段限速100 km/h，小型客车路侧事故概率为14.7%，而载重货车路侧事故概率增加到43.8%. 结果进一步表明，在车速大于80 km/h的情况下，载重货车比小型客车有更高的侧翻风险. 当然，涉及的变量越多，模型计算概率越准确.
Fig. 5
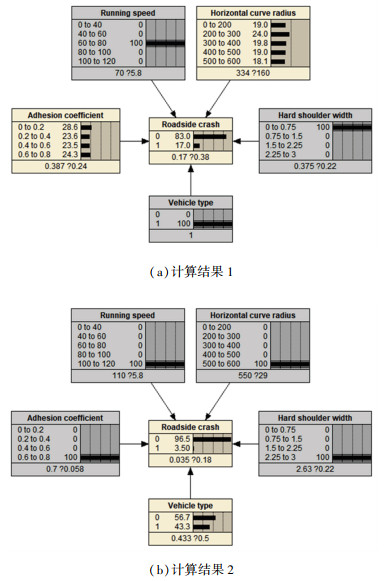图 5 路侧事故概率计算 Fig. 5 Probability calculation of roadside accidents 当各种变量处于趋向于避免路侧事故的极值状态，即使将车速设为100 km/h < v≤120 km/h，无论对于小型客车还是载重货车，路侧事故概率仅为3.5%，如图 5(b)所示，这充分说明了当无法对驾驶人行为有效控制的情况下，道路几何要素的合理设计对提升路侧安全的重要性. 因此，为了降低路侧事故率，应对导致路侧事故多发的风险因素阈值进行确定，从而提出路侧事故多发路段判别方法.
4 路侧事故多发路段判别基于贝叶斯网络概率预测结果，本文参考文献[17]关于事故多发判定方法的研究，认为当路侧事故发生概率大于75%时，定义为路侧事故多发. 因此，对应于不同的车速和车型，表 4给出了导致路侧事故多发的圆曲线半径、路面附着系数和硬路肩宽度风险因素阈值. 根据阈值划分结果可知，同一车速范围下对应于多种路侧事故多发判别规则，当某一路段各个风险因素取值满足其中任意一种判别规则时，则判定为路侧事故多发路段.
表 4
表 4 风险因素阈值 Tab. 4 Thresholds of risk factors 编号 车速/(km·h-1) 车型 圆曲线半径/m 硬路肩宽度/m 路面附着系数 概率/% 1 (60, 80] 载重货车 (200, 300] (0, 0.75] (0, 0.2] ≥77.4
2 (60, 80] 载重货车 (200, 300] (0, 0.75] (0, 0.6] ≥78.3
3 (60, 80] 载重货车 (0, 200] (0, 0.75] (0, 0.8] ≥75.9
4 (80, 100] 载重货车 (500, 600] (0, 0.75] (0, 0.2] ≥80.1
5 (80, 100] 载重货车 (400, 500] (0, 1.5] (0, 0.6] ≥75.4
6 (80, 100] 载重货车 (0, 400] (0, 2.25] (0, 0.8] ≥77.8
7 (100, 120] 载重货车 (400, 600] (1.5, 2.25] (0, 0.2] ≥82.1
8 (100, 120] 载重货车 (400, 600] (0, 1.5] (0, 0.8] ≥76.8
9 (100, 120] 载重货车 (0, 400] (0, 2.25] (0, 0.8] ≥78.1
10 (60, 80] 小型客车 (0, 200] (0, 0.75] (0, 0.2] ≥79.4
11 (80, 100] 小型客车 (400, 500] (0, 0.75] (0, 0.4] ≥75.2
12 (80, 100] 小型客车 (0, 400] (0, 1.5] (0, 0.8] ≥78.8
13 (100, 120] 小型客车 (300, 400] (0, 2.25] (0, 0.2] ≥81.2
14 (100, 120] 小型客车 (200, 300] (0, 1.5] (0.2, 0.6] ≥83.5
15 (100, 120] 小型客车 (200, 300] (0, 2.25] (0, 0.2] ≥75.8
16 (100, 120] 小型客车 (0, 200] (0, 3] (0, 0.8] ≥77.9
表 4 风险因素阈值 Tab. 4 Thresholds of risk factors
本文选取G105线K2639+498.02至K2679+170段用于验证路侧事故多发路段判别方法的有效性. G105线属于一级公路，设计速度为80 km/h. 通过收集道路设计文件和路段运行速度观测资料，根据表 4所示风险因素阈值判定K2666+181.158处为路侧事故多发路段. 该路段圆曲线半径为310 m，硬路肩宽度为1.5 m，85%的载重货车运行速度达82 km/h，85%的小型客车运行速度达93 km/h，上述指标分别满足表 4中第6种和第12种判别规则. 据交警部门事故记录和统计资料显示，上述路段在2015年—2018年共发生70余起路侧事故，已经被列为路侧事故多发路段. 综上分析可得，通过本文提出的路侧事故多发路段判别方法得到的结论与实际相符，由此验证了本文方法的可靠性.
5 结论1) 通过PC-crash仿真软件获取路侧事故数据，使用CHAID决策树技术识别了导致路侧事故发生的显著性风险因素，探讨了各种风险因素之间交互作用对路侧事故的影响，并利用贝叶斯网络构建了路侧事故概率预测模型，据此提出了路侧事故多发路段判别方法，并予以案例验证.
2) 所建立的贝叶斯网络预测模型能够计算任意数量(1~5)变量影响下的路侧事故概率，可实现对路侧事故概率的定量分析. 根据路侧事故概率预测结果，给出了对应不同车速和车型的圆曲线半径、路面附着系数和硬路肩宽度风险因素阈值，提出了路侧事故多发路段判别方法.
3) 显著性风险因素对路侧事故影响程度由大到小依次为车速、圆曲线半径、车型、路面附着系数和硬路肩宽度. 与小型客车相比，硬路肩宽度对载重货车路侧事故有更显著的影响，且载重货车更倾向于发生路侧事故，尤其是当车速大于80 km/h时最为明显.
4) 为减少路侧事故风险，在《公路路线设计规范》(JTG D20—2017)规定的基础上，对公路路线设计指标进一步优化. 建议：对于运行速度为40 km/h < v≤60 km/h且圆曲线半径≤200 m，以及运行速度为60 km/h < v≤80 km/h且圆曲线半径≤300 m的路段，应加强路面铺装防滑措施；对于运行速度为80 km/h < v≤100 km/h且圆曲线半径为300 m < R≤600 m的路段，应设置硬路肩宽度≥1.5 m；对于运行速度为100 km/h < v≤120 km/h且圆曲线半径为300 m < R≤600 m的路段，应设置硬路肩宽度≥2.25 m，以保障载重货车行驶安全.
参考文献
[1] MCLAUGHLIN S B, HANKEY J M, KLAUER S G, et al. Contributing factors to run-off-road accidents and near-accidents[R]. Washington DC: National Highway Traffic Safety Administration (NHTSA), 2009
[2] HUSSEIN M, SAYED T, ISMAIL K, et al. Calibrating road design guides using risk-based reliability analysis[J]. Journal of Transportation Engineering, 2014, 140(9): 36.
[3] LIU C, SUBRAMANIAN R.Factors related to fatal single-vehicle run-off-road accidents[R]. Washington DC: National Center for Statistics and Analysis, 2009
[4] ROQUE C, JALAYER M. Improving roadside design policies for safety enhancement using hazard-based duration modeling[J]. Accident Analysis and Prevention, 2018, 120(11): 165.
[5] LORD D, BREWER M A, FITZPATRICK K, et al. Analysis of roadway departure accidents on two lane rural roads in Texas[R]. Galveston: Texas Transportation Institute, 2011
[6] EWAN L, AL-KAISY A, HOSSAIN F. Safety effects of road geometry and roadside features on low-volume roads in Oregon[J]. Transportation Research Record, 2016, 2580(1): 47. DOI:10.3141/2580-06
[7] SAX C R, MAZE T H, SOULEYRETTE R R, et al. Optimum urban clear zone distance[J]. Transportation Research Record, 2010, 2195(1): 27. DOI:10.3141/2195-04
[8] LIU C, YE T J. Run-off-road accidents: an on-scene perspective[R]. Washington DC: National Highway Traffic Safety Administration, 2011
[9] 方勇, 郭忠印, 李志勇. 双车道公路路侧环境客观安全性评估模型[J]. 同济大学学报(自然科学版), 2013, 41(7): 1025.
FANG Yong, GUO Zhongyin, LI Zhiyong. Assessment model for roadside environment objective safety on two-lane highway[J]. Journal of Tongji University (Natural Science), 2013, 41(7): 1025. DOI:10.3969/j.issn.0253-374x.2013.07.011
[10] CHENG G, CHENG R, ZHANG S, et al. Risk evaluation method for highway roadside accidents[J]. Advances in Mechanical Engineering, 2019, 11(1): 1.
[11] ROQUE C, MOURA F, CARDOSO J L. Detecting unforgiving roadside contributors through the severity analysis of ran-off-road accidents[J]. Accident Analysis and Prevention, 2015, 80(7): 262. DOI:10.1016/j.aap.2015.02.012
[12] RAIHAN M A, ALLURI P, WU W, et al. Estimation of bicycle accident modification factors (CMFs) on urban facilities using zero inflated negative binomial models[J]. Accident Analysis and Prevention, 2019, 123(2): 303.
[13] ROSE N A, BEAUCHAMP G. Analysis of a dolly rollover with PC-crash[R]. New York: SAE International, 2009
[14] 中华人民共和国交通运输部. 公路路线设计规范: JTG D20—2017[S]. 北京: 人民交通出版社, 2017
Ministry of Transport of the People′s Republic of China. Design specification for highway alignment: JTG D20—2017[S]. Beijing: China Communications Press, 2017
[15] RITSCHARD G. CHAID and earlier supervised tree methods[M]. New York: Routledge, 2011: 70.
[16] PEARL J. Probabilistic reasoning in intelligent systems: networks of plausible inference[M]. Amsterdam: Elsevier, 2014: 56.
[17] 管满泉. 交通事故多发点鉴别方法的比较研究[J]. 公路, 2009(4): 191.
GUAN Manquan. Comparative study on identification methods of traffic accident hot spots[J]. Highway, 2009(4): 191.
